Data Collecting and Energy Charging Oriented Mobile Path Design for Rechargeable Wireless Sensor Networks
Abstract
Energy efficiency is one of the most important concerns in wireless sensor networks (WSNs). As far as we know, almost all energy efficiency researches of WSNs focus on energy conservation in some respects such as wireless data transmission and minimal data collection. Recently, wireless energy transfer has been a promising technology to prolong the lifetime of microsensor nodes, and so the traditional WSNs can be extended to rechargeable WSNs. Rechargeable WSNs is a new type of wireless sensor networks, where each sensor node can replenish energy through wireless charging. For rechargeable WSNs, it is powered by reusable energy or harvested energy, so the energy efficiency problem can be completely solved. Furthermore, mobile data collection has been well recognized to have significant advantages over sensory data collection manner using static sinks. In this paper, by employing one or multiple recharging sinks to replenish energy for sensor nodes and collect sensory data concurrently, we propose a novel wireless charging and mobile data collecting method based on self-organizing map (SOM) unsupervised learning for rechargeable WSNs. In other words, the sink mobility and energy replenishment are jointly considered in this paper. Finally, we evaluate the performance of the proposed algorithms through software simulation. Extensive results verify that the performance of the proposed algorithm can reduce the travel cost of mobile sink and improve the residual energy level for sensor nodes. As a results, it is very promising in the field of data acquisition in wireless sensor networks.
1. Introduction
Wireless sensor networks (WSNs) have been widely used in many applications such as environmental monitoring, military mission, smart agriculture, structural monitoring, and intelligent transportation [1–4]. Typically, there are a large number of sensor nodes and a data sink or base station in one WSNs, and thus, it is able to collect sensory data from its surrounding physical environments. As we all know, due to size and cost restrictions of sensor nodes, traditional wireless sensor networks are energy-limited and application-specific [5]. Hence, these two characteristics pose new challenges in terms of data collecting and energy supply. Sensor nodes in traditional WSNs are mainly powered by energy-limited batteries, so the lifetime of sensor networks is very limited. Generally speaking, sensor nodes are expected to operate over years with limited power supply. Thus, the energy consumption becomes the foremost design constraint.
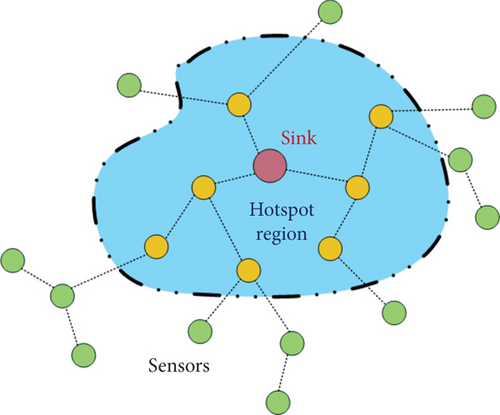
To prolong the lifetime of WSNs, extensive studies have been conducted in past years, which can be divided into two categories. One way is to reduce energy consumption as much as possible from all aspects. Much research effort has been dedicated to resolving energy conservation problem of WSNs such as energy-efficient communication protocols [6]. However, in classic wireless multi-hop transmission manner, in addition to transmitting their own sensory data, sensor nodes have to transmit relay data resulting in additional energy consumption. This situation is especially worse for those sensor nodes close to sink node, which is called “hotspot” problem [7]. As Figure 1, sensor nodes within “hotspot” region are prone to transmit or relay more data, so these nodes will consume more energy than others. In other words, sensor nodes near sink node have to transfer much more network flow, and therefore, they will deplete their energy much earlier [8]. This is an inherent defect of the traditional fixed-sink data acquisition manner. Fortunately, it will reduce energy consumption of sensor nodes with mobile data collecting method by utilizing mobility characteristic of mobile sinks. Usually, mobile vehicles with relatively more energy are usually taken as mobile data collectors. In this way, sensor nodes only need to transmit their own sensory data to mobile sinks with smaller transmission distances when mobile sinks get close to them.
For the second category, the stored energy of sensor nodes needs to be replenished, and most of recent researches focus on energy replenishment fundamental problem. Wireless energy transfer is a new technology that can be used to recharge sensor nodes’ batteries in wireless manner [9–11]. To prolong the lifetime of WSNs, a variety of wireless charging techniques have been proposed to provide additional energy supply for WSNs. With recent advances in radio energy harvesting techniques, it is possible to recharge sensor nodes in a relative long distance (>10 m away). Since the long-distance charging provides much weaker harvesting power, mobile charging method with short distance is often used to achieve high charging efficiency. In general, there are two different sensor charging categories [11]. One is to enable sensors to harvest energy from their surrounding environments. The main drawback of this method is that the energy harvesting rates are extremely unstable due to time-varying environments. The other is to employ mobile charging vehicles to travel to the vicinity of sensors and recharge them using wireless energy transfer method. Thus, sensor nodes can be charged via wireless energy transfer technology with highly stable charging rates [12]. Consequently, the energy replenishing problem can be transformed into a new problem of finding an optimized charging path. Hence, recent research resorts to the optimal or suboptimal recharging trajectory so as to improve charging effect.
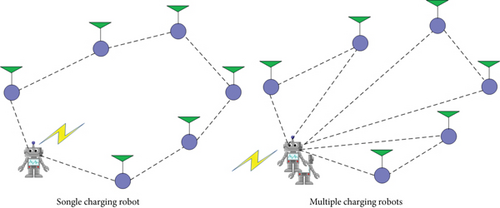
To solve energy problem, some researches jointly apply the emerging techniques of wireless power transfer and intelligent mobile vehicles to develop a new paradigm of rechargeable wireless sensor networks. As far as we know, there are few researches that consider mobile data collecting and wireless energy supply comprehensively. Moreover, the mobility of charging and data collectors brings new issues. In this paper, we study the interesting problem of co-locating one wireless charger and mobile sink on the same mobile platform, which is named as wireless charging vehicle (WCV) in this paper. The WCV travels along a preplanned path inside the region of interest (RoI) in wireless sensor networks. For example, as shown in Figure 2, six sensor nodes will be charged by one charging robot and three charging robots, respectively. Each charging robot or WCV starts from base station to charge sensor nodes and returns to base station after completing its charging task. The optimal goal is to minimize energy consumption of multiple WCVs and improve energy efficiency of wireless sensor networks. Extensive simulation results verify that the proposed method has a more efficient performance in terms of path length and energy consumption; thus, it is very suitable for mobile data collection in rechargeable WSNs.
Our main contributions are the following:
Statement of Contributions: (1) This paper investigates mobile sensory data collecting and long-distance wireless energy recharging concurrent strategy for sensor nodes, which is mapped to traditional Close-Enough Traveling Salesman Problem (CETSP); (2) this paper uses SOM (self-organizing feature map) based unsupervised learning algorithm to solve CETSP. To the best of our knowledge, this is the first report to design compatible considering both data collecting and energy charging mobile path for wireless sensor networks. The rest of this paper is organized as follows. Section 2 gives some related works on wireless energy transfer and mobile data collecting in wireless sensor networks. Section 3 presents the problem statement with rechargeable sensor networks. In Section 4, data collecting and energy charging oriented mobile path design algorithm based on SOM unsupervised learning and Bezier curve is presented in details. Simulation results are shown in Section 5 to verify our proposed algorithm, followed by the conclusions in Section 6.
2. Related Works and Preliminaries
Energy efficiency problem has been a fundamental constraint and challenge faced by many applications of WSNs. Due to the harshness of environments, unattended operability of WSNs for long time is desirable. Energy management mechanisms and routing protocols in traditional WSNs are no longer suitable for rechargeable WSNs, and new solutions must be proposed. To mitigate the limited energy problem in wireless sensor networks, some researchers have proposed different efficient approaches. Since it is not efficient to install densely located fixed sinks, expensive multi-hop transmission can be avoided using mobile sink mode. The traditional energy consumption in the sink information retrieval can be reduced by the factor of hop number. Consequently, the movement strategy of sink node is very crucial to the WSNs performance.
A recent breakthrough in the wireless power transfer technique based on strongly coupled magnetic resonances has drawn plenty of attentions [13, 14]. Wireless energy transfer (WET) is a new technology that can be used to charge the batteries of sensor nodes without wires. Although wireless, WET does require a charging station to be brought within reasonable range of a sensor node so that good energy transfer efficiency can be achieved [15]. Cheng et al. [16] survey the latest research on charging programming in rechargeable wireless sensor networks from different dimensions. Guo et al. [17] propose the VBMERS (mobile energy replenishment strategy with virtual backbone) algorithm to solve the fast energy expenditure problem of backbone nodes. Banoth et al. [18] propose a deep reinforcement learning-based mobile charger scheduling strategy called dynamic partial mobile charger scheduling using deep-Q-networks (DPMCS). It is generally accepted that, wireless power charging is a very promising technique to prolong the lifetime of WSNs. On the other hand, it has been well recognized that data collection with mobile robots has significant advantages over static one. Therefore, it is logical to consider these two methods together.
2.1. Mobile Data Collecting in Wireless Sensor Networks
The mobility management has received extensive research efforts in different areas of wireless sensor networks. These researches focus on different problems such as lifetime maximization, delay minimization, and trajectory optimization, in the way of sink mobility control. Gu et al. [19] exploit sink mobility to prolong the network lifetime in wireless sensor networks where the information delay caused by moving the sink should be bounded. Wang et al. [20] use multiple controllable sinks to travel among event locations to gather data efficiently. They considered issues like the mobile distance of a sink and time delay. Yun and Xia [21] jointly consider the multi-hop routing, sink mobility, and delay bound to improve the energy efficacy. Li et al. [22] present a localized geographic routing scheme to ensure data delivery to the mobile sink in a WSN. Mehto et al. [23] propose a squirrel search algorithm-based rendezvous points selection (SSA-RPS) method that chooses a set of optimal RPs for reliable data collection. In conclusion, these researches investigate mobility as a means of relieving traffic burden and enhancing energy efficiency of WSNs.
2.2. Wireless Energy Transfer in Wireless Sensor Networks
Wireless charging technology is considered as a promising solution to address the energy limitation problem for wireless sensor networks [24]. To minimize the network operational cost, Xu et al. [25] formulate a charging scheduling problem of dispatching multiple mobile charging vehicles to collaboratively charge sensors such that the sum of traveling distance (referred to as the service cost) of these vehicles for this monitoring period is minimized. Fu et al. [26] propose a novel energy-synchronized mobile charging (ESync) protocol, which simultaneously reduces both of them. For mobile charger, the optimization objective is to minimize its travel distance while performing the charging tasks [27]. These researches adopt the wireless energy replenishment to prolong the lifetime of WSNs, and a comprehensive survey is given in [28]. With the development of wireless charging technology, long-distance wireless charging can meet the function of energy supplement in wireless sensor networks. As we know, how to gain the optimal recharging trajectory belongs to NP-hardness optimization problem such as Traveling Salesman Problem (TSP); different approximation algorithms derived by heuristic solutions have been proposed to address this problem.
Unlike these mentioned studies, we herein consider mobile path design for sensory data collecting and sensor nodes’ energy recharging, and traditional CETSP model [29] for rechargeable wireless sensor networks is established to address our optimization problem. Moreover, self-organizing map-based unsupervised learning algorithm is applied to obtain suboptimal solution, so as to minimize the total traveling distance of mobile vehicles, which can reduce the network maintenance costs significantly.
3. Preliminaries and Problem Statement
In this section, we first introduce the network model and propose a novel simultaneous energy charging and data collecting model, and we then define the problems. Since ultra-fast charging batteries will be commercialized in the new future and will be widely used in wireless sensor networks, therefore, wireless charging takes far more time than wireless data transmission. As a result, we ignore the time spent by mobile chargers per charging round in the following sections.
Existing studies of sensor nodes’ energy replenishment via wireless charging vehicles assumed that either just one or multiple mobile charging vehicles are deployed. Our investigation focuses on sparsely deployed networks; the WCV operates on a rechargeable battery and has much higher computation and communication capabilities. Individual sensor nodes are immobile and store a number of packets for transmission to the WCV. We also assume that WCVs are aware of position of sensor nodes and number of packets on every node. This can be achieved by a traditional sensor node registration procedure.
For clarity, the principle topology of recharging wireless sensor networks is described in Figure 3. As depicted in Figure 3, there are n sensor nodes (Si, i = 1, 2, ⋯, n) with coordinates si = (xi, yi) ∈ ℝ2 and m mobile charging vehicles (MRj, j = 1, 2, ⋯, m) deployed randomly in the rectangle area. Sensor nodes can monitor and collect parameters of the surroundings and then transmit sensory data via wireless communication within maximal range. It is assumed that sensor nodes can replenish energy with long-distance wireless power transfer technology. Mobile WCVs have the ability of collecting data from sensor nodes while moving along the preset trajectory; moreover, they can provide power supply capability to such sensor nodes within maximal range of wireless power transfer. Additionally, it is assumed that battery-stored energy of mobile WCVs is enough to support the complete traversal of a scheduled trajectory and replenish all sensor nodes. With the development of new technology, long-distance wireless charging technology has become more and more mature. In this paper, we assume that the mobile WCVs have sufficient amount of energy to support its travel, data collection, and energy transfer to sensor nodes before they return to the service station.
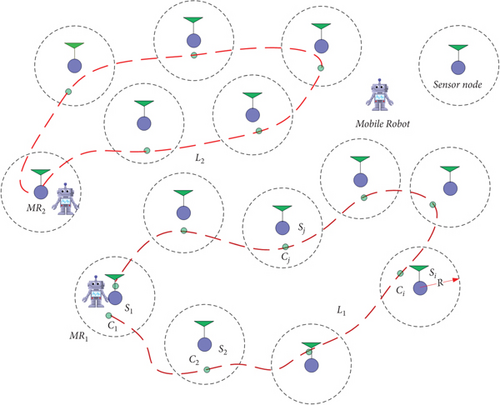
In order to illustrate design detailed methodology of proposed algorithm, we summarize the simplified notation in Table 1 for the reader’s convenience.
| Notation | Definition |
|---|---|
| Si | The ith sensor node, i = 1, ⋯, n |
| n | The total number of sensor nodes |
|
|
Set of sensor nodes |
| si | The coordinates of Si |
| ∥(si, sj)∥ | Euclidean distance between Si and Sj |
| MRj | The jth mobile WCV, j = 1, ⋯, m |
| m | Total number of mobile WCVs |
|
|
The set of mobile WCVs |
| Rs | The maximal wireless communication distance |
| R | The maximal wireless energy transfer distance |
|
|
Tour sequence for WCVs, k = 1, 2, ⋯, n − 1 |
|
|
Bezier based tour trajectory for WCVs, k = 1, 2, ⋯, n − 1 |
|
|
Tour length of sequence |
|
|
The total length of trajectory |
| Ei | The residual energy of ith sensor node |
| E0 | The initial energy of sensor nodes |
| Itermax | The maximal iteration number |
The detailed energy charging model and wireless energy charging model will be described as follows.
3.1. Mobile Data Collecting Model
In this paper, we assume a constant data generation rate from each sensor node. Moreover, each sensor node has the ability of cache data into its buffer, and the cached data to deliver of sensor node Si is Bi. Cached sensory data will be transmitted to mobile WCVs if and only if at least one WCV is approaching. That is to say, the distance of sensor node and WCV is less than the maximal wireless communication range Rs. For traditional sensor nodes, the amount of sensory data is relatively small. On the contrary, commonly used wireless communication also has high speed over several Kbps or Mbps and long distance over hundreds of meters. Moreover, wireless data transmission takes much faster than wireless power transmission, so the time required for wireless data transmission can be ignored comparing to wireless energy transfer. Therefore, the residence time near each sensor node is decided only by wireless charging time [28].
3.2. Wireless Energy Charging Model
3.3. Energy Consumption Model
3.4. Optimization Objective and Model
Based on the above framework, we develop a mathematical formulation that is a mixed integer nonlinear programming (MINLP) problem and is time-consuming to solve directly [31]. Following these above assumptions, the optimization objective is proposed in this subsection. The sensor node is considered to be visited if the mobile data collection path is the distance less or equal to the maximal range R. Thus, the range forms a disk-shaped neighborhood with the radius R around each sensor. Therefore, rather than the ordinary TSP, the problem can be formulated more specify as the disk-shaped neighborhood as the Close-Enough TSP (CETSP). The CETSP can be formulated as a combination of the combinatorial optimization to determine the sequence ∑ of visits to sensor nodes set together with the determination of most suitable locations such that each sensor Si has its location si within the distance R, i.e., ∥(si, pi)∥≤R.
The investigated problem is defined as follows:
4. Data Collecting and Energy Charging Oriented Path Design for Mobile WCVs
4.1. Mobile Data Collecting and Energy Recharging Application
The mentioned mobile data sinks and wireless chargers have the ability of passing through all predefined sensor nodes along a smooth trajectory to collect sensory data and recharge its closest sensor nodes. In this paper, the unsupervised learning framework based on self-organizing map is used to solve CETSP based path design, and moreover, we apply Bezier curve for mobile data collection. The procedure consists of three parts: topology data extraction, SOM-based optimization solution, and Bezier curve interpolation.
4.2. SOM-Based Heuristic Solution Algorithm
The SOM for CETSP follows the standard Kohonen’s SOM [32] with few modifications due to the solution of routing problems. It can be considered as a two-layered neural network as Figure 4, where the input layer serves for presenting the sensing sites (input signals) towards which the network is adapted using the unsupervised learning. The output layer is organized as an array of neurons, which defines a sequence of visits to the targets, and the neurons’ weights directly represent point locations in the input space. The neurons can be connected into a ring because of the array structure of output layer and thus represent a closed path in the input space.
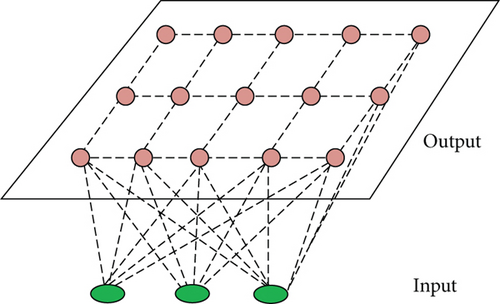
The SOM-based unsupervised learning is performed with an iterative procedure in which all the targets are presented to the network. The best matching neuron is selected in the winner selection procedure, and then the winner neuron is adapted towards the presented input together with neighboring neurons to the winner neuron with decreasing power of the adaptation defined by the neighboring function. The SOM based CETSP is a set of nodes S1, ⋯, Sn organized in a one-dimensional structure that is called an iterative ring of nodes. Therefore, the total iteration process of SOM-based CETSP is comprised of three main parts: (1) winner selection, (2) winner adaptation, and (3) results output.
Having the point , a new winner node v∗ is created and inserted between the respective vi nodes.
Since all winner nodes in the ring have associated waypoints, a feasible solution can be constructed by traversing the ring and connecting the waypoints.
4.3. Bezier Curve-Based Trajectory Design
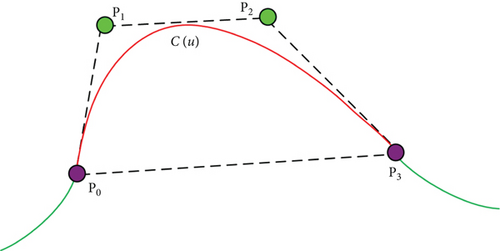
In order to make curves smooth and trajectory closed, the four control points of each cubic Bezier curve are selected following such definition in [36], which is shown as Figure 5.
4.4. Pseudo-Code of SOM-Based Mobile Path Design Algorithm
The detailed pseudo-code of SOM-based mobile path design algorithm is depicted in following Algorithm 1. It is worth noting that the computational complexity of the proposed unsupervised learning method does not significantly increase and will be bounded by O((n + m)3) [35].
As a typical heuristic solving Traveling Salesman Problem, the proposed SOM-based unsupervised learning procedure can extract suboptimal convergence solution with the computational complexity. However, the proposed algorithm belongs to one kind of centralized algorithm, so it is still based on the global information that is obtained from the whole network, which is quite harsh to meet in practice.
5. Simulation Results
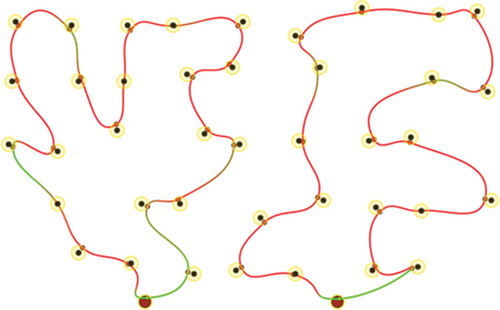
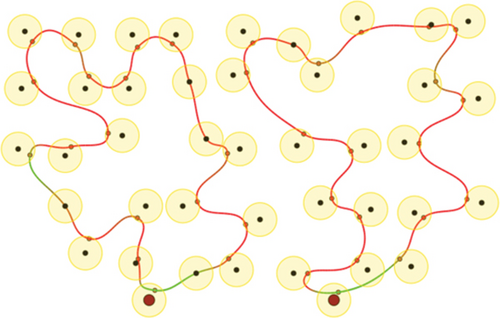
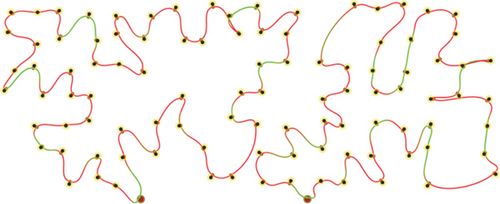
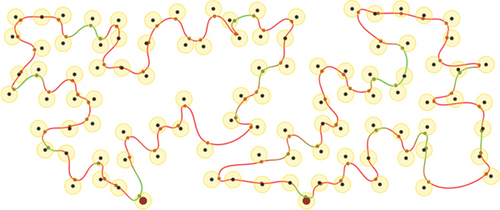
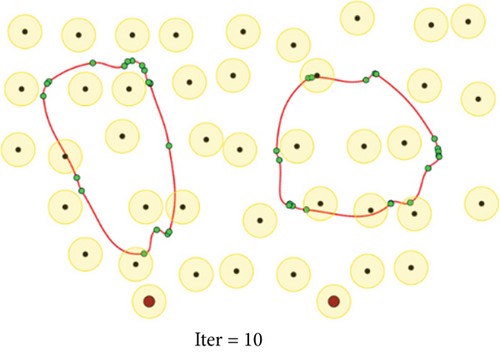
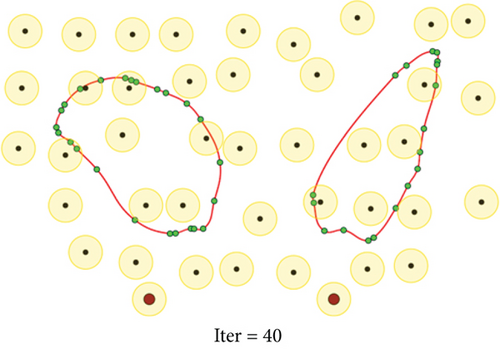
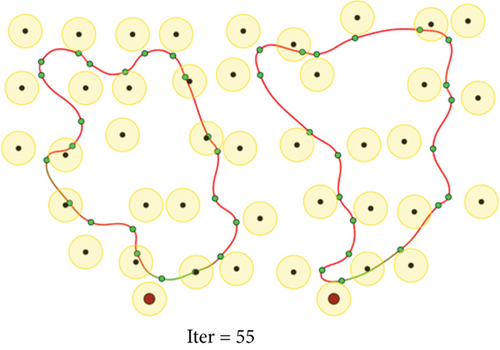
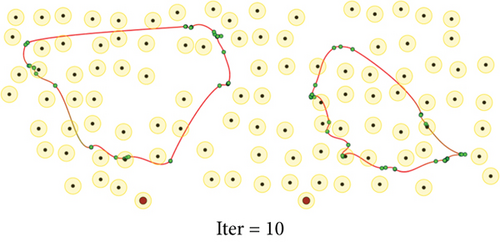
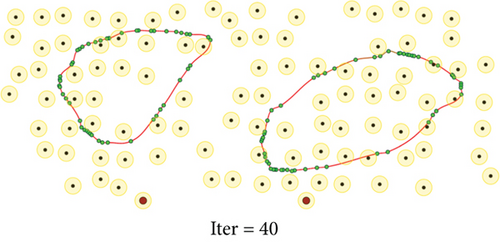
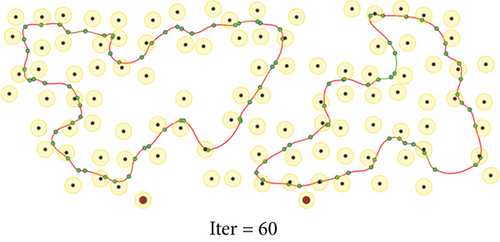
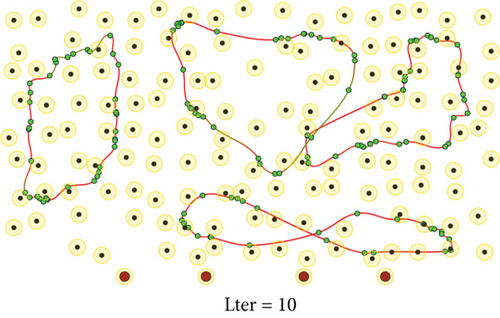
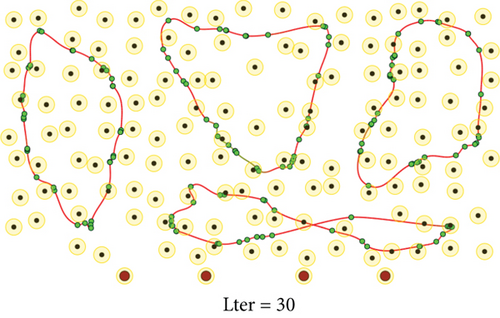
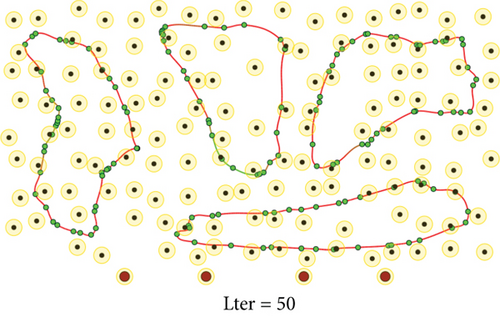
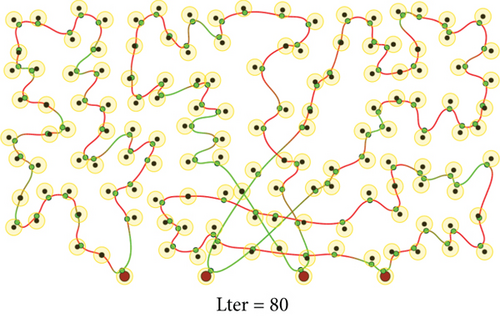
To evaluate the performance of the proposed method, we conduct a series of simulations with MATLAB software, by generating a series of random deployments of mobile WCVs and sensor nodes. In our simulation, there are n sensor nodes distributed in a rectangle region of L × W unit2 randomly, with different communication distance and recharging radius R. At present, the practical wireless power supply distance is several meters, not more than 10 meters. Nevertheless, the wireless data transmission range is much larger than 10 meters. Hence, for the sake of unification, we set both to the same value. Moreover, there are m mobile WCVs with wireless power supply capability used to collect sensory data from different sensor nodes. Therefore, battery energy of sensor nodes can be replenished when mobile WCVs approaching, i.e., the distance between certain WCV and sensor node is smaller than R. The MATLAB 2016b simulator is used as the simulation platform, and simulation trajectories under different network topology are exhibited. The simulations are repeated with 100 × n rounds, and the average value is derived to reflect the results. Some important parameters are listed in the following Table 2. The selection basis of main parameters is based on the existing literature integrating mobile data acquisition and wireless charging energy supply. In this section, simulation results are provided to demonstrate the performance of the proposed algorithm over existing algorithms. Figures 6–9 depict four derived trajectories of our simulation scenario when n = 40/100, m = 2, and R = 2/5. The iterative processes of our SOM-based solution method with n = 40, m = 2, and R = 5; n = 100, m = 2, and R = 5; and n = 140, m = 4, and R = 5 are shown in Figures 10–12, respectively. The average lengths of designed trajectory are shown in Table 3, which show that the total length of WCV will increase when the number of sensor nodes increase. Moreover, the total length of designed trajectories will decrease when the number of WCVs increase.
-
Algorithm 1: Data collecting and energy charging oriented mobile path design algorithm.
-
INPUT
-
S={S1, …Si, …, Sn}: a set of sensor nodes to be visited.
-
s={s1, …si, …, sn}: a set sensor locations to be visited with disk-shaped R-neighborhood of sensor nodes
-
set S.
-
(σ, μ, α, r): the unsupervised learning parameters.
-
(Σ,P): Σ defines the order of visits to the sensors S, P are the Bezier curve based tour path to visit sensor nodes.
-
iter = 1;
-
while iter < itermax do
-
STEP1. winner selection
-
for each Si ∈S do
-
Determine winner and insert it to winner set
-
N ←− insert_winner(N,v∗)
-
STEP2. winner adaptation
-
Adapt v using the neighbouring function
-
endfor
-
Update the best solution found now
-
Remove all no competing nodes from
-
iter + +
-
if (Σ′, P′)represents a shorter route than (Σ,P), then
-
(Σ, P) ←− (Σ′, P′)
-
STEP3. Results output
-
return (Σ,P)
-
endwhile
-
STEP4. Bezier curve transform
-
while k < n do
-
Tk ←−Pk
-
endwhile
-
OUTPUT
-
return (Σ, T)
| Parameters | Meanings | Values |
|---|---|---|
| n | Sensor nodes’ number | 40-160 |
| m | WCV’s number | 2-8 |
| L × W | Region size | 300 × 200 |
| R | Maximal range | 2/5 |
| σ (default) | Learning gain | 10 |
| α (default) | Gain decreasing rate | 0.0005 |
| μ (default) | Learning rate | 0.5 |
| r (default) | Neighbor node factor | 0.2 |
| E0 | Initial energy | 1 J |
| Bi | Transfer data in each round | 100 bytes |
| Itermax | Maximal iteration number | 100 |
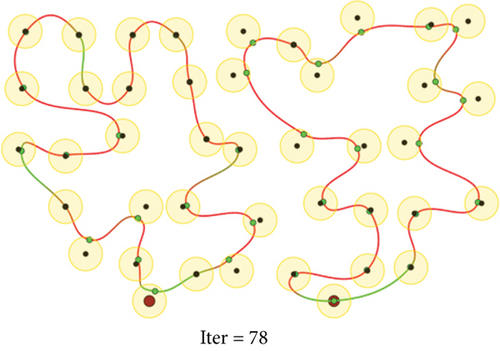
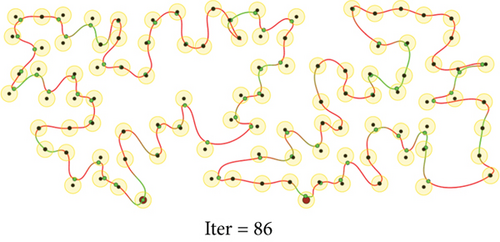
| Number of sensors and WCVs | m = 2 | m = 4 | m = 6 | m = 8 |
|---|---|---|---|---|
| n = 40 | 151.3 | 99.3 | 68.8 | 63.8 |
| n = 60 | 239.7 | 128.8 | 93.3 | 75.3 |
| n = 80 | 325.3 | 161.4 | 115.2 | 75.3 |
| n = 100 | 445.0 | 213.6 | 137.7 | 111.3 |
| n = 120 | 519.3 | 231.3 | 161.1 | 129.0 |
| n = 140 | 587.0 | 247.1 | 177.8 | 142.8 |
| n = 160 | 608.8 | 323.3 | 203.5 | 150.7 |
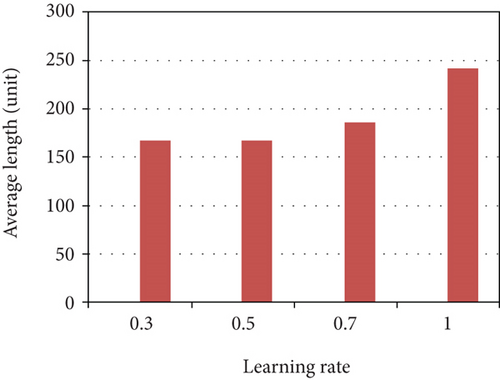
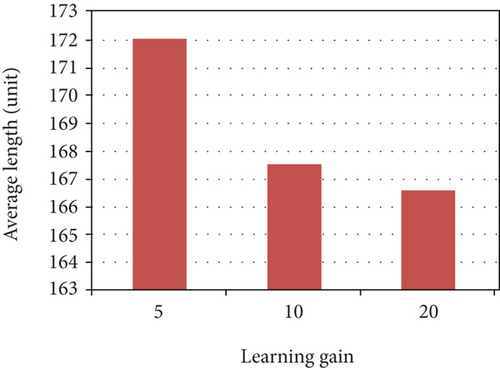
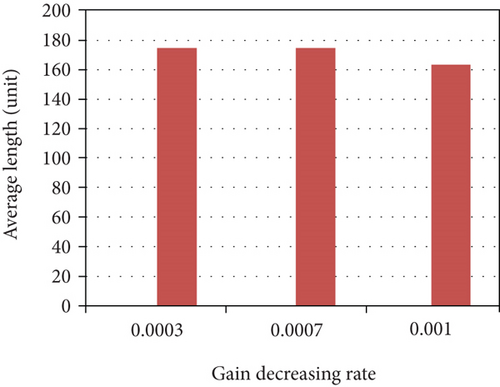
Furthermore, we test the performance changes with different parameters in SOM-based unsupervised learning method. There are four key parameters: learning gain σ, gain decreasing rate α, learning rate μ, and neighbor node factor r. In our simulations, using the same networks topology as n = 100, m = 4, and R = 5, we change these four important parameters to get final results as Figure 13. It is worth noting that when single parameter changes, other parameters are set according to the default settings in Table 2. Figure 13 verifies that our proposed algorithm satisfies the convergence property which is proven in [38]. Moreover, the comparison results provide a basis for selecting the optimal parameters in the following simulations.
Finally, we evaluate energy efficiency of the proposed algorithm. In our simulation, it is supposed that each WCV will stop at each site and replenish 0.1% energy, i.e., 1 mJ to its adjacent sensor node. In each round, each WCV will move to the next point, and each sensor node will transmit Bi cached data to mobile WCVs. For simplicity, the charging time and efficiency are considered to be fixed with a relatively small region. As we know, residual energy level is an important metric to address this problem, and it can prolong the life cycle of WSNs. Residual energy level denotes the ratio between average residual energy between initial energy after finishing 100 times WCVs’ cruising cycle. The derived energy efficiency results are illustrated in Figure 14; it is obvious that the residual energy level using multiple WCVs is able to maintain a relatively higher level than just using mobile sinks.
Furthermore, the proposed algorithm outperforms previous approaches for the CETSP in terms of the solution quality and required computational time. As a result, compared to traditional long-distance transmission manner, the proposed path planning method can improve the lifetime of wireless sensor networks from residual energy level.
6. Conclusions
This paper investigates optimal and suboptimal trajectory design model of mobile data collection and wireless energy supplement for rechargeable wireless sensor networks. At first, we model the optimal path design problem as a kind of CETSP problem. Then, SOM-based unsupervised learning algorithm is used to solve CETSP with one or more mobile WCVs as data collectors and wireless power suppliers. Simulation results demonstrate that the proposed algorithm can reduce the length of path trajectories and extend the network energy efficiency. The herein presented learning procedure is a conceptually simple algorithm which outperforms previous mobile path design approaches for the TSP in terms of the solution quality and required computational time. In our future works, path design with obstacle avoidance will be considered in the process of mobile data collection and wireless energy recharging.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Authors’ Contributions
M.Z. and W.C. proposed the main idea and generated the simulation results and drafted the manuscript. They also responded to the reviewers’ comments. These authors contributed equally to this work.
Acknowledgments
This research was partially supported by the Natural Science Foundation of Zhejiang Province (Grant Nos. LZJWY22E090001 and LZ22F010004), the National Natural Science Foundation of China (Grant Nos. 61801431 and 61871163), and the Fundamental Research Funds for the Provincial Universities of Zhejiang (No. GK209907299001-001).
Open Research
Data Availability
No data were used to support this study.




