Volume 2022, Issue 1 3996256

Research Article

Open Access

[Retracted] Approximations of Intuitionistic Fuzzy Ideals over Dual Spaces by Soft Binary Relations

Retraction(s) for this article

Muhammad Zishan Anwar,

Muhammad Zishan Anwar

Department of Mathematics, University of Gujrat, Gujrat 50700, Pakistan uog.edu.pk

Search for more papers by this author

Shahida Bashir,

Corresponding Author

Shahida Bashir

[email protected]

orcid.org/0000-0001-5869-9254

Department of Mathematics, University of Gujrat, Gujrat 50700, Pakistan uog.edu.pk

Search for more papers by this author

Muhammad Aslam,

Muhammad Aslam

Department of Mathematics, College of Sciences, King Khalid University, Abha 61413, Saudi Arabia kku.edu.sa

Search for more papers by this author

Muhammad Shabir,

Muhammad Shabir

Department of Mathematics, Quaid-i-Azam University, Islamabad, Pakistan qau.edu.pk

Search for more papers by this author

Muhammad Zishan Anwar,

Muhammad Zishan Anwar

Department of Mathematics, University of Gujrat, Gujrat 50700, Pakistan uog.edu.pk

Search for more papers by this author

Shahida Bashir,

Corresponding Author

Shahida Bashir

[email protected]

orcid.org/0000-0001-5869-9254

Department of Mathematics, University of Gujrat, Gujrat 50700, Pakistan uog.edu.pk

Search for more papers by this author

Muhammad Aslam,

Muhammad Aslam

Department of Mathematics, College of Sciences, King Khalid University, Abha 61413, Saudi Arabia kku.edu.sa

Search for more papers by this author

Muhammad Shabir,

Muhammad Shabir

Department of Mathematics, Quaid-i-Azam University, Islamabad, Pakistan qau.edu.pk

Search for more papers by this author

First published: 02 June 2022

https://doi.org/10.1155/2022/3996256

Citations: 1

Academic Editor: Ganesh Ghorai

Share a link

Email
Wechat
Bluesky

Abstract

The major advantage of this proposed work is to investigate roughness of intuitionistic fuzzy subsemigroups (RIFSs) by using soft relations. In this way, two sets of intuitionistic fuzzy (IF) soft subsemigroups, named lower approximation and upper approximation regarding aftersets and foresets, have been introduced. In RIFSs, incomplete and insufficient information is handled in decision-making problems like symptom diagnosis in medical science. In addition, this new technique is more effective as compared to the previous literature because we use intuitionistic fuzzy set (IFS) instead of fuzzy set (FS). Since the FS describes the membership degree only but often in real-world problems, we need the description of nonmembership degree. That is why an IFS is a more useful set due to its nonmembership degree and hesitation degree. The above technique is applied for left (right) ideals, interior ideals, and bi-ideals in the same manner as described for subsemigroups.

1. Introduction

We are facing critical problems involving uncertainty and impreciseness in everyday life. Inexact and incomplete information data has not complete and precise reasoning possibly. Nowadays, the gap between the world full of vagueness and traditional mathematics with precise concepts is going to reduce with highly appreciated mode. Researchers are keen to deal with different nature of uncertainty with different methods. In this regard, they studied many newly defined theories such as RSs, FSs, IFSs, and SSs. The FSs are very important to manage the uncertainties in real-world problems. They have numerous applications in several fields such as vacuum cleaner, control of subway systems, unmanned helicopters, transmission systems, models for new pricing, and weather forecasting systems. This logic has given new life to scientific fields and has been used in many fields such as electronics, image processing, and optimization [1]. The IFS theory introduced by Attanassov [2] is one of the generalizations of FS theory. In IFS, membership degree, degree of nonmembership, and degree of hesitation of every element are expressed whose sum must be equal to 1. As we know, IFSs have degree of membership and degree of nonmembership which are more valuable in medical field. Intuitionistic fuzzy environment is more suitable to diagnose disease than FS due to its nonmembership degree. The FSs have only degree of membership but IF soft sets (IFSSs) keep a controlled degree of the vagueness, and they transform an imprecise pattern classification problem into a well-defined and precise optimization problem because an IFS gives out the uncertainty by a nonmembership degree. In real-life problems, IF logic has more effective use to control and overcome the uncertainty than fuzzy logic [3–6].

The rough sets (RSs) were introduced by Pawlak [7, 8]. They attract many researchers and specialists because they handle vagueness, uncertainty, and impreciseness in a noncustomary manner and discover relationship of structures with FSs. They also help to make decisions in an eccentric way in daily life problems. The abdominal pain of children is a very serious issue in medical field which is due to different reasons, and this is a challenging issue for researchers to diagnose the reasons correctly. Researchers can use the RS theory to diagnose it and give further consultations. This theory is also used for feature extraction, decision rule generation, data reduction, and feature selection and also applied successfully to pattern recognition, intelligent systems, machine learning, mereology, expert systems, signal analysis, decision analysis, and more other fields.

In RS theory, we define approximation spaces as set with multiple memberships, but in FS theory, it concerns only with partial membership. In RS theory, we use indiscernibility to remove useless data without using basic knowledge-based data. Usually, we approximate a crisp set into two formal approximations, lower and upper approximation. Upper approximation is a set which has elements having possible belonging with target set and lower approximated set has objectives having positive belonging with the target set. In simple words, we can say that a RS is a nonempty set regarding its boundary region, and in other case, this set is crisp set [7–20].

The soft set (SS) theory is presented by Molodtsov [21], and this is a very suitable approach to remove those associated difficulties which the other theories were unable to tackle, like FS theory, interval mathematics, and probability theory. In this theory, parameters can be chosen by researchers with their form according to their needs. In industrialized countries, more visible reason for cancer death in men is prostate cancer, which depends on many factors such as age, family cancer history, the level of prostate-specific antigen in blood and ethnic background, etc. Many researchers are working on finding the risks of prostate cancer with the help of FSs and SSs [22]. Nowadays, the SS theory has many study work by different authors rapidly. Aktas and Cagman described soft groups [23]. Jun connected SSs with ideal theory ([24, 25]). Maji et al. [26] worked on IFSSs. Razak and Mohamad [27] worked on decision-making regarding fuzzy soft sets (FSSs) in connection with SSs [28].

Al-shami et al. [29, 30] introduced extended form of FS called square-root FS and contrast square-root FS with IFS and Pythagorean FS. Hariwan et al. [31] proposed a useful concept of (3,2)-fuzzy sets with connection of other types of fuzzy sets and discussed its basic properties and operations. (3,2)-Fuzzy sets are more useful than IFSs and Pythagorean FSs due to their larger range of membership grades. Since we know RSs are useful to deal with incompleteness and IFSs are useful to deal vagueness, SSs have rich operations due to its parameters. So the combination of IFSs, RSs, and SSs is a valuable combination to deal with impreciseness [32–36].

1.1. Related Works

Binary relations are always very important in information sciences and mathematics both. Extended form of ordinary binary relations is soft binary relation which is a family of parameters of binary relation to a universe. Anwar et al. [37] presented a suitable model of IFRS in terms of soft relations and algorithm for real-world problems. Later on, Anwar et al. [38, 39] worked on [37] based on multisoft relations and its algebraic properties with useful algorithms and introduced the optimistic multigranulation intuitionistic fuzzy rough set (OMGIFRS) and pessimistic multigranulation intuitionistic fuzzy rough set (PMGIFRS) in terms of multisoft relations.

1.2. Innovative Contribution

For several practical applications in real world, equivalence relation is much restrictive. Skowron and Stepaniuk [40] replaced equivalence relations by tolerance relations. The soft covering has also been discussed by Li et al. [41]. The rough approximation by soft binary relations handles multiple binary relations. Ali [42] presented the conceptual theory about soft binary relation, and he discussed the soft lower and soft upper approximation operations regarding soft equivalence relations. In rough approximations, only binary relations are addressed, but in any other case, there are different several binary relations in connection with rough approximations in terms of soft binary relations. Shabir et al. presented prime and semiprime L-fuzzy hyperideals in terms of soft sets. They also discussed applications of semihypergroups in terms of L-fuzzy soft sets and fuzzy ideals in connection with rough fuzzy ternary subsemigroups and 3-dimensional congruence relation in their previous publications [41–49]. In 2019, Kanwal and Shabir discussed the fuzzy set of semigroup in terms of rough approximation with soft relations [50]. In this research, we have studied the rough approximation of IF set in semigroups based on soft relations.

1.3. Motivation

The main motivation of this research study is to extend the concept of fuzzy ideals into IF ideals based on soft relations in terms of semigroups. Its related properties are also discussed. The semigroup attracts many algebraists due to their applications to formal languages, automata theory and network analogy, etc. The connection of semigroup theory and theory of machines increases the importance of both theories during the past few decades. In association with the study of machines and automata, other areas of applications have been improved such as formal languages, and the software uses the language of modern algebra in terms of Boolean algebra, semigroups, and others. The semigroup theory contributes in biology, psychology, biochemistry, and sociology [51]. The FS describes only degree of membership of each element which is insufficient to tackle uncertainty in several real-world problems. Here, we need IFS to describe degree of membership as well as degree of nonmembership of each element to control vagueness and impreciseness in real-world problems. In [52], Bashir et al. discussed a useful model of regular ternary semirings based on bipolar fuzzy sets and its algebraic properties. In Kanwal and Shabir’s paper [50], fuzzy ideals have been discussed, but in this paper, we discuss our proposed model in intuitionistic environment which is a more suitable environment to deal with incompleteness and uncertainty.

1.4. Organization of the Paper

The setting of the paper is as follows. In Section 2, a few basic concepts with SSs, soft binary relations, IFSs, and IF ideals are presented. In Section 3, we discussed an approximation of an IFS in terms of soft binary relations. We made approximations of IF set by the foresets and aftersets, and we get two IFSSs, called the upper approximation and lower approximation regarding foresets and aftersets. After applying these concepts, approximations of IF subsemigroups, IF left (right) ideals, IF interior ideals, and IF bi-ideals of semigroups are discussed with examples. In Section 4, we present the comparison with the previous work. In Section 5, conclusion is described to present this research work and future work.

See Table 1 for the acronyms.

Table 1. List of acronyms.

Acronyms	Representations
FSs	Fuzzy sets
IFSs	Intuitionistic fuzzy sets
RSs	Rough sets
SSs	Soft sets
FSSs	Fuzzy soft sets
IFSSs	Intuitionistic fuzzy soft sets
IFRSs	Rough intuitionistic fuzzy sets
MGRS	Multigranulation rough set
OMGRS	Optimistic multigranulation rough set
PMGRS	Pessimistic multigranulation rough set
RIFs	Rough intuitionistic fuzzy subsemigroups

2. Preliminaries and Basic Concepts

In this section, basic notions about IFSs, SSs, IFSSs, and some background materials are given. Throughout this paper, (U, ·) is semigroup and U₁ and U₂ represent two nonempty finite sets unless stated otherwise. Here, we recall some ideas and results which are useful for this paper.

We will denote the product of two elements x, y ∈ U by xy instead of x.y. In what follows by subsets, we always means nonempty ones. Let us consider two subsets A and B of U, and then, the product AB is defined as AB = {ab : a ∈ A, b ∈ B}.

Definition 1 (see [53].)A binary relation T from U₁ to U₂ is a subset of U₁ × U₂, and a subset of U₁ × U₁ is said to be a binary relation on U₁. If T is a binary relation on U₁, then T is said to be reflexive if (u, u) ∈ T for all u ∈ U₁, symmetric if (u, v) ∈ T implies (v, u) ∈ T for all u, v ∈ U₁, and transitive if (u, v) ∈ T and (v, w) ∈ T implies (u, w) ∈ T for all u, v, w ∈ U₁. If a binary relation T is reflexive, symmetric, and transitive, then it is called an equivalence relation. A set is partitioned into disjoint classes by an equivalence relation.

Definition 2 (see [54].)For any subset A of U if ab ∈ A for all a, b ∈ A, then A is called a subsemigroup of U. A left (right) ideal of U is a subset A of U such that UA⊆A(AU⊆A). A two-sided ideal is a subset A of U which is a left as well as right ideal of U. A subsemigroup A of U is said to be an interior ideal of U if UAU⊆A. A subsemigroup A of U is said to be a bi-ideal of U if AUA⊆A.

Definition 3 (see [2].)An intuitionistic fuzzy set (IFS) B in U₁ is an object having the shape B = {〈x, μ_B(x), γ_B(x)〉: x ∈ U₁}, where μ_B : U₁⟶0, 1⌉ and γ_B : U₁⟶0, 1⌉ satisfying 0 ≤ μ_B(x) + γ_B(x) ≤ 1 for all x ∈ U₁. The values μ_B(x) and γ_B(x) are called membership degree and nonmembership degree of x ∈ U₁ to B, respectively. The number π_B(x) = 1 − μ_B(x) − γ_B(x) is called the hesitancy degree of x ∈ U₁ to B. The collection of all IFS in U₁ is denoted by IF(U₁). In the remaining paper, we shall write an IFS by B = 〈μ_B, γ_B〉 instead of B = {〈x, μ_B(x), γ_B(x)〉: x ∈ U₁}. Let B = 〈μ_B, γ_B〉 and be two IFSs in U₁. Then, B⊆B₁ if and only if and for all x ∈ U₁. Two IFSs B and B₁ are said to be equal if and only if B⊆B₁ and B₁⊆B. The union and intersection of the two IFSs B and B₁ in U₁ are denoted and defined by and , where , , and .

Next, we define two special types of IFSs. The IF universe set U = 1_U = <1, 0> and IF empty set ∅ = 0_U = <0, 1>, where 1(x) = 1 and 0(x) = 0 for all x ∈ U. The complement of an IFS A = <μ, γ> is denoted and defined as A^c = <γ, μ>.

Definition 4 (see [21].)A pair (σ, A) is said to be a soft set (SS) over U if σ : A⟶P(U), where A⊆E, E is the set of parameters and the set U has power set P(U). Thus, σ(e) is a subset of U for all e ∈ A. Hence, a SS over U is a parametrized collection of subsets of U.

Definition 5 (see [26], [55].)A pair (σ, A) is called an intuitionistic fuzzy soft set (IFSS) over U if σ : A⟶IF(U) and A⊆E where E is the set of parameters. Thus, σ(e) is an IFS in U for all e ∈ A. Hence, an IFSS over U is a parametrized collection of IFSs in U.

If (σ, A) and (ρ, B) are two IFSSs over U, we say that (σ, A) is an IF soft subset of (ρ, B) if (1)A⊆B and (2)σ(e) is an IF subset of ρ(e) for all e ∈ A. If (σ, A) and (ρ, B) over U are IFSSs, then they called IF soft equal if (σ, A) is an IF soft subset of (ρ, B) and (ρ, B) is an IF soft subset of (σ, A). The union of two IFSSs (σ, A) and (ρ, A) over the common universe U is the IFSS (λ, A), where λ(e) = σ(e) ∪ ρ(e) for all e ∈ A. Over the common universe U, the intersection of two IFSSs (σ, A) and (ρ, A) is the IFSS (π, A), where π(e) = σ(e)∩ρ(e) for all e ∈ A.

Definition 6 (see [21].)An IFS B = 〈μ_B, γ_B〉 in U is called an IF subsemigroup of U if it satisfies the following:

(1)
μ_B(xy) ≥ μ_B(x)∧μ_B(y)
(2)
γ_B(xy) ≤ γ_B(x)∨γ_B(y) for all x, y ∈ U

An IFS B = 〈μ_B, γ_B〉 in a semigroup U is called an IF left (resp., right) ideal of U if it satisfies μ_B(xy) ≥ μ_B(y)(resp.μ_B(xy) ≥ μ_B(x)) and γ_B(xy) ≤ γ_B(y)(resp.γ_B(xy) ≤ γ_B(x)) for all x, y ∈ U. An IF left ideal and IF right ideal are called fuzzy ideals. An IF subsemigroup B = 〈μ_B, γ_B〉 in U is called an IF interior ideal of U if it satisfies μ_B(xay) ≥ μ_B(a) and γ_B(xay) ≤ γ_B(a) for all x, y, a ∈ U.

An IF subsemigroup B = 〈μ_B, γ_B〉 in U is called an IF bi-ideal of U if it satisfies the following:

(1)
μ_B(xwy) ≥ μ_B(x)∧μ_B(y)
(2)
γ_B(xwy) ≤ γ_B(x)∨γ_B(y) for all x, y, w ∈ U [2, 26, 56–58]

Definition 7 (see [59].)An IFSS (σ, A) over U is called IF soft subsemigroup (left ideal, right ideal, interior ideal, and bi-ideal) over U if each σ(e) is IF subsemigroup (left ideal, right ideal, interior ideal, and bi-ideal) of U for all e ∈ A.

Definition 8 (see [60].)A soft binary relation (σ, A) from U₁ to U₂ is a SS over U₁ × U₂, that is, σ : A⟶P(U₁ × U₂), where A⊆E.

Of course, (σ, A) is a parameterized collection of binary relations from U₁ to U₂; that is, for each e ∈ A, we have a binary relation σ(e) from U₁ to U₂.

Definition 9 (see [61].)A soft binary relation (σ, A) from a semigroup U₁ to a semigroup U₂ is said to be soft compatible if (p, q), (r, s) ∈ σ(e) implies (pr, qs) ∈ σ(e) for all p, r ∈ U₁ and q, s ∈ U₂.

In general, if (σ, A) is a soft compatible relation from U₁ to U₂, then pσ(e).qσ(e)⊆(pq)σ(e); indeed if a ∈ pσ(e) and b ∈ qσ(e), then (p, a) ∈ σ(e) and (q, b) ∈ σ(e). By compatibility of (σ, A), (pq, ab) ∈ σ(e); that is, ab ∈ (pq)σ(e). Similarly, σ(e)p.σ(e)q⊆σ(e)(pq). The following example shows that in general, pσ(e).qσ(e) ≠ (pq)σ(e) and σ(e)p.σ(e)q ≠ σ(e)(pq).

Example 1. Let U₁ = {p, q, r, s} and U₂ = {1, 2, 3, 4} be two semigroups, and their multiplication tables are as shown in Tables 2 and 3, respectively).

Table 2. Multiplication table for U₁.

.	p	q	r	s
p	p	p	p	s
q	p	q	p	s
r	p	p	r	s
s	s	s	s	s

Table 3. Multiplication table for U₂.

.	1	2	3	4
1	1	2	3	4
2	2	2	2	2
3	3	3	3	3
4	4	3	2	1

Let A = {e₁, e₂}. Define σ : A⟶P(U₁ × U₂) by

(1)

Then, (σ, A) is a soft compatible relation from U₁ to U₂.

(2)

But

(3)

Now,

(4)

But

(5)

Definition 10 (see [61].)A soft compatible relation (σ, A) from a semigroup U₁ to a semigroup U₂ is said to be soft complete regarding aftersets if pσ(e).qσ(e) = (pq)σ(e) for all p, q ∈ U₁ and e ∈ A and is said to be soft complete relation regarding foresets if σ(e)r.σ(e)s = σ(e)(rs) for all r, s ∈ U₂ and e ∈ A.

Definition 11 (see [37].)Let (σ, A) be a soft binary relation from U₁ to U₂ and B = 〈μ_B, γ_B〉 be an IFS in U₂. Then, the lower approximation and the upper approximation of B = 〈μ_B, γ_B〉 are IFSSs over U₁ and defined as

(6)

for all u₁ ∈ U₁, where u₁σ(e) = {a ∈ U₂ : (u₁, a) ∈ σ(e)} and is called the afterset of u₁ for u₁ ∈ U₁ and e ∈ A.

Definition 12 (see [37].)Let (σ, A) be a soft binary relation from U₁ to U₂ and B = 〈μ_B, γ_B〉 be an IFS in U₁. Then, the lower approximation and the upper approximation of B = 〈μ_B, γ_B〉 are IFSSs over U₂ and defined as

(7)

for all u₂ ∈ U₂ where σ(e)u₂ = {a ∈ U₁ : (a, u₂) ∈ σ(e)} and is called the foreset of u₂ for u₂ ∈ U₂ and e ∈ A.

Of course, , and , .

Theorem 13 (see [37].)Let (σ, A) be a soft binary relation from U₁ to U₂ that is σ : A⟶P(U₁ × U₂). For any IFSs and of U₂, the following hold.

(1)
D₁ ≤ D₂ implies
(2)
D₁ ≤ D₂ implies
(3)
(4)
(5)
(6)
(7)
if uσ(e) ≠ ∅
(8)
if uσ(e) ≠ ∅
(9)
if uσ(e) ≠ ∅
(10)
if uσ(e) ≠ ∅
(11)
if uσ(e) ≠ ∅

Theorem 14 (see [37].)Let (σ, A) be a soft binary relation from U₁ to U₂; that is, σ : A⟶P(U₁ × U₂). For any IFSs and of U₁, the following are true.

(1)
If implies
(2)
If D₁ ≤ D₂ implies
(3)
(4)
(5)
(6)
(7)
if uσ(e) ≠ ∅
(8)
if uσ(e) ≠ ∅
(9)
if uσ(e) ≠ ∅
(10)
if uσ(e) ≠ ∅
(11)

3. Approximations of IF Ideals in Semigroups by Soft Binary Relation

This is our major section of the paper. Our related work is narrated in this section. Here, we discuss the rough approximations of IF subsemigroup (IF left (right) ideal, IF interior ideal, and IF bi-ideal) in a semigroup regarding aftersets as well as regarding foresets by using soft compatible relation. We show that upper approximation of an IF subsemigroup (IF left (right), IF interior ideal, and IF bi-ideal) in a semigroup is an IF soft subsemigroup (IF soft left (right) ideal, IF soft interior ideal, and IF soft bi-ideal) and discuss examples which shows that its converse is not true. Similar results for lower approximation are also proved.

Theorem 15. Let (σ, A) be a soft compatible relation from a semigroup U₁ to a semigroup U₂.

(1)
If B₂ is an IF subsemigroup of U₂, then is an IF soft subsemigroup of U₁
(2)
If B₂ is an IF left (right, two-sided) ideal of U₂, then is an IF soft left (right, two-sided) ideal of U₁

Proof.

(1)
We assume that B₂ is an IF subsemigroup of U₂. Now for u, v ∈ U₁,

(8)

Similarly for s, t ∈ U₁,

(9)

Hence, is an IF subsemigroup of U₁ for all e ∈ A, so is an IF soft subsemigroup of U₁.

(2)
Assume that B₂ is an IF left ideal of U₂. Now for x, y ∈ U₁,

(10)

Similarly for x, y ∈ U₁,

(11)

Hence, is an IF left ideal of U₁ for each e ∈ A, so is an IF soft left ideal of U₁.

In Theorem 15 from part 1, soft compatible relations from U₁ to U₂ are given, and B₂ is an IF subsemigroup in U₂. After combining theme, we get generalized IF soft subsemigroups in U₁. Similarly, we take an IF left (right, two-sided) ideal B₂ of U₂, and we get generalized IF soft left (right, two-sided) ideal of U₁.

Theorem 16. Let (σ, A) be a soft compatible relation from a semigroup U₁ to a semigroup U₂:

(1)
If B₁ is an IF subsemigroup of U₁, then is an IF soft subsemigroup of U₂
(2)
If B₁ is an IF left (right, two-sided) ideal of U₁, then is an IF soft left (right, two-sided) ideal of U₂

Proof. It follows from Theorem 15.

In Theorem 16 from part 1, soft compatible relations from U₁ to U₂ are given, and B₁ is an IF subsemigroup in U₁. After combining them, we get generalized IF soft subsemigroups in U₂. Similarly, we take an IF left (right, two-sided) ideal B₁ of U₁, and we get generalized IF soft left (right, two-sided) ideal of U₂.

Now, we show that the converses of parts of the above theorem do not hold in general.

Example 2. Let U₁ = {p, q, r, s, t} and U₂ = {1, 2, 3, 4, 5} be two semigroups, and their multiplication tables are as follows in Tables 4 and 5, respectively.

Table 4. Multiplication table for U₁.

.	p	q	r	s	t
p	q	q	s	s	s
q	q	q	s	s	s
r	s	s	r	s	r
s	s	s	s	s	s
t	s	s	r	s	r

Table 5. Multiplication table for U₂.

.	1	2	3	4	5
1	1	5	3	4	5
2	1	2	3	4	5
3	1	5	3	4	5
4	1	5	3	4	5
5	1	5	3	4	5

Let A = {e₁, e₂}. Define σ : A⟶P(U₁ × U₂) by

(12)

Then, (σ, A) is a soft compatible relation from U₁ to U₂.

(13)

(1)
Define B₁ : U₂⟶[0, 1] (given in Table 6)

Table 6. Intuitionistic fuzzy set B₁.

B₁	1	2	3	4	5
	0.5	0.4	0.3	1	0.1
	0.4	0.5	0.7	0	0.8

Then, B₁ is not an IF subsemigroup of U₂ because if we take x = 1, y = 2, then and Upper approximation of B₁ is given in Table 7.

Table 7. Upper approximation of B₁.

p	q	r	s	t
0.5	0.5	0.3	1	0.1
0.4	0.4	0.7	0	0.8
0.5	0.5	0.3	1	0.1
0.4	0.4	0.7	0	0.8

Clearly,

and

are IF subsemigroups of U₁, so

is an IF soft subsemigroup of U₁.

(2)
Define B₂ : U₁⟶[0, 1] (given in Table 8)

Table 8. Intuitionistic fuzzy set B₂.

B₂	p	q	r	s	t
	0.2	0.7	0.8	0	0.9
	0.7	0.3	0.2	1	0.1

Then, B₂ is not an IF subsemigroup of U₁ because if we take x = t, y = t, then

and

Upper approximation of B₂ is given in Table 9. Clearly,

and

are IF subsemigroups of U₂, so

is an IF soft subsemigroup of U₂.

(3)
Define B : U₂⟶[0, 1] (given in Table 10)

Table 9. Upper approximation of B₂.

1	2	3	4	5
0.7	0.7	0.8	0	0.9
0.3	0.3	0.2	1	0.1
0.7	0.7	0.8	0	0.9
0.3	0.3	0.2	1	0.1

Table 10. Intuitionistic fuzzy set B.

B	1	2	3	4	5
μ_B	0.5	0.4	0.3	1	0.1
γ_B	0.4	0.6	0.6	0	0.8

Then, B is not an IF left ideal of U₂ because if we take x = 1, y = 2, then μ_B(12)≱μ_B(2) and γ_B(12)≰γ_B(2). Upper approximation of B is given in Table 11. Clearly,

and

are IF left ideals of U₁, so

is an IF soft left ideal of U₁.

(4)
Define H : U₁⟶[0, 1] (given in Table 12)

Table 11. Upper approximation of B.

p	q	r	s	t
0.5	0.5	0.3	1	0.1
0.4	0.4	0.6	0	0.8
0.5	0.5	0.3	1	0.1
0.4	0.4	0.6	0	0.8

Table 12. Intuitionistic fuzzy set H.

H	p	q	r	s	t
μ_H	0.2	0.7	0.8	0	0.9
γ_H	0.7	0.2	0.1	1	0.1

Then, H is not an IF left ideal of U₁ because if we take x = t, y = t, then μ_H(tt)≱μ_H(t) and γ_H(tt)≰γ_H(t). Upper approximation of H is given in Table 13.

Table 13. Upper approximation of H.

1	2	3	4	5
0.7	0.7	0.8	0	0.9
0.2	0.2	0.1	1	0.1
0.7	0.7	0.8	0	0.9
0.2	0.2	0.1	1	0.1

Clearly, and are IF left ideals of U₂, so is an IF soft left ideal of U₂.

Example 3. Consider the semigroups and soft binary relation of Example 2. Define B : U₂⟶[0, 1] (given in Table 14).

Table 14. Intuitionistic fuzzy set B.

B	1	2	3	4	5
μ_B	0.7	0.7	0.8	0	0.9
γ_B	0.2	0.3	0.1	1	0.1

Then, B is an IF left ideal of U₂. Lower approximation of B is given in Table 15.

Table 15. Lower approximation of B.

p	q	r	s	t
0.7	0.7	0.8	0	0.9
0.2	0.3	0.9	1	0.1

But is not an IF left ideal of U₁ because if we take x = r, y = t, then μ_B(rt)≱μ_B(t) and γ_B(rt)≰γ_B(t).

This example shows that if the soft relation is compatible, then lower approximation of an IF left ideal is not IF soft left ideal. However, the following result is true.

Theorem 17. Let (σ, A) be a soft complete relation regarding aftersets from a semigroup U₁ to a semigroup U₂.

(1)
If B is an IF subsemigroup of U₂, then is an IF soft subsemigroup of U₁
(2)
If B is an IF left (right, two-sided) ideal of U₂, then is an IF soft left (right, two-sided) ideal of U₁

Proof.

(1)
Assume that B is an IF subsemigroup of U₂. Now for x, y ∈ U₁,

(14)

Similarly, for x, y ∈ U₁,

(15)

Hence, is an IF subsemigroup of U₁ for each e ∈ A, so is an IF soft subsemigroup of U₁.

(2)
Suppose B is an IF left ideal of U₂. Now for x, y ∈ U₁,

(16)

Similarly, for x, y ∈ U₁,

(17)

Hence, is an IF left ideal of U₁ for all e ∈ A, so is an IF soft left ideal of U₁.

Theorem 18. Suppose (σ, A) is a soft complete relation regarding foresets from a semigroup U₁ to a semigroup U₂. Then, the following are true:

(1)
If B is an IF subsemigroup of U₁, then is an IF soft subsemigroup of U₂
(2)
If B is an IF left (right, two-sided) ideal of U₁, then is an IF soft left (right, two-sided) ideal of U₂

Proof. It follows from Theorem 17.

Example 4. Consider the semigroups of Example 1.

Let A = {e₁, e₂}. Define σ : A⟶P(U₁ × U₂) by

(18)

Then, (σ, A) is a soft complete relation from U₁ to U₂ with respect to the aftersets.

(19)

(1)
Define B : U₂⟶[0, 1] (given in Table 16)

Table 16. Intuitionistic fuzzy set B.

B	1	2	3	4
μ_B	0.2	0.4	0.6	0.8
γ_B	0.7	0.5	0.2	0.1

Then, B is not an IF subsemigroup of U₂ because if we take x = 4, y = 4, then μ_B(44)≱μ_B(4)∧μ_B(4) and γ_B(44)≰γ_B(4)∨γ_B(4). Lower approximation of B is given in Table 17.

Table 17. Lower approximation of B.

p	q	r	s
0.4	0.4	0.4	0.4
0.5	0.5	0.5	0.5
0.4	0.4	0.4	0.4
0.5	0.5	0.5	0.5

Clearly,

and

are IF subsemigroups of U₁, so

is an IF soft subsemigroup of U₁.

(2)
Define B₁ : U₂⟶[0, 1] (given in Table 18)

Table 18. Intuitionistic fuzzy set B₁.

B₁	1	2	3	4
	0.2	0.4	0.6	0.8
	0.7	0.5	0.2	0.1

Then, B₁ is not an IF left ideal of U₂ because if we take x = 3, y = 4, then and Lower approximations of B₁ are given in Table 19.

Table 19. Lower approximation of B₁.

p	q	r	s
0.4	0.4	0.4	0.4
0.5	0.5	0.5	0.5
0.4	0.4	0.4	0.4
0.5	0.5	0.5	0.5

Clearly, and are IF left ideals of U₁, so is an IF soft left ideal of U₁.

Now define σ : A⟶P(U₁ × U₂) by

(20)

These are soft complete relations from U₁ to U₂ with respect to the foresets.

(21)

(1)
Define B : U₁⟶[0, 1] (given in Table 20)

Table 20. Intuitionistic fuzzy set B.

	p	q	r	s
μ_B	0.1	0.3	0.5	0.7
γ_B	0.9	0.6	0.4	0.2

Then, B is not an IF subsemigroup of U₁ because if we take x = r, y = q, then μ_B(rq)≱μ_B(r)∧μ_B(q) and γ_B(rq)≰γ_B(r)∨γ_B(q). Lower approximation of B is given in Table 21.

Table 21. Lower approximation of B.

1	2	3	4
0.7	0.7	0.7	0.7
0.2	0.2	0.2	0.2
0.1	0.1	0.1	0.1
0.9	0.9	0.9	0.9

Clearly,

and

are IF subsemigroups of U₂, so

is an IF soft subsemigroup of U₂.

(2)
Define B₁ : U₁⟶[0, 1] (given in Table 22)

Table 22. Intuitionistic fuzzy set B₁.

p	q	r	s
0.1	0.3	0.5	0.7
0.8	0.6	0.5	0.2

Then, B₁ is not an IF left ideal of U₁ because if we take x = r, y = q, then and Lower approximation of B₁ is given in Table 23.

Table 23. Lower approximation of B₁.

1	2	3	4
0.7	0.7	0.7	0.7
0.2	0.2	0.2	0.2
0.1	0.1	0.1	0.1
0.8	0.8	0.8	0.8

Clearly, and are IF left ideals of U₂, so is an IF soft left ideal of U₂.

The next theorem shows that upper approximation of product of right and left IF ideals is contained in the intersection of their upper approximations.

Theorem 19. Suppose (σ, A) is a soft binary relation from a semigroup U₁ to a semigroup U₂; that is, σ : A⟶P(U₁ × U₂). Then, for an IF right ideal and for an IF left ideal of U₂, .

Proof. Assume that B₁ is an IF right ideal and B₂ is IF left ideal of U₂, so by definition, B₁B₂⊆B₁∩B₂.

It follows from Theorem 13,

(22)

Hence,

(23)

Also,

(24)

Hence,

(25)

Theorem 20. Suppose (σ, A) is a soft bianry relation from a semigroup U₁ to a semigroup U₂; that is, σ : A⟶P(U₁ × U₂). Then, for an IF right ideal and for an IF left ideal of U₁, .

Proof. It follows from Theorem 19.

Theorem 21. Let (σ, A) be a soft binary relation from a semigroup U₁ to a semigroup U₂; that is, σ : A⟶P(U₁ × U₂). Then, for an IF right ideal and an IF left ideal of U₂, .

Proof. Assume that B₁ is an IF right ideal and B₂ is IF left ideal of U₂, so by definition B₁B₂⊆B₁∩B₂.

It follows from Theorem 13,

(26)

Hence,

(27)

Also,

(28)

Hence,

(29)

Theorem 22. Suppose (σ, A) is a soft binary relation from a semigroup U₁ to a semigroup U₂; that is, σ : A⟶P(U₁ × U₂). Then for IF right ideal and IF left ideal of U₁, .

Proof. It follows from Theorem 21.

Now for IF interior ideals of a semigroup, we discuss a few properties.

Theorem 23. Let (σ, A) be a soft compatible relation from a semigroup U₁ to a semigroup U₂. If B is an IF interior ideal of U₂, then is an IF soft interior ideal of U₁.

Proof. Suppose that B is an IF interior ideal of U₂. Thus, B is an IF subsemigroup of U₂, so by Theorem 15, is an IF soft subsemigroup of U₁. Now for x, a, y ∈ U₁,

(30)

Similarly, for s, b, t ∈ U₁,

(31)

Hence, is an IF interior ideal of U₁ for all e ∈ A, so is an IF soft interior ideal of U₁.

For converse of above result, we show the following example.

Example 5. Let U₁ = {1, 2, 3} and U₂ = {p, q, r} be two semigroups, and their multiplication tables are as shown in Tables 24 and 25, respectively.

Table 24. Multiplication table for U₁.

.	1	2	3
1	1	2	3
2	1	2	3
3	1	2	3

Table 25. Multiplication table for U₂.

.	p	q	r
p	p	p	r
q	p	q	r
r	p	r	r

And A = {e₁, e₂}. Define σ : A⟶P(U₁ × U₂) by

(32)

Then, (σ, A) is a soft compatible relation from U₁ to U₂.

(33)

Define B : U₂⟶[0, 1] (given in Table 26).

Table 26. Intuitionistic fuzzy set B.

	p	q	r
μ_B	0	0.1	0.1
γ_B	0.9	0.8	0.9

Then, B is not an IF interior ideal of U₂ because if we take x = q, a = r, y = p, then μ_B(qrp)≱μ_B(r) and γ_B(qrp)≰γ_B(r). Upper approximation of B is given in Table 27.

Table 27. Upper approximation of B.

1	2	3
0.1	0.1	0.1
0.8	0.8	0.9
0.1	0.1	0.1
0.8	0.8	0.9

Clearly, and are IF interior ideals of U₁, so is an IF soft interior ideal of U₁.

Theorem 24. Let (σ, A) be a soft compatible relation from a semigroup U₁ to a semigroup U₂. If B is an IF interior ideal of U₁, then is an IF soft interior ideal of U₂.

Proof. It follows from Theorem 23.

For converse of above result, we show the following example.

Example 6. Consider the semigroups of Example 5.

And A = {e₁, e₂}. Define σ : A⟶P(U₁ × U₂) by

(34)

Then, (σ, A) is a soft compatible relation from U₁ to U₂.

(35)

Define B : U₁⟶[0, 1] (given in Table 28).

Table 28. Intuitionistic fuzzy set B.

	1	2	3
μ_B	0	0.1	0.1
γ_B	0.9	0.8	0.9

Then, B is not an IF interior ideal of U₁ because if we take x = 2, a = 3, y = 1, then μ_B(231)≱μ_B(3) and γ_B(231)≰γ_B(3). Upper approximation of B is given in Table 29.

Table 29. Upper approximation of B.

p	q	r
0.1	0.1	0.1
0.8	0.8	0.8
0.1	0.1	0.1
0.8	0.8	0.8

Clearly, and are IF interior ideals of U₂, so is an IF soft interior ideal of U₂.

Now for lower approximations of an IF interior ideal of a semigroup, we discuss some results.

Theorem 25. Suppose (σ, A) is a soft complete relation regarding aftersets from a semigroup U₁ to a semigroup U₂. If B is an IF interior ideal of U₂, then is an IF soft interior ideal of U₁.

Proof. Suppose that B is an IF interior ideal of U₂. Thus, B is an IF subsemigroup of U₂, so by Theorem 17, is an IF soft subsemigroup of U₁. Now for x, a, y ∈ U₁,

(36)

Similarly, for s, b, t ∈ U₁,

(37)

Hence, is an IF interior ideal of U₁ for all e ∈ A, so is an IF soft interior ideal of U₁.

From following example, we show the converse of above theorem which is not true.

Example 7. Consider the semigroups of Example 1.

Let A = {e₁, e₂}. Define σ : A⟶P(U₁ × U₂) by

(38)

Then, (σ, A) is a soft complete relation from U₁ to U₂ with respect to the aftersets.

(39)

(1)
Define B : U₂⟶0, 1] such that B = 〈μ_B, γ_B〉 (given in Table 30)

Table 30. Intuitionistic fuzzy set B.

	1	2	3	4
μ_B	0.4	0.6	0.8	1
γ_B	0.5	0.3	0.1	0

Then, B is not an IF interior ideal of U₂, because if we take x = 2, a = 3, y = 1, then μ_B(231)≱μ_B(3) and γ_B(231)≰γ_B(3). Lower approximation of B is given in Table 31.

Table 31. Lower approximation of B.

p	q	r	s
0.6	0.6	0.6	0.6
0.3	0.3	0.3	0.3
0.6	0.6	0.6	0.6
0.3	0.3	0.3	0.3

Clearly, and are IF interior ideals of U₁, so is an IF soft interior ideal of U₁.

Theorem 26. Suppose (σ, A) is a soft complete relation regarding foresets from a semigroup U₁ to a semigroup U₂. If B is an IF interior ideal of U₁, then is an IF soft interior ideal of U₂.

Proof. It follows from Theorem 25.

Example 8. Consider the semigroups of Example 1.

Define σ : A⟶P(U₁ × U₂) by

(40)

Then, (σ, A) is a soft complete relation from U₁ to U₂ with respect to the foresets.

(41)

Define B : U₁⟶[0, 1] (given in Table 32).

Table 32. Intuitionistic fuzzy set B.

	p	q	r	s
μ_B	0	0.3	0.5	0.7
γ_B	1	0.7	0.4	0.2

Then, B is not an IF interior ideal of U₁ because if we take x = q, a = r, y = p, then μ_B(qrp)≱μ_B(r) and γ_B(qrp)≰γ_B(r). Lower approximation of B is given in Table 33.

Table 33. Lower approximation of B.

1	2	3	4
0.7	0.7	0.7	0.7
0.2	0.2	0.2	0.2
0	0	0	0
1	1	1	1

Clearly, and are IF interior ideals of U₂, so is an IF soft interior ideal of U₂.

Now, we discuss properties for IF bi-ideals of a semigroup.

Theorem 27. Suppose (σ, A) is a soft compatible relation from a semigroup U₁ to a semigroup U₂. If B₁ is an IF bi-ideal of U₂ then is an IF soft bi-ideal of U₁.

Proof. Suppose that B₁ is an IF bi-ideal of U₂. Thus, B₁ is an IF subsemigroup of U₂, so by Theorem 15, is an IF soft subsemigroup of U₁. Now for x, a, y ∈ U₁,

(42)

Similarly, for x, a, y ∈ U₁,

(43)

Hence, is an IF bi-ideal of U₁ for all e ∈ A, so is an IF soft bi-ideal of U₁.

Theorem 28. Suppose (σ, A) is a soft compatible relation from a semigroup U₁ to a semigroup U₂. If B₁ is an IF bi-ideal of U₁, then is an IF soft bi-ideal of U₂.

Proof. It follows from Theorem 27.

Example 9. Consider the semigroups and soft relations of Example 2.

Define B₁ : U₁⟶[0, 1] (given in Table 34).

Table 34. Intuitionistic fuzzy set B₁.

	p	q	r	s	t
μ_B	1	0.5	0.7	0.9	0.2
γ_B	0	0.4	0.3	0.1	0.7

Then, B₁ is not an IF bi-ideal of U₁ because if we take x = p, w = s, y = p, then μ_B(psp)≱μ_B(p)∧μ_B(p) and γ_B(psp)≰γ_B(p)∨μ_B(p). Upper approximation of B₁ is given in Table 35.

Table 35. Upper approximation of B₁.

1	2	3	4	5
1	0.5	0.9	0.9	0.9
0	0.4	0.1	0.1	0.1
1	0.5	0.9	0.9	0.9
0	0.4	0.1	0.1	0.1

Clearly, and are IF bi-ideals of U₂, so is an IF soft bi-ideal of U₂.

Theorem 29. Let (σ, A) be a soft complete relation regarding aftersets from a semigroup U₁ to a semigroup U₂. If B₁ is an IF bi-ideal of U₂, then is an IF soft bi-ideal of U₁.

Proof. Suppose that B₁ is an IF bi-ideal of U₂. Thus, B₁ is an IF subsemigroup of U₂, so by Theorem 17, is an IF soft subsemigroup of U₁. Now for x, a, y ∈ U₁,

(44)

Similarly, for x, a, y ∈ U₁,

(45)

Hence, is an IF bi-ideal of U₁ for each e ∈ A, so is an IF soft bi-ideal of U₁.

Example 10. Taking the semigroups of Example 1.

Define σ : A⟶P(U₁ × U₂) by

(46)

Then, (σ, A) is a soft complete relation from U₁ to U₂ with respect to the aftersets.

(47)

Define B₁ : U₂⟶[0, 1] (given in Table 36).

Table 36. Intuitionistic fuzzy set B₁.

1	2	3	4
0.7	0.2	0.1	0.4
0.2	0.7	0.9	0.5

Then, B₁ is not an IF bi-ideal of U₂ because if we take x = 1, w = 4, y = 1, then and Lower approximation of B₁ is given in Table 37.

Table 37. Lower approximation of B₁.

p	q	r	s
0.1	0.1	0.1	0.1
0.9	0.9	0.9	0.9
0.2	0.2	0.2	0.2
0 : 7	0.7	0.7	0.7

Clearly, and are IF bi-ideals of U₁, so is an IF soft bi-ideal of U₁.

Theorem 30. Let (σ, A) be a soft complete relation with respect to the foresets from a semigroup U₁ to a semigroup U₂. If B₂ is an IF bi-ideal of U₁, then is an IF soft bi-ideal of U₂.

Proof. It follows from Theorem 29.

Example 11. Taking the semigroups of Example 1.

Define σ : A⟶P(U₁ × U₂) by

(48)

Then, (σ, A) is a soft complete relation from U₁ to U₂ with respect to the foresets.

(49)

Define B₂ : U₁⟶[0, 1] (given in Table 38).

Table 38. Intuitionistic fuzzy set B₂.

p	q	r	s
0.1	0.8	0.6	0.7
0.9	0.1	0.3	0.3

Then, B₂ is not an IF bi-ideal of U₁ because if we take x = q, w = r, y = q, then and Lower approximation of B₂ is given in Table 39.

Table 39. Lower approximation of B₂.

1	2	3	4
0.7	0.7	0.7	0.7
0.3	0.3	0.3	0.3
0.1	0.1	0.1	0.1
0.9	0.9	0.9	0.9

Clearly, and are IF bi-ideals of U₂, so is an IF soft bi-ideal of U₂.

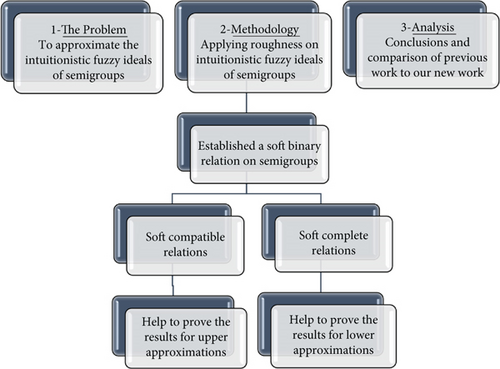
The flow chart of our proposed model is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Flow chart of proposed model.

4. Comparison with Previous Work

Our research work is a generalized form of rough approximation of an FS in semigroups based on soft relation which is discussed by Kanwal and Shabir in [50]. In this paper, we use an IFS in semigroups instead of only an FS. As we know, an IFS is better than an FS to control the vagueness and uncertainty in real-life problems. In FS theory, only membership function is discussed, but in IFS theory, functions of membership and nonmembership are also discussed. For example, if a person wants to buy a shirt with his choice, then he can buy his favourite shirt with specific design and colour by using this RIFS model. His preference will be calculated more effectively than Kanwal and Shabir’s technique [50] which is about an FS. Cagman and Engino [62] redefined the operations of SSs and proposed the products of SSs and uni-int decision function and their corresponding decision-making algorithm. Maji et al. [63] proposed a decision-making algorithm using SSs with RSs. In comparison with these two above methods, our proposed model is more reliable due to IFSs. Similarly, IFSs play an important role in medical field to detect intestinal bacteria such as Shigella and Salmonella which cause dysentery and typhoid, respectively. This is a challenging situation for microbiologists to diagnose these such deceases. Khatibi and Montazer (2009) presented value approach towards the bacteria classification problem to examine capabilities of FSs and IFSs in facing vagueness and uncertainty in the medical pattern recognition by using their five similarity measures. After comparing and illustrating the measures by experimental results, they obtained better detection rates of IFS Hausdorff and Mitchell similarity measures with valuable results 95.27% and 94.48% detection rate, respectively. On the other hand, the FS Euclidean distance yielded 85% detection rate only [64]. We can say that we make better decision by using RIFS model.

5. Conclusion

This paper has developed RIFS model in terms of soft binary relations. By using this approach, we obtain the upper approximation and lower approximation in the form of two pairs of IFSSs regarding aftersets and foresets. After applying these concepts, we discuss rough approximations of IF subsemigroups, IF left (right) ideals, IF interior ideals, and IF bi-ideals of semigroups. Earlier, rough approximation of an FS in semigroups based on soft binary relations has been discussed [50]. In an FS, only membership function is discussed, but in some critical situations of real world, we need nonmembership function to discuss uncertainty in good manner. Actually, the membership function alone is insufficient to deal vagueness. In such critical situations, an IFS is more useful set because its elements have membership function, nonmembership function, and the hesitation margin function. Since IFS has degree of membership, degree of nonmembership and hesitant degree with their sum of 1 but pythagorean FSs are more useful sets than IFSs because they cover more points that were not covered by IFSs. So Pythagorean FSs can describe the vagueness and impreciseness related to membership degree and nonmembership degree in a better way than IFSs.

5.1. Future Study

For future study, it is more considerable to make granulation roughness of an IFS and the roughness in interval valued set (IFS) under different several environments of soft binary relations. Study of this research work might be expanded to more outcomes in soft computing. For more research study, by taking on IF rough sets (IFRS), we can expand knowledge addition in IF information systems.

Conflicts of Interest

The authors declare that they have no conflict of interest.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha 61413, Saudi Arabia, for funding this work through research groups program under grant number R.G. P-2/98/43.

Open Research

Data Availability

We did not use any data for this research work.

References

1 Singh H. and Gupta M. M., Real-life applications of fuzzy logic, Advances in Fuzzy Systems. (2013) 2013, 3, 581879, https://doi.org/10.1155/2013/581879, 2-s2.0-84884258852.
10.1155/2013/581879
Google Scholar
2 Attanassov K. T., Intuitionistic fuzzy sets, Fuzzy Sets and Systems. (1986) 20, no. 1, 87–96, https://doi.org/10.1016/S0165-0114(86)80034-3, 2-s2.0-0002740725.
10.1016/S0165-0114(86)80034-3
Web of Science® Google Scholar
3 Kuroki N., On fuzzy ideals and fuzzy bi-ideals in semigroups, Fuzzy Sets and Systems. (1981) 5, no. 2, 203–215, https://doi.org/10.1016/0165-0114(81)90018-X, 2-s2.0-0011912417.
10.1016/0165-0114(81)90018-X
Web of Science® Google Scholar
4 Shabir M., Al-kenani A. N., Javed F., and Bashir S., An efficient approach to approximate fuzzy ideals of semirings using bipolar techniques, Mathematics. (2022) 10, no. 7, https://doi.org/10.3390/math10071009.
10.3390/math10071009
Web of Science® Google Scholar
5 Zhan J., Sun B., and Alcantud J. C. R., Covering based multigranulation (I, T)-fuzzy rough set models and applications in multi-attribute group decision-making, Information Sciences. (2019) 476, 290–318, https://doi.org/10.1016/j.ins.2018.10.016, 2-s2.0-85055212027.
10.1016/j.ins.2018.10.016
Web of Science® Google Scholar
6 Zhang L., Zhan J., and Xu Z. X., Covering-based generalized IF rough sets with applications to multi-attribute decision-making, Information Sciences. (2019) 478, 275–302, https://doi.org/10.1016/j.ins.2018.11.033, 2-s2.0-85056852367.
10.1016/j.ins.2018.11.033
Web of Science® Google Scholar
7 Pawlak Z., Rough sets, International Journal of Computer & Information Sciences. (1982) 11, no. 5, 341–356, https://doi.org/10.1007/BF01001956, 2-s2.0-27744565978.
10.1007/BF01001956
Google Scholar
8 Pawlak Z., Wong S. K. M., and Ziarko W., Rough sets: probabilistic versus deterministic approach, International Journal of Man-Machine Studies. (1988) 29, no. 1, 81–95, https://doi.org/10.1016/S0020-7373(88)80032-4, 2-s2.0-0024038052.
10.1016/S0020-7373(88)80032-4
Web of Science® Google Scholar
9 Ali M. I., Shabir M., and Tanveer S., Roughness in hemirings, Neural Computing and Applications. (2012) 21, no. S1, 171–180, https://doi.org/10.1007/s00521-011-0757-5, 2-s2.0-84865768084.
10.1007/s00521-011-0757-5
Web of Science® Google Scholar
10 Bonikowski Z., Bryniariski E., and Skardowska U. W., Extensions and intentions in the rough set theory, Information Sciences. (1998) 107, no. 1-4, 149–167, https://doi.org/10.1016/S0020-0255(97)10046-9, 2-s2.0-0032092163.
10.1016/S0020-0255(97)10046-9
Web of Science® Google Scholar
11 Bonikowski Z., A certain conception of the calculus of rough sets, Notre Dame Journal of Formal Logic. (1992) 33, no. 3, 412–421, https://doi.org/10.1305/ndjfl/1093634405, 2-s2.0-84972582671.
10.1305/ndjfl/1093634405
Google Scholar
12 Dubois D. and Prade H., Rough fuzzy sets and fuzzy rough sets, International Journal of General Systems. (1990) 17, no. 2-3, 191–209, https://doi.org/10.1080/03081079008935107, 2-s2.0-84963133436.
10.1080/03081079008935107
Web of Science® Google Scholar
13 Gehrke M. and Walker E., On the structure of rough sets, Bulletin of the Polish Academy of Sciences, Mathematics. (1992) 40, 235–245.
Google Scholar
14 Iwinski J., Algebraic approach to rough sets, Bulletin of the Polish Academy of Sciences, Mathematics. (1987) 35, 673–683.
Google Scholar
15 Jiawei H. and Jian P., In Data Mining, 2012, 3rd edition.
Google Scholar
16 Karavidic Z. and Projovic D., A multi-criteria decision-making (MCDM) model in the security forces operations based on rough sets, Decision Making Applications in Management and Engineering. (2018) 1, no. 1, 97–120, https://doi.org/10.31181/dmame180197k.
10.31181/dmame180197k
Google Scholar
17 Liu G. and Zhu W., The algebraic structures of generalized rough set theory, Information Sciences. (2008) 178, no. 21, 4105–4113, https://doi.org/10.1016/j.ins.2008.06.021, 2-s2.0-49849093407.
10.1016/j.ins.2008.06.021
Web of Science® Google Scholar
18 Mahmood T., Ali M. I., and Hussain A., Generalized roughness in fuzzy filters and fuzzy ideals with thresholds in ordered semigroups, Computational and Applied Mathematics. (2018) 37, 5013–5033, https://doi.org/10.1007/s40314-018-0615-5, 2-s2.0-85052400880.
10.1007/s40314-018-0615-5
Web of Science® Google Scholar
19 Pawlak Z. and Skowron A., Rough sets: some extensions, Information Sciences. (2007) 177, no. 1, 28–40, https://doi.org/10.1016/j.ins.2006.06.006, 2-s2.0-33749667344.
10.1016/j.ins.2006.06.006
Web of Science® Google Scholar
20 Shabir M. and Irshad S., Roughness in ordered semigroups, World Applied Sciences Journal. (2013) 22, 84–105.
Google Scholar
21 Molodtsov D., Soft set theory--First results, Computers & Mathematcs with Applications. (1999) 37, no. 4-5, 19–31, https://doi.org/10.1016/S0898-1221(99)00056-5.
10.1016/S0898-1221(99)00056-5
Web of Science® Google Scholar
22 Yuksel S., Dizman T., Yildizdan G., and Sert U., Application of soft sets to diagnose the prostate cancer risk, Journal of Inequalities and Applications. (2013) 2013, https://doi.org/10.1186/1029-242x-2013-229, 2-s2.0-84894582488.
10.1186/1029-242X-2013-229
Google Scholar
23 Aktas H. and Cagman N., Soft sets and soft groups, Information Sciences. (2007) 177, no. 13, 2726–2735, https://doi.org/10.1016/j.ins.2006.12.008, 2-s2.0-34147169878.
10.1016/j.ins.2006.12.008
Web of Science® Google Scholar
24 Jun Y. B., Soft BCK/BCI-algebras, Computers and Mathematics with Applications. (2008) 56, no. 5, 1408–1413, https://doi.org/10.1016/j.camwa.2008.02.035, 2-s2.0-46449100603.
10.1016/j.camwa.2008.02.035
Web of Science® Google Scholar
25 Jun Y. B., Lee K. J., and Kang M. S., Ideal theory in BCK/BCI-algebras based on soft sets and -structures, Discrete Dynamics in Nature and Society. (2012) 2012, 13, https://doi.org/10.1155/2012/910450, 2-s2.0-84861063935.
10.1155/2012/910450
Web of Science® Google Scholar
26 Maji P. K., Biswas R., and Roy A. R., Intuitionistic fuzzy soft sets, Journal of Fuzzy Mathematics. (2001) 9, no. 3, 677–692.
Google Scholar
27 Razak S. A. and Mohamad D., A decision making method using fuzzy soft sets, Malaysian Journal of Fundamental and Applied Sciences. (2014) 9, no. 2, 99–104.
Google Scholar
28 Mahmoood T., Shabir M., Ayub S., and Bashir S., Regular and intra-regular semihyper groups in terms of L-fuzzy softhyperideals, Journal of Applied Environmental and Biological Sciences. (2017) 7, no. 11, 115–137.
Google Scholar
29 Al-shami T. M., An improvement of rough sets' accuracy measure using containment neighborhoods with a medical application, Information Sciences. (2021) 569, 110–124, https://doi.org/10.1016/j.ins.2021.04.016.
10.1016/j.ins.2021.04.016
Web of Science® Google Scholar
30 Al-shami T. M., Hariwan Z., Ibrahim A., Azzam A., and Ahmad I., SR-fuzzy sets and their weighted aggregated operators in application to decision-making, Journal of Function Spaces. (2022) 2022, 14, 3653225, https://doi.org/10.1155/2022/3653225.
10.1155/2022/3653225
Web of Science® Google Scholar
31 Hariwan Z., Al-shami T. M., and Albarbary O. G., (3, 2)-Fuzzy sets and their applications to topology and optimal choices, Computational Intelligence and Neuroscience. (2021) 2021, 14, 1272266, https://doi.org/10.1155/2021/1272266.
10.1155/2021/1272266
PubMed Web of Science® Google Scholar
32 Bashir S., Fatima M., and Shabir M., Regular ordered ternary semigroups in terms of bipolar fuzzy ideals, Mathematics. (2019) 7, https://doi.org/10.3390/math7030233, 2-s2.0-85062947056.
10.3390/math7030233
Web of Science® Google Scholar
33 Bhunia S., Ghorai G., Kutbi M. A., Gulzar M., and Alam M. A., On the algebraic characteristics of fuzzy sub e-groups, Journal of Function Spaces. (2021) 2021, 7, 5253346, https://doi.org/10.1155/2021/5253346.
10.1155/2021/5253346
Web of Science® Google Scholar
34 Gulzar M., Abbas G., and Dilawar F., Algebraic properties of w-Q-fuzzy subgroups, International Journal of Mathematics and Computer Science. (2020) 15, 265–274.
Web of Science® Google Scholar
35 Gulzar M., Dilawar F., Alghazzawi D., and Mateen M. H., A note on complex fuzzy subfield, Indonesian Journal of Electrical Engineering and Computer Science. (2021) 21, no. 2, 1048–1056, https://doi.org/10.11591/ijeecs.v21.i2.pp1048-1056.
10.11591/ijeecs.v21.i2.pp1048-1056
Google Scholar
36 Gulzar M., Mateen M. H., Alghazzawi D., and Kausar N., A novel applications of complex intuitionistic fuzzy sets in group theory, IEEE Access. (2020) 8, 196075–196085, https://doi.org/10.1109/ACCESS.2020.3034626.
10.1109/ACCESS.2020.3034626
Web of Science® Google Scholar
37 Anwar M. Z., Bashir S., and Shabir M., An efficient model for the approximation of intuitionistic fuzzy sets in terms of soft relations with applications in decision making, Mathematical Problems in Engeerings. (2021) 2021, article 6238481, 19, https://doi.org/10.1155/2021/6238481.
10.1155/2021/6238481
Web of Science® Google Scholar
38 Anwar M. Z., Al-kenani A. N., Bashir S., and Shabir M., Pessimistic multigranulation rough set of intuitionistic fuzzy sets based on soft relations, Mathematics. (2022) 10, no. 5, https://doi.org/10.3390/math10050685.
10.3390/math10050685
Web of Science® Google Scholar
39 Anwar M. Z., Bashir S., Shabir M., and Alharbi M. G., Multigranulation roughness of intuitionistic fuzzy sets by soft relations and their applications in decision making, Mathematics. (2021) 9, no. 20, article 2587, https://doi.org/10.3390/math9202587.
10.3390/math9202587
Web of Science® Google Scholar
40 Skowron A. and Stepaniuk J., Tolerance approximation spaces, Fundamenta Informaticae. (1996) 27, no. 2,3, 245–253, https://doi.org/10.3233/FI-1996-272311.
10.3233/FI-1996-272311
Google Scholar
41 Li Z., Xie N., and Wen G., Soft coverings and their parameter reductions, Applied Soft Computing. (2015) 31, 48–60, https://doi.org/10.1016/j.asoc.2015.02.027, 2-s2.0-84924976130.
10.1016/j.asoc.2015.02.027
CAS Web of Science® Google Scholar
42 Ali M. I., A note on soft sets, rough soft sets and fuzzy soft sets, Applied Soft Computing. (2011) 11, no. 4, 3329–3332, https://doi.org/10.1016/j.asoc.2011.01.003, 2-s2.0-79954598734.
10.1016/j.asoc.2011.01.003
Web of Science® Google Scholar
43 Bashir S., Abbas H., Mazhar R., and Shabir M., Rough fuzzy ternary subsemigroups based on fuzzy ideals with three-dimensional congruence relation, Computational and Applied Mathematics. (2020) 39, no. 2, article 90, https://doi.org/10.1007/s40314-020-1079-y.
10.1007/s40314-020-1079-y
Web of Science® Google Scholar
44 Kanwal R. S. and Shabir M., An approach to approximate a fuzzy set by soft binary relation and corresponding decision making, 2019.
Google Scholar
45 Kanwal R. S. and Shabir M., Approximation of soft ideals by soft relations in semigroups, Journal of Intelligent & Fuzzy Systems. (2019) 7977–7989, https://doi.org/10.3233/jifs-190328.
10.3233/JIFS-190328
Web of Science® Google Scholar
46 Kazanci O. and Yamak S., Generalized fuzzy bi-ideals of semigroups, Soft Computing. (2008) 12, no. 11, 1119–1124, https://doi.org/10.1007/s00500-008-0280-5, 2-s2.0-45849153060.
10.1007/s00500-008-0280-5
Web of Science® Google Scholar
47 Shabir M., Ayub S., and Bashir S., Prime and semiprime L-fuzzy soft bi-hyperideals ideals, Journal of Hyperstructures. (2017) 6, no. 2, 109–119.
Google Scholar
48 Shabir M., Ayub S., and Bashir S., Applications of L-fuzzy soft sets in semihypergroups, Journal of Advanced Mathematical Studies. (2017) 10, no. 3, 367–385.
Google Scholar
49 Shabir M., Kanwal R. S., and Ali M. I., Reduction of an information system, Soft Computing. (2020) 24, no. 14, 10801–10813, https://doi.org/10.1007/s00500-019-04582-3.
10.1007/s00500-019-04582-3
Web of Science® Google Scholar
50 Kanwal R. S. and Shabir M., Rough approximation of a fuzzy set in semigroups based on soft relations, Computational and Applied Mathematics. (2019) 38, no. 2, https://doi.org/10.1007/s40314-019-0851-3, 2-s2.0-85064565699.
10.1007/s40314-019-0851-3
Web of Science® Google Scholar
51 Reddy P. S. and Dawud M., Applications of semigroups, Global Journey of Science Frontier Research (F). (2015) XV, no. III, Version 1.
Google Scholar
52 Bashir S., Mazhar R., Abbas H., and Shabir M., Regular ternary semirings in terms of bipolar fuzzy ideals, Computational and Applied Mathematics. (2020) 39, no. 4, https://doi.org/10.1007/s40314-020-01319-z.
10.1007/s40314-020-01319-z
Web of Science® Google Scholar
53 Brown R., Topology and groupoids, 2006, Booksurge LLC.
Google Scholar
54 Howie J. M., London Mathematical Society Monographs New Series, Fundamentals of semigroup theory, 1995, Clanderon Press.
Google Scholar
55 Xu Y., Sun Y., and Li D., Intuitionistic fuzzy soft set, 2nd International Workshop on Intelligent Systems and Applications, 2010, Wuhan China.
Google Scholar
56 Hur K., Jang S. Y., and Lim P. K., Intuitionistic fuzzy semigroups, International Journal of Fuzzy Logic and Intellegent Systems. (2008) 8, no. 3, 207–219, https://doi.org/10.5391/IJFIS.2008.8.3.207.
10.5391/IJFIS.2008.8.3.207
Google Scholar
57 Kim K. H. and Jun Y. B., Intuitionistic fuzzy interior ideals of semigroups, International Journal of Mathematics and Mathematical Sciences.(2001) 27, no. 5, 261–267, https://doi.org/10.1155/S0161171201010778.
10.1155/S0161171201010778
Google Scholar
58 Sumathi R. and Sathappan K. E., On intuitionistic L-fuzzy bi-ideals of semigroups, Journal of Discrete Mathematical Sciences and Cryptography. (2019) 22, no. 5, 801–807, https://doi.org/10.1080/09720529.2019.1685233.
10.1080/09720529.2019.1685233
Web of Science® Google Scholar
59 Zhau J., Li Y., and Yin Y., Intuitionistic fuzzy soft semigroups, Mathematica Aeterna. (2011) 1, no. 3, 173–183.
Google Scholar
60 Babitha K. V. and Sunil J. J., Soft set relations and functions, Computers and Mathematics with Applications. (2010) 60, no. 7, 1840–1849, https://doi.org/10.1016/j.camwa.2010.07.014, 2-s2.0-77956394869.
10.1016/j.camwa.2010.07.014
Web of Science® Google Scholar
61 Feng F., Ali M. I., and Shabbir M., Soft relations applied to semigroups, Filomat. (2013) 27, no. 7, 1183–1196, https://doi.org/10.2298/fil1307183f, 2-s2.0-84888126471.
10.2298/FIL1307183F
Web of Science® Google Scholar
62 Cagman N. and Engino S., Soft set theory and uni-int decision making, European Journal of Operational Research. (2010) 207, no. 2, 848–855, https://doi.org/10.1016/j.ejor.2010.05.004, 2-s2.0-77955559824.
10.1016/j.ejor.2010.05.004
Web of Science® Google Scholar
63 Maji P. K., Roy A. R., and Biswas R., An application of soft sets in a decision making problem, Computers and Mathematics with Applications. (2002) 44, no. 8-9, 1077–1083, https://doi.org/10.1016/S0898-1221(02)00216-X, 2-s2.0-0036772771.
10.1016/S0898-1221(02)00216-X
Web of Science® Google Scholar
64 Khatibi V. and Montazer G. A., Intuitionistic fuzzy set vs. fuzzy set application in medical pattern recognition, Artificial Intelligence in Medicine. (2009) 47, no. 1, 43–52, https://doi.org/10.1016/j.artmed.2009.03.002, 2-s2.0-68249107322, 19375899.
10.1016/j.artmed.2009.03.002
PubMed Web of Science® Google Scholar

Citing Literature

All articles

[Retracted] Approximations of Intuitionistic Fuzzy Ideals over Dual Spaces by Soft Binary Relations

Retraction(s) for this article

Retracted: Approximations of Intuitionistic Fuzzy Ideals over Dual Spaces by Soft Binary Relations

Abstract

1. Introduction

1.1. Related Works

1.2. Innovative Contribution

1.3. Motivation

1.4. Organization of the Paper

2. Preliminaries and Basic Concepts

3. Approximations of IF Ideals in Semigroups by Soft Binary Relation

4. Comparison with Previous Work

5. Conclusion

5.1. Future Study

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley