Volume 2022, Issue 1 3791662

Research Article

Open Access

A New Model for Microbial Desalination Cells: Model Formulation and Validation under Different Operating Conditions

Merna Hesham

orcid.org/0000-0001-6693-6088

Irrigation and Hydraulics Engineering Dept., Faculty of Engineering, Cairo University, El-Gamaa St., 12613 Giza, Egypt cu.edu.eg

Search for more papers by this author

Abdelsalam Elawwad,

Corresponding Author

Abdelsalam Elawwad

[email protected]

orcid.org/0000-0002-9202-870X

Environmental Engineering Dept., Faculty of Engineering, Cairo University, El-Gamaa St., 12613 Giza, Egypt cu.edu.eg

Search for more papers by this author

Ahmed Abd El Meguid,

Ahmed Abd El Meguid

orcid.org/0000-0002-9875-9132

Sanitary and Environmental Engineering Institute, Housing and Building National Research Center, 87 Tahir St., 11511 Dokki, Giza, Egypt

Search for more papers by this author

Mohamed Hamdy Nour,

Mohamed Hamdy Nour

orcid.org/0000-0001-6237-6853

Irrigation and Hydraulics Engineering Dept., Faculty of Engineering, Cairo University, El-Gamaa St., 12613 Giza, Egypt cu.edu.eg

Search for more papers by this author

Merna Hesham,

Merna Hesham

orcid.org/0000-0001-6693-6088

Irrigation and Hydraulics Engineering Dept., Faculty of Engineering, Cairo University, El-Gamaa St., 12613 Giza, Egypt cu.edu.eg

Search for more papers by this author

Abdelsalam Elawwad,

Corresponding Author

Abdelsalam Elawwad

[email protected]

orcid.org/0000-0002-9202-870X

Environmental Engineering Dept., Faculty of Engineering, Cairo University, El-Gamaa St., 12613 Giza, Egypt cu.edu.eg

Search for more papers by this author

Ahmed Abd El Meguid,

Ahmed Abd El Meguid

orcid.org/0000-0002-9875-9132

Sanitary and Environmental Engineering Institute, Housing and Building National Research Center, 87 Tahir St., 11511 Dokki, Giza, Egypt

Search for more papers by this author

Mohamed Hamdy Nour,

Mohamed Hamdy Nour

orcid.org/0000-0001-6237-6853

Irrigation and Hydraulics Engineering Dept., Faculty of Engineering, Cairo University, El-Gamaa St., 12613 Giza, Egypt cu.edu.eg

Search for more papers by this author

First published: 26 April 2022

https://doi.org/10.1155/2022/3791662

Citations: 2

Academic Editor: Zhang-Hui Lu

Share a link

Email
Wechat
Bluesky

Abstract

In this paper, a dynamic mathematical model was developed to simulate the processes in Microbial Desalination Cells (MDCs) operated in cyclic batch flow mode using ordinary differential equations found in the literature. In contrast to previous models, the proposed model was developed for fed-batch operations and considers the effects of temperature and substrate inhibition using simple equations for quick simulation. Local sensitivity analysis was performed to determine the parameters with the least impact on current, COD, and salt removal, which were then eliminated from the simplified model. These parameters were found to be the decay rates of anodophilic and methanogenic microorganisms (k_d,aand k_d,m) and the internal resistance parameters (R_anolyte and R_membrane). In addition, the best-performing parameters based on the sensitivity analysis results were selected for reestimation for model fitting. The reestimated parameters were mediator yield (Y), membrane salt transfer coefficient (d), maximum substrate utilization rate by methanogenic microorganisms (μ_s, _m, _max), and maximum anodophilic growth rate (μ_a, _max). The predictions of the model were consistent with both our previous experimental data and experimental studies found in the literature and can be easily used by experimentalists for the rapid simulation and prediction of an MDC’s performance under different operating conditions.

1. Introduction

In the present day, energy and water security are global challenges that have increased in importance due to increasing populations, rising energy demands, and water shortages. In addition, the growth of the economy and rapid urbanization around the world has led to high energy and water demands [1] According to the United Nations, 2.7 billion people will have difficulties accessing safe drinking water by 2025, and approximately 20% of countries will face serious water shortage problems [2]. Recently, water reclamation and desalination have become alternative sources of water to support the increasing demand for fresh water; however, traditional wastewater treatment and desalination technologies consume large amounts of energy. Conventional wastewater treatment systems, which are mainly based on activated sludge processes, are energy-intensive processes due to the high energy requirements of aeration. Although, energy recovery can be achieved using anaerobic wastewater treatment such as UASB [3]; however, it is a complicated process and required many steps such as gas treatment and fails at low temperatures and at low strength wastewater conditions. Regarding desalination, the most commercially used processes require large amounts of energy; for example, reverse osmosis requires 3–7 Kwh/m3 of energy [4]. Conventional desalination technologies are also a source of greenhouse gas emissions as they are mostly powered by fossil fuel sources [5]. Microbial desalination cells (MDCs) are one of the bioelectrochemical systems that desalinate salty water using current generated from the oxidation of organic matter, allowing it to achieve three primary goals: energy production, wastewater treatment, and desalination [6]. It is reported that an MDC can produce 1.8 kWh of bioenergy while desalinating 1 m³ of salty water with a desalination efficiency of more than 90% [7].

An MDC’s performance is controlled by operational, design, and biological parameters; hence, any large-scale applications require a strong understanding of the relationships between these various parameters to achieve optimal performance. MDC modeling is thus essential for studying this complicated system, which is affected by physical, chemical, biological, and electrochemical factors that are dynamically linked; doing so helps to optimize and scale up MDC operations [8]. Despite its relative importance, there are only a few MDC papers about modeling in the literature; the majority of these studies have been experimental. The Scopus database indicates that less than 178 articles have been published on MDCs as of 2020, and only a few of those were about MDC modeling [5].

One of the first well-established models was developed for continuous flow by Ping et al. [4]; this model was expanded by the same research group to include brackish water desalination [9]. These models aimed for a better prediction of the variations in salinity and the concentration of individual ions [9]. Both models [4, 9] were formulated based on ordinary differential equations (ODEs), which include mass balances for the substrate, microorganisms, mediators, and salt, as well as taking time into account; however, it does not consider spatial dimensions. In addition, the Monod model was used for microbial growth kinetics in both models; however, the first model assumed that salt removal occurred due to diffusion and potential gradients [4], while the improved model considered the dilution effect due to osmotic flow as an additional reason for salt removal [9]. In addition, the improved model incorporated current efficiency, restricted diffusion, and junction potential [9], leading to a more complex model. The first model was more appropriate for generating comprehensive predictions of the MDC’s three functions. Ping et al.’s models were expanded to study boron removal in different BEs [10] in a combined FO-MDC system [11] and to model predictive control [12–14].

This study was aimed at presenting a simple mathematical model that describes the important processes that occur in MDCs. The proposed model can help experimentalists rapidly predict the overall performance of the MDC, allowing them to optimize the system while carrying out experiments. The main difference between the proposed model and other previous models is that it was developed to predict the performance of fed-batch modes (cyclic batch flow). It also considers the effects of temperature and substrate inhibition, allowing the model to predict the performance of the MDC under different operating conditions. As the main goal of this paper was to propose a simplified model, the number of parameters was reduced via sensitivity analysis, eliminating the least effective parameters. The model was also validated using experimental data and the results of sensitivity analysis were used to determine the best-performing parameters that would be reestimated during model calibration and validation. The model was used to evaluate the effects of important operating parameters (external resistance, temperature, and salt and substrate concentrations) on key performance indicators of MDCs. The model predictions were subsequently compared with trends observed in experimental results.

2. Materials and Methods

2.1. Model Assumptions and Development

The main assumptions of the model are as follows:

(i)
the MDC is operated in fed-batch mode
(ii)
the substrate in the anode chamber is homogenized, and microorganisms are uniformly distributed across the anode biofilm
(iii)
the presence of anodophilic microorganisms, which are responsible for the release of electrons, as well as methanogenic microorganisms, which compete with anodophilic microorganisms for the substrate but do not contribute to current production
(iv)
microbial growth kinetics as described using the Haldane model
(v)
the intracellular electron transfer mediator is assumed to be constant
(vi)
the pH is constant
(vii)
salt removal in the middle chamber is due to both potential and the salt concentration gradient

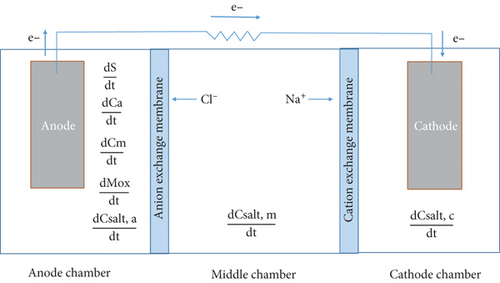
The structure of the model was developed using mass balance equations for the concentration of the substrate, microorganisms, and oxidized mediators in the anode chamber and salt concentrations in all chambers. The model was implemented in MATLAB using ode15s for solving stiff differential equations and DAEs. The equations that define the model are described in the following subsections. A conceptual schematic of an MDC is shown in Figure 1.

Details are in the caption following the image — Open in figure viewer PowerPoint

2.2. Mass Balance of the Substrate

The variation of substrate concentration in the anode chamber due to its consumption by anodophilic and methanogenic microorganisms is described as follows [15]:

(1)

where t is the time (d); S is the concentration of the substrate (mg∙L^-1); C_a and C_m are the concentrations for anodophilic and methanogenic microorganisms, respectively (mg∙L^-1); μ_s,a and μ_s,m are the substrate consumption rate by anodophilic and methanogenic microorganisms, respectively (mg∙mg^-1∙d^-1).

2.3. Mass Balances for Microorganisms

The rate of change of the concentration of microorganisms due to the consumption of substrate is described as follows [15]:

(2)

(3)

where μ_a and μ_m are the growth rate of anodophilic and methanogenic microorganisms, respectively (d^-1); and k_d,a and k_d,m are the decay rate of anodophilic and methanogenic microorganisms, respectively.

2.4. Mass Balance of the Mediator

The concentration of the intracellular total mediator is constant and is equal to the sum of its oxidized and reduced forms. The variation in concentration of the oxidized mediator is described as follows [4, 15, 16]:

(4)

(5)

where M_red and M_total are the fraction of the reduced and total mediator concentrations per anodophilic microorganisms, respectively (mg·mg⁻¹); Y is the mediator yield (mg.mg^-1); I_MDC is the current produced by MDC (A); F is the Faraday constant (A∙s∙ mole^-1); γ is the molar mass of the mediator (mg∙mol_med^-1); and ne is the number of electrons transferred per mole of the mediator (mol∙mol^-1).

2.5. Microbial Kinetics Equations

The microbial kinetics equations are presented in Equations (6)–(9). The consumption of the substrate and the microbial growth rate were described using the Haldane model [17]. The consumption rate of the substrate by anodophilic microorganisms and the corresponding microbial growth rate are a function of the concentration of the substrate and oxidized mediator, while the consumption rate of the substrate by methanogenic microorganisms and the corresponding microbial growth rate are a function of substrate concentration only. Since biochemical reactions are similar to chemical reactions and occur more rapidly at higher temperatures, a modified Arrhenius equation was used in the microbial kinetics equations as it is widely used to evaluate the effect of temperature on microbial growth and the substrate consumption rate [18].

(6)

(7)

(8)

(9)

where μ_a,max and

are the maximum growth rate of anodophilic and methanogenic microorganisms, respectively (d⁻¹); μ_s,a,max and μ_s,m,max are the maximum substrate utilization rate by anodophilic and methanogenic microorganisms, respectively (mg∙mg^-1∙d⁻¹); K_a and K_m are the half-saturation constants for anodophilic and methanogenic microorganisms, respectively (mg∙L^-1); K_M is the half-saturation constant for mediators (mg∙L^-1); k_i,m and k_i,a are the inhibition constants for anodophilic and methanogenic microorganisms, respectively (mg∙L^-1); T₁ and T₂ are the initial and final temperature in Celsius; and θ is the temperature coefficient.

2.6. Mass Balance for Salt Concentrations

Quantification of the concentration of salt in all chambers is described as follows [4]:

(10)

(11)

(12)

where C_salt,m, C_salt,a, and C_salt,c are the concentrations of salts in the salt, anode, and cathode chambers, respectively (mol∙L^-1); d is the salt transfer coefficient of the membrane (day⁻¹); and V_salt is the volume of the salt chamber (L).

2.7. Electrochemical Equations

The current in the MDC was determined by Ohm’s law as follows [4, 9]:

(13)

(14)

(15)

(16)

(17)

where V_oc is the open-circuit voltage (V); E_min and E_max are the minimum and maximum observed open-circuit voltages, respectively, (V); R_min and R_max are the minimum and maximum observed internal resistances, respectively, (Ω); k_r is a constant that determines the extent to which a change in the concentration of anodophilic microorganisms affects the internal resistance (L·mg^-1); R is the ideal gas constant (J∙K^-1∙mole^-1); R_salt is the resistance of salt solution (Ω); R_membrane is the mass transfer resistance through an exchange membrane; R_anolyte is the resistance of anolyte solution; R_ext is the external resistance; a_ion,a, a_ion,c, and a_ion,m are the ionic activity in the anode, cathode, and middle chambers, respectively, which can be assumed to be from the total dissolved salts; Z_ion is the ionic charge; and t_AEM and t_CEM are the transport numbers of ionic species in AEM and CEM, respectively.

2.8. Sensitivity Analysis

A sensitivity analysis for the model parameters was conducted to eliminate any ineffectual parameters and reestimate the best-performing parameters for model fitting. A local sensitivity analysis [19] was used to calculate the ratio between the model outputs (changes in substrate concentration in the anode chamber, saltwater in the middle chamber, and current) to the changes in each of the individual parameters. The following equation was used to determine the sensitivity of parameters on the model:

(18)

where T_j is the dependent time sensitivity for any parameter j, P is the output value, x_j is the value of parameter j, and δx_j is the change in x_j (δx_j = 0.01x_j).

Based on the results of the sensitivity analysis, the best-performing parameters were reestimated using experimental data. The values of the other parameters were chosen based on a literature review. To determine the values of parameters to be reestimated during model fitting and validation, a criterion was used that minimized the error between the model predictions and the experimental results for COD removal efficiency, maximum current, desalination efficiency, and the Coulombic efficiency.

2.9. Analysis and Calculations

Equations (19)–(22) were used to evaluate the performance of the MDC:

(19)

(20)

(21)

(22)

In addition, the Coulombic efficiency is an important metric that indicates the extent of electron recovery from the substrate. It is defined as the ratio between the total number of electrons recovered at the anode chamber and the maximum theoretical number of electrons that can be recovered assuming that all the consumed substrate was completely oxidized to current [20]. The equation that expresses this value is as follows:

(23)

where M is the molecular weight of oxygen (32 g∙mol^-1), b is the number of electrons exchanged per mole of oxygen (4 electrons), v is the volume of the anode chamber, and ∆COD is the change in the concentration of substrate over cycle time.

3. Results and Discussion

3.1. Model Reduction

Model reduction is an important step that simplifies the equations in a model, reducing computation time. Based on the results of the sensitivity analysis, the parameters that had the smallest effect on the performance of the MDC (in terms of current, COD, and salt removal) were k_d,a, k_d,m, R_anolyte, and R_membrane. The decay rate of anodophilic and methanogenic microorganisms represents 0.02 of their maximum growth rate [17]. Previously reported values of the anolyte and membrane resistance were low [4] and they were not considered in the calculations of resistances in some other models [15, 16]. The internal resistance already takes into account the resistance of the membrane and anolyte [21]; specifically, the maximum and minimum internal resistance values were already based on the sum of internal resistances, including anolyte and membrane resistances. Therefore, k_d,a, k_d,m, R_anolyte, and R_membrane were eliminated from the equations by assuming their values were equal to zero for the purposes of model simplification. The equations obtained after this model reduction step are as follows:

(24)

(25)

(26)

(27)

(28)

(29)

(30)

3.2. Effect of External Resistance

External resistance is an important parameter that affects the amount of current produced and the competition between electrogenic and nonelectrogenic microorganisms [22]. Experimental literature data for cyclic batch flow MDCs from our previously published work [23], which was operated under a range of external resistances, were used to validate the MDC model developed in this study and evaluate its predictions across a range of external resistances. The model was fit at an external resistance of 10 Ω and then validated at the following external resistances: 100 Ω -500 Ω -5000 Ω -10000 Ω. The concentrations of the substrate (sodium acetate) and salt (NaCl) were 500 mg/l and 10 g/L during the three-day cycle, respectively. Any parameters that had been judged to be important based on sensitivity analysis, but could not be quantified from the experiments, were reestimated. The rest of the parameters were estimated based on values from the literature as shown in Table 1. Based on the sensitivity analysis, the reestimated parameters, which has the largest effect on MDC performance, were mediator yield (Y), membrane salt transfer coefficient (d), maximum substrate utilization rate by methanogenic microorganisms, and maximum anodophilic growth rate.

1. Model parameters values based on previous work.

Parameter	Value	Dimensions	Ref.
Y	23	[mg-M.- mg-S^-1]	Estimated
d	0.024	[d^-1]	Estimated
μ_a,max	0.3	[d^-1]	Estimated
μ_s,m,max	11.3	[mg-S-mg-x^-1 d^-1]	Estimated
μ_m,max	0.1	[d^-1]	[4]
μ_s,a,max	5.32	[mg-S -mg-x^-1 d^-1]	[4]
K_a	20	[mg-S L^-1]	[4]
K_m	80	[mg-S L^-1]	[4]
K_M	0.2^∗M_tot	[mg-M mg-x^-1]	[16]
K_i	3748	[mg-S L^-1]	[27]
θ	1.07	Unitless	[28]
R	8.314472	[J K^{-1 M}ol^-1]	Physical constant
T	300	[K]	Physical constant
ne	2	[mol-e-mol-mediator^-1]	[16]
F	96485	[As mole^-1]	Physical constant
M_to_t	0.05	[mg-M mg-x^-1]	[16]
K_r	0.082	[L mg-x^-1]	[4]
γ	663,400	[mg-M mol_med^-1]	[16]

The model results (Figure 2) were consistent with the experimental results across all external resistances except for COD removal efficiency. The experimental observations followed a nonlinear trend as the COD removal efficiency was semiconstant between 10 and 100 Ω, increased to a maximum at 500 Ω, and then decreased between 500 and 10000 Ω. The low COD removal efficiencies at high external resistances were attributed to the consumption of energy during the production of extracellular polymeric substances (EPS). In addition, the Coulombic efficiency followed a nonlinear trend between 10 and 500 Ω; this may be due to factors related to the operating conditions and uncontrolled interactions within the cell.

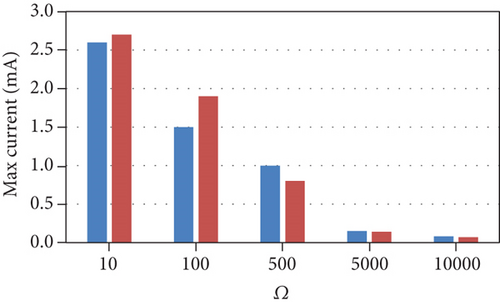
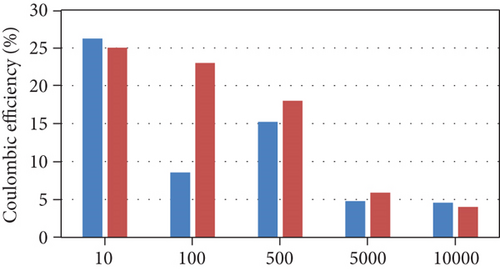
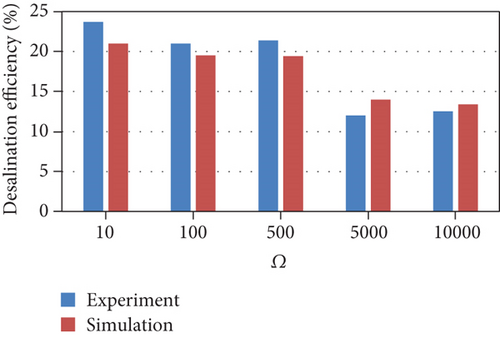
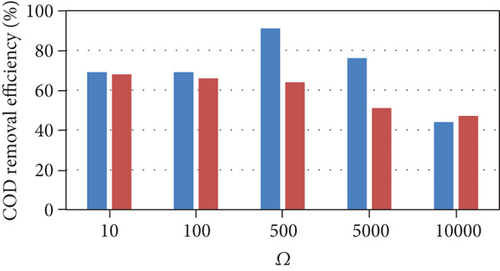
The current model indicates that an increase in external resistance causes a decrease in the current produced; consequently, the desalination rate decreases. The COD removal rate also decreases because the growth rate and substrate consumption rate of anodophilic microorganisms are a function of the concentration of the oxidized form of the mediator, which decreases as current decreases. As a result, the substrate becomes more readily available for methanogenic microorganisms, leading to a decrease in the Coulombic efficiency. This indicates that lower resistances are better for anodophilic microbial growth.

The model trends are consistent with many other experimental results. Lower external resistances lead to the generation of higher current due to high electron transfer to the cathode and high electrogenic activity [24, 25]. As the current produced from the oxidation of organic matter is the main driving force for the desalination process, lower resistances increase the speed of the desalination process [23, 24]. In addition, many experimental studies reported that COD removal efficiency decreases with increasing external resistance [25, 26]. Pinto et al. [16] reported that at higher external resistances, the methane production increases. A high external resistance also lowers the potential of the anode, allowing fermentative and anaerobic microorganisms to become dominant; conversely, lower external resistances are more favorable for electrogenic microorganisms, resulting in a decrease in the Coulombic efficiency as external resistances increase [26].

3.3. Effect of Temperature

Experimental literature data of cyclic batch flow MDCs from our previous published work [29] were also used to validate the proposed MDC model. The MDCs were operated under different temperatures (12, 27, and 45°C). The model was fitted at a temperature of 12°C; the model was subsequently validated at a temperature of 27°C, while substrate (sodium acetate) and salt (NaCl) concentrations were 1000 mg/l and 20 g/L over a two-day cycle, respectively. The reestimated parameters were mediator yield (Y), membrane salt transfer coefficient (d), maximum substrate utilization rate by methanogenic microorganisms, and maximum anodophilic growth rate; these were estimated to be 8 mg∙mg^-1, 0.018 d^-1, 11.3 mg∙mg^-1∙d^-1, and 0.3 d^-1, respectively. The results of model fitting and validation are shown in Table 2.

2. Model calibration at different temperatures.

	COD Removal Eff. %	Desalination Eff. %	Max current mA	Coulombic Eff. %
Temperature 12 Celsius
Experiment	46 ± 10	9.4 ± 4.3	0.08 ± 0.04	1.04 ± 0.56
Simulation	38	6.3	0.11	1.91
Temperature 27 Celsius
Experiment	86 ± 5.7	9.7 ± 1.35	2.1 ± 0.55	10.22 ± 3.14
Simulation	89	10.9	2.1	9.65

The experimental and model results show that COD removal, Coulombic efficiency, salt removal, and current increase as temperature increases from 12 to 27°C. However, at 45°C, the experimental results exhibit a nonlinear trend as the maximum current density, COD removal, and Coulombic efficiency decrease; in contrast, the salt removal increases. These results were not consistent with the linear trend of the model, which used a modified Arrhenius equation, so it can be used until the optimum temperature.

Several experimental studies have evaluated the effect of temperature on bioelectrochemical systems to determine the optimal operating temperature. Feng et al. [30] observed a linear increase in the performance of fed-batch MFCs in terms of COD removal efficiency, voltage and power output, and Coulombic efficiency % as temperatures were increased from 15 to 30°C. Behera et al. [31] found that batch MFC achieved maximum COD removal efficiency, Coulombic efficiency, and power density at 40°C when operated across a range of temperatures between 20 and 55°C. Moon et al. [32] found that the performance of MFCs improved between 24 and 35°C and then decreased between 38 and 41°C. Gadkari et al. [8] observed that the MFCs achieved the maximum power density at 34°C when operated at temperatures ranging between 20 and 40°C. Li et al. [33] reported that fed-batch MFCs reached their maximum power density and COD removal efficiency at 37°C, and their maximum Coulombic efficiency at 43°C when operated within a temperature range of 10 to 55°C. Based on the results of the aforementioned experimental studies, and considering that the modified Arrhenius equation exhibits errors of around 15% at 40°C and 25% at 50°C [34], the model calibration indicates the model can be used within a temperature range of 12 to 35°C.

3.4. Effect of the Initial Concentration of the Substrate

The current model suggests that at low substrate concentrations, the rate of substrate consumption and growth rate of microorganisms increases when the substrate concentration increases until they reach a maximum rate, following which they decrease due to the inhibition effect. In addition, the current increases due to an increase in the concentration of anodophilic microorganisms, which favors the migration of ions in the salt chamber. There is also an inverse relationship between the initial substrate concentration and Coulombic efficiency because the high availability of substrate causes an increase in the competition between the microorganisms. This affects not only the production of current by anodophilic microorganisms but also its consumption by methanogenic microorganisms. These trends are consistent with previous experimental results [35, 36]. However, at high substrate concentrations, the growth rate of microorganisms and the substrate consumption rate decrease, negatively affecting the performance of the MDC; this has been reported in several publications [23, 37]. The model’s predictions of MDC performance as a function of different initial substrate concentrations are shown in Figure 3.

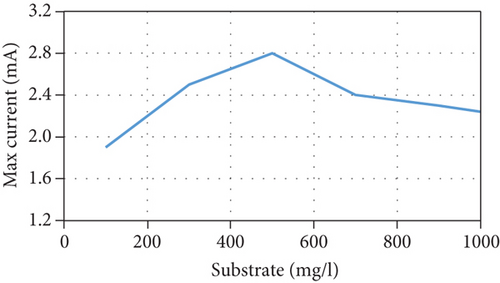
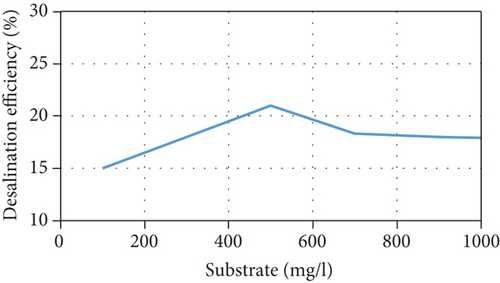
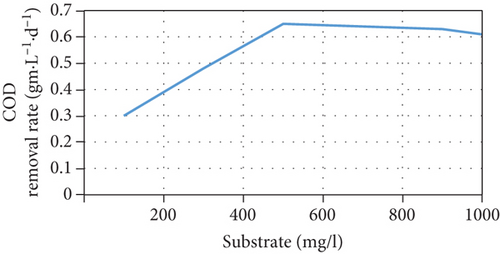
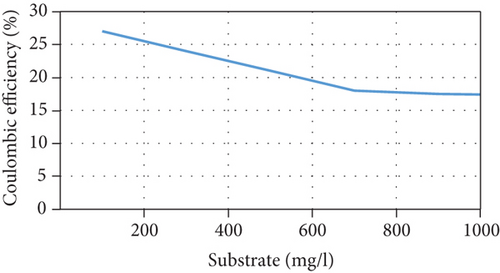
3.5. Effect of the Initial Salt Concentration

The current model indicates that an increase of initial salt concentrations results in the steepening of the concentration gradient between chambers, improving the desalination rate. In addition, the current increases due to the increase in junction potential, consequently increasing the removal of salts and the Coulombic efficiency, as well as a slight increase of COD removal efficiency. The model’s predictions are consistent with experimental results [38, 39]. The model’s predictions of the performance of the MDC as a function of different initial salt concentrations are shown in Figure 4.

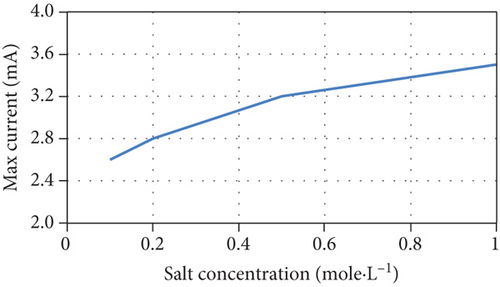
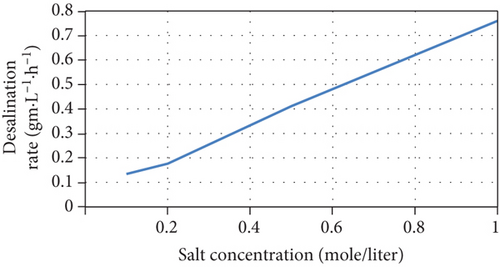
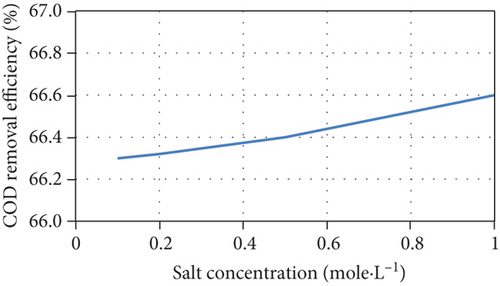
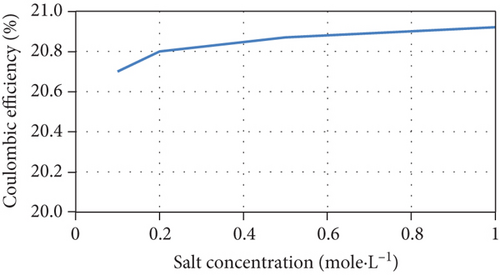
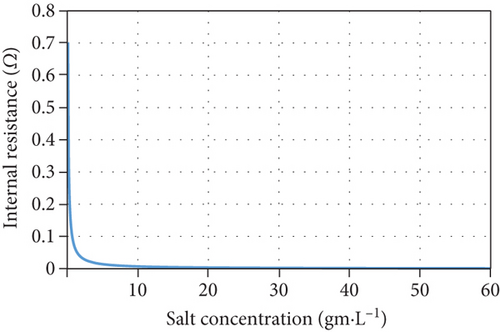
However, it was reported that another reason for the increase in salt removal and current production is the increase in electrical conductivity and the corresponding decrease in internal resistance when salt concentrations increase [40]. Although the model considers salt resistance to be a function of salt concentration, Equation (16) cannot be used for all MDC configurations and middle chamber volumes as it underestimates the effect of salt concentration on internal resistance as shown in Figure 5 when compared with other experimental data in literature [41, 42].

To improve the accuracy of the model predictions when varying the initial salt concentration in an MDC, the salt resistance equation should be in a general form such that coefficients can be calibrated for different configurations and chamber volume ratios as follows:

(31)

4. Conclusion

This work represents an attempt to understand the complicated system of MDCs through the use of a simple yet comprehensive mathematical model. The model was used to predict the performance of MDCs under different operating parameters; the outputs of the model were evaluated and compared with experimental results. The predictions of the final MDC model were found to be mostly consistent with the results of experimental studies; this suggests that the model can evaluate the performance of MDCs under different operating conditions. The proposed model can be used by experimentalists to rapidly predict the performance of MDCs in terms of current, COD, and salt removal and can be used to understand the processes involved in MDC before performing detailed numerical studies. While the model predictions were consistent with the experimental results under most different operating conditions, there were still some trends that differed between the two. These could be due to factors related to the design and configuration of the MDC, or due to complex interactions within the MDC that require further experimental and numerical studies to fully understand. Future studies should be focused on improving the accuracy of the proposed model. The equations that describe the effects of temperature should be modified such that their range can be extended to predict the performance of the MDC at temperatures greater than the optimum. A study on the effects of pH on the MDC is also recommended, as this is a parameter that can affect microbial activity, which consequently affects the current production and desalination rate. In addition, cathode reactions and their effect on the performance of MDC should be considered. Also, the effect of fouling of exchange membranes on the performance of MDC should be considered for better model predictions in the long run.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

All the data used to support the findings of this study are included within the article.

References

1 Alhimali H., Jafary T., Al-Mamun A., Baawain M. S., and Vakili-Nezhaad G. R., New insights into the application of microbial desalination cells for desalination and bioelectricity generation, Biofuel Research Journal. (2019) 6, no. 4, 1090–1099, https://doi.org/10.18331/BRJ2019.6.4.5.
10.18331/BRJ2019.6.4.5
Web of Science® Google Scholar
2 Yang E., Chae K. J., Choi M. J., He Z., and Kim I. S., Critical review of bioelectrochemical systems integrated with membrane-based technologies for desalination, energy self-sufficiency, and high-efficiency water and wastewater treatment, Desalination. (2019) 452, 40–67, https://doi.org/10.1016/j.desal.2018.11.007, 2-s2.0-85056625525.
10.1016/j.desal.2018.11.007
CAS Web of Science® Google Scholar
3 Elawwad A. and Hazem M., Minimization of sludge production in an integrated UASB–continuous flow sequencing batch reactor system, Desalination and Water Treatment. (2017) 91, 206–213, https://doi.org/10.5004/dwt.2017.20643, 2-s2.0-85037050979.
10.5004/dwt.2017.20643
CAS Web of Science® Google Scholar
4 Ping Q., Zhang C., Chen X., Zhang B., Huang Z., and He Z., Mathematical model of dynamic behavior of microbial desalination cells for simultaneous wastewater treatment and water desalination, Environmental Science and Technology.(2014) 48, no. 21, 13010–13019, https://doi.org/10.1021/es504089x, 2-s2.0-84908582600, 25316438.
10.1021/es504089x
CAS PubMed Web of Science® Google Scholar
5 Rahman S., Jafary T., Al-Mamun A., Baawain M. S., Choudhury M. R., Alhaimali H., Siddiqi S. A., Dhar B. R., Sana A., Lam S. S., Aghbashlo M., and Tabatabaei M., Towards upscaling microbial desalination cell technology: a comprehensive review on current challenges and future prospects, Journal of Cleaner Production. (2021) 288, article 125597, https://doi.org/10.1016/j.jclepro.2020.125597.
10.1016/j.jclepro.2020.125597
Web of Science® Google Scholar
6 Elawwad A., Husein D. Z., Ragab M., and Hamdy A., Enhancing the performance of microbial desalination cells using δMnO₂/graphene nanocomposite as a cathode catalyst, Journal of Water Reuse and Desalination. (2020) 10, no. 3, 214–226, https://doi.org/10.2166/wrd.2020.011.
10.2166/wrd.2020.011
CAS Web of Science® Google Scholar
7 Jacobson K. S., Drew D. M., and He Z., Use of a liter-scale microbial desalination cell as a platform to study bioelectrochemical desalination with salt solution or artificial seawater, Environmental Science and Technology. (2011) 45, no. 10, 4652–4657, https://doi.org/10.1021/es200127p, 2-s2.0-79956041957.
10.1021/es200127p
CAS PubMed Web of Science® Google Scholar
8 Gadkari S., Gu S., and Sadhukhan J., Towards automated design of bioelectrochemical systems: a comprehensive review of mathematical models, Chemical Engineering Journal. (2018) 343, 303–316, https://doi.org/10.1016/j.cej.2018.03.005, 2-s2.0-85043231660.
10.1016/j.cej.2018.03.005
CAS Web of Science® Google Scholar
9 Ping Q., Huang Z., Dosoretz C., and He Z., Integrated experimental investigation and mathematical modeling of brackish water desalination and wastewater treatment in microbial desalination cells, Water Research. (2015) 77, 13–23, https://doi.org/10.1016/j.watres.2015.03.008, 2-s2.0-84964252266, 25839832.
10.1016/j.watres.2015.03.008
CAS PubMed Web of Science® Google Scholar
10 Ping Q., Abu-reesh I. M., and He Z., Boron removal from saline water by a microbial desalination cell integrated with donnan dialysis, Desalination. (2015) 376, 55–61, https://doi.org/10.1016/j.desal.2015.08.019, 2-s2.0-84940486978.
10.1016/j.desal.2015.08.019
CAS Web of Science® Google Scholar
11 Yuan H., Abu-Reesh I. M., and He Z., Mathematical modeling assisted investigation of forward osmosis as pretreatment for microbial desalination cells to achieve continuous water desalination and wastewater treatment, Journal of Membrane Science. (2016) 502, 116–123, https://doi.org/10.1016/j.memsci.2015.12.026, 2-s2.0-84952802081.
10.1016/j.memsci.2015.12.026
CAS Web of Science® Google Scholar
12 Wang J. and Wang Q., Intelligent explicit model predictive control based on machine learning for microbial desalination cells, Proceedings of the Institution of Mechanical Engineers. Part I: Journal of Systems and Control Engineering. (2019) 233, no. 7, 751–763, https://doi.org/10.1177/0959651818816845, 2-s2.0-85060526755.
10.1177/0959651818816845
Web of Science® Google Scholar
13 Wang J. and Wang Q., Output-tracking explicit nonlinear model predictive control for microbial desalination cells, 2018 5th International Conference on Control, Decision and Information Technologies (CoDIT), 2018, Thessaloniki, Greece, 929–934, https://doi.org/10.1109/CoDIT.2018.8394948, 2-s2.0-85050241651.
10.1109/CoDIT.2018.8394948
Google Scholar
14 Shi Y. and Wang J., Generalized predictive control for microbial desalination cells, 2017 Chinese Automation Congress (CAC), 2017, Jinan, China, 5839–5844, https://doi.org/10.1109/CAC.2017.8243827, 2-s2.0-85050375262.
10.1109/CAC.2017.8243827
Google Scholar
15 Gadkari S., Shemfe M., and Sadhukhan J., Microbial fuel cells: a fast converging dynamic model for assessing system performance based on bioanode kinetics, International Journal of Hydrogen Energy. (2019) 44, no. 29, 15377–15386, https://doi.org/10.1016/j.ijhydene.2019.04.065, 2-s2.0-85064664330.
10.1016/j.ijhydene.2019.04.065
CAS Web of Science® Google Scholar
16 Pinto R. P., Srinivasan B., Manuel M. F., and Tartakovsky B., A two-population bio-electrochemical model of a microbial fuel cell, Bioresource Technology. (2010) 101, no. 14, 5256–5265, https://doi.org/10.1016/j.biortech.2010.01.122, 2-s2.0-77950341486.
10.1016/j.biortech.2010.01.122
CAS PubMed Web of Science® Google Scholar
17 Andrews J. F., A mathematical model for the continuous culture of microorganisms utilizing inhibitory substrates, Biotechnology and Bioengineering. (1968) 10, no. 6, 707–723, https://doi.org/10.1002/bit.260100602, 2-s2.0-84984082223.
10.1002/bit.260100602
CAS Web of Science® Google Scholar
18 Grady C. P. L., Daigger G. T., and Lim H. C., Biological wastewater treatment, 1999, Marcel Dekker, New York.
Google Scholar
19 Zeng Y., Choo Y. F., Kim B. H., and Wu P., Modelling and simulation of two-chamber microbial fuel cell, Journal of Power Sources. (2010) 195, no. 1, 79–89, https://doi.org/10.1016/j.jpowsour.2009.06.101, 2-s2.0-69549088017.
10.1016/j.jpowsour.2009.06.101
CAS Web of Science® Google Scholar
20 Logan B. E., Hamelers B., Rozendal R., Schröder U., Keller J., Freguia S., Aelterman P., Verstraete W., and Rabaey K., Microbial fuel cells: methodology and technology, Environmental Science and Technology. (2006) 40, no. 17, 5181–5192, https://doi.org/10.1021/es0605016, 2-s2.0-33748566549.
10.1021/es0605016
CAS PubMed Web of Science® Google Scholar
21 Fan Y., Sharbrough E., and Liu H., Quantification of the internal resistance distribution of microbial fuel cells, Environmental Science and Technology. (2008) 42, no. 21, 8101–8107, https://doi.org/10.1021/es801229j, 2-s2.0-55349136222, 19031909.
10.1021/es801229j
CAS PubMed Web of Science® Google Scholar
22 Kloch M. and Toczylowska-Maminska R., Toward optimization of wood industry wastewater treatment in microbial fuel cells-mixed wastewaters approach, Energies (Basel). (2020) 13, no. 1, https://doi.org/10.3390/en13010263.
10.3390/en13010263
Web of Science® Google Scholar
23 Ragab M., Elawwad A., and Abdel-Halim H., Simultaneous power generation and pollutant removals using microbial desalination cell at variable operation modes, Renewable Energy. (2019) 143, 939–949, https://doi.org/10.1016/J.RENENE.2019.05.068, 2-s2.0-85066428674.
10.1016/j.renene.2019.05.068
CAS Web of Science® Google Scholar
24 Sevda S. and Abu-Reesh I. M., Energy production in microbial desalination cells and its effects on desalinatio, Journal of Energy and Environmental Sustainability. (2017) 3, 71–76, https://doi.org/10.47469/jees.2017.v03.100035.
10.47469/JEES.2017.v03.100035
Google Scholar
25 Jang J. K., Pham T. H., Chang I. S., Kang K. H., Moon H., Cho K. S., and Kim B. H., Construction and operation of a novel mediator- and membrane-less microbial fuel cell, Process Biochemistry. (2004) 39, no. 8, 1007–1012, https://doi.org/10.1016/S0032-9592(03)00203-6, 2-s2.0-1942489157.
10.1016/S0032-9592(03)00203-6
CAS Web of Science® Google Scholar
26 González Del Campo A., Cañizares P., Lobato J., Rodrigo M., and Fernandez Morales F. J., Effects of external resistance on microbial fuel cell’s performance Environment, energy and climate change II, 2016, 34, springer, 175–197, https://doi.org/10.1007/698-2014-290, 2-s2.0-84944145198.
Google Scholar
27 Wu H. H., Feng Y., Li H., Wang H., and Wang J., Co-metabolism kinetics and electrogenesis change during cyanide degradation in a microbial fuel cell, RSC advances. (2018) 8, no. 70, 40407–40416, https://doi.org/10.1039/c8ra08775j, 2-s2.0-85058243804.
10.1039/C8RA08775J
CAS PubMed Web of Science® Google Scholar
28 Myszograj S., Reaction rate coefficient k20 and temperature coefficient Θ in organic waste thermal disintegration, ITM Web of Conferences. (2018) 23, https://doi.org/10.1051/itmconf/20182300026.
10.1051/itmconf/20182300026
Google Scholar
29 Ragab M., Elawwad A., and Abdel-Halim H., Evaluating the performance of microbial desalination cells subjected to different operating temperatures, Desalination. (2019) 462, 56–66, https://doi.org/10.1016/j.desal.2019.04.008, 2-s2.0-85064071079.
10.1016/j.desal.2019.04.008
CAS Web of Science® Google Scholar
30 Feng Y., Lee H., Wang X., and Liu Y., Electricity generation in microbial fuel cells at different temperature and isolation of electrogenic bacteria, 2009 Asia-Pacific Power and Energy Engineering Conference, 2009, Wuhan, China, 1–5, https://doi.org/10.1109/APPEEC.2009.4918327, 2-s2.0-84869985170.
10.1109/APPEEC.2009.4918327
Google Scholar
31 Behera M., Murthy S. S. R., and Ghangrekar M. M., Effect of operating temperature on performance of microbial fuel cell, Water Science and Technology. (2011) 64, no. 4, 917–922, https://doi.org/10.2166/wst.2011.704, 2-s2.0-80052055384, 22097080.
10.2166/wst.2011.704
CAS PubMed Web of Science® Google Scholar
32 Moon H., Chang I. S., and Kim B. H., Continuous electricity production from artificial wastewater using a mediator- less microbial fuel cell, Bioresource Technology. (2006) 97, no. 4, 621–627, https://doi.org/10.1016/j.biortech.2005.03.027, 2-s2.0-28844483665, 15939588.
10.1016/j.biortech.2005.03.027
CAS PubMed Web of Science® Google Scholar
33 Li L. H., Sun Y. M., Yuan Z. H., Kong X. Y., and Li Y., Effect of temperature change on power generation of microbial fuel cell, Environmental Technology (United Kingdom). (2013) 34, no. 13-14, 1929–1934, https://doi.org/10.1080/09593330.2013.828101, 2-s2.0-84886039973, 24350446.
10.1080/09593330.2013.828101
CAS PubMed Google Scholar
34 Sheridan C., Petersen J., and Rohwer J., Technical note On modifying the Arrhenius equation to compensate for temperature changes for reactions within biological systems, Water SA. (2012) 38, no. 1, 149–151, https://doi.org/10.4314/wsa.v38i1.18.
10.4314/wsa.v38i1.18
CAS Web of Science® Google Scholar
35 Ullah Z. and Zeshan S., Effect of substrate type and concentration on the performance of a double chamber microbial fuel cell, Water Science and Technology. (2020) 81, no. 7, 1336–1344, https://doi.org/10.2166/wst.2019.387, 32616686.
10.2166/wst.2019.387
PubMed Web of Science® Google Scholar
36 Feng Y., Wang X., Logan B. E., and Lee H., Brewery wastewater treatment using air-cathode microbial fuel cells, Applied Microbiology and Biotechnology. (2008) 78, no. 5, 873–880, https://doi.org/10.1007/s00253-008-1360-2, 2-s2.0-41049085567, 18246346.
10.1007/s00253-008-1360-2
CAS PubMed Web of Science® Google Scholar
37 Ghoreyshi A. A., Jafary T., Najafpour G. D., and Haghparast F., Effect of type and concentration of substrate on power generation in a dual chambered microbial fuel cell, 57, Proceedings of the World Renewable Energy Congress–Sweden, 2011, Linköping, Sweden, 1174–1181, https://doi.org/10.3384/ecp110571174.
10.3384/ecp110571174
Google Scholar
38 Ebrahimi A., Yousefi Kebria D., and Darzi G. N., Improving bioelectricity generation and COD removal of sewage sludge in microbial desalination cell, Environmental Technology (United Kingdom). (2018) 39, no. 9, 1188–1197, https://doi.org/10.1080/09593330.2017.1323958, 2-s2.0-85019076838, 28443368.
10.1080/09593330.2017.1323958
CAS PubMed Google Scholar
39 Habibi A., Abbaspour M., Javid A. H., and Hassani A. H., An investigation on using MDCs for an efficient desalination process as pretreatment of reverse osmosis, Journal of Water Supply: Research and Technology-Aqua. (2020) 69, no. 4, 322–331, https://doi.org/10.2166/AQUA.2020.073.
10.2166/aqua.2020.073
Web of Science® Google Scholar
40 Ashwaniy V. R. V. and Perumalsamy M., Microbial desalination cell: an integrated technology for desalination, wastewater treatment and renewable energy generation, materials research foundations Microbial Fuel Cells: Materials and Applications, 2019, Materials Research Forum LLC, https://doi.org/10.21741/9781644900116-9.
Google Scholar
41 Khazraee Zamanpour M., Kariminia H. R., and Vosoughi M., Electricity generation, desalination and microalgae cultivation in a biocathode-microbial desalination cell, Chemical Engineering. (2017) 5, no. 1, 843–848, https://doi.org/10.1016/j.jece.2016.12.045, 2-s2.0-85009085058.
10.1016/j.jece.2016.12.045
CAS Web of Science® Google Scholar
42 Wen Q. X., Yang H., Chen Z. Q., and Zhang H. C., Microbial desalination cell combined with capacitive deionization/membrane capacitive deionization to desalinate seawater, Advanced Materials Research. (2013) 807-809, 373–379, https://doi.org/10.4028/WWW.SCIENTIFIC.NET/AMR.807-809.373, 2-s2.0-84886813560.
10.4028/www.scientific.net/AMR.807-809.373
CAS Google Scholar

Citing Literature

All articles

A New Model for Microbial Desalination Cells: Model Formulation and Validation under Different Operating Conditions

Abstract

1. Introduction