Volume 2022, Issue 1 3621403

Research Article

Open Access

[Retracted] Computation of Vertex Degree-Based Molecular Descriptors of Hydrocarbon Structure

Retraction(s) for this article

Zeeshan Saleem Mufti,

Zeeshan Saleem Mufti

orcid.org/0000-0002-6765-6595

Department of Mathematics and Statistics, The University of Lahore, Lahore Campus, Pakistan uol.edu.pk

Search for more papers by this author

Rukhshanda Anjum,

Rukhshanda Anjum

orcid.org/0000-0001-8736-0006

Department of Mathematics and Statistics, The University of Lahore, Lahore Campus, Pakistan uol.edu.pk

Search for more papers by this author

Ayesha Abbas,

Ayesha Abbas

Department of Mathematics and Statistics, The University of Lahore, Lahore Campus, Pakistan uol.edu.pk

Search for more papers by this author

Shahbaz Ali,

Shahbaz Ali

orcid.org/0000-0002-5998-0053

Department of Mathematics, Khawaja Fareed University of Engineering and Information Technology, Rahim Yar Khan 64200, Pakistan

Search for more papers by this author

Muhammad Afzal,

Muhammad Afzal

Department of Mathematics, Division of Science and Technology, University of Education, Lahore, Pakistan ue.edu.pk

Search for more papers by this author

Ashraful Alam,

Corresponding Author

Ashraful Alam

[email protected]

orcid.org/0000-0001-9152-2573

Department of Mathematics, Jahangirnagar University, Savar, Dhaka, Bangladesh juniv.edu

Search for more papers by this author

Zeeshan Saleem Mufti,

Zeeshan Saleem Mufti

orcid.org/0000-0002-6765-6595

Department of Mathematics and Statistics, The University of Lahore, Lahore Campus, Pakistan uol.edu.pk

Search for more papers by this author

Rukhshanda Anjum,

Rukhshanda Anjum

orcid.org/0000-0001-8736-0006

Department of Mathematics and Statistics, The University of Lahore, Lahore Campus, Pakistan uol.edu.pk

Search for more papers by this author

Ayesha Abbas,

Ayesha Abbas

Department of Mathematics and Statistics, The University of Lahore, Lahore Campus, Pakistan uol.edu.pk

Search for more papers by this author

Shahbaz Ali,

Shahbaz Ali

orcid.org/0000-0002-5998-0053

Department of Mathematics, Khawaja Fareed University of Engineering and Information Technology, Rahim Yar Khan 64200, Pakistan

Search for more papers by this author

Muhammad Afzal,

Muhammad Afzal

Department of Mathematics, Division of Science and Technology, University of Education, Lahore, Pakistan ue.edu.pk

Search for more papers by this author

Ashraful Alam,

Corresponding Author

Ashraful Alam

[email protected]

orcid.org/0000-0001-9152-2573

Department of Mathematics, Jahangirnagar University, Savar, Dhaka, Bangladesh juniv.edu

Search for more papers by this author

First published: 05 January 2022

https://doi.org/10.1155/2022/3621403

Citations: 2

Academic Editor: Shaohui Wang

Share a link

Email
Wechat
Bluesky

Abstract

Topological indices are such numbers or set of numbers that describe topology of structures. Nearly 400 topological indices are calculated so far. The prognostication of physical, chemical, and biological attributes of organic compounds is an important and still unsolved problem of computational chemistry. Topological index is the tool to predict the physicochemical properties such as boiling point, melting point, density, viscosity, and polarity of organic compounds. In this study, some degree-based molecular descriptors of hydrocarbon structure are calculated.

1. Introduction

The invention of graph theory in 18^th century was a biggest game changer in the field of mathematics by a Swiss Mathematician Leonard Euler (1702–1782). He used graphs to tackle the famous problem of Konigsberg bridge [1, 2]. In this study, is a simple undirected graph containing a set of vertices and an edges set [3]. The number of lines connected to a vertex is called a degree of a vertex and is denoted by Deg_u.

Topological indices investigate the features of graphs that persist constant after continual changing in graph. They describe symmetry of chemical structures with a number and then work for the improvement of QSAR and QSPR which both are employed to build a connection among the molecular structure and mathematical tools. These indices are useful to associate physiochemical properties of compounds (such as entropy, boiling and melting point, flammability, and many more).

Topological indices are invariants of structures, so they are independent of pictorial representation [4]. Among three categories of molecular descriptors, vertex degree-based indices are considerably significant. Medicine industries are producing new and advanced medicines which are effective for mankind and ecology. Graph theory and molecular descriptors are playing a significant role in analysing the physiochemical properties of organic compounds.

Hydrocarbon structure is an aromatic hydrocarbon and a unique structure composed of benzene through covalent bond. There are six sigma and six pi bonds in each benzene ring present in this compound. It is a nonpolar structure, and each benzene has a bond angle of 120°. It can be used in making of plastic, nylon, and dyes. It cannot be dissolved in water but in organic solvents. It has a sharp melting point because of the presence of benzene but does not have high boiling point. The structure is flammable and also show resonance.

1.1. Derivation of Degree-Based Topological Indices

1.1.1. First General Zagreb Index

The 1st general Zagreb index was introduced by Li and Zhao and is given as [5]

(1)

Classes of Zagreb Indices. We have two Zagreb groups of indices, first Zagreb index and second Zagreb index denoted by M₁ and M₂ [6–8]. They are proposed in late seventies by Gutman and Tranjistic.

1.1.2. First Zagreb Index

The first Zagreb index can be written as [9, 10]

(2)

1.1.3. Second Zagreb Index

The mathematical form is [9]

(3)

Multiple and Polynomial Zagreb Indices. In 2012, advanced forms of Zagreb descriptors were suggested, with names 1st and 2nd multiple Zagreb descriptors given as PM₁(G^∗) and PM₂(G^∗) [8]. The polynomials are helpful to calculate Zageb index. 1st and 2nd Zagreb polynomial descriptors are denoted as M₁(G^∗, j) and M₂(G^∗, j).

1.1.4. First and Second Multiple Zagreb Indices

The 1st and 2nd multiple Zagreb indices are

(4)

(5)

1.1.5. First and Second Polynomial Zagreb Indices

The 1st and 2nd polynomial Zagreb indices are

(6)

(7)

1.1.6. Modified Zagreb Index

The modified form of Zagreb index was put forward in 2013 by G. H Shirdil, H. Rezapour, and A.M.Sayadi.

(8)

1.1.7. Second Modified Zagreb Index

The 2^nd modified Zagreb index is

(9)

1.1.8. Reduced 2nd Zagreb Index

It was written by Furtula, and its formula is

(10)

1.1.9. Atom Bond Connectivity Index

Ernesto Estrada and Torres defined the abovementioned index [8, 11]. It is helpful in modeling thermodynamic properties of hydrocarbons.

(11)

1.1.10. Atom Bond Connectivity Index of 4th Order

Ghorbani and Ghazi suggested this index [7].

(12)

1.1.11. General Randić Connectivity Index

Millan Randić introduced molecular descriptors for the first time based on degree of vertices. Initially, it was coined as branching index [10] and familiar to find the branching of hydrocarbons. In 1998, Eddrös and Bollobás suggested the general form of this index by switching the factor (−1/2) with αεIR [12].

(13)

1.1.12. Randić Index

We may call this index as first-degree-based topological index [8].

(14)

1.1.13. Reciprocal Randić Index (RRI)

Favaron, Mahéo, and Saclé invented a new index RRI [13].

(15)

1.1.14. RRR Index

It is equivalent of RR index [13]. It can be written as

(16)

1.1.15. GA Index

Vukicevic̀ and Furtula proposed the GA index [4, 7, 8].

(17)

1.1.16. GA₅ Index

Grovac et al. suggested the GA₅ index in 2011.

(18)

1.1.17. Forgotten Index

Gutman and Futula suggested an index [14]. It is represented by F(G^∗).

(19)

1.1.18. General Sum Connectivity Index

Zhou and Trinajstić proposed new index [8, 15]. It is defined as

(20)

where αεIR.

1.1.19. SD Index

In 2010, D.vukicevic and Furtula proposed this useful index denoted by SD (G) [17–21].

(21)

1.1.20. Harmonic Index

Siemion Fajtlowicz prepared a computer program that is helpful in automatic generation of conjectures [8] and also suggested a degree-based element; then, Zhang unwrapped this element and named harmonic index [22–25].

(22)

2. Topological Indices of Hydrocarbon Structure

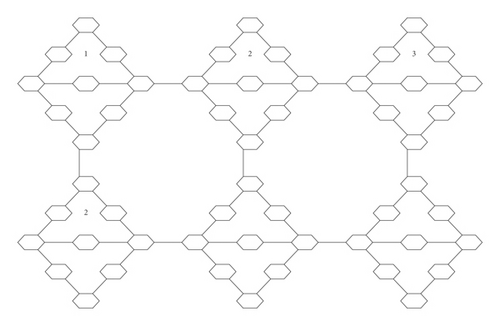
In this study, numbers of molecular descriptors of the hydrocarbon structure are computed (Figure 1).

Details are in the caption following the image — Open in figure viewer PowerPoint

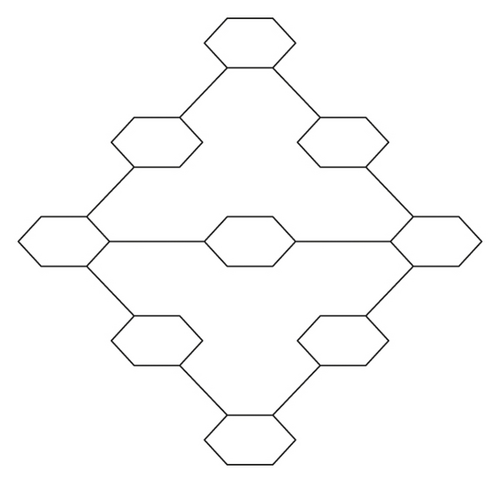
2.1. Description of Graph of Hydrocarbon Structure

Chemical properties of graph shown in Figure 2 are given (Tables 1–4).

1. Chemical properties of graph G^∗.

Chemical formula	C₅₄H₃₄
Exact mass	682.27
Molecular weight	682.85
Elemental analysis	C, 94.98; H, 5.02

2. Partition of graph G^∗ on the basis of degrees.

Degree of vertex	Number of vertices
2	30pq + 2p + 2q
3	24pq − 2p − 2q
Sum	66pq − q − p

3. Edge partition of graph G^∗ with respect to starting and ending vertices of each edge.

(Deg_p, Deg_q) where p, q εE (G)	Number of vertices
(2,2)	112pq + 4p + 4q
(2,3)	36pq − 4p − 4q
(3,3)	18pq − p − q
Sum	66pq − p − q

4. Edge grouping of a graph G^∗ of hydrocarbon structure with accordance of degree summation of adjoining end vertices of every edges.

Degree of vertices	Number of vertices
(4, 4)	2p
(4, 5)	4p + 4q
(5, 5)	12pq − 2p
(5, 7)	22pq − 2p
(5, 8)	2pq + 2p + 4q
(6, 7)	6pq − 2p − 4q
(6, 8)	6pq − 2p − 4q
(7, 7)	2pq − p − q
(7, 8)	8pq
(7, 9)	2pq
(8, 8)	2pq
(8, 9)	4pq
Sum	66pq − p − q

Our concerned graph is shown in Figure 2, and it is denoted by G^∗.

Theorem 1. G^∗ is a graph of hydrocarbon structure, and its first general Zagreb index is given as follows:

(23)

Proof. Consider graph G^∗, i.e., shown in Figure 2. G^∗ has 54pq points in which 30pq + 2p + 2q of degree 2 vertices and 24pq − 2p − 2q of degree 3.

By applying the definition of M_α(G^∗) (1),

(24)

we have the required results:

(25)

Theorem 2. First Zagreb index of graph G^∗ is given as follows:

(26)

Proof. of G^∗ is divided into 3 groups.

holds 12pq + 4p + 4q arcs pq, here Deg_p = Deg_q = 2
has 36pq − 4p − 4q arcs pq, here Deg_p = 2, Deg_q = 3
contains 18pq − q − p arcs pq, here Deg_p = 3, Deg_q = 3
Consider

From equation (6), we get

(27)

Theorem 3. First and second polynomial and multiple Zagreb indices of (hydrocarbon structure) G^∗ are given as follows:

(1)
PM₁(G^∗) = 4^{12 pq+4 p+4 q} × 5^{36 pq−4 p−4 q} × 6^{18 pq− q− p};
(2)
PM₂(G^∗) = 4^{12 pq+4 p+4 q} × 6^{36 pq−4 p−4 q} × 9^{18 pq− q− p};
(3)
M₁(G^∗, j) = (12pq + 4p + 4q)j⁴ + (36pq − 4p − 4q)j⁵ + (18pq − p − q)j⁶;
(4)
M₂(G^∗, j) = (12pq + 4p + 4q)j⁴ + (36pq − 4p − 4q)j⁶ + (18pq − p − q)j⁹;

Proof. is grouped in 3 edge partitions depending on end vertices degrees. contains 12pq + 4p + 4q edges, where Deg_p = Deg_q = 2. has 36pq − 4p − 4q edges pq, where Deg_p = 2 and Deg_q = 3. has 18pq − p − q lines pq, where Deg_p = 3 and Deg_q = 3. Consider , , and .

By utilizing the definition of PM₁(G^∗),

(28)

Now,

(29)

By utilizing M₁(G^∗, j) from (6),

(30)

From equation (7), we have

(31)

This completes the proof.

Theorem 4. Harmonic index, second Zagreb index, and reduced second Zagreb index of G^∗ are as follows:

(1)
Hyper-Zagreb index of graph G^∗ is
(32)
(2)
Second Zagreb index is
(33)
(3)
Reduced 2^nd Zagreb index is
(34)

Proof. is grouped in 3 partitions. holds 12pq + 4p + 4q edges, where Deg_p = Deg_q = 2. supports 36pq − 4p − 4q edges pq, where Deg_p = 2 and Deg_q = 3. keeps 18pq − q − p edges, where Deg_p = 3 and Deg_q = 3. Consider , , and .

From (8), we define HM(G^∗) as

(35)

By using the definition of M₂(G^∗),

(36)

By substituting the values in equation (10),

(37)

With the help of (3) and (4), we have

(38)

Theorem 5. ABC index of graph hydrocarbon structure is given as follows:

(39)

Proof. G^∗ encounters 66pq − p − q number of edges and 54pq vertices. Vertex count of degree 2 is 30pq + 2p + 2q and of degree 3 is 24pq − 2p − 2q. The cardinality arc group E of G^∗ is 66pq − p − q. grouped into 3 disjoint arc groups, i.e., . has 12mn + 4n + 4m edges pq, where Deg_p = Deg_q = 2. supports 36pq − 4p − 4q edges pq, where Deg_p = 2 and Deg_q = 3. has 18pq − p − q arcs pq, where Deg_p = Deg_q = 3.

We use ABC(G^∗) in (11) as

(40)

Theorem 6.

(1)
ABC₄(G^∗) of G^∗ is
(41)
(2)
GA₅(G^∗) is
(42)

Proof. The graph G^∗ has 66pq − q − p number of edges. can be distributed into twelve disunite groups of edges.

, i = 4,5,6 … , 15. .

has 2n lines pq, where S_p = S_q = 4. supports 4p + 4q lines pq, where S_p = 4 and S_q = 5. contains 12pq − 2p edges, where S_p = S_q = 5. contains 22pq − 2p edges, where S_p = 5 and S_q = 7. keeps 2pq + 2p + 4q edges, where S_p = 5 and S_q = 8. E₉(G^∗) contains 6pq − 2p − 4q edges, where S_p = 6 and S_q = 7. contains 6pq − 2p − 4q edges, where S_p = 6 and S_q = 8. contains 2pq − p − q edges, where S_p = S_q = 7. holds 8pq edges, where S_p = 7 and S_q = 8. holds 2pq edges, where S_p = 7 and S_q = 9. The edge set keep 2mn edges, where S_p = S_q = 8. holds 4mn edges, here pq, where S_p = 8 and S_q = 9.

The index is defined in equation (12):

(43)

(44)

After substituting the values , we get

(45)

After simplification, we get

(46)

By utilizing the definition of GA₅(G^∗) from equation (18),

(47)

(48)

After substituting the values , we get

(49)

After simplification,

(50)

Theorem 7. Consider the following:

(1)
The general Randić index of graph G^∗ is given as follows:
(51)
(2)
Randić index of graph G^∗ is
(52)
(3)
Reduced reciprocal Randić index of graph G^∗ is
(53)
(4)
Reciprocal Randić index of graph G^∗ is
(54)

Proof. G^∗ encounters 66pq − p − q lines and 54pq vertices. Vertices of degree 2 are 30pq + 2p + 2q and of degree 3 are 24pq − 2p − 2q. The cardinality of of G^∗ is 66pq − p − q. is divided into 3 dissociate edge groups that rely on the degrees of the end points, i.e., . has 12pq + 4p + 4q edges pq, where Deg_p = Deg_q = 2. has 36pq − 4p − 4q edges pq, where Deg_p = 2 and Deg_q = 3. has 18pq − p − q arcs pq, where Deg_p = Deg_q = 3.

We use general Randic index in (13) as

(55)

Now, we have

(56)

After simplification, we get

(57)

By the use of Randić index (14),

(58)

After simplification,

(59)

Definition of RRR(G^∗) index from equation (16) is

(60)

Now, by utilizing the definition of reduced Randić index from equation (15),

(61)

Theorem 8. We have graph G^∗ and its different indices are explained here.

(1)
GA index is as follows:
(62)
(2)
Sum connectivity index is given as follows:
(63)
(3)
Forgotten index of G^∗ is
(64)

Proof. G^∗ encounters 66pq − p − q edges and 54pq vertices. Vertex count of degree 2 are 30pq + 2p + 2q and of degree 3 are 24pq − 2p − 2q. The cardinality line group of G^∗ is 66pq − p − q. E(G^∗) is classified into three disjoint edge groups, i.e., . has 12pq + 4p + 4q edges pq, where Deg_p = Deg_q = 2. has 36pq − 4p − 4q edges pq, where Deg_p = 2 and Deg_q = 3. has 18pq − p − q edges pq, where Deg_p = Deg_q = 3.

We use geometric arithmetic index in (17) as

(65)

After simplification, we obtain

(66)

From equation (20), we get

(67)

We use forgotten index in (19) as

(68)

Theorem 9. Let G^∗ be graph:

(1)
Symmetric division index is
(69)
(2)
Harmonic index is
(70)

Proof. G^∗ encounters 66pq − p − q edge and 54pq points. Vertex counts of degree 2 are 30pq + 2p + 2q and of degree 3 are 24pq − 2p − 2q. The edge set E(G^∗) splits into three distinct line groups.

has 12pq + 4p + 4q lines pq, where Deg_p = Deg_q = 2. has 36pq − 4p − 4q lines pq, where Deg_p = 2 and Deg_q = 3. has 18pq − p − q lines pq, where Deg_p = Deg_q = 3.

From equation (21), we obtain

(71)

From equation (22),

(72)

3. Conclusion

We find some topological descriptors of hydrocarbon structure. Randić index has well known applications in the study of physicochemical characteristics of alkane, for example, surface area, enthalpy of formation, boiling point, and melting point. The index has the most functional role in pharmacology. Similarly, forgotten index is helpful to figure out the strength of organic structures. Symmetric division index has productive applications to find heat formation of chemical structures. GA index can forecast biological activities of compounds. ABC index has an outstanding role in finding strain energy and stability of isoparaffins. Our results will be helpful to estimate the physicochemical properties of hydrocarbon structures.

4. Future Work

In future, we will find the distance-based and spectrum-based topological indices of hydrocarbon structures.

Conflicts of Interest

The authors declares that there are no conflicts of interest.

Acknowledgments

This project was supported by the Jahangirnagar University, Savar, Dhaka, Bangladesh.

Open Research

Data Availability

No data were used to support this study.

References

1 Chassapis D. and Kotsakosta M., Crossing the bridges of Konigsberg in a primary mathematics classroom, Mathematics in School. (2003) 32, no. 1, 11–13.
Google Scholar
2 F. Harary, A Seminar on Graph Theory, 2015, Courier Dover Publications, Mineola, NY, USA.
Google Scholar
3 Bondy J. A. and Murty U. S. R., Graph Theory with Applications, 1976, 290, Macmillan, London, UK.
10.1007/978-1-349-03521-2
Google Scholar
4 Rodriguez J. M. and Sigarreta J. M., On the geometric-arithmetic index, MATCH Communications in Mathematical and in Computer Chemistry. (2015) 74, 103–120.
Web of Science® Google Scholar
5 Zhang S. and Zhang H., Unicyclic graphs with the first three smallest and largest first general Zagreb index, MATCH Communications in Mathematical and in Computer Chemistry. (2006) 55, no. 20.
Web of Science® Google Scholar
6 Fath-Tabar G. H., Old and new Zagreb indices of graphs, MATCH Communications in Mathematical and in Computer Chemistry. (2011) 65, 79–84.
Web of Science® Google Scholar
7 Ghorbani M. and Ghazi M., Computing some topological indices of triangular Benzenoid, Digest Journal of Nanomaterials and Biostructures. (2010) 5, no. 4, 1107–1111.
Web of Science® Google Scholar
8 Gutman I., Degree-based topological indices, Croatica Chemica Acta. (2013) 86, no. 4, 351–361, https://doi.org/10.5562/cca2294, 2-s2.0-84897584934.
10.5562/cca2294
CAS Web of Science® Google Scholar
9 Das K. C. and Gutman I., Some properties of the second Zagreb index, MATCH Communications in Mathematical and in Computer Chemistry. (2004) 52, no. 1, 3–1.
Google Scholar
10 Deutsch E. and Klavžar S., M-polynomial and degree-based topological indices, 2014, https://arxiv.org/abs/1407.1592.
Google Scholar
11 Das K. C., Gutman I., and Furtula B., On atom-bond connectivity index, Chemical Physics Letters. (2011) 511, no. 4–6, 452–454, https://doi.org/10.1016/j.cplett.2011.06.049, 2-s2.0-79960929524.
10.1016/j.cplett.2011.06.049
CAS Web of Science® Google Scholar
12 Li X. and Shi Y., A survey on the Randic index, MATCH Communications in Mathematical and in Computer Chemistry. (2008) 59, no. 1, 127–156.
CAS Web of Science® Google Scholar
13 Gutman I., Furtula B., and Elphick C., Three new/old vertex-degree-based topological indices, MATCH Communications in Mathematical and in Computer Chemistry. (2014) 72, no. 3, 617–632.
Web of Science® Google Scholar
14 Siddiqui H. A. J. R. A. and Farahani M. R., Forgotten polynomial and forgotten index of certain interconnection networks, Open Journal of Mathematical Analysis. (2017) 1, no. 1, 45–60.
Google Scholar
15 Zhou B. and Trinajstić N., On general sum-connectivity index, Journal of Mathematical Chemistry. (2010) 47, no. 1, 210–218, https://doi.org/10.1007/s10910-009-9542-4, 2-s2.0-72949100341.
10.1007/s10910-009-9542-4
CAS Web of Science® Google Scholar
16 Ali A., Elumalai S., and Mansour T., On the symmetric division deg index of molecular graphs, MATCH Communications in Mathematical and in Computer Chemistry. (2020) 83, 205–220.
Web of Science® Google Scholar
17 Baca M., Horváthová J., Mokrišová M., and Suhányiová A., On topological indices of fullerenes, Applied Mathematics and Computation. (2015) 251, 154–161.
10.1016/j.amc.2014.11.069
Web of Science® Google Scholar
18 Basak S. C., Balaban A. T., Grunwald G. D., and Gute B. D., Topological indices: their nature and mutual relatedness, Journal of Chemical Information and Computer Sciences. (2000) 40, no. 4, 891–898, https://doi.org/10.1021/ci990114y, 2-s2.0-0000226523.
10.1021/ci990114y
CAS PubMed Web of Science® Google Scholar
19 Das K. C., Gutman I., and Furtula B., Survey on geometric-arithmetic indices of graphs, MATCH Communications in Mathematical and in Computer Chemistry. (2011) 65, no. 3, 595–644.
CAS Web of Science® Google Scholar
20 Das K. C., On geometric-arithmetic index of graph, MATCH Communications in Mathematical and in Computer Chemistry. (2010) 64, no. 3, 619–630.
Web of Science® Google Scholar
21 Gozalbes R., Doucet J., and Derouin F., Application of topological descriptors in QSAR and drug design: history and new trends, Current Drug Targets - Infectious Disorders. (2002) 2, no. 1, 93–102, https://doi.org/10.2174/1568005024605909, 2-s2.0-0035986794.
10.2174/1568005024605909
CAS PubMed Google Scholar
22 Imran M., Hayat S., and Mailk M. Y. H., On topological indices of certain interconnection networks, Applied Mathematics and Computation. (2014) 244, 936–951, https://doi.org/10.1016/j.amc.2014.07.064, 2-s2.0-84907317006.
10.1016/j.amc.2014.07.064
Web of Science® Google Scholar
23 Kulli V. R., Reduced second hyper-Zagreb index and its polynomial of certain silicate networks, Journal of Mathematics and Informatics. (2018) 14, 11–16, https://doi.org/10.22457/jmi.v14a2.
10.22457/jmi.v14a2
Google Scholar
24 Mondal B. and De K., An overview applications of graph theory in real field, International Journal of Scientific Research in Computer Science, Engineering and Information Technology. (2017) 2, no. 5, 751–759.
Google Scholar
25 Nikoliç S., Kovaçeviç G., Miliçeviç A., and Trinajstiç N., The Zagreb indices 30 years after, Croatica Chemica Acta. (2003) 76, no. 2, 113–124.
CAS Web of Science® Google Scholar

Citing Literature

All articles

[Retracted] Computation of Vertex Degree-Based Molecular Descriptors of Hydrocarbon Structure

Retraction(s) for this article

Retracted: Computation of Vertex Degree-Based Molecular Descriptors of Hydrocarbon Structure

Abstract

1. Introduction

1.1. Derivation of Degree-Based Topological Indices

1.1.1. First General Zagreb Index

1.1.2. First Zagreb Index

1.1.3. Second Zagreb Index

1.1.4. First and Second Multiple Zagreb Indices

1.1.5. First and Second Polynomial Zagreb Indices

1.1.6. Modified Zagreb Index

1.1.7. Second Modified Zagreb Index

1.1.8. Reduced 2nd Zagreb Index

1.1.9. Atom Bond Connectivity Index

1.1.10. Atom Bond Connectivity Index of 4th Order

1.1.11. General Randić Connectivity Index

1.1.12. Randić Index

1.1.13. Reciprocal Randić Index (RRI)

1.1.14. RRR Index

1.1.15. GA Index

1.1.16. GA5 Index

1.1.17. Forgotten Index

1.1.18. General Sum Connectivity Index

1.1.19. SD Index

1.1.20. Harmonic Index

2. Topological Indices of Hydrocarbon Structure

2.1. Description of Graph of Hydrocarbon Structure

3. Conclusion

4. Future Work

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information

1.1.16. GA₅ Index