The many publications related to the gyroscope theory consider the action of the inertial torques on the spinning disc. All of them have simplified expressions for the inertial torques and mathematical models of the gyroscope motions do not validate by practice. Recent research in the theory of the gyroscopic effects for rotating objects solved problems with mathematical models for interrelated inertial torques generated by the spinning disc, bar, and ring and their motions. Practitioners of engineering designed gyroscopic devices with spinning rotors whose geometry can be an annulus or similar designs. Such spinning annulus generates inertial torques whose expressions differ from the disc bar and ring and hence another mathematical model describes the motions of the gyroscopic devices. The value of gyroscopic effects of the devices with spinning annulus is bigger than for the disc-type rotor. This manuscript presents mathematical models for the inertial torques generated by the spinning annulus and the interrelated angular velocities of the gyroscopic devices about axes of rotation.

1. Introduction

The gyroscopic effects in engineering mechanics are the most complex problems that are being unsolved for a long time [1–5]. Beginning from the Industrial Revolution, scientists yield only partial analytical solutions but did not solve the entire gyroscopic effects. For practical applications were worked out numerical models with the expensive software for gyroscopic effects. The physics of the gyroscopic effects of the simple spinning disc remained unexplained and mysterious for a couple of centuries [6–10]. Scientists and researchers of our time continue to describe gyroscopic effects without success which can be seen in many publications each year [11–19]. Recent investigations of the gyroscopic effects showed their nature is more complex and based on several physical principles that were discovered at different times. Scientists of 18-19 centuries could not solve gyroscopic effects in principle because the concept of mechanical energy conservation was formulated at the beginning of twenty century. From this time, researchers have all the analytical tools for formulation of the gyroscope theory but did not do it.

The latest studies of the physics of the gyroscopic effects yield mathematical models for the inertial torques and the interrelated dependency of the angular velocities of the spinning disc motions about axes of rotation. The solution to gyroscopic effects is based on the principle of mechanical energy conservation [20–22]. The method of deriving mathematical models for inertial torques shows the action of the system of the centrifugal, Coriolis forces generated by the rotating mass, and the change in the angular momentum of the spinning disc. The dependency of the angular velocities of the spinning disc around axes of motions interrelates the inertial torques. Table 1 presents the expressions of inertial torques acting on the spinning disc and the dependency of the angular velocities of it's motions.

1. Equations of the inertial torques acting on the spinning disc.

Type of the torque generated by	Acton	Equation
Centrifugal forces	Resistance	T_ct = (4/9)π²Jωω_x
Centrifugal forces	Precession	T_ct = (4/9)π²Jωω_x
Coriolis forces	Resistance	T_cr = (8/9)Jωω_x
Change in angular momentum	Precession	T_am = Jωω_x
Dependency of angular velocities of spinning disc rotations about axes		ω_y = (8π² + 17)ω_x

The practice tests validate the action of the system of the interrelated inertial torques on the spinning disc. Practitioners should use the derived method for the modeling of the gyroscopic effects for any designs of the spinning objects [22]. The mathematical models for the inertial torques generated by the centrifugal and Coriolis forces and the change in the angular momentum acting on the spinning flat annulus and its interrelated motions around two axes are present as the contribution of the manuscript.

2. Centrifugal Forces and Torques Acting on a Spinning Annulus

The method for the analytical solution for all inertial torques acting on the spinning disc is described in several publications [21, 22]. The inertial torques are generated by the distributed mass elements of the spanning disc disposed on the circle of 2/3 of its radius. This method can be applied to rotating objects of different forms. For the annulus, the radius of the disposition of the distributed mass elements on the circle should be defined. The rotating mass elements produce the plane of centrifugal forces of the spinning annulus around axis oz with an angular velocity of ω in a counter-clockwise direction considered in Figure 1. The mass element m is disposed on the circle of radius r which is perpendicular to the axis of the spinning annulus.

Details are in the caption following the image — Open in figure viewer PowerPoint

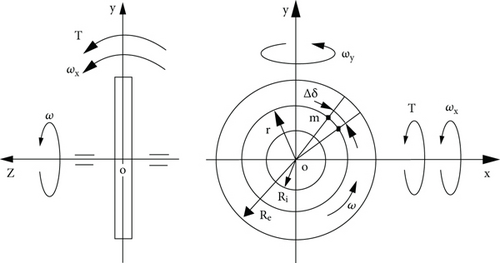
The radius r of disposing of the mass elements of the annulus is defined from the truncated sector with the small angle Δδ and the arcs of the external and internal radii R_e and R_i, respectively. The rotating mass elements generate centrifugal forces. The action of the external torque to the spinning annulus has manifested the inclination of its plane with the rotating centrifugal forces and the turns of the annulus around axes. These motions are presented at the Cartesian 3D coordinate system Σoxyz in Figure 1. The external torque applied to the spinning annulus generates several inertial torques (Figure 2).

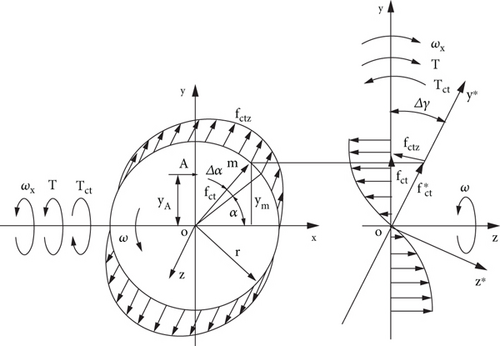
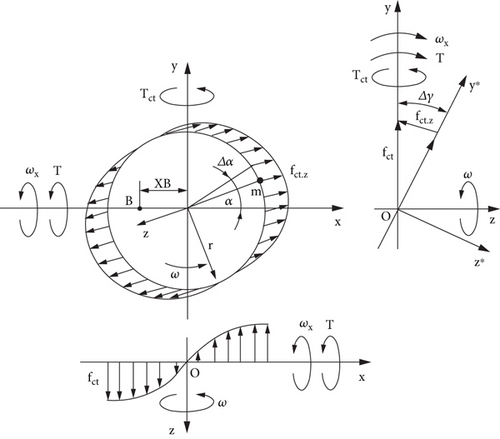
The plane of the rotating centrifugal forces turns around axis ox along the diameter line and changes in the directions of centrifugal force vectors f_ct of the mass elements. The inclined plane of rotating centrifugal forces on angle Δγ around axis ox is presented in the plane xoy∗. The action of the centrifugal force vectors f_ct is radial and their components f∗ _ct produce the torques around axes ox and oy. The values of torques acting around axis ox are maximal at 90^o and 270^o and zero at 0^o and 180^o (Figure 2(a)). The values of torques acting around axis oy are maximal at 0^o and 180^o and zero at 90^o and 270^o (Figure 2(b)). The integrated product of the components’ vector of the centrifugal forces f_ct.z and their radii relative to axes ox and oy give the torques T_ct acting around two axes. The torque acting around axis ox resists the action of the external torque T. The torque acting around axis oy turns the spinning annulus in the counter-clockwise direction.

The mathematical models for the inertial torques generated by the centrifugal forces of the mass elements are expressed as follows:

(1)

(2)

where ΔT_ct is the centrifugal torque generated by the mass element; f_ct.z is the component of the centrifugal force; y_m and x_m are the distance from the mass element to axes oy and ox, respectively; m is the mass element of the annulus disposed on the circle of the radius r; a_z = rω² is the radial acceleration; ω is the angular velocity of the spinning annulus; the signs (+) and (-) mean the counter-clockwise and clockwise direction, respectively.

The following equations express the component of the centrifugal force acting along axis oz:

(i)
Around axis ox
(3)
(ii)
Around axis oy
(4)
where f_ct = mrω² = (Mrω²/2π)Δδ is the centrifugal force of the mass element m; m = (M/2πr)Δδr = (M/2π)Δδ in which M is the mass of the annulus; Δδ is the sector’s angle of the mass element’s disposition; α is the angle of the mass element’s disposition; Δγ is the angle of turn for the annulus plane, sinΔγ = Δγ is the trigonometric identity for the small values of the angle.

The radius r of the circle of disposing of the mass elements m of the annulus is defined from the truncated sector with the small angle Δδ and the arcs of the external and internal radii R_e and R_i, respectively (Figure 1). The radius r is expressed by the equation of the centroid of the truncated sector

(5)

where

and

are the area of the sectors of radii R_e and R_i and (2/3)R_e and (2/3)R_i are the radii of the mass elements disposition, respectively;

is the area of the truncated sector.

Substituting the expressions of f_ct.z of Equations (3)–(5) into Equations (1) and (2) and transformation yield the expressions of the inertial centrifugal torques produced by the mass element.

(6)

(7)

where y_m = rsinα and x_m = rcosα are the distance from the mass element of the annulus relative to axes ox (Figure 2(a)) and to axis oy (Figure 2(b)), respectively; and the other components are as specified above.

The centrifugal torques are distributed on the circle where the mass elements of the annulus are located (Figures 2(a) and 2(b)). The action of the torques is defined by a concentrated load at the centroid points at the semi-circles along axes oy and ox. The known integrated equation calculates the disposition of the centroid (point A of Figure 2(a) and point B of Figure 2(b)) [6–9].

(8)

where

, l_i is the centroid for the semi-circle i, and l_m is y_m or x_m.

Substituting Equations (4) and (5) and other components into Equation (8) and transformation yield the following expression.

(i)
About axis ox
(9)
(ii)
About axis oy
(10)
where the expression is constant of Equations (9) and (10); the expressions sin²α = (1 − cos2α)/2 and cos²α = (1 + cos2α)/2 are a trigonometric identity, and other parameters are as specified above.

Equations (6) and (7) are presented in differential and integral forms. Substituting expressions of Equations (9) and (10) into Equations (6) and (7), replacing

and

by the integral expressions with defined limits, respectively, the following equations emerge:

(i)
About axis ox
(11)
(ii)
About axis oy
(12)

Solutions of integral Equations (11) and (12) yield the following:

(i)
About axis ox
(13)
(ii)
About axis oy
(14)

that gave rise to the following:

(i)
About axis ox
(15)
(ii)
About axis oy
(16)
where all components are as specified above.

Equations (15) and (16) are almost identical except for the signs (±) of counter and clockwise action around axes ox and oy. The inertial torque T_ct depends on the variable angle γ that expresses the angular velocity ω_x of the annulus rotation about axis ox per time t. The differential equation expresses the change in torque T_ct per time

(17)

where t = α/ω is the time taken relative to the angular velocity of the annulus.

The differential of time t is dt = dα/ω; the expression dγ/dt = ω_x is the angular velocity of the spinning annulus around axis ox. Substituting the defined components into Equation (17) and transforming yield:

(18)

Separation of the variables of Equation (18), transformation, and presentation by the integral form with defined limits yield:

(19)

Solution of Equation (19) yields

(20)

The centrifugal torques act on the upper and lower sides of the annulus about axis ox, and its left and right sides about axis oy. Then, the total torque T_ct acting about axes ox and oy is increased double.

(21)

where

is the annulus moment of inertia, and other components are as specified above.

3. Coriolis Forces and Torques Acting on a Spinning Annulus

The Coriolis acceleration and force generated by mass elements are revealed when the spinning annulus turns around axis perpendicular to its axle. The integrated Coriolis force produced by the rotating mass elements of the annulus generates the torque counteracting the external torque [10]. Figure 3 shows the rotation of the mass element m of the annulus that turns on the angle Δγ around axis ox. The turn of the annulus around axis ox changes the direction of the tangential velocity vectors of mass elements. The change in the tangential velocity of mass elements produces the acceleration in which a product with a mass yields the Coriolis forces of the mass elements, where ΔV = VsinΔγ, V = rcosα × ω, and sinΔγ = Δγ for the small angle (Figure 3). The maximal changes of the velocity vectors V∗ are on the line of axis ox. The tangential velocity V whose vector is parallel to axis ox, i.e., on 90^o and 270^o does not change. The changes in tangential velocity vectors are presented by the components V_z that are parallel to the annulus axle oz.

The torque generated by the Coriolis force of the rotating mass element is expressed by

(22)

where ΔT_cr is the torque generated by Coriolis force f_cr of the annulus mass element m; a_z is the Coriolis acceleration along with axis oz; y_m = rsinα is the distance from the mass element to axis ox; the sigh (-) means the action in the clockwise direction around axis ox, and the other components are represented in Equation (2).

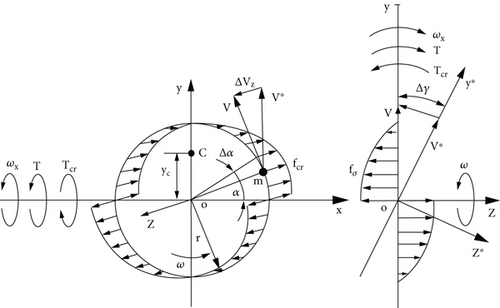
The differential form of changes in tangential velocity vectors is dV/dt = a_z and change in the angle of rotation around axis ox is dγ/dt = ω_x.

Then, the Coriolis acceleration is:

(23)

The Coriolis force of the mass element is presented:

(24)

Then, the Coriolis torque is:

(25)

where all parameters are as specified above.

The centroid for the torque ΔT_cr is point C of Figure 3, which is defined by Equation (8).

(26)

Substituting Equation (26) into Equation (25), replacing

by the integral expression with defined limits, and presenting other components by the integral forms, the following equation emerges:

(27)

Solution of integral Equation (27) yields:

(28)

that gave rise to the following:

(29)

where all components are as specified above.

The inertial torque T_cr acts on the upper and lower sides of the annulus. Multiplying Equation (29) by two yields the full expression of T_cr:

(30)

where

is the annulus moment of inertia; the sign (-) expresses the clockwise direction.

4. Attributes of Inertial Torques Acting on a Spinning Annulus

The load torque applied to the spinning annulus produces the system of the inertial torques generated by the rotating mass [22]. Among them is the change in the angular momentum of a spinning disc, which is Euler’s fundamental principle of gyroscope theory [1–5]. The motion of the spinning annulus around axis oy (Figure 3) manifests the change in the annulus angular momentum in the counter-clockwise direction which is called precession. The expression of the change in the angular momentum is T_am = Jωω_x where all components are presented above. The system of the inertial torques produces the resistance and precession torques and motions of the spinning annulus around axes of the rotation. Table 2 represents expressions of the inertial torques generated by pseudo forces of the spinning annulus.

2. The inertial torques acting on the spinning annulus generated by the external torque.

Type of the torque generated by	Action	Equation
Centrifugal forces, T_ct	Resistance
Centrifugal forces, T_ct	Precession
Coriolis forces, T_cr	Resistance
Change in angular momentum, T_am	Precession	T_am = Jωω_x
Dependency of angular velocities of spinning disc rotations about axes

The external torque T generates all inertial torques that depend on the mass moment of the annulus’s inertia J, its angular velocity ω, and the angular velocity ω_x of the spinning annulus about axis ox.

The action of all torques around axes ox and oy on the spinning object is shown in Figure 4 for the given symmetrical disposing of its supports [22]. The interrelated action of the inertial torques is considered for the horizontal disposition of the spinning object.

The action of the inertial torques of the spinning annulus around axes ox and oy expresses analytically the equality of their mechanical energies that enables for deriving of the dependency of its interrelated angular velocities around axes of motions (Figure 4) [22].

(31)

where expressions of the inertial torques are presented by Equations (21) and (30), and T_am = Jωω_x.

Substituting expressions of the defined torques into Equation (31) yields the following:

(32)

where the signs (-) and (+) mean the clockwise and counter-clockwise directions of the action of the inertial torques around two axes, respectively.

Simplification and transformation of Equation (32) yield the following:

(33)

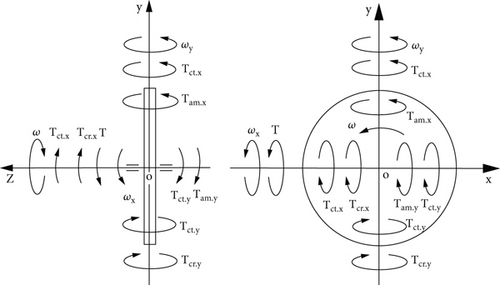
The expressions of the inertial torques and their action, and the dependency of interrelated angular velocities of the spinning annulus around axes are presented in Table 2.

The expressions of torques and the dependency angular velocities (Table 2) formulate the mathematical models for the motions of the gyroscopic devices with the annulus rotor. Comparative analysis of formulas for the spinning annulus shows when its internal radius R_i =0, all of them are converted to the formulas for the disc-type rotor presented in Table 1. This fact validates the mathematical correctness of the formulas. The values of formulas in Table 2 give results bigger than the formulas in Table 1.

5. Working Example

The annulus has a mass of 1.0 kg and the external and internal radii of 0.1 m and 0.06 m, respectively. The annulus rotates at 3000 rpm around the axle and precesses with an angular velocity of 0.06 rpm. Determine the values of the torques generated by the centrifugal and Coriolis force, the change in the angular momentum, and the angular velocity of precession. Substituting the data into equations of Table 2 and transformation yields the following results.

(i)
The torque T_ct generated by the centrifugal forces
(34)
(ii)
The torque generated by Coriolis T_cr forces
(35)
(iii)
The torque T_am of the change in the angular momentum
(36)
(iv)
The angular velocity of precession
(37)

For the disc-type rotor (Table 1), the dependency of the angular velocities is obtained if the R_i =0 in Table 2. Substituting data of the working example and computing yield:

(38)

The comparative results of the dependency of the angular velocities rotation around axes of motions for the annulus and disc-type rotor show their big differences. The radius of disposition of the distributed mass of the annulus is bigger than for the disc-type rotor. Analysis of them yields the spinning annulus generates bigger values of the inertial torques and the dependency of the angular velocities than the spinning disc-type rotor.

6. Results and Discussion

Gyroscopic effects are remaining as sophisticated mathematical problems because the inertial torques generated by the rotating mass depend on the geometry of the spinning objects. The practice of engineering designs of the gyroscopic devices shows different geometry of their main components which are the rotors. The value of the inertial torques generated by the spinning rotors depends on their technical data. The working example shows the spinning annulus generates bigger values of the inertial torques and the dependency of the angular velocities than the disc-type rotor. This result gives the tip for the practitioners to design gyroscopic devices with a high value of the inertial torques and the angular velocity of precession. Practitioners can design gyroscopic devices with a necessary output of technical data that depends on the geometry of the spinning rotor. This result opens a new analytical approach to finding optimal designs of the spinning rotor that respond to the quality of gyroscope work.

7. Conclusion

Aerospace and engineering industries try to solve gyroscopic problems and find optimal designs for gyroscopic devices that give the necessary technical data. The new theory of gyroscopic effects for rotating objects opens new methods for computing the technical data for gyroscopic devices. The method for deriving mathematical models for the gyroscopic effects enables finding the output data of gyroscopic devices that depend on the geometry of the main unit which is the spinning rotor. Optimization of the rotor’s design by criteria of the aerospace industry is a new direction for investigations in engineering. The fundamental principles of the theory of gyroscopic effects for rotating objects and methods enable solving them in engineering. The known numerical modeling for gyroscopic effects with expensive software is going past and engineering science receives new analytical methods.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

The authors declare that the data supporting the findings of this study are available within the article. R. Usubamatov wrote the mathematical models of inertial torques. S. Kapayea corrected the text and references.

References

1 Cordeiro F. J. B., The Gyroscope, 2015, Createspace, NV, USA.
Google Scholar
2 Greenhill G., Report on Gyroscopic Theory, 2015, Relink Books, Fallbrook, CA, USA.
Google Scholar
3 Scarborough J. B., The Gyroscope Theory and Applications, 2014, Nabu Press, London.
Google Scholar
4 Weinberg H., Gyro mechanical performance: the most important parameter. Analog Devices, 2011, 1–5, Technical Article MS2158.
Google Scholar
5 Apostolyuk V., Coriolis Vibratory Gyroscopes, 2016, Springer International Publishing Switzerland, https://doi.org/10.1007/978-3-319-22198-4, 2-s2.0-84943147931.
10.1007/978-3-319-22198-4
Google Scholar
6 Hibbeler R. C. and Yap K. B., Mechanics for Engineers-Statics and Dynamics, 2020, 14th edition., Prentice Hall, Pearson, Singapore.
Google Scholar
7 Gregory D. R., Classical Mechanics, 2012, Cambridge University Press, New York.
Google Scholar
8 Taylor J. R., Classical Mechanics, 2005, University Science Books, California, USA.
Google Scholar
9 Aardema M. D., Analytical Dynamics, 2005, Academic/Plenum Publishers, New York, Theory and Application, https://doi.org/10.1007/b116020, 2-s2.0-84895239535.
10.1007/b116020
Google Scholar
10 Scheck F., Mechanics, 2018, Springer-Verlag, Berlin Heidelberg, https://doi.org/10.1007/978-3-662-55490-6.
10.1007/978-3-662-55490-6
Google Scholar
11 Bhatti M. M. and Michaelides E. E., Oldroyd 6-constant electro-magneto-hydrodynamic fluid flow through parallel micro-plates with heat transfer using Darcy-Brinkman-Forchheimer model: a parametric investigation, Mathematics in Engineering. (2022) 5, no. 3, 1–19, https://doi.org/10.3934/mine.2023051.
10.3934/mine.2023051
Google Scholar
12 Liang W. C. and Lee S. C., Vorticity, gyroscopic precession, and spin-curvature force, Physical Review D. (2013) 87, no. 4, article 044024, https://doi.org/10.1103/PhysRevD.87.044024, 2-s2.0-84874038229.
10.1103/PhysRevD.87.044024
Web of Science® Google Scholar
13 Crassidis J. L. and Markley F. L., Three-axis attitude estimation using rate-integrating gyroscopes, Journal of Guidance, Control, and Dynamics. (2016) 39, no. 7, 1513–1526, https://doi.org/10.2514/1.G000336, 2-s2.0-84975090497.
10.2514/1.G000336
Web of Science® Google Scholar
14 Nanamori Y. and Takahashi M., An integrated steering law considering biased loads and singularity for control moment gyroscopes, AIAA Guidance, Navigation, and Control Conference, January 2015, Kissimmee, Florida, https://doi.org/10.2514/6.2015-1091.
10.2514/6.2015-1091
Google Scholar
15 Chu Y. and Fei J., Adaptive global sliding mode control for MEMS gyroscope using RBF neural network, Mathematical Problems in Engineering. (2015) 2015, 9, 403180, https://doi.org/10.1155/2015/403180, 2-s2.0-84927135772.
10.1155/2015/403180
Google Scholar
16 Doukhi Q., Fayjie A. R., and Jin Lee F. D., Intelligent controller design for quad-rotor stabilization in presence of parameter variations, Journal of Advanced Transportation. (2017) 2017, 10, 4683912, https://doi.org/10.1155/2017/4683912, 2-s2.0-85041425877.
10.1155/2017/4683912
Google Scholar
17 Xu B. and Zhang P., Minimal-learning-parameter technique based adaptive neural sliding mode control of MEMS gyroscope, Complexity. (2017) 2017, 8, 6019175, https://doi.org/10.1155/2017/6019175, 2-s2.0-85027361061.
10.1155/2017/6019175
Google Scholar
18 Wang W., Ma H., Xia M., Weng L., and Ye X., Attitude and altitude controller design for quad-rotor type MAVs, Mathematical Problems in Engineering. (2013) 2013, 9, 587098, https://doi.org/10.1155/2013/587098, 2-s2.0-84878667263.
10.1155/2013/587098
Web of Science® Google Scholar
19 Zhu Z., Bo Y., and Jiang C., A MEMS gyroscope noise suppressing method using neural architecture search neural network, Mathematical Problems in Engineering. (2019) 2019, 9, 5491243, https://doi.org/10.1155/2019/5491243.
10.1155/2019/5491243
Web of Science® Google Scholar
20 Usubamatov R., Physics of gyroscope’s “antigravity effect”, Advances in Mathematical Physics. (2019) 2019, 7, 4197863, https://doi.org/10.1155/2019/4197863.
10.1155/2019/4197863
Web of Science® Google Scholar
21 Usubamatov R. and Allen D., Corrected inertial torques of gyroscopic effects, Advances in mathematical physics. (2022) 2022, 7, 3479736, https://doi.org/10.1155/2022/3479736.
10.1155/2022/3479736
Web of Science® Google Scholar
22 Usubamatov R., Theory of Gyroscope Effects for Rotating Objects, 2022, 2nd edition., Springer, Cham, Switzerland, https://doi.org/10.1007/978-3-030-99213-2.
10.1007/978-3-030-99213-2
Google Scholar

All articles

Inertial Forces and Torques Acting on a Spinning Annulus

Abstract

1. Introduction

2. Centrifugal Forces and Torques Acting on a Spinning Annulus

3. Coriolis Forces and Torques Acting on a Spinning Annulus

4. Attributes of Inertial Torques Acting on a Spinning Annulus

5. Working Example

6. Results and Discussion

7. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Inertial Forces and Torques Acting on a Spinning Annulus

Abstract

1. Introduction

2. Centrifugal Forces and Torques Acting on a Spinning Annulus

3. Coriolis Forces and Torques Acting on a Spinning Annulus

4. Attributes of Inertial Torques Acting on a Spinning Annulus

5. Working Example

6. Results and Discussion

7. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Figures

References

Related

Information