Volume 2022, Issue 1 3205521

Research Article

Open Access

Static Characteristics of Improved Composite Box Girder with Corrugated Steel Webs

Shijin Wang,

Corresponding Author

Shijin Wang

[email protected]

orcid.org/0000-0001-6018-4284

School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China lzjtu.edu.cn

School of Civil and Architectural Engineering, Shandong University of Technology, Zibo 255000, China sdut.edu.cn

Search for more papers by this author

Genhui Wang,

Genhui Wang

School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China lzjtu.edu.cn

Search for more papers by this author

Zichen Zhang,

Zichen Zhang

School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China lzjtu.edu.cn

Search for more papers by this author

Shijin Wang,

Corresponding Author

Shijin Wang

[email protected]

orcid.org/0000-0001-6018-4284

School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China lzjtu.edu.cn

School of Civil and Architectural Engineering, Shandong University of Technology, Zibo 255000, China sdut.edu.cn

Search for more papers by this author

Genhui Wang,

Genhui Wang

School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China lzjtu.edu.cn

Search for more papers by this author

Zichen Zhang,

Zichen Zhang

School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China lzjtu.edu.cn

Search for more papers by this author

First published: 28 September 2022

https://doi.org/10.1155/2022/3205521

Citations: 1

Academic Editor: Wen-Da Wang

Share a link

Email
Wechat
Bluesky

Abstract

In order to accurately calculate the cross-sectional stresses and deflections of the improved composite box girder with corrugated steel webs, the control differential equations and boundary conditions are established based on the energy variational principle, taking into account the effects of corrugated steel web properties, shear lag, and shear deformation. A cantilever composite box girder is used as a numerical example. The influence of width span ratio and corrugated steel web bending angle on the shear lag and fold effect is analyzed. The results show that the analytical solution is in good agreement with the finite element solution. A shear lag effect and a negative shear lag effect exist in the cantilever composite box girder under uniform load. The fold effect under concentrated load has a greater influence on the mechanical properties of the wing plate than under uniform load. With the increase of the width span ratio, the effects of both shear lag and fold effect increases. With the increase of the corrugated steel web bending angle, the fold effect is obviously enhanced, but the change of the bending angle has little effect on the shear lag effect.

1. Introduction

The improved composite box girder with corrugated steel webs is a new composite structure composed of concrete plate, corrugated steel webs, and steel bottom plate (CSWCB), which is an improvement of the traditional composite girder with corrugated steel webs (CSWs). This bridge type [1] has the following advantages: beautiful appearance and novel shape; light self-weight, large span capacity; avoiding the crack of the bottom plate of the composite girder with CSWs [2–6]; and realizing formwork-free construction. The composite box girder with CSWCB has been widely promoted and applied in Gansu Province of China, for example, the interchange reconstruction projects of Zhongchuan Airport Terminals T2 and T3, and the Dingxi-Lintao Expressway—in which the maximum span of this kind of continuous composite box girder with CSWCB has reached 90 m.

At present, there is more research on the composite girder with CSWs [7–11], but less work on the static performance of the composite box girder with CSWCB [12–17]. The effect of corrugated steel web, shear lag effect, and shear deformation are not considered simultaneously for the composite box girder with CSWCB, thus the analysis of this structure has some limitations [18]. The control differential equations and boundary conditions of the composite girder with CSWCB are established based on the principle of energy variation. The influence of shear lag, shear deformation, width span ratio, and corrugated steel web bending angle are comprehensively considered in the numerical example. The analytical method used in this paper extends the analytical theory of the composite box girder with CSWCB.

2. Control Differential Equations of the Composite Girder with CSWCB and Its Solutions

2.1. Basic Assumptions of Calculation

Combined with the stress characteristics of the section of the composite box girder with CSWCB, the following basic assumptions are given: ① In the elastic working range of the composite box girder with CSWCB, there is no relative slip between web and roof; ② the upper and lower wing plates of the composite box girder with CSWCB always meet the “quasi plane section assumption”; and ③ the corrugated steel web bears all shear, and the shear stress is evenly distributed along the vertical direction.

2.2. Calculation Model of the Composite Box Girder with CSWCB

The geometric parameters of corrugated steel webs are shown in Figure 1, and the calculation formula of the effective shear modulus G_w [19] of corrugated steel web is calculated as follows:

(1)

where L₁ is the plate length, L₂ is the inclined plate length, δ is the bending angle, E_s is the elastic modulus of steel, and ʋ_s is Poisson’s of steel.

Details are in the caption following the image — Open in figure viewer PowerPoint

During the theoretical calculation, the steel bottom plate of the composite box girder with CSWCB is converted into an equivalent concrete plate, and the equivalent geometric characteristics are as follows:

(2)

where E_c is the elastic modulus of the concrete, and t₂ is the equivalent concrete plate thickness.

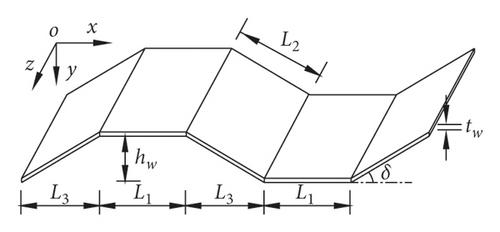
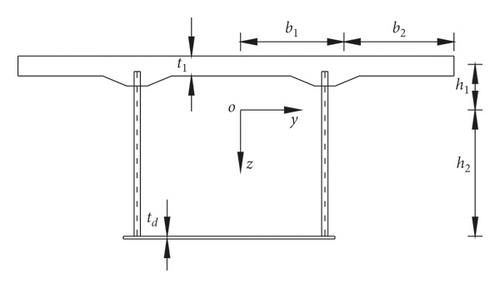
The geometric parameters of the corrugated steel webs are shown in Figure 2. Where b₂ is the width of the cantilever plate, 2b₁ is the width of the concrete top plate and the steel bottom plate, t₁ and t_d are the thickness of the upper flange concrete and the steel bottom plate, respectively; h₁ and h₂ are the distance from the upper flange and the bottom plate to the neutral axis, respectively. The z-axis is the height direction of the composite box girder; and the y-axis is the width direction.

2.3. Formula Derivation

Considering the influence of shear deformation, the longitudinal displacement of the top plate u₁(x, y), the cantilever plate u₂(x, y), and the bottom plate u₃(x, y) can be expressed as follows:

(3)

where U₁(x) and U₂(x) are the function of the maximum longitudinal displacement difference from top to bottom plate and the cantilever plate, respectively, and θ(x) is the vertical rotation angle of the box girder section relative to the y-axis.

The strain energy of top plate is:

(4)

The strain energy of the cantilever plate is:

(5)

The strain energy of bottom plate is:

(6)

where ε_xi = ∂u_i(x, y, z)/∂x(i = 1,2,3) , γ_xi = ∂u_i(x, y, z)/∂y(i = 1,2,3) , and G is the shear modulus of concrete.

The external potential energy of the composite box girder under bending is:

(7)

where M₁ and M₂ are to the y-axis bending moment caused by the shear lag effect of the cantilever plate; Q(x) and q(x) are shear force and vertical distributed load, respectively; M(x) is the bending moment about the y-axis when the vertical rotation angle θ(x) is generated at the end of beam section; and w(x) is the vertical deflection of composite box girder.

The shear strain energy of corrugated steel web is:

(8)

where A_w is the cross-section area of the corrugated steel web.

The total potential energy of the composite box girder is:

(9)

Based on the principle of minimum potential energy, it is known that the total potential energy of the structural system under the action of external forces is zero [20–23], and according to the energy variation method, the differential equations of elastic control of the composite box girder can be obtained as follows:

(10)

(11)

(12)

(13)

where I₁ is the sum moment of inertia of the top plate and the bottom plate to the y-axis, and I₂ is the moment of inertia of the cantilever plate to the y-axis.

Similarly, the boundary conditions of the composite box girder can be obtained as follows:

(14)

(15)

(16)

(17)

where I is the moment of inertia of the composite box girder.

The derivative expression of U₁(x) can be obtained by deformation of (13), and the differential equations of θ(x) and U₂(x) can be obtained by bringing the derivative U₁(x) into (12) and (14). The equation of θ(x) can be obtained after sorting and replacing the differential equations of θ(x) and U₂(x) with (13). Combined with (12), the differential equation of w(x) can be obtained as follows:

(18)

where

From (20), the solution of characteristic equation is as follows:

(19)

According to the properties of differential equation (14), the general solution of (20) is as follows:

(20)

where n₁ = α₁ + β₁i, n₂ = α₂ + β₂i.

According to the properties of ordinary differential equations and the principle of identity, the solution of the θ(x) equation can be obtained as follows:

(21)

Similarly, the solutions of U₁(x) and U₂(x) are obtained as follows:

(22)

2.4. Boundary Conditions

The boundary conditions of the cantilever composite box girder with CAWCB under uniform load q are as follows:

(23)

The boundary conditions of the cantilever composite box girder under concentrated load p are as follows:

(24)

The boundary conditions of the simply supported composite box girder under uniform load q are as follows:

(25)

The boundary conditions of the simply supported composite box girder under concentrated load p are as follows:

(26)

3. Numerical Example

3.1. Example 1

Taking the single box and single cell simply supported composite box girder with CSWCB in document 18 as an example, the span length is 8 m, reference 18 for other dimensions and material parameters. Table 1 shows the midspan deflections of the single box and single cell simply supported composite box girder with CSWCB based on the present method and the test values provided by Ma et al. (2021). It can be seen that the calculated values are in good agreement with the test values, thus the accuracy of this method is verified.

1. Midspan deflections of the single box and single cell simply supported composite box girder with CSWCB (unit: mm).

Working condition	Load amplitude	Measured value	Calculated value
Concentrated load	17.6 kN	1.705	1.912
	35.2 kN	3.325	3.824
	63.2 kN	6.140	6.866
	71.2 kN	7.405	7.735

Uniform load	2.250 kN/m	1.330	1.224
	3.983 kN/m	2.225	2.135
	5.625 kN/m	3.185	3.241
	7.500 kN/m	4.335	4.158

3.2. Example 2

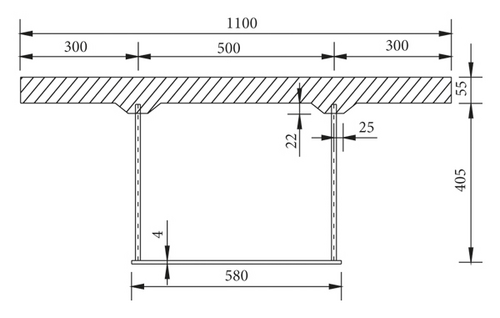
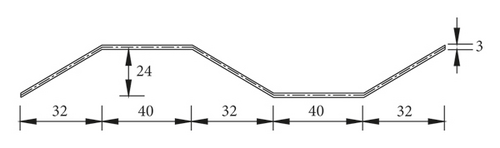
A cantilever composite box girder is designed and the span is 2.45 meters. The concrete material of the composite box girder top plate is C50, and the elastic modulus is 34.5 GPa; Q345 steel is used for corrugated steel webs and bottom plate, and the elastic modulus is 206 GPa. The cross section and steel web dimensions of the composite box girder are shown in Figure 3.

The finite element model is established by the ANSYS finite element software. The concrete top plate is simulated by SOLID65 element, the steel bottom plate and corrugated steel webs are simulated by SHELL63 element. The top and bottom plates are connected to the corrugated webs by means of the common node. All nodes of the cantilever fixed section are set as rigid constraints, and the finite element model is shown in Figure 4.

Tables 2–5 show the normal stresses distribution and fold effect of the top plate at the fixed end of the cantilever composite girder under different loads (Error in table and = (theoretical calculated value-finite element value)/finite element value ×100%; fold effect = (stress value of the composite box girder with SCWCB-stress value of composite box girder with flat steel webs)/stress value of the composite box girder with flat steel webs ×100%).

2. Stress values in the top plate of the cantilever composite box girder (MPa) (x = 0, concentrated load).

Calculation method	Transverse coordinates of the top plate (m)
Calculation method	0.00	0.05	0.10	0.15	0.20	0.25	0.30	0.35	0.40	0.45	0.50	0.55
Method of this paper	1.950	1.976	2.055	2.185	2.368	2.603	2.402	2.240	2.113	2.023	1.968	1.951
Finite element method	1.893	1.957	1.969	2.096	2.374	2.612	2.411	2.178	2.079	1.962	1.886	1.893
& (%)	3.011	0.971	4.368	4.246	−0.253	−0.345	−0.373	2.847	1.635	3.109	4.348	3.064
Fold effect (%)	13.22	14.36	17.25	20.18	22.45	26.31	23.71	21.46	19.96	18.30	15.74	14.32

3. Stress values in the bottom plate of the cantilever composite box girder (MPa) (x = 0, concentrated load).

Calculation method	Horizontal coordinates of the bottom plate (m)
Calculation method	0.00	0.05	0.10	0.15	0.20	0.25
Method of this paper	−52.608	−53.306	−55.402	−58.924	−63.813	−70.118
Finite element method	−51.873	−52.145	−53.917	−56.721	−60.614	−68.525
& (%)	1.222	2.226	2.754	3.884	5.278	2.325
Fold effect (%)	18.34	20.53	21.97	23.05	25.21	28.45

4. Stress values in the top plate of the cantilever composite box girder (MPa) (x = 0, uniform load).

Calculation method	Transverse coordinates of the top plate (m)
Calculation method	0.00	0.05	0.10	0.15	0.20	0.25	0.30	0.35	0.40	0.45	0.50	0.55
Method of this paper	1.370	1.404	1.521	1.704	2.005	2.339	1.972	1.721	1.537	1.387	1.303	1.287
Finite element method	1.405	1.422	1.497	1.651	1.892	2.268	1.915	1.689	1.561	1.425	1.364	1.352
& (%)	−2.491	−1.266	1.603	3.210	5.973	3.131	2.977	1.895	−1.537	−2.667	−4.472	−4.808
Fold effect (%)	6.97	7.02	7.04	6.95	7.03	7.05	7.02	6.97	6.99	7.03	7.01	6.98

5. Stress values in the bottom plate of the cantilever composite box girder (MPa) (x = 0, uniform load).

Calculation method	Horizontal coordinates of the bottom plate (m)
Calculation method	0.00	0.05	0.10	0.15	0.20	0.25
Method of this paper	−39.814	−40.954	−44.375	−50.071	−58.046	−68.303
Method of finite element	−37.659	−39.241	−42.653	−49.035	−56.204	−66.316
& (%)	5.722	4.365	4.037	2.113	3.277	2.996
Fold effect (%)	13.82	13.84	13.96	14.11	14.24	14.41

From Tables 2–5, it can be seen that the calculation results of the method in this paper agree well with the finite element values, and the error is basically controlled at about 5%, thus verifying the accuracy of the method. The fold effect at the intersection of the web and the top and bottom plate under the concentrated load is 26.31% and 28.45%, respectively. Under uniform load, the fold effect at the intersection of the web and the top and bottom plates is about 7% and 14%, respectively. The reason for the fold effect is that after the flat steel web is replaced by the corrugated web, its longitudinal stiffness becomes smaller, and the deformation of the flange and the web is incompatible under the vertical load, resulting in additional strain at the connection between the flange and the web.

Figures 5 and 6 show the variation law of the shear lag coefficient along the longitudinal direction of the cantilever composite box girder under uniform loads and concentrated loads, respectively, and the shear lag coefficients are taken from the junction of the upper flange with the corrugated steel web (y = 0.25 m) and the centre of the top plate (y = 0.00 m). Figure 7 shows the transverse distribution curves of the shear lag coefficients of two different sections under vertical bending loads, with the maximum shear lag effect occurring at the fixed end section (x = 0.00 m) and a more serious negative shear lag effect at the section (x = 2.00 m).

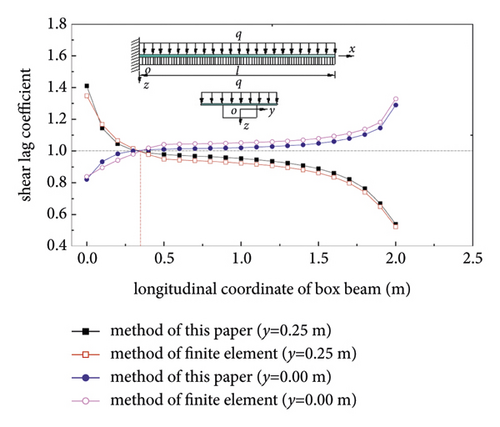
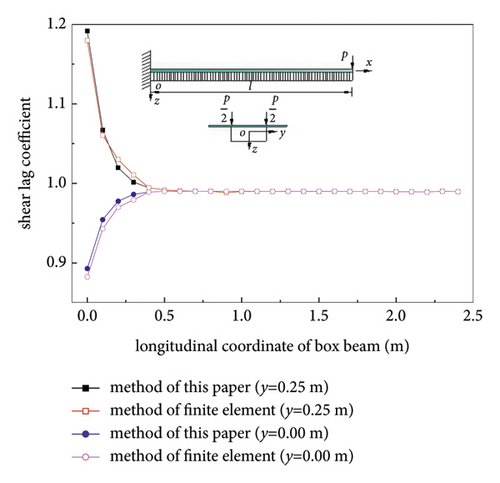
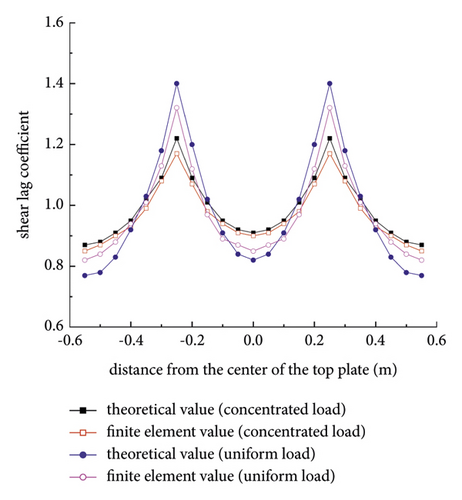
From Figures 5–7, it can be seen that the corresponding shear lag coefficients obtained from the theory and finite element method in this paper are basically consistent with the variation law along the longitudinal direction of the box girder. For cantilever composite box beams, the shear lag effect under uniform load is stronger than that under concentrated load. Under uniform load, not only shear lag effect occurs in cantilever composite box girder but also negative shear lag effect occurs at about 0.31 m away from fixed end, but no such phenomenon occurs under concentrated load. This phenomenon indicates that the load formed is one of the main factors for the negative shear lag effect of the structure, while the shear lag effect tends to be stronger with the increase of the distance from the fixed end. The shear lag effect of the section near the fixed end under the concentrated load is obvious and then decreases along the span direction.

The calculated results of the longitudinal deflection curves of cantilever composite box girders under concentrated load and uniform load are shown in Figures 8 and 9 respectively, and the comparison of the deflection of cantilever end section is shown in Table 5.

From Figures 8 and 9 and Table 6, it can be seen that the theoretical calculations in this paper agree well with the finite element values and the theoretical values of the Timoshenko girder theory, which verifies the rationality of the theoretical method. The deflection error of the theoretical calculation of the Euler beam has exceeded 9.6%. The additional deflection of shear deformation and shear lag increases from the fixed end to the cantilever end, and the additional deflection of shear deformation and shear lag of the cantilever end section under the concentrated load accounts for 22.26% and 7.82% of the primary girder deflection, respectively, indicating that shear lag and shear deformation cannot be ignored in the deflection calculation of this type of cantilever composite girder. The theoretical method in this paper can accurately calculate the longitudinal deflection curve of a cantilever composite box girder.

6. Comparison of deflection at cantilever end section.

Position	Concentrated load					Uniform load
Position	w/mm	f₁/mm	f₂/mm	(f₁/w)/%	(f₂/w)/%	w/mm	f₁/mm	f₂/mm	(f₁/w)/%	(f₂/w)/%
Section of the cantilever end	1.496	0.333	0.117	22.26	7.82	1.007	0.213	0.064	21.15	6.36

Note: w is the theoretical deflection value of Euler, f₁ is the additional deflection value of shear deformation, and f₂ is the additional deflection value of the shear lag.

4. Parameters Analysis

Based on the model beam in example 2, the influence of the width span ratio of the cantilever composite box girder and the bending angle of corrugated steel webs on shear lag and fold effect is analyzed by the ANSYS finite element method.

4.1. Width Span Ratio

The influence of width span ratio 2b1/l is analyzed by changing the flange width 2b1 of the cantilever corrugated web box girder. The parameter range of the wide span ratio is 0.163, 0.204, 0.245, 0.286, and 0.327. The maximum shear lag coefficient and fold effect of the fixed-end section wing under different width span ratios are compared, and the results are shown in Figure 10. Z1 and Z2 represent the maximum fold effect of the wing plate and the bottom plate under concentrated load, respectively. Z3 and Z4 represent the maximum fold effect of the wing plate and the bottom plate under uniform load, respectively. J5 and J6 represent the maximum shear lag effect of the wing plate under uniform load and concentrated load, respectively.

It can be seen from Figure 10 that when the width span ratio increases from 0.163 to 0.327, the maximum shear lag coefficient of the wing plate under uniform load increases from 1.24 to 1.57, and the maximum shear lag coefficient of the wing plate under concentrated load increases from 1.06 to 1.36. Therefore, the shear lag coefficient of the fixed end section of the cantilever composite box girder shows an upward trend with the increase of the width span ratio. The maximum fold effect of the wing plate under concentrated load increases from 24.19 to 28.05 and there is a positive correlation between shear lag effect and fold effect.

4.2. Corrugated Steel Web Bending Angle

Keeping the cross-sectional dimensions and span of the box girder unchanged, the corrugated steel webs were selected from three commonly used types, namely: 1600, 1200, and 1000, corresponding to corrugated angles of 30.74°, 36.53°, and 45°, respectively. Comparing the maximum shear lag coefficient and fold effect of the fixed end section flange under different corrugated angles, the results are shown in Figure 11.

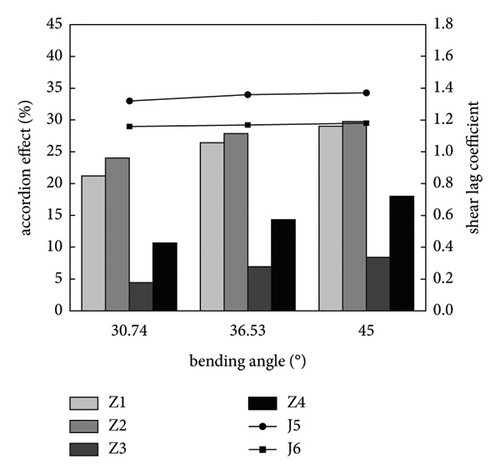
It can be seen from Figure 11 that when the bending angle increases from 30.74° to 45°, the shear lag coefficient of the fixed end section of the cantilever composite box girder shows an upward trend under the vertical load, but the amplitude is very small, and the maximum increase is 0.05, so it can be considered that the bending angle has no effect on the shear lag coefficient. Under the concentrated load, the maximum fold effect value of the wing plate of the fixed end section rises from 21.19 to 28.99, with an increase of 36.81%. Therefore, with the increase of the bending angle, the fold effect of the composite box girder is obviously enhanced.

5. Conclusion

In this work, the following conclusions were obtained:

(1)
Based on the energy variation principle, the calculation method which can accurately calculate the deflection and stresses of the composite box girder with CSWCB is proposed by comprehensively considering shear lag, shear deformation, and fold effect.
(2)
The fold effect generated by corrugated steel webs has a certain effect on the mechanical properties of the cantilever composite girder wings, and the effect of the fold effect is greater under concentrated loads than under uniform loads.
(3)
The deflection error of the composite box girder with CSWCB calculated by the Euler beam theory exceeds 9.6%, and the shear deformation and shear lag additional deflection of the cantilever end section under concentrated load account for 22.26% and 7.82% of the deflection of the primary girder, respectively, indicating that shear lag and shear deformation cannot be ignored in the deflection calculation of this type of girder.
(4)
Only a shear lag effect occurs in a cantilever composite box girder under concentrated load, while shear lag and negative shear lag effects exist simultaneously under uniform load, and the effects of both shear lag and negative shear lag tend to be stronger as the width span ratio increases.
(5)
With the increase in the width span ratio, the effects of shear lag and fold effect of the composite box girder show a consistent increase. With the increase of the bending angle, the fold effect of the composite box girder with CSWCB is obviously enhanced, but the change in the bending angle has a negligible effect on the shear lag effect.

Conflicts of Interest

The authors declare that there are no conflicts of interest.

Acknowledgments

Science and Technology Plan of Gansu Province of China (19ZD2GA002).

Open Research

Data Availability

The data generated or used during the study are included within the article.

References

1 Nie J. G., Zhu Y. J., Tao M. X., Guo C. R., and Li Y. X., Optimized prestressed continuous composite girder bridges with corrugated steel webs, Journal of Bridge Engineering. (2017) 22, no. 2, 1–17, https://doi.org/10.1061/(asce)be.1943-5592.0000995, 2-s2.0-85009726432.
10.1061/(ASCE)BE.1943-5592.0000995
Web of Science® Google Scholar
2 Li Y., Chen L., and Liu B., Analytical solution derivation and parametrical analysis of bending-torsional effects of curved composite beam with corrugated steel webs, Journal of the China Railway Society. (2019) 41, no. 1, 101–108.
Google Scholar
3 Hu H., Li J., and Qiang S., Study on shear buckling property of corrugated steel web PC combined box girder, Journal of Railway Engineering Society. (2011) 149, no. 2, 80–83.
Google Scholar
4 Li L., Hou L., and Sun J., Research on shear mechanical property of corrugated steel webs, Journal of Hunan University. (2015) 42, no. 11, 56–63.
CAS Google Scholar
5 Driver R. G., Abbas H. H., and Sause R., Shear behavior of corrugated web bridge girders, Journal of Structural Engineering. (2006) 132, no. 2, 195–203, https://doi.org/10.1061/(asce)0733-9445(2006)132:2(195), 2-s2.0-30844431516.
10.1061/(ASCE)0733-9445(2006)132:2(195)
Web of Science® Google Scholar
6 Elgaaly M., Hamilton R. W., and seshadri A., Shear strength of beams with corrugated webs, Journal of Structural Engineering. (1996) 122, no. 4, 390–398, https://doi.org/10.1061/(asce)0733-9445(1996)122:4(390), 2-s2.0-0030126208.
10.1061/(ASCE)0733-9445(1996)122:4(390)
Web of Science® Google Scholar
7 Gan Y., Wang G., and Jin X., Research on the statics properties of composite I-beams with corrugated steel webs, Journal of Railway Engineering Society. (2020) 258, no. 3, 27–33.
Google Scholar
8 Chan C. L., Khalid Y. A., and Sahari B. B., Finite element analysis of corrugated web beams under bending, Journal of Constructional Steel Research. (2002) 58, no. 11, 1391–1406, https://doi.org/10.1016/s0143-974x(01)00075-x, 2-s2.0-0037179435.
10.1016/S0143-974X(01)00075-X
Web of Science® Google Scholar
9 Wang Z. and Zhang Y., Research on transverse internal force of single box double cell composite box girder with corrugated steel web, Journal of the China Railway Society. (2019) 41, no. 12, 106–112.
Google Scholar
10 Zhao P. and Ye J., Analysis of transverse temperature effects on the deck of box girder with corrugated steel webs, Journal of Harbin Engineering University. (2019) 40, no. 5, 974–978.
Google Scholar
11 Deng W., Mao Z., and Liu D., Analysis and experimental study on torsion and distortion of single box three-cell cantilever girder with corrugated steel webs, Journal of Building Structures. (2020) 41, no. 2, 173–181.
Google Scholar
12 Zhang Z. and Wang G., Study on the influence of folding effect on the mechanical characteristics of new composite box girder, Journal of Railway Science and Engineering. (2019) 16, no. 10, 2491–2496.
Google Scholar
13 Hassanein M. F. and Kharoob O. F., Shear buckling behavior of tapered bridge girders with steel corrugated webs, Engineering Structures. (2014) 74, 157–169, https://doi.org/10.1016/j.engstruct.2014.05.021, 2-s2.0-84901976722.
10.1016/j.engstruct.2014.05.021
Web of Science® Google Scholar
14 Yi J., Gil H., and Youm K., Interactive shear buckling behavior of trapezoidally corrugated steel webs, Engineering Structures. (2008) 30, no. 6, 1659–1666, https://doi.org/10.1016/j.engstruct.2007.11.009, 2-s2.0-43449096022.
10.1016/j.engstruct.2007.11.009
Web of Science® Google Scholar
15 Ma C., Liu S., and Li A., Shear lag effect of continuous corrugated steel web-steel bottom-concrete top composited box girders, Applied Mathematics and Mechanics. (2020) 41, no. 5, 517–529.
Google Scholar
16 Wang G., Fan J., and Cao J., Research on the vertical bending mechanical behaviors of new composite box girders, Journal of Railway Engineering Society. (2019) 252, no. 9, 23–30.
Google Scholar
17 Li J., The Study on Torsional Behavior of Steel Box Composite Beams with Corrugated Web, 2018, Ph.D. thesis Zhengzhou University, Zhengzhou, China.
Google Scholar
18 Ma C., Liu S. Z., Jin J., and Zhang R. J., Analysis of pure bending vertical deflection of improved composite box girders with corrugated steel webs, Advances in Civil Engineering. (2021) 2021, 6617846, https://doi.org/10.1155/2021/6617846.
10.1155/2021/6617846
Web of Science® Google Scholar
19 Ling L., Hikosaka H., and Komine K., Simulation of accordion effect in corrugated steel web with concrete flanges, Computers & Structures Structures. (2004) 82, no. 23-26, 2061–2069, https://doi.org/10.1016/j.compstruc.2003.07.010, 2-s2.0-4944256851.
10.1016/j.compstruc.2003.07.010
Web of Science® Google Scholar
20 Zhang Y., Hu Y., and Lin L., Analysis on shear lag effect of thin-walled box girders based on a modified warping displacement mode, China Civil Engineering Journal. (2015) 48, no. 6, 44–50.
Google Scholar
21 Reissner E., Analysis of shear lag in box beams by the principle of minimum potential energy, Quarterly of Applied Mathematics. (1946) 4, no. 3, 268–278, https://doi.org/10.1090/qam/17176.
10.1090/qam/17176
Web of Science® Google Scholar
22 Zhou S. J., Finite beam element considering shear-lag effect in box girder, Journal of Engineering Mechanics. (2010) 136, no. 9, 1115–1122, https://doi.org/10.1061/(asce)em.1943-7889.0000156, 2-s2.0-78651381170.
10.1061/(ASCE)EM.1943-7889.0000156
Web of Science® Google Scholar
23 Zhang Z., Jin X., and Gan Y., Vertical bending mechanical properties of box composite girder with corrugated steel webs, China Railway Science. (2019) 40, no. 6, 52–59.
Google Scholar

Citing Literature

All articles

Static Characteristics of Improved Composite Box Girder with Corrugated Steel Webs

Abstract

1. Introduction