Dynamical Analysis of Nonlocalized Wave Solutions of (2 + 1)-Dimensional CBS and RLW Equation with the Impact of Fractionality and Free Parameters
Abstract
This study retrieves some new exact solutions to the (2 + 1)-dimensional Calogero-Bogoyavlenskii-Schilf (CSB) equation and regularized long wave (RLW) equation in the context of nonlinear traveling wave phenomena. In this regard, the advanced exp(−φ(ξ))-expansion method is imposed to the (2 + 1)-dimensional CBS and RLW equation, and consequently, rogue, kink, singular kink, periodic, singular, and multiple soliton solutions are exhibited in terms of trigonometric, hyperbolic, and rational function solutions. To enucleate the underlying nonlocalized traveling wave features, accomplished exact solutions are established by making their dynamic behavior of the exact solutions exhibited in three-dimensional (3D) and two-dimensional (2D) combined chart with the help of computational software Maple 18. All of our accomplished solutions are claimed to be new in the sense of conformable derivative, chosen a unique fractional type wave transformation, dynamical behavior of fractionally and free variable, and the imposed method on our preferred equations.
1. Introduction
Most of the physical problems are now formatted into mathematical schemes through partial differential equations (PDEs). In recent years, calculus of fractional nonlinear differential condition is one of the rising concern of nonlinear dynamics as well as plays an eventual role in real-life problems such as plasma physics [1], quantum mechanics [2], fluid mechanics [3], optical fibers [4], and other fields of applied mathematics and engineering. Calculus of fractional derivative is the generality of the traditional order of integration and differentiation and a conventional technique for demonstrating complex physical behavior, especially of the nonlinear mathematical science of engineering and physics. In the recent past, nonlinear fractional partial differential equations (FPDEs) have been inventing a potential platform for the researchers to interpret the tangible phenomena. As a result, some significant, concise, and original methods have been explored and explain to exact closed solutions of nonlinear FPDEs, videlicet, namely, the Hirota bilinear method [5, 6], modified extended tanh-function method [7], (G′/G)-expansion method [8], fractional subequation method [9], modified trial equation method [10], advanced exp(−φ(ξ)) method [11], tan(−φ(ξ))-expansion method [12], and improved Kudryashov method [13]. Recently, some researchers, like, Ferdous et al. [14], attained exact wave solutions to the extended Zakharov–Kuzetsov equation by implementing the generalized exp(−φ(ξ))-expansion method. Alike, adopting the exp(−φ(ξ))-expansion modified technique, Khater [15] has established three different types of nonlocalized traveling wave solutions to the generalized Hirota-Satsuma (HS) couple KdV system. Encouraged by ongoing research on related topics, we extract the recent and more common precise solitary wave solutions to some nonlinear FPDEs, described earlier by proposing the advanced method of exp(−φ(ξ))-expansion, which can be considered the generalization of the generalized form of exp(−φ(ξ))-expansion [16].
Our current study mainly explores the dynamical changes of conformable time-fractional (2 + 1)-dimensional CSB equation [17] and regularized long wave (RLW) equation by employing the new progressive exp(−φ(ξ))-expansion technique. Recent past, Rahman et al. [18] imposed this technique on some nonfractional NLEEs, but they did not show any productive concept to conformable nonlinear time fractional sense of NPEEs. We decisively believe that our stated advanced exp(−φ(ξ)) modified method will be frolicked a significant role in investigating the traveling wave arrangements of nonlinear science and mathematical physics. Here it is significant to note that our stated fractional equations are in a conformable sense so we have converted our equations in fractional form.
where 0 < θ ≤ 1.
The RLW equation is a particular class of nonlinear conformable fractional equations that generates fruitful models for predicting the water wave and physical phenomena [32]. Many authoritative approaches have been the subject of investigating the RLW equation, such as the Fourier leap-frog method [33], finite difference method [34], Hirota direct method approach [35], and modified extended tanh method [36]. Whereas so far we know, with the sense of conformable derivative, there is no prolific results have not yet been established about our declared technique to simplify the RLW equation. The exact wave solutions of RLW equation we attained are completely new in respect of our mentioned method.
Recently, Ferdous et al. [14] proposed a generalized exp(−φ(ξ))-expansion method by choosing the auxiliary ODE of the form φ′(ξ) − λ exp(φ(ξ)) − μ exp (−φ (ξ)) = r. In our mentioned method, we take the auxiliary nonlinear ODE of the form φ′(ξ) − λ exp (φ (ξ)) − μ exp (−φ (ξ)) = 0 by setting r = 0. Here λ and μ are real type parameters, and reasonably, our said supplementary form affords much better complete solutions to the FPDEs as well as has a more comprehensive operational physical explanation than the findings of Ferdous et al. [14]. The important favor of our specified technique over the other approaches [15, 18] is that it provides some straight and succinct form of new exact wave solution, as well as it is very useful, well-organized, and responsive applicable in presenting of exact and explicit wave solutions to NPDEs, arises in science, mathematical physics, and engineering.
We have employed successfully the exp(−φ(ξ) method on CBS and RLW equations to treasure the meticulous traveling wave solutions which have not appeared beforehand in publications.
We believe that our discoveries might be used to computer simulations of water waves in shallow water, to the study of the propagation of small amplitude long waves on the surface of shallow water, and to the advancement of scientific knowledge. Theoretical physicists, applied mathematicians, and ocean engineers who are interested in the precise solutions to moving rogue waves should all find this paper to be of interest. When this project is successfully completed, it may be possible to forecast the sea level of a coastal area during natural catastrophes. Low pressure systems like cyclones are the main culprits in natural disasters.
The paper’s structure is as follows: the conformable derivative’s narration and its elementary possessions are given in Section 2. The advanced exp(−φ(ξ)) expansion scheme has been outlined in Section 3. In Section 4, we apply this approach to the time-fractional (2 + 1)-dimensional equation of CBS and RLW. The findings and the debate are discussed in Section 5, and the conclusions are provided in Section 6.
2. Inceptions and Procedures
2.1. Definition and Some Features of Conformable Fractional Derivative
Khalil et al. [37] primarily exposed the sense of conformable derivative with a limit operator.
Definition 1. If , then the conformable derivative with the fractional sense of f order δ is defined as
Later, in the fractional-order method, Abdeljawad [38] also discussed chain law, Gronwall’s inequality, exponential functions, definite and infinite component integration, Taylor power series expansions, and Laplace transform conformable derivative. The difficulty of exiting the modified Riemann-Liouville derivative description [39] will efficiently resolve the concept of a conformable fractional-order derivative.
Theorem 2.
Let ω ∈ (0, 1] and f = f(t), g = g(t) be ω-conformably differentiable at a point t > 0; then,
- (i)
- (ii)
- (iii)
- (iv)
Moreover, if the function f is differentiable, then .
Theorem 3. Consider f : (0, ω)⟶R be a real type function such that f is differentiable and ω-conformable derivable. Also, assume that g be a derivable function well-defined in the range of f. Then, we have , where prime indicates the simple derivatives with respect to the point t.
In this research, we have careful about the preferred equation with the concept of conformable-based derivative. In circumstance of basic calculus, numerous functions do not expand Taylor’s power-order illustrations on specific points but in the technique of conformable-order derivative, they do consume the existence. CD accomplishes good in the product and chain rule while complicated plans appear in logic of basic fractional geometry. The CD of a constant type function is correspondent to zero wherever it is not the topic for Riemann derivative of fractional order. Mittag Leffler functions show a noteworthy authoritative in fractional-order calculus as interpretation to exponential function where the fractional-order form of exponential type function of the form f(t) = e(tα/α) seems in circumstance of CD.
3. Overview of the Method
Step 1. We deliberate a traveling variable for transferring the mentioned equation to nondimensionality. We alter all self-governing variable into a single variable, by the following way.
By employing mentioned variable, Equation (7) allows us in dropping Equation (6) in ODE for Π(x, t) = u(ξ) in the type
Step 2. Let us consider that a polynomial can begin the solution of OD Equation (8) in the
Here N is the positive integer, which can be integrated by consistency of the highest order of derivatives to the highest order of nonlinear portions, performed in Equation (8).
Also, the differential of φ(ξ) satisfies ODE in the subsequent form
Case 1. The function solutions are hyperbolic (when λμ < 0):
Case 2. The function solutions are trigonometric (when λμ > 0):
Case 3. When μ > 0 and λ = 0,
Case 4. When μ = 0 and ,
where C is defined as constant, λμ < 0 , or λμ > 0 is conditional on the symbol of μ.
Step 3. By submitting Equation (9) into Equation (8) and finally consuming Equation (6), assemble all like term of order of exp(−qφ (ξ)), q = 0, ±1, ±2, ±3..⋯ prearranged; then, we achieve a polynomial form of exp(−qφ (ξ)) and connecting each coefficient of the gotten polynomial corresponding to zero, yields system of algebraic equations (SAE).
Step 4. Assume the constants’ determination be attained as one or more results by determining the mathematical conditions in phase 3. Putting the constant designs laterally with the measures for Equation (7), from the evaluation equation, we can attain up-to-date, extensive, and exhaustive dynamic wave propagation (6).
4. Application of the Suggested Method
4.1. Application of (2 + 1) CBS Equation
Hereafter differentiating Equation (18) regarding ξ and putting the value u, u′, u‴ into Equation (17), we obtain the same polynomial set.
Now solving the system of equations, we get one set of solutions.
Case 1. When λμ < 0, the following solutions are obtained for hyperbolic functions:
Family 1
Family 2
Case 2. The function solutions are trigonometric when λμ > 0.
Family 1
Family 2
Case 3. When μ > 0 and λ = 0, the solution is not sufficient, so we can neglect this case.
Case 4. u5(x, y, t) = A0 + 12/(α + β)(ξ + C), where, ξ = x + y and C is an arbitrary constant.
4.2. Application of RLW Equation
Hereafter, we differentiate Equation (28) regarding ξ and putting the required value u, u2, u″ in Eq.(17).
Now by solving this system of equations, we find two sets of solutions as below.
Case 1. when λμ < 0, the following solutions are obtained for hyperbolic functions:
Set 1.
Family 1
Family 2
where .
Set 2
Family 1
Family 2
where .
Case 2. The function solutions are trigonometric when λμ > 0.
Set 1
Family 1
where .
Family 2
where .
Set 2
Family 1
where .
Family 2
where .
5. Results and Discussion
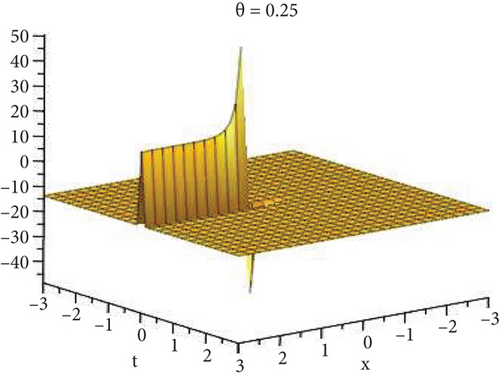
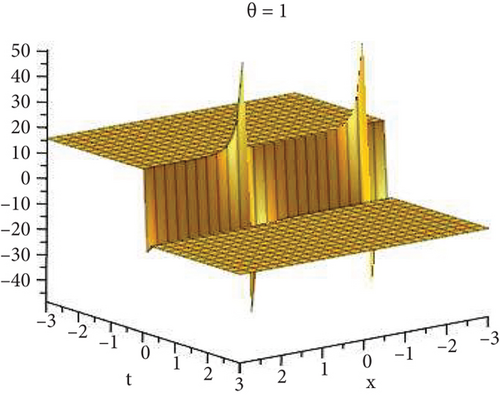
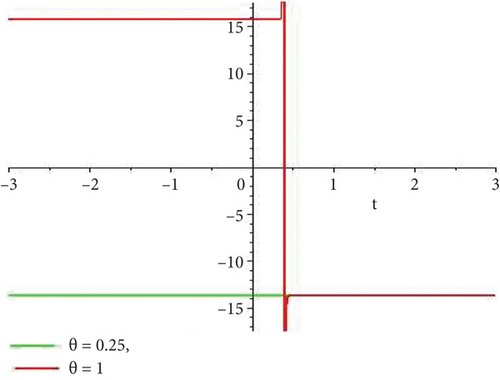
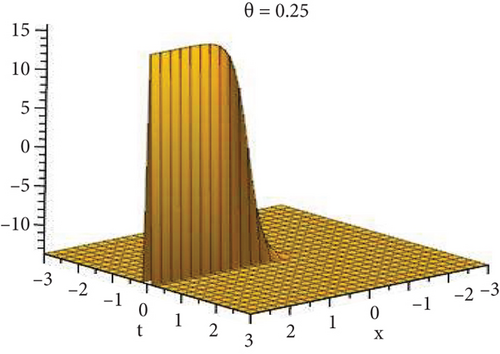
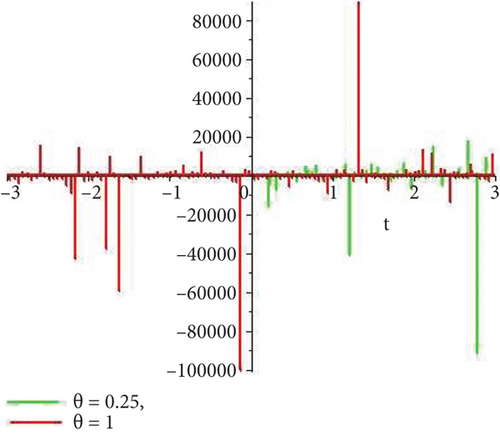
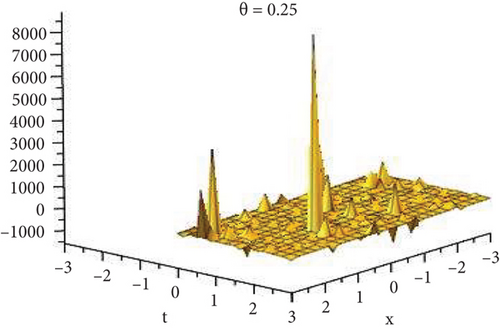
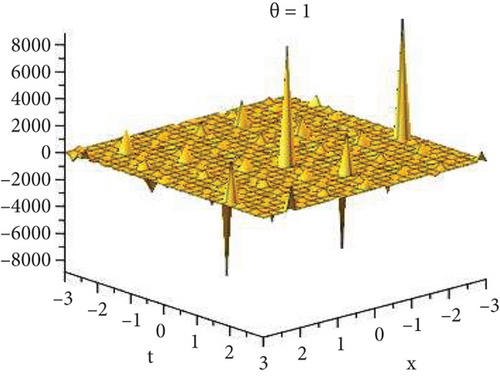
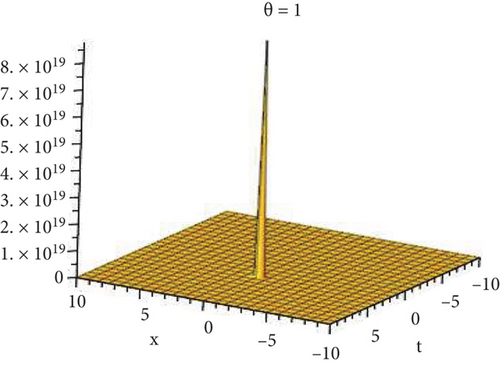
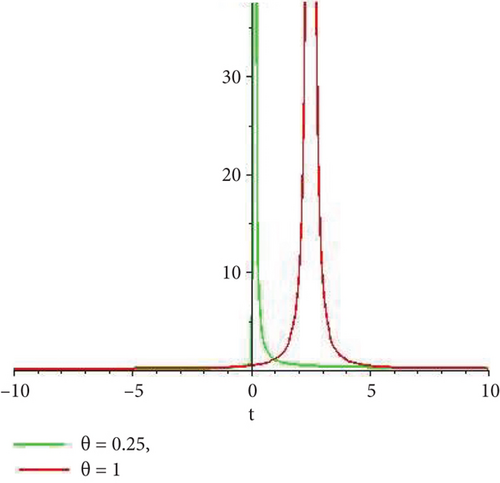
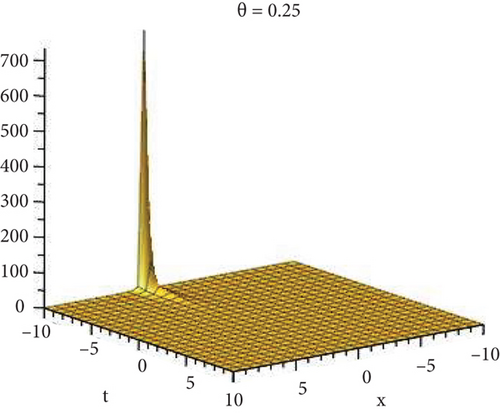
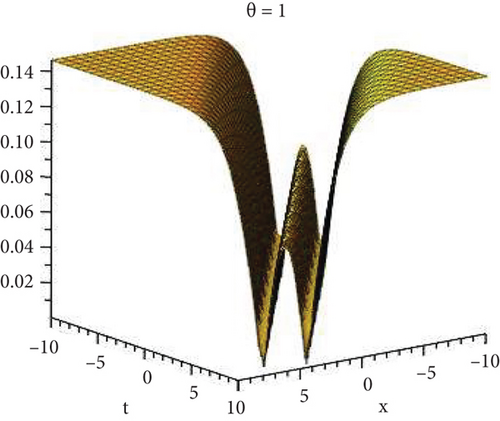
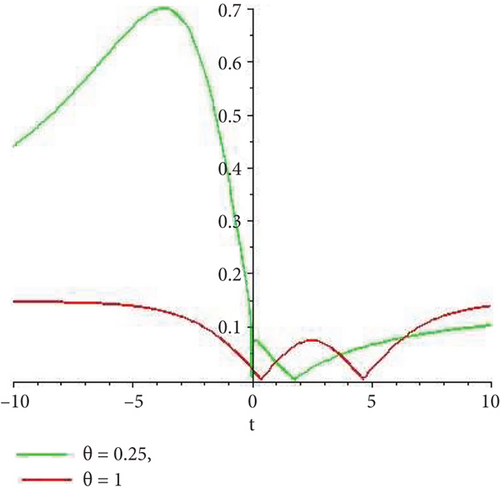
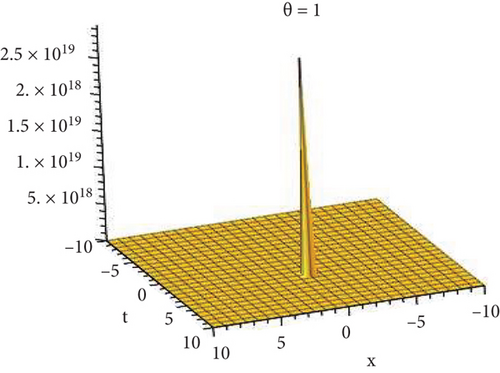
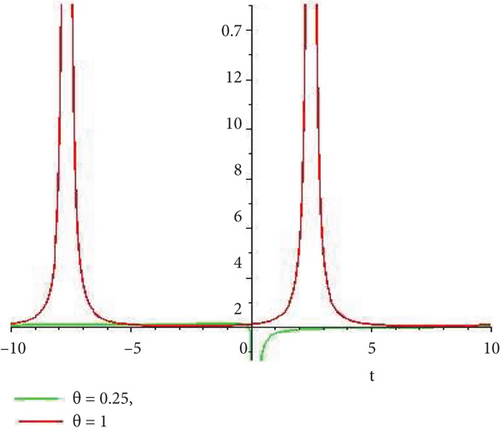
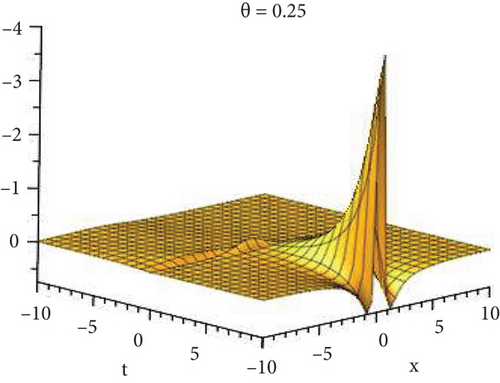
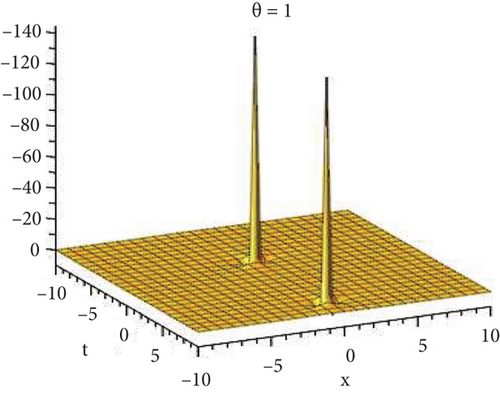
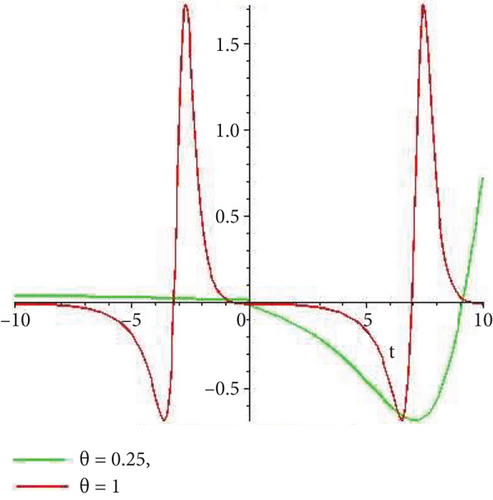
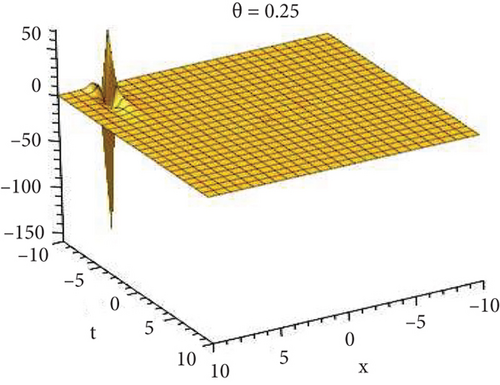
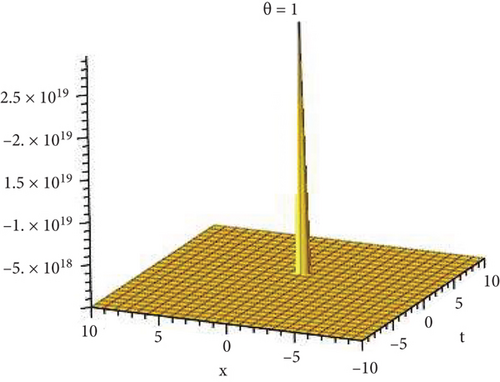
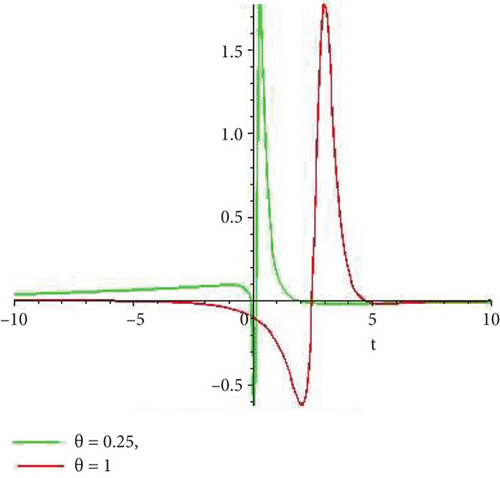
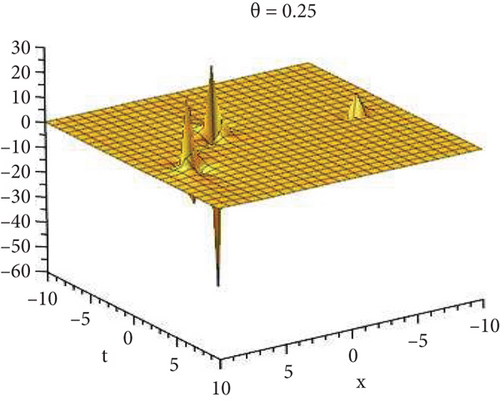
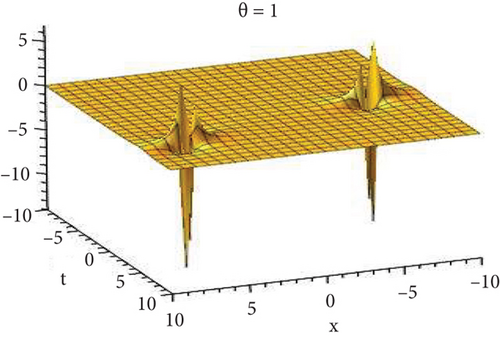
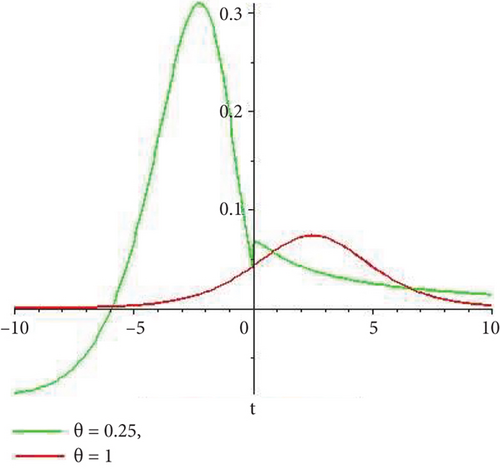
Physical and graphical representation of newly established solutions of the (2 + 1)-dimensional CBS and RLW equation will be well-defined in this segment. Pictorial representation is the absolute means of envisioning the complete tangible sense of real-life concerns. We also showed the graphical depiction of our resultant solutions exhausting the computational Maple features to designate the fractional-order derivative by selecting suitable fractional values of θ. We have assigned specific high costs to the unidentified parameters to envision the consequent solutions’ natural features. The established equations are presented in Figures 1–13, which have been designed.
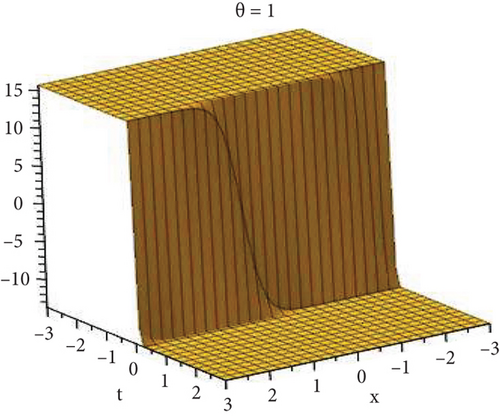
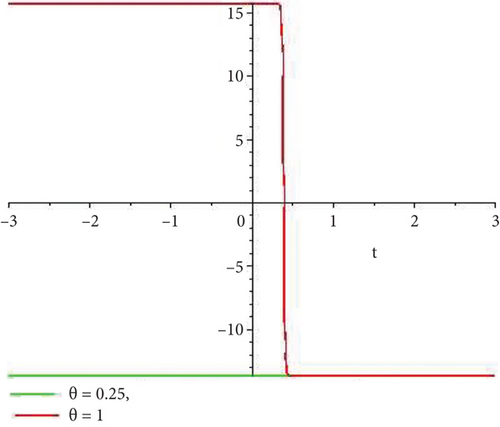
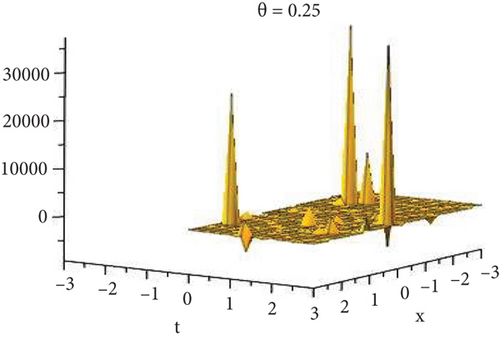
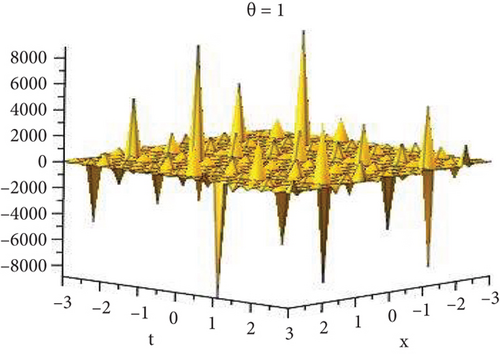
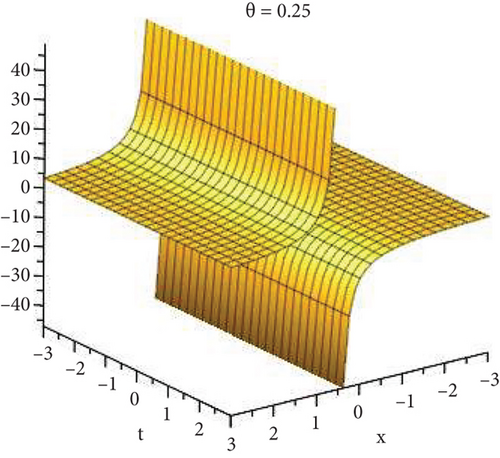
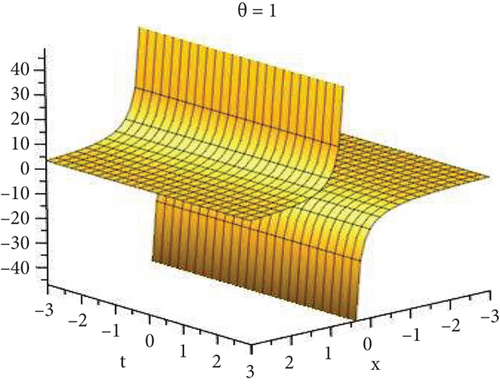
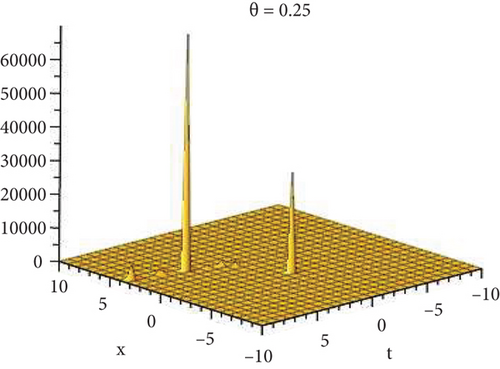

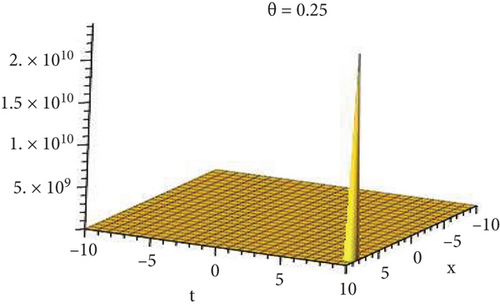
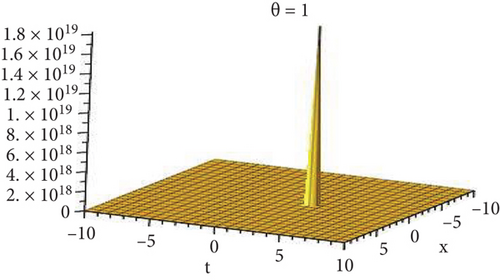
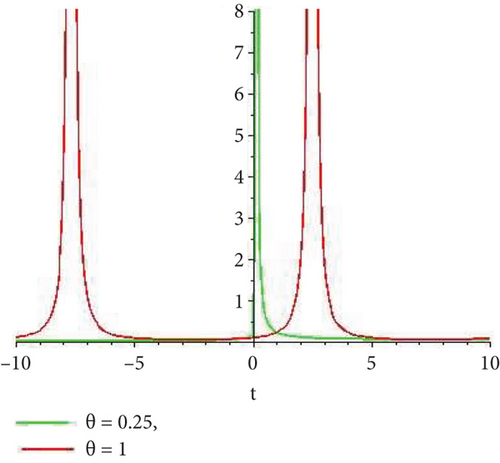
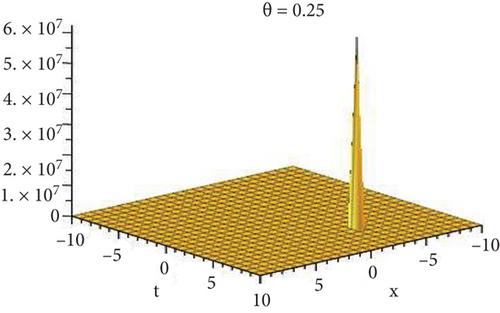
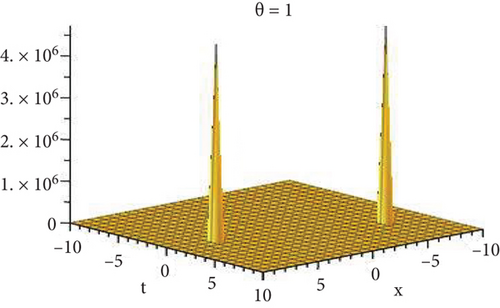
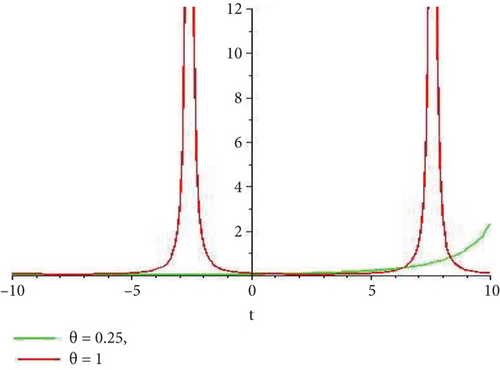
5.1. Physical Explanation
This subsection will focus on the physical elucidation of the (2 + 1)-dimensional CBS and RLW equation exact solutions by utilizing the advanced exp(−φ(ξ))-expansion scheme. The attained solutions u1(x, y, t), u2(x, y, t), u8,9(x, t), u10,11(x, t), and u12, 13(x, t) are hyperbolic function solutions, u3(x, y, t), u4(x, y, t), u14,15(x, t), u6,7(x, t)u16,17(x, t), u18,19(x, t), and u20,21(x, t) are trigonometric function solutions, and u5(x, t) is an algebraic solution. Figures 1–5 are presented from CBS equation. Figures 6–13 are from the RLW equation. In every set of figures, we have changed the free parameter of our preferred equation and fractional-order derivative θ = 0.25 to 1 with other suitable parameters to show the dynamical behavior of attained solutions. Figure 1 represents the singular soliton shape u1(x, y, t) for the fractional value θ = 0.25 with the suitable parameters λ = 3, μ = −2, C = −0.5, A = 1, α = 1, and β = 1; with the change of fractional parameter, θ = 0.25 to 1, the solution shape changes its amplitude and size only, but there have no changes for the variety of free parameters α and β. Figure 2 represents the bright soliton solution shape u2(x, y, t) for the fractional value θ = 0.25 with the suitable parameters λ = 3, μ = −2, C = −0.5, A = 1, α = 1, and β = 1. With the change of fractional parameter, θ = 0.25 to 1, the solution shape turns into the dark soliton shape. Here for the evolution of free parameters α and β, the solution shape changes its amplitude and size only. Figures 3 and 4 represent the periodic singular solution shape u3(x, y, t) and u4(x, y, t) for the fractional value θ = 0.25 with the suitable parameters. With the variety of fractional parameters θ = 0.25 to 1 and free parameters, the solution has no dynamical change but only its amplitude and size. Figure 5 represents the singular soliton solution shape u5(x, y, t) for the fractional value θ = 0.25 with the suitable parameters λ = 2, μ = 0, C = −0.5, A = 1, α = 1, and β = 1. With the variety of fractional parameters θ = 0.25 to 1 and free parameters, the solution has no dynamical change. Figures 6–9 belong to the set-1 solution set, and Figures 10–13 belong to the set-2 solution set of the RLW equation. Figure 6 represents the two soliton solution shape of u6(x, t) for the fractional value θ = 0.25 with the suitable parameters λ = 3, μ = −0.2, C = −0.5, n = −0.4, α = 6, and β = 10. With the variety of fractional parameters, θ = 0.25 to 1, the two-soliton shape turns into the one-soliton shape and has no change with free parameters. Figure 7 represents the one-soliton solution shape u7(x, t) for the fractional value θ = 0.25 with the right parameters λ = 3, μ = −0.2, C = −0.5, n = −0.4, α = 6, and β = 10. Shape moves to W-shaped solution shape for the transformation of fractional-order derivative θ = 0.25 to 1. Herewith, with the change of free parameters α and β, the solution shape changes its amplitude and size only. Figures 8 and 9 represent the singular soliton shape of u14,15(x, t) and u16,17(x, t) for the fractional value θ = 0.25 with the suitable parameters λ = 3, μ = −0.2, C = −0.5, n = −0.4, α = 6, and β = 10. With the variety of fractional parameters, θ = 0.25 to 1, the singular soliton shape turns into the two-soliton shape and has no change with free parameters. Figure 10 represents the rogue wave soliton shape u10,11(x, t) for the fractional value θ = 0.25 with the suitable parameters λ = 3, μ = −0.2, C = 1, n = −0.4, α = 6, and β = 10. With the variety of fractional parameter, θ = 0.25 to 1, the rogue wave turns into the singular soliton shape. Figure 11 represents the rogue wave soliton shape u12,13(x, t) for the fractional value θ = 0.25 with the suitable parameters λ = 3, μ = −0.2, C = 1, n = −0.4, α = 6, and β = 10. With the variety of fractional parameter, θ = 0.25 to 1, the rogue wave changes its amplitude and size only. Figures 12 and 13 represent the singular soliton shape of u18,19(x, t) and u20,21(x, t) for the fractional value θ = 0.25 with the suitable parameters λ = 3, μ = −0.2, C = 1, n = −0.4, α = 6, and β = 10. With the variety of fractional parameters, θ = 0.25 to 1, the singular soliton shape turns into the two-soliton shape.
5.2. Graphical Representation
The graphical decorations of our attained solutions of the (2 + 1)-dimensional CBS and RLW equation have exposed in this subsection. Our preferred equations are resolved, and attained solutions are extracted from the trigonometric and hyperbolic function by computational tool Maple 21. For detailed physical clarity, all precise solution charts are exhibited in 3D as well as 2D combined stripe charts.
6. Conclusions
In the above study, exact wave solutions with several types of wave constructions for time fractional (2 + 1)-dimensional CBS and RLW equation have been accumulated through the advanced exp(−φ(ξ)) expansion technique. The dissimilar wave structures characterized the attained solutions’ dynamical behavior in this system. Preferred fractional and free parameters have significant insinuations, such as putting the dissimilar magnitude of the fractional and free parameters from a separate function of meaningful solutions can be originated exclusively and variation of suitable parameters has a significant impact on the wave. Moreover, we claim that our obtained traveling solutions are new in the sense of conformable derivative and could be operative in the research of nonlinear physical phenomena. It is very clear to decide that our promoted technique is effective, reliable, and friendly applicable and delivers sufficient well-matched explanations to NLFEEs arise in engineering, applied mathematics, nonlinear dynamics, and mathematical physics.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Acknowledgments
The authors like to express their gratitude to the Bangladesh University of Engineering and Technology (BUET), Bangladesh, for providing financial support under the Basic Research Grant No. 1111202109017. The second author (Foyjonnesa) specially wants to express her deepest gratitude to the Bangladesh University of Engineering and Technology (BUET), for selecting her as a PG Fellow (Ph.D. Mathematics).
Open Research
Data Availability
All required data were included in the manuscript and cited appropriately when it was required.




