Volume 2022, Issue 1 2880340

Research Article

Open Access

[Retracted] Assessment of the Business Proposals Using Frank Aggregation Operators Based on Interval-Valued T-Spherical Fuzzy Information

Retraction(s) for this article

Amir Hussain

orcid.org/0000-0002-3535-9414

Department of Mathematics, Riphah Institute of Computing and Applied Sciences, Riphah International University Lahore, Lahore 54000, Pakistan riphah.edu.pk

Search for more papers by this author

Kifayat Ullah,

Kifayat Ullah

orcid.org/0000-0002-1438-6413

Department of Mathematics, Riphah Institute of Computing and Applied Sciences, Riphah International University Lahore, Lahore 54000, Pakistan riphah.edu.pk

Search for more papers by this author

Haolun Wang,

Corresponding Author

Haolun Wang

[email protected]

orcid.org/0000-0001-7189-0264

School of Economics and Management, Nanchang University, Nanchang 330031, China ncu.edu.cn

Research Center of the Central China for Economic and Social Development, Nanchang 330031, China

Search for more papers by this author

Mehwish Bari,

Mehwish Bari

orcid.org/0000-0003-2652-0402

Riphah International College Bahawalpur Campus, Bahawalpur, Pakistan

Search for more papers by this author

Amir Hussain,

Amir Hussain

orcid.org/0000-0002-3535-9414

Department of Mathematics, Riphah Institute of Computing and Applied Sciences, Riphah International University Lahore, Lahore 54000, Pakistan riphah.edu.pk

Search for more papers by this author

Kifayat Ullah,

Kifayat Ullah

orcid.org/0000-0002-1438-6413

Department of Mathematics, Riphah Institute of Computing and Applied Sciences, Riphah International University Lahore, Lahore 54000, Pakistan riphah.edu.pk

Search for more papers by this author

Haolun Wang,

Corresponding Author

Haolun Wang

[email protected]

orcid.org/0000-0001-7189-0264

School of Economics and Management, Nanchang University, Nanchang 330031, China ncu.edu.cn

Research Center of the Central China for Economic and Social Development, Nanchang 330031, China

Search for more papers by this author

Mehwish Bari,

Mehwish Bari

orcid.org/0000-0003-2652-0402

Riphah International College Bahawalpur Campus, Bahawalpur, Pakistan

Search for more papers by this author

First published: 08 April 2022

https://doi.org/10.1155/2022/2880340

Citations: 12

Academic Editor: Hanan A. Al-Olayan

Share a link

Email
Wechat
Bluesky

Abstract

An interval-valued T-spherical fuzzy set (IVTSFS) is an efficient framework to treat ambiguous and vague information more efficiently. It has four functions consisting of the information in intervals. With the help of these functions, IVTSFS is a more reliable framework than the other existing frameworks. This article aims to establish algebraic operations of IVTSFSs named Frank sum, Frank multiplication, and Frank scalar multiplication stranded on Frank t-norm and t-conorm. Further, some averaging and geometric aggregation operators (AOs), i.e., interval-valued T-spherical fuzzy Frank weighted averaging (IVTSFFWA) and interval-valued T-spherical fuzzy Frank weighted geometric (IVTSFFWG) operators are established based on the defined operations, and then the properties of these operators are observed. The proposed approach is supported by an illustrative example, in which we have applied our proposed approach to a multiattribute group decision-making (MAGDM) problem. For the significance of the proposed approach, a comparative study is done. The various effects of the variation of parameters are also investigated which plays an important role in the final results.

1. Introduction

Mathematicians have been dealing with uncertainties and vagueness in data for many years. For this purpose, Zadeh [1] introduced the concept of fuzzy set (FS), where a membership grade (MG) is used to describe the uncertainty of an object, where m ∈ [0, 1]. Atanassov [2] introduced the model of an intuitionistic fuzzy set (IFS), in which he used two grades, MG m and a nonmembership grade (NMG) n to describe the uncertain situation. Yager [3] extended this concept to Pythagorean fuzzy set (PyFS), where the sole purpose was to increase the range of the IFS by allowing the sum of the squares of m and n in [0, 1]. Despite, the frame of PyFS provides a wider range for m and n to be taken, but still, it has limitations in some cases and hence does not guarantee the independency of the MG and the NMG. To enlarge the space for assigning m and n, Yager [4] proposed the notion of q-rung orthopair fuzzy set (qROFS) where the range for assigning the MG and the NMG is taken to a limitless level using a variable parameter q.

The literature in [1–4] only used two grades, i.e., the MG and NMG of an object for its description in an uncertain environment. But in many real-life problems, opinion about a phenomenon or an object may not be of two types only as discussed in the layout of IFS, PyFS, and qROFS. Cuong [5] observed that opinion about someone or something may have four aspects including favor, abstinence, disfavor, and refusal. To express such kind of opinion, Cuong [5] introduced the notion of picture fuzzy set (PFS) where he portrayed uncertain information using four types of memberships known by an MG, an abstinence grade (AG), NMG, and a refusal grade (RG), hence generalizing the notion IFSs by covering larger information than IFSs. The frame of PFS greatly reduces information loss by taking into account the AG and the RG, yet it has a certain restriction on the MG, NMG, and the AG. Mahmood et al. [6] observed that the frame of PFS has a limited choice for decision-makers to dispense the values of their concern to MG, AG, and NMG. To overcome this problematic situation, Mahmood et al. [6] introduced the model of the spherical fuzzy set (SFS) and analogously T-spherical fuzzy sets (TSFS) with the independent choice to assign the values to MG, AG, and NMG. TSFSs covered a big loss of information. However, Ullah et al. [7] introduced interval-valued TSFS (IVTSFS) having four functions with intervals to cover more information.

MAGDM became a very significant concept in FS theory due to its effects in the fields of engineering, management, and social sciences. FS theory has been applied to treat MAGDM problems for many years. It had started in 1970 when Bellman [8] used FS in decision-making. To treat MAGDM problems, IFS was used by Xu [9] with its aggregation tools. Rahman et al. [10] and Yager et al. [11] presented some AOs for PyFSs with a larger range for MG and NMG and used these AOs to deal with multiattribute decision-making (MADM) problems. In [12, 13], the authors developed AOs in the framework of PFSs and used them in MADM. Mahmood et al. [6] developed AOs for SFSs and TSFSs having no restrictions for MG, AG, and NMG. Ullah et al. [7] established AOs in the framework of interval-valued TSFSs (IVTSFSs) and solved the financial policy evaluation problem. Guleria and Bajaj [14] introduced AOs for T-spherical fuzzy (TSF) soft sets and utilized these AOs to solve multiattribute decision-making (MADM) problems. Karaaslan and Dawood [15] established complex (TSF) Dombi aggregation operators and used them in MAGDM. Xu et al. [16] solved the MADM problem by introducing an interval-valued q-Rung dual hesitant uncertain linguistic set. In [17] the authors developed AOs in an environment of IFS to solve the MADM problem. Wang and Li [18] developed AOs for hesitant PFS and used them in MADM. Akram et al. [19] introduced complex picture fuzzy Hamacher AOs and studied their application in MADM. In [20] Riaz and Hashmi developed the AOs in the environment of cubic m-polar fuzzy sets and applied them to solve MAGDM. Peng and Yang [21] developed AOs the phenomenon of interval-valued Pythagorean fuzzy (PyFS) and applied in MAGDM. Fahmi et al. [22] introduced cubic fuzzy Einstein AOs and applied them to the MAGDM problem. Ullah et al. [23] introduced TSF Hamacher AOs and applied them in the evaluation of the performance of robots. Garg et al. [24] developed TSF power AOs and applied them in MAGDM. Akram et al. [25] introduced IVTSFS Bonferroni mean AOs and applied them in the evaluation of solar energy cells.

All the described AOs are grounded on some t-norm and t-conorm. The frequently used t-norm and t-conorm is the product and probabilistic sum [26] because computation becomes very laidback by using this dual. But the deficiency of flexibility and robustness are the major negatives of these triangular norms. So, some AOs are familiarized with other t-norm and t-conorms to astound these drawbacks. Xia et al. [27] proposed AOs for IFSs information grounded on Archimedean t-norm and t-conorms. Liu and Wang [28] proposed a family of some AOs in the environment of IFSs based on Einstein t-norm and t-conorms. Shahzadi [29] inspected Hamacher hybrid AOs in the framework of Fermatean fuzzy number and applied them in MAGDM. Jin et al. [30] developed the aggregation operators for IVTSFS based on Hamacher t-norm and t-conorm. Jana [31] explored some MADM problems based on SVNTH methods. Jana et al. [32] introduced AOs in the environment of qROFS using Dombi t-norm and t-conorm and applied in MAGDM. Seikh and Mandal [33] introduced AOs in the framework of IFS using Dombi t-norms and t-conorms and applied them in MAGDM. Jana et al. [34] developed bipolar fuzzy Dombi AOs and applied them in MAGDM. Ullah et al. [35] developed IVTSF Dombi AOs and studied their application in MAGDM. Ullah [36] introduced picture fuzzy (PF) Maclaurin symmetric mean operators and applied them in MADM problems. Some remarkable work can be seen in [37–39].

By the use of the aforementioned t-norms and t-conorms, the level of robustness enlarged. However, the abovementioned t-norm and t-conorm are not much flexible to include all opinions (information) to model real-world MAGDM problems. To overcome the gap, Frank [40] generalized the Lukasiewicz and probabilistic t-norm and t-conorm to propose Frank t-norm and t-conorm, a flexible family of triangular norms. The inclusion of parameters in Frank t-norm and t-conorm makes them more malleable in the fusion of information and more appropriate to model the DM problems. Sarkoci [41] studied the comparison between Hamacher and Frank t-norms and found the same family of two different t-norms.

After the introduction of Frank t-norm and t-conorms, the mathematicians developed AOs by using this pair of norms. Zhang [42] introduced Frank AOs (FAOs) for IVIFSs and observed their application in MAGDM problems. Qin et al. [43] proposed FAOs for triangular interval type-2 fuzzy information based on Frank t-norms and t-conorms and applied them to MAGDM problems. In [44] the FAOs are developed in probabilistic hesitant fuzzy sets and their application in MAGDM. Tang et al. [45] proposed the FAOs in the framework of dual hesitant fuzzy information.

After the introduction of IVTSFSs, the decision-makers have become independent in expressing their information using the MGs, AGs, and NMGs in intervals with greater flexibility. Due to this property of IVTSFSs, and the significance of Frank t-norm and t-conorm, the concept FAOs in the framework of IVTSFSs is eminent and has some desirable properties. It is also noted that there is a lack of study of the effects of changing the behavior of the parameters of the FAOs in MAGDM problems. This fact motivated me to study the family of FAOs and their properties in the framework of IVTSFSs, grounded on frank t-norm and t-conorm, and consequently to apply to the MAGDM problem.

We divide the remaining paper into 9 further sections. We stated some basic concepts of IVTSFS and Frank t-norm and t-conorm in Section 2. In Section 3, we defined Frank operations of sum and multiplication in the framework of IVTSFSs. In Section 4, we defined the IVTSFFWA operator and investigate some basic properties of the IVTSFFWA operator. In Section 5, we define the IVTSFFWG operator and observe its basic properties. In Section 6, we planned an approach to apply IVTSFFWA and IVTSFFWG operators to a MAGDM problem. In Section 7, we applied proposed operators in the MAGDM problem with help of an illustrative example and observed the influence of parameters in Section 8. In Section 9, we investigated a comparative study with other AOs. In Section 10, we concluded our article.

2. Preliminaries

In this section, first, we will introduce fundamental concepts Frank t-norm and t-conorm and IVTSFFs which are used to understand the proposed approach. IVTSFS is a stimulating technique to deal with data, especially in uncertain and ambiguous situations. Due to the involvement of intervals, IVTSFS grabs more information from real-life situations whenever human opinions evolved and hence greatly reduces information loss. In Definition 1, we define IVTSFS as follows:

Definition 1 (see [7].)Let X be the universe of discourse, an IVTSFS T in X is defined as

(1)

where s, i, d : X⟶[0, 1] are MG, AG, and NMG such that s = [s^l, s^u], i = [i^l, i^u] and d = [d^l, d^u] with condition

. The RG of IVTSFS is defined as

and (s, i, d) is IVTSF number (IVTSFN).

Ullah et al. [7] defined the score function for IVTSFNs given as follows.

Definition 2. Let sc(α) denotes the score value of IVTSFN α, and score function can be defined as

(2)

All the operators defined on the FSs have been playing an important role since starting. These operators are grounded on the general concept of t-norms and t-conorms [27]. The definitions of the t-norm and t-conorm introduced by Frank [36] are the following:

Definition 3. The Frank t-norms and t-conorms are functions from [0, 1]² to [0, 1] which are below:

(3)

Based on t-norms and t-conorms, we can define the generalized union and generalized intersection of two IVTSFSs as follows:

Definition 4. Let for j = 1, 2 be two IVTSFSs, and then the generalized union and intersection can be defined as

(4)

where we can utilize any pair of t-norm and t-conorm.

Definition 5. Let and be two IVTSFNs; the generalized union and intersection between t₁ and t₂ can be defined as

(5)

where we can utilize any pair of t-norm and t-conorm.

3. Frank Aggregation Operators for IVTSFNs

In this section, we will describe the introduction of some operations for IVTSFNs grounded on the Frank t-norm and t-conorm and investigate some properties of these operations.

Assume T denotes the t-norm and S denotes t-conorm, and let T_F is theFrank product and S_F is the Frank sum, and then the generalized union and intersection of two IVTSFNs

and

become the Frank sum and Frank product, symbolically denoted by μ₁⨁_Fμ₂ and μ₁⨂_Fμ₂, respectively. The sum and product are as follows:

(6)

where θ > 1

(7)

where θ > 1.

Now, we describe some properties of IVTSFNs in the environment of Frank t-norm and t-conorm. It is observed that the sum of two IVTSFNs is also an IVTSFN. In Theorem 6, we will prove that the sum of two IVTSFNs is again an IVTSFN.

Theorem 6. Let and be two IVTSFNs, and let μ₃ = μ₁⨂_Fμ₂ and μ₄ = μ₁⨁_Fμ₂, then both μ₃ and μ₄ are also IVTSFNs.

Proof. Since 0 ≤ s_j, i_j, d_j ≤ 1 and for both lower and upper intervals values, then we have

(8)

(9)

Similarly

(10)

which, indicates that μ₃ is an IVTSFN.

Accordingly, we can also prove that μ₄ is also IVTSFN. Thus, proof of Theorem 6 is completed.

We can also multiply a positive number to an IVTSFN, which results another IVTSFN. In Theorem 7, we will describe scalar multiplication of IVTSFN with a positive integer.

Theorem 7. If n is any positive integer and μ = ([s^l, s^u], [i^l, i^u], [d^l, d^u]) is anIVTSFN, then n ._Fμ is a mapping from Z⁺ × μ to μ:

(11)

where n._Fμ = μ⊕_Fμ⊕_Fμ⊕_F ⋯ μ⊕_F(ntimes). Moreover, n._Fμ is an IVTSFN for every positive real number n.

Proof. First, we can prove this equation true for Z⁺ by mathematical induction as follows:

For n = 1

(12)

The equation is true for n = 1.

Now we have to prove for n = k + 1 by assuming true for n = k, i.e.

(13)

Using the hypothesis that equation is true for n = k, then the left-hand side can be written as (k + 1)._Fμ = (k._Fμ)⨁_Fμ and on the basis of the Frank sum operation of two IVTSFNs as follows:

(14)

The equation is true for n = k + 1. Thus, it is true for all positive integers.

Further, we can prove

(15)

(16)

Even n ∈ R⁺.

Since 0 ≤ s^l, i^l, d^l ≤ 1 and

, thus we have

(17)

Similarly, we can easily prove for the upper values of interval. Hence, it is verified that n._Fμ is IVTSFN for any positive real number n.

On the basis of Theorem 7, we can define scalar multiplication for any IVTSFN μ = ([s^l, s^u], [i^l, i^u], [d^l, d^u]) and any positive real number ϵ > 0 as follows:

(18)

In Theorem 8, we define an operation for any real number to the power of the IVTSFN as follows:

Theorem 8. If n ∈ Z⁺ and μ = ([s^l, s^u], [i^l, i^u], [d^l, d^u]) is an IVTSFN, then the exponential operation is a mapping Z⁺ × μ⟶μ:

(19)

where

(n times).

Moreover, is an IVTSFN for very positive real n.

On the basis of Theorem 8, for any real number ϵ > 0 and an IVTSFN μ = ([s^l, s^u], [i^l, i^u], [d^l, d^u]), we can define exponential operation

(20)

In addition, we investigated the following properties and some interesting laws in Theorem 9, as follows:

Theorem 9. For any two IVTSFNs μ₁ and μ₂, we have the following properties:

(21)

4. IVTSF Frank Averaging Aggregation Operators

In this section, we will define IVTSFFWA operator and investigate some basic properties.

Definition 10. Let be set of IVTSFNs, having be the weight vector of μ_j(j = 1, 2, 3, ⋯, n) with w_j ∈ [0, 1] and (note that we shall use w in next discussion for weight vector having same characteristics). Then, IVTSFFWA operator is a mapping μⁿ⟶μ such that

(22)

Particularly, if

, then the IVTSFFWA operator reduces to the IVTSFFA operator:

(23)

It is noted that the value obtained after the aggregation of IVTSFNs is also an IVTSFN. In Theorem 11, we will state that the number obtained after aggregation by IVTSFFWA operator is also an IVTSFN.

Theorem 11. Let set of IVTSFNs, and let w be the weight vector, and then the value obtained after aggregation by using the IVTSFFWA operator is also IVTSFN, and

(24)

Theorem 11 can be easily proved by operations defined above. The proof is skipped to avoid the extra length of this article.

Now, we shall discuss the properties of IVTSFFWA operator in the following. As we know that the aggregation operators hold three basic properties idempotency, monotonicity, and boundedness. In Theorem 12, we will prove the idempotency of IVTSFFWA operator, as follows:

Theorem 12. Let is set of IVTSFNs; if all are same, i.e., μ_j = μ = ([s^l, s^u], [i^l, i^u], [d^l, d^u]) for all j, then IVTSFFWA(μ₁, μ₂, ⋯, μ_n) = IVTSFFWA(μ, μ, ⋯, μ) = μ which is called idempotency.

Proof.

(25)

This completes proof.

In Theorem 13, we will prove monotonicity of IVTSFFWA operator, as follows:

Theorem 13. Let and be two collections of IVTSFNs; if , and , for all j, then IVTSFFWA(μ₁, μ₂, ⋯, μ_n) ≤ IVTSFFWA(φ₁, φ₂, ⋯, φ_n) which is called monotonicity.

Proof. For two collections of IVTSFNs and , if and , for all j, then

(26)

Similarly,

(27)

By definition of score function

(28)

By definition

(1)
If then IVTSFFWA(μ₁, μ₂, ⋯, μ_n) < IVTSFFWA(φ₁, φ₂, ⋯, φ_n)
(2)
If then IVTSFFWA(μ₁, μ₂, ⋯, μ_n) > IVTSFFWA_τ(φ₁, φ₂, ⋯, φ_n)
(3)
If then IVTSFFWA(μ₁, μ₂, ⋯, μ_n) = IVTSFFWA(φ₁, φ₂, ⋯, φ_n)

Then by equations

(29)

Similarly,

(30)

which shows that IVTSFFWA(μ₁, μ₂, ⋯, μ_n) = IVTSFFWA(φ₁, φ₂, ⋯, φ_n). Hence proof is completed.Note that the proofs of further theorems are skipped to control the length of the article.

Theorem 14. Let be the collection of IVTSFNs and

(31)

then

(32)

which is called the boundedness.

Theorem 15. Let is set of IVTSFNs, and let w be the weight vector of μ_j(j = 1, 2, 3, ⋯, n); if r > 1 is real number, then

(33)

Theorem 16. Let be set of IVTSFNs, and let w is weight vector; if μ = ([s^l, s^u], [i^l, i^u], [d^l, d^u]) is a IVTSFN, then

(34)

By Theorem 15 and Theorem 16, we can obtain Theorem 17 as follows:

Theorem 17. Let be collection of IVTSFNs, and let w is weight vector; if r > 1 is real number, then

(35)

Theorem 18. Let and be two collections of IVTSFNs, and let w be weight vector, then IVTSFFWA(μ₁⨁_Fφ₁, μ₂⊕_Fφ₂, ⋯μ_n⨁_Fφ_n) = IVTSFFWA(μ₁, μ₂, ⋯, μ_n)⨁_FIVTSFFWA(φ₁, φ₂, ⋯, φ_n)

Now we shall investigate some special cases of IVTSFFWA operator in following.

Let be collection of IVTSFNs, and let w then

(1)
The IVTSFFWA operator is reduced to IVTSFWA by applying θ⟶1.

(36)

(2)
The IVTSFFWA operator is reduced into traditional arithmetic weighted average operator when θ⟶+∞:
(37)

5. IVTSF Frank Geometric Aggregation Operator

In this section, on the basis of the IVTSFFWA operator and the geometric mean, we define IVTSFFWG operator, as follows:

Definition 19. Let be collection of IVTSFNs, and let w be weight vector. Then, IVTSFFWG operator is a mapping Gⁿ⟶G such that

(38)

Particularly, if , then the IVTSFFWG operator reduces to the IVTSFFG operator:

(39)

Similar to the IVTSFFWA operator, the IVTSFFWG operator have some basic properties, which are discussed in following. Note that most of the properties of IVTSFFWG operator are similar to the IVTSFFWA operator. That is why, we state only the properties which are different.

Theorem 20. Let be collection of IVTSFNs, and let w be the weight vector; if r > 1 is real number, then

(40)

Theorem 21. Let be collection of IVTSFNs, and let w be weight vector; if μ = ([s^l, s^u], [i^l, i^u], [d^l, d^u]) is a IVTSFN, then

(41)

Theorem 22. Let be collection of IVTSFNs, and let w be weight vector; if r > 1 is real number, then

(42)

Theorem 23. Let and be two collections of IVTSFNs, and let w be the weight vector, then IVTSFFWG(μ₁⨂_Fφ₁, μ₂⨂_Fφ₂, ⋯μ_n⨂_Fφ_n) = IVTSFFWG(μ₁, μ₂, ⋯, μ_n)⨂_FIVTSFFWG(φ₁, φ₂, ⋯, φ_n).

We next give some special cases of IVTSFFWG operator, which are similar to the IVTSFFWA operator, as follows:

Let be collection of IVTSFNs, and let w be the weight vector, then

(1)
The IVTSFFWG operator is reduced to IVTSFWG operator by applying θ⟶1.
(43)
(2)
The IVTSFFWG operator is reduced into traditional weighted geometric operator when θ⟶+∞:
(44)

In the last of this section, we give relationship between the IVTSFFWA and the IVTSFFWG operator, which is given as

Theorem 24. Let be set of IVTSFNs, and let w be the weight vector, then

(45)

Lemma 25. Let z_j > 0, δ_j > 0, j = 1, 2, 3, ⋯, n and, then

(46)

where

if and only if z₁ = z₂ = ⋯ = z_n.

Theorem 26. Let be set of IVTSFNs, and let w the weight vector, then

(47)

6. Application of Proposed Approach in MAGDM

In this section, we will explore the application of IVTSFFAOs in MAGD problem with IVTSF information.

For a MAGDM problem with IVTSF information, let Z = {z₁, z₂, ⋯, z_m} is set of m alternatives to be selected; let S = {s₁, s₂, ⋯, s_m} be set of attributes having weight vector w and D = {d₁, d₂, ⋯, d_k} are k decision-makers having weight vector ω. Let be the Atanassov’s IVTSF decision matrix, where the attribute value provided by decision-maker d_k is denoted by anIVTSFN for the alternative z_j with respect to attribute s_l, where the degree range of satisfaction of attribute s_l by the alternative z_j is denoted by , is degree range that an alternative does not satisfy an attribute, and is degree range that of hesitancy for an alternative with the condition.

Generally, there are two types of attributes, benefit attributes and cost attributes in MAGDM problems. Different types of attributes values have different impact. Different impact of attribute values should be eliminated by transformation of attributes into same type. We transform the cost attributes values in benefit attribute values without loss of generality, and we obtain

, where

(48)

Then we develop an approach to MAGDM to IVTSF information by utilizing IVTSFFWA/IVTSFFWG operator, which has following steps:

Step 1. We investigate the IVTSF information for parameter q.

Step 2. We take the decision information from given decision matrix and utilize IVTSFFWA/IVTSFFWG operator; the individual total IVTSF preference value of alternative z_j is derived as follows; or for aggregation of all individual IVTSF decision matrices into collective IVTSF decision matrix.

Step 3. In this step, we aggregate individual all the preference values to obtain collective overall preference value using IVTSFFWA or IVTSFFWG operator.

Step 4. By using ranking method, we rank all the obtained values.

Step 5. Finally, we select the best alternative by ranking all of them, the best one in ranking, the better the alternative.

7. Illustrative Example

In this section of our article, we use an illustrative example for the selection of a business proposal to support proposed approach. We shall solve this example to select the best business proposal among some business proposals.

Example 1. A company desires to select a new business proposal in order to invest in new field. After initial screening, four alternatives z_i = (i = 1, 2, 3, 4) have remained in list. Three experts ε_k = (1, 2, 3) form a decision-maker committee having weight vector w = (0.25,0.40,0.35)^T. Four considered attributes are (1) time duration (c_i), (2) cost of investment (c₂), (3) requirement of equipment (c₃), and (4) expected rate of return (c₄) having ω = (0.25,0.3,0.35,0.2)^T. Three IVTSF decision matrix are obtained after evaluating proposals by experts. Table 1 has been obtained by expert 1, Table 2 by expert 2, and Table 3 by expert 3, as follows;

Table 1. Decision matrix D1 provided by expert 1.

	z₁					z₂
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
c₁	0.23	0.35	0.43	0.5	0.55	0.6	0.5	0.62	0.34	0.45	0.3	0.56
c₂	0.45	0.5	0.68	0.7	0.77	0.8	0.55	0.7	0.24	0.36	0.3	0.43
c₃	0.23	0.45	0.34	0.39	0.49	0.61	0.43	0.54	0.33	0.36	0.2	0.45
c₄	0.67	0.7	0.34	0.43	0.77	0.81	0.54	0.65	0.36	0.49	0.2	0.6
	z₃					z₄
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
c₁	0.5	0.72	0.2	0.4	0.4	0.5	0.7	0.8	0.34	0.65	0.32	0.45
c₂	0.44	0.67	0.3	0.7	0.4	0.56	0.6	0.75	0.43	0.46	0.44	0.56
c₃	0.32	0.54	0.5	0.6	0.2	0.39	0.4	0.56	0.53	0.65	0.43	0.57
c₄	0.5	0.76	0.4	0.6	0.3	0.65	0.5	0.76	0.4	0.56	0.57	0.67

Table 2. Decision matrix D2 provided by expert 2.

z₁							z₂
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
c₁	0.6	0.7	0.2	0.32	0.2	0.5	0.5	0.7	0.32	0.46	0.2	0.34
c₂	0.5	0.6	0.3	0.32	0.3	0.35	0.4	0.6	0.44	0.52	0.5	0.56
c₃	0.2	0.4	0.35	0.36	0.6	0.7	0.35	0.45	0.31	0.62	0.6	0.71
c₄	0.4	0.5	0.4	0.47	0.4	0.52	0.53	0.67	0.37	0.62	0.3	0.35
z₃							z₄
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
c₁	0.5	0.4	0.5	0.3	0.44	0.5	0.2	0.52	0.4	0.45	0.34	0.45
c₂	0.5	0.8	0.81	0.43	0.53	0.2	0.54	0.63	0.35	0.54	0.45	0.56
c₃	0.5	0.7	0.73	0.45	0.56	0.54	0.4	0.52	0.34	0.54	0.44	0.67
c₄	0.5	0.5	0.62	0.53	0.65	0.43	0.15	0.42	0.36	0.56	0.54	0.74

Table 3. Decision matrix D3 provided by expert 3.

z₁							z₂
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
c₁	0.6	0.7	0.3	0.55	0.2	0.34	0.4	0.49	0.43	0.54	0.2	0.43
c₂	0.5	0.6	0.4	0.53	0.3	0.43	0.43	0.56	0.23	0.43	0.5	0.6
c₃	0.2	0.5	0.29	0.35	0.6	0.67	0.42	0.62	0.42	0.54	0.6	0.8
c₄	0.4	0.5	0.34	0.46	0.4	0.51	0.5	0.67	0.52	0.72	0.3	0.6
z₃							z₄
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
c₁	0.4	0.55	0.2	0.35	0.5	0.65	0.3	0.47	0.26	0.5	0.3	0.45
c₂	0.45	0.56	0.25	0.45	0.2	0.45	0.4	0.55	0.29	0.49	0.23	0.47
c₃	0.54	0.67	0.52	0.7	0.2	0.54	0.42	0.56	0.31	0.45	0.34	0.43
c₄	0.39	0.54	0.29	0.44	0.3	0.44	0.32	0.51	0.33	0.39	0.41	0.57

Attribute c₂ is of the cost type, and all others are benefit type, the attributes have two different types, and thus, we need to normalize the decision matrix (see Tables 4, 5, and 6). To normalize the matrix, we take compliment of the cost type attribute. In Tables 4, 5, and 6, we took the compliment of the attribute c₂.

Table 4. Decision matrix R1.

	z₁						z₂
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
c₁	0.23	0.35	0.43	0.5	0.55	0.6	0.5	0.62	0.34	0.45	0.3	0.56
c₂	0.77	0.8	0.68	0.7	0.45	0.5	0.3	0.43	0.24	0.36	0.55	0.7
c₃	0.23	0.45	0.34	0.39	0.49	0.61	0.43	0.54	0.33	0.36	0.2	0.45
c₄	0.67	0.7	0.34	0.43	0.77	0.81	0.54	0.65	0.36	0.49	0.2	0.6
	z₃						z₄
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
c₁	0.5	0.72	0.2	0.4	0.4	0.5	0.7	0.8	0.34	0.65	0.32	0.45
c₂	0.4	0.56	0.3	0.7	0.44	0.67	0.6	0.75	0.43	0.46	0.44	0.56
c₃	0.32	0.54	0.5	0.6	0.2	0.39	0.4	0.56	0.53	0.65	0.43	0.57
c₄	0.5	0.76	0.4	0.6	0.3	0.65	0.5	0.76	0.4	0.56	0.57	0.67

Table 5. Decision matrix R2.

	z₁						z₂
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
c₁	0.6	0.7	0.2	0.32	0.2	0.5	0.5	0.7	0.32	0.46	0.2	0.34
c₂	0.3	0.35	0.3	0.32	0.5	0.6	0.5	0.56	0.44	0.52	0.4	0.65
c₃	0.2	0.4	0.35	0.36	0.6	0.7	0.35	0.45	0.31	0.62	0.6	0.71
c₄	0.4	0.5	0.4	0.47	0.4	0.52	0.53	0.67	0.37	0.62	0.3	0.35
	z₃						z₄
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
c₁	0.4	0.5	0.3	0.44	0.5	0.65	0.2	0.52	0.4	0.45	0.34	0.45
c₂	0.2	0.45	0.43	0.53	0.8	0.81	0.5	0.56	0.35	0.54	0.54	0.63
c₃	0.7	0.73	0.45	0.56	0.54	0.65	0.4	0.52	0.34	0.54	0.44	0.67
c₄	0.5	0.62	0.53	0.65	0.43	0.55	0.15	0.42	0.36	0.56	0.54	0.74

Table 6. Decision matrix R3.

	z₁						z₂
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
c₁	0.6	0.7	0.3	0.55	0.2	0.34	0.4	0.49	0.43	0.54	0.2	0.43
c₂	0.3	0.43	0.4	0.53	0.5	0.6	0.5	0.6	0.23	0.43	0.43	0.56
c₃	0.2	0.5	0.29	0.35	0.6	0.67	0.42	0.62	0.42	0.54	0.6	0.8
c₄	0.4	0.5	0.34	0.46	0.4	0.51	0.5	0.67	0.52	0.72	0.3	0.6
	z₃						z₄
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
c₁	0.4	0.55	0.2	0.35	0.5	0.65	0.7	0.8	0.34	0.65	0.32	0.45
c₂	0.2	0.45	0.25	0.45	0.45	0.56	0.6	0.75	0.43	0.46	0.44	0.56
c₃	0.54	0.67	0.52	0.7	0.2	0.54	0.3	0.47	0.26	0.5	0.3	0.45
c₄	0.39	0.54	0.29	0.44	0.3	0.44	0.41	0.57	0.33	0.39	0.32	0.51

7.1. Rank the Alternatives by the Developed Approach

In this section, we use both IVTSFFWA and IVTSFFWG operators to solve the MADM problem and see the impact of the variable parameters on ranking.

7.1.1. By Using IVTSFFWA Operator

In the following, IVTSFFWA operator is used to obtain optimal alternative, which involves following steps:

Step 1. First of all, we aggregate all the individual values of the IVTSF decision matrix without loss of generality by using IVTSFFWA operator (let θ = 2). The preferences values are obtained, given in Table 7:

Step 2. Secondly, we apply IVTSFFWA operator on preferences values to get collective preference value r_j for the alternative z_j which are given as follows in Table 8:

Step 3. We calculate the score values of obtained collective preference values by using Definition 2 of Section 2, as follows:

(49)

Since sc(z₁) > sc(z₂) > sc(z₃) > sc(z₄), thus z₁≻z₂≻z₃≻z₄, where ^"≻ ^" denotes “be superior to.” Therefore, z₁ is the best proposal.

Table 7. Decision matrix obtained after IVTSFFWA operator.

	z₁						z₂
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
c₁	0.562	0.820	0.285	0.459	0.245	0.428	0.4560	0.7959	0.375	0.496	0.216	0.423
c₂	0.504	0.782	0.409	0.483	0.489	0.578	0.4732	0.783	0.282	0.439	0.442	0.612
c₃	0.206	0.756	0.316	0.360	0.576	0.666	0.4039	0.7843	0.365	0.520	0.485	0.692
c₄	0.486	0.781	0.357	0.456	0.458	0.560	0.5176	0.8220	0.436	0.639	0.276	0.512
	z₃						z₄
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
c₁	0.4243	0.7910	0.2259	0.3851	0.4783	0.6174	0.4518	0.7950	0.3123	0.5112	0.3155	0.45
c₂	0.2686	0.7591	0.30	0.5175	0.5364	0.6509	0.6070	0.7173	0.3713	0	0.3431	0
c₃	0.579	0.8240	0.4941	0.6356	0.2704	0.5361	0.4102	0.7793	0.3552	0.5123	0.3851	0.5212
c₄	0.4523	0.805	0.3713	0.5276	0.3344	0.509	0.350	0.7864	0.3520	0.4681	0.4762	0.6378

Table 8. Collective preferences values.

	z₁						z₂
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
r_i	0.4669	0.7943	0.322	0.4304	0.4297	0.5543	0.4667	0.8063	0.3336	0.5169	0.345	0.5596
	z₃						z₄
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
r_i	0.478	0.8096	0.3324	0.5322	0.3630	0.560	0.4938	0.7805	0.330	0	0.3541	0

7.1.2. By Using IVTSFFWG Operator

In the following, we IVTSFFWG operator is used to get optimal alternative, which involves following steps:

Step 1. In the first step, we aggregate all the individual values of the IVTSF decision matrix without loss of generality by using IVTSFFWG operator (let θ = 2). The preferences values are obtained in Table 9:

Step 2. In the second step, we apply IVTSFFWG operator on preferences values to get collective preference value r_j for the alternative z_j which are given in Table 10, as follows:

Step 3. We calculate the score values of obtained collective preference values by Definition 2 of Section 2, as follows:

(50)

Since sc(z₂) > sc(z₃) > sc(z₄) > sc(z₁), thus z₂≻z₃≻z₄≻z₁,where ^"≻ ^" denotes “be superior to.” Therefore, z₂ is the best proposal.

Table 9. Decision matrix obtained after IVTSFFWG operator.

	z₁						z₂
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
c₁	0.4983	0.6132	0.3176	0.4923	0.3455	0.4677	0.4474	0.5730	0.3862	0.5020	0.2277	0.4441
c₂	0.3650	0.4608	0.4765	0.5409	0.4909	0.5832	0.452	0.550	0.3265	0.451	0.4527	0.622
c₃	0.2056	0.4580	0.3205	0.3616	0.5818	0.6690	0.3996	0.5486	0.3764	0.5445	0.5617	0.7345
c₄	0.444	0.5355	0.3669	0.4574	0.5361	0.6138	0.5167	0.6659	0.4573	0.6595	0.2852	0.5503
	z₃						z₄
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
c₁	0.4184	0.565	0.2394	0.3913	0.4835	0.6269	0.3166	0.541	0.3301	0.5275	0.3170	0.45
c₂	0.2299	0.4703	0.3342	0.5465	0.6197	0.6857	0.561	0	0.3864	0	0.3458	0
c₃	0.5282	0.6593	0.497	0.646	0.3795	0.5599	0.4098	0.5477	0.3855	0.5312	0.3942	0.5553
c₄	0.4418	0.6039	0.4137	0.5555	0.3502	0.5311	0.2798	0.5231	0.3551	0.4916	0.4929	0.6537

Table 10. Collective preferences values.

	z₁						z₂
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
r_i	0.314	0.481	0.392	0.476	0.525	0.615	0.425	0.558	0.391	0.552	0.462	0.645
	z₃						z₄
	s^l	s^u	i^l	i^u	d^l	d^u	s^l	s^u	i^l	i^u	d^l	d^u
r_i	0.367	0.555	0.416	0.577	0.499	0.620	0.378	0.000	0.377	0.475	0.401	0.517

From the above value, we obtained same ranking orders of alternatives by using IVTSFFWA and IVTSFFWG operators. We can see that the IVTSFFWA operator is based on the arithmetic average, which emphasize on the group opinion about the alternative, but the IVTSFFWG operator is based on the geometric mean which mainly emphases on the individual opinion between arguments. Hence, the IVTSFFWG gives the better results.

8. The Influence of Parameters

The AOs discussed above depends upon two parameters θ and q. In this section, we observed the influence of these parameters on our results.

8.1. The Influence of θ

It can be observed that we considered θ = 2 in our example. However, value of θ can be changed by the interest of the decision maker. In the following, Table 11 and Table 12 represent very interesting behavior of variation of ranking orders in IVTSFFWA and IVTSFFWG operator, respectively.

Table 11. Variation of ranking with θ in IVTSFFWA operator.

θ	Ranking of score values
2	sc(z₁) > sc(z₂) > sc(z₃) > sc(z₄)
3	sc(z₃) > sc(z₄) > sc(z₁) > sc(z₂)
4	sc(z₃) > sc(z₄) > sc(z₂) > sc(z₁)
5	sc(z₃) > sc(z₂) > sc(z₄) > sc(z₁)
6	sc(z₃) > sc(z₂) > sc(z₄) > sc(z₁)
7	sc(z₃) > sc(z₂) > sc(z₄) > sc(z₁)
8	sc(z₃) > sc(z₂) > sc(z₄) > sc(z₁)
9	sc(z₃) > sc(z₂) > sc(z₄) > sc(z₁)
10	sc(z₃) > sc(z₂) > sc(z₄) > sc(z₁)
15	sc(z₃) > sc(z₂) > sc(z₄) > sc(z₁)
30	sc(z₃) > sc(z₂) > sc(z₄) > sc(z₁)
50	sc(z₃) > sc(z₂) > sc(z₄) > sc(z₁)
100	sc(z₃) > sc(z₂) > sc(z₄) > sc(z₁)

Table 12. Variation of ranking with θ in IVTSFFG operator.

θ	Ranking of score values
2	sc(z₂) > sc(z₃) > sc(z₄) > sc(z₁)
3	sc(z₂) > sc(z₃) > sc(z₄) > sc(z₁)
4	sc(z₂) > sc(z₃) > sc(z₄) > sc(z₁)
5	sc(z₂) > sc(z₃) > sc(z₄) > sc(z₁)
6	sc(z₂) > sc(z₃) > sc(z₄) > sc(z₁)
7	sc(z₂) > sc(z₃) > sc(z₄) > sc(z₁)
8	sc(z₂) > sc(z₃) > sc(z₄) > sc(z₁)
9	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)
10	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)
15	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)
30	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)
50	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)
100	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)

We can observe the behavior of variation of ranking values by changing θ in IVTSFFWA operator in Table 11. When we increase value of θ from 2, we note that the IVTSFFWA operator gives same ranking order. Hence, we recommend the decision-maker to use value of θ greater than 2.

We also plotted the variation in ranking values by changing in θ in Figure 1. It can be observed from Figure 1 that there is linear change in score values, as follows:

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Variation of ranking by θ and its effect on ranking.

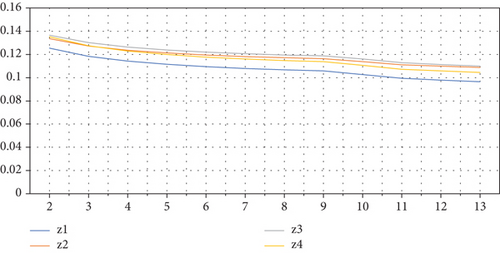
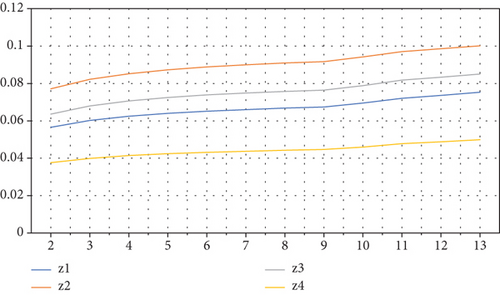
From above tables, it is noted that the ranking of score values do not fluctuate with the values of parameter θ also in IVTSFFWG operator. We varied θ up to 100, but we found the same ranking of alternatives as in Table 12. The decision-makers are independent to use any value of θ while using IVTSFFWG operator. In Figure 2, we can observe the stability of score values graphically, as given in following.

8.2. The Influence of q

The variation in ranking of score values is not influenced only by θ; it also depends upon the value of q. The variation of ranking by changing the value of q is given in following tables:

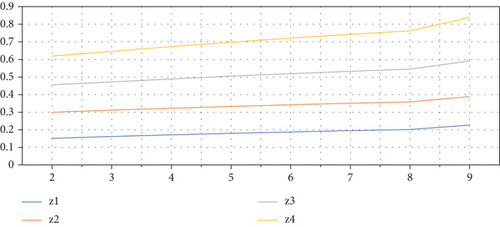
In Table 13, we can observe the variation in ranking of score values of alternatives using IVTSFFWA operator. As the framework of IVTSFS has a variable parameter "q", and the value of "q" can be assigned the by decision makers subject to the staisfaction of essential conditions. However, we may get some stable results after q = 6. It is also noted that if decision-maker assigns significantly large value, then the results can be impossible.

Table 13. Variation of ranking with q in IVTSFFWA operator.

q	Ranking of score values
3	sc(z₁) > sc(z₂) > sc(z₃) > sc(z₄)
4	sc(z₄) > sc(z₃) > sc(z₂) > sc(z₁)
5	sc(z₄) > sc(z₃) > sc(z₁) > sc(z₂)
6	sc(z₄) > sc(z₁) > sc(z₃) > sc(z₂)
7	sc(z₄) > sc(z₁) > sc(z₃) > sc(z₂)
8	sc(z₄) > sc(z₁) > sc(z₃) > sc(z₂)
9	sc(z₄) > sc(z₁) > sc(z₃) > sc(z₂)
10	sc(z₄) > sc(z₁) > sc(z₃) > sc(z₂)
15	sc(z₄) > sc(z₁) > sc(z₃) > sc(z₂)

The variation behavior of ranking of score values of alternatives can be presented in Figure 3 graphically, as follows:

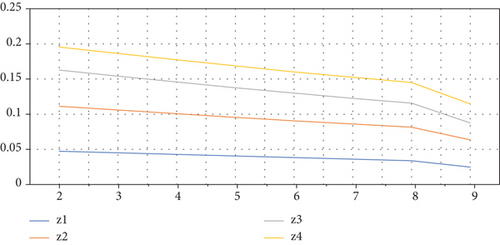
Unlike to variation in IVTSFFWA operator, the variations of ranking values in IVTSFFWG operator by q are observed in Table 14. It is observed that in IVTSFFWG operator, the results are stable for all values of q. However, we also observed these results can be impossible on significantly large value of q. The variation of ranking of score values is presented graphically in Figure 4, as the following:

Table 14. Variation of ranking with q in IVTSFFWG operator.

q	Ranking of score values
3	sc(z₂) > sc(z₃) > sc(z₄) > sc(z₁)
4	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)
5	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)
6	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)
7	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)
8	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)
9	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)
10	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)
15	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)

9. Comparison with Other Operators

Ullah et al. [7] developed aggregation operators for the environment of IVTSFSs based on which they investigated the evaluation of an investment policy. Jin et al. [30] proposed Hamacher aggregation operator for the environment of IVTSFSs and applied in MAGDM. Ullah et al. [35] introduced aggregation operator for IVTSFSs based on Dombi t-norm and t-conorm. In the following, we will study comparison of our proposed AOs with approaches mentioned above, and then we will mention advantages of our proposed AOs. To do this, let us solve Example 1 of Section 7 by AOs in [7, 30, 35]; we get the ranking of score values of alternatives which is given in Table 15 and Table 16. By using AOs in [7, 35], we note z₃ alternative is the best. According to AOs in [30] z₁ is the best alternative. But the ranking of alternatives depends upon the value of parameters and changed up to specific value. While using our proposed approach, it is noted that the ranking of alternatives is more stable as in Tables 11, 12, and 13 and Table 14. This describes the significance of our proposed AOs. In addition, the proposed approach has following advantages:

(1)
The AOs defined in [7] simply aggregate the IVTSF information, but IVTSFFWA and IVTSFFWG operators are based on Frank t-norm and t-conorm; hence, these AOs have more flexibility
(2)
As Frank t-norm and t-conorm are more flexible than the Dombi and Hamacher pair of norms, hence IVTSFFWA and IVTSFFWG operators are the more appropriate AOs to aggregate IVTSF information
(3)
Since IVTSFFWA and IVTSFFWG operators have two parameters θ and q, hence the decision-makers can assign the value of their own interest (studied in Subsection 8.1).

Table 15. Comparison with IVTSFFWA operator.

Operator	Ranking of score values
IVTSFWA	sc(z₃) > sc(z₂) > sc(z₁) > sc(z₄)
IVTSFHWA	sc(z₁) > sc(z₄) > sc(z₃) > sc(z₂)
IVTSFDWA	sc(z₃) > sc(z₂) > sc(z₁) > sc(z₄)

Table 16. Comparison with IVTSFFWG operator.

Operator	Ranking of score values
IVTSFWG	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)
IVTSFHWG	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)
IVTSFDWG	sc(z₂) > sc(z₃) > sc(z₁) > sc(z₄)

The comparison of IVTSFFWA operator with IVTSF Hamacher (IVTSFHWA), IVTSF Dombi (IVTSFDWA), and IVTSF weightage averaging (IVTSFWA) operator is given following in Table 15.

Similarly, the comparison of the geometric operators is given following in Table 16:

We also plot the score values obtained by different operators mentioned in Tables 15 and 16, as follows in Figures 5 and 6:

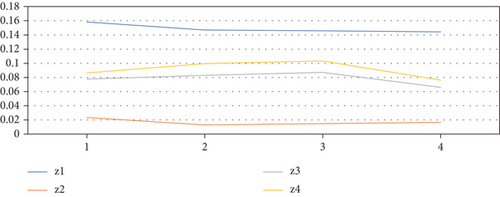
10. Conclusion

In this paper, we have studied Frank AOs for the atmosphere of IVTSFSs in detail. To do this, first, we prolonged the Frank t-norm and t-conorm in the environment of IVTSFSs, defined some new operations for the environment of IVTSFNs, and studied their properties in detail. We introduced new AOs such as IVTSFFWA operator and IVTSFFWG operator which are based on Frank t-norm t-conorm. Numerous properties and the relation between these AOs have investigated in detail. These AOs have applied to the MAGDM problem with the help of an illustrative example. The variations of ranking of alternatives have observed by the change in values of parameters q and θ, i.e.:

(i)
When we change the value of θ, the ranking of the score values obtained by the IVTSFFWA operator remains unchanged after θ = 2. The ranking of alternatives slightly differs at θ = 2
(ii)
Interestingly, the IVTSFFWG operator gives the same ranking of score values for all values of θ
(iii)
When we change the values of q, the ranking of score values of alternatives slightly differ up to q = 5. For the values of q > 5, the ranking remains the same. So q > 5 is recommended value for decision-makers, while using the IVTSFFWA operator. However, it is also noted that the score values approach zero for a significantly large value of q
(iv)
We noted that the ranking of score values of alternatives remain unchanged when we varied the value of q in the IVTSFFWG operator. Hence the decision-makers are independent of the values of q while using the IVTSFFWG operator. However, the score values also approach zero for significantly large values of q

The behavior of variation in the ranking of alternatives with the change of parameters has also been represented graphically. In the last, these AOs have been compared to Dombi, Hamacher, and traditional AOs. In the future we aim to extend this idea of Frank AOs in the environment of PFS, spherical fuzzy sets [6], complex TSFSs [46], and some decision theories [47]. In the future, we shall also study the application of IVTSFFAOs in other fields except for MAGDM like game theory, uncertain programming, and pattern recognition due to their flexibility and interesting properties.

Conflicts of Interest

The authors have no conflict of interest regarding this paper.

Acknowledgments

The authors are thankful to the Office of Research, Innovation and Commercialization (ORIC) of Riphah International University for supporting this research under the project: Riphah-ORIC-21-22/FEAS-20. This work is supported by the Humanities and Social Sciences Foundation of Ministry of Education of the People’s Republic of China (No. 19YJC630164) and the Postdoctoral Science Foundation of Jiangxi Province (No. 2019KY14). The authors are also thankful to the office of Research, Innovation and Commercialization (ORIC) of Riphah International University Lahore for supporting this research under the project: R-ORIC-21/FEAS-09.

Open Research

Data Availability

No data were used to support this study.

References

1 Zadeh L. A., Fuzzy sets, Information and Control. (1965) 8, no. 3, 338–353, https://doi.org/10.1016/S0019-9958(65)90241-X, 2-s2.0-34248666540.
10.1016/S0019-9958(65)90241-X
CAS Web of Science® Google Scholar
2 Atanassov K. T., Intuitionistic fuzzy sets, Fuzzy Sets and Systems. (1986) 20, no. 1, 87–96, https://doi.org/10.1016/S0165-0114(86)80034-3, 2-s2.0-0002740725.
10.1016/S0165-0114(86)80034-3
Web of Science® Google Scholar
3 Yager R. R., Pythagorean fuzzy subsets, In Proceedings of the IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), 2013, Edmonton, AB, Canada.
Google Scholar
4 Yager R. R., Generalized orthopair fuzzy sets, IEEE Transactions on Fuzzy Systems. (2017) 25, no. 5, 1222–1230, https://doi.org/10.1109/TFUZZ.2016.2604005, 2-s2.0-85032276362.
10.1109/TFUZZ.2016.2604005
Web of Science® Google Scholar
5 Cuong B. C., Picture fuzzy sets, Journal of Computer Science and Cybernetics. (2015) 30, https://doi.org/10.15625/1813-9663/30/4/5032.
10.15625/1813-9663/30/4/5032
Google Scholar
6 Mahmood T., Ullah K., Khan Q., and Jan N., An approach towards decision making and medical diagnosis problems using the concept of spherical fuzzy sets, Neural Computing and Applications. (2018) 31, 7041–7053, https://doi.org/10.1007/s00521-018-3521-2, 2-s2.0-85047123393.
10.1007/s00521-018-3521-2
Web of Science® Google Scholar
7 Ullah K., Hassan N., Mahmood T., Jan N., and Hassan M., Evaluation of investment policy based on multi-attribute decision-making using interval-valued T-spherical fuzzy aggregation operators, Symmetry. (2019) 11, no. 3, https://doi.org/10.3390/sym11030357, 2-s2.0-85064944326.
10.3390/sym11030357
Web of Science® Google Scholar
8 Bellman R. E. and Zadeh L. A., Decision-making in a fuzzy environment, Management Science. (1970) 17, no. 4, B-141–B-164, https://doi.org/10.1287/mnsc.17.4.B141.
10.1287/mnsc.17.4.B141
Web of Science® Google Scholar
9 Xu Z., Intuitionistic fuzzy aggregation operators, IEEE Transactions on Fuzzy Systems. (2007) 15, no. 6, 1179–1187, https://doi.org/10.1109/TFUZZ.2006.890678, 2-s2.0-37249067095.
10.1109/TFUZZ.2006.890678
Web of Science® Google Scholar
10 Rahman K., Ali A., Shakeel M., Khan M., and Ullah M., Pythagorean fuzzy weighted averaging aggregation operator and its application to decision-making theory, Nucleus. (2017) 54, 190–196.
Google Scholar
11 Yager R. R. and Abbasov A. M., Pythagorean membership grades, complex numbers, and decision making, International Journal of Intelligent Systems. (2013) 28, no. 5, 436–452, https://doi.org/10.1002/int.21584, 2-s2.0-84875259751.
10.1002/int.21584
Web of Science® Google Scholar
12 Wei G., Picture fuzzy aggregation operators and their application to multiple attribute decision making, Journal of Intelligent Fuzzy Systems. (2017) 33, no. 2, 713–724, https://doi.org/10.3233/JIFS-161798, 2-s2.0-85025681338.
10.3233/JIFS-161798
Web of Science® Google Scholar
13 Garg H., Some picture fuzzy aggregation operators and their applications to multicriteria decision-making, Arabian Journal for Science and Engineering. (2017) 42, no. 12, 5275–5290, https://doi.org/10.1007/s13369-017-2625-9, 2-s2.0-85033672854.
10.1007/s13369-017-2625-9
Web of Science® Google Scholar
14 Guleria A. and Bajaj R. K., T-spherical fuzzy soft sets and its aggregation operators with application in decision-making, Scientia Iranica. (2021) 28, no. 2, 1014–1029, https://doi.org/10.24200/sci.2019.53027.3018.
10.24200/sci.2019.53027.3018
Web of Science® Google Scholar
15 Karaaslan F. and Dawood M. A., Complex T-spherical fuzzy Dombi aggregation operators and their applications in multiple-criteria decision-making, Complex & Intelligent Systems.(2021) 7, no. 5, 2711–2734, https://doi.org/10.1007/s40747-021-00446-2, 34777971.
10.1007/s40747-021-00446-2
PubMed Web of Science® Google Scholar
16 Xu W., Shang X., Wang J., and Xu Y., Multi-attribute decision-making based on interval-valued q-rung dual hesitant uncertain linguistic sets, IEEE Access. (2020) 8, no. 8, 26792–26813, https://doi.org/10.1109/ACCESS.2020.2968381.
10.1109/ACCESS.2020.2968381
Web of Science® Google Scholar
17 Jiang W. and Wei B., Intuitionistic fuzzy evidential power aggregation operator and its application in multiple criteria decision-making, International Journal of Systems Science. (2018) 49, no. 3, 582–594, https://doi.org/10.1080/00207721.2017.1411989, 2-s2.0-85038005586.
10.1080/00207721.2017.1411989
Web of Science® Google Scholar
18 Wang R. and Li Y., Picture hesitant fuzzy set and its application to multiple criteria decision-making, Symmetry. (2018) 10, no. 7, https://doi.org/10.3390/sym10070295, 2-s2.0-85050374873.
10.3390/sym10070295
PubMed Web of Science® Google Scholar
19 Akram M., Bashir A., and Garg H., Decision-making model under complex picture fuzzy Hamacher aggregation operators, Computational and Applied Mathematics. (2020) 39, no. 3, 1–38, https://doi.org/10.1007/s40314-020-01251-2.
10.1007/s40314-020-01251-2
Web of Science® Google Scholar
20 Riaz M. and Hashmi M. R., MAGDM for agribusiness in the environment of various cubic m-polar fuzzy averaging aggregation operators, Journal of Intelligent Fuzzy Systems. (2019) 37, no. 3, 3671–3691, https://doi.org/10.3233/JIFS-182809, 2-s2.0-85073734049.
10.3233/JIFS-182809
Web of Science® Google Scholar
21 Peng X. and Yang Y., Fundamental properties of interval-valued Pythagorean fuzzy aggregation operators, International Journal of Intelligent Systems. (2016) 31, no. 5, 444–487, https://doi.org/10.1002/int.21790, 2-s2.0-84959451457.
10.1002/int.21790
Web of Science® Google Scholar
22 Fahmi A., Amin F., Abdullah S., and Ali A., Cubic fuzzy Einstein aggregation operators and its application to decision-making, International Journal of Systems Science. (2018) 49, no. 11, 2385–2397, https://doi.org/10.1080/00207721.2018.1503356, 2-s2.0-85052099294.
10.1080/00207721.2018.1503356
Web of Science® Google Scholar
23 Ullah K., Mahmood T., and Garg H., Evaluation of the performance of search and rescue robots using T-spherical fuzzy Hamacher aggregation operators, International Journal of Fuzzy Systems. (2020) 22, no. 2, 570–582, https://doi.org/10.1007/s40815-020-00803-2.
10.1007/s40815-020-00803-2
Web of Science® Google Scholar
24 Garg H., Ullah K., Mahmood T., Hassan N., and Jan N., T-spherical fuzzy power aggregation operators and their applications in multi-attribute decision making, Journal of Ambient Intelligence and Humanized Computing. (2021) 12, no. 10, 9067–9080, https://doi.org/10.1007/s12652-020-02600-z.
10.1007/s12652-020-02600-z
PubMed Web of Science® Google Scholar
25 Akram M., Ullah K., and Pamucar D., Performance evaluation of solar energy cells using the interval-valued T-spherical fuzzy Bonferroni mean operators, Energies. (2022) 15, no. 1, https://doi.org/10.3390/en15010292.
10.3390/en15010292
Google Scholar
26 Deschrijver G. and Kerre E. E., Uninorms in L*-fuzzy set theory, Fuzzy Sets and Systems. (2004) 148, no. 2, 243–262, https://doi.org/10.1016/j.fss.2003.12.006, 2-s2.0-5644277804.
10.1016/j.fss.2003.12.006
Web of Science® Google Scholar
27 Xia M., Xu Z., and Zhu B., Some issues on intuitionistic fuzzy aggregation operators based on Archimedean t-conorm and t-norm, Knowledge-Based Systems. (2012) 31, 78–88, https://doi.org/10.1016/j.knosys.2012.02.004, 2-s2.0-84862777933.
10.1016/j.knosys.2012.02.004
PubMed Web of Science® Google Scholar
28 Wang W. and Liu X., Intuitionistic fuzzy information aggregation using Einstein operations, IEEE Transactions on Fuzzy Systems. (2012) 20, no. 5, 923–938, https://doi.org/10.1109/TFUZZ.2012.2189405, 2-s2.0-84865685565.
10.1109/TFUZZ.2012.2189405
PubMed Web of Science® Google Scholar
29 Shahzadi G., Muhiuddin G., Arif Butt M., and Ashraf A., Hamacher interactive hybrid weighted averaging operators under Fermatean fuzzy numbers, Journal of Mathematics. (2021) 2021, 17, https://doi.org/10.1155/2021/5556017, 5556017.
10.1155/2021/5556017
Web of Science® Google Scholar
30 Jin Y., Kousar Z., Ullah K., Mahmood T., Yapici Pehlivan N., and Ali Z., Approach to multi-attribute decision-making methods for performance evaluation process using interval-valued T-spherical fuzzy Hamacher aggregation information, Axioms. (2021) 10, no. 3, https://doi.org/10.3390/axioms10030145.
10.3390/axioms10030145
Web of Science® Google Scholar
31 Jana C., Muhiuddin G., and Pal M., Multiple-attribute decision making problems based on SVTNH methods, Journal of Ambient Intelligence and Humanized Computing. (2020) 11, no. 9, 3717–3733, https://doi.org/10.1007/s12652-019-01568-9.
10.1007/s12652-019-01568-9
Web of Science® Google Scholar
32 Jana C., Muhiuddin G., and Pal M., Some Dombi aggregation of Q-rung orthopair fuzzy numbers in multiple-attribute decision making, International Journal of Intelligent Systems. (2019) 34, no. 12, 3220–3240, https://doi.org/10.1002/int.22191, 2-s2.0-85073695849.
10.1002/int.22191
Web of Science® Google Scholar
33 Seikh M. R. and Mandal U., Intuitionistic fuzzy Dombi aggregation operators and their application to multiple attribute decision-making, Granular Computing.(2021) 6, no. 3, 473–488, https://doi.org/10.1007/s41066-019-00209-y.
10.1007/s41066-019-00209-y
Google Scholar
34 Jana C., Pal M., and Wang J. Q., Bipolar fuzzy Dombi aggregation operators and its application in multiple-attribute decision-making process, Journal of Ambient Intelligence and Humanized Computing. (2019) 10, no. 9, 3533–3549, https://doi.org/10.1007/s12652-018-1076-9, 2-s2.0-85055560918.
10.1007/s12652-018-1076-9
Web of Science® Google Scholar
35 Ullah K., Garg H., Gul Z., Mahmood T., Khan Q., and Ali Z., Interval valued T-spherical fuzzy information aggregation based on Dombi t-norm and Dombi t-conorm for multi-attribute decision making problems, Symmetry. (2021) 13, no. 6, https://doi.org/10.3390/sym13061053.
10.3390/sym13061053
Web of Science® Google Scholar
36 Ullah K., Picture fuzzy Maclaurin symmetric mean operators and their applications in solving multi-attribute decision-making problems, Mathematical Problems in Engineering. (2021) 2021, 1098631, https://doi.org/10.1155/2021/1098631.
10.1155/2021/1098631
Web of Science® Google Scholar
37 Power average of trapezoidal intuitionistic fuzzy numbers using strict t-norms and t-conorms, IEEE Transactions on Fuzzy Systems. (2016) 24, no. 5, 1035–1047, https://doi.org/10.1109/TFUZZ.2015.2501408, 2-s2.0-84990941224.
10.1109/TFUZZ.2015.2501408
Web of Science® Google Scholar
38 Wan S. P., Cheng W. B., and Dong J. Y., Interactive multi-criteria group decision-making with probabilistic linguistic information for emergency assistance of COVID-19, Applied Soft Computing. (2021) 107, article 107383, https://doi.org/10.1016/j.asoc.2021.107383.
10.1016/j.asoc.2021.107383
PubMed Web of Science® Google Scholar
39 Wan S. P., Zou W. C., Dong J. Y., and Martí�nez L., A consensual fuzzy multi-criteria group decision-making for linguistic intuitionistic information, Information Sciences. (2022) 582, 797–832, https://doi.org/10.1016/j.ins.2021.10.030.
10.1016/j.ins.2021.10.030
Web of Science® Google Scholar
40 Frank M. J., On the simultaneous associativity of F(x, y) and x + y − F(x, y), Aequationes Mathematicae. (1979) 19, 194–226.
10.1007/BF02189866
Google Scholar
41 Sarkoci P., Domination in the families of Frank and Hamacher t-norms, Kybernetika. (2005) 41, 349–360.
Web of Science® Google Scholar
42 Zhang X., Liu P., and Wang Y., Multiple attribute group decision-making methods based on intuitionistic fuzzy frank power aggregation operators, Journal of Intelligent Fuzzy Systems. (2015) 29, no. 5, 2235–2246.
10.3233/IFS-151699
Web of Science® Google Scholar
43 Qin J. and Liu X., Frank aggregation operators for triangular interval type-2 fuzzy set and its application in multiple attribute group decision making, Journal of Applied Mathematics. (2014) 2014, 923213, https://doi.org/10.1155/2014/923213, 2-s2.0-84937046624.
10.1155/2014/923213
Google Scholar
44 Yahya M., Abdullah S., Chinram R., Al-Otaibi Y. D., and Naeem M., Frank aggregation operators and their application to probabilistic hesitant fuzzy multiple attribute decision-making, International Journal of Fuzzy Systems. (2021) 23, no. 1, 194–215, https://doi.org/10.1007/s40815-020-00970-2.
10.1007/s40815-020-00970-2
Web of Science® Google Scholar
45 Tang X., Yang S., and Pedrycz W., Multiple attribute decision-making approaches based on dual hesitant fuzzy Frank aggregation operators, Applied Soft Computing. (2018) 68, 525–547, https://doi.org/10.1016/j.asoc.2018.03.055, 2-s2.0-85045716311.
10.1016/j.asoc.2018.03.055
Web of Science® Google Scholar
46 Nasir A., Jan N., Yang M. S., and Khan S. U., Complex T-spherical fuzzy relations with their applications in economic relationships and international trades, IEEE Access. (2021) 9, 66115–66131, https://doi.org/10.1109/ACCESS.2021.3074557.
10.1109/ACCESS.2021.3074557
Web of Science® Google Scholar
47 Wan S. and Dong J., Decision Making Theories and Methods Based on Interval-Valued Intuitionistic Fuzzy Sets, 2020, Springer, Singapore.
10.1007/978-981-15-1521-7
Google Scholar

Citing Literature

All articles

[Retracted] Assessment of the Business Proposals Using Frank Aggregation Operators Based on Interval-Valued T-Spherical Fuzzy Information

Retraction(s) for this article

Retracted: Assessment of the Business Proposals Using Frank Aggregation Operators Based on Interval-Valued T-Spherical Fuzzy Information

Abstract

1. Introduction

2. Preliminaries

3. Frank Aggregation Operators for IVTSFNs

4. IVTSF Frank Averaging Aggregation Operators

5. IVTSF Frank Geometric Aggregation Operator

6. Application of Proposed Approach in MAGDM

7. Illustrative Example