This study focuses on solving three-dimensional non-linear Klein-Gordon equations of four variables by using the quadruple Laplace transform method coupled with the iterative method. This study was designed in order to show the quadruple Laplace transform with an iterative method for solving three-dimensional nonlinear Klein-Gordon equations. The quadruple Laplace transform with the iterative method was aimed at getting analytical solutions of three-dimensional nonlinear Klein-Gordon equations. Exact solutions obtained through the iterative method have been analytically evaluated and presented in the form of a table and graph. The analytical solutions of these equations have been given in terms of convergent series with a simply calculable system, and the nonlinear terms in equations can easily be solved by the iterative method. Illustrative examples are also provided to demonstrate the applicability and efficiency of the method. The result renders the applicability and efficiency of the applied method. Finally, the quadruple Laplace transform and iterative method is an excellent method for the solution of nonlinear Klein-Gordon equations.

1. Introduction

Partial differential equation has big importance in mathematics and other fields of science. Therefore, it is very important to know methods to solve such partial differential equations. As [1], the investigation of the exact solutions of nonlinear partial differential equations plays an important role in the study of nonlinear physical phenomena. In order to better understand these non-linear phenomena, many mathematicians and physical scientists make efforts to seek more exact solutions to them [2].

Nonlinear systems of partial differential equations (PDEs) play an important role in various areas of modern physics and engineering such as fluid mechanics, optical fibers, and quantum mechanics. Additionally, nonlinear partial differential equations arise various areas of nonlinear science such as hydrodynamics, plasma physics, molecular biology, quantum mechanics, nonlinear optics, surface water waves, etc. As mentioned in the work of [3].

Moreover, nonlinear partial differential equations (NLPDEs) and fractional differential equations (FDEs) are of massive concern for engineers, physicists, and mathematicians as the generality of physical systems is intrinsically nonlinear in nature. The solitary solutions of nonlinear PDEs and FDEs can demonstrate quite a few phenomenon in physics and may also provide farther understanding of the physical aspects of problems [4] and see also in the work of [5].

The Klein-Gordon equation is a relativistic version of the Schrodinger equation describing free particles, which was proposed by Oskar Klein and Walter Gordon in 1926. It has many applications in physics and engineering such as quantum field theory of relativistic physics, dispersive wave phenomena, plasma physics, and nonlinear optics. Various methods have been developed to get approximate and numerical solutions of linear Klein-Gordon (LKG) and nonlinear Klein-Gordon (NLKG) equations. [6] used the Adomain decomposition method (ADM) by Adomain in 1994 for solving LKG and NLKG equations. [7] used the variational iteration method to obtain an approximate solution of the NLKG equation. Khuri used a modified Laplace decomposition method proposed by [8] to solve the KG equation. As mentioned in the work of [9], the Laplace decomposition method and the Adomain decomposition method used to solve NLKG equations.

Consequently, one of the consummate known methods to solve partial differential equations is the integral transform method. In mathematics, physics, engineering, and throughout the sciences, the Laplace transform is a widely used integral transform method. P. S. Laplace (1749–1827) introduced the idea of the Laplace transform in 1782, in his celebrated study of probability theory and celestial mechanics. Laplace’s classic treatise on LaTh’eorie Analytique des Probabilities (analytical theory of probability) contained some basic results of the Laplace transform which is one of the longest-lived and most commonly used linear integral transforms available in the mathematical literature. This has effectively been used in finding the solutions of linear differential, difference, and integral equations as explained by [10, 11].

In mathematics, partial differential equations (PDEs) are equations that contain unknown multivariate functions and their partial derivatives. PDEs are used to formulate problems involving functions of several variables and are either solved by hand or used to create a relevant computer model. The Laplace transform method is any of several methods for solving ordinary and partial differential equations in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation and the convolution into multiplication leads one to the solution as it is simple to solve algebraic equations. Mainly, the advantage of the Laplace transform method is that it evaluates exact solutions while the iteration method mainly leads to approximate solutions. The method of Laplace transform has been used intensively for solving different linear and nonlinear equations as [12].

The Laplace transform method (LTM) is the basic scheme for finding exact solutions of linear and nonlinear differential equations. This method has many applications in different fields of science and engineering. LTM helps to convert differential equations and the convolution part is changed into multiplications which easily leads one to the solution as LTM reduces a linear/non-linear differential equation to simple and solvable equations. So, these equations are evaluated by the basic definition of algebra and by applying the inverse Laplace transform to the original differential equation. Nowadays, different kinds of differential equations such as linear, nonlinear, functional, integral, and fractional differential equations [13–16] solved by using the double Laplace transform method to solve a one-dimensional boundary value problem from the extension of the single Laplace transform.

In addition, different researchers apply the concept of double Laplace transform method to study triple Laplace transform in order to solve two dimensional nonlinear partial differential equations getting up in different fields of physics, engineering, and other related study areas. Different biographer nearly new triple Laplace transform method to find different differential equations as explained from the works of [17–19]. Khan et al. applied the concept of triple Laplace transform and the work is very effective for solving such kinds of differential equations involving triple integrals, see from [20, 21].

In the same way, an iterative method (IM) is an applicable method in a branch of computational mathematics in order to get the solution of nonlinear differential equations. An iterative process direct to a series of procedures which is helpful to get an analytical solution which are approximated in a suitable condition (see [22]). An iterative method shows an effective and rapid convergent series solution as described by [13]. Our main intent is to apply quadruple Laplace transform coupled with an iterative method to find analytical solutions of three-dimensional nonlinear Klein-Gordon equations dependent on initial and boundary conditions and bluster terms that disappear from the iteration process. Finally, we get the required analytical solution.

This study mainly considers three-dimensional nonlinear Klein-Gordon equations with four variables:

()

With initial conditions as follows:

()

Boundary conditions are as follows:

()

where c and a are constants with necessary initial and boundary conditions. Where x, m, v, t are positive a and c are real numbers. N(u(x, m, v, t)) is a nonlinear term and h(x, m, v, t) is a source function.

At present, there is a very little work available on the triple Laplace transform of three positive variables and their properties. So, the major objective of this work is to study the quadruple Laplace transform and its properties with examples of three-dimensional nonlinear Klein-Gordon equations using the quadruple Laplace transform coupled with an iterative method. The main focus of this work is relating to QLT coupled with IM to examine exact solutions to three-dimensional 3D nonlinear KGEs using initial and boundary value problems to establish the advantages and effectiveness of the method in applied mathematics and mathematical physics.

The organization of this article is as follows: section 1 is about the introduction, in section 2 the definition of quadruple Laplace transform, properties of quadruple Laplace transform and iterative method and its convergence conditions are mentioned, section 3 contains analytical, graphical, tabular results and discussion and section 5 about conclusion.

Recalling the following definition for the purpose of integration of important concepts.

Definition 1. Let f(x) be a piecewise continuously differentiable function in every finite interval and is absolutely integrable function on the whole real line. The Fourier integral formula of f is defined by

()

where k a complex number is taken as the variable of the transform.

2. Definition of Quadruple Laplace Transform

A continuous function F(x, m, v, t) of four variables x, m, vandt quadruple Laplace transform is defined by the quadruple integral in the form

()

Provided the integral exists.

Definition 2. (see [23]). For a continuous function F(x, m, v, t) of four variables, then the quadruple

Laplace transform is defined as follows:

()

With x, m, v, t > 0 by considering e, y, g and h are Laplace variables.

Theorem 1. Let F^xmvt(e, y, g, h) is a function, then the inverse quadruple Laplace transform

()

is given by the complex quadruple integral formula as follows:

()

where F(e, y, g, h) must be an analytic function for each e, y, g and h in the given region defined by the inequality ℝee ≥ α, ℝey ≥ β, ℝeg ≥ η, ℝeh ≥ ζ where α, β, η, and ζ are real constants to be chosen suitably based on [23]. To verify this we recall the Fourier integral formula given by (4) which expresses the representation of a function g(x) defined on −∞ < x < ∞, in the form

()

This can be set as the concept of Heaviside function

()

where c is a positive fixed number. Now (9) becomes

()

2.1. Using a Change of Variables

c + ik = s and i dk = ds (11) can be equivalently written in the form

()

From (12) we get the formal definition of the Laplace transform of f(t):

()

where, e^−st is the kernel of the transform and s is the transform variable which is a complex number. Thus, (12) can be used to give the formal definition of the inverse Laplace transform

()

Hence, from (14) one can deduce that

()

Further, [18] key rules of quadruple Laplace transforms of functions of four variables are given as follows:

(1)
For first order partial derivatives of functions of four variables is as follows:
()
(2)
For second order partial derivative of functions of four variables is as follows:

()

2.2. Existence of Quadruple Laplace Transform

Definition 3. A function f(x, m, v, t) is said to be of exponential order a > 0, b > 0, c > 0 and d > 0 on 0 ≤ x < ∞, 0 ≤ m < ∞, 0 ≤ v < ∞ and 0 ≤ t < ∞. If a positive constant k exists for every x > X, m > M, v > V and t > T, |f(x, m, v, t)|≤ke^ax+bm+cv+dt and write

()

Such a function f(x, m, v, t) is simply called an exponential order as x⟶∞, m⟶∞, v⟶∞, t⟶∞ based on the exponential order ke^ax+bm+cv+dt as x⟶∞, m⟶∞, v⟶∞, t⟶∞ grow more faster as described by [14].

Theorem 2. (Existence): For a continuous function f(x, m, v, t) in every finite intervals (0, x), (0, m), (0, v) and (0, t) and of exponential order e^ax+bm+cv+dt, then the quadruple Laplace transform of f(x, m, v, t) exists for all e, g, y and h provided that ℝee > a, ℝey > b, ℝeg > c and ℝeh > d.

Proof. We have

()

For ℝee > a, ℝey > b, ℝeg > c and ℝeh > d. It follows from this (18) that

()

This proves the existence of quadruple Laplace transform. This result can be regarded as the limiting property of the quadruple Laplace transform, clearly,

()

is not quadruple Laplace transform of any function f(x, m, v, t) because F^xmvt(e, y, g, h) does not tend to zero as x⟶∞, m⟶∞, v⟶∞, t⟶∞. On the other hand,

cannot have quadruple Laplace transform even through it is continuous but is not of the exponential order because x⟶∞, m⟶∞, v⟶∞, t⟶∞. Then

as [14].

Theorem 3. (Uniqueness): For any two continuous functions f(x, m, v, t) and q(x, m, v, t) defined for x, m, v, t≥ 0 and having Laplace transforms, F^xmvt(e, y, g, h) and Q^xmvt(e, y, g, h) , respectively, if

()

as described on [23].

Proof. Based on the definition of the inverse Laplace transform, if α, β, η and ζ are sufficiently large, then the integral expression,

()

By hypothesis, we have that F^xmvt(e, y, g, h) = Q^xmvt(e, y, g, h),

Then replacing this in the previous expression, we have the following:

()

Use the above relation, F^xmvt(e, y, g, h) = Q^xmvt(e, y, g, h), (18) can be rewritten as

()

This completes the required proof. And this proves the uniqueness of the quadruple Laplace transform.

2.3. Main Properties of Quadruple Laplace Transform

The properties of quadruple Laplace transform are mentioned and proved in this section. Note that these properties follow from those of the double Laplace transform described by [17] from the source [24], properties of the triple Laplace transform from [17]. Some properties of quadruple transform as follows:

Property 1. (Linearity of quadruple Laplace transform): As presented on [10] for triple Laplace transform and [23] for quadruple Laplace transform linearity property. If F(x, m, v, t) and Q(x, m, v, t) are two functions with variables of x, m, v and t such that

()

Then, ℒ_xℒ_mℒ_vℒ_t{αF(x, m, v, t) + βQ(x, m, v, t)}

()

with α and β as constants.

Property 2. Linearity of inverse of quadruple Laplace transform: Based on property (1), the inverse quadruple Laplace transform

()

is defined by the quadruple integral formula as folllows:

()

It shows that satisfies the linearity property

()

with α and β as constants.

is also a linear transformation.

Property 3. (Change of scale property): as described on [10]. Let ℒ_xℒ_mℒ_vℒ_t{F(x, m, v, t)} = f(e, y, g, h) then

()

where α, β, η and ζ are nonzero constants.

Proof. From the definition of quadruple Laplace transform

()

Applying change of variables

()

where α, β, ηandζ are nonzero constants.

Property 4. (First shifting property): As explained by [10]: Let

()

Proof. By definition of quadruple Laplace transform (19) can be solved as

()

The interior integral with respect to t in (36) can be solved next to proper substitution as

()

(36) becomes

()

The next inner integral with respect to v in (38) can be solved after proper substitution as

()

After substituting the value from (39) in (37), we can get

()

On the same procedure integrating (40) with respect to m and can be solved after proper substitution as

()

On the last process of integration of (41) with respect to x and can be solved after proper substitution as

()

As the required proof of (35).

2.4. An Iterative Method

In computational mathematics, an iterative method with a powerful set of rules that must be followed when solving a particular problem such as linear and nonlinear ordinary and partial differential equations. The analysis takes place by means of numerical examples. This method in solving the above types of equations is used to want linearization which verifies the capacity, exactness, and directness of the given method in contrast with some of the other methods as explained in the work of [25].

Consider the following general functional equation, as described by [22]:

()

From the Banach space N : B⟶B where N is a nonlinear operator as f is a common function.

We are cast about a solution y in (43) having the sequence:

()

The disintegrate form of the nonlinear operator N is given as follows:

()

From (43)–(45) is equivalent to

()

Now, define H₀ = N(y₀)

Consider the sequence given by

()

We define the recurrence relation:

()

Then,

()

And hence,

()

If N is contraction, i.e., N(x) − N(y) ≤ kx − y, 0 < k < 1 then y_m+1 = N(y₀ + …+y_m) − N(y₀ + …+y_m−1) ≤ ky_m ≤ k^my₀, m = 0,1,2, … and the series

The Banach fixed point theorem shows (43) has unique, absolute, and uniform converges to a solution as explained by [26]. Consequently, the m^th comparative solution of (43) is disposed as follows:

()

2.5. Taylor Series and New Iterative Method

Consider the sequence given by (47) as shown on [1].

()

Then

()

Similarly,

()

Generally,

()

Now in equation (28) to (39) we have,

()

Hence, the simplified form of (57) is given by

()

Hence, (58) is the Taylor series expansion of N(y) around y₀, and this shows that the new iterative method is equivalent to Taylor’s expansion around y₀ as described by [22].

2.6. The New Iterative Method and Its Convergence

Theorem 4. For a continuously differentiable function N a neighborhood of y₀ and

()

For each M the series converges absolutely as described by [22].

Proof. The recurrence relation

()

Consider ξ₀ = M and η_m = ξ_m − ξ_{(m − 1)}, m = 1,2,3, … based on (48) and (56) and the idea of theorem (4), we observe that

()

Take

()

Note that and

Moreover, ξ_m > ξ_{(m − 1)} > 0 , hence, ∑η_m is the series of positive real numbers. Note that

()

. In general,0 < ξ_m < 1. Hence, σ_m = ξ_m − ξ₀ < 1 which yields that bounded and convergent. Consequently, by comparison test ∑G_m is absolutely convergent. So, the new iterative method proves the existence of analytical solution.

3. Numerical Solutions

The aim of this study is to obtain analytical solution of three-dimensional NLKGE by using coupled QLTIM. This is done by extending the work of [9] that was used to solve NLKGE by using coupled DLTIM. So, the definitions, theorems, and some derivations related to quadruple Laplace transform was mentioned in the preceding section would be applied here. Consider the three dimensional nonlinear Klein-Gordon equation of four variables given in (1).

()

With initial conditions

()

Boundary conditions

()

Where x, m, v, t are positive a and c are real numbers N(u(x, m, v, t)) is a nonlinear term and h(x, m, v, t) is a source function. In order to solve such problem we first decompose the source function h(x, m, v, t) into h₁(x, m, v, t) and h₂(x, m, v, t). Where h₁(x, m, v, t) is the term in (1) which leads to express in a simple algebra when applying the inverse quadruple Laplace transform. Whereas h₂(x, m, v, t) is the nonlinear term of (1) helps to reject a complicated term in the process of iteration. Perform quadruple Laplace transform in opposite sides of (1) by using (17), we obtain,

()

Where u, u_t, u_x, u_m, u_v, and h₁ are Laplace transforms of functions of four variables. Note that the existence of Laplace transform of functions of four variables is shown in section (2.1). Next, perform triple Laplace transform of both ICs and BCs of equation (46) and equation (47), yields

()

Here f_i = 1,2; and g_i = 1,2, …, 6; are the Laplace transforms of functions of three variables. Based on the concept of [17]. Then, plugging these ICs and BCs into (67) and using the properties of quadruple Laplace transform as follows, we obtain

()

Where,

()

Applying the definition of inverse quadruple Laplace transform on (70) we obtain

()

Now start the iterative process. Consider

()

Substitute (73) in (72) we obtain,

()

Now, by (45), the iterated portion of non-linear term of (74) decomposed as

()

Again, by (46), we substitute (75) in (74) to obtain

()

Now, define the recurrence relation which is explained in equations (30) to (34):

()

Constructing in this manner, the (n + 1)^th term approximation of the unknown functions u(x, m, v, t) is given by

()

Using (51) the solution u(x, m, v, t) can be constructed in the form of:

()

Hence, by theorem (4) the series is convergent and by equation (27) we conclude that equation (60) is the analytical solution of three dimensional NLKGE.

4. Results and Discussion

In this section the validity and effectiveness of the coupled quadruple Laplace transform and iterative method has been shown.

Example 1. Consider the three dimensional NLKGE

()

With IC’s

()

BC’s

()

Applying quadruple Laplace transform in opposite sides of (81), we obtain

()

Now, applying the triple Laplace transform on both initial conditions and boundary conditions of (82) and (83), we obtain

()

Substituting these initial and boundary conditions values in (84)

()

Applying inverse quadruple Laplace transform in (86), we get

()

Now, perform the process of iteration and substitute (87) on (86) based on (73) and applying equations from (57) to (60), we get

()

From this iteration we conclude that

()

Thus,

()

Note that,

()

And, therefore, N^(k)(u(x, m, v, t)) = 0 for all k ≥ 1. Thus, for all x, m, v, t ≥ 0.

We have,

()

Then the convergence condition of

()

is satisfied. Therefore, by applying the new iterative method we get the solution series,

()

That converges for all x, m, v, t ≥ 0 and hence the required exact solution of example 1 is

()

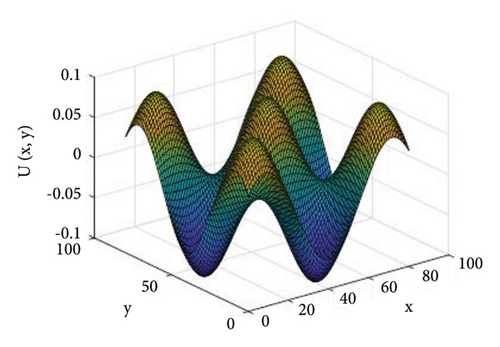
The corresponding graphical representation of three dimensional NLKGE of example 1 is given as follows:

The above Figure 1 shows the exact solution of example (4.1) with 0 ≤ x ≤ 100,0 ≤ y ≤ 100 and. −0.1 ≤ t ≤ 0.1.

Details are in the caption following the image — Open in figure viewer PowerPoint

Example 2. Consider the three dimensional NLKGE of

()

With IC’s

()

BC’s

()

Applying quadruple Laplace transforms both sides of the given (96).

()

Now, applying triple Laplace on both IC’s and BC’s

()

Then substituting these IC’s and BC’s in (99).

()

Applying inverse quadruple Laplace transform on (101), we obtain

()

Now, perform the process of iteration and substitute (102) on (101) based on

(76) and applying equation from (57) to (58), we get

()

From this iteration we conclude that

()

Thus,

()

Note that,

()

And therefore, ‖N^(k)(u₀(x, m, v, t))‖ = 0

for all k ≥ 1 Thus, for all x, m, v, t ≥ 0 we have,

()

for all k ≥ 1. Then by theorem (4), the convergence condition of

()

is satisfied. Therefore, by applying the new iterative method we get the solution series,

()

That converges for all x, m, v, t ≥ 0 and hence the required exact solution of example 2 is

()

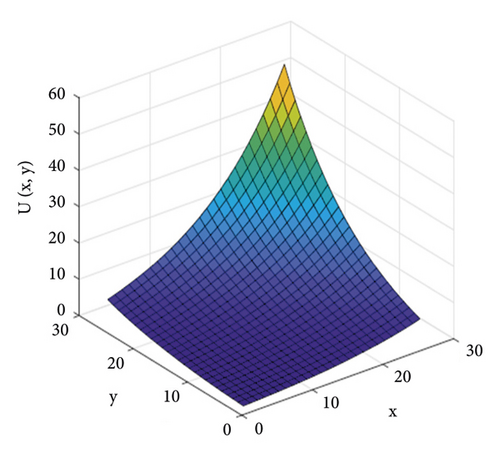
The corresponding graphical representation of three dimensional NLKGE of example 2 is given as follows.

The above Figure 2 shows the exact solution of example (4.2) with 0 ≤ x ≤ 30,0 ≤ y ≤ 30 and. 0 ≤ t ≤ 60,

4.1. Tabular Results

Table 1 shows the exact solutions of the above two examples of nonlinear Klein-Gordon equations using coupled quadruple Laplace transform with iterative method.

1. Tabular values of the above examples (1) and (2), respectively.

	Functions f(x, m, v, t)	Quadruple laplace transform of F(x, m, v, t)
1	cos x cos m sin v sin t	ey/(e² + 1)(y² + 1)(g² + 1)(h² + 1)
2	e^x+m+v+4t	1/(e − 1)(y − 1)(g − 1)(h − 4)

5. Conclusions

In this study quadruple Laplace transform coupled with iterative method was employed for solving three dimensional non-linear Klein-Gordon equations. The main mathematical basics of non-linear Klein-Gordon equation, including a method that describes how to solve partial differential equations of second order were identified and used. To further clarify the theoretical basics some examples have been given, where tables of quadruple Laplace transform also given in order to cross check the exact solutions of examples and there corresponding graphical simulation also presented. The coupled methods applied to obtain analytical solutions of three dimensional non-linear Klein-Gordon equation with initial and boundary conditions in the sense of decomposition of

()

consists only one term, which is

()

From this practical observation we conclude that the quadruple Laplace transform coupled with iterative method helps to find nice practical analytical results with less computation procedures.

Conflicts of Interest

The authors declare that there are no conflicts of interest.

Acknowledgments

The authors would like to express their sincere thanks to the anonymous referees for their insightful remarks and suggestions on the manuscript.

Open Research

Data Availability

The data used to support the findings of the study are included in the article.

References

1 Ali L., Islam S., Gul T., and Amiri I. S., Solution of nonlinear problems by a new analytical technique using Daftardar-Gejji and Jafari polynomials, Advances in Mechanical Engineering. (2019) 11, no. 12, 168781401989696, https://doi.org/10.1177/1687814019896962.
10.1177/1687814019896962
Web of Science® Google Scholar
2 Chand F. and Malik A. K., Exact traveling wave solutions of some nonlinear equations using G, G-expansion Method International Journal of Nonlinear Science. (2012) 14, no. 4, 416–424.
Google Scholar
3 Baskonus H. M., Sulaiman T. A., and Bulut H., On the new wave behavior to the Klein–Gordon–Zakharov equations in plasma physics, Indian Journal of Physics. (2019) 93, no. 3, 393–399, https://doi.org/10.1007/s12648-018-1262-9, 2-s2.0-85063146321.
10.1007/s12648-018-1262-9
CAS Web of Science® Google Scholar
4 Khan N. A., Riaz F., and Ara A., A note on soliton solutions of Klein-Gordon-Zakharov equation by variational approach, Nonlinear Engineering. (2016) 5, no. 3, 135–139, https://doi.org/10.1515/nleng-2016-0001, 2-s2.0-84989160040.
10.1515/nleng-2016-0001
Google Scholar
5 Khalid M., Sultana M., Zaidi F., and Arshad U., Solving linear and nonlinear Klein-Gordon equations by new perturbation iteration transform method, TWMS Journal of Applied and Engineering Mathematics. (2016) 6, no. 1, 115–125.
Web of Science® Google Scholar
6 Wazwaz A. M., The modified decomposition method for analytic treatment of differential equations, Applied Mathematics and Computation. (2006) 173, no. 1, 165–176, https://doi.org/10.1016/j.amc.2005.02.048, 2-s2.0-32144452761.
10.1016/j.amc.2005.02.048
Web of Science® Google Scholar
7 He J. H., Variational iteration method–a kind of non-linear analytical technique: some examples, International Journal of Non-Linear Mechanics. (1999) 34, no. 4, 699–708, https://doi.org/10.1016/s0020-7462(98)00048-1.
10.1016/S0020-7462(98)00048-1
Web of Science® Google Scholar
8 Khuri S. A., A Laplace decomposition algorithm applied to a class of nonlinear differential equations, Journal of Applied Mathematics. (2001) 1, no. 4, 141–155, https://doi.org/10.1155/s1110757x01000183, 2-s2.0-33744989624.
10.1155/S1110757X01000183
Google Scholar
9 Dhunde R. R. and Waghmare G., Analytical solution of the nonlinear Klein-Gordon equation using double Laplace transform and iterative method, American Journal of Computational and Applied Mathematics. (2016) 6, no. 6, 195–201.
Google Scholar
10 Thakur A., Kumar A., and Suryavanshi H., The triple Laplace transforms and their properties, International Journal of Applied Mathematics & Statistical Sciences. (2018) 7, no. 4, 33–44.
Google Scholar
11 Bhadane P. R., Applications of triple laplace transformation to volterra integro partial differential equation, Turkish Journal of Computer and Mathematics Education (TURCOMAT). (2021) 12, no. 13, 3089–3093.
Google Scholar
12 Jamil M., Khan R. A., and Shah K., Exact analytical solutions of linear DissipativeWave equations via laplace transform method, Punjab University Journal of Mathematics. (2021) 53, no. 6, 425–434, https://doi.org/10.52280/pujm.2021.530605.
10.52280/pujm.2021.530605
Google Scholar
13 Deresse A. T., Mussa Y. O., and Gizaw A. K., Solutions of two-dimensional nonlinear sine- Gordon equation via triple laplace transform coupled with iterative method, Journal of Applied Mathematics. (2021) 2021, 2115, 9279022, https://doi.org/10.1155/2021/9279022.
10.1155/2021/9279022
Google Scholar
14 Debnath L., The double Laplace transforms and their properties with applications to functional, integral and partial differential equations, International Journal of Algorithms, Computing and Mathematics. (2016) 2, no. 2, 223–241, https://doi.org/10.1007/s40819-015-0057-3, 2-s2.0-84994452075.
10.1007/s40819-015-0057-3
Google Scholar
15 Eltayeb H. and Kilic¸man A., A note on double Laplace transform and telegraphic equations Abstract and Applied Analysis, 2013, 2013, Hindawi, 6, 932578, https://doi.org/10.1155/2013/932578, 2-s2.0-84874831615.
Google Scholar
16 Elagan S., Sayed M., and Higazy M., An analytical study on fractional partial differential equations by Laplace transform operator method, International Journal of Applied Engineering Research. (2018) 13, no. 1, 545–549.
Google Scholar
17 Atangana A., A note on the triple Laplace transform and its applications to some kind of third-order differential equation Abstract and Applied Analysis, 2013, 2013, Hindawi, 10, 769102, https://doi.org/10.1155/2013/769102, 2-s2.0-84880172399.
Google Scholar
18 Thakur A. and Panda S., Some properties of triple Laplace transform, Journal of Mathematics and Computer Applications Research. (2015) 2250.
Google Scholar
19 Alfaqeih S. and Zis T., Note on fractional triple aboodh transform and its properties, International Journal of Engineering and Information Systems (IJEAIS). (2019) 3, no. 5.
Google Scholar
20 Khan A., Khan A., Khan T., and Zaman G., Extension of triple Laplace transform for solving fractional differential equations, Discrete & Continuous Dynamical Systems-S. (2020) 13, no. 3, 755–768, https://doi.org/10.3934/dcdss.2020042.
10.3934/dcdss.2020042
Google Scholar
21 Khan T., Shah K., Khan A., and Khan R. A., Solution of fractional order heat equation via triple Laplace transform in 2 dimensions, Mathematical Methods in the Applied Sciences. (2018) 41, no. 2, 818–825.
10.1002/mma.4646
Web of Science® Google Scholar
22 Bhalekar S. and Daftardar-Gejji V., Convergence of the new iterative method, International Journal of Differential Equations. (2011) 2011, 1–10, https://doi.org/10.1155/2011/989065, 2-s2.0-84874914808.
10.1155/2011/989065
Google Scholar
23 Rehman H. U., Iftikhar M., Saleem S., Younis M., and Mueed A., A computational quadruple Laplace transform for the solution of partial differential equations, Applied Mathematics. (2014) 05, no. 21, 3372–3382, https://doi.org/10.4236/am.2014.521314.
10.4236/am.2014.521314
Google Scholar
24 Kılıc¸man A. and Eltayeb H., A note on the classifications of hyperbolic and elliptic equations with polynomial coefficients, Applied Mathematics Letters. (2008) 21, no. 11, 1124–1128, https://doi.org/10.1016/j.aml.2007.11.002, 2-s2.0-51049113592.
10.1016/j.aml.2007.11.002
Google Scholar
25 Hemeda A., New iterative method: an application for solving fractional physical differential equations Abstract and Applied Analysis, 2013, 2013, Hindawi, 9, 617010, https://doi.org/10.1155/2013/617010, 2-s2.0-84878689795.
Google Scholar
26 Daftardar-Gejji V. and Jafari H., An iterative method for solving nonlinear functional equations, Journal of Mathematical Analysis and Applications. (2006) 316, no. 2, 753–763, https://doi.org/10.1016/j.jmaa.2005.05.009, 2-s2.0-29844442304.
10.1016/j.jmaa.2005.05.009
Web of Science® Google Scholar

All articles

Solutions of Three Dimensional Nonlinear Klein-Gordon Equations by Using Quadruple Laplace Transform

Abstract

1. Introduction

2. Definition of Quadruple Laplace Transform

2.1. Using a Change of Variables

2.2. Existence of Quadruple Laplace Transform

2.3. Main Properties of Quadruple Laplace Transform

2.4. An Iterative Method

2.5. Taylor Series and New Iterative Method

2.6. The New Iterative Method and Its Convergence

3. Numerical Solutions

4. Results and Discussion

4.1. Tabular Results

5. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Solutions of Three Dimensional Nonlinear Klein-Gordon Equations by Using Quadruple Laplace Transform

Abstract

1. Introduction

2. Definition of Quadruple Laplace Transform

2.1. Using a Change of Variables

2.2. Existence of Quadruple Laplace Transform

2.3. Main Properties of Quadruple Laplace Transform

2.4. An Iterative Method

2.5. Taylor Series and New Iterative Method

2.6. The New Iterative Method and Its Convergence

3. Numerical Solutions

4. Results and Discussion

4.1. Tabular Results

5. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Related

Information