Volume 2022, Issue 1 2537513

Research Article

Open Access

[Retracted] A Novel Multiple-Criteria Decision-Making Approach Based on Picture Fuzzy Sets

Retraction(s) for this article

Hanen Karamti

Department of Computer Sciences, College of Computer and Information Sciences, Princess Nourah Bint Abdulrahman University, P.O.Box 84428, Riyadh 11671, Saudi Arabia pnu.edu.sa

Search for more papers by this author

Muhammad Sarwar Sindhu,

Muhammad Sarwar Sindhu

Department of Mathematics, Virtual University of Pakistan, Lahore, Pakistan vu.edu.pk

Search for more papers by this author

Muhammad Ahsan,

Muhammad Ahsan

Department of Mathematics, Virtual University of Pakistan, Lahore, Pakistan vu.edu.pk

Search for more papers by this author

Imran Siddique,

Corresponding Author

Imran Siddique

[email protected]

orcid.org/0000-0002-5060-7906

Department of Mathematics, University of Management and Technology, Lahore 54770, Pakistan umt.edu.pk

Search for more papers by this author

Ibrahim Mekawy,

Corresponding Author

Ibrahim Mekawy

[email protected]

orcid.org/0000-0003-1014-7041

Department of Mathematics, College of Science and Arts, Qassim University, Ar Rass, Saudi Arabia qu.edu.sa

Search for more papers by this author

Hamiden Abd El-Wahed Khalifa,

Hamiden Abd El-Wahed Khalifa

Department of Operations Research, Faculty of Graduate Studies for Statistical Research, Cairo University, Giza 12613, Egypt cu.edu.eg

Department of Mathematics, College of Science and Arts, Qassim University, Al-Badaya 51951, Saudi Arabia qu.edu.sa

Search for more papers by this author

Hanen Karamti,

Hanen Karamti

Department of Computer Sciences, College of Computer and Information Sciences, Princess Nourah Bint Abdulrahman University, P.O.Box 84428, Riyadh 11671, Saudi Arabia pnu.edu.sa

Search for more papers by this author

Muhammad Sarwar Sindhu,

Muhammad Sarwar Sindhu

Department of Mathematics, Virtual University of Pakistan, Lahore, Pakistan vu.edu.pk

Search for more papers by this author

Muhammad Ahsan,

Muhammad Ahsan

Department of Mathematics, Virtual University of Pakistan, Lahore, Pakistan vu.edu.pk

Search for more papers by this author

Imran Siddique,

Corresponding Author

Imran Siddique

[email protected]

orcid.org/0000-0002-5060-7906

Department of Mathematics, University of Management and Technology, Lahore 54770, Pakistan umt.edu.pk

Search for more papers by this author

Ibrahim Mekawy,

Corresponding Author

Ibrahim Mekawy

[email protected]

orcid.org/0000-0003-1014-7041

Department of Mathematics, College of Science and Arts, Qassim University, Ar Rass, Saudi Arabia qu.edu.sa

Search for more papers by this author

Hamiden Abd El-Wahed Khalifa,

Hamiden Abd El-Wahed Khalifa

Department of Operations Research, Faculty of Graduate Studies for Statistical Research, Cairo University, Giza 12613, Egypt cu.edu.eg

Department of Mathematics, College of Science and Arts, Qassim University, Al-Badaya 51951, Saudi Arabia qu.edu.sa

Search for more papers by this author

First published: 27 February 2022

https://doi.org/10.1155/2022/2537513

Citations: 3

Academic Editor: Ganesh Ghorai

Share a link

Email
Wechat
Bluesky

Abstract

Experts are using picture fuzzy sets (PFSs) in their probes to resolve the uncertain and vague information during the process of decision making because PFSs describe human attitudes naturally. Divergence measure (DM) plays a dominant role in discriminating between two distributions of probability and extracting consequences from that discrimination. In the present work, a novel picture fuzzy divergence measure (PF-DM) is developed between two PFSs. Some of the suggested measure’s important qualities are also discussed with particular situations to validate it. Based on the suggested PF-DM, a multiple-criteria decision-making (MCDM) model is established to grab the fuzzy information. The suggested measure’s performance is compared to that of various existing measures in the literature. An MCDM model has been proven for the usefulness of the suggested technique in dealing with real-life scenarios in the context of dengue sickness and pattern identification. Validation of the suggested MCDM model has been further investigated using validity testing. To improve the generated model, a thorough comparison with several current methodologies has been carried out while taking the time complexity (TC) factor into account.

1. Introduction

Handling vagueuncertain information in real-life situations has trouble. Therefore, various techniques, such as the theory of fuzzy sets (FSs), have been examined to address the ambiguity and uncertainty found in the real world. Zadeh [1] introduced the concept of FSs in 1965 to tackle the imprecise, unclear data and applied them in decision-making complications by considering diverse perspectives. Although the FS theory has been applied to a variety of sectors, some circumstances in actual life appear to be beyond its capabilities. To capture such occurrences, Atanassov [2] suggested intuitionistic fuzzy sets (IFSs). IFSs are a generalization of FSs made up of two degrees: membership degree (MD) and non-membership degree (NMD), with 0 ≤ MD + NMD ≤ 1. Innumerable investigators contributed their work in this extension, for example, based on the Hamming distance, Szmidt and Kacprzyk [3] developed a similarity measure (SM) between IFSs. Xu and Xia [4] categorized SM and the geometric distance of IFSs for group decision-making problems. Several scholars have begun research on Atanassov’s intuitionistic fuzzy theory due to its elasticity and effective applications. Furthermore, stimulating solicitations in specific areas such as risk analysis, image processing, and medical diagnosis have been established in [5, 6].

This cosmos is full of uncertainty, inconsistency, and ambiguity. In reality, the great majority of the concepts we discuss include ambiguity instead of exact information. Addressing fear or uncertainties is a major difficulty in many professions, including sociology, natural science, engineering, medicine, and economics. Recently, a lot of authors have expressed a significant interest in depicting ambiguity. Traditional hypotheses, such as FS [1], vague sets [7], and rough sets [8], are well known and play a significant role in demonstrating uncertainty. Molodtsov [9] defined soft sets as an entirely new scientific instrument for coping with uncertainty.

Regardless, IFSs have been used in many fields of life. However, there are a variety of situations in which IFSs cannot be used. For example, casting a vote and dealing with issues such as yes, neutral, rejection, and refusal, which restricts the use of IFSs. Cuong [10] developed a generalization of FS called picture fuzzy (PF) sets (PFSs) to address such issues. PFSs have considered three factors from their inception: neutral membership degree (NMD), acceptance membership degree (AMD), and refusal membership degree (RMD). The requirement 0 ≤ AMD + NMD + RMD ≤ 1 was met by these three features. From its beginning to the current day, PFSs have been verified for treating unclear circumstances in real-life issues, for example, decision making, pattern recognition, clustering, etc.

Based on PFSs, numerous researchers have worked in different fields, for instance, Thong [11] put forward an algorithm for fuzzy clustering that depicts the benefits of PFSs, Wei [12] developed the PF cross-entropy model for MCDM problems, Ashraf et al. [13] explained several procedures to MCDM issues under PF framework, and Sindhu et al. [14] implemented PFSs to select the best alternative. Recently, Zhao et al. [15] presented a dynamic distance measure of PFS depending on a PF point operator to resolve the real-life problem. Duong and Thao established a dissimilarity measure on PFSs and applied it MCDM problem to choose the optimal option. Verma and Rohtagi [16] presented the similarity measures based on PFSs to diagnose diseases and pattern recognition. Gocer [17] created a group decision-making technique based on interval-valued PFSs and then used it to determine a sustainable supply chain strategy. Sustainable supply chain strategy is a complex MCDM issue involving multiple parameters that may be contradictory at the same time. Luo et al. [18] proposed the SM based on relationship matrix and showed that it satisfied all the conditions of SM and then implemented the established SM to resolve the MCDM problem.

DM is useful for discriminating between two probability distributions and extracting conclusions from that discrimination. With the use of HFSs [19] and IFSs [20], many academics have worked and developed to answer decision-making difficulties. DM has also been utilized in MCDM problems by several experts [21, 22]. The PFS has been regarded as an extension of the FS and IFSs. As a result of the findings of the study on FS measures, the IFSs for the PFSs are likewise natural and necessary. This is the motivation behind our research into the DM of PFSs, both in theory and in practice. The major aims and contributions of this study are as follows:

(i)
A novel PF divergence measure (PF-DM) is proposed along with its properties.
(ii)
PF-DM is developed to measure the degree of fuzziness.
(iii)
Two examples, one related to medical diagnosis and the other to pattern recognition, are used to reveal the strength and reliability of the newly developed PF-DM.

Since the inception of the current MCDM theory in the early 1960s, MCDM has been developing to aid decision making to meet various applications [23]. Its importance in numerous application fields has grown significantly, particularly when new techniques are developed and existing ones are improved. MCDM approaches can provide powerful tools for allocating resources inside difficult operations, as well as in complicated exercises such as picking alternatives, weighing criteria, and establishing priorities. MCDM strategies are techniques and ways that attempt to find an optimal solution when there are several competing criteria. The selection of the most appealing DM goals from a wide number of available options while taking into account a variety of physical and abstract features or attributes [24] is at the heart of MCDM techniques. MCDM is a discipline that supports decision makers in making the best decision possible from a set of options based on several factors [25]. Several MCDM approaches have been created in the current decade [26] and used in many fields, such as supplier selection [27, 28] and project management development [29]. Sindhu et al. [30, 31] proposed a TOPSIS-based assessment approach for PFSs to address MCDM problems.

The remainder of the paper is organized as follows. Some basic and related knowledge is penned in Section 2. Novel PF-DM and its properties are discussed comprehensively in Section 3. An MCDM model based on PF-DM is established to resolve the uncertain information. Section 5 comprises two MCDM problems related to medical diagnosis and pattern recognition. In Section 6, the validity of the suggested model is investigated. A comprehensive comparison based on TC is analyzed in Section 6.3. Finally, Section 7 points out some conclusions.

2. Basic Concepts

Some basic ideas connected to the present work like FSs, IFSs, and PFSs and their operational laws are briefly penned in this section.

Definition 1 (see [1].)Let Y be a discourse set such that Y = {y₁, y₂, …, y_n}; then, a FS ℱ over Y can be illustrated as

(1)

where μ_ℱ(y)) : X⟶[0,1] is a MD so that y ∈ Y to ℱ.

Definition 2 (see [2].)Suppose that Y is a fixed set, and an IFS ℐ on Y is illustrated as

(2)

where α_ℐ(y) and β_ℐ(y) ∈ [0,1] are called the MD and NMD of y ∈ Y to ℐ, respectively, with the condition: 0 ≤ α_ℐ(y) + β_ℐ(y) ≤ 1, for all y ∈ Y.For all y ∈ Y, η_I(y) is known as hesitancy degree of y ∈ ℐ where η_I(y) = 1 − α_ℐ(y) − β_ℐ(y).

Definition 3 (see [10].)A PFS on Y = {y₁, y₂, …, y_n} is penned as follows:

(3)

where α_P(y), β_P(y), and η_P(y) ∈ [0,1] are called the MD, neutral degree, and NMD of y ∈ Y to the set P; subsequently, α_P(y), η_P(y), and β_P(y) fulfil the condition: 0 ≤ α_P(y) + η_P(y) + β_P(y) ≤ 1, for all y ∈ Y. Also, η_P(y) = 1 − α_P(y) − η_P(y) − β_P(y); then, η_P(y) is supposed to represent a degree of refusal membership of y ∈ Y in P. For simplicity, PFS over a fixed set Y is read as PFS (Y).

Definition 4 (see [10].)Let , , and P = (α_P(y), η_P(y), β_p(y)) be three PFSs on Y; then, some arithmetic operations are described as follows:

(1)
P₁⊆P₂ iff and for all y ∈ Y.
(2)
P₁ = P₂ iff P₁⊆P₂ and P₂⊆P₁.
(3)
.
(4)
.
(5)
P^C = {〈y, β_P(y), η_P(y), α_P(y)〉|y ∈ Y}.

3. Novel Divergence Measure for PFSs

In the present work, a novel PF-DM is proposed.

(i)
.
(ii)
.

Definition 5. Let PFSs. The function D: PFS × PFS R is called a PF-divergence measure (PF-DM) denoted by if it satisfies

Definition 6. Let PFSs. Then, a PF-DM is defined by

(4)

where

and

Theorem 1. Let PFSs. Then, the measure is valid PF-divergence measure.

Proof.

(i)
The following inequality holds for any two real numbers a, b ∈ [0,1]:
.
Since .
.
.
.
(ii)
Suppose that ; therefore, α₁(y_i) = α₂(y_i), η₁(y_i) = η₂(y_i), β₁(y_i) = β₂(y_i), ∀i = 1,2, …, n. Then, (4) becomes

(5)

Conversely, assume .

(6)

This is possible if and only if α₁(y_i) = α₂(y_i), η₁(y_i) = η₂(y_i), β₁(y_i) = β₂(y_i), ∀i = 1,2, …, n.

This proves that .

Since the measure holds the postulates of Definition 5, is an appropriate divergence measure for PFSs.

Theorem 2. Let PFSs (Y); then, the measure satisfies the following axioms:

.
, we have
.
.

Proof.

(i)
It is easy to understand.
(ii)
(a) Let ; then, for any 0 ≤ i ≤ n,
α₁(y_i) ≤ α₂(y_i) ≤ α₃(y_i),
η₁(y_i) ≤ η₂(y_i) ≤ η₃(y_i),
and β₁(y_i) ≤ β₂(y_i) ≤ β₃(y_i), and we obtain
.
Hence, . Similarly, we can verify axiom (b).

Theorem 3. Let PFSs. Then, for , we get

(1)
,
(2)
,
(3)
or , we get
- (i)
  ,
- (ii)
  .

Proof.

(1)
Since , ,
, ; then,
,
.
(2)
,
,
(ii) .
(3)
(i) Take ; then, , also, .
Now if , then ; also, .
That is, if or , we get .
(ii) Its proof is simple.

4. MCDM Process Based on PF-DM

In this section, a decision-making process based on PF-DM has been provided, followed by practical examples to demonstrate the concept. Suppose a collection of n alternatives represented by A = {A₁, A₂, …, A_n} that has been investigated by the decision maker by considering the collection of m different criteria Q = {Q₁, Q₂, …, Q_m} having weight vectors is

so that

. Consider the decision maker assessing the rating of an alternative A_i, (1 ≤ i ≤ n) on the criteria G_j, (1 ≤ j ≤ m) in the form of PFSs. To arrive at the best solution, MCDM takes the following actions.

Step 1. Gather data in the form of PF decision matrix. .
.
Step 2. Evaluate the ideal solution .
Step 3. Based on (4), compute the PF-DM.
Step 4. Arrange the values of PF-DM from lower order to top order.
Step 5. Based on Step 4, choose the best alternative.

5. Solution of Problems Based on PF-DM

The authors used the proposed MCDM model to recognize the pattern and breakout of dengue disease in this section.

Step 1. Picture fuzzy (PF) decision matrix is denoted in Table 1.
Step 2. The ideal solution N = {(y₁,0.1000, 0.1000, 0.1000), (y₂,0,0.1000, 0.3000), (y₃,0.3000, 0.1000, 0.1000), (y₄, 0.2000, 0.1000,0.1000), (y₅,0.1000,0.1000, 0.2000)}.
Step 3. The PF-DM values among the symptoms B₁, B₂, B₃, B₄, and B₅ and the ideal solution N are
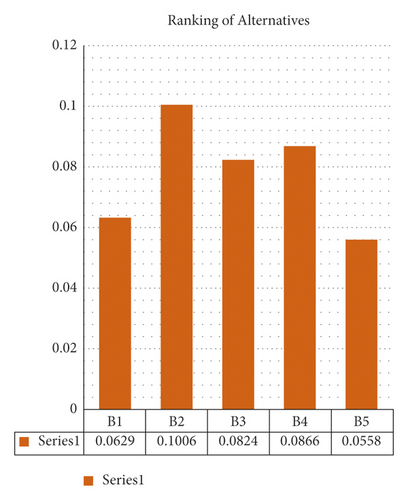
D_m(B₁, N) = 0.0629, D_m(B₂, N) = 0.1006,
D_m(B₃, N) = 0.0824,
D_m(B₄, N) = 0.0866, D_m(B₅, N) = 0.0558.
Step 4. Arrange the values of PF-DM from lower order to top order such that B₅≺B₁≺B₃≺B₄≺B₂.
Step 5. The most frequent symptom is B₅ which can be seen in Figure 1.

Table 1. PF decision matrix.

Symptoms
B₁	{(y₁, 0.1, 0.4, 0.3), (y₂, 0.4, 0.1, 0.3), (y₃, 0.3, 0.2, 0.4),(y₄, 0.2, 0.3, 0.5), (y₅, 0.5, 0.1, 0.3)}
B₂	{(y₁, 0.3, 0.3, 0.3), (y₂, 0.0, 0.2, 0.7), (y₃, 0.6, 0.1, 0.1),(y₄, 0.4, 0.4, 0.2), (y₅, 0.1, 0.5, 0.3)}
B₃	{(y₁, 0.5, 0.1, 0.3), (y₂, 0.3, 0.4, 0.3), (y₃, 0.6, 0.1, 0.3),(y₄, 0.4, 0.4, 0.1), (y₅, 0.1, 0.5, 0.2)}
B₄	{(y₁, 0.6, 0.2, 0.1), (y₂, 0.3, 0.2, 0.4), (y₃, 0.4, 0.2, 0.3),(y₄, 0.6, 0.1, 0.1), (y₅, 0.4, 0.2, 0.2)}
B₅	{(y₁, 0.1, 0.4, 0.3), (y₂, 0.4, 0.1, 0.3), (y₃, 0.3, 0.2, 0.4),(y₄, 0.2, 0.3, 0.4), (y₅, 0.5, 0.1, 0.3)}

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Ranking of symptoms by PF-DM.

Example 1. In the context of dengue disease, it is critical to provide a productive path in crisis response in order to avoid additional misfortunes and save people’s lives. As a result of such a life-threatening situation, health professionals must respond quickly in order to effectively control the situation and prevent further deaths. There are five major symptoms, namely, aching muscles and joints (B₁), body rash that can disappear and then reappear (B₂), high fever (B₃), intense headache (B₄), and vomiting and feeling nauseous (B₅), that can be investigated to diagnose this disease. All symptoms, B₁, B₂, B₃, B₄, and B₅, are penned in terms of PFSs in Table 1.

An unknown pattern is classified into a specific pattern using numerous fuzzy information parameters such as distance, similarity, accuracy, and others. For pattern recognition, we employ the proposed PF-DM. A pattern recognition problem is phrased as follows in the picture fuzzy environment.

(i)
Step 1. PF decision matrix is denoted in Table 2.
Step 2. An unknown pattern represented by N is:
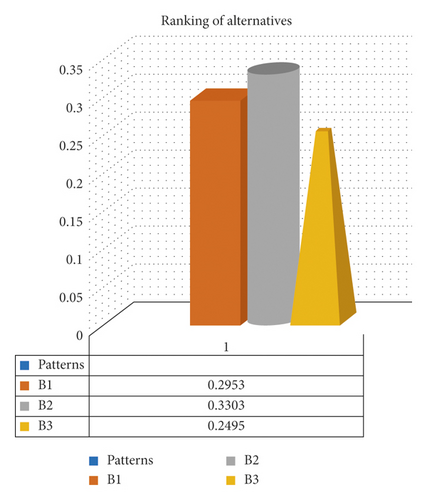
Step 3. The PF-DM values among the alternatives B₁, B₂, and B₃ and the unknown pattern are
, , .
Step 4. Arrange the values of PF-DM from lower order to top order such that B₃≺B₁≺B₂.
Step 5. Hence, B₃ is an optimal pattern. Figure 2 illustrates the ranking order of the alternatives.

Table 2. PF decision matrix.

Patterns
B₁	{(y₁, 0.4, 0.3, 0.1), (y₂,0.5, 0.3, 0.2), (y₃,0.4, 0.3, 0.0), (y₄,0.7, 0.0, 0.2), (y₅,0.6, 0.1, 0.1)}
B₂	{(y₁, 0.7,0.1, 0.1), (y₂, 0.2, 0.3, 0.4), (y₃,0.2, 0.1, 0.5), (y₄,0.1, 0.5, 0.2), (y₅,0.3, 0.3, 0.3)}
B₃	{(y₁, 0.1, 0.3, 0.4), (y₂,0.4, 0.3, 0.1), (y₃,0.3, 0.4, 0.2), (y₄,0.2, 0.5, 0.3), (y₅,0.5, 0.3, 0.1)}

Example 2. Suppose A = {B₁, B₂, B₃} are some well-known patterns distinguished by PFSs in the universal set Y = {Y₁, Y₂, Y₃, Y₄, Y₅} which are given in the table below.

Because determining which option is the best match for a particular choice issue is impractical in real life, Wang and Triantaphyllou [32] developed testing criteria to examine the validity of MCDM approaches, which are as follows.

6. Validity Testing of Criteria for the Proposed MCDM Model

Criterion 1. An effective MCDM approach should not change the indication of the best option when replacing a non-optimal option with a worse option without changing the relative relevance of any decision criterion.

Criterion 2. The transitive property should be followed by an effective MCDM approach.

Criterion 3. When an MCDM problem is broken down into smaller problems and the same MCDM method is used to assess the options on the smaller problems, the combined ranking of the alternatives should equal the undecomposed problem’s original rating. These testing criteria are being used to evaluate the proposed PF-DM MCDM model’s validity.

6.1. Testing Criterion 1

Decision matrix provided in Table 3 is attained by altering the AMD and RMD of the alternative B₁ (non-favorable) and B₂ (inferior) in the original decision matrix to check the efficacy of the suggested model under test criterion 1 of Example 1.

Table 3. PF decision matrix.

Symptoms
B₁	{(y₁, 0.3, 0.4, 0.1), (y₂, 0.3, 0.1, 0.4), (y₃, 0.4 0.2, 0.3),(y₄, 0.5, 0.3, 0.2), (y₅, 0.3, 0.1, 0.5)}
B₂	{(y₁,0.3, 0.3, 0.3), (y₂, 0.70, 0.2, 0.0), (y₃, 0.1, 0.1, 0.6),(y₄, 0.2, 0.4, 0.4), (y₅, 0.3, 0.5, 0.1)}
B₃	{(y₁, 0.5, 0.1, 0.3), (y₂, 0.3, 0.4, 0.3), (y₃, 0.6, 0.1, 0.3),(y₄, 0.4, 0.4, 0.1), (y₅, 0.1, 0.5, 0.2)}
B₄	{(y₁, 0.6, 0.2, 0.1), (y₂, 0.3, 0.2, 0.4), (y₃, 0.4, 0.2, 0.3),(y₄, 0.6, 0.1, 0.1), (y₅, 0.4, 0.2, 0.2)}
B₅	{(y₁, 0.1, 0.4, 0.3), (y₂, 0.4, 0.1, 0.3), (y₃, 0.3, 0.2, 0.4),(y₄, 0.2, 0.3, 0.4), (y₅, 0.5, 0.1, 0.3)}

The PF-DM values among the symptoms B₁, B₂, B₃, B₄, and B₅ and the ideal solution N are D_m(B₁, N) = 0.0660, D_m(B₂, N) = 0.1037, D_m(B₃, N) = 0.0855, D_m(B₄, N) = 0.0896, and D_m(B₅, N) = 0.0590. As a result, the proposed technique supported test criterion 1 provided in [32].

6.2. Testing Criteria 2 and 3

To validate the suggested approach, use test criterion 2 and test criterion 3. The MCDM problem presented in Example 1 has been divided into five smaller subsets such as {B₁, B₂, B₃, B₄}, {B₁, B₂, B₃, B₅}, {B₁, B₃, B₄, B₅}, {B₁, B₂, B₃, B₅}, and {B₂, B₃, B₄, B₅}. We may obtain the following arrangements for each subset using the suggested MCDM model: B₁≺B₃≺B₄≺B₂, B₅≺B₁≺B₃≺B₂, B₅≺B₃≺B₄≺B₁, B₅≺B₁≺B₃≺B₁, and B₅≺B₃≺B₄≺B₂, respectively. By aggregating all these arrangements, overall ranking B₅≺B₁≺B₃≺B₄≺B₂ is obtained which is identical to the original one. Thereby, the suggested MCDM model is validated under the test criteria 2 and 3 presented in [32].

6.3. Comparison Based on Time Complexity

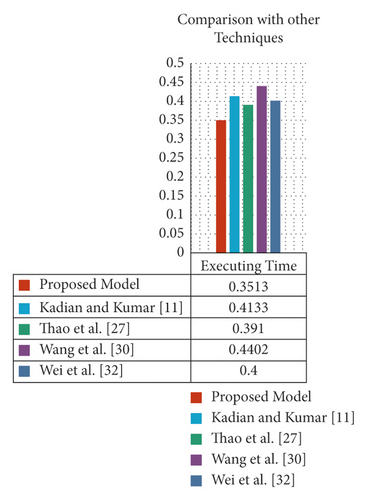
In order to strengthen the results obtained from the proposed MCDM model, TC analysis is performed in this section. TC is the time required to execute an algorithm to reach the final result. TC is measured among the proposed and the existing techniques presented by Kadian and Kumar [6], Thao et al. [33], Wang et al. [34], and Wei et al. [35]. The executing time of each technique is evaluated with the help of MATLAB which is presented in Table 4, and its graphical view is drawn in Figure 3. From Table 4, our approach takes less time as compared to others, and hence the proposed MCDM model is more effective and resolves the issues rapidly.

Table 4. TC among the proposed and existing techniques.

Techniques	Executing time
Proposed model	0.3513 seconds
Kadian and Kumar [6]	0.4133 seconds
Thao et al. [33]	0.3910 seconds
Wang et al. [34]	0.4402 seconds
Wei et al. [35]	0.4000 seconds

7. Conclusions

A PF-DM is proposed in this study, along with proof of its validity, and some of its features are studied. Existing DMs for PFSs are less feasible than the suggested DM. The suggested divergence metric surpasses other current similarities and DMs by illustrating real challenges in medical analysis and pattern recognition. It can be seen that in pattern recognition, the suggested divergence metric can assign an unknown pattern to one of the previously recognized patterns. Diseases are diagnosed in medical analysis based on their symptoms, which are represented by visual fuzzy numbers. In addition, pattern recognition employs the proposed divergence measure. It holds in both circumstances.

As a result, the proposed DM is useful for pattern identification as well as medical diagnostics. In addition, the following are the study’s long-term goals. (i) It is possible to develop a parametric generalized divergence measure. (ii) PFS can be enhanced by including a third parameter, the degree of refusal. (iii) The suggested divergence metric may be expanded and implemented in an image fuzzy soft set environment. (iv) The suggested DMs may be used to a wide range of real-world problems [36].

Abbreviations	Description
DM	Divergence measure
FSs	Fuzzy sets
IFSs	Intuitionistic fuzzy sets
MD	Membership degree
MCDM	Multiple-criteria decision making
NMD	Non-membership degree
PFSs	Picture fuzzy sets
PF-DM	Picture fuzzy divergence measure
SM	Similarity measure

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This research was supported by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R192), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Open Research

Data Availability

No data were used to support this study.

References

1 Zadeh L. A., Fuzzy sets, Information and Control. (1965) 8, no. 3, 338–353, https://doi.org/10.1016/s0019-9958(65)90241-x, 2-s2.0-34248666540.
10.1016/S0019-9958(65)90241-X
CAS Web of Science® Google Scholar
2 Atanassov K. T., Intuitionistic fuzzy sets, Fuzzy Sets and Systems. (1986) 20, no. 1, 87–96, https://doi.org/10.1016/s0165-0114(86)80034-3, 2-s2.0-0002740725.
10.1016/S0165-0114(86)80034-3
Web of Science® Google Scholar
3 Szmidt E. and Kacprzyk J., Distances between intuitionistic fuzzy sets, Fuzzy Sets and Systems. (2000) 114, no. 3, 505–518, https://doi.org/10.1016/s0165-0114(98)00244-9, 2-s2.0-0000041473.
10.1016/S0165-0114(98)00244-9
Web of Science® Google Scholar
4 Xu Z. S. and Xia M. M., Some new similarity measures for intuitionistic fuzzy values and their application in group decision making, Journal of Systems Science and Systems Engineering. (2010) 19, 430–452.
10.1007/s11518-010-5151-9
Web of Science® Google Scholar
5 Joshi R., A novel decision-making method using R-norm concept and VIKOR approach under picture fuzzy environment, Expert Systems with Applications. (2020) 147, https://doi.org/10.1016/j.eswa.2020.113228.
10.1016/j.eswa.2020.113228
Web of Science® Google Scholar
6 Kadian R. and Kumar S., A novel intuitionistic Renyi’s-Tsallis discriminant information measure and its applications in decision-making, Granular Computing. (2021) 6, 901–913, https://doi.org/10.1007/s41066-020-00237-z.
10.1007/s41066-020-00237-z
Google Scholar
7 Gau W.-L. and Buehrer D. J., Vague sets, IEEE Transactions on Systems, Man, and Cybernetics. (1993) 23, no. 2, 610–614, https://doi.org/10.1109/21.229476, 2-s2.0-0027555609.
10.1109/21.229476
Web of Science® Google Scholar
8 Pawlak Z., Grzymala-Busse J., Slowinski R., and Ziarko W., Rough sets, Communications of the ACM. (1995) 38, no. 11, 88–95, https://doi.org/10.1145/219717.219791, 2-s2.0-0029405527.
10.1145/219717.219791
Web of Science® Google Scholar
9 Molodtsov D., Soft Set theory-first results, Computers & Mathematics with Applications. (1999) 37, no. 4-5, 19–31, https://doi.org/10.1016/s0898-1221(99)00056-5.
10.1016/S0898-1221(99)00056-5
Web of Science® Google Scholar
10 Cuong B. C., Picture fuzzy sets, a new concept for computational intelligence problems, Proceedings of the third world congress on information and communication technologies, December 2013, Hanoi, Vietnam, 1–6, https://doi.org/10.1109/wict.2013.7113099, 2-s2.0-84949928814.
10.1109/wict.2013.7113099
Google Scholar
11 Thong P. H., Some novel hybrid forecast methods based on picture fuzzy clustering for weather now casting from satellite image sequences, Applied Intelligence. (2017) 46, 1–15.
10.1007/s10489-016-0811-1
Web of Science® Google Scholar
12 Wei G., Picture fuzzy aggregation operators and their application to multiple attribute decision making, Journal of Intelligent and Fuzzy Systems. (2017) 33, no. 2, 713–724, https://doi.org/10.3233/jifs-161798, 2-s2.0-85025681338.
10.3233/JIFS-161798
Web of Science® Google Scholar
13 Ashraf S., Mahmood T., Abdullah S., and Khan Q., Different approaches to multi-criteria group decision making problems for picture fuzzy environment, Bulletin of the Brazilian Mathematical Society, New Series. (2019) 50, no. 2, 373–397, https://doi.org/10.1007/s00574-018-0103-y, 2-s2.0-85049799434.
10.1007/s00574-018-0103-y
Google Scholar
14 Sindhu M. S., Rashid T., and Kashif A., Modeling of linear programming and extended TOPSIS in decision making problem under the framework of picture fuzzy sets, PLoS One. (2019) 14, no. 8, e0220957, https://doi.org/10.1371/journal.pone.0220957, 2-s2.0-85070628440.
10.1371/journal.pone.0220957
CAS PubMed Web of Science® Google Scholar
15 Zhao R., Luo M., and Li S., A dynamic distance measure of picture fuzzy sets and its application, Symmetry. (2021) 13, no. 3, https://doi.org/10.3390/sym13030436.
10.3390/sym13030436
Web of Science® Google Scholar
16 Verma R. and Rohtagi B., Novel similarity measures between picture fuzzy sets and their applications to pattern recognition and medical diagnosis, Granular Computing. (2022) 1–17, https://doi.org/10.1007/s41066-021-00294-y.
10.1007/s41066-021-00294-y
Google Scholar
17 Gocer F., A novel interval value extension of picture fuzzy sets into group decision making: an approach to support supply chain sustainability in catastrophic disruptions, IEEE Access. (2021) 9, 117080–117096, https://doi.org/10.1109/access.2021.3105734.
10.1109/ACCESS.2021.3105734
Web of Science® Google Scholar
18 Luo M., Zhang Y., and Fu L., A new similarity measure for picture fuzzy sets and its application to multi-attribute decision making, Informatica. (2021) 32, 1–22, https://doi.org/10.15388/21-infor452.
10.15388/21-infor452
Web of Science® Google Scholar
19 Kobza V., Janiš V., and Montes S., Divergence measures on hesitant fuzzy sets, Journal of Intelligent and Fuzzy Systems. (2017) 33, no. 3, 1589–1601, https://doi.org/10.3233/jifs-161430, 2-s2.0-85028535253.
10.3233/JIFS-161430
Web of Science® Google Scholar
20 Mishra A. R., Kumari R., and Sharma D. K., Intuitionistic fuzzy divergence measure-based multi-criteria decision-making method, Neural Computing & Applications. (2019) 31, no. 7, 2279–2294, https://doi.org/10.1007/s00521-017-3187-1, 2-s2.0-85028777657.
10.1007/s00521-017-3187-1
Web of Science® Google Scholar
21 Mishra A. R., Rani P., Pardasani K. R., Mardani A., Stević Ž., and Pamučar D., A novel entropy and divergence measures with multi-criteria service quality assessment using interval-valued intuitionistic fuzzy TODIM method, Soft Computing. (2020) 24, no. 15, 11641–11661, https://doi.org/10.1007/s00500-019-04627-7.
10.1007/s00500-019-04627-7
Web of Science® Google Scholar
22 Zhou Q., Mo H., and Deng Y., A new divergence measure of pythagorean fuzzy sets based on belief function and its application in medical diagnosis, Mathematics. (2020) 8, no. 1, https://doi.org/10.3390/math8010142.
10.3390/math8010142
Web of Science® Google Scholar
23 Kahraman C., Onar S. C., and Oztaysi B., Fuzzy multicriteria decision-making: a literature review, International Journal of Computational Intelligence Systems. (2015) 8, no. 4, 637–666, https://doi.org/10.1080/18756891.2015.1046325, 2-s2.0-84930983878.
10.1080/18756891.2015.1046325
Web of Science® Google Scholar
24 Buyuukozkan G., Gocer F., and Feyzioglu O., Cloud computing technology selection based on interval-valued intuitionistic fuzzy MCDM methods, Soft Computing. (2018) 22, no. 15, 5091–5114.
10.1007/s00500-018-3317-4
Web of Science® Google Scholar
25 Antucheviciene J., Kala Z., Marzouk M., and Vaidogas E. R., Solving civil engineering problems by means of fuzzy and stochastic MCDM methods: current state and future research, Mathematical Problems in Engineering. (2015) 2015, 1–16, https://doi.org/10.1155/2015/362579, 2-s2.0-84944198696.
10.1155/2015/362579
Web of Science® Google Scholar
26 Mardani A., Jusoh A., Md Nor K., Khalifah Z., Zakwan N., and Valipour A., Multiple criteria decision-making techniques and their applications - a review of the literature from 2000 to 2014, Economic Research-Ekonomska Istraživanja. (2015) 28, no. 1, 516–571, https://doi.org/10.1080/1331677x.2015.1075139, 2-s2.0-84990984121.
10.1080/1331677X.2015.1075139
Web of Science® Google Scholar
27 Kannan D., Jabbour A. B. L. d. S., and Jabbour C. J. C., Selecting green suppliers based on GSCM practices: using fuzzy TOPSIS applied to a Brazilian electronics company, European Journal of Operational Research. (2014) 233, no. 2, 432–447, https://doi.org/10.1016/j.ejor.2013.07.023, 2-s2.0-84893686242.
10.1016/j.ejor.2013.07.023
Web of Science® Google Scholar
28 Liu P. and Zhang X., Research on the supplier selection of a supply chain based on entropy weight and improved electre-III method, International Journal of Production Research. (2011) 49, no. 3, 637–646, https://doi.org/10.1080/00207540903490171, 2-s2.0-78649898211.
10.1080/00207540903490171
Web of Science® Google Scholar
29 San Cristóbal J. R., Multi-criteria decision-making in the selection of a renewable energy project in Spain: the Vikor method, Renewable Energy. (2011) 36, no. 2, 498–502, https://doi.org/10.1016/j.renene.2010.07.031, 2-s2.0-77957327723.
10.1016/j.renene.2010.07.031
Web of Science® Google Scholar
30 Sindhu M. S., Ahsan M., Rafiq A., and Khan I. A., Multiple criteria decision making based on bipolar picture fuzzy sets and extended TOPSIS, The Journal of Mathematics and Computer Science. (2021) 23, no. 1, 49–57.
10.22436/jmcs.023.01.05
Web of Science® Google Scholar
31 Sindhu M. S., Rashid T., and Kashif A., An approach to select the investment based on bipolar picture fuzzy sets, International Journal of Fuzzy Systems. (2021) 23, 1–13, https://doi.org/10.1007/s40815-021-01072-3.
10.1007/s40815-021-01072-3
Web of Science® Google Scholar
32 Wang X. and Triantaphyllou E., Ranking irregularities when evaluating alternatives by using some ELECTRE methods, Omega. (2008) 36, no. 1, 45–63, https://doi.org/10.1016/j.omega.2005.12.003, 2-s2.0-34247194905.
10.1016/j.omega.2005.12.003
CAS Web of Science® Google Scholar
33 Thao N. X., Ali M., Nhung L. T., Gianey H. K., and Smarandache F., A new multi-criteria decision making algorithm for medical diagnosis and classification problems using divergence measure of picture fuzzy sets, Journal of Intelligent and Fuzzy Systems. (2019) 37, no. 6, 7785–7796, https://doi.org/10.3233/jifs-182697.
10.3233/JIFS-182697
Web of Science® Google Scholar
34 Wang R., Wang J., Gao H., and Wei G., Methods for MADM with picture fuzzy Muirhead mean operators and their application for evaluating the financial investment risk, Symmetry. (2019) 11, no. 1, https://doi.org/10.3390/sym11010006, 2-s2.0-85061083486.
10.3390/sym11010006
Web of Science® Google Scholar
35 Wei G., Lu M., and Gao H., Picture fuzzy heronian mean aggregation operators in multiple attribute decision making, International Journal of Knowledge-Based and Intelligent Engineering Systems. (2018) 22, no. 3, 167–175, https://doi.org/10.3233/kes-180382, 2-s2.0-85057758241.
10.3233/KES-180382
Google Scholar
36 Duong T. T. T. and Thao N. X., A novel dissimilarity measure on picture fuzzy sets and its application in multi-criteria decision making, Soft Computing. (2021) 25, no. 1, 15–25, https://doi.org/10.1007/s00500-020-05405-6.
10.1007/s00500-020-05405-6
Web of Science® Google Scholar

Citing Literature

All articles

[Retracted] A Novel Multiple-Criteria Decision-Making Approach Based on Picture Fuzzy Sets

Retraction(s) for this article

Retracted: A Novel Multiple-Criteria Decision-Making Approach Based on Picture Fuzzy Sets

Abstract

1. Introduction

2. Basic Concepts

3. Novel Divergence Measure for PFSs

4. MCDM Process Based on PF-DM

5. Solution of Problems Based on PF-DM