1. Introduction

A great many of engineering applications are performed in rock masses, including tunnel excavations, mining activities, and personnel protective structures [1–3]. Consequently, the rock is frequently subjected to dynamic loadings resulted from drill and blast, rockburst, and projectile penetration. Unlike quasi-static loading, the dynamic loading applied on the rock is intensive together with high pressure and high temperature. Therefore, it is of great significance to understand the response of rocks subjected to dynamic loadings, which benefits the safe design and the safety of personnel and device in rock engineering projects.

To date, numerous experiments have been performed in laboratory and filed scale to assess the dynamic response of various rocks. For example, Zhang and Zhao [4] employed the Split and Hopkinson Pressure Bar (SHPB) in conjunction with digital image correlation technique and high-speed camera to explore the mechanical behaviour (e.g., strain localization and evolution, onset of fracture, and material property) of Fangshan marble under dynamic uniaxial compression, Brazilian disc, and notched semi-circular bending tests. They observed that the fracture initiation toughness, tensile strength and uniaxial compression strength of Fangshan marble increases significantly with the increase of strain rate, and the strain rate effect results from the transition of fracture mode. Marurer and Rinehart [5] carried out spherical steel projectile penetration tests on sandstone and granite with various velocities and impact angles. They concluded that the crater formed in the sandstone and granite is induced by the crushing in front of projectile and the fracturing extension to the free surface, and the crushed and fracturing volumes are relating to the first and second power of impact velocity, respectively. In addition, they noticed that the penetration varies linearly with the impact velocity and is inversely proportional to the specific acoustic resistance of rock. Chi et al. [6] performed blast experiments on six granite cubes with two charge weights, and the fracturing process is monitored with the use of digital correlation technique and high-speed camera. They found that the charge wight influences the number and opening velocity of dominant vertical cracks, the initiation time of macroscopic cracks, and the velocity of fragment.

Numerical approach is an alternative of experiment to investigate the dynamic response of rock materials [7–9]. Compared with experiment, the numerical approach is more cost-effective and easier to repreat. In addition, the numerical approach can be used to investigate the micro-mechanical parameters that influence the dynamic response of rock, which is difficult to be incorporated in experiments [10]. The commonly used numerical methods include finite element method, finite-discrete element method, discrete element method, peridynamic method, and Smoothed-particle hydrodynamics method [11–13]. Through these methods, the response of rock under various dynamic loadings are explored. For example, Xie et al. [14] investigated the effect of free-surface boundary conditions, in-situ stress and the coefficient of lateral pressure on the granite response subjected to cut blasting with the use of finite element method. An et al. [15] used the discrete element method to evaluate the confinement effect on the on the blasting performance in narrow vein mining, and they found that the blasting confinement results in underbreak or overbreak. Saksala and Ibrahimbegovic [16] developed a combined continuum viscodamage-embedded discontinuity model to figure out the thermal shock weakening effect on the dynamic response of granite, and they reported that the rock gravel and rubble crushing can be enhanced by the heat shock pretreatment. Zhao et al. [17] examined the bedding effect on the dynamic Brazilian tensile strength of coal in the SHPB test with distinct lattice spring method. It is found that the dynamic indirect tensile strength of coal positively correlates to the impact velocity, bedding direction, bedding roughness, and bedding discontinuity. Moreover, much effort has been paid to develop new isotropic and anisotropic constitutive models for more accurately and reasonably describing the rock and rock-like materials’ response under dynamic loadings [18–25].

To sum up, the studies mentioned above have provided insights on the dynamic response of rock materials under various dynamic loading scenarios, such as SHPB tests, projectile penetrations and blast loadings. Most of these studies focused on the effect of external factors, e.g., in-situ stress and impact velocity, but the influence of intrinsic factors, including rock types and rock’s material property is lesser explored. Therefore, this study aims to numerically investigate the rock response under blast loadings with a special focus on the effect of rock types and explosive configuration. Specially, four types of rock, including Chuanshan limestone, Gaolishan sandstone, Mineralized limestone and Xixia limestone, are selected, and their material properties are first determined with uniaxial and triaxial compression tests in the laboratory. Then, 3D rock panels are established in the finite element tool LS-DYNA [26], and each type of rock panel is subjected to four blast loadings with different scaled distances, i.e., 0.15 m/kg^1/3, 0.30 m/kg^1/3, 0.60 m/kg^1/3, 1.20 m/kg^1/3. Finally, the effects of rock type and scaled distance of TNT on the damage distribution inside rock panels are quantitively and qualitatively discussed.

2. Experimental and Numerical Approaches

2.2. Parameters Determination

The required parameters of Mohr-Coulomb model can be determined based on the uniaxial and triaxial compression tests on rock materials. Here, four types of rocks, i.e., mineralized limestone, Gaolishan sandstone, Chuanshan limestone, and Xixia limestone, are drilled from the −475 m underground sublevel of a lead-zinc-silver deposit located in Nanjing, China. Then, these rock cores are cut into cylinders with a dimension of 54 mm × 110 mm (diameter × height). Later, these cylinders are ground flat at their two ends. After that, these cylinders are subjected to uniaxial and triaxial compression tests according to the ASTM D7012-14e1 standard method. During the test, a thin layer of Vaseline is put on two ends of the sample to reduce the friction between the sample and the loading platens. The confining pressures include 0 MPa (uniaxial compression), 10 MPa, 15 MPa, and 20 MPa.

The fracture patterns of mineralized limestone under various confining pressures are given as an example and illustrated in Figure 1. It is evident from Figure 1 that when the confining pressure is smaller than 15 MPa, the shear failure is the dominated fracture type of mineralized limestone, and under a high confining pressure (20 MPa in this study) the mineralized limestone fails in a crushing mode. Based on the uniaxial and triaxial compression data of these four rocks, their material properties can be determined as listed in Table 1. In the table, E, v, UCS, and BTS denote Young’s modulus, Poisson ratio, uniaxial compressive strength and Brazilian tensile strength, respectively.

1. Material properties of tocks.

Rock	Density (kg/m3)	E(MPa)	v	C (MPa)	ϕ	UCS (MPa)
Mineralized limestone	2725	43722	0.268	5.094	45	78.70
Gaolishan sandstone	2610	28168	0.358	1.146	32	35.14
Chuanshan limestone	2659	26911	0.151	3.438	39	72.92
Xixia limestone	2649	30691	0.141	2.496	34	76.83

2.3. Blast Loading Modelling

The keyword “Load_Blast_Enhanced” is used to create the air blast pressure history induced by conventional explosives in LS-DYNA [28], which is an empirical function proposed based on a large amount of experimental data. Numerous studies have demonstrated the accuracy and efficiency of this function in modelling the blast loading on panels made of rock-like materials [29, 30], and only the equivalent mass of TNT, type of blast, and the detonation centre of the explosive needs to be predefined in this function. Thus, this keyword is also used to generate the TNT blast loading on the rock panels herein, and its pressure history in a free-air explosion can be described as

$$ (5)

where P is the blast pressure varying with duration time t; P_max is the incident overpressure; t₊ is the positive duration time; and a is waveform number.

The theory and experiments denote that the blast pressure shows a large degree of self-similarity in terms of the scaled distance which is written as

$$ (6)

where Z is the scaled distance; R is the distance from explosive centre to the target surface; and M is explosive mass. In this study, four scaled distances are used to investigate the mechanical behaviour of various rock panels subjected to varying degrees of blast loading, i.e., 0.15 m/kg^1/3 (R = 0.119 m, M = 0.50 kg), 0.30 m/kg^1/3 (R = 0.30 m, M = 1.0 kg), 0.6 m/kg^1/3 (R = 0.756 m, M = 2.0 kg), and 1.20 m/kg^1/3 (R = 1.905 m, M = 4.0 kg). The generated blast pressure history curves by these four scaled distances are illustrated in Figure 2. As can be seen, with the increase of scaled distance, the maximum incident overpressure on the rock panel’s surface decreases from 182.345 MPa to 2.9 MPa, and the arrival time increases from 0.029 ms to 1.2 ms. The negative pressure is also accommodated in the “Load_Blast_Enhanced” approach using the Friedlander equation [28], and its minimum values are −90.4091 Pa, −90.28 Pa, −60.015 Pa, −102.2 Pa for the scaled distances of 0.15 m/kg^1/3, 0.30 m/kg^1/3, 0.6 m/kg^1/3, and 1.2 m/kg^1/3, respectively. It is worth mentioning that the blast pressure history is not influenced by the rock type. The density and Chapman-Jouguet detonation velocity of standard TNT in LS-DYNA are 1.57 g/cm3 and 0.693 cm/µs, respectively.

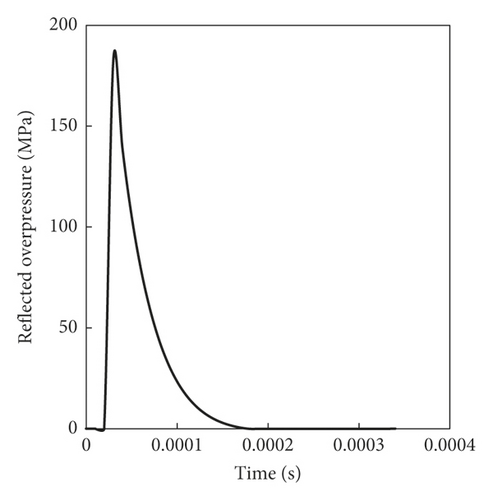
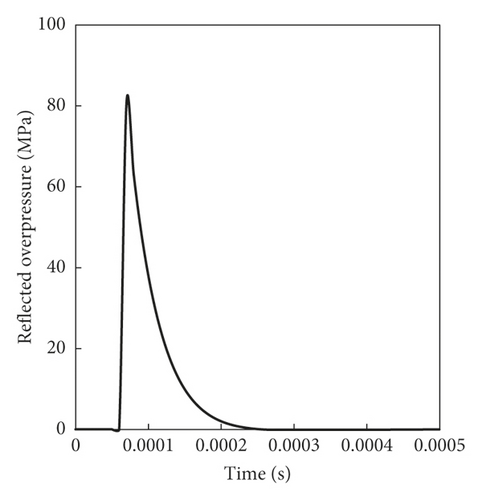
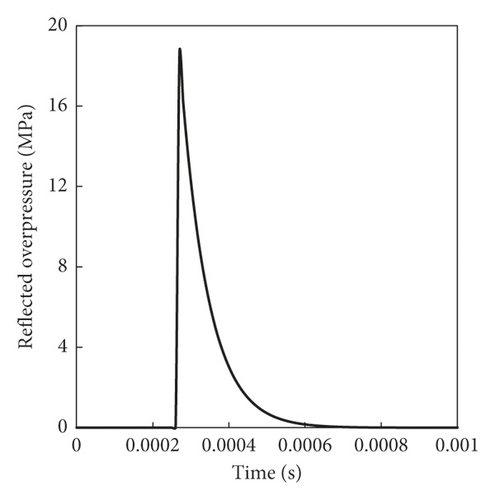
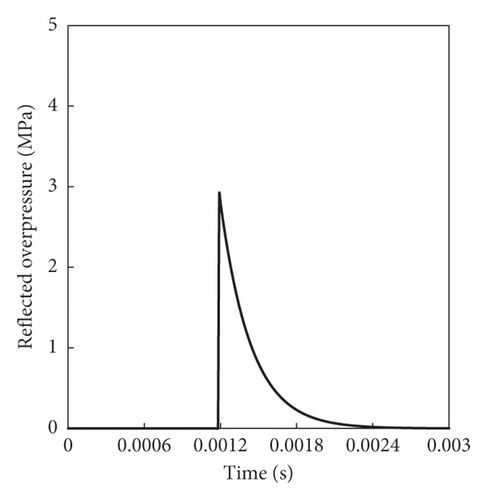
2.4. Numerical Model Setup

A numerical model with a dimension of 700 mm × 700 mm × 75 mm is established with eight-node constant solid stress elements as shown in Figure 3, and the Lagrangian formulation is employed in the modelling. The mesh size is 5 mm, and a total of 294, 000 elements is used in the numerical model after mesh convergence study to avoid mesh dependency as much as possible and make a trade-off between numerical accuracy and computational efficiency. The vertical displacements of two edges along the Y direction in the bottom face are fixed to avoid bouncing back up. Also, the hourglass control is adopted in the explicitly dynamic simulation. Recall that in this study, four kinds of rocks are selected, and each type of rock is subjected to blast load with four scaled distances. Therefore, a total of 16 simulations are conducted in this study, and the termination time for each simulation is 0.02 s to ensure the complete blast related response of rock panels. Note that the strength property (e.g., uniaxial compressive and tensile strengths) of rock materials is rate sensitive, and an obvious strength gain can be obtained under high strain rates. The rate sensitivity of rock is material dependent, that is, different types of rock materials show different strength enhancement under the same strain rate. In the numerical modelling, the strain rate effect can be described by using the dynamic increase factor formula. Per the author’s knowledge, there is no specified dynamic increase factor formulas for the four kinds of rock materials investigated in this study. In consequence, the strain rate effect on the is not considered here.

3. Results and Discussion

After explosive action, the effective plastic strain distributed within the rock panels are illustrated in Figures 4 and 5. It is worth mentioning that in this study, the finite element with an effective plastic strain (eps) larger than 0 denotes that it has been damaged. Figure 4 plots that the damage decreases with the increasing scaled distance. When the scaled distance is small, i.e., 0.15 m/kg^1/3, the circular damage area with high eps values localises in the top middle of the rock panels. As the scaled distance increases, the damage pattern changes to a rectangular band across the panel with lower eps values.

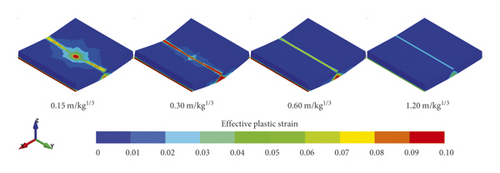
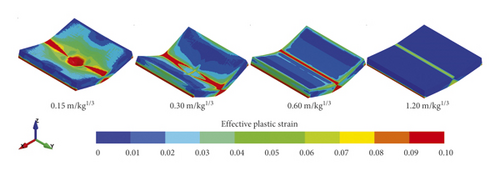
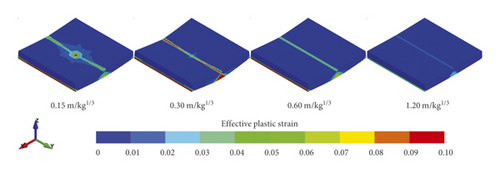
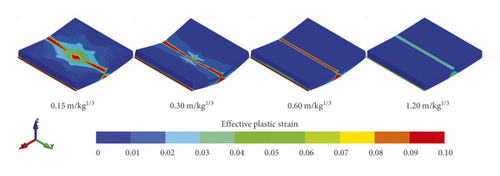
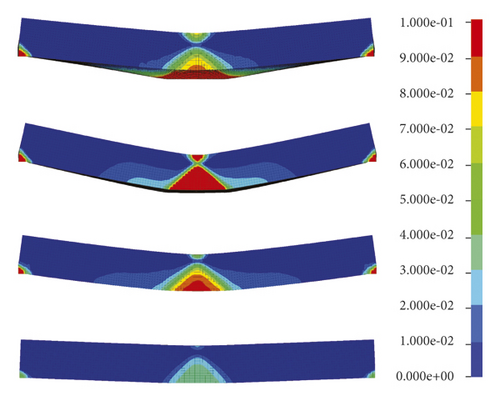
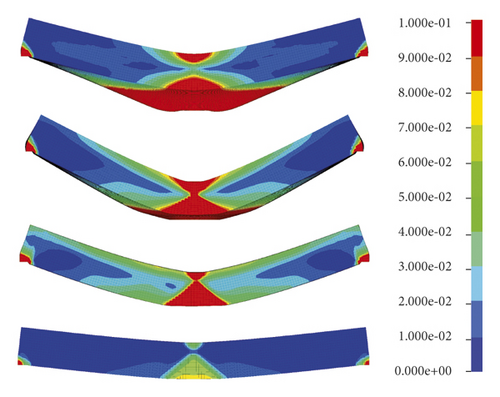
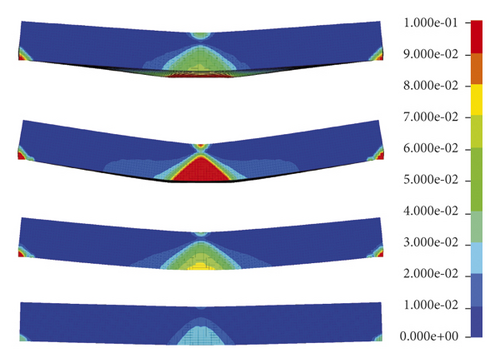
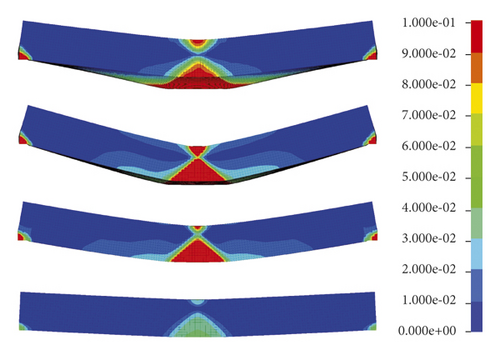
The sides views of rock panels in Figure 4 demonstrate that all the panels are overall damaged in flexural mode with eps mainly distributed in the middle span and gradually smeared to the edges. In fact, it is reasonable as such damage pattern absorbs most of the energy generated by the charge explosion. For a given rock type, e.g., the Chuanshan limestone shown in Figure 4(a), the damage decreases with the increases of scaled distance overall. The diameter of the front face at the side view decreases, but the damage diameter of the distal face at the side view increases first and then decreases as the scaled distance increases. It is interesting to note that the Chuanshan limestone with a scaled distance of 0.15 m/kg^1/3 is damaged much more severe than the scaled distance of 0.30 m/kg^1/3 at its distal face where the noticeable bulge is noticed, but its damage diameter of the distal face at side view is smaller. The reason can be explained by the fact that when the scaled distance is small, the local damage occurs in the rock panel centre due to the punching induced by the high-intensity shear force generated by the blast wave [31]. When the scaled distance is big, i.e., 0.30 m/kg^1/3 or larger, the rock panel is mainly damaged due to the bending force. Note that a similar trend can be concluded for another three types of rock panels as shown in Figures 5(b)–5(d), which is not repeated herein. In addition, it can be observed from Figures 4 and 5 that the Gaolishan sandstone is the most damaged for a given scaled distance, followed by the Xixia limestone, Chuanshan limestone, and mineralized limestone. It is because Gaolishan sandstone has the lowest cohesion strength and friction angle.

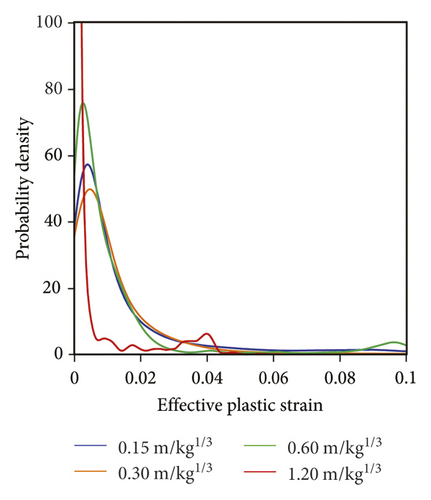
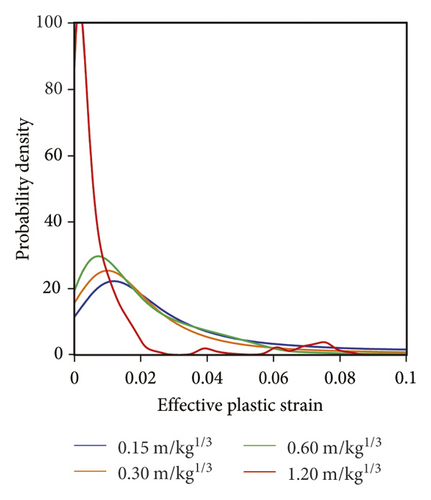
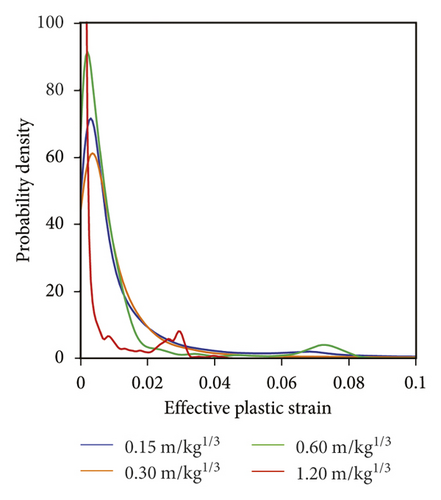
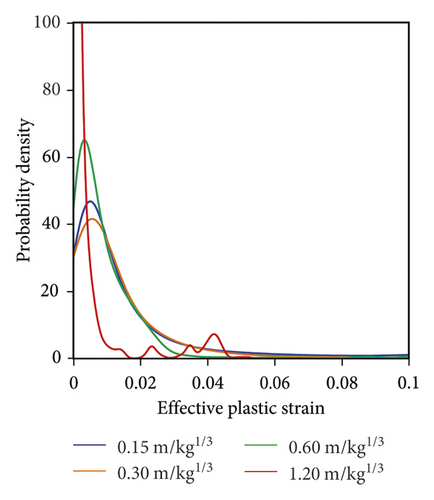
To quantify the damage induced by the explosive action with different scaled distances, the probability density of eps in these four types of rocks is illustrated in Figure 6. As seen, for the Chuanshan limestone shown in Figure 6(a), its probability density value of eps = 0 decreases first and then increases, and the lowest probability density value of eps = 0 is noticed in the case of scaled distance equal to 0.30 m/kg^1/3. Note that a smaller probability density of eps = 0 means that more finite elements are damaged, and thus the Chuanshan limestone panel with a scaled distance of 0.30 m/kg^1/3 has the largest number of damaged elements. In addition, as the scaled distance increases, the eps corresponding to the peak value of probability density increases first and then decreases. It denotes that their damage degree for these damaged elements is severest in the Chuanshan limestone panel with a scaled distance of 0.30 m/kg^1/3. For the Gaolishan sandstone shown in Figure 6(b), it is found that with the increase of scaled distance, the probability density of eps = 0 increases significantly. As a result, the number of damaged elements, and the damaged degree decreases with the increase of scaled distance. As for the mineralized limestone and Xixia limestone panels, they behave like the Chuanshan limestone, as shown in Figures 6(c) and 6(d). In fact, the above conclusions can be supported by the average eps of each rock panel. For example, under the scaled distance of 0.15 m/kg^1/3, 0.30 m/kg^1/3, 0.60 m/kg^1/3, 1.20 m/kg^1/3: (a) the average eps values of the Chuanshan limestone panels are 0.0192, 0.0224, 0.0132, and 0.0037, respectively; (b) the average eps values of the Gaolishan sandstone panels are 0.0472, 0.0471, 0.0320, and 0.0094, respectively; (c) the average eps of the mineralized limestone panels are 0.0152, 0.0181, 0.0104, and 0.0028, respectively; and (d) the average eps of the Xixia limestone panels are 0.0232, 0.0268, 0.0154, and 0.00429, respectively. In addition, the percentage of damage elements in the rock panels subjected to the blast loadings with different scaled distances are compared in Table 2. It can be seen from Table 2 that the damage percentage shows the same trend as the probability density value illustrated in Figure 6.

4. Conclusions

In this study, the dynamic performance of four types of rock panels (e.g., Chuanshan limestone, Gaolishan sandstone, Mineralized limestone and Xixia limestone) subjected the explosive action with four scaled distances (0.15 m/kg^1/3, 0.30 m/kg^1/3, 0.60 m/kg^1/3, 1.20 m/kg^1/3) is investigated with the finite element tool. Mohr-Coulomb criterion is used to describe the mechanical behaviour of rock panels, and its input parameters are determined by the triaxial compression tests with confining pressures between 0 MPa and 20 MPa. The damage, which is represented by the effective plastic strain, induced by the explosive action is qualitatively and quantitively analyzed. The simulation results demonstrate that the effect of scaled distance on the damage distribution of rock panels is material dependent. The Gaolishan sandstone is damaged most severely, followed by the Xixia limestone, Chuanshan limestone, and mineralized limestone for a given scaled distance. Whether the increase of scaled distance leading to a smaller damage degree depends on the rock type. In general, there is a critical scaled distance for most of rocks, e.g., 0.30 m/kg^1/3 in this study. Below this critical value, the scaled distance has a negative impact on the damage degree of rock, but the larger scaled distance leads to a lower damage degree after exceeding this critical value. However, such a critical scaled distance is not observed in the Gaolishan sandstone panels, as the damage induced by explosive action decrease apparently with increasing the scaled distance. The modelling highlights that the blast design and support schemes need to be adjusted when conducting excavation activities in different rock mass, even though these rock masses locate in the same sublevel. In the future study, the heterogeneity rate-dependency of rock’s material property need to be taken into account in the blast modelling.

Conflicts of Interest

The authors declare that they have no conflicts of interest.