The application of graph theory in the study of molecular physical and chemical properties involves theoretical mathematical chemistry. Atoms, represented by vertices, and edges, represented by bonds between them, are detailed in simple graphs called chemical graphs. The mathematical derivation of the numerical value of a graph is called the molecular descriptor of the graph. Any connected graph wherein no edge is contained in exclusive of a single cycle is called a cactus graph. In the research in this article, expressions for various molecular descriptors of line graph of the graph obtained by the rooted product of the cycle and path graphs are constructed. This article obtained the calculation of molecular descriptors for line graphs of chain ortho cactus and chain para cactus graphs. To predict the biological activity of a compound, the generalized Zagreb index, the first Zagreb index M₁(G), the second Zagreb index M₂(G), the F-index, the general Randic index, the symmetric division, the atom bond connectivity (ABC), and the geometric arithmetic (GA) descriptors are created.

1. Introduction

The branch of mathematical chemistry that relates to other sciences, engineering, and especially chemistry is called chemical graph theory. An ordered pair of a couple of sets (V(G), E(G)), where (V(G)) is called the set of vertices and E(G) the set of edges, constitutes the graph G. The number of vertices of a graph apart from the vertex v that are incident on v is a natural number that is termed as the degree of the veterx v denoted by dv or d_G(v). A graph obtained by some other graph wherein the vertices of the resulting graph are edges of the original graph G is called a line graph L(G) of the original graph G. The number mathematically determined by the graph is called the topological index of the graph, and this number remains constant for isomorphic graphs. Lately, many researchers have discovered quite a few number of molecular descriptors that cover a wide range of chemistry applications and cover biochemistry, medicine, and other fields to theoretically understand the physicochemical properties of chemical compounds. The blocks of a chain cactus graph can either be edges or cycles. If all the blocks of a chain cactus graph are triangular, then it will be termed as a triangular cactus graph. Chain square cactus graphs are those in which the triangles in the chain have been replaced with cycles of length 4. The articulation points in case of ortho chain square cactus are contiguous as against para chain square cactus wherein the articulation points are not contiguous. Sadeghieh et al. [1] performed a derivation of Hosoya polynomial of quite a few chain cactus and studied quite a few molecular descriptor in [1]lately. For further research on cactus diagrams, we kindly refer the reader to [2–5] This article examines the mathematical properties of the general Zagreb indices and their special cases of the line diagrams of ortho cactus and para cactus chains, such as the line graph of the triangular chain cactus L(T_n), the line graph of the square chain cactus L(S_q), and the hexagonal chain cactus L(H_o) are considered in the document. This article derives some expressions for molecular descriptors based on graph vertex degrees, such as the general Zagreb index, the F-index, the redefined Zagreb index, the first Zagreb index, the second Zagreb index, the general Randic index, and the symmetric division index.

(1)

(2)

In the same paper [6], the “forgotten topological index” or F-index was defined as

(3)

In 2003, Ranjini et al. redefined the Zagreb index in [7] and is defined as

(4)

The symmetric division index of a graph is defined as

(5)

For further study about indices index, we refer [7–9]. In 2011, Azari et al. introduced a generalized version of vertex degree-based topological index, named as generalized Zagreb index or the (a, b)-Zagreb index and is defined as

(6)

We refer [7–11] for further study about different indices.

It is clear that all the topological indices discussed previously, can be obtained from (a, b)-Zagreb index for some particular values of a and b.

2. Main Results

In this section, we consider line graph of para cacti chain, ortho cacti chain, and rooted product of cycle and path. We first take a line graph of para cacti chain of cycles C_p of length q. Suppose line graph of para cacti chain is denoted by . In our first theorem, we calculate an exact result of general Zagreb index of line graph of para cacti chain .

Theorem 1. Let be the line graph of para cacti chain of cycles for p ≥ 4, q ≥ 2. Then

Proof. The order and size of line graph of para cacti chain of cycles are p, q, and pq + 4q − 4. The edge set of can be partitioned into subsets given in

(7)

where the number of elements of

, and

are 2m − 6, 2m − 4, and mn − 4m + 4n + 6, respectively.

From the definition of general Zagreb index, we have

(8)

Corollary 2. Let be the line graph of para cacti chain of cycles for (m ≥ 3, n ≥ 2). Then

(1)
,
(2)
,
(3)
,
(4)
,
(5)
.

The expressions for different indices about line graph of para squares cactus chain L(S_q) can be obtained from Theorem 1 by taking p = 4 The representation of L(S_q) is shown in Figure 1.

Corollary 3. Let L(S_q) be the line graph of para chain square cactus graph for q ≥ 2

(9)

Proof. If we take p = 4 in Theorem 1, we have our this result.

Details are in the caption following the image — Open in figure viewer PowerPoint

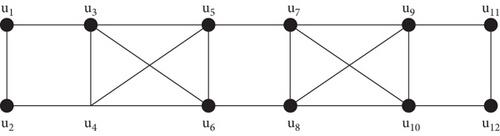
From Corollary 3, the result obtained for line graph of para chain square cactus is q ≥ 2.

Corollary 4. Let L(S_q) be the line graph of para chain square cactus for q ≥ 2. Then

(1)
Z₁[L(S_q)] = Z_{(1, 0)}[L(s_q)] = 8(4q − 5),
(2)
Z₂[L(S_q)] = 1/2Z_{(1, 1)}[L(s_q)] = 8(8q − 5),
(3)
F[L(S_q)] = Z_{(2, 0)}[L(s_q)] = 64(2q − 1),
(4)
RZ[L(S_q)] = Z_{(2, 1)}[L(s_q)] = 32[16q − 9],
(5)
SD[L(S_q)] = Z_(1,−1)[L(s_q)] = 9q + 6.

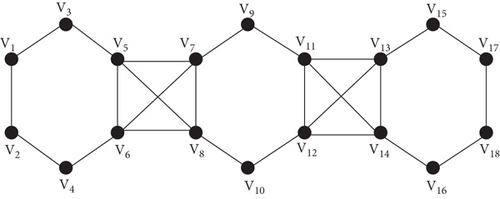
The generalized Zagreb index of line graph of para chain hexagenal cactus L(H_q) can be obtained from the theorem 1 by putting p = 6. The line graph of para chain hexagonal cactus is shown in Figure 2 .From the general result, the following are topological indices for line graph of para chain hexagonal cactus for q ≥ 3.

Corollary 5. Let L(H_q) be the line graph of para chain hexagonal cactus for q ≥ 3. Then

(10)

Corollary 6. Let L(H_q) be the line graph of para chain hexagonal cactus for q ≥ 3. Then

(1)
Z₁[L(H_q)] = Z_{(1, 0)}[L(H_q)] = 8(5q − 6),
(2)
Z₂[L(H_q)] = 1/2Z_{(1, 1)}[L(H_q)] = 8(10q − 7),
(3)
F[L(H_q)] = Z_{(2, 0)}[L(H_q)] = 80(2q − 1),
(4)
RZ[L(H_q)] = Z_{(2, 1)}[L(H_q)] = 32[20q − 21],
(5)
SD[L(S_q)] = Z_(1,−1)[L(H_q)] = 11q + 16.

Theorem 7. is the line graph of para chain cactus with q cycles and p vertices. Then

(i)
General Randic index

(11)

(ii)
Atom bond connectivity index

(12)

(iii)
Geometric arithmetic (GA) index

(13)

(iv)
Harmonic index

Proof. Edge partition of is the same as the in Theorem 1.

(i)
General Randic index

(14)

(ii)
Using

(15)

We have

(16)

(iii)
Formula for geometric arithmetic index

(17)

We have

(18)

(iv)
Harmonic index

(19)

Next, when cut vertices are adjacent, then such type of chain is said to be ortho chain cactus. Suppose ortho chain cactus is represented by where m is length of each cycle and n is length of chain. is line graph of ortho chain cactus. Number of vertices and edge of are mn and mn + 4n − 4. In next two theorems, we find different topological indices for line graph of ortho.chain cactus.

Theorem 8. Let be the line graph of ortho chain cactus of cycles for m ≥ 3, n ≥ 2. Then

(20)

Proof. Partition of edge set of is given

(21)

where the number of element in above sets are 2m − 6, 2m − 2, m + n and mn − 5m + 3n + 4, respectively.

From definition of Zagreb index

(22)

Corollary 9. is the line graph of ortho chain cactus of cycle for m ≥ 3, n ≥ 2. Then, first Zegred and second Zegreb are forgotten. Redefined Zagreb and symmetric divisions indices are

(i)
,
(ii)
,
(iii)
,
(iv)
,
(v)
.

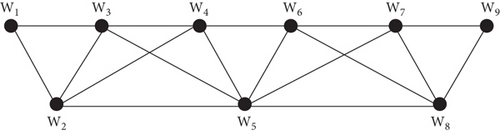
Now we consider line graph of triangular ortho chain cactus shown in Figure 3 denoted by L(T_n)

Corollary 10. L(T_n) is line graph of triangular ortho chain cactus of cycle with n ≥ 2

(23)

Proof. By putting m = 3 in Theorem 8, we get desired result.

Corollary 11. L(T_n) is the line graph of triangular ortho chain cactus of cycles with n ≥ 2; expressions for different topological indices for L(T_n) are given

(i)
M₁[L(T_n)] = Z_{(1, 0)}[L(T_n)] = 2(32n − 37),
(ii)
M₂[L(T_n)] = Z_{(1, 1)}[L(T_n)] = 16(19n+−26),
(iii)
F[L(T_n)] = Z_{(2, 0)}[L(T_n)] = 4(82n − 111),
(iv)
ReZ[L(T_n)] = Z_{(2, 1)}[L(T_n)] = 16(94n − 141)
(v)
SD[L(T_n)] = Z_(1,−1)[L(T_n)] = 1/6(84n − 65).

Theorem 12. Let L(RC_kP_l) be the line graph of rooted product of cycleC_k of k vertices and path P_l of vertices l with k ≥ 3, l ≥ 4. Then

(24)

Proof. Order and size of line graph of rooted product graph of cycle and path are kl and k(l + 1). Partition of edge set is as under

(25)

where the number of elements in these sets are k, k(l − 4), k, 2k, k, respectively, using

(26)

Corollary 13. G = L(ZC_kP_l) is line graph of rooted product of cycle C_k and path P_l expressions for first, second Zagreb, forgotten, redefined Zagreb, and symmetric division indices are

(27)

3. Conclusion

In this study, the computation of the first Zagreb index, the second Zagreb index, the F-index, the general Randic index, and the redefined Zagreb index has been made, and their comparisons have been drawn with their corresponding (a, b)-Zagreb indices for the line graph of the graph obtained by the rooted product of the cycle and the path graphs. A few closed expressions for the general Zagreb index of the line graph of some cactus chain graphs have also been obtained in this research which has also led to some other significant degree base molecular descriptors for some particular values of a and b. The Zagreb indices of line graphs of some other graph structures can also be calculated for further investigation.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

No data were used to support this study.

References

1 Sadeghieh A., Alikhani S., Ghanbari K., and A J, Hosoya polynomial of some cactus chain, Cogent Mathematics. (2017) 4, no. 1, 1–7, https://doi.org/10.1080/23311835.2017.1305638.
10.1080/23311835.2017.1305638
Google Scholar
2 Ahmad A., On the degree based topological indices of benzene ring embedded in the P-type-surface in 2D network, Hacettepe Journal of Mathematics and Statistic. (2017) 47, no. 1, 9–18.
Web of Science® Google Scholar
3 Aslam A., Faisal Nadeem M., Zahid Z., Zafar S., and Gao W., Computing certain topological indices of the line graphs of subdivision graphs of some rooted product graphs, Mathematics. (2019) 7.
10.3390/math7050393
Web of Science® Google Scholar
4 Vukicevic D. and Furtula B., Topological index based on the ratios of geometrical and arithmetic means of end-vertex degree of edges, Journal of Mathematical Chemistry. (2009) 46, 1369–1376, https://doi.org/10.1007/s10910-009-9520-x, 2-s2.0-70350166990.
10.1007/s10910-009-9520-x
CAS Web of Science® Google Scholar
5 Estrada E., Torres L., Rodriguez L., and Gutman I., An atom-bond connectivity index,Modelling the enthalpy of formation of alkanes, Indian Journal of Chemistry. (1998) 37A, 849–855.
CAS Google Scholar
6 Gutman I. and Trinajstić N., Graph theory and molecular orbitals total p-electron energy of alternant hydrocarbons, Chemical Physics Letters. (1972) 17, no. 4, 535–538, https://doi.org/10.1016/0009-2614(72)85099-1, 2-s2.0-33845352210.
10.1016/0009-2614(72)85099-1
CAS Web of Science® Google Scholar
7 Ranjini P. S., Lokesha V., and Usha A., Relation between phenylene and hexagonal squeeze using harmonic index, International Journal of Graph Theory. (2013) 1, 116–121.
Google Scholar
8 Sarkar P., De N., and Pal A., The generalized Zagreb index of some carbon structures, Acta Chemica Iasi. (2018) 26, no. 1, 91–104, https://doi.org/10.2478/achi-2018-0007.
10.2478/achi-2018-0007
CAS Google Scholar
9 Sarkar P., De N., and Pal A., Generalized Zagreb index of some dendrimer structures, Universal Journal of Mathematics and Applications. (2018) 26, no. 1, 91–104, https://doi.org/10.2478/achi-2018-0007.
10.2478/achi-2018-0007
CAS Google Scholar
10 Azeem M., Aslam A., Iqbal Z., Binyamin M. A., and Gao W., Topological aspects of 2D structures of trans-Pd(NH2)S lattice and a Metal-organic Superlattice, Arabian Journal of Chemistry. (2021) 14, article 102963, https://doi.org/10.1016/j.arabjc.2020.102963.
10.1016/j.arabjc.2020.102963
Web of Science® Google Scholar
11 Ali N., Koam A., Ahmad A., and Nadeem M. F., Comparative study of valency-based topological descriptor for hexagon star network, Computer Systems Science and Engineering. (2021) 36, no. 2, 293–306, https://doi.org/10.32604/csse.2021.014896.
10.32604/csse.2021.014896
Web of Science® Google Scholar

Citing Literature

All articles

[Retracted] Molecular Descriptors on Line Graphs of Cactus Chains and Rooted Products Graphs

Retraction(s) for this article

Retracted: Molecular Descriptors on Line Graphs of Cactus Chains and Rooted Products Graphs

Abstract

1. Introduction

2. Main Results

3. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

[Retracted] Molecular Descriptors on Line Graphs of Cactus Chains and Rooted Products Graphs

Retraction(s) for this article

Retracted: Molecular Descriptors on Line Graphs of Cactus Chains and Rooted Products Graphs

Abstract

1. Introduction

2. Main Results

3. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information