[Retracted] Decompositions of Circulant-Balanced Complete Multipartite Graphs Based on a Novel Labelling Approach
Abstract
For applied scientists and engineers, graph theory is a strong and vital tool for evaluating and inventing solutions for a variety of issues. Graph theory is extremely important in complex systems, particularly in computer science. Many scientific areas use graph theory, including biological sciences, engineering, coding, and operational research. A strategy for the orthogonal labelling of a bipartite graph G with n edges has been proposed in the literature, yielding cyclic decompositions of balanced complete bipartite graphs Kn,n by the graph G. A generalization to circulant-balanced complete multipartite graphs is our objective here. In this paper, we expand the orthogonal labelling approach used to generate cyclic decompositions for Kn,n to a generalized orthogonal labelling approach that may be used for decomposing . We can decompose into distinct graph classes based on the proposed generalized orthogonal labelling approach.
1. Introduction
As is well known, discrete mathematics is a field of mathematics that deals with countable processes and components. One of the most significant and intriguing disciplines in discrete mathematics is graph theory [1–3]. Graph theory is the study of structural models called graphs, which are made up of a collection of vertices and edges. Graph theory is extremely important in complex systems, particularly in computer science. Many scientific areas use graph theory, including engineering, coding [4, 5], operational research, biological sciences, and management sciences. For applied scientists and engineers, graph theory is a strong and vital science for evaluating and inventing solutions for a variety of issues. Graphs have recently been utilized as structural models for characterizing World Wide Web connections and the number of links necessary to move between web pages [6].
Circulant graphs are a significant category of graphs [7–10]. Circulant graphs have gained a lot of attention in recent decades. The circulant graphs class includes complete graphs and classic rings topologies. The algebraic properties of circulant graphs have been studied in thousands of publications. Circulant graphs have been handled in a variety of graph applications, including wide area communication graphs, local area computer graphs, parallel processing architectures, very large-scale integrated circuit design, and distributed computing [11–13].
Several traditional parallel and distributed systems were built on the foundation of circulant graphs [14–16]. Circulant graphs have a wide range of practical uses, such as a structure in chemical reaction models [17], multiprocessor cluster systems [18], small-world graph models [19], discrete cellular neural graphs [20], and as a basic structure for optical graphs [21], and so on.
The study of circulant graphs, including their characterization, analysis, and applications, is currently a popular issue in research. Several papers have been published that deal with graph decompositions by simpler graphs [22–24]. Decompositions of circulant graphs have several excellent contributions. For Cayley graphs labelled with Abelian groups, the Hamilton decomposition was investigated in [25]. The circulant graph is a particular case of the Cayley graph. It has been demonstrated that two Hamilton cycles may be used to decompose four-regular connected Cayley graphs [26].
For a certain recursive circulant graph, the Hamilton decompositions have been proven [27]. Every circulant graph has a corresponding circulant matrix [28]. Excellent descriptions of circulant matrices have been published in [28].
Definition 1. A circulant-balanced complete multipartite graph is a simple graph having vertices. The vertices of are divided into m partitions of cardinality n; two vertices are said to be adjacent if they are found in two different partitions. The graph has a degree equal to (m − 1)n. The circulant graph can be divided into
Definition 2. A caterpillar graph Ca(b1, b2, ⋯, ba) is a tree formed by the path Pa = y1y2 ⋯ ya by linking a vertex yi to bi new vertices where a ≥ 1, b1, b2, ⋯, ba are integers greater than zero, b1, ba ≥ 1 and bi ≥ 0 for i ∈ {2, 3, ⋯, a − 1}.
El-Mesady et al. have proposed an orthogonal labelling approach to decompose a certain circulant graph class with 2n vertices and n degree [29]. Circulant-balanced complete bipartite graphs are the name for this type of graph which is denoted by Kn,n. In cognitive radio graphs and cloud computing, bipartite circulant graphs can address a variety of challenges. For a good survey on several decompositions of circulant graphs, see [30–34].
In this study, we generalize the orthogonal labelling approach proposed in [29] to create edge decompositions of the graphs which are considered a generalization to the graphs Kn,n. The following sections make up the current paper: The second section deals with the proposed novel orthogonal labelling approach. In the third section, the graph is decomposed by infinite classes of graphs. We generate many decompositions of by connected caterpillars in the fourth section. The fifth section introduces concluding remarks and future work.
2. A Novel Labelling Approach
Consider now the circulant-balanced complete multipartite graph with vertex set where V, l ∈ {0, 1, ⋯, m − 1} are m independent sets of vertices. There are bijective mappings φl : Vl⟶ℤn × {l}, l ∈ {0, 1, ⋯, m − 1} where the vertices in Vl are labelled by ℤn × {l}, see Figure 1.
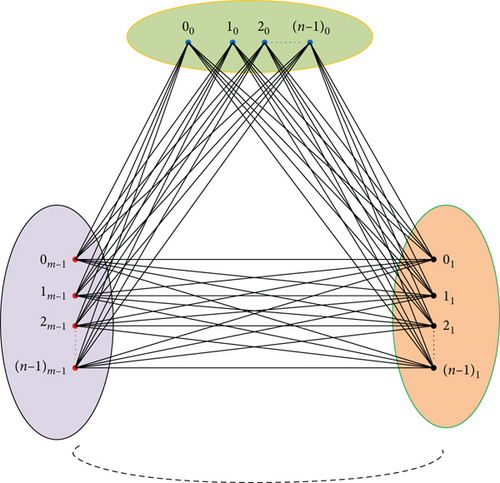
- (i)
Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, the length 0 is found once in and the length n/2 is found once in if n is even
- (ii)
For every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G has precisely edges of length λ,
- (iii)
The length 0 is found times in G,
- (iv)
The length n/2 is found times in G if n is even
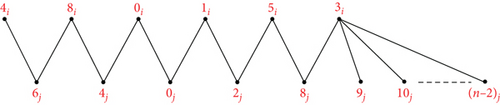
Example 1. An orthogonal labelling of is shown in Figure 2.
Definition 3. Suppose G is a subgraph of Then G + x with E(G + x) = {{a + x, b + x}: {a, b} ∈ E(G)} is called the x-translate of G.

The edge decomposition of circulant-balanced complete multipartite graphs and orthogonal labelling are linked in the next proposition.
Proposition 4. If and only if there is an orthogonal labelling of an edge decomposition of can be constructed by G.
Proof. Our goal is to show that E(Gi,j + ω)∩E(Gi,j + σ) = ϕ for all ω, σ ∈ ℤn. We assume, by way of contradiction, that |E(Gi,j + ω)∩E(Gi,j + σ)| | ≥1 for ω, σ ∈ ℤn with ω ≠ σ. For the lengths λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, which are repeated twice in Gi,j, let {a, b} and {c, d} be two edges of E(Gi,j + ω)∩E(Gi,j + σ) with length λ, then {a − ω, b − ω}, {c − ω, d − ω} and {a − σ, b − σ}, {c − σ, d − σ} are various edges with length λ in E(Gi,j). However, this is a contradiction because Gi,j verifies the orthogonal labelling requirement (i). Let {a, b} belong to E(Gi,j + ω)∩E(Gi,j + σ) with length l ∈ {0, n/2}, n is even, then {a − ω, b − ω} and {a − σ, b − σ} are distinct edges in E(Gi,j), both with length l. However, this is a contradiction because Gi,j verifies the orthogonal labelling requirement (i). Hence, Also, for every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G has precisely edges with length λ, the length 0 is only found times in G, the length n/2 is only found times in G if n is even. Consequently,
Example 2. An example of edge decomposition of K3,3,3 by is shown in Figure 3.
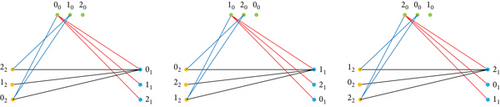
3. Decompositions of by Several Classes of Graphs
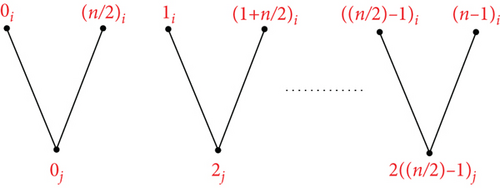
Theorem 5. Let n ≥ 5, m ≥ 2 be integers. Then, there is an orthogonal labelling for .
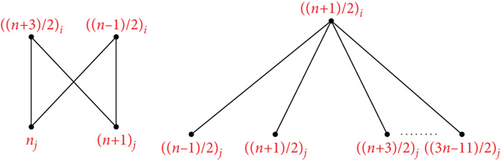
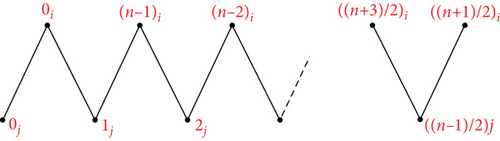
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G1, which can be defined by which is defined by ψk(v0) = ((n + 3)/2)i, ψk(v1) = ((n − 1)/2)i, ψk(v2) = ((n + 1)/2)i, ψk(vs+3) = (((n − 1)/2) + s)j, s ∈ {0, ⋯, n − 5}, and the edge set of is
see Figure 4. From the edge set of G1, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, the length 0 is found once in the length n/2 is found once in if n is even, for every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G1 has precisely edges of length λ, the length 0 is found times in G1, and the length n/2 is found times in G1 if n is even. Hence, can be decomposed by G1.
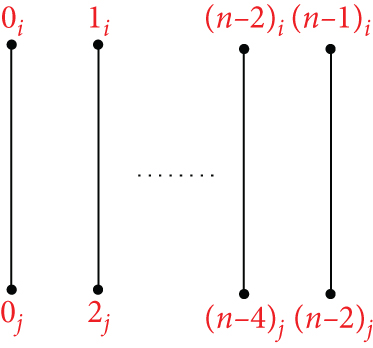
Theorem 6. Let n > 1, m ≥ 2 be integers. Then, there is an orthogonal labelling for .
Proof. Suppose is The mapping ψk can be used to define an orthogonal labelling for the subgraph G2, which can be defined by which is defined by
see Figure 5. From the edge set of G2, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(2n − 1)/2⌋}, the length 0 is found once in the length n is found once in , for every λ ∈ {1, 2, ⋯, ⌊(2n − 1)/2⌋}, G2 has precisely edges of length λ, the length 0 is found times in G2, and the length n is found times in G2. Hence, can be decomposed by G2.
Theorem 7. Let n ≡ 2 mod 6 or n ≡ 4 mod 6, m ≥ 2. Then, there is an orthogonal labelling for
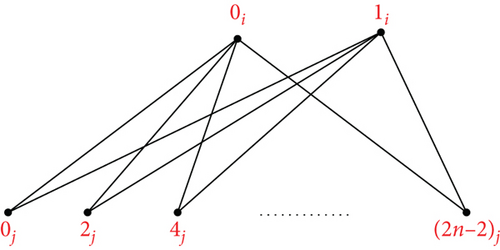
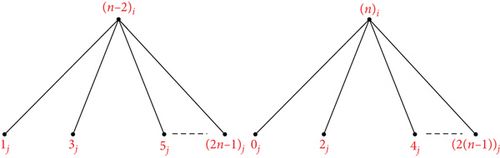
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G3, which can be defined by which is defined by ψk(vs) = si, s ∈ {0, 1, ⋯, n − 1}, ψk(vn+s) = ((2s)(modn))j, s ∈ {0, 1, ⋯, n − 1}, and the edge set of is see Figure 6. From the edge set of G3, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, the length 0 is found once in the length n/2 is found once in for every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G3 has precisely edges of length λ, the length 0 is found times in G3, and the length n/2 is found times in G3. Hence, can be decomposed by G3.
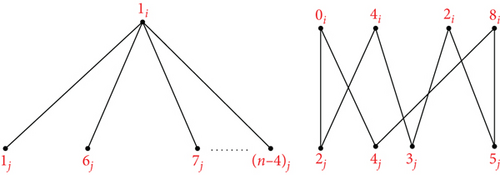
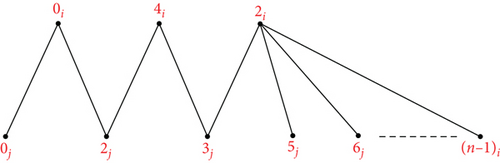
Theorem 8. Let n ≥ 9, m ≥ 2 be integers. Then, there is an orthogonal labelling for
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G4, which can be defined by which is defined by
∪{{1i, sj}: s ∈ {6, 7, ⋯, n − 4}}, see Figure 7. From the edge set of G4, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, the length 0 is found once in the length n/2 is found once in if n is even, for every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G4 has precisely edges of length λ, the length 0 is found times in G4, and the length n/2 is found times in G4 if n is even. Hence, can be decomposed by G4.
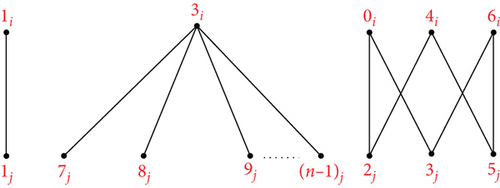
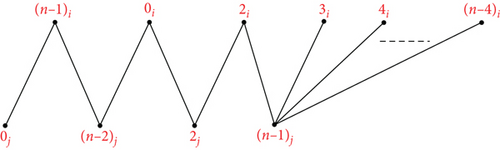
Theorem 9. Let n ≥ 7, m ≥ 2 be integers. Then, there is an orthogonal labelling for .
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G5, which can be defined by ψk : V(K1,1 ∪ C6 ∪ K1,n−7)⟶ℤn × {i, j} which is defined by
ψk(v8) = 5j, ψk(vs) = (s − 2)j, s ∈ {9, ⋯, n + 1}, and the edge set of is
see Figure 8. From the edge set of G5, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, the length 0 is found once in the length n/2 is found once in if n is even, for every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G5 has precisely edges of length λ, the length 0 is found times in G5, and the length n/2 is found times in G5 if n is even. Hence, can be decomposed by G5.
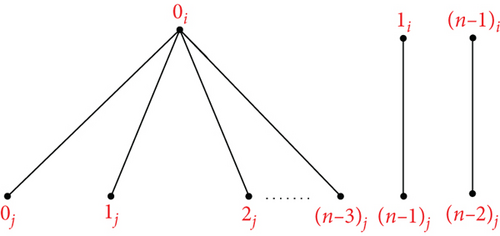
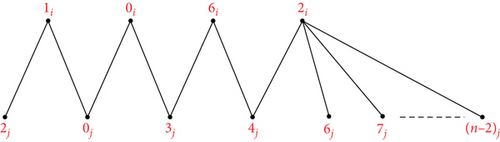
Theorem 10. Let n ≥ 5, m ≥ 2 be integers. Then, there is an orthogonal labelling for .
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G6, which can be defined by which is defined by
and the edge set of is
see Figure 9. From the edge set of G6, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, the length 0 is found once in the length n/2 is found once in if n is even, for every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G6 has precisely edges of length λ, the length 0 is found times in G6, and the length n/2 is found times in G6 if n is even. Hence, can be decomposed by G6.
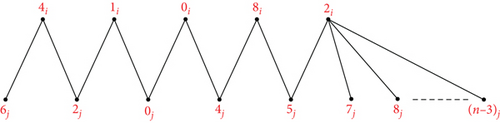
Theorem 11. Let n > 1, m ≥ 2 be integers. Then, there is an orthogonal labelling for .
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G7, which can be defined by which is defined by
s ∈ {0, 1, ⋯, (n − 1)/2}, and the edge set of is .{{((n − s)(modn))i, (s + α)j}: s ∈ {0, 1, ⋯, (n − 3)/2}, α ∈ {0, 1}}, see Figure 10. From the edge set of G7, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, the length 0 is only present once in the length n/2 is found once in if n is even, for every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G7 has precisely edges of length λ, the length 0 is found times in G7, and the length n/2 is found times in G7 if n is even. Hence, can be decomposed by G7.
Theorem 12. Let n ≡ 1mod6, n ≡ 5mod6, m ≥ 2 be an integer. Then, there is an orthogonal labelling for by
Proof. Suppose is The mapping ψk can be used to define an orthogonal labelling for the subgraph G8, which can be defined by which is defined by ψk(vs) = si, s ∈ {0, 1, ⋯, n − 1}, ψk(vn+s−1) = ((2(s − 1))modn)j, s ∈ {1, 2, ⋯, n}, and the edge set of is see Figure 11. From the edge set of G8, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, the length 0 is found once in the length n/2 is found once in if n is even, for every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G8 has precisely edges of length λ, the length 0 is found times in G8, and the length n/2 is found times in G8 if n is even. Hence, can be decomposed by G8.
Theorem 13. Let n ≥ 1, m ≥ 2 be integers. Then, there is an orthogonal labelling for
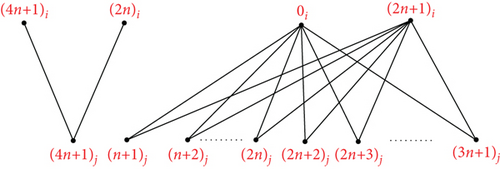
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G9, which can be defined by which is defined by
ψk(vs) = (n + s − 4)j, s ∈ {5, ⋯, n + 4}, ψk(vn+s) = (2n + s − 3)j, s ∈ {5, ⋯, n + 4}, and the edge set of is
see Figure 12. From the edge set of G9, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(4n + 1)/2⌋}, the length 0 is found once in the length 2n + 1 is found once in for every λ ∈ {1, 2, ⋯, ⌊(4n + 1)/2⌋}, G9 has precisely edges of length λ, the length 0 is found times in G9, and the length 2n + 1 is found times in G9. Hence, can be decomposed by G9.
Theorem 14. Let n ≥ 2, m ≥ 2 be integers. Then, there is an orthogonal labelling for
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G10, which can be defined by which is defined by ψk(v0) = (n − 2)i, ψk(v1) = ni, ψk(vs+2) = sj, s ∈ {0, ⋯, 2n − 1}, and the edge set of is see Figure 13. From the edge set of G10, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(2n − 1)/2⌋}, the length 0 is found once in the length n is found once in for every λ ∈ {1, 2, ⋯, ⌊(2n − 1)/2⌋}, G10 has precisely edges of length λ, the length n is found times in G10, and the length 0 is found times in G10. Hence, can be decomposed by G10.
Theorem 15. For all positive integers n with gcd (n, 3) = 1, m ≥ 2. Then, there is an orthogonal labelling for
Proof. Suppose is The mapping ψk can be used to define an orthogonal labelling for the subgraph G11, which can be defined by which is defined by
and the edge set of is
From the edge set of G11, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(4n − 1)/2⌋}, the length 0 is found once in the length 2n is found once in , for every λ ∈ {1, 2, ⋯, ⌊(4n − 1)/2⌋}, G11 has precisely edges of length λ, the length 0 is found times in G11, and the length 2n is found times in G11. Hence, can be decomposed by G11.
Theorem 16. Let n ≥ 3, m ≥ 2 be integers. Then, there is an orthogonal labelling for
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G12, which can be defined by which is defined by ψk(v0) = 0i, ψk(v1) = 2i, ψk(v2) = 4i, ψk(vs) = (3(s − 3))j, s ∈ {3, ⋯, n + 2}, and the edge set of is see Figure 14. From the edge set of G12, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(3n − 1)/2⌋}, the length 0 is only present once in the length 3n/2 is found once in if n is even, for every λ ∈ {1, 2, ⋯, ⌊(3n − 1)/2⌋}, G12 has precisely edges of length λ, the length 0 is found times in G12, and the length 3n/2 is found times in G12 if n is even. Hence, can be decomposed by G12.
Theorem 17. Let n ≥ 4, m ≥ 2 be integers. Then, there is an orthogonal labelling for
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G13, which can be defined by which is defined by
and the edge set of is
see Figure 15. From the edge set of G13, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, n}, the length 0 is found once in for every λ ∈ {1, 2, ⋯, n}, G13 has precisely edges of length λ, and the length 0 is found times in G13. Hence, can be decomposed by G13.

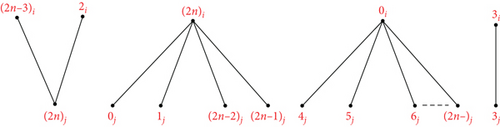
4. Decompositions of by Connected Caterpillars
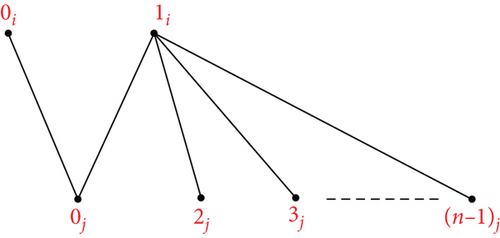
Theorem 18. Let n ≥ 2, m ≥ 2 be integers. Then, there is an orthogonal labelling for
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G14, which can be defined by which is defined by
and the edge set of is
see Figure 16. From the edge set of G14, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, the length 0 is found once in the length n/2 is found once in for every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G14 has precisely edges of length λ, the length n/2 is found times in G14, and the length 0 is found times in G14. Hence, can be decomposed by G14.
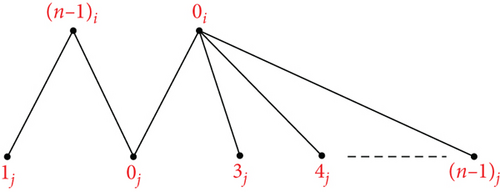
Theorem 19. Let n ≥ 3, m ≥ 2 be integers. Then, there is an orthogonal labelling for
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G15, which can be defined by which is defined by ψk(v0) = 0i, ψk(v1) = (n − 1)i, ψk(v2) = 0j, ψk(v3) = 1j, ψk(vs) = (s − 1)j, s ∈ {4, 5, ⋯, n}, and the edge set of is
see Figure 17. From the edge set of G15, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, the length 0 is found once in the length n/2 is found once in if n is even, for every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G15 has precisely edges of length λ, the length n/2 is found times in G15 if n is even, and the length 0 is found times in G15. Hence, can be decomposed by G15.
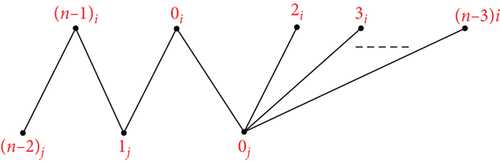
Theorem 20. Let n ≥ 4, m ≥ 2 be integers. Then, there is an orthogonal labelling for
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G16, which can be defined by which is defined by
s ∈ {2, 3, ⋯, n − 3}, and the edge set of is
see Figure 18. From the edge set of G16, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, the length 0 is found once in the length n/2 is found once in if n is even, for every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G16 has precisely edges of length λ, the length n/2 is found times in G16 if n is even, and the length 0 is found times in G16. Hence, can be decomposed by G16.
Theorem 21. Let n ≥ 5, m ≥ 2 be integers. Then, there is an orthogonal labelling for
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G17, which can be defined by which is defined by
and the edge set of is
see Figure 19. From the edge set of G17, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, the length 0 is found once in the length n/2 is found once in if n is even, for every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G17 has precisely edges of length λ, the length n/2 is found times in G17 if n is even, and the length 0 is found times in G17. Hence, can be decomposed by G17.
Theorem 22. Let n ≥ 6, m ≥ 2 be integers. Then, there is an orthogonal labelling for
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G18, which can be defined by which is defined by
ψk(v6) = (n − 1)j, ψk(vs+4) = si, s ∈ {3, 4, ⋯, n − 4}, and the edge set of is
see Figure 20. From the edge set of G18, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, the length 0 is only present once in the length n/2 is found once in if n is even, for every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G18 has precisely edges of length λ, the length n/2 is found times in G18 if n is even, and the length 0 is found times in G18. Hence, can be decomposed by G18.
Theorem 23. Let n ≥ 7, m ≥ 2 be integers. Then, there is an orthogonal labelling for
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G19, which can be defined by which is defined by ψk(v0) = 2j, ψk(v1) = 1i, ψk(v2) = 0j, ψk(v3) = 0i, ψk(v4) = 3j, ψk(v5) = 6i, ψk(v6) = 4j, ψk(v7) = 2i, ψk(vs+2) = sj, s ∈ {6, 7, ⋯, n − 2}, and the edge set of is
Theorem 24. Let n ≥ 8, m ≥ 2 be integers. Then, there is an orthogonal labelling for
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G20, which can be defined by which is defined byψk(v0) = 6i, ψk(v1) = 5j, ψk(v2) = 4i, ψk(v3) = 2j, ψk(v4) = 0i, ψk(v5) = 0j, ψk(v6) = 3i, ψk(v7) = 6j.
ψk(v8) = 2i, φ(vi+2) = i1, i ∈ {7, 8, ⋯, n − 2}, and the edge set of is
see Figure 22. From the edge set of G20, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, the length 0 is found once in the length n/2 is found once in if n is even, for every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G20 has precisely edges of length λ, the length n/2 is found times in G20 if n is even, and the length 0 is found times in G20. Hence, can be decomposed by G20.
Theorem 25. Let n ≥ 9, m ≥ 2 be integers. Then, there is an orthogonal labelling for
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G21, which can be defined by which is defined byψk(v0) = 6j, ψk(v1) = 4i, ψk(v2) = 2j, ψk(v3) = 1i, ψk(v4) = 0j, ψk(v5) = 0i, ψk(v6) = 4j, ψk(v7) = 8i.
ψk(v8) = 5j, ψk(v9) = 2i, ψk(vs+3) = sj, s ∈ {7, 8, ⋯, n − 3}, and the edge set of is
see Figure 23. From the edge set of G21, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, the length 0 is found once in the length n/2 is found once in if n is even, for every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G21 has precisely edges of length λ, the length n/2 is found times in G21 if n is even, and the length 0 is found times in G21. Hence, can be decomposed by G21.
Theorem 26. Let n ≥ 10, m ≥ 2 be integers. Then, there is an orthogonal labelling for
Proof. Suppose The mapping ψk can be used to define an orthogonal labelling for the subgraph G22, which can be defined by which is defined by
and the edge set of is
see Figure 24. From the edge set of G22, the following conditions are verified: Each graph has precisely two edges of length λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, the length 0 is found once in the length n/2 is found once in if n is even, for every λ ∈ {1, 2, ⋯, ⌊(n − 1)/2⌋}, G22 has precisely edges of length λ, the length n/2 is found times in G22 if n is even, and the length 0 is found times in G22. Hence, can be decomposed by G22.

5. Conclusion
As known, there are several types of graphs labelling. Herein, we are concerned with orthogonal labelling notion. As a generalization to the orthogonal labelling approach provided in the literature for finding the decomposition of circulant-balanced complete bipartite graphs Kn,n, we have developed a generalized orthogonal labelling approach for decomposing the circulant-balanced complete multipartite graphs in this study. In the future, we will work to improve the orthogonal labelling approach so that it may be used with all types of circulant graphs.
Nomenclatures
-
- Km:
-
- Complete graph having m vertices
-
- kH:
-
- k disjoint unions of graph H
-
- Km,n:
-
- Complete bipartite graph with size m + n, where the vertex set is divided into two sets with sizes m and n
-
- Cx:
-
- Cycle graph on x vertices
-
- Pm:
-
- Path graph on m vertices
-
- V(G):
-
- Vertex set of graph G
-
- E(G):
-
- Edge set of graph G
-
- G ∪ H:
-
- Disjoint union of graphs G and H.
Conflicts of Interest
The authors declare no conflict of interest.
Open Research
Data Availability
The data used to support the findings of this study are available from the corresponding author on request.




