Volume 2022, Issue 1 1988302

Research Article

Open Access

Criterion for Hydraulic Fracture Propagation Behavior at the Interface of a Coal Measure Composite Reservoir

Yifeng Guo

College of Safety and Emergency Management Engineering, Taiyuan University of Technology, Taiyuan 030024, China tyut.edu.cn

Search for more papers by this author

Runxu Zhang,

Corresponding Author

Runxu Zhang

[email protected]

orcid.org/0000-0002-6487-1695

College of Safety and Emergency Management Engineering, Taiyuan University of Technology, Taiyuan 030024, China tyut.edu.cn

Search for more papers by this author

Xinghua Zhang,

Xinghua Zhang

College of Safety and Emergency Management Engineering, Taiyuan University of Technology, Taiyuan 030024, China tyut.edu.cn

Search for more papers by this author

Kangkang Han,

Kangkang Han

Shanxi Blue Flame Holding Company Limited, Jincheng 048000, China

Search for more papers by this author

Fazhi Yan,

Fazhi Yan

orcid.org/0000-0001-7355-1004

College of Safety and Emergency Management Engineering, Taiyuan University of Technology, Taiyuan 030024, China tyut.edu.cn

Search for more papers by this author

Cunbao Deng,

Cunbao Deng

College of Safety and Emergency Management Engineering, Taiyuan University of Technology, Taiyuan 030024, China tyut.edu.cn

Search for more papers by this author

Zhixin Jin,

Zhixin Jin

College of Safety and Emergency Management Engineering, Taiyuan University of Technology, Taiyuan 030024, China tyut.edu.cn

Search for more papers by this author

Yifeng Guo,

Yifeng Guo

College of Safety and Emergency Management Engineering, Taiyuan University of Technology, Taiyuan 030024, China tyut.edu.cn

Search for more papers by this author

Runxu Zhang,

Corresponding Author

Runxu Zhang

[email protected]

orcid.org/0000-0002-6487-1695

College of Safety and Emergency Management Engineering, Taiyuan University of Technology, Taiyuan 030024, China tyut.edu.cn

Search for more papers by this author

Xinghua Zhang,

Xinghua Zhang

College of Safety and Emergency Management Engineering, Taiyuan University of Technology, Taiyuan 030024, China tyut.edu.cn

Search for more papers by this author

Kangkang Han,

Kangkang Han

Shanxi Blue Flame Holding Company Limited, Jincheng 048000, China

Search for more papers by this author

Fazhi Yan,

Fazhi Yan

orcid.org/0000-0001-7355-1004

College of Safety and Emergency Management Engineering, Taiyuan University of Technology, Taiyuan 030024, China tyut.edu.cn

Search for more papers by this author

Cunbao Deng,

Cunbao Deng

College of Safety and Emergency Management Engineering, Taiyuan University of Technology, Taiyuan 030024, China tyut.edu.cn

Search for more papers by this author

Zhixin Jin,

Zhixin Jin

College of Safety and Emergency Management Engineering, Taiyuan University of Technology, Taiyuan 030024, China tyut.edu.cn

Search for more papers by this author

First published: 11 October 2022

https://doi.org/10.1155/2022/1988302

Academic Editor: Wen-long Shen

Share a link

Email
Wechat
Bluesky

Abstract

Regarding the three expansion modes of hydraulic fractures at the interface of a coal measure composite reservoir (arrested, deflection, and penetration), based on the coupling theory of fluid flow and solid elastic deformation, a criterion that considers the influences of the injection parameters (fracturing fluid injection rate and viscosity) is established to predict the propagation path of hydraulic fractures at the interface of a composite reservoir. The criterion judges the propagation behavior of the fractures by comparing the water pressure in the wellbore and the critical seam pressure of the penetration and deflection. The controlled variable method is used to analyze the influences of the various factors on the propagation behavior of hydraulic fractures at the interface between layers. The results show that the differences in in situ stress, the interface cohesion, and the included angle mainly affect the critical seam pressure of the fracture deflection. The differences in elastic modulus, fluid injection rate, and fracturing fluid viscosity directly affect the water pressure in the wellbore. The difference in the fracture toughness mainly affects the crack propagation path by affecting the critical seam pressure of the deflection. The smaller the difference in the in situ stress is, the more likely it is that the hydraulic fractures will penetrate the layer. Larger differences in the fracture toughness between layers, interfacial cohesion, fluid injection rate, and fracturing fluid viscosity are more conducive to the hydraulic fractures penetrating the layer. When the angle between the hydraulic fractures and the interface is 25–55°, the hydraulic fracture is more likely to expand along the interface. This criterion takes into account the influences of the injection parameters and is of great significance to gaining a better understanding of the propagation behavior of hydraulic fractures at an interlayer interface.

1. Introduction

Coal measure gas, which is characterized by the coexistence of coalbed methane, tight sandstone gas, and shale gas, is an important type of unconventional natural gas resource [1, 2]. In the combined fracturing of a coal measure composite reservoir, the vertical expansion range of the hydraulic fractures determines the sharing degree of the stimulation measures, which is the key factor determining the success or failure of the fracturing operation [3]. Therefore, before combined fracturing of a coal measure composite reservoir is conducted, it is necessary to predict the vertical expansion range and shape of the hydraulic fractures and to predict whether the hydraulic fractures will penetrate the layers. The corresponding criterion is the basis for determining whether a hydraulic fracture can penetrate through a layer, and understanding the factors influencing the fracture’s ability to penetrate the layer is the premise.

The propagation behavior of hydraulic fractures at the interface of a composite reservoir is mainly controlled by geological factors, including the differences in the physical properties (e.g., the elasticity modulus, Poisson’s ratio, fracture toughness, and in situ stress) and the characteristics of the interface between the different types of reservoirs (i.e., the interfacial bond strength and inclination angle). Through theoretical derivation and numerical simulation, Fung et al., Gu and Siebrits, and Li et al. [4–6] determined that the difference in the elastic moduli of the layers has little effect on the fracture height, and even if the elastic modulus of the crack initiation layer differs by a factor of 10 from that of the adjacent layer, the hydraulic fracture will penetrate the interface and extend into the layer with the higher modulus. Laboratory and field tests also revealed that the difference in the elastic moduli of the layers does not substantially affect the penetration of the cracks. However, the elastic modulus may affect the intrafracture pressure. In a reservoir with a large elastic modulus, the intrafracture pressure of the hydraulic fractures will also be relatively large, so the fracture is more likely to enter the layer with the lower elastic modulus from the layer with the higher elastic modulus [7]. Thiercelin et al. and Wu et al. [8, 9] studied the effects of the differences in the interlaminar fracture toughness and Poisson’s ratio on vertical crack propagation. They found that when the fracture toughness or Poisson’s ratio of the crack initiation layer is greater than that of the adjacent layer, this can promote the propagation of the crack through the layer; otherwise, it will inhibit the crack penetration. However, the ranges of the fracture toughnesses and Poisson’s ratios of different lithologic reservoirs are very small, so the influences of the fracture toughness and Poisson’s ratio on fracture penetration are very limited. The difference in the minimum horizontal in situ stress of different reservoirs is the most critical factor inhibiting fracture penetration [10]. Tan et al. [11] conducted fracturing tests on layered rock samples and found that when the difference in the minimum horizontal in situ stress of the layers is greater than 2 MPa, the penetration range of the hydraulic fractures is significantly reduced; and when the difference in the minimum horizontal in situ stress of the layers is greater than 4 MPa, the hydraulic fractures are basically confined within the initiation layer. Warpinski et al. also reported that when the difference in the minimum horizontal in situ stress of the layers is greater than 10 MPa, the cracks will not be able to propagate through the interface into the adjacent layers [12]. The properties of the interface are also an important factor affecting the propagation behavior of hydraulic fractures at an interface in a composite reservoir. Daneshy [13] studied the effect of the interfacial strength on the vertical expansion of a fracture through fracturing tests on layered rock combination samples and concluded that when the bonding strength of the interlayer interface is high enough, the interface basically does not undergo slip failure, and the fracture can easily penetrate the interface and propagate into the other layers. Later, this conclusion was also confirmed by Teufel and Clark, Wang et al., and Gao et al. [14–17]. The inclination angle of the interface is also an important factor affecting the vertical penetration of the fracture. Tan et al. [18] concluded through numerical simulation that the greater the inclination angle, the more likely the interface is to slip and fail, and the more difficult it is for the fractures to penetrate the layer.

When hydraulic fractures encounter natural weak surfaces such as natural fractures, bedding planes, and weakly bonded interfaces in order to predict the propagation behavior of the hydraulic fractures, scholars in China and abroad have successively proposed various criteria, such as the Warpinski criterion [19], R&P criterion [20], e-R&P criterion [21], and Llanos criterion [22]. These criteria are mainly used to discriminate the intersection behavior of hydraulic fractures and natural fractures. There are few criteria for discriminating the propagation behavior of hydraulic fractures when they encounter an interlayer interface. Zhao and Chen [23] adopted the method of rock fracture mechanics and fully considered the influence of the layered in situ stress, layered rock mechanical parameters, formation interface properties, and reservoir thickness to calculate the critical seam pressure for hydraulic fracture cessation, deflection, and penetration. The fracture propagation behavior is determined by comparing the water pressure in the wellbore with the two critical fracture pressures. However, this criterion only considers the case in which the hydraulic fracture is perpendicular to the interlayer interface. Due to the arbitrary distribution of the interfaces in a coal measure composite reservoir, it is necessary to extend this criterion to cases where the hydraulic fracture and the interface are not orthogonal. Moreover, this criterion does not consider the effects of the injection parameters on the crack propagation behavior at the interface.

In view of this, based on the research of Zhao et al. and the theories of fluid flow and solid elastic deformation, a criterion for fracture propagation through an interface in a coal measure composite reservoir for any interface dip angle was developed in this study. The criterion focuses on the influences of the fracturing fluid parameters on the pressure in the fracture. The propagation behavior of the hydraulic fracture at the interface between layers is determined by comparing the critical seam pressure for deflection, the critical seam pressure for penetration, and the water pressure in the wellbore. Based on the experimental data obtained in previous studies, the accuracy of the discriminant results of this criterion was compared under the same conditions. Finally, the control variable method was used to analyze the sensitivities of the influencing parameters.

2. Establishing the Judgment Criterion

2.1. Physical Model and Basic Assumptions

The expansion form of hydraulic fractures in a formation is shown in Figure 1. Figure 1(a) is a schematic diagram of the fracture propagation shape during the hydraulic fracturing process, and Figure 1(b) is a schematic diagram of the relative positions of the hydraulic fractures when they meet an interface in a coal measure composite reservoir. In Figure 1, σ_h is the horizontal minimum in situ stress of the composite reservoir; σ_V is the vertical in situ stress of the composite reservoir; h is the height of the hydraulic fracture; α is the angle between the hydraulic fracture and the interface between the layers; O is the crack initiation position; and A and B are the upper and lower ends of the hydraulic fracture in the height direction, respectively.

Details are in the caption following the image — **Figure 1 (a) Hydraulic fracture morphology**
Open in figure viewer PowerPoint

Schematic diagrams of the physical model.

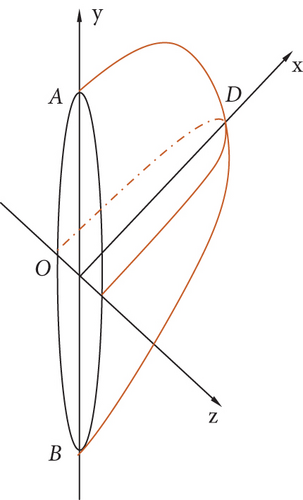
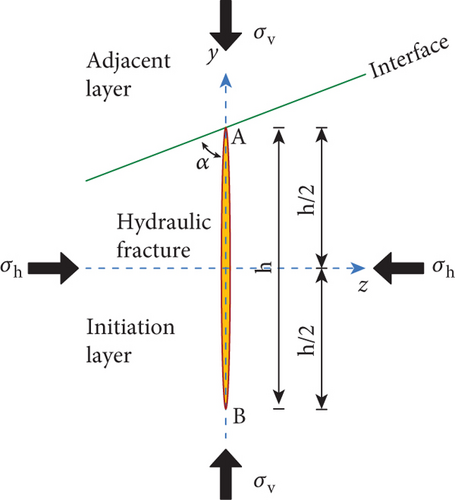
To simplify the calculations, the following basic assumptions were made in the model. (1) The hydraulic fracture is a quasi-three-dimensional elliptical fracture when a single formation expands, and the fracture surface is perpendicular to the direction of the minimum in situ stress and extends statically. (2) In the fracture expansion process, there is a tiny fracture process zone at the tip. (3) Each reservoir of the composite coal measure reservoir is an ideal homogeneous and isotropic body, the interlayer interface is well cemented, and the rock fracture obeys the theory of elastic fracture mechanics. (4) The flow of the fracturing fluid is one-dimensional laminar flow along the fracture length, the fluid is incompressible, and the filtration of the fracturing fluid is not considered.

2.2. Model of Water Pressure Distribution in Fractures

There is a pressure drop in the fracturing fluid in both the fracture length and fracture height directions. The longitudinal pressure drop of the fracturing fluid affects the extension of the hydraulic fractures at the interface between layers. Neglecting the longitudinal pressure drop will lead to a larger deviation. To be more consistent with the actual situation, after introducing the pressure drop gradient in the fracture height direction, the water pressure P_F(y) in the center of the fracture along the fracture height direction y can be obtained as follows:

(1)

where y is the coordinate of a point in the direction of the fracture height (m), P₀ is the water pressure in the wellbore (MPa), and g_v is the pressure drop gradient in the direction of the slit height (MPa/m).

Based on the basic assumptions, it can be concluded that the flow of the fracturing fluid in the fracture is simple one-dimensional laminar flow along the length of the fracture, and the fluid is incompressible. The flow rate at different locations within the fracture is not constant, and it is a complex function that changes as the fracture grows. Based on the first-order linear partial differential equation for fluid pressure in elliptical pipes, the continuous equation for one-dimensional laminar flow of the fracturing fluid along the fracture length direction, and the expression for the fracture width, the integral terms that cannot be simply analytically expressed can be properly approximated. The simple analytical solution of P₀ is as follows [24, 25]:

(2)

where q is the displacement of the fracturing fluid (m³/s), ρ is the fluid density (kg/m³), h is the height of the fracture (m), γ is the fracturing fluid’s viscosity (mPa·s), E is the elastic modulus of the reservoir (GPa), K_IC is the type-I fracture toughness of the reservoir (MPa·m^1/2), and l is the half-length of the fracture (m).

2.3. Critical Fracture Pressure for Different Propagation Behaviors of Fractures

2.3.1. The Cracks Directly Pass through the Interlayer Interface

If the interlayer interface is well consolidated, when the hydraulic fracture reaches the interlayer interface, it will directly pass through the interface and enter the adjacent layer. According to the basic assumptions, when the hydraulic fracture intersects the interlayer interface,

(3)

At this time, the critical condition for the crack to pass through the interface into the adjacent layer and continue to expand is

(4)

where K_AC is the fracture toughness of the adjacent layer (MPa·m^1/2) and K_A is the stress intensity factor of the fracture tip when the hydraulic fracture reaches the interlayer interface (MPa·m^1/2). Under plane strain conditions, the stress intensity factor of a hydraulic fracture with height h is [26]

(5)

where P(y) is the distribution function of the net pressure within the fracture. When the hydraulic fracture reaches the interlayer interface, assuming that the critical pressure in the center of the fracture required for the critical seam pressure of penetration is P₁, the stress decomposition diagram of the fracture profile is shown in Figure 2.

Based on the stress decomposition of the fracture profile, the distribution function P(y) of the net pressure in the fracture can be obtained as follows:

(6)

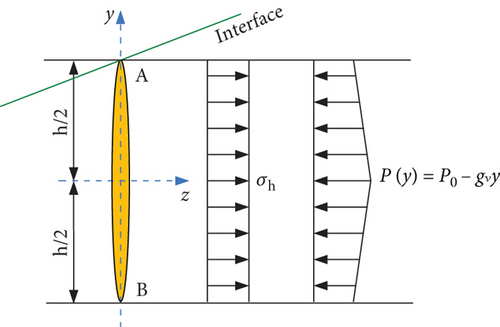
By simultaneously solving Equations (3)–(6), the critical fracture pressure P₁ at which the hydraulic fracture directly penetrates the interface and enters the adjacent layer can be obtained.

2.3.2. The Fractures Propagate along the Interlayer Interface

The bond strength and dip angle of the interlayer interface play important roles in the crack propagation. When the strength of the interlayer interface is weak or the dip angle is large, the hydraulic fracture may expand along the interface after intersecting with the interface. At this time, shear slip failure mainly occurs at the interlayer interface, and the critical condition for the hydraulic fractures to propagate along the interface is [27]

(7)

where τ_rθ is the shear stress acting on the interface (MPa), τ_I is the shear strength of the interface (MPa), μ is the friction factor of the interface, σ_n is the normal stress acting on the interface (MPa), and C is the cohesive force of the interface (MPa). When the hydraulic fracture reaches the interlayer interface, based on elastic-plastic theory, the stress field at the tip of the hydraulic fracture can be expressed as follows [28]:

(8)

where σ_z, σ_y, and τ_zy are the stress components at the tip of the hydraulic fracture (MPa), r and θ are the polar coordinates of the tip of the hydraulic fracture, σ_V is the vertical in situ stress (MPa), and σ_h is the minimum horizontal in situ stress (MPa). When the dip angle of the interlayer interface is α, the stress component of the stress field at the tip of the hydraulic fracture at the interface is

(9)

where σ_r, σ_θ, and τ_rθ are the axial stress, normal stress, and tangential stress at any point on the interlayer interface, respectively (MPa). By substituting Equation (9) into Equation (10), we can obtain the stress component of the stress field at the tip of the hydraulic fracture at the formation interface under the combined action of the in situ stress and the water pressure in the fracture:

(10)

According to fracture mechanics, there is a fracture process zone at the tip of a hydraulic fracture, in which the material undergoes plastic deformation. It is generally considered that the stress in the fracture process zone is less than or equal to the stress at its edges; that is, the stress in the fracture process zone does not exceed the stress when r = r_c. r_c is the radius of the fracture process zone at the tip of the hydraulic fracture (m). Assuming that the critical pressure at the center of the fracture required for the hydraulic fracture to expand along the interface is P₂, the distribution function P(y) of the net pressure in the fracture can be obtained as follows:

(11)

When the hydraulic fracture spreads along the interface, the following relationship is satisfied:

(12)

By combining Equations (5), (7), (10), (11), and (12), the critical fracture pressure P₂ can be obtained when the hydraulic fractures expand along the interlayer interface.

2.4. Criterion

(1)
If P₀ < min(P₁, P₂), the hydraulic fracture stops spreading after it intersects with the interlayer interface
(2)
If min(P₁, P₂) = P₂ and P₀ > P₂, then the hydraulic fracture will spread along the interlayer interface after intersecting with the interlayer interface
(3)
If min(P₁, P₂) = P₁ and P₀ > P₁, then the hydraulic fracture intersects with the interlayer interface and passes directly through the interface into the adjacent layer

3. Verification of Discriminant Criteria

To test the accuracy of the criterion, the accuracy of the criterion was verified by comparing the results of the criterion under the same conditions with the experimental data of Zhou et al. [29] and the laboratory data of Jiang et al. [28]. The initial experimental parameters of Zhou et al. and Jiang et al. are presented in Table 1.

Table 1. Initial experimental parameters of Zhou et al. and Jiang et al.

Experimental group		E (GPa)	v	K_IC (MPa·m^1/2)	C (MPa)	μ	γ (mPa·s)	q (m³/min)
Zhou et al.	Initiation layer	8.402	0.23	0.59			135	2.52 × 10⁻⁷
	Adjacent layer	8.402	0.23	0.59
	Interface				3.2	0.89
Jiang et al.	Initiation layer	3.63	0.19	0.52			1	2 × 10⁻⁵
	Adjacent layer	2.75	0.23	0.20
	Interface				0	0.32

Table 2 presents the results obtained in Zhou et al.’s experiments and the judgment results of the discriminant criteria developed in this study, and it compares the two sets of results. The symbol ✔ in the table indicates that the judgment results are consistent with the experimental results, and the symbol ✘ indicates that the judgment results are inconsistent with the experimental results. Comparison of the results revealed that except for the last set of experiments, the judgment results of the criterion developed in this study are in good agreement with the experimental results of Zhou et al., which verifies the accuracy of the criterion.

Table 2. Comparison of Zhou et al.’s experimental results and the results of the proposed criterion.

No.	α (°)	σ_h (MPa)	σ_v (MPa)	∆σ (MPa)	r_c (m)	Experimental results	Criterion results	Uniformity
1	90	5	10	5	0.0011	Penetration	Penetration	✔
2	90	3	10	7	0.0019	Penetration	Penetration	✔
3	60	3	13	10	0.0026	Penetration	Penetration	✔
4	60	5	8	3	0.0026	Penetration	Penetration	✔
5	60	3	10	7	0.0026	Deflection	Deflection	✔
6	30	5	8	3	0.0012	Deflection	Deflection	✔
7	30	5	10	5	0.0012	Deflection	Deflection	✔
8	30	3	13	10	0.0021	Arrested	Deflection	✘

Jiang et al.’s experimental results were used to further verify the judgment method developed in this study. Table 3 presents Jiang et al.’s experimental results and the calculation results of the discriminant criteria developed in this study, and it compares the two sets of results. It can be seen from Table 3 that the results obtained using the judgment criterion developed in this study are consistent with Jiang et al.’s test results, which further verifies the accuracy of the criterion. It can be seen from the comparison of the results that only the last set of experimental comparison results is inconsistent. This is because the criterion established in this paper is based on the assumption that each coal measure is homogeneous and isotropic. Furthermore, the rock materials used in the actual fracturing tests were not uniform. There were obvious dents near the interface of the rock layer in the eighth group of tests (Table 2), and the heterogeneity near the interface was stronger than that of the previous seven groups, which in turn affected the propagation path of the hydraulic fractures in this set of experiments. Overall, the judgment results of the criterion developed in this study are in good agreement with Zhou et al.’s experimental results, which verifies the accuracy of the criterion.

Table 3. Comparison of Jiang et al.’s experimental results and the results of the proposed criterion.

No.	α (°)	σ_h (MPa)	σ_v (MPa)	∆σ (MPa)	r_c (m)	Experimental results	Criterion results	Uniformity
1	90	6	3	3	0.0011	No penetration	Deflection	✔
2	90	7	3	4	0.0019	No penetration	Deflection	✔
3	90	8	3	5	0.0026	No penetration	Deflection	✔
4	90	9	3	6	0.0026	Penetration	Penetration	✔

4. Parametric Analysis

Taking the sand-mudstone composite reservoir of the Shihezi Formation in the Linxing Block in the Ordos Basin as the geological background, the effects of the differences in the in situ stress, rock mechanical properties (elastic modulus and fracture toughness), fluid injection parameters (injection rate and viscosity of fracturing fluid), and interface properties (interface dip angle and cohesion) on the propagation behavior of the hydraulic fractures at the interface in the coal measure composite reservoir were studied. The hydraulic fracture propagation behavior at the interface in the coal measure composite reservoir under the influences of the different parameters was analyzed based on the critical seam pressure for the fracture deflection P₁, the critical seam pressure for the fracture penetration P₂, and the water pressure in the wellbore P₀. Table 4 presents the basic parameters of the sand-mudstone composite reservoir.

Table 4. Basic parameters.

Type	Parameter	Number
Mudstone	Elastic modulus (GPa)	20
	Poisson’s ratio	0.25
	Density (g/mm³)	1.94
	Tensile strength (MPa)	4.1
	Fracture toughness (MPa·m^1/2)	0.416
	Horizontal minimum ground stress (MPa)	25
	Horizontal maximum ground stress (MPa)	30
	Overburden pressure (MPa)	40
	Layer thickness (m)	10
Sandstone	Elastic modulus (GPa)	25
	Poisson’s ratio	0.2
	Density (g/mm³)	2.45
	Tensile strength (MPa)	6.7
	Fracture toughness (MPa·m^1/2)	0.995
	Horizontal minimum ground stress (MPa)	25
	Horizontal maximum ground stress (MPa)	30
	Overburden pressure (MPa)	40
	Layer thickness (m)	20
Interface	Tensile strength (MPa)	1.78
	Cohesion (MPa)	1.15
	Friction factor	0.15

4.1. Difference in In Situ Stress

The main parameters of the model were set according to Table 4. The angle between the hydraulic fracture and the interface was set as 45°, and the vertical in situ stress of the reservoir was gradually changed. The difference between the ground stress and the horizontal minimum principal stress was set as 0, 2.5, 5, 7.5, 10, 12.5, and 15 MPa in sequence. The influence of the difference in the in situ stress on the propagation behavior of the hydraulic fractures at the interface in the coal measure composite reservoir was analyzed by studying the variations in the critical seam pressure for fracture deflection P₁, the critical seam pressure for fracture penetration P₂, and the water pressure in the wellbore P₀ under different in situ stress differences. The results are shown in Figure 3.

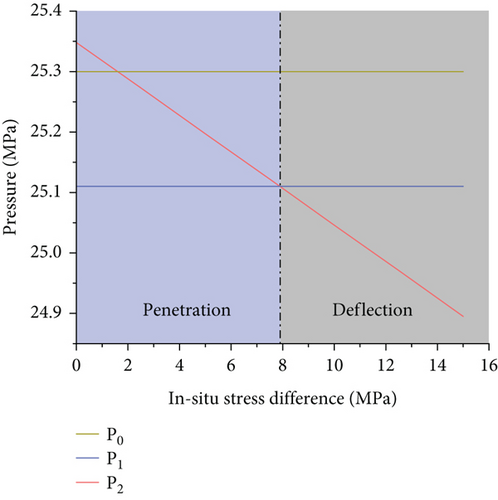
It can be seen from Figure 3 that the water pressure in the wellbore P₀ and the critical seam pressure for deflection P₁ basically do not change under the different in situ stress differences. The critical seam pressure for penetration P₂ decreases linearly as the in situ stress difference increases, and it intersects the line where the critical seam pressure for deflection P₁ is located at point (7.9, 25.11). Since the water pressure in the wellbore P₀ is always greater than the critical seam pressure for deflection P₁ under these parameter values, the established criterion shows that when P₁ is less than P₂, the fracture spreads through the layer. Thus, when the in situ stress difference is less than 7.9 MPa (light blue area in Figure 3), the hydraulic fractures propagate through the layers at the interlayer interface; and when the in situ stress difference is greater than 7.9 MPa (light gray area in Figure 3), the hydraulic fractures propagate along the interface at the interlayer interface. It can be seen that the in situ stress difference is the main factor affecting the propagation path of the hydraulic fractures at the interlayer interface. When the other conditions remain unchanged, the in situ stress difference mainly changes the relationship between the three pressures by affecting the critical seam pressure for fracture deflection P₂, thereby affecting the propagation path of the hydraulic fractures.

4.2. Rock Mechanical Properties

4.2.1. Difference in Elastic Moduli

The main parameters of the model were set according to Table 4, the angle between the hydraulic fracture and the interface was set as 45°, and the elastic modulus of the reservoir was gradually changed (24, 24.5, 25, 25.5, and 26 GPa). The difference in the elastic moduli was set as 4, 4.5, 5, 5.5, and 6 GPa. The effect of the difference in the elastic moduli of the reservoir layers on the propagation behavior of the hydraulic fractures at the interface in the coal measure composite reservoir was analyzed by studying the variations in the critical seam pressure for fracture deflection P₁, the critical seam pressure for fracture penetration P₂, and the water pressure in the wellbore P₀ under different elastic moduli differences. The results are shown in Figure 4.

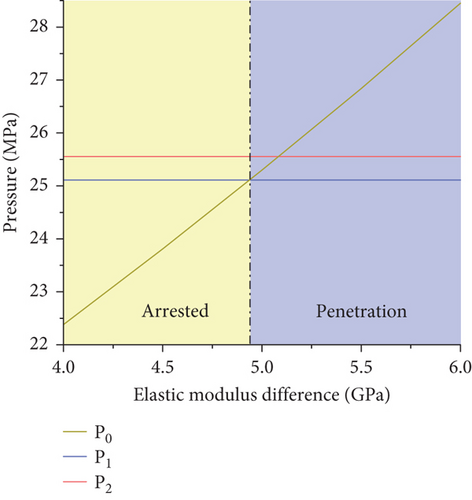
It can be seen from Figure 4 that the critical seam pressure for deflection P₁ and the critical seam pressure for penetration P₂ under the different elastic moduli differences basically do not change. The water pressure in the wellbore P₀ increases linearly as the difference in the elastic moduli increases, and it intersects the line where the critical seam pressure for deflection P₁ is located at point (7.9, 25.11). Because the critical seam pressure for penetration P₁ is always smaller than the critical seam pressure for deflection P₂ under these parameter settings, according to the established criterion, when P₀ is less than P₁, the fracture stops expanding after intersecting with the interlayer interface. Therefore, when the difference in the elastic moduli is less than 4.9 GPa (light orange area in Figure 4), and the fracture stops spreading after it intersects with the interlayer interface. When the difference in the elastic moduli is greater than 4.9 GPa (light blue area in Figure 4), the hydraulic fracture propagates through the layer at the interlayer interface. Thus, the difference in the elastic moduli of the reservoir layers affects the propagation path of the hydraulic fractures at the interface between layers. When the other conditions remain unchanged, the difference in the elastic moduli of the layers mainly changes the relationship between the three pressures by affecting the water pressure in the wellbore P₀, thereby affecting the propagation path of the hydraulic fractures.

4.2.2. Difference in Fracture Toughness

The main parameters of the model were set according to Table 4. The angle between the hydraulic fracture and the interface was set as 75°, and the fracture toughness of the interlayer was gradually changed (0.395, 0.595, 0.795, 0.995, 1.195, 1.395, and 1.595 MPa∙m^1/2). The difference in the fracture toughness between the reservoir and the interlayer was set as 0.6, 0.4, 0.2, 0, −0.2, −0.4, and 0.6 MPa∙m^1/2. The effect of the difference in the fracture toughness on the propagation behavior of the hydraulic fractures at the interface in the coal measure composite reservoir was analyzed by studying the variations in the critical seam pressure for fracture deflection P₁, the critical seam pressure for fracture penetration P₂, and the water pressure in the wellbore P₀ under different fracture toughness differences. The results are shown in Figure 5.

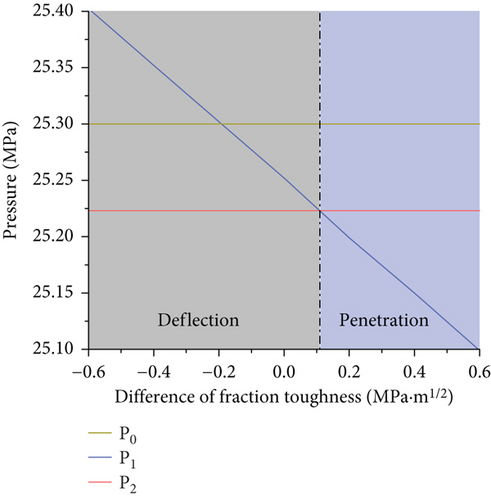
It can be seen from Figure 5 that the water pressure in the wellbore P₁₀ and the critical seam pressure for penetration P₂ basically do not change with the differences in the fracture toughness. The critical seam pressure for penetration P₁ decreases linearly as the difference in the fracture toughness increases, and it intersects the line where the deflection critical fracture pressure P₂ is located at point (0.1, 25.223). Since the water pressure in the wellbore P₀ is always greater than the critical seam pressure for deflection P₂ under these parameter settings, according to the established criterion, the fracture expands along the interface when P₁ is greater than P₂. Thus, when the fracture toughness difference is less than 0.1 MPa∙m^1/2 (light gray area in Figure 5), the hydraulic fractures propagate along the interface at the interlayer interface; and when the fracture toughness difference is greater than 0.1 MPa∙m^1/2 (light blue area in Figure 5), the hydraulic fractures propagate through the layers at the interlayer interface. It can be seen that the difference in the fracture toughness affects the propagation path of the hydraulic fractures at the interlayer interface. When the other conditions remain unchanged, the difference in the fracture toughness mainly changes the distance between the three pressures by affecting the critical seam pressure for fracture penetration P₁, which in turn affects the propagation path of the hydraulic fractures.

4.3. Fracturing Parameters

4.3.1. Fracturing Fluid Injection Rate

The fracturing fluid injection rate is easy to control in engineering. Studying the effect of the fracturing fluid injection rate on the hydraulic fracture propagation behavior is helpful in determining whether the hydraulic fracture propagation mode can be directly controlled by controlling the fracturing fluid injection rate. The main parameters of the model were set according to Table 4. The angle between the hydraulic fracture and the interface was set as 90°. The fracturing fluid injection rate was gradually changed (3.444, 3.456, 3.468, 3.48, 3.492, 3.504, 3.516, 3.528, 3.54, 3.552, 3.564, and 3.576 m³/min). The effect of the liquid injection rate on the propagation behavior of the hydraulic fractures at the interface in the coal measure composite reservoir was analyzed by studying the variations in the critical seam pressure for fracture deflection P₁, the critical seam pressure for fracture penetration P₂, and the water pressure in the wellbore P₀ under different fracturing fluid injection rates. The results are shown in Figure 6.

It can be seen from Figure 6 that the critical seam pressure for deflection P₁ and the critical seam pressure for deflection P₂ do not change substantially with the injection rate. The water pressure in the wellbore P₀ increases linearly with increasing injection rate, and it intersects the line where the critical seam pressure of deflection P₁ is located at point (3.484, 25.11). Since the critical seam pressure for deflection P₁ is always lower than the critical seam pressure for deflection P₂ under these parameter settings, according to the established criterion, the fracture stops expanding when P₀ is less than P₁. Thus, when the injection rate is less than 3.484 m³/min (light gray area in Figure 6), after the hydraulic fracture intersects with the interlayer interface, the expansion stops. When the injection rate is greater than 3.484 m³/min (light blue area in Figure 6), the hydraulic fracture propagates through the layer at the interlayer interface. It can be seen that the injection rate directly affects the propagation path of the hydraulic fractures at the interlayer interface. When the other conditions remain unchanged, the injection rate mainly changes the relationship between the three pressures by affecting the water pressure in the wellbore P₀, which in turn affects the propagation path of the hydraulic fractures.

4.3.2. Fracturing Fluid Viscosity

The main parameters of the model were set according to Table 4. The angle between the hydraulic fracture and the interface was set as 90°, and the viscosity of the fracturing fluid was gradually changed (1.4, 1.45, 1.5, 1.55, and 1.6 mPa∙s). The effect of the fracturing fluid’s viscosity on the propagation behavior of the hydraulic fractures at the interface in the coal measure composite reservoir was analyzed by studying the variations in the critical seam pressure for fracture deflection P₁, the critical seam pressure for fracture penetration P₂, and the water pressure in the wellbore P₀ under different fracturing fluid viscosities. The results are shown in Figure 7.

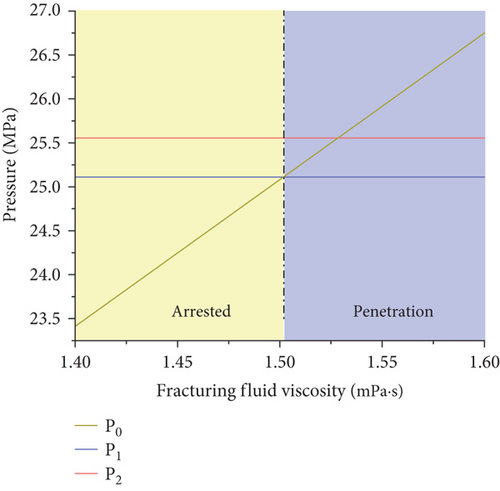
It can be seen from Figure 7 that the critical seam pressure for deflection P₁ and the critical seam pressure for penetration P₂ do not change substantially with the fracturing fluid viscosity. The water pressure in the wellbore P₀ gradually increases with increasing fracturing fluid viscosity, and it intersects with the line where the critical seam pressure for deflection P₁ is located at point (1.5, 25.11). Since the critical seam pressure for deflection P₁ is always lower than the critical seam pressure for penetration P₂ under these parameter settings, according to the established criterion, the fracture stops expanding when P₀ is less than P₁. Therefore, when the viscosity of the fracturing fluid is less than 1.5 mPa∙s (light gray area in Figure 7), the hydraulic fracture stops spreading after it intersects with the interface; and when the viscosity of the fracturing fluid is greater than 1.5 mPa∙s (light blue area in Figure 7), the hydraulic fractures propagate through the layers at the interlayer interface. It can be seen that changing the viscosity of the fracturing fluid affects the propagation path of the hydraulic fractures at the interface between the layers. When the other conditions remain unchanged, the viscosity of the fracturing fluid mainly changes the relationship between the three pressures by affecting the water pressure in the wellbore P₀, which in turn affects the propagation path of the hydraulic fractures.

4.4. Interface Properties

4.4.1. Interface Dip Angle

The main parameters of the model were set according to Table 4. The angle between the hydraulic fracture and the interlayer interface was gradually changed (10°, 20°, 30°, 40°, 50°, 60°, 70°, 80°, and 90°). The influence of the interface dip angle on the propagation behavior of the hydraulic fractures at the interface in the coal measure composite reservoir was analyzed by studying the variations in the critical seam pressure for fracture deflection P₁, the critical seam pressure for fracture penetration P₂, and the water pressure in the wellbore P₀ under different interface dip angles. The results are shown in Figure 8.

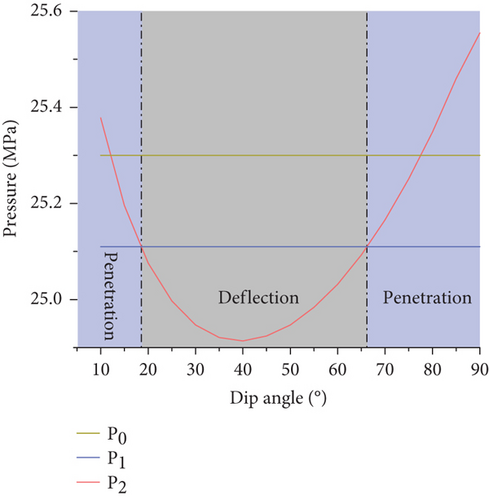
It can be seen from Figure 8 that the water pressure in the wellbore P₀ and the critical seam pressure for penetration P₁ basically do not change with the interface dip angle. The critical seam pressure for deflection P₂ initially decreases and then increases with increasing interface inclination angle, and it intersects the line where the critical seam pressure for penetration P₁ is located at points (18.6, 25.11) and (66.16, 25.11). Under these parameter settings, the water pressure P₀ in the wellbore is always greater than the critical seam pressure for penetration P₁, while the critical seam pressure for deflection P₂ changes from greater than the critical seam pressure for penetration P₁ to less than the critical seam pressure for penetration P₁ with increasing interface dip angle. According to the established criterion, when P₁ is less than P₂, the fracture propagates through the layer; and when P₁ is greater than P₂, the fracture expands along the interface. Thus, when the interface dip angle is less than 18.6° (light blue area in Figure 8), the hydraulic fractures spread through the layers at the interlayer interface. When the interface dip angle is 18.6–66.16° (light gray area in Figure 8), the hydraulic fractures spread along the interface at the interlayer interface. When the interface dip angle is greater than 66.16° (light blue area in Figure 8), the hydraulic fractures propagate through the layers at the interlayer interface. It can be seen that the interface dip angle affects the propagation path of the hydraulic fractures at the interlayer interface. When the other conditions remain unchanged, the interface dip angle mainly changes the relationship between the three pressures by affecting the critical seam pressure for fracture deflection P₂, thereby affecting the propagation path of the hydraulic fractures.

4.4.2. Interfacial Cohesion

The main parameters of the model were set according to Table 4. The angle between the hydraulic fracture and the interface was set as 60°, and the interfacial cohesion between the reservoir layers was gradually changed (0, 1, 2, 3, 4, 5, and 6 MPa). The effect of the interfacial cohesion on the propagation behavior of the hydraulic fractures at the interface in the coal measure composite reservoir was analyzed by studying the variations in the critical seam pressure for fracture penetration P₁, the critical seam pressure for fracture deflection P₂, and the water pressure in the wellbore P₀ under different interfacial cohesion values between the reservoir layers. The results are shown in Figure 9.

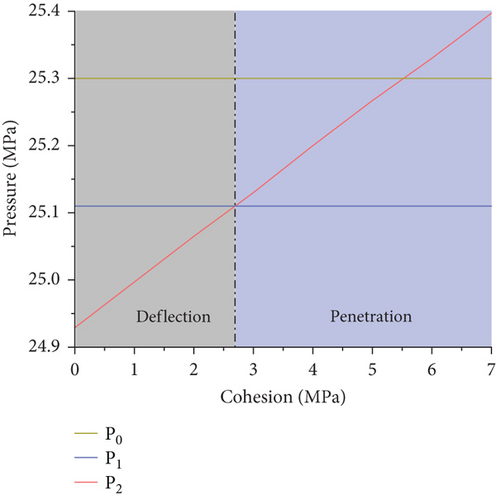
It can be seen from Figure 9 that the water pressure in the wellbore P₀ and the critical seam pressure for penetration P₁ basically do not change with the interfacial cohesion. The critical seam pressure for deflection P₂ increases linearly with increasing interfacial cohesion, and it intersects the line where the critical seam pressure for penetration P₁ is located at point (2.7, 25.11). Since the water pressure in the wellbore P₀ is always greater than the critical seam pressure for penetration P₁, under these parameter settings, according to the established criterion, the fracture expands along the interface when P₂ is less than P₁. Thus, when the interfacial cohesion is less than 2.7 MPa (light gray area in Figure 9), the hydraulic fracture spreads along the interface at the interlayer interface; and when the interfacial cohesion is greater than 2.7 MPa (light blue area in Figure 9), the hydraulic fracture spreads through the layer at the interlayer interface. It can be seen that changing the interfacial cohesion affects the propagation mode of the hydraulic fractures at the interlayer interface. When the other conditions remain unchanged, the interfacial cohesion mainly changes the relationship between the three pressures by affecting the critical seam pressure for fracture deflection P₂, thereby affecting the propagation mode of the hydraulic fractures.

5. Conclusions

Based on the theories of fluid flow in fractures and elastic deformation of solids, in this study, the influences of the injection parameters on the fracture propagation path were investigated, and a criterion for judging the propagation of hydraulic fractures through an interface in a coal measure composite reservoir with any interface dip angle was developed. The criterion was used to judge the propagation behavior of cracks at an interlayer interface by comparing three pressures (the water pressure in the wellbore and the critical seam pressures for penetration and deflection). The results obtained using the proposed criterion were found to be in good agreement with previous experimental data. The other interesting conclusions obtained from the parametric sensitivity analysis of this criterion are as follows.

(1)
The difference in the in situ stress, the interface dip angle, and the interfacial cohesion directly affect the critical seam pressure for deflection P₂ when the fracture propagates along the interface. The critical seam pressure for deflection P₂ decreases linearly as the in situ stress difference increases. When the in situ stress difference is less than 7.9 MPa, the hydraulic fracture spreads through the layer. The critical seam pressure for deflection P₂ increases linearly with increasing interfacial cohesion. When the interfacial cohesion is greater than 2.7 MPa, the hydraulic fracture propagates through the layer. As the interface dip angle increases, the critical seam pressure for deflection P₂ initially decreases and then increases, and the hydraulic fracture expands when the interface dip angle is 25–55°. This means that the smaller the in situ stress difference is, the greater the interfacial cohesion is, and the easier it is for the hydraulic fracture to spread through the layer. When the interface dip angle is 25–55°, the hydraulic fracture is more likely to expand along the interface
(2)
The difference in the elastic moduli, the fluid injection rate, and the fracturing fluid’s viscosity directly affect the water pressure in the wellbore P₀. As the difference in the elastic moduli, the injection rate, and the fracturing fluid’s viscosity increase, the water pressure in the wellbore P₀ increases linearly. When the difference in the elastic moduli is greater than 4.9 GPa, the hydraulic fractures propagate through the layer; when the injection rate is greater than 3.484 m³/min, the hydraulic fractures propagate through the layer; and when the fracture fluid viscosity is greater than 1.5 mPa∙s, the hydraulic fractures propagate through the layer. The larger the difference in the interlayer elastic modulus, the faster the fluid injection rate, the greater the viscosity of the fracturing fluid, and the more likely it is that the hydraulic fractures will propagate through the layers
(3)
The difference in the fracture toughness mainly changes the relationship between the three pressures by affecting the critical seam pressure for penetration P₁, thereby changing the propagation mode of the hydraulic fractures. The critical seam pressure for propagation P₁ decreases linearly as the difference in the fracture toughness increases. When the fracture toughness difference is greater than 0.1 MPa∙m^1/2, the hydraulic fracture propagates through the layer at the interlayer interface, indicating that the larger the interlayer fracture toughness difference is, the more likely it is that the hydraulic fracture will penetrate the layer

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

The authors would like to give their sincere gratitude for the financial support from the National Natural Science Foundation of China (grant number 42102222).

Open Research

Data Availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Qin Y., Shen J., and Shen Y. L., Joint mining compatibility of superposed gas-bearing systems: a general geological problem for extraction of three natural gases and deep CBM in coal series, Journal of China Coal Society. (2016) 41, no. 1, 14–23.
Google Scholar
2 Liang B., Shi Y. S., Sun W. J., and Liu Q., Reservoir forming characteristics of “the three gases” in coal measure and the possibility of commingling in China, Journal of China Coal Society. (2016) 41, no. 1, 167–173.
CAS Google Scholar
3 Meng S. Z., Hou B., Zhang J., Tan P., and Xiong Z. Y., Experimental research on hydraulic fracture propagation through mixed layers of shale, tight sand and coal seam, Journal of China Coal Society. (2016) 41, no. 1, 221–227.
Google Scholar
4 Fung R. L., Vijayakumar S., and Cormack D. E., Calculation of vertical fracture containment in layered formations, SPE Formation Evaluation. (1987) 2, no. 4, 518–522, https://doi.org/10.2118/14707-PA, 2-s2.0-0023546051.
10.2118/14707-PA
Google Scholar
5 Gu H. R. and Siebrits E., Effect of formation modulus contrast on hydraulic fracture height containment, SPE Production & Operations. (2008) 23, no. 2, 170–176, https://doi.org/10.2118/103822-PA.
10.2118/103822-PA
CAS Web of Science® Google Scholar
6 Li Y., Deng J. G., Yu B. H., Liu W., and Chen J. G., Effects of reservoir rock/barrier and interfacial properties on hydraulic fracture height containment, Petroleum Drilling Techniques. (2014) 42, no. 6, 80–86.
Google Scholar
7 Li D. Q., Zhang S., and Zhang S. A., Experimental and numerical simulation study on fracturing through interlayer to coal seam, Journal of Natural Gas Science & Engineering. (2014) 21, 386–396, https://doi.org/10.1016/j.jngse.2014.08.022, 2-s2.0-84907463685.
10.1016/j.jngse.2014.08.022
Web of Science® Google Scholar
8 Thiercelin M., Jeffrey R. G., and Naceur K. B., Influence of fracture toughness on the geometry of hydraulic fractures, SPE Production Engineering. (1989) 4, no. 4, 435–442, https://doi.org/10.2118/16431-PA.
10.2118/16431-PA
Google Scholar
9 Wu R., Deng J. G., Yu B. H., Liu W., Li Y., and Li M., Numerical modeling of hydraulic fracture containment of tight gas reservoir in Shihezi Formation, Linxing Block, Journal of China Coal Society. (2017) 42, no. 9, 2393–2401.
Google Scholar
10 Li X. L., Chen S. J., Wang S., Zhao M., and Liu H., Study on in situ stress distribution law of the deep mine: taking Linyi mining area as an example, Advances in Materials Science and Engineering. (2021) 2021, 11, 5594181, https://doi.org/10.1155/2021/5594181.
10.1155/2021/5594181
Web of Science® Google Scholar
11 Tan P., Jin Y., Han K., Zheng X. J., Hou B., Gao J., Chen M., and Zhang Y. Y., Vertical propagation behavior of hydraulic fractures in coal measure strata based on true triaxial experiment, Journal of Petroleum Science and Engineering. (2017) 158, 398–407, https://doi.org/10.1016/j.petrol.2017.08.076, 2-s2.0-85032909046.
10.1016/j.petrol.2017.08.076
CAS Web of Science® Google Scholar
12 Warpinski N. R., Schmidt R. A., and Northrop D. A., In-situ stresses: the predominant influence on hydraulic fracture containment, Journal of Petroleum Technology. (1982) 34, no. 3, 653–664, https://doi.org/10.2118/8932-PA, 2-s2.0-0020102435.
10.2118/8932-PA
Web of Science® Google Scholar
13 Daneshy A. A., Hydraulic fracture propagation in layered formations, Society of Petroleum Engineers Journal. (1978) 18, no. 1, 33–41, https://doi.org/10.2118/6088-PA.
10.2118/6088-PA
Web of Science® Google Scholar
14 Teufel L. W. and Clark J. A., Hydraulic fracture propagation in layered rock: experimental studies of fracture containment, Society of Petroleum Engineers Journal. (1984) 24, no. 1, 19–32, https://doi.org/10.2118/9878-PA, 2-s2.0-0021375676.
10.2118/9878-PA
Web of Science® Google Scholar
15 Wang H., Liu H., Wu H. A., and Wang X. X., A 3D numerical model for studying the effect of interface shear failure on hydraulic fracture height containment, Journal of Petroleum Science and Engineering. (2015) 133, 280–284, https://doi.org/10.1016/j.petrol.2015.06.016, 2-s2.0-84934282172.
10.1016/j.petrol.2015.06.016
CAS Web of Science® Google Scholar
16 Gao J., Hou B., Tan P., Guo X. F., and Chang Z., Propagation mechanism of hydraulic fracture in sand coal interbedding, Journal of Petroleum Science and Engineering. (2017) 42, no. S2, 428–433.
Google Scholar
17 Li X. L., Chen S. J., Liu S. M., and Li Z. H., AE waveform characteristics of rock mass under uniaxial loading based on Hilbert-Huang transform, Journal of Central South University. (2021) 28, no. 6, 1843–1856, https://doi.org/10.1007/s11771-021-4734-6.
10.1007/s11771-021-4734-6
Web of Science® Google Scholar
18 Tan P., Jin Y., Hou B., Han K., Zhou Y. C., and Meng S. Z., Experimental investigation on fracture initiation and non-planar propagation of hydraulic fractures in coal seams, Petroleum Exploration and Development. (2017) 44, no. 3, 470–476, https://doi.org/10.1016/S1876-3804(17)30054-X, 2-s2.0-85020854355.
10.1016/S1876-3804(17)30054-X
Web of Science® Google Scholar
19 Warpinski N. R., Lorenz J. C., Branagan P. T., Myal F. R., and Gall B. L., Examination of a cored hydraulic fracture in a deep gas well, SPE Production & Facilities. (1993) 8, no. 3, 150–158, https://doi.org/10.2118/22876-PA.
10.2118/22876-PA
CAS Google Scholar
20 Renshaw C. E. and Pollard D. D., An experimentally verified criterion for propagation across unbounded frictional interfaces in brittle, linear elastic materials, International Journal of Rock Mechanics & Mining Sciences. (1995) 32, no. 3, 237–249, https://doi.org/10.1016/0148-9062(94)00037-4, 2-s2.0-0029513261.
10.1016/0148-9062(94)00037-4
Web of Science® Google Scholar
21 Sarmadivaleh M. and Rasouli V., Modified Reinshaw and Pollard criteria for a non-orthogonal cohesive natural interface intersected by an induced fracture, Rock Mechanics & Rock Engineering. (2014) 47, no. 6, 2107–2115, https://doi.org/10.1007/s00603-013-0509-1, 2-s2.0-84920708015.
10.1007/s00603-013-0509-1
Web of Science® Google Scholar
22 Llanos E. M., Jeffrey R. G., Hillis R., and Zhang X., Hydraulic fracture propagation through an orthogonal discontinuity: a laboratory, analytical and numerical study, Rock Mechanics and Rock Engineering. (2017) 50, no. 8, 2101–2118, https://doi.org/10.1007/s00603-017-1213-3, 2-s2.0-85017099504.
10.1007/s00603-017-1213-3
Web of Science® Google Scholar
23 Zhao H. F. and Chen M., Extending behavior of hydraulic fracture when reaching formation interface, Rock Mechanics & Rock Engineering. (2010) 74, no. 1-2, 26–30, https://doi.org/10.1016/j.petrol.2010.08.003, 2-s2.0-78650001637.
10.1016/j.petrol.2010.08.003
CAS Google Scholar
24 Zhang G. Q. and Chen M., Dynamic fracture propagation in hydraulic re-fracturing, Journal of Petroleum Science & Engineering. (2010) 70, no. 3-4, 266–272, https://doi.org/10.1016/j.petrol.2009.11.019, 2-s2.0-74149091220.
10.1016/j.petrol.2009.11.019
CAS Web of Science® Google Scholar
25 Zhang R. X., Zhang X. Y., Kang T. H., and He F. F., Dynamic fracture propagation model for oriented perforation steering fracturing in low permeability reservoir based on microelement method, Journal of Natural Gas Science and Engineering. (2020) 74, no. 21-22, article 103105.
10.1016/j.jngse.2019.103105
Web of Science® Google Scholar
26 Zhang R. X., Kang T. H., Kang J. T., Guo J. Q., Li L. G., and Zhao G. F., Influence of horizontal control holes on fracture height containment in low permeability layered coal measure gas reservoirs, Journal of Petroleum Science & Engineering. (2019) 179, 104–111, https://doi.org/10.1016/j.petrol.2019.04.066, 2-s2.0-85064520042.
10.1016/j.petrol.2019.04.066
CAS Web of Science® Google Scholar
27 Zhao Y., He P. F., Zhang Y. F., and Wang C. L., A new criterion for a toughness-dominated hydraulic fracture crossing a natural frictional interface, Rock Mechanics and Rock Engineering. (2019) 52, no. 8, 2617–2629, https://doi.org/10.1007/s00603-018-1683-y, 2-s2.0-85057627679.
10.1007/s00603-018-1683-y
Web of Science® Google Scholar
28 Jiang Y. L., Lian H. J., Nguyen V. P., and Liang W. G., Propagation behavior of hydraulic fracture across the coal-rock interface under different interfacial friction coefficients and a new prediction model, Journal of Natural Gas Science and Engineering. (2019) 68, article 102894, https://doi.org/10.1016/j.jngse.2019.05.007, 2-s2.0-85066290651.
10.1016/j.jngse.2019.05.007
Web of Science® Google Scholar
29 Zhou J., Chen M., Jin Y., and Zhang G. Q., Analysis of fracture propagation behavior and fracture geometry using a tri-axial fracturing system in naturally fractured reservoirs, International Journal of Rock Mechanics and Mining Sciences. (2008) 45, no. 7, 1143–1152, https://doi.org/10.1016/j.ijrmms.2008.01.001, 2-s2.0-43449131525.
10.1016/j.ijrmms.2008.01.001
Web of Science® Google Scholar

All articles

Criterion for Hydraulic Fracture Propagation Behavior at the Interface of a Coal Measure Composite Reservoir

Abstract

1. Introduction

2. Establishing the Judgment Criterion

2.1. Physical Model and Basic Assumptions

2.2. Model of Water Pressure Distribution in Fractures