In the GNSS-challenged/denied environments, compared with other aided navigation systems, synthetic aperture radar- (SAR-) aided navigation systems can achieve all-weather, all-day, and global positioning. This paper is aimed at designing a reliable navigation system for the supersonic vehicle in the whole flight phase. Considering the SAR is of great significance for the reliable and precise navigation of the supersonic vehicle, we introduce it to the terminal phase to cope with the interference of the global navigation satellite system (GNSS). At the same time, to accelerate the speed of SAR positioning, a positioning method based on the area feature and stack sequential decoding algorithm (SSDA) is designed. Then, applying the SAR positioning under the framework of the Kalman filter (KF), we propose a tightly coupled strapdown inertial navigation system (SINS)/SAR/GNSS integration algorithm, which can achieve positioning without a complicated fusion method between the front phase and terminal phase. The flight experiment results show that the proposed method can correct the average position error to 1.7 m within 1 cycle.

1. Introduction

At present, medium-range supersonic vehicle rely more on global navigation satellite system (GNSS) and inertial navigation system (INS) [1]. However, the significant problem with using GNSS technology is that the signals are very weak [2]. Taking GNSS as an example, the signals are transmitted at two L-band frequencies: L1 = 1 : 575 42 GHz and L2 = 1 : 2276 GHz from a set of orbiting satellites located at an altitude of ~20,200 Km [3]. Since the global positioning system (GPS) signals are transmitted at only ~25 W, the received signal at a typical GPS receiver is on the order of -155 to 160 dBW, which makes GNSS signals extremely susceptible to interference [4–6]. Therefore, in this case, how to design the navigation system for medium-range supersonic vehicle is vital.

To tackle the positioning problem in the GPS-denied environment, Poulose et al. proposed a novel fusion algorithm based on the traditional inertial measurement unit (IMU) and magnetometer, which firstly completes the sensor fusion algorithm for pitch and roll estimation and then completes the sensor fusion algorithm for heading estimation. Furthermore, based on an accuracy generalization benchmark for indoor localization [7], experimental results show that the proposed position-estimation algorithm achieves high position accuracy that significantly outperforms that of conventional estimation methods [8]. Gao et al. proposed a SINS/SAR loosely integrated method based on the Lupin adaptive filter, which establishes the SINS state equation as a linear model and uses SAR latitude, longitude, and height as the observation to establish the observation equation. Compared with the traditional adaptive Kalman filter, it can suppress the state divergence caused by the state noise and the observation noise [9]. Xiao et al. designed a switching mechanism between SINS/GPS and SINS/SAR to reduce the impact of matching errors on the combined system during the SAR image matching process [10]. In addition to using the latitude and longitude provided by SAR as the observation data, Xu et al. proposed an SINS/SAR loosely integrated method, which makes full use of the heading angle provided by the SAR scene matching and the east and north velocity as observations. It improves the integrated accuracy of SINS/SAR navigation information [11]. Jiang et al. proposed a SINS/SAR loosely integrated method, which uses the interferogram obtained by interferometric synthetic aperture radar (InSAR) to obtain three-dimensional positioning latitude and longitude. Compared with SAR, InSAR can obtain higher precision elevation and provide high-precision elevation correction for SINS [12]. Yandong et al. based on the SINS linear error model and SAR measurement of latitude and longitude designed an adaptive Kalman filter method to complete the SINS/SAR combination [13]. Similarly, Gao et al. designed an error suppression adaptive Kalman filter to complete the SINS/SAR combination [14]. In the latter, they proposed a SINS/GPS/SAR tightly integrated method, which uses SAR azimuth, elevation, GPS pseudorange, and pseudorange rate to establish a measurement model. As the author mentioned, the advantage of this method is that the GPS and SAR can calibrate each other under extreme conditions. However, when the GPS interferes, it is difficult to ensure the high accuracy of carrier positioning only using SAR azimuth and elevation angles [15]. Lu et al. designed an SINS/SAR tightly integrated method, which focused on the impact of the single-sided and double-sided distribution of control points on the INS/SAR combined accuracy [16].

(i)
A SINS/SAR/GNSS tightly integrated navigation system architecture is proposed based on KF, which is equipped with a partial feedback update algorithm to tackle the high requirements for the convergence speed and equipped with an approximate extrapolation to solve nonequidistance and delayed measurement of SAR
(ii)
Aiming at the problem of SAR delayed measurement, a SINS/SAR/GNSS measurement update algorithm is proposed, which can be performed in real-time in FPGA

The rest of this paper is organized as follows: in Section 2, we introduce the tightly coupled SINS/SAR/GNSS model based on the Kalman filter, which equipped with a partial feedback update algorithm to tackle the high requirements for the convergence speed and equipped with an approximate extrapolation to solve nonequidistance and delayed measurement of SAR. In Section 3, we conduct a flight experiment to verify the effectiveness of the proposed algorithm, and the position error is discussed. In Section 4, we discuss the experiment results, the proposed method, and the future work. Finally, conclusions are given in Section 5.

2. Methods

In short, the mainstream of the SINS/SAR can be divided into three parts according to the fusion algorithm. The first is taking the system model as nonlinear and then designing SINS/SAR integrated methods based on PF and its improved methods. It can be predicted that these methods are time-consuming. The second is taking the system model as linear and then designing SINS/SAR loosely integrated methods based on KF and its improved method, but only using the SAR observation longitude, latitude, height, and heading angle as measurements, which was greatly affected by the SAR matching accuracy. The third is taking the system model as linear and then designing SINS/SAR integrated methods based on KF and its improved methods, but considering the nonequidistance and delayed measurement of the actual SAR sensor, these methods did not give corresponding solutions.

Different from the existing algorithm, this paper proposes a tightly coupled SINS/SAR/GNSS integration algorithm for the navigation of the supersonic vehicle in the whole flight phase, as described in Section 2.1. The SAR positioning algorithm is described in Section 2.2. The system model and fusion algorithm are described in Section 2.3. Aiming at the problem of SAR delayed measurement, a SINS/SAR/GNSS measurement update algorithm is proposed, as described in Section 2.4.

2.1. System Architecture

As shown in Figure 1, the typical flight phase of a medium-range supersonic vehicle consists of three stages [17]. In the boost phase and the midcourse phase, the GNSS signal is valid, and the tightly coupled SINS/GNSS is used as the navigation method. When the supersonic vehicle enters into the terminal phase, the GNSS would be interfered, so the SAR-aided navigation system is introduced. Considering the relative position of the vehicles and jamming radar in the terminal phase, the satellite signals may not be completely jammed [18]; thus, a tightly coupled SINS/SAR/GNSS algorithm is proposed in the terminal phase.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The typical flight phase of a supersonic vehicle.

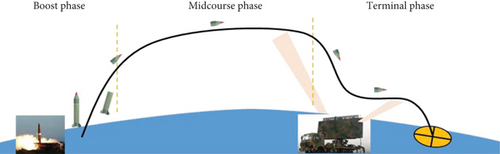
In the boost phase and midcourse phase, since the GNSS is not interfered, the tightly SINS/GNSS integrated navigation system is used for navigation. Meanwhile, the high power consumption of SAR only allows limited use, so SAR will not be used in the two-phase. Then, in the terminal phase, when the GNSS is interfered, the tightly SINS/SAR/GNSS integrated navigation system is performed. And if the GNSS is interfered completely, the system degenerates to SINS/SAR.

As illustrated in Figure 2, the proposed system can be divided into four parts: SINS mechanization, system model, integration Kalman filter, and measurement processing. Considering the real-time performance of the vehicle-borne solution, we adopt the quaternion attitude update algorithm described in [19, 20] and the velocity and position update algorithm proposed in [21–23].

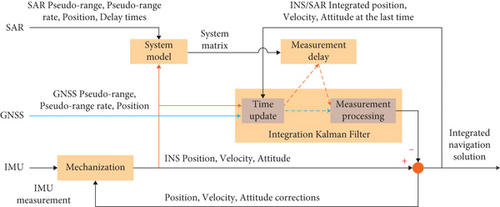
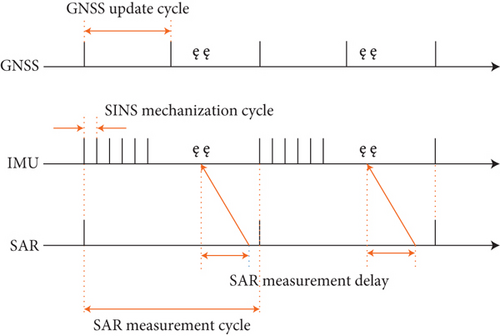
In general, the update period of SAR measurement is greater than that of GNSS and greater than that of IMU. When the single-sample algorithm is used, the update period of SINS is the same as that of IMU. Considering that the SAR measurement sequence will inevitably be nonequidistance and delayed because of the high time consuming when processing the SAR echo, which can be seen in Figure 3, an approximate extrapolation algorithm is proposed under the framework of KF. And the measurement processing is introduced in Section 2.4.

2.2. SAR Positioning by Template Match

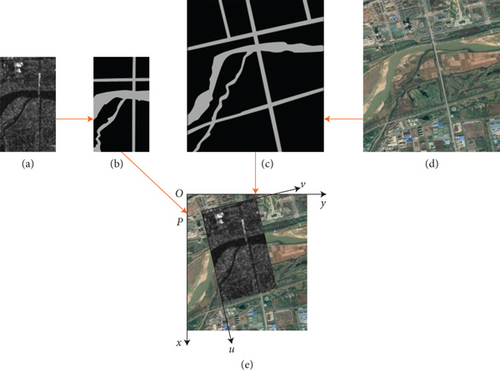
Although the measurement delay of SAR is inevitable, the shorter the matching time, the higher the accuracy of the integrated navigation system. At present, image matching is commonly conducted by feature extracting and matching, such as the ORB, SAR-SIFT, and LSD. However, all of these methods are extremely time-consuming. To tackle this, we proposed an area feature extraction and match algorithm based on the area feature and SSDA. Since SAR imaging is largely determined by the reflectivity of the echo from the ground, we utilize the pixel value to extract the scatter feature and then utilize the region growing method to generate the area feature, which is described in Figures 4(a) and 4(b). Considering that before the launch of the vehicle, the maximum position errors could be inferred based on the sensor error. Thus, the reference map is made by 1.5 times the range direction and 2.5 times the azimuth direction, respectively, of the SAR, which is described in Figure 4(c). After the area features of the real-time SAR image are extracted, we perform the SSDA (sequential similarity detection algorithm) to match it (P-uv) with the reference map (O-xy), which is described in Figure 4(e).

We conduct a comparative experiment on the mainstream feature algorithm of LSD [24], SAR-SIFT [25], ORB [26], and our method with the computer of Intel Core i5-4690K. The experiment results are shown in Table 1. Compared with other methods, our method requires fewer calculations and can achieve higher accuracy.

Table 1. The comparative experiment results of feature algorithms.

Feature algorithm	Matching algorithm	SAR image size	Average position error (pixel)	Average time of the whole process (s)
ORB	FLANN [27]	650∗1800	1.7	0.11
SAR-SIFT	FLANN [27]	650∗1800	1.6	0.14
LSD	LSD	650∗1800	2.4	0.19
Ours	SSDA	650∗1800	1.9	0.09

2.3. System Model

With the navigation frame defined in the east-north-up (E-N-U) geography frame, the SINS/SAR integrated system model can be written as:

(1)

where X (t) is the error-state vector of SINS which has 17 dimensions, F (t) is the state transition matrix which is 17∗17 dimensions, r is the vector of process noise which has 17 dimensions, q is the vector of measurement noise which has 17 dimensions, Z (t) is the vector of measurement which has 6 dimensions, and H (t) is the observation matrix constructed based on pseudorange and pseudorange rate which is 6∗17 dimensions.

As expressed in (2), the state vector X has 17 dimensions, which is composed by 3-dim attitude errors, 3-dim velocity errors, 3-dim position errors, 3-dim gyroscope drifts, 3-dim accelerometer drifts, 1-dim pseudorange error, and 1-dim pseudorange rate error:

(2)

Based on the state vector, the state transition matrix F can be written as:

(3)

For the convenience of algorithmic calculation, the pseudorange and pseudorange rate in measurement equation are calculated in the ECEF (Earth-Centered Earth-Fixed) frame. We firstly transform them to the ECEF frame:

(4)

where [L_I, λ_I, h_I] is the position of the SINS mechanization and [x_I, y_I, z_I] is the position of SINS in the ECEF frame. Similarly, [L_S, λ_S, h_S] and [x_S, y_S, z_S] denote the position of measurement sensors (control points of SAR of satellite).

Then, a first-order approximation at the true value of position [x, y, z] is carried out to calculate the pseudorange ρ_I and pseudorange rate

, and we can get the following equations after dropping higher-order error terms:

(5)

Thus, according to the measurement pseudorange and pseudorange rate, the measurement model in Equation (1) can be calculated as:

(6)

where the Z_r(t) is the pseudorange measurement model and the Z_v(t) is the pseudorange rate measurement model. And the

is the transformation of velocity from the navigation frame system to the ECEF frame:

(7)

In Equation (6), the observation matrix is given as:

(8)

where the P is the retraction of:

(9)

The Q is the retraction of:

(10)

The

is the retraction of:

(11)

The

is the retraction of the transformation between [δL, δλ, δh] and [δx, δy, δz]:

(12)

2.4. Kalman Filter with Feedback and Measurement Delay

The time update step of Kalman filter with feedback can be written as:

(13)

where for the convenience of algorithmic calculation, the discrete form of error-state is expressed as: F_k = I_17∗17 + F(t)T. The P_k is the state covariance matrix at k frame. The Q_k is the process noise covariance matrix which is usually a constant value. Further, the measurement update step of Kalman filter with feedback can be written as:

(14)

where the K_k is the gain matrix of the Kalman filter. When multiple pseudorange and pseudorange rate data are received, whether they are from GNSS or SAR, performing multiple iterations according to (12), followed with Kalman filter, the mechanization results of the velocity

, attitude matrix

, and position [λ_k, L_k, h_k] at k frame are corrected by:

(15)

After the process of correction, we set the attitude error, velocity error, and the pseudorange error to zero as the feedback. Considering the measurement delay of SAR, we utilize the approximate extrapolation algorithm to calculate the state at k frame.

Firstly, the state

that is at the actual measurement frame of SAR is calculated by:

(16)

where the delay period N_dl can be calculated based on the delay time returned by the SAR measurement. The T_nav is the mechanization period of navigation. The

is calculated and saved according to Equation (13).

Then, the measurement update at current time can be calculated as:

(17)

Note that when the SAR measurement comes, the chi-square test is used to judge the validity of the measurement. Firstly, we calculate the innovation variance matrix by based on the saved historical data. Then, we calculate the innovation matrix by I = Z_k − H_kX_k/k−1. The measurement is valid only when the data in the vector I is less than 3 times the diagonal data in the matrix PI.

3. Experiment and Result Discussion

To testify the effectiveness of the proposed algorithm, a flight experiment is carried out. The velocity of the vehicle in the whole flight phase is within 900-1100 m/s, and the flight time is about 160 s in the terminal phase of 120-200 Km. The experiment setup in this experiment is described in Section 3.1. The parameters of the algorithm are given in Section 3.2. The experiment results are described in Section 3.3.

3.1. Experiment Setup

The parameters of SINS, SAR, and GNSS receiver are given in Tables 2, 3, and 4, respectively. Due to the limited experimental conditions, we do not conduct GNSS jamming tests. But after analyzing the experimental data, we divided the flight phase based on the flight mileage. In the terminal phase, we select satellite data from 0 to 1 randomly as the GNSS data for the tightly coupled integrated navigation system, which can be regarded as the case of GNSS interference.

Table 2. Parameters of SINS.

Parameters	Unit	Value
Accelerometer bias	μg	100 (1σ)
Accelerometer scale factor	ppm	100 (1σ)
Accelerometer installation	arcsec	20 (1σ)
Accelerometer white noise		30 (1σ)
Gyroscope bias	^°/h	0.1 (1σ)
Gyroscope scale factor	ppm	100 (1σ)
Gyroscope installation	arcsec	20 (1σ)
Gyroscope white noise		0.03 (1σ)
Update cycle	ms	0.002
Mechanization cycle	ms	0.004

Table 3. Parameters of SAR.

Parameters	Unit	Value
Update cycle	s	2
Pseudorange error	m	2 (1σ)
Pseudorange rate error	m/s	0.1 (1σ)

Table 4. Parameters of GNSS receiver.

Parameters	Unit	Value
Update cycle	ms	100
Clock correction cycle	ms	100
Pseudorange error	m	6.5
Pseudorange rate error	m/s	0.9

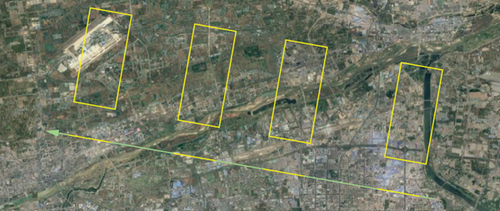
Due to the high power consumption of SAR, we perform four imaging in the terminal phase, which provides four measurement information and is described in Figure 5.

3.2. Experiment Parameters

The setting of the initial value of the state covariance matrix P, the value of the process noise covariance matrix Q, and the value of the measurement noise covariance matrix R play an important role in the convergence and convergence speed of the filter.

As for the 17-dimensional diagonal matrix P, the covariance of the velocity and position is set according to the initial error. The covariance of the attitude is set according to the statistical variance of the alignment result. The covariance of gyro and the accumulator bias are set according to their repeatability. The covariance of pseudorange error and the pseudorange rate error is set according to the clock error parameters and the clock rate error parameters of the measurement. Based on the rules above, in the flight experiment the initial value of the P is set to:

(18)

Furthermore, both Q and R are set to constant values. The component noise covariance corresponding to the attitude and velocity in the Q is set to the noise of the gyro and accelerometer separately, and the rest are small values. The component noise covariance corresponding to the pseudorange of the R matrix is set to 1, and the component corresponding to the pseudorange rate is set to 0.1.

3.3. Results

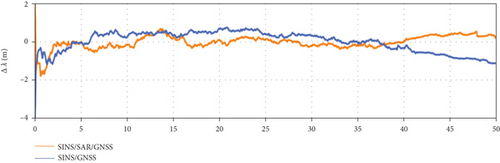
The experiment results of longitude error, latitude error, and altitude error are given in Figures 6, 7, and 8, respectively. At 42 s, the GNSS signals began to be jammed. Thus, in the time range of [0, 41.9] s and [42.0, 50.0] s, we perform the tightly coupled SINS/GNSS and tightly coupled SINS/SAR/GNSS integration algorithm, respectively.

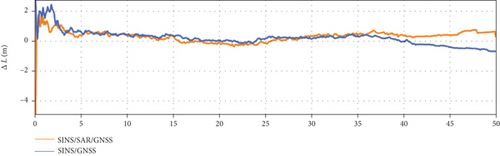
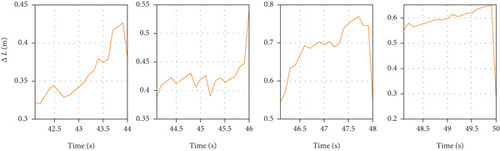
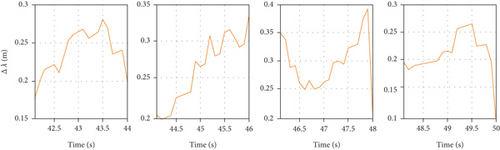
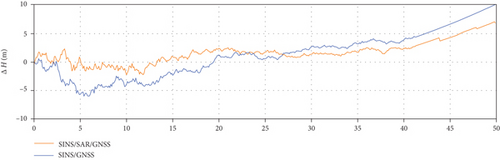
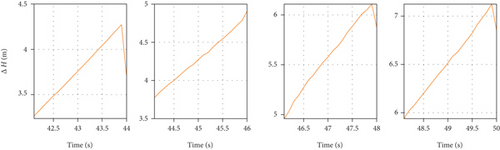
As shown above, when the GNSS signal is interfered, the SINS/GNSS will cause an average position error of 2.8 m within 2 seconds, which is intolerable for supersonic vehicles in the terminal phase. At the moment of 43.9 s, 45.9 s, 47.9 s, and 49.9 s, the SINS/SAR/GNSS algorithm is utilized, and the average position error could be corrected to 1.7 m within 1 cycle. With the relatively few measurement times and the long measurement cycle, the measurement of SAR can suppress the divergence of SINS/GNSS positioning, and the proposed algorithm can achieve high positioning accuracy, which meets the requirements of supersonic vehicles.

4. Discussion

4.1. Discussion of the Experiment Results

The longitude and latitude error is shown in Figures 7 and 8, separately. Due to the different initial values, we only show the details of the SINS/SAR/GNSS error without drawing the details of the SINS/GNSS error in the subfigure. However, it can be clearly seen from the comparison curve in the range of [42.0, 50.0] s that the SAR measurement plays an important role in correcting the positioning of the navigation system when the GNSS is interfered. At the moment of 43.9 s, 45.9 s, 47.9 s, and 49.9 s, when the SAR measurement comes, the SINS/SAR/GNSS algorithm is utilized, and the average position error could be corrected to 1.7 m within 1 cycle.

As for the tightly SINS/SAR/GNSS integrated navigation system, there are few descriptions in the current published literature. At the same time, due to the uncertain delay of SAR measurement, few literatures have been found to propose a system solution. Therefore, this paper only compares the proposed method with the classical tightly SINS/GNSS integrated method.

4.2. Discussion of the Proposed System

The purpose of the proposed system is to design a SINS/SAR/GNSS integrated navigation system for the medium-range supersonic vehicle in the whole flight phase to tackle the interference of GNSS. In the early phase of the flight process, when the GNSS signal is not interfered with, the tightly SINS/GNSS integrated navigation system is used for navigation. Considering that the vehicle flies in its own territory in the early phase, the GNSS will not be interfered. Furthermore, the high power consumption of SAR only allows limited use, so SAR will not be used in this phase. In the terminal phase when the GNSS signal has interfered, the tightly SINS/SAR/GNSS integrated navigation system is performed.

To cope with the SAR measurement delay, we design an approximate extrapolation algorithm under the framework of Kalman filter. This is an engineering solution, and the convergence of the method has not been proved theoretically. However, qualitative analysis can show that the approximate extrapolation algorithm has limited influence on the Kalman filter. This method will indeed bring about approximate errors which depend on the difference between the change of actual navigation information and the simulated linear change. In fact, considering that the attitude and velocity changes of the supersonic vehicle after the boost phase are small, the navigation change of the navigation state is small. Thus, the navigation state can be considered as linear, which is the basis of the application of this method. Moreover, it should be noted that this method can only be performed at discrete moments; thus, the shorter the SINS mechanization period, the higher the accuracy of the integrated navigation.

4.3. Discussion of the Future Work

According to Equation (11), when the SAR measurement fails and the GNSS is completely interfered with, the tightly SINS/SAR/GNSS integrated navigation system degenerates into a SINS navigation system. Actually, for general supersonic vehicles, after the boost phase, the velocity of the vehicle is within 900-1100 m/s, and the flight time is still about 160 s in the terminal phase of 120-200 Km. This allows sufficient time for SAR measurement, and it will generally return 4-25 effective measurements in the terminal phase, which is sufficient for the integrated system. Thus, the most important thing is the matching accuracy, which determines the positioning accuracy of the vehicle. At the same time, according to our experiments, different SAR matching rules should be designed in different environments to improve the matching accuracy, such as towns, rivers, mountains, plateaus, and other places.

Therefore, in the future, we will study SAR matching and positioning in various complex environments and, at the same time, design automatic selection rules for different matching areas and increase the matching success rate to 99%. Furthermore, we will carry out research on the matching of SAR images and satellite images based on neural networks and, at the same time, explore its deployment on the vehicle processor.

5. Conclusions

Since GNSS signals are easily interfered, this paper proposes a tightly coupled SINS/SAR/GNSS integration algorithm, which can complete the navigation of supersonic vehicles in the whole flight phase even if the GNSS signal is interfered completely. In the boost and midcourse phase, we use the tightly coupled SINS/GNSS integration as the navigation method. In the terminal phase, we introduce the SAR-aided navigation system and proposed a tightly coupled SINS/SAR/GNSS integration algorithm to cope with the interference of the GNSS. In order to accelerate the speed of SAR positioning and improve the accuracy of position at the same time, we design a positioning method based on the area feature and SSDA. The comparison experiment shows that our method possesses the highest accuracy and speed. Finally, the experiment results show that the proposed tightly coupled SINS/SAR/GNSS integration algorithm can correct the average position error to 1.7 m within 1 cycle. In short, the proposed SINS/SAR/GNSS algorithm can complete the navigation in the whole phase and suppress the divergence in terminal phase compared with conventional SINS/GNSS.

Conflicts of Interest

The authors declare no conflict of interest.

Acknowledgments

This work was supported by the National Defense Fundamental Scientific Research of the Central Military Commission (CMC) under grant 2019-JCJQ-2D-078.

Open Research

Data Availability

The data supporting the findings of this study are available within the paper. The raw data of SINS, SAR, image, and GNSS can be obtained through email with the permission of the authors.

References

1 Hyslop G., Gerth D., and Kraemer J., GPS/INS integration on the standoff land attack missile (SLAM), IEEE Aerospace and Electronic Systems Magazine. (1990) 5, no. 7, 29–34, https://doi.org/10.1109/62.134218, 2-s2.0-0025460923.
10.1109/62.134218
Google Scholar
2 Van den Bergh B. and Pollin S., Keeping UAVs under control during GPS jamming, IEEE Systems Journal. (2019) 13, no. 2, 2010–2021, https://doi.org/10.1109/JSYST.2018.2882769, 2-s2.0-85067050922.
10.1109/JSYST.2018.2882769
Web of Science® Google Scholar
3 Sun W. and Amin M. G., A self-coherence anti-jamming GPS receiver, IEEE Transactions on Signal Processing. (2005) 53, no. 10, 3910–3915, https://doi.org/10.1109/TSP.2005.855428, 2-s2.0-27844473182.
10.1109/TSP.2005.855428
Web of Science® Google Scholar
4 Keller S. D., Weiss S. J., Maloney J. A., Kwon D. -H., Janaswamy R., and Morley J., Design considerations for a wearable anti-jam GPS antenna, 2018 2nd URSI Atlantic Radio Science Meeting (AT-RASC), 2018, Gran Canaria, Spain, 1–4, https://doi.org/10.23919/URSI-AT-RASC.2018.8471663, 2-s2.0-85055858834.
10.23919/URSI-AT-RASC.2018.8471663
Google Scholar
5 Rezazadeh N. and Shafai L., A compact antenna for GPS anti-jamming in airborne applications, IEEE Access. (2019) 7, 154253–154259, https://doi.org/10.1109/ACCESS.2019.2948823.
10.1109/ACCESS.2019.2948823
Web of Science® Google Scholar
6 Braasch M. S. and van Dierendonck A. J., GPS receiver architectures and measurements, Proceedings of the IEEE. (1999) 87, no. 1, 48–64, https://doi.org/10.1109/5.736341, 2-s2.0-0032715744.
10.1109/5.736341
Web of Science® Google Scholar
7 Poulose A., Eyobu O. S., and Han D. S., An indoor position-estimation algorithm using smartphone IMU sensor data, IEEE Access. (2019) 7, 11165–11177, https://doi.org/10.1109/ACCESS.2019.2891942, 2-s2.0-85061152960.
10.1109/ACCESS.2019.2891942
Google Scholar
8 Eyobu O. S., Poulose A., and Han D. S., An accuracy generalization benchmark for wireless indoor localization based on IMU sensor data, 2018 IEEE 8th International Conference on Consumer Electronics-Berlin (ICCE-Berlin), 2018, Berlin, Germany, 1–3, https://doi.org/10.1109/ICCE-Berlin.2018.8576213, 2-s2.0-85060306798.
10.1109/ICCE-Berlin.2018.8576213
Google Scholar
9 Gao S., Zhong Y., and Wei L., Robust adaptive filtering method for SINS/SAR integrated navigation system, Aerospace Science and Technology. (2011) 15, no. 6, 425–430, https://doi.org/10.1016/j.ast.2010.08.007, 2-s2.0-80052260166.
10.1016/j.ast.2010.08.007
Web of Science® Google Scholar
10 Xiao M., Li W., Hu T., Liang P., Shen L., and Yanlong B., SAR aided navigation based on FAST feature, 2013 IEEE 4th International Conference on Software Engineering and Service Science, 2013, Beijing, China, 861–864, https://doi.org/10.1109/ICSESS.2013.6615441, 2-s2.0-84890057695.
10.1109/ICSESS.2013.6615441
Google Scholar
11 Xu G., Wang Y., and Gong Y., The novel method with sequence SAR imagery for INS/SAR integrated navigation system, 2019 6th Asia Pacific Conference on Synthetic Aperture Radar (APSAR), 2019, Xiamen, China, 1–4, https://doi.org/10.1109/APSAR46974.2019.9048511.
10.1109/APSAR46974.2019.9048511
Google Scholar
12 Jiang S., Wang B., Xiang M., Fu X., and Sun X., Method for InSAR/INS navigation system based on interferogram matching, IET Radar, Sonar and Navigation. (2018) 12, no. 9, 938–944, https://doi.org/10.1049/iet-rsn.2018.5118, 2-s2.0-85052297184.
10.1049/iet-rsn.2018.5118
Web of Science® Google Scholar
13 Yandong S., Chunmeng S., and Shesheng G., Adaptive filtering for INS/SAR integrated navigation system, 2009 2nd Asian-Pacific Conference on Synthetic Aperture Radar, 2009, Xi’an, China, 884–887, https://doi.org/10.1109/APSAR.2009.5374197, 2-s2.0-77949609565.
10.1109/APSAR.2009.5374197
Google Scholar
14 Gao S., Jiao Y., Gu Y., and Zhong Y., Error-resistant adaptive filtering for INS/SAR integrated navigation system, 2009 2nd international congress on image and signal processing, 2009, Tianjin, China, 1–4, https://doi.org/10.1109/CISP.2009.5301104, 2-s2.0-73849101759.
10.1109/CISP.2009.5301104
Google Scholar
15 Gao S., Zhong Y., Zhang X., and Shirinzadeh B., Multi-sensor optimal data fusion for INS/GPS/SAR integrated navigation system, Aerospace Science and Technology. (2009) 13, no. 4-5, 232–237, https://doi.org/10.1016/j.ast.2009.04.006, 2-s2.0-67649311245.
10.1016/j.ast.2009.04.006
Web of Science® Google Scholar
16 Lu J., Ye L., and Han S., A deep fusion method based on INS/SAR integrated navigation and SAR bias estimation, IEEE Sensors Journal. (2020) 20, no. 17, 10057–10070, https://doi.org/10.1109/JSEN.2020.2991870.
10.1109/JSEN.2020.2991870
Google Scholar
17 Moon K., Kwon H., Ryoo C., and Sim H., Trajectory estimation for a ballistic missile in ballistic phase using IR images, 2018 9th International Conference on Mechanical and Aerospace Engineering (ICMAE), 2018, Budapest, Hungary, 173–177, https://doi.org/10.1109/ICMAE.2018.8467635, 2-s2.0-85055493551.
10.1109/ICMAE.2018.8467635
Google Scholar
18 Wang Y. and Wang S., Research on GPS anti-jam technologies of GPS/INS integrated guidance for ground-to-ground missile, Tactical Missile Technology. (2004) 23, no. 3, 47–50.
Google Scholar
19 Qin Y. Y., Inertial Navigation, 2006, Science Press, Beijing, China.
Google Scholar
20 Cui X., Mei C., Qin Y., Yan G., and Fu Q., In-motion alignment for lowcost SINS/GPS under random misalignment angles, Journal of Navigation. (2017) 70, no. 6, 1224–1240, https://doi.org/10.1017/S037346331700039X, 2-s2.0-85021125335.
10.1017/S037346331700039X
Web of Science® Google Scholar
21 Wu Y. and Pan X., Velocity/position integration formula part I: application to in-flight coarse alignment, IEEE Transactions on Aerospace and Electronic Systems. (2013) 49, no. 2, 1006–1023, https://doi.org/10.1109/TAES.2013.6494395, 2-s2.0-84876130385.
10.1109/TAES.2013.6494395
Web of Science® Google Scholar
22 Wu Y. and Pan X., Velocity/position integration formula part II: application to strapdown inertial navigation computation, IEEE Transactions on Aerospace and Electronic Systems. (2013) 49, no. 2, 1024–1034, https://doi.org/10.1109/TAES.2013.6494396, 2-s2.0-84876129163.
10.1109/TAES.2013.6494396
Web of Science® Google Scholar
23 Wu Y., iNavFIter: next-generation inertial navigation computation based on functional iteration, IEEE Transactions on Aerospace and Electronic Systems. (2020) 56, no. 3, 2061–2082, https://doi.org/10.1109/TAES.2019.2942471.
10.1109/TAES.2019.2942471
Google Scholar
24 Grompone von Gioi R., Jakubowicz J., Morel J., and Randall G., LSD: a fast line segment detector with a false detection control, IEEE Transactions on Pattern Analysis and Machine Intelligence. (2010) 32, no. 4, 722–732, https://doi.org/10.1109/TPAMI.2008.300, 2-s2.0-77649270310, 20224126.
10.1109/TPAMI.2008.300
PubMed Web of Science® Google Scholar
25 Dellinger F., Delon J., Gousseau Y., Michel J., and Tupin F., SAR-SIFT: a SIFT-like algorithm for SAR images, IEEE Transactions on Geoscience and Remote Sensing. (2015) 53, no. 1, 453–466, https://doi.org/10.1109/TGRS.2014.2323552, 2-s2.0-84906500760.
10.1109/TGRS.2014.2323552
Web of Science® Google Scholar
26 Mur-Artal R., Montiel J. M. M., and Tardós J. D., ORB-SLAM: a versatile and accurate monocular SLAM system, IEEE Transactions on Robotics. (2015) 31, no. 5, 1147–1163, https://doi.org/10.1109/TRO.2015.2463671, 2-s2.0-84988339174.
10.1109/TRO.2015.2463671
Web of Science® Google Scholar
27 Muja M. and Lowe D. G., Fast approximate nearest neighbors with automatic algorithm configuration, International Conference on Computer Vision Theory and Applications (VISAPP'09), 2009, Lisboa, Portugal.
Google Scholar

Citing Literature

All articles

Reliable SINS/SAR/GNSS Integrated Navigation System for the Supersonic Vehicle

Abstract

1. Introduction