A Privacy-Preserving Biometric Recognition System with Visual Cryptography
Abstract
The popularity of more powerful and smarter digital devices has improved the quality of life and poses new challenges to the privacy protection of personal information. In this paper, we propose a biometric recognition system with visual cryptography, which preserves the privacy of biometric features by storing biometric features in separate databases. Visual cryptography combines perfect ciphers and secret sharing in cryptography with images, thus eliminating the complex operations in existing privacy-preserving schemes based on cryptography or watermarking. Since shares do not reveal any feature about biometric information, we can efficiently transmit sensitive information among sensors and smart devices in plain. To abate the influence of noise in visual cryptography, we leverage the generalization ability of transfer learning to train a visual cryptography-based recognition network. Experimental results show that our proposed method keeps the high accuracy of the feature recognition system when providing security.
1. Introduction
With the help of smartphones equipped with rich sensors and high-bandwidth 5G networks and beyond [1], now we can share information at any time and any place [2]. Face images have been the most widely used perceptual information transmitted on the Internet [3, 4]. With people paying more attention to the privacy of personal information, it has been a major concern for ensuring privacy in these crucial services provided on public networks [5]. Traditional cryptography methods based on a password or ID card have shortcomings including easy to forge, easy to forget, and computation complexity, which prevents them from widespread applications [6].
Visual cryptography (VC) [7, 8] (also known as k-out-of-n VC) is a secret-sharing method aiming at images. It splits a secret image into n shares. The threshold characteristic makes it impossible to restore the secret image unless stacking k, (k < n) or more shares together. The human visual system (HVS) can recover secret information by simply printing shares on transparencies and stacking them, without any digital device. VC provides a simple and effective method for the distributed storage of feature data, where there is no need to maintain keys in encryption. These features of VC are particularly suitable for scenarios in a limited-computing and untrusted networking environment. VC eliminates the complex computation required by traditional watermarking or cryptography. However, recovery images from a VC scheme (VCS) have poor quality and expanding size [9].
- (1)
We construct a meaning VCS, where HVS can print shares on transparencies and recover secret images
- (2)
We propose a secure storage method for biometric features by the secret sharing of images
- (3)
We keep the recognition performance of images recovered from VC with the strong generalization of transfer learning
The structure of the rest of the paper is as follows. Section 2 provides helpful background on feature recognition and improved VCSs. Section 3 describes our privacy-preserving recognition model. Section 4 evaluates the performance of our approach on two classic datasets. Finally, we summarize our contributions in Section 5.
2. Related Work
2.1. Feature Recognition
The past decades have witnessed the explosion of advances in feature recognition [12]. By collecting massive samples with big data technologies, deep neural networks (DNN) [13, 14] can use an artificial neural network to directly give inference results.
Metric learning [15] is an emerging feature recognition method that can verify whether two embedding samples belong to the same identity or not. Authors [16] use a DNN to transform a face image into a vector and then calculate and compare the Euclidean distance between two vectors. Directly using Euclidean distance is equivalent to considering the only intraclass distance. However, sometimes the intraclass distance may be larger than the interclass distance. To address the shortcomings of Euclidean distance, FaceNet [17] used a triplet-based loss function to embed face images. Minimizing the triplet loss function is both minimizing the distance of similar samples and maximizing the distance of nonsimilar samples at the same time.
To train a model enhancing the discrimination of learned features, Wen et al. [18] join supervision of center loss and softmax cross-entropy loss as the loss function of neural networks, thus significantly accelerating the convergence of training models.
2.2. Visual Cryptography
VC is a (k, n) threshold scheme for images. The simple decryption makes VC surpass other cryptographic schemes based on cryptography or watermark [19]. VC expands the application scenarios of secret sharing. It has been an emerging research field in the field of image cryptography since born in 1995 [9, 20, 21]. The conditional VCS encrypts a secret image into shares pixel-by-pixel, hence resulting in pixel expansion. It can eliminate pixel expansion by mapping a block in the secret image into an equal-sized block at the corresponding position of shares. Through vertical arrangements and elaborately processing the correspondence between the secret block and share blocks, we can keep the size and obtain a higher contrast than previous schemes. Another scheme keeping the size of recovery images is the probabilistic VCS which firstly randomly selects a column from a basis matrix and then distributes each pixel in the column to the corresponding position of shares.
The EVCS is also known as friendly VCS[22], which issues the management difficulty caused by noise-like shares in VCS. Ateni [23] proposed a general technique to implement EVCS for any access structure by hypergraph coloring. Due to the pixel-by-pixel encryption mechanism, restored images remain the problem of pixel expansion. Lee [24] proposed a novel algorithm of general access structures to cope with the pixel expansion problem. Instead of the traditional VC-based approach, this scheme first constructed meaningless shares using an optimization technique and then solved it by a simulated-annealing algorithm. Then, the method generates meaningful shares by adding cover images into shares with a stamping algorithm. No computational devices are needed for decryption in this scheme. However, it is only appliable to black-and-white images and needs a lot of time to generate shares.
To address the risk of leakage in biometric features, Jinu [25] proposed a multifactor authentication scheme based on VC and Siamese networks. However, the VCS adopted needs a key to encrypt, which destroys the printable characteristic of VC. Ross [26] preserved the privacy of face template data through a trusted third party and EVCS. In this scheme, shares for decoupling secret face data come from a group of general face images. To improve the quality of restored images, it may use up to 100 shares to encrypt a face image. How to transmit these shares will be a large challenge. Requiring huge storage blocks its application in many scenarios. The accuracy of face recognition decreases because of the interference of VC or EVC in these schemes.
3. A Privacy-Preserving Biometric Recognition System with Visual Cryptography
Combining feature identification and cryptography can effectively build a secure feature recognition system. In this section, we first present our novel EVCS to address the pixel expansion and vulnerability of noise-like shares, and then we use the proposed scheme to securely distribute face images in separate databases. In the end, to keep the accuracy of face recognition, we leverage the transfer learning method to mitigate the quality degradation of recovery images.
3.1. Expansion-Free EVCS
In the traditional pixel-by-pixel encryption of VC, there is a corresponding matrix collection C0 and C1, for a white (w) or black (b) pixel in a secret image. The matrix in C0 or C1 consists of n × m Boolean values. When encrypting, we randomly select a matrix from C0 or C1 and assign n rows of pixels of the matrix to the corresponding n shares. Each row contains m subpixels which are reinterpreted as recovery w or b pixel.
- (i)
For any matrix S0 in C0, H(V) < d − am is satisfied when overlaying any k of n row vectors in S0
- (ii)
For any matrix S1 in C1, H(V) ≥ d is satisfied when overlaying any k of n row vectors in S1
- (iii)
For any subset with q, q < k rows, rows overlaying of q × m matrices are indistinguishable, which implies the black-and-white pixels in combined shares have a uniform probability distribution
Conditions (i) and (ii) make images visible when overlaying. The condition (iii) implies that fewer than k shares cannot gain any information about the secret pixel.
Taking the (2, 2)-VCS with two participants for example, if the pixel arrangement held by the other participant is complementary to itself, all black pixels will appear, while if pixels held by the other are the same as itself, it will generate half black and half white gray pixels after superimposing. The proportion of black-and-white pixels in each share is fixed, so it will not reveal any information about a secret image.
The disadvantage of VC is that generated shares are meaningless noisy-like images. Although such images will not reveal any information about secret images, they will increase the burden of management and pique the interest of attackers. If these images are tempered by malicious attackers, it is difficult to detect.
The difference between VCS and EVCS is that EVCS has to take into account the color of shares besides the secret image we want to get [27], hence we can see n + 1 meaningful images in an EVCS. Table 1 shows collections for traditional (2,2)-EVCS and recovered subpixels, where the gray-level 1(0) denotes a white (black) pixel (w, b). Each secret pixel is expanded to 4 subpixels in the EVCS (m = 4). Only when enough participants show held shares can the secret images be restored. For example, if the pixel is black in the secret image, black in Share1, and white in Share2, the share subpixels will be selected from the third row and second column of Table 1, that is, the [0 1 0 0] and [1 0 1 0] subpixel blocks. After superimposing the two rows, we get a subpixel with four black pixels. The subpixel blocks [0 1 0 0] and [1 0 1 0] may also appear in other basis matrices (e g., and ), hence the secret information is not exposed in the cover images. When encrypting a black secret pixel, regardless of which basis matrix is selected to generate the corresponding subpixels, we can obtain a whole black subpixel block ([0 0 0 0]), while for white secret pixel, we can only obtain a subpixel block with three black pixels and one white pixel ([1 0 0 0]), which is interpreted as a white pixel in the recovery image, hence the recovery pixel shows a contrast of 1/4 (three white pixels are lost). It can also be verified that for the (2,2)-EVCS, the contrast values of the covers image also are a = 1/4. No matter which basic matrix we choose, the white pixel in Share1 or Share2 is represented by a subpixel with two black pixels and two white pixels, while the black pixel is represented by a subpixel with three black white pixels and one black pixel, so the contrast in cover images is 2/4 − 1/4 = 1/4.
| Secret pixels | Recovery subpixels | |||
|---|---|---|---|---|
| White pixel (1) | Black pixel (0) | White pixel | Black pixel | |
| Basis matrix | ||||
To eliminate the pixel expansion problem in the traditional EVCS model, we can use the block-wise operation instead of pixel-by-pixel encryption [28]. We first divide a gray-level image into n nonoverlapping black-and-white pixel blocks Bi, Bi∩Bj = ∅, for1 ≤ i ≠ j ≤ n. Bi and halftoned blocks Bh are the same in size. The number of black pixels in Bi and Bh must satisfy the following: bBi = sl/(sb + 1) × (sl − ∑Bi/255), where sl denotes the size of candidate black levels, bBi denotes the gray-level of cover blocks, and sb denotes the block size. To meet the security requirement of VC, the contrast of black-and-white blocks cannot be any, which results in contrast loss after halftoning.
We reinterpret the image blocks as white and black pixels based on the original EVCS. For example, for the (2,2)-EVCS, we will dither a secret gray-level block into the closest equal-sized pixel block with 3 or 4 black pixels and dither a cover block into the closest equal-sized pixel block with 2 or 3 black pixels. If the encryption block has three black pixels (e.g., [1 0 0 0]) and cover blocks have two black (e.g., [0 1 1 0]) and three black pixels, e.g., [0 1 0 0], respectively, then we will set cs to w and ch1, ch2 to w, b. Therefore, we will select as the basis matrix and randomly permuting all columns of to obtain the collections C. At last, we select a matrix Cp from C and dispatch each row of Cp to the corresponding blocks in sharei, i ∈ [i ∈ 1, …, n].
After processing the secret image by the limited halftoning, we can reuse the underlying EVCS directly to encrypt the secret image into meaningful share images without pixel expansion. Ateni [23] et al. describe a general construction method for EVCS in detail.
3.2. The Recognition of Face Images Recovered from EVC
In this section, we will propose a new embedding method for VC-recovered images to maintain high accuracy in feature identification. Although the proposed EVCS solves the problems of size expansion and noise-like shares, it still cannot achieve perfect image restoration. For existing feature identification methods, the use of VC can alleviate the leakage of centralized storage of template data, but it will also mix noise into sample images, which will reduce the performance of feature recognition.
Witnessing the recent success of DNN, we hope to use these methods to solve the problem of noise interference caused by the introduction of VC in feature identification [6]. Figure 1 shows the flowchart of the proposed approach for distributing and matching face images. In a high-precision neural network model for face images, the face data is converted into the corresponding weights in the network. Using transfer learning [29], we can extract and transfer these weights to other neural networks (e.g., reduced images mixed with noisy signals). Transfer learning allows sharing the learned model parameters and structures to a new model in a specific way, thus speeding up and optimizing the learning efficiency of the model and avoiding learning from scratch. We first train a softmax classifier on the training data using a pretrained neural network model and then fine-tune the weights of the last layer or layers using a dataset recovered from EVCS. To avoid affecting learned weighted when training, we freeze the pretrained model and add multiple fully connected layers at the end of the network. After embedding reduced images, we select a loss function to efficiently obtain a high-precision model. When used as a classification task, the model selects the most similar image class ID in the training set to the test image as the output.

In deep learning, many methods use pairs of samples to compute gradient loss and update model parameters [15]. We use the triplet loss [17] gradient optimization in the face recognition system. Although center loss [18] may have a faster convergence rate, triplet loss is more robust for image quality degradation. The basic idea of triplet loss is to make the distance between negative sample pairs larger than that between positive sample pairs. In the training process, positive sample pairs and negative sample pairs are selected at the same time, and the anchor of the positive and negative sample pairs is the same. Choosing which triplets to train is important for achieving good performance. When the distance between the negative sample and the positive sample pairs is greater than a threshold, the model sets the loss to 0 and ignores the sample pairs. Because the distance between positive and negative samples and anchor points is considered at the same time, the performance using triplet loss is often better than that of contrastive loss [30].
The triplet loss minimizes L, then d(a, p)⟶0, d(a, n)⟶margin. The goal is to shorten the distance between a and p and lengthen the distance between a and n. For the case L = 0, that is, d(a, p) + margin < d(a, n), this is an easily discernible triple and does not need to optimize, because a and p and a and n are far apart; for the case d(a, p) < d(a, n) < d(a, p) + margin, the triples are in the fuzzy region. This case is the focus of our training.
The same deep neural network is used to extract the features of these three images to obtain three embedding vectors, which are input parameters of triple loss. The model is updated by using a backpropagation algorithm according to loss and iterated until a stable neural network model is obtained. When inferring samples, we first generate triplet image pairs and then output the distances between anchor, positive, and negative embedding [31]. After transforming the distances into probability models, we can get desired results. During the registration process, we decompose the private face data into two or more meaningful images. After dispatching shares, the system discards the original data. The encrypted face data are stored in two or more database servers. Unless these servers collude, the private data will not be revealed to any server. In the authentication stage, the feature recognition system sends requests to database servers to transmit corresponding shares to it. Once finishing the classification recognition or similarity matching task, our system will discard the reconstructed secret image. In the whole registration and recognition process, the secret image will be only recovered in use. Because private biometrics cannot be extracted from any single database or server, the whole authentication does not reveal any feature information.
4. Experiments and Results
In this section, we first evaluate the effectiveness of the proposed method. We select the TensorFlow [32] framework to develop the Siamese network [31] model and the test application using Python rapidly.
Table 2 shows a triple example in the IMM dataset [33]. Every embedding has three input images, which are anchor, positive, and negative images, respectively. The proposed EVCS keeps the image size before and after encryption. All images are 640 × 480 in size.
| Type | Secret image | Share1 | Share2 | Decrypted image |
|---|---|---|---|---|
| Anchor |  |
 |
 |
 |
| Positive |  |
 |
 |
 |
| Negative |  |
 |
 |
 |
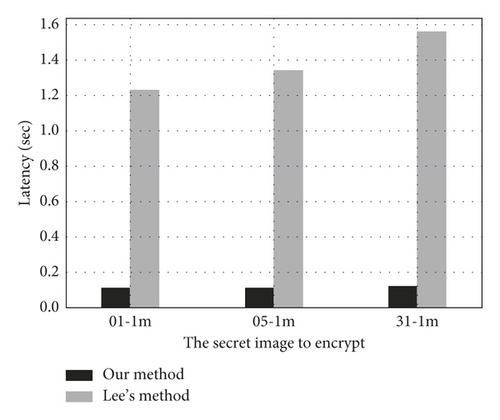
Figure 2 shows the encryption time comparison between our and Lee’s [24] schemes for three images from the IMM dataset. When encrypting one image, we selected two other images separately as cover images. It can be seen that Lee's method took a lot of time in the encryption process, which was 10X that of our method. It is because Lee’s method developed a complex simulated-annealing-based method to generate an optimized arrangement when encrypting the cover images, while our algorithm can directly obtain the encrypted pixels for each share from the base matrix. So, the encryption performance of our algorithm is better.
We further test the recognition system on the IMM and LFW datasets. We choose ResNet18 [14] as the backbone network and use pretrained weights from the ImageNet [34] dataset. The IMM Face Database comprises 240 still images of 40 different human faces. LFW (Labeled Faces in the Wild) [35] is the de-facto benchmark for face verification, also known as pair matching. The dataset contains more than 13,000 labeled images of faces collected from the web. 1680 of the people pictured have two or more distinct photos in the dataset.
Table 3 shows the performance including accuracy, precision, recall, and f1-score of our networks on IMM and LFW datasets for normal and images recovered from the proposed EVCS, respectively. Because the normal data is unencrypted, the recognition performance is higher. For the dataset recovered from the proposed EVCS, the recognition performance is lower than that of normal data because the image is lossy. However, this experiment shows the trained model can archive results of more than 0.92 on all metrics, which implies we can still keep the inferred performance of the trained model when securing face images. The reason the metrics on the LFW dataset are lower than IMM is that the face consists of more complex patterns. The proposal processes every pixel in the face image one by one while preserving the gray-level density. This transformation corresponds to adding a global white noise to the image, which does not destroy the features and patterns in face images, so it does not affect the final prediction accuracy.
| Accuracy | IMM | Normal | 0.97 |
|---|---|---|---|
| Our | 0.95 | ||
| LFW | Normal | 0.95 | |
| Our | 0.93 | ||
| Precision | IMM | Normal | 0.97 |
| Our | 0.96 | ||
| LFW | Normal | 0.97 | |
| Our | 0.93 | ||
| Recall | IMM | Normal | 0.98 |
| Our | 0.92 | ||
| LFW | Normal | 0.92 | |
| Our | 0.90 | ||
| F1-score | IMM | Normal | 0.98 |
| Our | 0.94 | ||
| LFW | Normal | 0.93 | |
| Our | 0.92 |
5. Conclusions
With the development of next-generation networks and smart devices with rich sensors, it is convenient to sense and transmit images anytime and anywhere. There is an urgent need to protect the security and privacy of easily collected information and efficiently transfer them in untrusted networks. In this paper, we propose a novel feature recognition method taking advantage of VC and use transfer learning to improve the recognition system. This proposed method eliminates the complex computation in traditional cryptography. To solve the problems of pixel expansion and noise-like shares in VC, we propose a novel EVCS to keep the size of recovered images by block encryption before and after encryption. We further utilize the strong generalization ability of transfer learning to eliminate the interference of noise for images recovered from EVCS. The experimental results show our method can keep the high accuracy of feature recognition when preserving privacy.
In future work, we will combine VC with other methods like QR codes to provide richer forms for the transmission of private images. We will also test the performance of the proposed method in other biometrics such as fingerprints and voiceprints to verify its popularity.
Conflicts of Interest
All authors have no conflicts of interest to declare.
Acknowledgments
This work is supported in part by the National Key Research and Development Program of China (2019YFB1706003), and the Natural Science Foundation of Guangdong Province, China (2214050004382).
Open Research
Data Availability
The data used to support the findings of this study are available from the corresponding author upon request.




