Analytical Solutions for the Nonlinear Partial Differential Equations Using the Conformable Triple Laplace Transform Decomposition Method
Abstract
In this paper, a novel analytical method for solving nonlinear partial differential equations is studied. This method is known as triple Laplace transform decomposition method. This method is generalized in the sense of conformable derivative. Important results and theorems concerning this method are discussed. A new algorithm is proposed to solve linear and nonlinear partial differential equations in three dimensions. Moreover, some examples are provided to verify the performance of the proposed algorithm. This method presents a wide applicability to solve nonlinear partial differential equations in the sense of conformable derivative.
1. Introduction
Fractional calculus has attracted many researchers in the last decades. The impact of this fractional calculus on both pure and applied branches of science and engineering has been increased. Many researchers started to approach with the discrete versions of this fractional of calculus which are summarized into two approaches: nonlocal (classical) and local. Most popular definitions in the area of nonlocal fractional calculus are the Riemann–Liouville, Caputo, and Grunwald–Letnikov definitions. The obtained fractional derivatives lack some basic properties such as chain rule and Leibniz rule for derivatives [1]. However, the semigroup properties of these fractional operators behave well in some cases. In [2], later on, Khalil et al. (2014) presented a new definition of a local fractional derivative, known as conformable derivative, which is well behaved and obeys the Leibniz rule and chain rule for derivatives. While conformable derivative has been criticized in [3, 4], we believe that the new definition deserves to be explored further with its analysis and applications because many research studies have been conducted on this definition and its applications to various phenomena in physics and engineering. Therefore, throughout this paper, we will call this definition as conformable derivative. It is defined as follows.
For this derivative, Atanganana et al. (2018) presented new properties [5] which have been analysed for real valued multivariable functions [6] by Gozutok et al. (2018). In [7], conformable gradient vectors are defined, and a conformable sense Clairaut’s theorem has also been proven. In [8–14], the researchers have worked on the linear ordinary and partial differential equations based on the conformable derivatives. Namely, two new results on homogeneous functions involving their conformable partial derivatives are introduced, specifically, homogeneity of the conformable partial derivatives of a homogeneous function and the conformable version of Euler’s theorem. The conformable Laplace transform was studied and modified by Jarad et al. (2019) [15]. The conformable double Laplace transform was defined and applied in [16]. The conformable Laplace transform is not only useful to solve local conformable fractional dynamical systems but also it can be employed to solve systems within nonlocal conformable fractional derivatives that were defined and used in [17]. Finally, it is also a remarkable fact that there are a large number of studies in the theory and application of fractional differential equations based on this new definition of derivative, which have been developed in a short time. We refer to [4, 18–35] that many researchers have been worked on different analogues methods to solve partial fractional differential in conformable sense. Numerical and analytical techniques for solving conformable partial differential equations and conformable initial boundary value problems have been investigated in [36, 37], respectively. In addition, some interesting problems have been studied in the sense of conformable derivative such as conformable gradient-based dynamical system for constrained optimization problem [38], conformable heat equation on radial symmetric plate [39], and optimal control problem for conformable heat conduction equation [40]. Several equations have been formulated with the help of conformable formulations to study their solutions such as the (2 + 1)-dimensional Ablowitz–Kaup–Newell–Segur equations [25] where the complex soliton solutions were investigated and the Date–Jimbo–Kashiwara–Miwa equation [26] where new travelling wave solutions were obtained. In addition, the conformable formulations of the coupled nonlinear Schrodinger equations [30] and Fokas–Lenells equation [35] were studied to obtain travelling wave solutions and optical solutions, respectively. The triple Laplace Adomian decomposition method and modified variational iteration Laplace transform method were studied in [27, 28], respectively. Similarly, a combined method of both of the Laplace transform and resolvent kernel methods was introduced in [31]. Motivated by all these studies, we come up with the idea to study the nonlinear partial fractional differential equations by defining a function in 3-dimensional space. Therefore, a conformable triple Laplace transform is defined and coupled with Adomian decomposition method to solve systematic nonlinear partial fractional differential equations. The triple Laplace transform has been rarely discussed in the literature which makes this topic as an open research topic. Therefore, exploring new results concerning this interesting topic is always important. The main advantage of this method will give accurate solutions to nonlinear partial fractional derivatives in three-dimensional space.
This paper is divided into the following sections. In Section 2, some basic definitions on conformable partial derivatives are introduced. In Section 3, the main results and theorems on the conformable triple Laplace transform are investigated. In Section 4, a general nonlinear nonhomogeneous partial fractional differential equation is solved using the proposed method. In Section 5, numerical experiment is conducted using the proposed method to validate the obtained results. In Section 6, a conclusion of our research work is provided.
2. Basic Definitions and Tools
In this section, we provide some fundamental definitions on conformable partial derivatives.
Definition 1. Given a function f : R+ × R+ × R+⟶R, the conformable partial fractional derivatives (CPFDs) of orders α, β, and γ of the function f(x, y, t) are defined as follows:
We prove the basic Theorem 1 and the relation between the CPFDs and partial derivatives as follows.
Theorem 1. Let α, β, γ ∈ (0,1] and f(x, y, t) be a differentiable at a point for x, y, t > 0. Then,
- (i)
- (ii)
- (iii)
Proof. By the definition of CFPD,
Similarity, we can prove the results (ii) and (iii).
In the next preposition, we mention the conformable partial fractional derivative of some functions. By using Theorem 1, it can be verified easily.
Proposition 1. Let α, β, γ ∈ (0,1] and a, b ∈ R, l, m, n ∈ N. Then, we have the following:
- (1)
(∂α/∂xα)(au(x, y, t) + bv(x, y, t)) = a(∂α/∂xα)u(x, y, t) + b(∂α/∂xα)v(x, y, t)
- (2)
(∂α+β+γ/∂xα∂yβ∂tγ)(xl ym tn) = lmn xl−α ym−β tn−γ
- (3)
,
- (4)
(∂α/∂xα)(sin(xα/α)cos(tγ/γ)) = cos(xα/α)cos(tγ/γ)
- (5)
(∂β/∂yβ)(sin(xα/α)cos(yβ/β)cos(tγ/γ)) = −sin(xα/α)sin(yβ/β)cos(tγ/γ)
3. Some Results and Theorems of the Conformable Triple Laplace Transform
In this section, we recall some basic definitions on conformable Laplace transform and some results which will be used later on. We refer the reader to some related research studies in [4, 15–29]. Also, we define conformable triple Laplace transform, which is defined in equation (6).
Definition 2. Let the function u : (0, ∞)⟶R and 0 < α ≤ 1 be the piecewise continuous function. Then, the conformable Laplace transform (CLT) of function u of exponential of order α is defined and denoted by
Definition 3. Let u(x, y) be a piecewise continuous function on the domain D of R+ × R+ of exponential order α and β. Then conformable double Laplace Transform (CDLT) of u(x, y) is defined and denoted by
Now, we define the conformable triple Laplace transform, for α, β, γ ∈ (0,1], and p, q, s ∈ ∁ are the Laplace variables.
Definition 4. Let u(x, y, t) be a real valued piecewise continuous function of x, y, and t defined on the domain D of R+ × R+ × R+ of exponential order α, β, and γ, respectively. Then, the conformable triple Laplace transform (CTLT) of u(x, y, t) is defined as follows:
The conformable inverse triple Laplace transform, denoted by u(x, y, t), is defined by
Definition 5. A unit step or Heaviside unit step function is defined as follows:
Theorem 2. If , , and A, B, and C are constants, then
- (a)
Linearity property:
() - (b)
, where C is the constant.
- (c)
, where Γ(⋅) is the gamma function. Note that Γ(n + 1) = n!, for n = 0, 1, 2, 3, …
- (d)
The first shifting theorem for conformable triple Laplace transform:
-
If , then
() - (e)
, then
() - (f)
()
Proof. From results (a)–(d) and (f), it can be easily proved by using the definition of conformable triple Laplace transform (CTLT). Here only we see the proof of result (e).
So, by the definition of CTLT (equation (6)), we have
By differentiating with respect to p, l-times, we get
It reduces to
Now, we again differentiate with respect to q and s, m- and n-times, respectively, and we obtain the simplification as follows:
Now, we multiply (−1)l+m+n, on both sides, and we get the required result:
Theorem 3. If , then
Proof. By applying the definition of CTLT, we have
Now, using the definition of Heaviside unit step function H(x, y, t), we have
By putting , we have
Theorem 4. The conformable triple Laplace transform of the function , and (∂β+γ/∂yβ∂tγ)(u(x, y, t)) is given by
- (a)
- (b)
- (c)
- (d)
Proof. By applying the definition of CTLT and Theorem 2 (e), till equation (15) can be the required result (a). Remaining results (b)–(d) can be obtained via the same process.
Theorem 5. For α, β, γ ∈ (0,1]. Let u(x, y, t) = u(xα/α, yβ/β, tγ/γ) be the real valued piecewise continuous function x, y, and t of the domain D on (0, ∞) × (0, ∞) × (0, ∞). The CTLT (conformable triple Laplace transform) of the conformable partial fractional derivatives of order α, β, and γ is given by
- (a)
- (b)
- (c)
- (d)
- (e)
- (f)
- (g)
Proof. Here, we go for proof of result (a), and the remaining results (b)–(g) can be proved. To obtain conformable triple Laplace transform of the fractional partial derivatives, we use integration by parts and Theorem 1.
By applying the definition of CTLT, we have
Since we have Theorem 1, (∂α(u)/∂xα) = x1−α (∂u/∂x). We use this result in equation (23).
Therefore, equation (23) becomes
The integral inside the bracket is given by
By substituting equation (25) in equation (24), and simplifying, we get the required result (a), that is
In general, the above results in Theorem 5 can be extended as follows:
- (a)
()
- (b)
If , then
()
4. Solving Nonlinear Partial Fractional Differential Equation Using the Conformable Triple Laplace Transform Decomposition Method
-
Step 1: applying the conformable triple Laplace transform to equation (29) on both sides, we have
() -
Using Theorem 5 and equation (30), in equation (31),
() -
Step 2: divide by sm, and apply the conformable inverse triple Laplace transform to equation (32); it reduces to
() -
where G(x, y, t) represents the term coming from the source term and prescribed initial conditions.
-
Step 3: considering the conformable triple Laplace transform decomposition method, let the solution of equation (29) be an infinite series
() -
and the nonlinear term can be decomposed as
() -
where An is called Adomian polynomials of u1, u2, u3, …, un, and it can be calculated by the following formula:
() -
Substituting equations (35) and (36) in equation (34), we have
() -
Step 4: now, by comparing on both sides of equation (37), we get
()and so on…
5. Applications
In this section, a numerical experiment is done using the conformable triple Laplace decomposition method to solve nonlinear homogeneous and nonhomogeneous partial fractional differential equation in 3-dimensional space.
Example 1. To illustrate the proposed method, let us consider the following nonlinear partial fractional differential equation:
Solution 1. Rewrite equation (41) as
Taking the conformable triple Laplace transform on both sides of equation (42), we have
Recalling Theorem 5 (c), .
So, equation (43) reduces to
Since u(x, y, 0) = xy, we have
Now, by applying the conformable inverse triple Laplace transform to equation (44) and using initial condition equation (45), we obtain from equation (44)
By applying the proposed method, in particular, equations (35)–(37), let u0(x, y, t) = xy, and the recursive relation is given by
Let the nonlinear term be represented as
Substituting equation (49) in equation (48), and also calculating (∂2αun/∂x2α), the resulting expression of equation (47) reduces to the following.
For n = 0,
We have
For n = 1,
Using equation (51), u0, and u1 and simplifying, equation (52) becomes
We have
Simplifying equation (54), we have
For n = 2,
Substituting u0, u1, and u2 in equation (56) and simplifying, we obtain
Therefore, we have
Simplifying equation (58), we have
The approximate series solution is expressed as
From equation (60), if we consider α = β = γ = 1, then the solution of equation (41) reduces to
Figures 1 and 2 show the 3D graphical representations of equation (60) with various values of α and β.
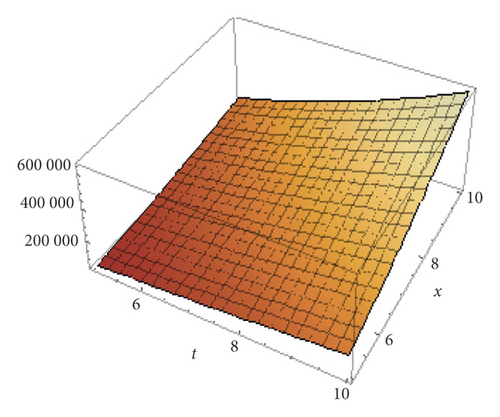
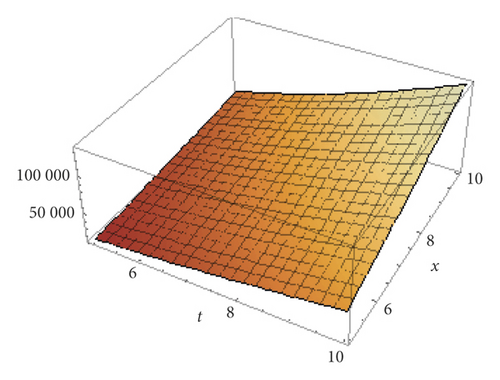
Example 2. Consider a nonlinear nonhomogeneous partial fractional differential equation, for α, β, γ ∈ (0,1], x, y, t∈[0, ∞).
Solution 2. Rewrite equation (62) as
Imposing the conformable triple Laplace transform to both sides,
Recalling Theorem 5 (d),
Equation (66) becomes
Using initial condition (equation (63)) and taking the inverse triple Laplace transform on equation (67), we obtain
By applying the proposed method, we have the following.
Let u0 = yt − x, and the recursive relation is
Let the nonlinear term be represented as
Note that, in Adomian relation, the linear term can be considered, in place of nonlinear. So, you may take f(u) = u, and it leads to the same answer. So, this method is also valid for linear partial fractional differential equation.
For n = 0,
The approximate series solution is written as
For α, β, γ ∈ ( 0,1, [x, y, t∈]0, ∞ ).
From equation (73), note that for α, β, γ = 1, the solution of equation (63) reduces to
Figures 3 and 4 show the 3D graphical representations of equation (74) with various values of γ and β.
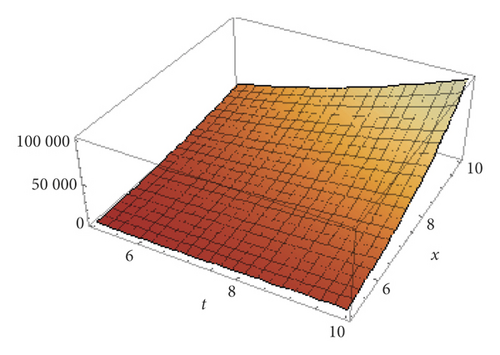
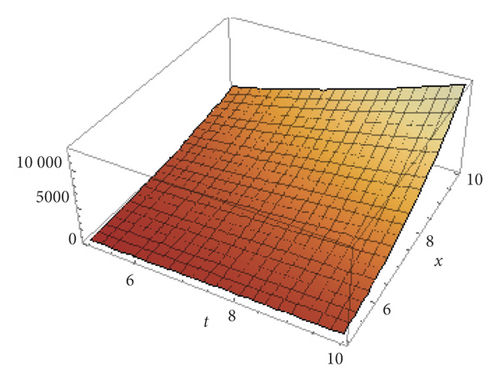
6. Conclusion
In this work, the conformable triple Laplace transform has been investigated using all our obtained novel results and theorems. The new conformable triple Laplace transform decomposition method is applied to find the solution of linear and nonlinear homogeneous and nonhomogeneous partial fractional differential equations. A numerical experiment has been conducted using this proposed method. This proposed method can be applied for simultaneous two or more than two linear and nonlinear partial fractional differential equations. Note that, if we take α, β, γ = 1, in Examples 1 and 2, we obtain an exact solution which was considered in [27]. Our results shed the light on the significance of exploring new generalized methods for solving partial differential equations, particularly nonlinear ones, due to the essential need to explore new analytical solutions to understand the dynamics of solutions for such important equations in physics and engineering.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this study.
Open Research
Data Availability
No data were used to support this study.




