The security of wireless information transmission in large-scale multi-input and multioutput (MIMO) is the focus of research in wireless communication. Recently, a new artificial noise—SCO-AN which shows no orthogonality to the channel, is proposed to overcome the shortcomings of traditional artificial noise. In the previous research, the optimization function of SCO-AN is not convex, and its extremum cannot be obtained. Usually, nonconvex optimization algorithms or iterative relaxation algorithms are used to get the maximum value of the optimization objective function. Nonconvex optimization algorithms or iterative relaxation algorithms are greatly affected by the initial value, and the extremum cannot be obtained by a nonconvex optimization algorithm or iterative relaxation algorithm. In this paper, we creatively apply the strong law of large numbers to obtain the optimal value of the optimization function of SCO-AN under the condition of large-scale MIMO: the strong law of large numbers is applied to obtain the ergodic lower bound (ELB) expression of SC for SCO-AN. The power allocation (PA) problem of the SCO-AN system is discussed. We use a statistical method to get the formula for calculating the optimal power distribution coefficient of the SCO-AN system. The transmitter can use the optimal power ratio of PA to distribute the transmitted power without using the PA algorithm. The effect of imperfect channel state information is discussed. Through simulation, we found that more power should be generated for SCO-AN if the channel estimation is imperfect and the proposed method can achieve better security performance in the large-scale MIMO system.

1. Introduction

Security is the core issue of wireless communication [1]. In this paper, the security of wireless information transmission is discussed. Since the wireless communication signal is transmitted in broadcast ways, the wireless communication signal can be received by eavesdroppers without restriction. Since the eavesdropper cannot be prevented from obtaining the transmitted information, previous research on secure communication is focused on using the principles of encryption to prevent eavesdroppers from deciphering the obtained information. However, encryption cannot fundamentally solve secure transmission problem if the eavesdropper obtains the key of the information or has enough computing power to crack the information. The secure transmission of information based on cryptography will fail. Therefore, reducing the amount of information obtained by eavesdroppers is the correct way to achieve secure communication. In recent years, physical layer security (PLS) technology has become a new research focus.

The PLS technology was proposed in [2]. In [2], a classic model for secure communication model is proposed. In [3], the secure communication model is extended to the field of wireless communication, the channels in the secure communication models are all broadcast channels.

The application of MIMO provides an opportunity for the development of PLS. In [4], the concept of secrecy capacity (SC) is outlined by Barros and Rodrigues. The numerical expression of SC is studied in [5]. In [6], Zhu studies the SC of wiretap fading channels in a massive MIMO communication system. Zeng proposes the SC of downlink massive MIMO-NOMA networks [7]. A novel method to select the proper antenna and PA in massive MIMO is proposed in [8], the algorithm in [8] makes the wireless communication system to adjust the PA coefficient, and the communication quality of eavesdropper is reduced effectively.

SC is determined by the capacity of legitimate and eavesdropping channels. Generally, increasing the capacity of the legitimate channel or decreasing the capacity of the eavesdropping channel could increase SC [9–11]. However, for a particular communication system, the capacity of the legitimate channel is challenging to change. Therefore, previous studies focus on reducing the capacity of eavesdropping channels [12–14].

Artificial noise (AN) is a specific application for PLS technology [15]. AN is orthogonal to the receiver’s channel, so AN will not affect the legitimate channel. However, AN is not orthogonal to the eavesdropping channel; AN will affect the eavesdropping channel. Adding AN to the transmitted signals will raise the SC of secure transmission.

However, the design of AN is under strict restriction. H denotes the legitimate channel state information (CSI), and w_k denotes the AN. By definition of AN, Hw_k = 0. w_k is the zero solution of homogeneous linear equation group HX = 0. The dimension of H is m × n. If X is nonzero, the rank (H) must be guaranteed that rank (H) < min (m, n). It means that the number of transmitting and receiving antennas has to be different. However, transmitting antennas have the same number as receiving antennas in most MIMO real-life communication systems. We have to reduce the transmitting or receiving antennas. Meanwhile, the capacity of legitimate channel is reduce.

SCO-AN is proposed in [16] to solve the problem. SCO-AN does not show orthogonality to the legitimate and eavesdropping channels. Therefore, SCO-AN is achievable in any situation. Although this method has a certain degree of negative impacts on the legitimate channel, SCO-AN has a greater degree of negative impacts on the eavesdropping channel. SCO-AN is considered to increase the SC to a greater degree when compared to the traditional AN. SCO-AN is a tool that converts the receiver’s antinoise ability into SC.

Recently, intelligent reflecting surface (IRS) technology has become a research hotspot in communication technology [17, 18]. Because the channel of IRS is divided into uplink and downlink. Artificial noise is only valid in the uplink or downlink so that AN cannot be applied to IRS. The nonorthogonal characteristic of SCO-AN makes it a perfect application in IRS. In 2020, [19] applied nonorthogonal artificial noise to improve the security performance of IRS systems. It should be pointed out that the idea of nonorthogonal artificial noise was first put forward in [16].

We should consider the transmission power limits. It is important to allocate the power of the SCO-AN system [20]. The objective function of SCO-AN PA is nonconvex. It has been proved that we cannot get the optimal PA coefficient of the SCO-AN system. In general, nonconvex optimization algorithm or relaxation iteration algorithm is used to optimize nonconvex functions [21–24]. The simulation result has proved that these two algorithms are greatly affected by initial states of the communication models. We can only adopt an iterative approach to calculate the maximum of the objective function in a certain range. However, in the massive MIMO communication system, we can use strong law of large numbers to approximate the ELB of SC. Based on the ELB of SC, the optimal PA coefficient of SCO-AN is obtained as well. The expression for ELB on SC in fading channels which adds SCO-AN is derived. The optimal ratio of PA of the SCO-AN system is then deduced.

Base on the optimal PA coefficient, in a large-scale MIMO system, we can allocate the power without calculating. Furthermore, the effects of the perfect CSI and the imperfect CSI on the ELB of SC are discussed. The study of this paper is highly compatible with the features of 6G networks which equip massive MIMO communication system [25]. Therefore, the application introduced in this paper is a promising solution in addressing security threats for 6G networks.

The contributions of this paper are as follows:

(i)
The nonconvexity of the SCO-AN PA function makes it impossible to obtain the maximum value. In this paper, the SCO-AN PA function is reconstructed creatively using statistical theory, and the reconstructed PA function approximates the theoretical limit. From the reconstructed PA function, we can deduce the channel capacity of the legitimate channel and eavesdropping channel in large-scale MIMO. Thereby, the secrecy capacity in large-scale MIMO is deduced. We reach a crucial conclusion: the PA objective function of the channel between transmitter and receiver depends mainly on the partition of power and the number of transmitting antennas
(ii)
Based on the reconstructed PA function, we derive the optimal PA coefficient. In large-scale MIMO, PA can be carried out according to this coefficient without calculation, and the system can achieve excellent security performance. To simplify the calculation, the precision of the traditional PA algorithm based on statistics is very low. We improve the traditional PA algorithm based on statistics and propose a new PA algorithm based on statistics. The accuracy of the PA algorithm is improved
(iii)
We consider the effect of the imperfect CSI. An expression for ELB of SC with imperfect CSI is derived. Based on the expression, we conclude that we should generate more power for SCO-AN once the level of imperfect CSI increases. The negative effect of imperfect CSI on PA is proved by simulation

The rest of the paper is organized as follows: Section 2 introduces the related work. Section 3 defines the system, channel, and signal model. Section 4 investigates the ELB of SC. The optimal PA for the proposed system model is discussed in Section 5. The effect of the imperfect is studied in Section 6. Simulation results are given in Section 7. Finally, concluding remarks are given in Section 8.

2. Related Work

SCO-AN was first proposed in [16]. In this paper, the author proposes an SCO-AN to overcome the defects caused by the orthogonality of traditional artificial noise. For a long time, SCO-AN is not drawing attention. In recent years, the intelligent reflecting surface is a hot spot in the field of communication technology. IRS has two channels—uplink and downlink channels, and artificial noise cannot be orthogonal with two channels simultaneously. The nonorthogonal SCO-AN is perfectly suitable for intelligent reflecting surface technology; it also brought new prospects for the application of SCO-AN. Hong et al. have started to add nonorthogonal artificial noise to the intelligent reflection surface and achieved excellent security performance [19].

Here, we briefly introduce the principle of AN. Let H be the CSI matrix. H is a N_h × N_h matrix. AN is a N_h × 1 vector. AN is orthogonal to channel H. AN should satisfy:

(1)

w_k denotes AN. We find that AN can hardly be designed in the simulation. AN does not exist, especially when the number of transmitting antennas equals the number of receiving antennas. According to matrix theory, for a linear equation Hw_k = 0, if H is not full rank, that is, |H| = 0, Hw_k = 0 has a nonzero solution. However, in wireless communication, |H| = 0 almost does not exist. Therefore, for real-life communication, AN has only zero solutions, and AN cannot be designed.

SCO-AN is designed to solve the orthogonality defect of AN. SCO-AN is not orthogonal to channel H; that is,

(2)

w_m denotes SCO-AN; α is a N_h × 1 vector, and each elements in α is arbitrarily small. When designing SCO-AN, α satisfies condition rank(H) = rank(H, α). According to matrix theory, SCO-AN must have a nonzero design scheme. The design of SCO-AN does not meet any restrictions.

We have performed a thousand simulation experiments to design AN and SCO-AN. From Table 1, it can be seen that when rank (H) is equal to N_h, in 1000 experiments, AN is not designed successfully in any experiments. Only when rank (H) is less than N_h, AN can be designed successfully. The design of SCO-AN is not affected by the rank(H).

Table 1. Design feasibility of AN and SCO-AN.

	AN	SCO-AN
Rank(H) = N_h	0	1000
Rank(H) < N_h	1000	1000

Table 2 shows the number of solution vectors for AN and SCO-AN under different channel conditions, N₁ is the number of solution vectors for AN, and N₂ is the number of solution vectors for SCO-AN. When rank(H) is equal to N_h, the number of solution vectors for AN is 0, that is, AN cannot be designed, and the number of solution vectors of SCO-AN is 1, that is, under a specific power limit, there is only one design scheme of SCO-AN. When rank(H) − N_h = 1, under a specific power limit, the number of AN solution vectors is 1; that is, under a specific power limit, there is only one design solution for AN. Moreover, there are countless kinds of SCO-AN design schemes. Only when rank(H) − N_h > 1, the solution vectors of AN and SCO-AN are both infinite, which also shows that SCO-AN is a more designable than artificial noise.

Table 2. Solution space size of AN and SCO-AN.

	AN	SCO-AN
Rank(H) = N_h	N₁ = 0	N₂ = 1
Rank(H) − N_h = 1	N₁ = 1	N₂ = ∞
Rank(H) − N_h > 1	N₁ = ∞	N₂ = ∞

A comparison of AN and SCO-AN secrecy performance is shown in Figure 1. The previous analysis shows that, in most cases, the design of AN is very few or even unique, so for a particular channel, the improvement of AN for SC is limited; while the number of design scheme for SCO-AN is infinite, SCO-AN has no theoretical upper limit for the improvement of SC. Therefore, the SC of SCO-AN is always higher than that of AN.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The SC of AN and SCO-AN versus different SNR.

In the real-life communication environment, Alice must consider the influence of power when transmitting signals. A reasonable power allocation will effectively increase the SC of the system. After considering the transmission power, the SC of the system is as follows:

(3)

In (3), H and G are legitimate channel CSI and eavesdropping channel CSI, respectively.

and

are the variance of noise in legitimate channel and eavesdropping channel, respectively.

is the power of the transmitted signal, and the power of SCO-AN is

; therefore,

. If the variables in (3) are

and

, the Hessian matrix of (3) is nonpositive definite so that (3) is nonconvex.

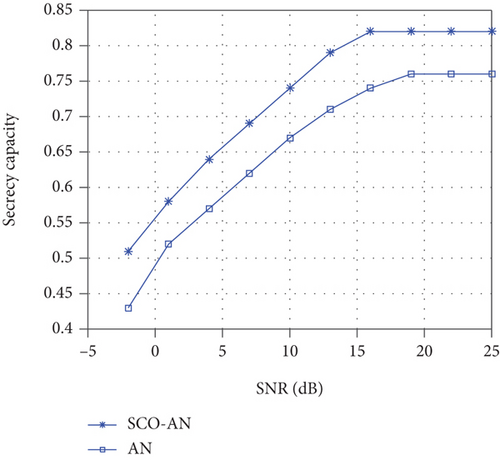
Due to the nonconvex property of the SCO-AN PA function, the extremum of the function and the optimal power allocation cannot be obtained. The iterative algorithms in [26–29] are applied to derive the maximum for PA function within a specific range. The iterative algorithms are affected by the initial value seriously and have a limited optimization effect.

Figure 2 shows a comparison of the different nonconvex optimization algorithms.

From Table 3, we can see that the different initial states of the transmitted signal and SCO-AN can lead to different optimization results, which is caused by the nonconvexity of the PA function. Therefore, traditional nonconvex optimization algorithms cannot get excellent optimization results. SQP is a classic iterative optimization algorithm. In the following sections, we continue to study the optimal PA and lower bound of secrecy capacity of SCO-AN under ideal conditions.

Table 3. The initial state influence on SC.

Algorithm	Initial (,)	Initial SC	Optimized SC
SQP	(5,5)	0.5612	0.6375
SQP	(3,7)	0.4785	0.5364
SQP	(1,9)	0.3821	0.4357

3. Problem State

3.1. System Model

In Figure 3, the system model of MIMO communication with eavesdroppers is shown. The noncolluding and colluding eavesdropper cases are discussed in this paper. Therefore, the system model has two scenarios: noncolluding and colluding eavesdroppers.

Alice is the transmitter of information. The number of Alice’s antennas is N_K. Bob is the receiver of information. The number of Bob’s antennas is N_P. Eve is the eavesdropper of information.

There are N_L eavesdroppers in the system. For colluding scenario, the N_L eavesdroppers can eavesdrop on information, which means that the eavesdropped information will be exchanged and processed jointly. The noncolluding eavesdropper is a special scenario that these N_L eavesdroppers independently eavesdrop on information. When studying this scenario, we conducted research on each independent eavesdropper, which can be considered N_L = 1. Similar settings can be found in [15, 30]. For the facilitation of discussion, we assumed N_K > N_L and N_K = N_P.

Here we have the following:

(4)

(5)

y_B is Bob’s received signal, and y_E is Eve’s eavesdropping signal. H is the CSI matrix of the legitimate channel. The dimension of H is N_K × N_P. G is the CSI of eavesdropping channel. For the colluding scenario, G is a matrix and the dimension of G is N_K × N_L; for the noncolluding scenario, G is a vector and the dimension of G is N_K × 1. Each element in H and G is zero-mean complex Gaussian random variables and independent identically distributed (i.i.d). x is signal transmitted by Alice. n and e are the additive Gaussian white noise (AWGN) in legitimate and eavesdropping channels. The variance of n is . The variance of e is .

Because AN is orthogonal to H, according to the theory of matrices, AN cannot be designed when N_K = N_P. The key idea of SCO-AN is to design a signal which does not show orthogonality to legitimate and eavesdropping channels. SCO-AN effectly reduces eavesdropping channel capacity while slightly reducing the capacity of legitimate channels [16]. Therefore, SCO-AN will improve the SC of the communication system.

We design the transmitted signal as below: x is a vector, the dimension of x is N_K × 1. x = r₁u + r₂v, where r₁ = H^†/‖H‖. u is the signal which bears the information. The power of u is

. v is the SCO-AN. The elements of v are i.i.d. In v, each power of the N_K − 1 column vectors is

. [∗]^† is the conjugate transpose operation of ∗. ‖∗‖ is the norm of ∗. So the legitimate receiving and eavesdropping signal becomes the following:

(6)

(7)

where H₁ = Hr₂, G₁ = Gr₁, and G₂ = Gr₂.

Let the power for each transmission be P,

. The proportion of SCO-AN to P is ϕ. Here,

(8)

(9)

From (8) and (9), we can come to the conclusion that Alice could adjust the PA strategy by adjusting ϕ.

4. ELB of SC for SCO-AN

The ELB of SC for SCO-AN is derived in this section. The legitimate channel capacity is as follows:

(10)

In (10), for the facilitation of discussion, we hypothesize the signal-noise-ratio (SNR) of communication is high enough, so P ≫ 1. Therefore, the ‖H‖²P is much larger than

is an arbitrarily small number which can be ignored. (10) is written as follows:

(11)

From (11), we can conclude that the capacity of the legitimate channel is mainly related to N_k and ϕ in a high SNR regime. Alice can adjust the capacity of the legitimate channel by adjusting ϕ and N_K.

Alice has no knowledge of SNR of G. In order to enable secure communication, we assume that is arbitrarily tiny, which means the eavesdropper has the best communication environment.

Therefore, the upper bound on the eavesdropping channel capacity without considering

is as follows:

(12)

r is the inverse of ϕ, r = ϕ⁻¹.

R = [r₁r₂] is a unitary matrix. GR = [G₁ G₂] is a complex Gaussian matrix, and G₁ and G₂ are independent. Therefore,

is equivalent to the signal-to-interference ratio of a N_L − branch mininum mean square error (MMSE) diversity combiner with N_K − 1 interferers. According to [30, 31], the complementary cumulative distribution function of

is as follows:

(13)

According to (13), we can rewrite (12) as follows:

(14)

In (14), Bet(·) is the function of beta distribution and Bet(a, b) = Γ(a)Γ(b)/Γ(a + b). K₁(·) is Gaussian hypergeometric function. Formula (14) uses conclusion in [31].

From [5], the ELB of SC is

and [a]⁺ denotes max{0, α}. The ELB of SC is as follows:

(15)

In the following sections, the simplified and approximated expressions on ELB of SC will be discussed.

In (15), from [32], here we have

(16)

(17)

where (m)_n is the rising factorial. So,

(18)

In [32], we know K₁(1, 1; 2; y) = −ln(1 − y)/y. Therefore, here, we have

(19)

Substituting (19) into (18), we can obtain the following:

(20)

From (20), it is easy to obtain

(21)

4.1. The Noncolluding Eavesdropper Case for SC

In the noncolluding eavesdroppers case, there is no cooperation between each eavesdropper; therefore, N_L = 1. Then,

(22)

(22) is derived by applying the Gaussian hypergeometric function. The ELB of SC for noncolluding eavesdroppers is given by the following:

(23)

4.2. The Colluding Eavesdropper Case for SC

In this subsection, the ELB of SC is discussed when N_K is large enough. We know that

when we use the strong law of large numbers. So (12) can be written as follows:

(24)

where E_k( ) is the generalized exponential integral. The channel response of Rayleigh fading channel is an exponential function. So

is a Gamma function. The paramater of

is (N_L, 1).

When N_K is large enough, the ELB of SC is

(25)

From (25), we can conclude that the ELB of SC relates to N_k and r. The optimal PA can be obtained by deriving the ELB of SC. The optimal PA is a function of N_k and r.

5. Optimal PA of SCO-AN

The ELB of SC is discussed in the last section. In this section, the optimal PA of the SCO-AN system is studied. The ELB of SC for noncolluding eavesdroppers and infinite N_K are obtained by (23) and (25). For the facilitation of calculation and discussion, the expressions obtained in the last sections will be applied in this section.

5.1. Optimal PA: Noncolluding Eavesdropper

For the noncolluding case, the N_L = 1, and the ELB of SC in last sections helps us to find the optimal values for the PA coefficients r and ϕ.

The first derivatives of (23)—the ELB of SC—concerning the PA coefficient r will help us to find the optimal PA coefficient. Therefore, the first derivative of (23) satisfies the following:

(26)

From (26), the optimal PA coefficient should satisfy

(27)

(27) is a higher-order equation of r on N_K. Its closed-form solution is challenging to find or even nonexistent. Moreover, according to the difference of N_K, its root-finding formula is also different. Therefore, in the following research content, we provide some of the optimal PA coefficients with a particular number of commonly used antennas.

5.2. Optimal PA: Colluding Eavesdroppers

In this subsection, the colluding eavesdropper’s case is studied. We improve the optimal PA coefficient algorithm under colluding eavesdroppers in the classic paper [30].

In [30], for the convenience of calculation, is simplified to exp(r − 1)E_k(r − 1). The first N_L − 1 items in have been omitted. This will cause large errors in the calculation results. So we will improve this formula in order to get better calculation results.

Considering the expression of C in (25) and taking its derivative concerning r, the optimal r satisfies the following:

(28)

Hence, we have shown that for sufficiently large N_K, the optimal PA is given by (28). The solution of Equation (28) is the optimal PA coefficient. The optimal ratio of PA depends on N_L and N_K.

In Table 4, we provide the optimal PA coefficients for some commonly used transmitting and eavesdropping antennas. Alice can allocate power to the transmitted signal by looking up the table instead of using an algorithm for power allocation. From Table 4, we can also see that when the number of eavesdropping antennas increases, it is wise to allocate more power to the SCO-AN to confuse the eavesdropper. At the same time, when N_K increases, the capacity of the legitimate channel increases, which can reduce the power allocated for SCO-AN.

Table 4. Optimal ϕ for different N_K and N_L.

Number of N_K	Number of N_L	Optimal ϕ
2	1	0.292
2	2	0.313
2	4	0.327
2	8	0.339
4	1	0.271
4	2	0.282
4	4	0.312
4	8	0.327
8	1	0.255
8	2	0.262
8	4	0.272
8	8	0.284
16	1	0.232
16	2	0.238
16	4	0.252
16	8	0.267
32	1	0.207
32	2	0.212
32	4	0.232
32	8	0.242
64	1	0.185
64	2	0.202
64	4	0.231
64	8	0.252
128	1	0.171
128	2	0.190
128	4	0.201
128	8	0.224

6. Secrecy Capacity: Imperfect Channel State Information

The previous section explored the ELB of SC obtained with the perfect CSI. We will continue to discuss the effect of the imperfect CSI.

The CSI estimation error introduces extra noise into the legitimate channel. Bob uses the channel estimation algorithm to get the CSI. The CSI is imperfect due to the Gaussian noise. Therefore,

(29)

where

denotes the channel state information obtained by MMSE channel estimate and

denotes the channel estimation error.

and

are uncorrelated due to the property of the MMSE estimation. Therefore,

(30)

r₁ is designed as

, and the symbol received by Bob is

(31)

where H₁ = Hr₂. R is a unitary matrix, so the distribution of

and

is the same. Therefore, the ELB of SC for the legitimate channel is

(32)

With

normalized to unity, we have

. Each subchannel between Alice and Bod obeys exponential distribution. Therefore,

follows a Gamma distribution with parameter (

). Here, we have

(33)

In (33), h(x) is the inverse function (

) of (32), and g(x) is the first derivative of h(x). Therefore,

(34)

(35)

The error of channel estimation does not affect Eve’s channel. Therefore, the ELB of SC is as follows:

(36)

where Γ( ) denotes the Gamma function and Ψ⁽ⁿ⁾( ) denotes the n_th derivative of the polygamma function.

7. Results and Discussion

7.1. Simulation Parameters

In the simulation, the legitimate and eavesdropping channels are Rayleigh fading channels. The relevant simulation parameters are shown in Table 5.

Table 5. Simulation environment.

Parameters	Values
N_k	From 1 to 256
N_L	From 1 to 256
Power for each transmission	10 (W)
Mean of legitimate and eavesdropping channels	0
Variances of legitimate and eavesdropping channels	0.5
SNR of legitimate and eavesdropping channels	From -5 to 30 (dB)

7.2. Simulation Results and Discussion

Figure 4 shows how ELB of SC changes with N_k and N_l. The ELB of SC is calculated by (15) with the optimal ϕ. It can be seen from Figure 4 that when the number of transmitting antennas N_k increases, the SC also increases. It can also be seen from (15) that N_k is located on the molecule, and N_k plays a positive role in the promotion of SC. Similarly, the increase in the number of eavesdropping antennas will reduce the SC of the system. The above conclusions are easy to understand. The increase in the number of transmitting antennas represents an increase in the capacity of the legitimate channel. Therefore, the SC will increase. Similarly, the increase in the number of eavesdropping antennas will result in a decrease in the SC.

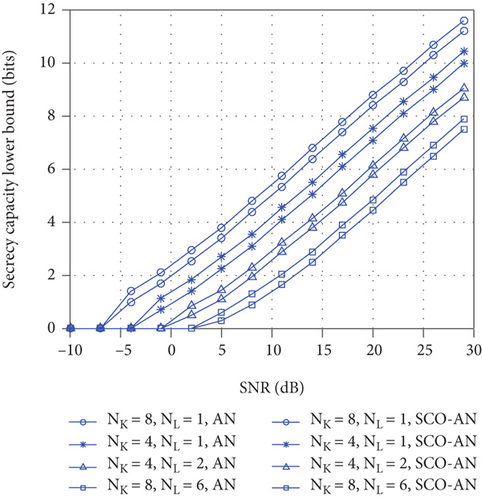
Figure 5 shows the effect of the number of eavesdropping antennas on the SC. It can be seen that with the increase in the number of eavesdropping antennas, the SC of the wireless communication system decreases under the condition that the legitimate channel remains unchanged. At the same time, Figure 5 shows the SC of the wireless communication system for AN and SCO-AN when N approaches infinity. It can be seen that the ELB on SC of SCO-AN is higher than that of AN.

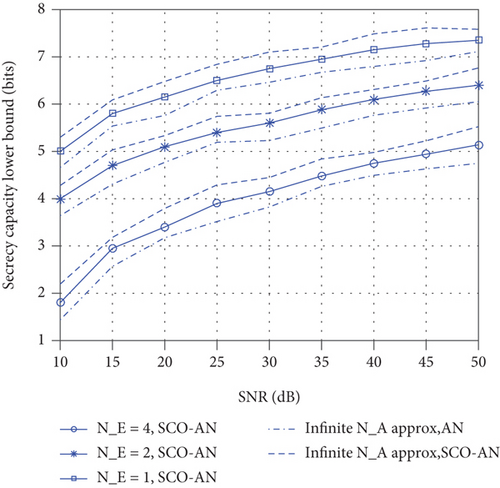
Figure 6 shows the ELB of SC in (15) with the optimal ϕ. For comparison, the ELB of SC for AN with equal power allocation is indicated by solid lines. ELB of SC for SCO-AN is always greater than that for AN. The SC increases as N_K grows. The optimal ϕ of SCO-AN is much smaller than that of SC for AN, which means SCO-AN has a better secrecy performance with less power for extra artificial noise. It proves that SCO-AN is a better artificial noise when compared to AN. The SC of the wireless communication system decreases, which shows that the channel estimation error has a counterproductive effect on the security performance of the wireless communication system, which is also in line with reality. The imperfect CSI will cause Alice to error in the distribution of transmitting power, which will leads to a decrease in the SC.

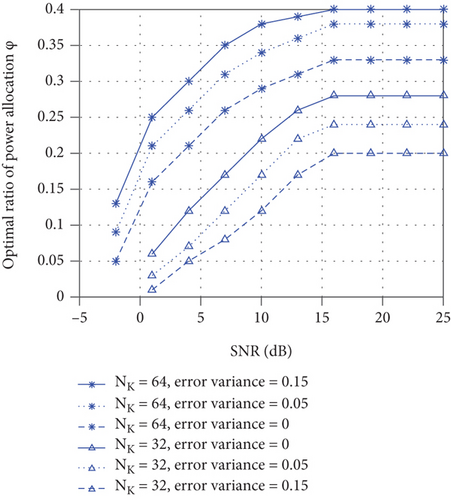
The AWGN produces the CSI estimation error. So the CSI estimation error decreases with SNR. The deviation of the PA ratio between the practical system and the perfect CSI system becomes smaller with the increase of SNR. We should consider the channel estimation error when SNR is low in a practical system.

Figure 7 shows the SC with optimal ϕ and different types of (LS and MMSE) [31]. MMSE and LS are classic channel estimation algorithms. It can be seen that for the influence of different levels of imperfect CSI on SC, the influence of wireless communication systems using MMSE channel estimation is always less than that of LS, which is because the MMSE channel estimation accuracy is higher than that of the LS, so the MMSE channel estimation has less influence on Alice’s power allocation. At the same time, the increase of the channel estimation error level will cause the decrease of SC.

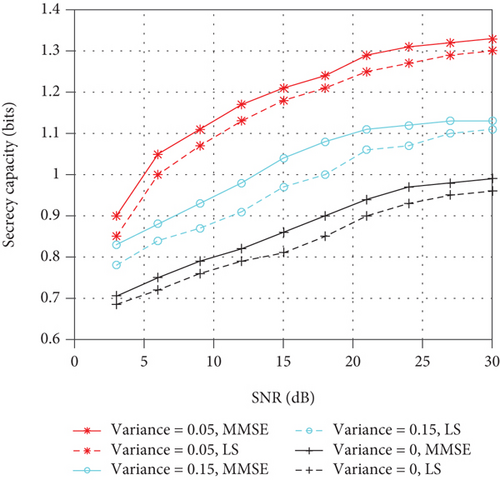
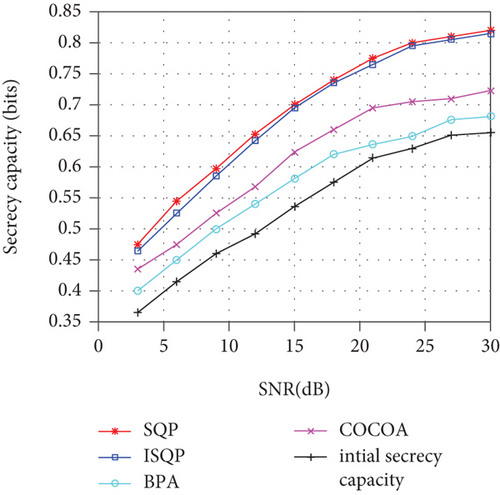
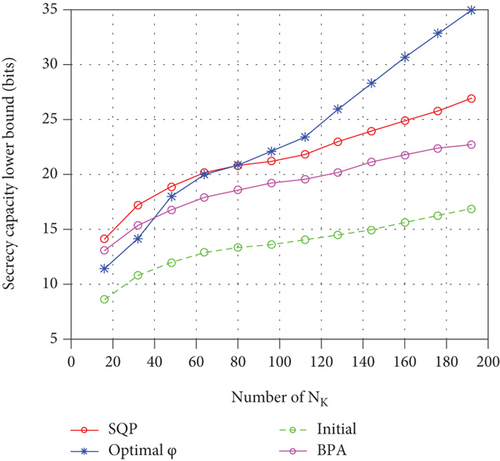
Figure 8 shows the ELB of SC with different PA methods. We use SQP and BPA algorithms [26] to compare with the optimal PA coefficient presented in this paper. We can see from Figure 8 that under the condition that transmitting antennas’ number is small, the ELB of SC using the optimal power distribution coefficient is smaller than that of SQP; when the number of antennas increases, the SC using the optimal power distribution coefficient increases significantly, which is consistent with the theory in this paper. Since the conclusions derived in this paper are derived using the strong law of large numbers, which is a statistical theory, the larger the number of samples, the more accurate the results of the theoretical derivation. Therefore, in the case of a small number of antennas, the algorithm in this paper is not as good as the traditional iterative optimization algorithm. But when the number of antennas is large enough, the algorithm in this paper is far better than the traditional iterative optimization algorithm. Since the optimal power distribution coefficient is based on statistics, the optimal power distribution coefficient can be used well for massive MIMO.

Figures 9 and 10 show optimal power distribution coefficient in (28) with different N_K and N_L. Figures 9 and 10 show optimal ϕ reduces as N_L grows; we should allocate more power to SCO-AN as N_L increases. On the contrary, when N_K increases, less power should be allocated to SCO-AN. Figures 9 and 10 also show that we should generate more power to the information-bearing signal with the SNR increase.

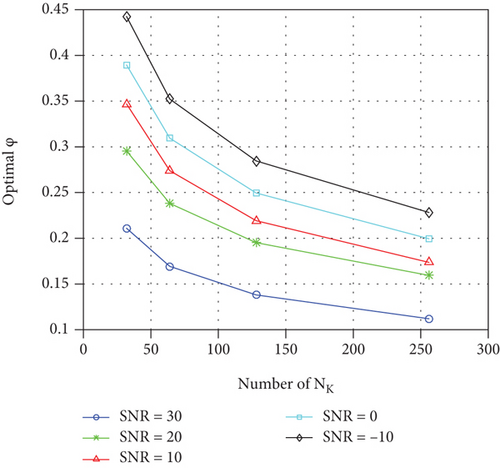
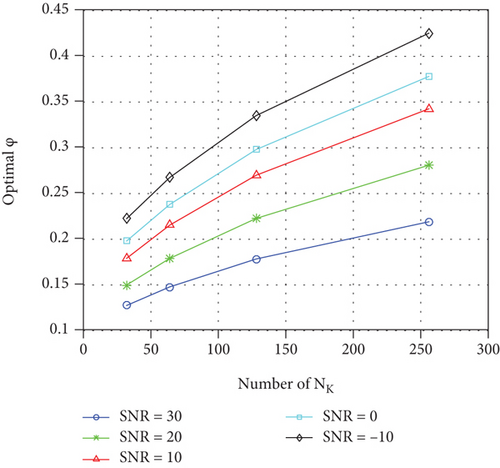
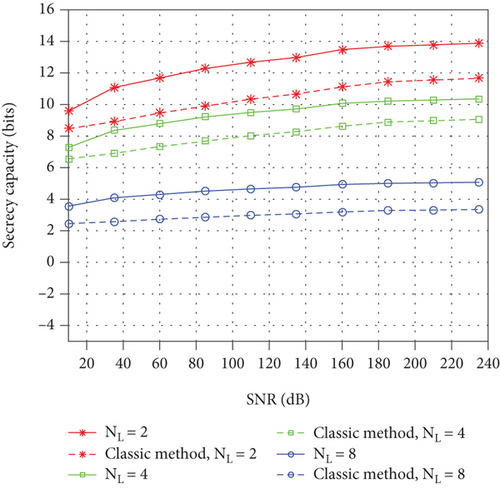
Figure 11 shows the comparison between the algorithm in this paper and the algorithm in the classic paper [30]. The solid line SC in Figure 11 is calculated by the optimal PA coefficient obtained by (28). The dotted SC is calculated by the best PA coefficient obtained in the classic paper [30]. Under the same conditions of N_k and N_L, the algorithm in this paper has a better improvement on SC, while the algorithm in the classic paper [30] discards too many items, resulting in a significant error in the optimal PA coefficient, and the effect of improving the SC is reduced.

8. Conclusion

This paper researches ELB of SC under large-scale MIMO. Aiming at the problem that traditional optimization algorithms cannot find the maximum value of nonconvex PA function, this paper uses statistical methods to study the PA technology of SCO-AN in large-scale MIMO systems. First, this paper derives the expression of ELB of SC. Then, the best PA coefficient function based on this expression of ELB of SC is derived. According to the optimal PA coefficient function, the optimal PA coefficient under the conditions of different transmitting antennas and the number of eavesdropping antennas can be deduced. The application of the PA coefficient can significantly improve the SC without the optimization algorithm. This paper also considers the impact of imperfect CSI on PA; when N_K increases or N_L decreases, the power of SCO-AN should be reduced. At the same time, when the level of imperfect CSI increases, more power should be allocated to SCO-AN.

Abbreviations

AN:: Artificial noise
SCO-AN:: Secrecy capacity optimization artificial noise
MIMO:: Multiple-input multiple-output
CSI:: Channel state information
SC:: Secrecy capacity
PA:: Power allocation
ELB:: Ergodic lower bound
IRS:: Intelligent reflecting surface.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

1 Hashem T. and Hasan R., Method and system for secure transmission of information, 2004, US Patent 6-792544.
Google Scholar
2 Wyner A., The wire-tap channel, Bell System Technical Journal. (1975) 54, no. 8, 1355–1387, https://doi.org/10.1002/j.1538-7305.1975.tb02040.x, 2-s2.0-0016562514.
10.1002/j.1538-7305.1975.tb02040.x
Web of Science® Google Scholar
3 Csiszar I. and Korner J., Broadcast channels with confidential messages, IEEE Transactions on Information Theory. (2003) 24, 339–348.
10.1109/TIT.1978.1055892
Web of Science® Google Scholar
4 Barros J. and Rodrigues M., Secrecy capacity of wireless channels, 2006 IEEE international symposium on information theory, 2006, Seattle, 356–360.
Google Scholar
5 Oggier F. and Hassibi B., The secrecy capacity of the MIMO wiretap channel, IEEE Transactions on Information Theory. (2011) 57, no. 8, 4961–4972, https://doi.org/10.1109/TIT.2011.2158487, 2-s2.0-79960996804.
10.1109/TIT.2011.2158487
Web of Science® Google Scholar
6 Zhu J., Robert S., and Vijay K., Linear precoding of data and artificial noise in secure massive MIMO systems, IEEE Transactions on Wireless Communications. (2015) 15, 2245–2261.
10.1109/TWC.2015.2500578
Web of Science® Google Scholar
7 Zeng M., Securing downlink massive MIMO-NOMA networks with artificial noise, IEEE Journal of Selected Topics in Signal Processing. (2019) 15, 685–699.
10.1109/JSTSP.2019.2901170
Google Scholar
8 Jo M., Gao H., Su Y., Zhang S., and Hou Y., Joint antenna selection and power allocation for secure co-time co-frequency full-duplex massive mimo systems, IEEE Transactions on Vehicular Technology. (2021) 70, 655–665.
10.1109/TVT.2020.3048854
Web of Science® Google Scholar
9 Wu Y., Schober R., Ng D. W. K., Xiao C., and Caire G., Secure massive MIMO transmission with an active eavesdropper, IEEE Transactions on Information Theory. (2016) 62, no. 7, 3880–3900, https://doi.org/10.1109/TIT.2016.2569118, 2-s2.0-84969998525.
10.1109/TIT.2016.2569118
Web of Science® Google Scholar
10 Ekrem E. and Ulukus S., The secrecy capacity region of the Gaussian MIMO multi-receiver wiretap channel, IEEE Transactions on Information Theory. (2011) 57, no. 4, 2083–2114, https://doi.org/10.1109/TIT.2011.2111750, 2-s2.0-79952846257.
10.1109/TIT.2011.2111750
Web of Science® Google Scholar
11 Ciuonzo D., Aubry A., and Carotenuto V., Vincenzo. C, Rician MIMO channel-and jamming-aware decision fusion, IEEE Transactions on Signal Processing. (2017) 65, no. 15, 3866–3880, https://doi.org/10.1109/TSP.2017.2686375, 2-s2.0-85028306056.
10.1109/TSP.2017.2686375
Web of Science® Google Scholar
12 Chakravarty J., Johnson O., and Piechocki R., A convex scheme for the secrecy capacity of a MIMO wiretap channel with a single antenna eavesdropper, 2019 IEEE International Conference on Communications (ICC), 2019, Shanghai, 1–5.
Google Scholar
13 Jia Y., Zhong Z., and Gao F., On the conditioning channel capacity of MIMO two-way relay networks against eavesdropper, 10th International Conference on Communications and Networking in China, 2015, Shanghai, 199–204.
Google Scholar
14 He X. and Yener A., MIMO wiretap channels with arbitrarily varying eavesdropper channel states, IEEE Transactions on Information Theory. (2017) 60, 6844–6869.
10.1109/TIT.2014.2359192
Google Scholar
15 Negi R. and Goel S., Secret communication using artificial noise, IEEE Vehicular Technology Conference, 2005, Dallas.
Google Scholar
16 Yebo G., Zhilu W., Zhendong Y., and Xiaojun Z., The secrecy capacity optimization artificial noise: a new type of artificial noise for secure communication in MIMO system, IEEE Access. (2019) 7, 58353–58360.
10.1109/ACCESS.2019.2905764
Web of Science® Google Scholar
17 Guan X., Wu Q., and Rui Z., Intelligent reflecting surface assisted secrecy communication: is artificial noise helpful or not?, IEEE Wireless Communications Letters. (2020) 9, 778–782, https://doi.org/10.1109/lwc.2020.2969629.
10.1109/LWC.2020.2969629
Web of Science® Google Scholar
18 Zhang X., Guo D., An K., Ma W., and Guo K., Secure transmission and power allocation in multiuser distributed massive MIMO systems, Wireless Networks. (2020) 26, no. 2, 941–954, https://doi.org/10.1007/s11276-018-1840-y, 2-s2.0-85053877801.
10.1007/s11276-018-1840-y
Web of Science® Google Scholar
19 Hong S., Pan C., Ren H., Wang K., and Nallanathan A., Artificial-noise-aided secure MIMO wireless communications via intelligent reflecting surface, IEEE Transactions on Communications. (2020) 68, no. 12, 7851–7866, https://doi.org/10.1109/TCOMM.2020.3024621.
10.1109/TCOMM.2020.3024621
Web of Science® Google Scholar
20 Gu Y., Huang B., and Wu Z., Power allocation for secrecy-capacity-optimization-artificial-noise secure MIMO precoding systems under perfect and imperfect channel state information, Apply Sciences. (2021) 11, no. 10, https://doi.org/10.3390/app11104558.
10.3390/app11104558
Google Scholar
21 Khan F., Malik Z., Nasir A., and Masood M., Relay selection & power allocation for maximizing sum-throughput of a buffered relay network, IEEE Communications Letters. (2020) 99, 1318–1322, https://doi.org/10.1109/lcomm.2020.2981882.
10.1109/LCOMM.2020.2981882
Google Scholar
22 Zhu J., On optimal power allocation for downlink non-orthogonal multiple access systems, IEEE Journal on Selected Areas in Communications. (2017) 35, 2744–2757.
Web of Science® Google Scholar
23 Zhang H., Downlink energy efficiency of power allocation and wireless backhaul bandwidth allocation in heterogeneous small cell networks, IEEE Transactions on Communications. (2017) 66, 1705–1716.
10.1109/TCOMM.2017.2763623
Web of Science® Google Scholar
24 Chen M. and Yener A., Power allocation for F/TDMA multiuser two-way relay networks, IEEE Transactions on Wireless Communications. (2010) 9, no. 2, 546–551.
10.1109/TWC.2010.02.090336
PubMed Web of Science® Google Scholar
25 Jiang Y., Zou Y., Guo H., Zhu J., and Gu J., Power allocation for intelligent interference exploitation aided physical-layer security in ofdm-based heterogeneous cellular networks, IEEE Transactions on Vehicular Technology. (2020) 69, no. 3, 3021–3033, https://doi.org/10.1109/TVT.2020.2966637.
10.1109/TVT.2020.2966637
Web of Science® Google Scholar
26 Büskens C. and Maurer H., SQP-methods for solving optimal control problems with control and state constraints: adjoint variables, sensitivity analysis and real-time control, Journal of Computational and Applied Mathematics. (2000) 120, no. 1-2, 85–108, https://doi.org/10.1016/S0377-0427(00)00305-8, 2-s2.0-0034255101.
10.1016/S0377-0427(00)00305-8
Web of Science® Google Scholar
27 Tse D., Optimal power allocation over parallel Gaussian broadcast channels, Proceedings of IEEE International Symposium on Information Theory, 1997, Ulm, Germany.
Google Scholar
28 Zhao Y., Raviraj A., and Teng J., Improving amplify-and-forward relay networks : optimal power allocation versus selection, IEEE International Symposium on Information Theory, 2006, Seattle, 1234–1238.
Google Scholar
29 Ding Z., Perlaza S. M., Esnaola I., and Poor H. V., Power allocation strategies in energy harvesting wireless cooperative networks, IEEE Transactions on Wireless Communications. (2014) 13, no. 2, 846–860, https://doi.org/10.1109/twc.2013.010213.130484, 2-s2.0-84896342581.
10.1109/TWC.2013.010213.130484
Web of Science® Google Scholar
30 Zhou X. and Matthew R., Secure transmission with artificial noise over fading channels: achievable rate and optimal power allocation, IEEE Transactions on Vehicular Technology. (2010) 59, no. 8, 3831–3842, https://doi.org/10.1109/TVT.2010.2059057, 2-s2.0-77958083375.
10.1109/TVT.2010.2059057
Web of Science® Google Scholar
31 Gao H., Smith P., and Clark V., Theoretical reliability of MMSE linear diversity combining in Rayleigh-fading additive interference channels, IEEE Transactions on Communications. (1998) 46, no. 5, 666–672, https://doi.org/10.1109/26.668742, 2-s2.0-0032074954.
10.1109/26.668742
Web of Science® Google Scholar
32 Abramowitz M., Stegun I., and Romain I., Handbook of Mathematical Functions, with Formulas, Graphs, and Mathematical Tables, Physics Today. (1966) 19, no. 1, 120–121, https://doi.org/10.1063/1.3047921.
10.1063/1.3047921
Web of Science® Google Scholar

All articles

Secrecy-Capacity-Optimization-Artificial-Noise in Large-Scale MIMO: Ergodic Lower Bound on Secrecy Capacity and Optimal Power Allocation

Abstract

1. Introduction

2. Related Work

3. Problem State

3.1. System Model

4. ELB of SC for SCO-AN

4.1. The Noncolluding Eavesdropper Case for SC

4.2. The Colluding Eavesdropper Case for SC

5. Optimal PA of SCO-AN

5.1. Optimal PA: Noncolluding Eavesdropper

5.2. Optimal PA: Colluding Eavesdroppers

6. Secrecy Capacity: Imperfect Channel State Information

7. Results and Discussion

7.1. Simulation Parameters

7.2. Simulation Results and Discussion

8. Conclusion

Abbreviations

Conflicts of Interest

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley