Volume 2021, Issue 1 9230714

Research Article

Open Access

A New Numerical Technique for Solving Volterra Integral Equations Using Chebyshev Spectral Method

Corresponding Author

Ahmed A. Khidir

[email protected]

orcid.org/0000-0002-2053-6377

Faculty of Technology of Mathematical Sciences and Statistics, Alneelain University, P.O. Box 12702, Khartoum, Sudan neelain.edu.sd

Department of Mathematics, Faculty of Sciences, University of Tabuk, P.O. Box 741, Tabuk, Saudi Arabia ut.edu.sa

Search for more papers by this author

Ahmed A. Khidir,

Corresponding Author

Ahmed A. Khidir

[email protected]

orcid.org/0000-0002-2053-6377

Faculty of Technology of Mathematical Sciences and Statistics, Alneelain University, P.O. Box 12702, Khartoum, Sudan neelain.edu.sd

Department of Mathematics, Faculty of Sciences, University of Tabuk, P.O. Box 741, Tabuk, Saudi Arabia ut.edu.sa

Search for more papers by this author

First published: 03 September 2021

https://doi.org/10.1155/2021/9230714

Citations: 4

Academic Editor: Bosheng Song

Share a link

Email
Wechat
Bluesky

Abstract

In this work, we propose a new method for solving Volterra integral equations. The technique is based on the Chebyshev spectral collocation method. The application of the proposed method leads Volterra integral equation to a system of algebraic equations that are easy to solve. Some examples are presented and compared with some methods in the literature to illustrate the ability of this technique. The results demonstrate that the new method is more efficient, convergent, and accurate to the exact solution.

1. Introduction

Many mathematical formulations of physical phenomena contain integral equations; these equations arise in many fields including biology, economics engineering, and medicine; for more details, see [1–4]. Finding solutions of linear or nonlinear Volterra integral equations is highly interesting for researchers and scientists in this field and there are available studies to find analytical or numerical solutions for Volterra integral equations (see [5–8]). In fact, Volterra integral equations are usually difficult to solve analytically, so we resort to finding approximate solutions to the problems using numerical or analytical approximation methods. The main purpose of this work is to introduce a new method for solving Volterra integral equations that uses Chebyshev spectral collocation method. Chebyshev spectral collocation methods have been applied successfully in different areas of sciences and engineering because of their ability to give highly accurate solutions of single or system of boundary value problems [9–13]. Chebyshev spectral methods are defined everywhere in the computational domain. Therefore, it is easy to compute high accurate values of a considered function at any point of the domain.

In the proposed method, we introduce a new integral transformation that is the replacement of an integral term in the Volterra integral equation by Chebyshev spectral differential matrix of known elements. The advantages of this approach over the standard same approaches are as follows: (i) the current technique suggests a standard way of choosing the auxiliary linear operator of the integral equation which is the main motivation behind the selection of the current algorithm whereas the other methods are choosing a linear operator to be simple in order to ensure that the integral or integrodifferential equations can be easily integrated and (ii) this algorithm transforms the integral equation(s) into a system of linear algebraic equations which is easier and faster to solve when compared to a system of integral equations. One of the disadvantages of this method is that it cannot be applied directly to the nonlinear integral equations; therefore, we need first to linearized the nonlinear integral equation using any available method such as the successive linearization method [14–17]. The applicability, accuracy, and reliability of the proposed method are confirmed by solving the various Volterra integral equations.

This paper is organized as follows: in Section 2, we introduce a description of the proposed method. In Section 3, the proposed method is implemented in some cases. The numerical results are discussed and investigated in Section 4. Finally, the paper is concluded in Section 5.

2. Description of the Method

Let us consider the Volterra integral equation of the second kind defined as

(1)

with

(2)

where u(x) is an unknown function and the kernel K(x, t) and the source term function f(x) are given functions.

In the proposed method, we are seeking for for solving the linear Volterra integral equation of the form (1) using the Chebyshev collocation method. This method is based on approximating the unknown function u(x) by the Chebyshev interpolating polynomials at the Gauss–Lobatto collocation points defined on the domain [0, x_N] by [18–20]

(3)

The unknown function u(x) is approximated as a truncated series of Chebyshev polynomials of the form

(4)

where T_k is the k th Chebyshev polynomial and u_k are the Chebyshev coefficients. The derivatives of u(x) at the collocation points are represented as

(5)

where r is the order of differentiation,

is the Chebyshev differentiation matrix, and N + 1 is the number of collocation points. We express the entries of the differentiation matrix

as [18–20]

(6)

We introduce the following simple integral equation:

(7)

where v(t) is a known function. Clearly, the existence of the function ϕ(x) depends on the existence of the integral. One approach is to note that the integral equation (7) is a special case of an initial value problem expressed as

(8)

This differential equation can be solved using the Chebyshev spectral collocation method by replacing the differential operator d/dx with the transformed Chebyshev differentiation matrix D defined on the domain x ∈ [0, x_N] (see [21]) and also the functions v(x) and u(x) are written in vectors forms of sizes (N + 1) × 1; this yields

(9)

where ϕ_i = ϕ(x_i), u_i = u(x_i), and v_i = v(x_i) and the superscript T denotes the transpose.

From the solution of the initial value problem (9), the integral equation (7) can be written in matrices form of unknown function u(x) as follows:

(10)

where u₀ and v₀ are known values; here, the first row of transformed Chebyshev differential matrix D in equation (10) is interchanging by the row

. This is caused by the condition ϕ(0) = 0.

Now, according to equations (7) and (10), we introduce the following transformation.

2.1. Definition

Let u(x) and v(x) be continuous functions on [0, x_N]; then, the integral

is transformed into matrices form as follows:

(11)

where L is a square matrix of size (N + 1) × (N + 1) defined as

(12)

and L_v is a multiplication of matrix L by the vector v defined by

(13)

where

is the modified matrix D after implementing initial condition. It is clear that this transformation is linear and it is easy to show this property.

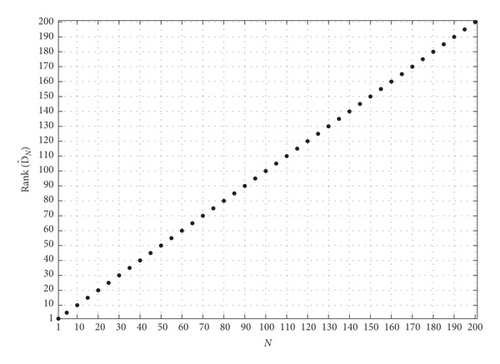
The existence and uniqueness of the linear transformation L defined in (12) depend on the existence and uniqueness of the inverse of matrix . In linear algebra, if A is a square matrix of size N × N, then (i) A is invertible if and only if rank (A) = N and (ii) if A is invertible, then its inverse is unique [22]. We applied this theorem to all square matrices to show that these matrices are invertible. In Figure 1, we display all the sizes of the matrices of sizes (N + 1) × (N + 1) against the corresponding ranks for 1 ≤ N ≤ 200. We notice that, from Figure 1, the rank of the matrix is equal to its size for all those values of N; that is, the matrix is invertible and consequently the inverse is unique.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Ranks of matrices .

For the kernel K(x, t) of the Volterra integral equation (1), we assume that the function K(x, t) can be separated into two multiplied functions w(x) and v(t) as follows:

(14)

Substituting (5), (11), and (14) in equation (1) gives the following system of linear equations:

(15)

in which A is an (N + 1) × (N + 1) square matrix and F is (N + 1) × 1 column vector obtained by

(16)

where diag […] is the diagonal matrix of size (N + 1) × (N + 1) that puts the vector […] of size (N + 1) × 1 on the main diagonal and I is an identity matrix of size (N + 1) × (N + 1). Finally, the solution of the Volterra integral equation (1) is obtained by solving the linear system (15) as

(17)

The general idea underpinning the use of the proposed method is the replacement of a linear Volterra integral equation by a system of linear algebraic equations that replace the integral part in the integral equation by the introduced integral transformation. The obtained linear algebraic equations can easily be solved with the help of symbolic computation software such as Maple, Mathematica, MATLAB, and other symbolic computer packages.

3. Numerical Examples

To illustrate the effectiveness and accuracy of the proposed technique in the present work, several examples are carried out in this section.

Example 1. Consider the following Volterra integral equation:

(18)

The exact solution is u(x) = −xe^x. According to (14), we have

(19)

To apply the proposed method to this test problem, we rewrite equation (19) in the following system of linear equations:

(20)

where

, and

Thus, the final solution is obtained as

(21)

Example 2. Consider the following Volterra–Fredholm integral equation [23]:

(22)

where

. The exact solution is

. According to (14), we have

(23)

Applying the proposed method to this problem, equation (23), we obtain the system of linear equations:

(24)

where A = I − diag[x]L_x + Rdiag[x] − diag[x]R,

, and

; the rows of the matrix R are obtained by subtracting the first row from the last row of the matrix:

(25)

Thus, the final solution of the Volterra–Fredholm integral equation (22) is obtained as

(26)

Example 3. Consider the following system of linear Volterra integral equations [24]:

(27)

with

(28)

where the exact solution is u(x) = sin x and g(x) = e^x. To illustrate the use of the proposed method to approximate the solution of this integral equations system, we rewrite the system as

(29)

Now, converting the system above into a system of linear algebraic equations using the proposed method gives

(30)

where

and

. Finally, the solution of the system of integral equations (30) is obtained as

(31)

where u, F, and A are defined as

(32)

Example 4. Consider the following quadratic nonlinear Volterra integral equation [25]:

(33)

with

. The exact solution is u(x) = e^x.

For solving the nonlinear Volterra integral equation (33), we first use the successive linearization method (SLM) [14–17] to linearize the nonlinear integral equation (33). The SLM was recently introduced as an efficient linearization algorithm and robust method for solving boundary value problems. The procedure of the SLM is based on transforming the governing nonlinear equation into an iterative scheme made up of linear equations which is subsequently solved using the proposed method. In applying the SLM, we assume that the solution of (33) is obtained by

(34)

where m is the iteration of SLM and u_m(x) are unknown functions that are obtained by solving the linearized integral equation assuming that u_m−1(x) are known functions from previous iterations. The procedure starts with an initial guess u₀(x) which is chosen to satisfy the condition u₀(0) = f(0). A suitable initial guess that satisfies this condition of equation (33) is

(35)

The linearized integral equation to be solved is obtained by substituting equation (34) in integral equation (33) and deleting the nonlinear terms. Thus, the linearized equation is expressed as

(36)

where

. Applying the proposed method on (36) gives the following matrices system:

(37)

where

(38)

where

and v₂ = 1/(1 + u_m). Finally, the solution of the integral equation (33) is given by

(39)

Example 5. Consider the following system of nonlinear Volterra integral equations [26, 27]:

(40)

with the exact solution (u(x), g(x)) = (sin x, cos x). To apply the proposed method to this test problem, we first linearize the equations using the SLM; we start by assuming that the solution of system (40) may be obtained by

(41)

Substituting (41) into (40) gives the linearized form

(42)

The suitable initial guesses for u₀(x) and g₀(x) are u₀(x) = sin x − x and g₀(x) = cos x − (sin² x/2). Applying the proposed method on (42) gives the following m th approximations of the linear system of equations:

(43)

with

(44)

where u_m, g_m, F_1,m−1, and F_1,m−1 are (N + 1) × 1 column vectors. System (43) leads to the matrix equation given as

(45)

where U_m, F_m−1, and A_m−1 are defined as

(46)

Thus, the final solution of the integral equations (40) for u(x) and g(x) is obtained as

(47)

4. Results and Discussion

In this section, we present the numerical results obtained using the proposed method for solving the Volterra integral equations. Implementation of the numerical schemes was performed using the personal computer of 2.5 GHz CPU speed including MATLAB 2017 package to perform the simulation results. The accuracy of the method is demonstrated by presenting infinity error norms u_E(x) between exact and approximate solutions computed as

(48)

where u(x) and

are the exact and the numerical solutions, respectively. The accuracy of the current results was checked by comparing them with other methods reported in the literature. We also generate the computational times of the results to show the computational efficiency of the proposed method. The results of our solutions for all introduced cases in this work are displayed in the tables and graphs and discussed below.

Table 1 gives a comparison between the absolute errors of the present results and the Adomian Decomposition Method (ADM) at different iterations at selected nodes for Example 1. A striking feature of the proposed method is that a high level of accuracy is achieved at the first order of approximation than the ADM, for example, whereas the proposed method gives the exact value at only one iteration for the 14^th digits. This is because the proposed method selects all the terms as linear operator.

Table 1. Comparison between absolute errors of present and AMD results at different iterations of u(x) for Example 1.

x	ADM iterations				Current results
x	1^st iteration	2^nd iteration	3^rd iteration	4^th iteration	1^st iteration
0	0	0	0	0	0
0.25	7.214e − 005	5.318e − 007	2.960e − 009	1.323e − 011	1.665e − 015
0.50	1.385e − 003	2.931e − 005	4.719e − 007	6.123e − 009	3.220e − 015
0.75	6.417e − 003	2.226e − 004	5.924e − 006	1.276e − 007	7.105e − 015
1.00	1.679e − 002	7.669e − 004	2.710e − 005	7.781e − 007	1.421e − 014
1.25	3.241e − 002	1.743e − 003	7.312e − 005	2.503e − 006	2.665e − 015
1.50	5.201e − 002	3.087e − 003	1.443e − 004	5.520e − 006	7.994e − 015
1.75	7.398e − 002	4.664e − 003	2.334e − 004	9.594e − 006	3.730e − 014
2.00	9.688e − 002	6.334e − 003	3.312e − 004	1.427e − 005	7.461e − 014

Table 2 shows a comparison between the results obtained by the current method and Shifted Chebyshev Collocation (SCC) method reported by Youssri and Hafez [23]; both methods have been applied to the Volterra–Fredholm integral equation (Example 2). It is noticed that accurate results with errors of order up to eight digits are observed using the proposed method while the SCC method is accurate up to six digits when applied to this example. Also, we notice that increasing the values of N leads to improvement in the accuracy of the solution using the SCC method whereas increasing the values of N does not affect the improvement in the accuracy of the solution using the proposed method.

Table 2. Comparison of the absolute errors with various choices of N and x for Example 2.

x	N = 8	N = 12	N = 16	Current method
	Youssri and Hafez [23]			Current method
0.1	2.96e − 003	5.97e − 004	3.02e − 005	7.30e − 009
0.2	8.79e − 004	5.75e − 004	3.00e − 004	2.30e − 009
0.3	7.10e − 004	3.63e − 004	1.33e − 004	2.70e − 009
0.4	9.59e − 004	1.64e − 004	4.62e − 005	7.81e − 009
0.5	1.75e − 005	6.72e − 006	3.24e − 006	1.31e − 008
0.6	7.12e − 004	1.31e − 004	2.19e − 005	1.87e − 008
0.7	2.48e − 004	1.43e − 004	6.51e − 005	2.49e − 008
0.8	1.87e − 004	1.75e − 004	6.74e − 005	3.19e − 008
0.9	4.93e − 004	4.87e − 005	9.79e − 006	4.02e − 008
1.0	5.12e − 004	1.71e − 004	7.71e − 005	5.03e − 008

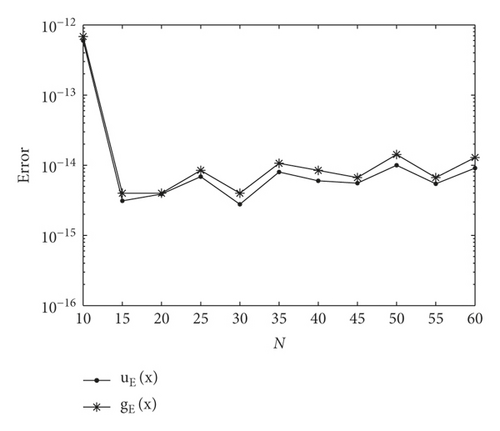
In Table 3, we present the numerical results of the absolute errors u_E(x) and g_E(x) for u(x) and g(x), respectively, at selected nodes obtained by the proposed method, the Bernstein Polynomials Expansion (BPE) method [24], the Artificial Neural Network (ANN) method [24], and the Trapezoidal Quadrature Rule (TQR) method [28] for Example 3. It is remarkable to note that accurate results with errors of order up to sixteen digits are obtained using the proposed method while the BPE, ANN, and TQR methods are accurate up to only two, five, and two digits, respectively. This indicates that the proposed method converges much faster than the BPE, ANN, and TQR methods. Table 4 shows the maximum absolute errors u_E(x) and g_E(x) for u(x) and g(x), respectively, obtained by the proposed method using different values of N. The maximum absolute errors are very small for small values of N. Also, increasing the number of nodes (increasing N) does not result in a significant improvement in the accuracy of the current approximation. We also note that the present method is computationally fast as accurate results are generated in a fraction of a second. In Figure 2, a convergence analysis graph for Example 3 is presented. Figure 2 presents a variation of the error norm at various values of nodes (N). It can be seen that the values of nodes start from N = 10 to converge fully. The accuracy of the method does not improve when increasing grid points N.

Table 3. Errors of the BPE, ANN, TQR methods and the present results for Example 3.

x = 1/2^r	BPE method	ANN method	TQR method	Presented results
u_E(x)
r = 1	2.66e − 005	1.160e − 002	8.320e − 003	5.551e − 017
r = 2	5.85e − 005	4.300e − 003	2.140e − 002	5.551e − 017
r = 3	8.55e − 005	2.040e − 003	3.010e − 002	6.106e − 016
r = 4	6.14e − 005	1.730e − 003	3.910e − 002	5.551e − 017
r = 5	3.89e − 005	8.010e − 004	1.120e − 001	7.355e − 016
r = 6	2.12e − 005	6.230e − 004	3.620e − 001	4.823e − 016
r = 7	1.11e − 005	5.370e − 004	8.540e − 002	1.422e − 016
r = 8	5.70e − 006	4.950e − 004	6.370e − 002	3.209e − 017
r = 9	2.90e − 006	4.750e − 004	8.640e − 002	4.597e − 017

g_E(x)
r = 1	4.92e − 005	9.280e − 004	8.070e − 003	2.220e − 016
r = 2	1.37e − 005	1.480e − 03	4.810e − 003	2.220e − 016
r = 3	2.04e − 005	4.430e − 003	3.710e − 002	2.220e − 016
r = 4	4.11e − 005	5.910e − 003	3.160e − 002	6.661e − 016
r = 5	9.44e − 005	7.940e − 003	4.240e − 001	4.441e − 016
r = 6	5.17e − 005	1.940e − 002	2.800e − 001	0
r = 7	2.71e − 005	4.130e − 002	1.780e − 001	4.441e − 016
r = 8	1.38e − 005	6.890e − 002	7.070e − 002	0
r = 9	7.01e − 006	9.400e − 002	9.040e − 003	0

Table 4. Errors of the approximate solutions u(x) and g(x) for increasing values of N for Example 3.

N	u_E(x)	g_E(x)	CPU time (sec)
10	5.961e − 013	6.817e − 013	0.044
15	3.109e − 015	3.997e − 015	0.004
20	3.886e − 015	3.997e − 015	0.001
30	2.776e − 015	3.997e − 015	0.002
60	9.104e − 015	1.288e − 014	0.008
100	9.215e − 015	1.110e − 014	0.021

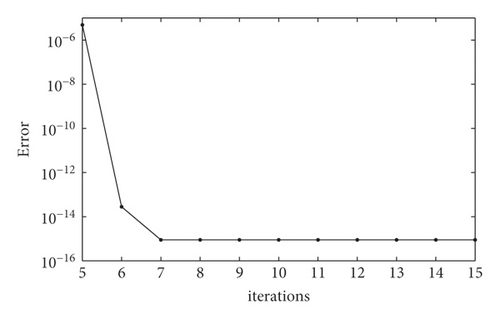
In Table 5, we have compared between the errors of present results for Example 4 corresponding to different values of collocation points N and those obtained by Maleknejad’s method (MAL) reported in [29] and Mean Value Theorem (MVT) reported in [25]. It can be seen that the present method converges rapidly compared to the MAL and MVT for this example. Full convergence to the 7 decimal places’ accurate results reported by MAL and MVT is achieved for the values N = 50 and N = 100 while high convergence is achieved to the 16 decimal places’ accurate results for the present method for all values of N ≥ 12. Table 6 shows the maximum absolute errors of u(x) for Example 4 at different orders of approximation at selected nodes. The maximum absolute errors are generally very small. A high level of accuracy is achieved at very low orders of approximation. We remark that increasing the number of nodes (i.e., increasing N) does not result in a significant improvement in the accuracy of the approximation. Figure 3 displays the errors against the iterations of the solution for Example 4 when N is fixed at 20. From Figure 3, it can be seen that the current solution rapidly converges, but the accuracy does not improve after 7 iterations.

Table 5. Comparison between the errors of the MAT, MVT, and present solutions at various values of N for Example 4.

N	MAT	MVT	Present method
5	—	—	7.287e − 008
12	—	—	8.882e − 016
15	—	—	4.441e − 016
50	2.435e − 007	1.669e − 007	8.882e − 016
100	1.166e − 007	3.057e − 008	4.441e − 016

Table 6. The errors of the present solutions for Example 4 at various values of N and iterations.

N	1^st iteration	2^nd iteration	3^rd iteration	4^th iteration
10	4.849e − 006	1.483e − 013	1.741e − 013	1.741e − 013
12	4.849e − 006	2.842e − 014	8.882e − 016	8.882e − 016
14	4.849e − 006	2.753e − 014	4.441e − 016	4.441e − 016
16	4.849e − 006	2.709e − 014	4.441e − 016	4.441e − 016
20	4.849e − 006	2.753e − 014	4.441e − 016	4.441e − 016

CPU time (sec)	0.037166	0.037443	0.037711	0.037975

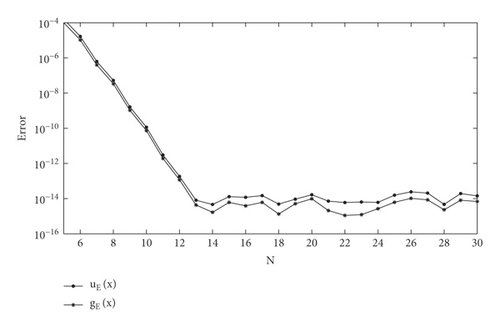
In Table 7, we have compared between the errors of present results for Example 5 corresponding to different values of x and those obtained by Single-Term Walsh Series (STWS) reported in [26] and Homotopy Perturbation Method (HPM) reported in [27]. Table 7 indicates that 15 decimal places’ accurate results are obtained using the present technique for large values of x while only 2 and 6 decimal places’ accurate results are obtained using HPM and STWS, respectively. It is interesting to note from Table 7 that when x increases, this would lead to a decrease in the absolute error for HPM and STWS, while increasing x does not result in a decrease in the accuracy of the current approximation. This shows that the present method is more efficient than the method of STWS and HPM. Table 8 shows the maximum absolute errors u_E(x) and g_E(x) of the present method at different orders of approximation for different values of N for Example 5. It can be seen that the maximum absolute errors are very small and further decrease with an increase in the order of the solution. Also, a large increase in the number of nodes (increasing N) does not result in a significant improvement in the accuracy of the present solution. In Figure 4, we display the absolute errors of u(x) and g(x) against collocation points N between the present results of Example 5 at the fifth iteration. From Figure 4, it is clear that the present method rapidly converges, and also, we notice that the accuracy does not improve for N > 13.

Table 7. Comparison between absolute errors of HPM, STWS, and present results of u(x) and g(x) at different values of x for Example 5.

x	Errors in HPM [26]		Errors in STWS [27]		Errors in present method
x	u(x)	g(x)	u(x)	g(x)	u(x)	g(x)
0.1	1.10e − 007	2.40e − 007	1.67e − 006	8.31e − 008	1.04e − 015	6.66e − 016
0.2	3.97e − 006	1.09e − 005	3.32e − 006	3.30e − 007	5.55e − 016	5.55e − 016
0.3	5.55e − 005	1.19e − 004	4.97e − 006	7.33e − 007	3.61e − 015	3.33e − 016
0.4	3.81e − 004	6.27e − 004	6.59e − 006	1.28e − 006	2.61e − 015	2.22e − 016
0.5	1.64e − 003	2.20e − 003	8.20e − 006	1.95e − 006	7.22e − 016	2.22e − 016
0.6	5.20e − 003	5.96e − 003	9.79e − 006	2.73e − 006	7.77e − 016	4.44e − 016
0.7	1.32e − 002	1.33e − 002	1.14e − 005	3.58e − 006	5.11e − 015	1.11e − 015
0.8	2.86e − 002	2.59e − 002	1.30e − 005	4.47e − 006	4.33e − 015	1.55e − 015
0.9	5.41e − 002	4.49e − 002	1.47e − 005	5.36e − 006	4.66e − 015	1.67e − 015
1.0	9.21e − 002	7.07e − 002	1.65e − 005	6.22e − 006	3.33e − 015	1.78e − 015

Table 8. Errors of u(x) and g(x) at different orders of approximation for different values of N for Example 5.

N	3^rd iteration	4^th iteration	5^th iteration	6^th iteration
u_E(x)
10	6.024e − 005	1.028e − 010	1.145e − 010	1.145e − 010
12	6.027e − 005	1.278e − 010	1.841e − 013	1.834e − 013
14	6.026e − 005	1.311e − 010	4.663e − 015	4.774e − 015
18	6.026e − 005	1.317e − 010	4.885e − 015	5.218e − 015
22	6.026e − 005	1.317e − 010	5.967e − 015	6.189e − 015

CPU time (sec)	0.002304	0.002993	0.003679	0.004365

g_E(x)
10	1.938e − 005	6.811e − 011	7.369e − 011	7.369e − 011
12	1.939e − 005	3.733e − 011	1.179e − 013	1.177e − 013
14	1.939e − 005	3.901e − 011	1.665e − 015	1.776e − 015
18	1.939e − 005	3.929e − 011	1.332e − 015	1.332e − 015
22	1.939e − 005	3.929e − 011	1.110e − 015	1.110e − 015

CPU time (sec)	0.002329	0.003601	0.004878	0.006196

5. Conclusion

In this paper, we have proposed a new method for solving linear and nonlinear Volterra integral equations. The technique has been constructed by introducing a new integral transformation together with Chebyshev pseudospectral method. The main difference between this collocation method and the other collocation methods is the replacement of the integral terms by a linear transformation using the Chebyshev differential matrix. The numerical results have been shown and compared with the exact solutions and other methods in the literature. These results are shown in the tables and figures for all cases considered in this work. To give a sense of the computational efficiency of the technique, the CPU computational time to generate the results is presented in the tables. It can be seen that high accuracy and less computational time (less than 0.02 seconds) substantiate our proposed method is a powerful numerical method for solving linear or nonlinear Volterra integral equations even for large values of grid points or iterations. The main conclusions emerging from this study may be summarized as follows:

(1)
The method is more flexible than other numerical methods such as BPE, ANN, TQR, STWS, HPM, MAT, and MVT since it allows us to choose the integral operators in the integral equations in terms of the Chebyshev spectral collocation differentiation matrix.
(2)
The proposed method is highly accurate and efficient, converges rapidly, and is sufficient to give good agreement with the exact solution.
(3)
The suggested technique does not depend on the number of collocation points N and it requires a few numbers of collocation points to achieve high accuracy of results.

Finally, we note that the proposed method described above is a powerful method that is appropriate in solving Volterra integral equations and can be generalized for Volterra and Fredholm integral equations. In future, we intend to show that the proposed method can be extended to coupled Volterra integrodifferential equations.

Conflicts of Interest

The author declares that there are no conflicts of interest.

Open Research

Data Availability

No data were used to support this study.

References

1 Kythe P. K. and Puri P., Computational Methods for Linear Integral Equations, 1992, University of New Orleans, New Orleans, LA, USA.
Google Scholar
2 Wazwaz A.-M., A comparison study between the modified decomposition method and the traditional methods for solving nonlinear integral equations, Applied Mathematics and Computation. (2006) 181, no. 2, 1703–1712, https://doi.org/10.1016/j.amc.2006.03.023, 2-s2.0-33750489744.
10.1016/j.amc.2006.03.023
Web of Science® Google Scholar
3 Wazwaz A. M., Linear and Nonlinear Integral Equations, 2011, Springer, Berlin, Germany.
10.1007/978-3-642-21449-3
Google Scholar
4 Brunner H., Volterra integral equations: an introduction to theory and applications, Cambridge Monographs on Applied and Computational Mathematics, 2017, 30, Cambridge University Press, Cambridge, UK.
10.1017/9781316162491
Google Scholar
5 Aziz I., Siraj-Ul I., and Khan F., A new method based on haar wavelet for the numerical solution of two-dimensional nonlinear integral equations, Journal of Computational and Applied Mathematics. (2014) 272, 70–80, https://doi.org/10.1016/j.cam.2014.04.027, 2-s2.0-84901426011.
10.1016/j.cam.2014.04.027
Web of Science® Google Scholar
6 Doucet A., Johansen A. M., and Tadić V. B., On solving integral equations using Markov chain Monte Carlo methods, Applied Mathematics and Computation. (2010) 216, no. 10, 2869–2880, https://doi.org/10.1016/j.amc.2010.03.138, 2-s2.0-77953233577.
10.1016/j.amc.2010.03.138
Web of Science® Google Scholar
7 Loh J. R. and Phang C., A new numerical scheme for solving system of Volterra integro-differential equation, Alexandria Engineering Journal. (2018) 57, no. 2, 1117–1124, https://doi.org/10.1016/j.aej.2017.01.021, 2-s2.0-85011928537.
10.1016/j.aej.2017.01.021
Web of Science® Google Scholar
8 Higazy M., Aggarwal S., and Nofal T. A., Sawi decomposition method for Volterra integral equation with application, Journal of Mathematics. (2020) 2020, 13, 6687134, https://doi.org/10.1155/2020/6687134.
10.1155/2020/6687134
Web of Science® Google Scholar
9 Khater A. H., Temsah R. S., and Hassan M. M., A Chebyshev spectral collocation method for solving Burgers’-type equations, Journal of Computational and Applied Mathematics. (2008) 222, no. 2, 333–350, https://doi.org/10.1016/j.cam.2007.11.007, 2-s2.0-53449090789.
10.1016/j.cam.2007.11.007
Web of Science® Google Scholar
10 Olmos D. and Shizgal B. D., A pseudospectral method of solution of Fisher’s equation, Journal of Computational and Applied Mathematics. (2006) 193, no. 1, 219–242, https://doi.org/10.1016/j.cam.2005.06.028, 2-s2.0-33646192333.
10.1016/j.cam.2005.06.028
Web of Science® Google Scholar
11 Javidi M., Spectral collocation method for the solution of the generalized Burger-Fisher equation, Applied Mathematics and Computation. (2006) 174, no. 1, 345–352, https://doi.org/10.1016/j.amc.2005.04.084, 2-s2.0-33344459415.
10.1016/j.amc.2005.04.084
Web of Science® Google Scholar
12 Javidi M., A numerical solution of the generalized Burger’s-Huxley equation by spectral collocation method, Applied Mathematics and Computation. (2006) 178, no. 2, 338–344, https://doi.org/10.1016/j.amc.2005.11.051, 2-s2.0-33746228097.
10.1016/j.amc.2005.11.051
Web of Science® Google Scholar
13 Dehghan M. and Fakhar-Izadi F., Pseudospectral methods for Nagumo equation, International Journal for Numerical Methods in Biomedical Engineering. (2011) 27, no. 4, 553–561, https://doi.org/10.1002/cnm.1319, 2-s2.0-79953035899.
10.1002/cnm.1319
Web of Science® Google Scholar
14 Motsa S. S., New algorithm for solving non-linear BVPs in heat transfer, International Journal of Modeling, Simulation & Scientific Computing. (2011) 2, no. 3, 355–373, https://doi.org/10.1142/s1793962311000499, 2-s2.0-80051956361.
10.1142/S1793962311000499
Google Scholar
15 Awad F. G., Sibanda P., Motsa S. S., and Makinde O. D., Convection from an inverted cone in a porous medium with cross-diffusion effects, Computers & Mathematics with Applications. (2011) 61, no. 5, 1431–1441, https://doi.org/10.1016/j.camwa.2011.01.015, 2-s2.0-79951723259.
10.1016/j.camwa.2011.01.015
Web of Science® Google Scholar
16 Makukula Z. G., Sibanda P., and Motsa S. S., A novel numerical technique for two-dimensional laminar flow between two moving porous walls, Mathematical Problems in Engineering. (2010) 2010, 15, 528956, https://doi.org/10.1155/2010/528956, 2-s2.0-77957848766.
10.1155/2010/528956
Web of Science® Google Scholar
17 Motsa S. S. and Shateyi S., A new approach for the solution of three-dimensional magnetohydrodynamic rotating flow over a shrinking sheet, Mathematical Problems in Engineering. (2010) 2010, 586340, https://doi.org/10.1155/2010/586340, 2-s2.0-79251534995.
10.1155/2010/586340
Web of Science® Google Scholar
18 Canuto C., Hussaini M. Y., Quarteroni A., and Zang T. A., Spectral Methods in Fluid Dy- Namics, 1988, Springer-Verlag, Berlin, Germany.
10.1007/978-3-642-84108-8
Google Scholar
19 Don W. S. and Solomonoff A., Accuracy and speed in computing the Chebyshev collocation derivative, SIAM Journal on Scientific Computing. (1995) 16, no. 6, 1253–1268, https://doi.org/10.1137/0916073.
10.1137/0916073
Web of Science® Google Scholar
20 Trefethen L. N., Spectral methods in MATLAB, 2000, SIAM, Philadelphia, PA, USA, https://doi.org/10.1137/1.9780898719598.
10.1137/1.9780898719598
Google Scholar
21 Agbolade O. A. and Anake T. A., Solutions of first-order Volterra type linear integrodifferential equations by collocation method, Journal of Applied Mathematics. (2017) 2017, 5, 1510267, https://doi.org/10.1155/2017/1510267, 2-s2.0-85017143944.
10.1155/2017/1510267
Google Scholar
22 Howard A. and Chris R., Elementary Linear Algebra:applications Version, 2013, 11th edition, Wiley, Hoboken, NJ, USA.
Google Scholar
23 Youssri Y. H. and Hafez R. M., Chebyshev collocation treatment of Volterra-Fredholm integral equation with error analysis, Arabian Journal of Mathematics. (2020) 9, no. 2, 471–480, https://doi.org/10.1007/s40065-019-0243-y.
10.1007/s40065-019-0243-y
Web of Science® Google Scholar
24 Jafarian A., Measoomy Nia S., Golmankhanh A. K., and Baleanu D., Numerical solution of linear integral equations system using the Bernstein collocation method, Advances in Difference Equations. (2013) 2013, 1–15, 2013, -123, https://doi.org/10.1186/1687-1847-2013-123, 2-s2.0-84893984155.
10.1186/1687-1847-2013-123
Google Scholar
25 De Angelis P., De Marchis R., and Martire A. L., A new numerical method for a class of Volterra and Fredholm integral equations, Journal of Computational and Applied Mathematics. (2020) 379, 112944, https://doi.org/10.1016/j.cam.2020.112944.
10.1016/j.cam.2020.112944
Web of Science® Google Scholar
26 Biazar J. and Ghazvini H., He’s homotopy perturbation method for solving systems of Volterra integral equations of the second kind, Chaos, Solitons & Fractals. (2009) 39, no. 2, 770–777, https://doi.org/10.1016/j.chaos.2007.01.108, 2-s2.0-62749090990.
10.1016/j.chaos.2007.01.108
Web of Science® Google Scholar
27 Chandra Guru Sekar R. and Murugesan K., STWS approach for Hammerstein system of nonlinear Volterra integral equations of the second kind, International Journal of Computer Mathematics. (2017) 94, no. 9, 1867–1878, https://doi.org/10.1080/00207160.2016.1247444, 2-s2.0-84995654940.
10.1080/00207160.2016.1247444
Web of Science® Google Scholar
28 Jafarian A. and Measoomy Nia S., Utilizing feed-back neural network approach for solving linear Fredholm integral equations system, Applied Mathematical Modelling. (2013) 37, no. 7, 5027–5038, https://doi.org/10.1016/j.apm.2012.09.029, 2-s2.0-84872601602.
10.1016/j.apm.2012.09.029
Web of Science® Google Scholar
29 Maleknejad K., Torabi P., and Sauter S., Numerical solution of a non-linear Volterra integral equation, Vietnam Journal of Mathematics. (2016) 44, no. 1, 5–28, https://doi.org/10.1007/s10013-015-0149-8, 2-s2.0-84960920275.
10.1007/s10013-015-0149-8
Google Scholar

Citing Literature

All articles

A New Numerical Technique for Solving Volterra Integral Equations Using Chebyshev Spectral Method

Abstract

1. Introduction

2. Description of the Method

2.1. Definition

3. Numerical Examples

4. Results and Discussion

5. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A New Numerical Technique for Solving Volterra Integral Equations Using Chebyshev Spectral Method

Abstract

1. Introduction

2. Description of the Method

2.1. Definition

3. Numerical Examples

4. Results and Discussion

5. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information