International Journal of Differential Equations

Volume 2021, Issue 1 8673020

Research Article

Open Access

Mathematical Analysis and Optimal Control of Giving up the Smoking Model

Omar Khyar,

Corresponding Author

Omar Khyar

[email protected]

orcid.org/0000-0003-1169-4733

Laboratory of Mathematics and Applications, Faculty of Sciences and Technologies, Hassan II University of Casablanca, P.O. Box 146, 20650 Mohammedia, Morocco uh2c.ac.ma

Search for more papers by this author

Jaouad Danane,

Jaouad Danane

Hassan First University, National School of Applied Sciences, Laboratory of Systems, Modelization and Analysis for Decision Support, Berrechid, Morocco uh1.ac.ma

Search for more papers by this author

Karam Allali,

Karam Allali

orcid.org/0000-0002-9463-4295

Laboratory of Mathematics and Applications, Faculty of Sciences and Technologies, Hassan II University of Casablanca, P.O. Box 146, 20650 Mohammedia, Morocco uh2c.ac.ma

Search for more papers by this author

Omar Khyar,

Corresponding Author

Omar Khyar

[email protected]

orcid.org/0000-0003-1169-4733

Laboratory of Mathematics and Applications, Faculty of Sciences and Technologies, Hassan II University of Casablanca, P.O. Box 146, 20650 Mohammedia, Morocco uh2c.ac.ma

Search for more papers by this author

Jaouad Danane,

Jaouad Danane

Hassan First University, National School of Applied Sciences, Laboratory of Systems, Modelization and Analysis for Decision Support, Berrechid, Morocco uh1.ac.ma

Search for more papers by this author

Karam Allali,

Karam Allali

orcid.org/0000-0002-9463-4295

Laboratory of Mathematics and Applications, Faculty of Sciences and Technologies, Hassan II University of Casablanca, P.O. Box 146, 20650 Mohammedia, Morocco uh2c.ac.ma

Search for more papers by this author

First published: 25 November 2021

https://doi.org/10.1155/2021/8673020

Citations: 3

Academic Editor: Andrea Scapellato

Share a link

Email
Wechat
Bluesky

Abstract

In this study, we are going to explore mathematically the dynamics of giving up smoking behavior. For this purpose, we will perform a mathematical analysis of a smoking model and suggest some conditions to control this serious burden on public health. The model under consideration describes the interaction between the potential smokers (P), the occasional smokers (L), the chain smokers (S), the temporarily quit smokers , and the permanently quit smokers . Existence, positivity, and boundedness of the proposed problem solutions are proved. Local stability of the equilibria is established by using Routh–Hurwitz conditions. Moreover, the global stability of the same equilibria is fulfilled through using suitable Lyapunov functionals. In order to study the optimal control of our problem, we will take into account a two controls’ strategy. The first control will represent the government prohibition of smoking in public areas which reduces the contact between nonsmokers and smokers, while the second will symbolize the educational campaigns and the increase of cigarette cost which prevents occasional smokers from becoming chain smokers. The existence of the optimal control pair is discussed, and by using Pontryagin minimum principle, these two optimal controls are characterized. The optimality system is derived and solved numerically using the forward and backward difference approximation. Finally, numerical simulations are performed in order to check the equilibria stability, confirm the theoretical findings, and show the role of optimal strategy in controlling the smoking severity.

1. Introduction

Smoking is a behavior in which a substance is heated or burned, and the derived smoke is breathed through the mouth or the nose and goes directly to the lungs. The active substances of the smoke are rapidly transmitted from the lungs to the bloodstream and therefore to the brain where they operate. The most common smoking substance is known as tobacco which is consumed by nearly 1.3 billion smokers worldwide [1]. More than 9% of all deaths are related to tobacco consumption [2], making the burden of smoking a global health priority. Smoking is one of the main risk factors of many noncommunicable diseases such as diabetes, cancer, cardiovascular, and chronic respiratory diseases [3–8].

Smoking dynamics were modelled by several authors in order to study the interaction between the model compartments. The simplest system that describes such dynamics was introduced in 1997 by Castillo-Garsow et al. [9], in which we find three main classes representing the potential smokers (P), the chain smokers (S), and the permanently quit smokers

. The authors studied the local stability of the equilibria and suggest a nonlinear smoking relapse model. Later, in 2008, another compartment of temporarily quit smokers

was added to the previous one [10]. Both the local and the global stability of the equilibria were performed depending on the smoking generation number. The stochastic study of the

smoking model was tackled in [11]; the authors consider Brownian motion as perturbation of their equations and establish the sufficient condition for mean square stability. Recently, the class of occasional smokers (L) was taken into account in [12]. The authors studied the following

smoking model:

(1)

where Λ is the recruitment rate, β is the transmission rate of potential smokers to occasional smoking class, σ denotes the rate of becoming chain smoker for a occasional smoker, and γ is the rate of becoming quit smoker. Furthermore, the natural death rate of all of the subpopulations is denoted by μ and their death rate related to smoking behavior is denoted by δ. Here, the incidence rate is given by I_R(P, L) : = ((2PL)/(P + L)). We note that for square-root incidence function

, and the

smoking problem is tackled by [13]; while with bilinear incidence function I_R(P, L) : = PL, the

smoking problem is studied in [14].

In this paper and inspired by the previous works, we are interested in studying

smoking problem by taking into consideration the saturated incidence rate I_R(P, L) : = ((2PL)/(P + L)); indeed, this saturated rate describes the crowding effect of potential and occasional smokers in smoking areas. The problem under consideration will take the following form:

(2)

The reversion to the smoking phenomenon is highlighted in this model by the parameter α which represents the ratio of temporarily quit smokers who start to smoke again, while η is the portion of quitters who quit smoking permanently. The flowchart of our suggested smoking model is illustrated in Figure 1. Our main interest is to study the equilibria stability of model (2) and to study the role of the optimal control strategy in reducing the number of smokers. For this last reason, we will introduce two controls; the first will represent the government prohibition of smoking in public areas, while the second control will symbolize the educational campaigns and the increase of cigarette cost. It will worthy to notice that the optimal control strategy have shown its efficiency in controlling many diseases such as tuberculosis and COVID-19 [15, 16]. Also, the optimal control has been studied in some fractional mathematical models [17]. Finally, as applications of many fractional derivatives on smoking modelling issues, we can cite [18–23].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The flowchart of the smoking model.

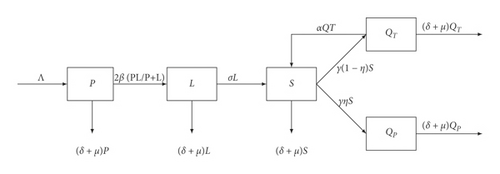
Different studies on smoking [16] have shown the clear impact of tobacco consumption on the rapid deterioration of health in COVID-19 patients. In fact, smokers are more vulnerable to COVID-19 because they already have respiratory problems, which considerably increase the risk that their condition worsens more quickly than nonsmokers. Hence, our main ambition is to check the role of governement of prohibition of smoking in public area, education campaign, and the increase of cigarette cost in controlling the severity of the smokers’ addiction.

This paper is organized as follows. In Section 2, we will establish the wellposedness of our suggested mathematical model by proving the existence, positivity, and boundedness of solutions. We fulfilled the mathematical analysis of the model, by proving the local and global stability of the equilibria in Sections 3 and 4. The optimization analysis of our model is given in Section 5; in Section 6 an appropriate numerical algorithm is constructed and some numerical simulations are given. The numerical results will show the importance of the optimal control in reducing the smokers’ addiction. In Section 7, we will give concluding remarks.

2. The Wellposedness Result and Smokers’ Generation Number

2.1. The Wellposedness Result

Let be the Banach space of continuous functions mapping ℝ⁺ into ℝ⁵ with the topology of uniform convergence. By using the fundamental theory of functional differential equations [24], we prove that there exists a unique local solution of system (2) with initial data . The following proposition guarantees that this solution exists globally.

Proposition 1. The solution of the studied model (2) remains positive and bounded for all t ≥ 0. Moreover, we have

(3)

Proof. The solution P(t) is nonnegative, for all t ≥ 0. Supposing the contrary, let t₀ > 0 be the first time such that P(t₀) = 0 and . From the first equation of system (2), we have , which leads a contradiction. Similar proofs show the positivity of L(t), S(t), , and , for all t ≥ 0. Indeed, according to system (2), we have , , , and . This completes the proof of positivity.

About boundedness, let the total population .

From system (2), we have

(4)

Therefore,

(5)

At t = 0, we have

(6)

Then,

(7)

Consequently,

(8)

Since 0 < e^{−(δ + μ)t} ≤ 1, for all t ≥ 0, we conclude that N(t) ≤ (Λ/(δ + μ)) + N(0).

2.2. The Smokers’ Generation Number

The smokers’ generation number is defined as the average number of new smokers resulting from one smoker, in a population consisting of potential smokers only. We use the next generation matrix FV⁻¹ to calculate the smokers’ generation number R₀ [25].

The formula that gives us the smokers’ generation number is R₀ = ρ(FV⁻¹), where ρ stands for the spectral radius, F is the nonnegative matrix of new smokers, and V is the matrix of smoking transition associated with model (2). After a simple resolution, we obtain

(9)

3. The Problem Equilibria and Local Stability

3.1. The Smoking Problem Equilibria

It is straightforward to check that model (2) has two steady states developed as follows:

(i)
The smoking-free equilibrium state is E₀((Λ/(δ + μ)), 0,0,0,0).
(ii)
The smoking-present equilibrium point is such that
(10)

3.1.1. Local Stability of the Smoking-Free Equilibrium

The local stability of the smoking-free equilibrium E₀((Λ/(δ + μ)), 0,0,0,0) is given by the following result.

Proposition 2.

(1)
If R₀ < 1, then the smoking-free equilibrium, E₀, is locally asymptotically stable.
(2)
If R₀ > 1, then E₀ is unstable.

Proof. The Jacobian matrix of system (2) at E₀ is given by

(11)

The characteristic polynomial of

(12)

Therefore, the eigenvalues of J(E₀) are given as follows:

(13)

with Δ = ((γ + δ + μ)(α + δ + μ))² − 4[(γ + δ + μ)(α + δ + μ) − αγ(1 − η)]. It is clear that λ₂ < 0 and λ₃ < 0 if R₀ < 1.

We conclude that E₀ is locally asymptotically stable when R₀ < 1.

3.1.2. Local Stability of the Smoking-Present Equilibrium

In order to study the local stability of the smoking-present equilibrium

, let us first give the Jacobian matrix of system (2) at E^∗:

(14)

The characteristic polynomial of

(15)

with

(16)

such that p = (1/R₀) and q = 1 − (1/R₀) (remark that p + q = 1).

The first eigenvalue of the above characteristic polynomial is ξ₁ = −(δ + μ) < 0; the second eigenvalue is ξ₂ = −(2βq² + δ + μ) < 0.

If R₀ > 1, then [(2βq² + δ + μ)(σ + δ + μ) − 2β(δ + μ)p²] > 0; consequently, a₁ > 0.

Thus, it is easy to verify that a₂ > 0, a₁a₂ − a₃ > 0, and a₃ > 0. Then, by application of Routh–Hurwitz theorem, the other eigenvalues, ξ₃, ξ₄, and ξ₅, have negative real parts.We conclude that E^∗ is locally asymptotically stable in case when R₀ > 1.

4. The Smoking Problem Global Stability Analysis

4.1. Global Stability of the Smoking-Free Equilibrium

Theorem 1. If R₀ ≤ 1, then the smoking-free equilibrium E₀ is globally asymptotically stable.

Proof. First, we denote d = δ + μ, P_f = (Λ/(δ + μ)), and we consider the following Lyapunov function defined in

(17)

The time derivative is given by

(18)

If R₀ ≤ 1, then ; consequently, according to the Lyapunov theorem, the smoking-free equilibrium E₀ is globally asymptotically stable.

4.2. Global Stability of the Smoking-Present Equilibrium

Theorem 2. If R₀ > 1, then the smoking-present equilibrium point E^∗ is globally asymptotically stable.

Proof. We consider the following Lyapunov function defined in

as follows:

(19)

The time derivative is given by

(20)

It is easy to verify that

(21)

So,

(22)

Then,

(23)

Therefore,

(24)

By application of the relation between geometric and arithmetic means, we obtain

(25)

Since R₀ > 1, we have that R₀ − 1 > 0. Consequently, .

We conclude that the smoking-present equilibrium point E^∗ is globally asymptotically stable when R₀ > 1.

5. Optimal Control of Smoking Problem

5.1. The Smoking Optimization Problem

In order to formulate our smoking optimization problem, we will introduce to problem (2) two controls u₁ and u₂. The smoking problem with controls becomes

(26)

with P(0) ≥ 0, L(0) ≥ 0, S(0) ≥ 0,

, and

The first control u₁ represents the government prohibition of smoking in public area, while the second control u₂ symbolizes the education campaign and the increase of cigarette cost. The aim of the first control is to reduce the contact between nonsmokers and smokers; the role of the second control is to prevent occasional smokers to become chain smokers. Since the two controls represent the effectiveness of each strategy, we will have the fact that u_i ∈ [0,1].

The smoking optimization problem consists in maximizing the objective functional defined as follows:

(27)

where t_f represents the time needed for the undertaken control measures and the two positive constants C₁ and C₂ are based on the costs of each strategy u₁(t) and u₂(t), respectively. The interest is to maximize the objective functional (27) which would mean that we want to increase the nonsmokers’ number and to decrease the cost of each strategy. More precisely, we are looking for optimal controls

such that

(28)

where U is the control set defined by

(29)

5.2. The Smoking Optimality System

Pontryagin’s minimum principle [26] transforms our optimization problem into a Hamiltonian maximization problem, where the Hamiltonian ℋ is given by

with

(30)

The optimality system is summarized by the following result.

Proposition 3. For any solution of the smoking optimization problem, there exist the adjoint variables, ϕ₁, ϕ₂, ϕ₃, ϕ₄, and ϕ₅, satisfying the system of equations

(31)

under the transversality conditions,

(32)

In addition, the optimal control is given by

(33)

Proof. The five adjoint equations and the transversality conditions can be obtained via Pontryagin’s minimum principle [26] such that

(34)

Simple calculations lead to

(35)

The two optimal controls and can be found from the following optimality conditions:

(36)

However, we have

(37)

Since the two controls belong to the interval [0,1], we will have

(38)

In addition, we have

(39)

6. Numerical Simulations

In order to solve numerically the optimization system, we will use the classical discretized scheme based on forward and backward finite-difference approximation scheme [28–30]. The numerical method will be implemented under Algorithm 1. The parameters values of our numerical simulations are given in Table 1.

Algorithm 1:

Step 1 (initial conditions):
P⁰, L⁰, S⁰, , , , .
.
Step 2 (numerical solving):
fori = 0, …, n − 1, do:
,
,
,
,
,
,
,
,
,
,
,
,
end for
Step 3 (the solution and optimal controls):
fori = 1, …, n, write
,
.
end for

Table 1. The estimation of the problem parameters.

Parameters	Figure 2	Figure 3	Figure 4	Reference
Λ	0.25	0.25	0.25	[12, 27]
β	0.006	0.032	0.032	[12, 27]
μ	0.08	0.0111	0.0111	[12, 27]
δ	4 × 10⁻⁵	0.0019	0.0019	[12, 27]
σ	0.02	0.021	0.021	[12, 27]
γ	2.74 × 10⁻⁴	0.041	0.041	[12, 27]
η	0.8	0.6	0.6	Estimated
α	0.0014	0.014	0.014	Estimated

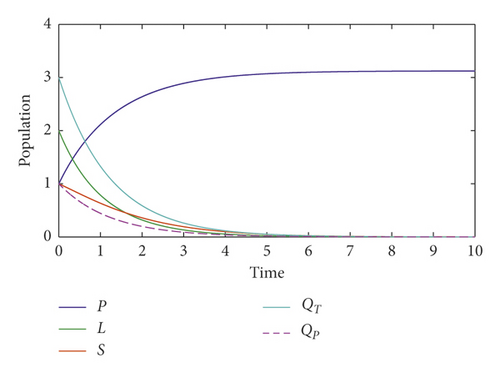
The smoking-free equilibrium stability result is illustrated numerically in Figure 2. In fact, we clearly see that the number of potential smokers increase and reach its maximum value. However, the other components of our smoking problem representing occasional smokers, chain smokers, temporarily quit smokers, and permanently quit smokers vanish. Within the used parameters in this figure (see Table 1), we can easily calculate the smokers’ generation number, R₀ = 0.119952, which means that this number is less than unity, and we have confirmation, from our theoretical findings, that the smoking-free equilibrium is stable. Moreover, we observe that all the curves converge toward the smoking-free equilibrium E_f = (3.12, 0,0,0,0) which means that our numerical result supports the theoretical result concerning the stability of the first steady state.

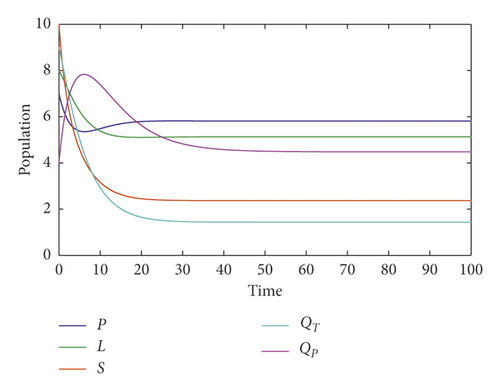
On the contrary, the smoking-present equilibrium stability is represented in Figure 3. Here, all the smoking problem compartments remain at strictly positive levels. From Table 1, we can calculate the smokers’ generation number relative to this figure, R₀ = 1.88. Since it is greater than unity, we have confirmation from our theoretical results that the smoking-present equilibrium is stable. Both the numerical and the theoretical results agree about the stability of the smoking-present equilibrium. From this same figure, we see the convergence of the different curves toward the smoking-present equilibrium E^∗ = (5.81, 5.13, 2.36, 1.43, 4.48) which means this second steady state can be found numerically or calculated theoretically. We conclude that the local and global theoretical results concerning the stability of the smoking-free and the smoking-present equilibria are in good agreement with our numerical results.

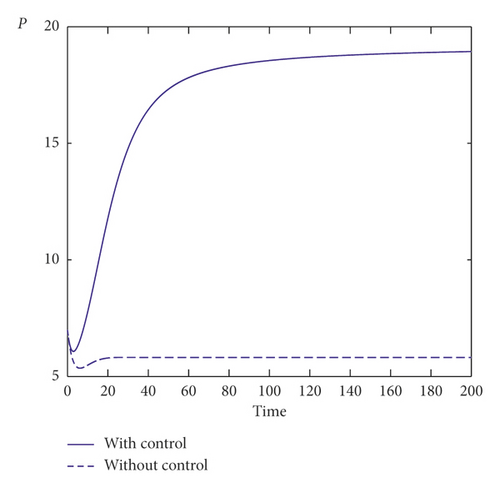
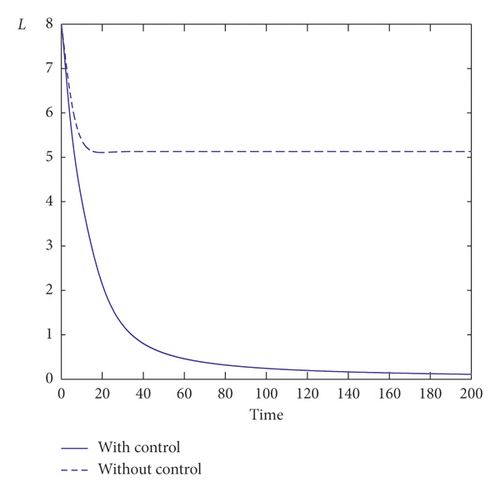
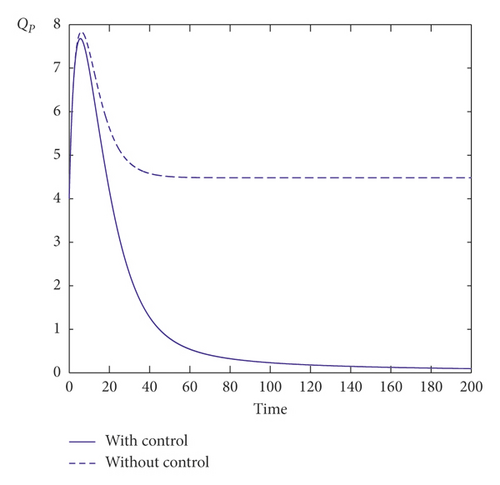
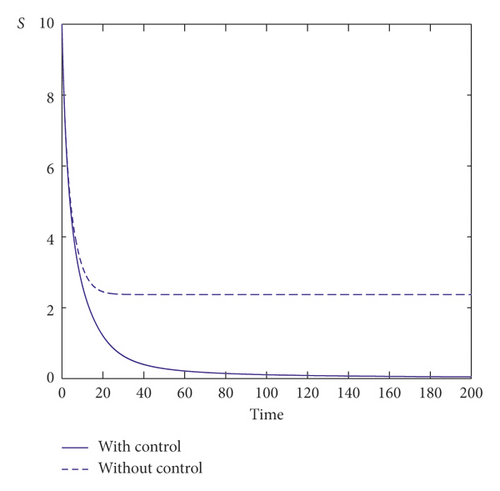
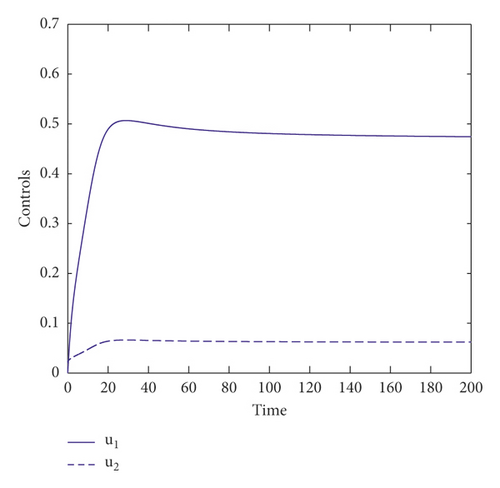
Our third numerical result concerns the comparison between the model with control strategy and the model without any control. Indeed, Figure 4 shows the evolution of potential smokers, occasional smokers, chain smokers, temporarily quit smokers, permanently quit smokers, and the two controls as the function of time. We clearly observe that, with control strategy, we will have more potential smokers than without control measures. Also, it is clearly seen that, with control measures, a significant reduce of occasional and chain smokers is observed. This means the roles of control strategies are to reduce the number of occasional and chain smokers which can lead to save many lives in smoking population. Besides, with control strategy, we observe that, without any control strategy, the curves representing the different smoking compartment converge toward E^∗ = (5.81, 5.13, 2.36, 1.43, 4.48). However, with taking significant control measures, those curves converge toward which confirms the role of control in reducing the smoking habit. In addition, we remark from the two controls’ behavior that we should give more importance to the first control than the second. It is also observed that the two controls should be also maintained at a constant level in order to have the desired good result.

7. Conclusion

We have studied in this paper mathematically and numerically the dynamics of giving up smoking behavior. The suggested smoking model consists of a system of five differential equations representing the potential smokers, the occasional smokers, the chain smokers, the temporarily quit smokers, and the permanently quit smokers. We have established the wellposedness result of our smoking problem by proving the existence, positivity, and boundedness of the smoking problem solution. Both the equilibria local and the global stability results are fulfilled. To study the role of control measures on our smoking problem dynamics, two different controls are introduced to the model. The role of the first control is to reduce the contact between nonsmokers and smokers, while the objective of the second is to prevent occasional smokers to become chain smokers. The existence and the characterization of the two optimal controls are discussed by using the Pontryagin minimum principle. The optimality system is solved numerically using the classical forward and backward difference numerical scheme. It was established that the numerical simulations concerning the stability of the smoking-free and the smoking-present equilibria are in good agreement with the local and global theoretical results. Moreover, the numerical results confirm the important role of control measures in reducing the number of occasional and chain smokers which may save significant number of lives in the smoking population.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this study.

Open Research

Data Availability

No data were used to support this study.

References

1 Jha P., Smoking cessation and e-cigarettes in China and India, BMJ. (2019) 367, https://doi.org/10.1136/bmj.l6016, 2-s2.0-85073592539.
10.1136/bmj.l6016
Google Scholar
2 Perez-Warnisher M. T., de Miguel M. P. C., and Seijo L. M., Tobacco use worldwide, legislative efforts to curb consumption, Annals of Global Health. (2019) 85, no. 1, 1–9, https://doi.org/10.5334/aogh.2417, 2-s2.0-85061247602.
10.5334/aogh.2417
PubMed Web of Science® Google Scholar
3 Boutayeb A. and Boutayeb S., The burden of non communicable diseases in developing countries, International Journal for Equity in Health. (2005) 4, no. 1, 2–8, https://doi.org/10.1186/1475-9276-4-2, 2-s2.0-14544289581.
10.1186/1475-9276-4-2
PubMed Google Scholar
4 Anand K., Shah B., Yadav K., Singh R., Mathur P., Paul E., and Kapoor S. K., Are the urban poor vulnerable to non-communicable diseases? A survey of risk factors for non-communicable diseases in urban slums of Faridabad, The National Medical Journal of India. (2007) 20, no. 3, 115–120.
CAS PubMed Web of Science® Google Scholar
5 Berlin I., Thomas D., Le Faou A. L., and Cornuz J., COVID-19 and smoking, Nicotine Tobacco Research. Official Journal of the Society for Research on Nicotine and Tobacco. (2020) 22, no. 9, 1650–1652, https://doi.org/10.1093/ntr/ntaa059.
10.1093/ntr/ntaa059
CAS PubMed Web of Science® Google Scholar
6 Alqahtani J. S., Oyelade T., Aldhahir A. M., Alghamdi S. M., Almehmadi M., Alqahtani A. S., Quaderi S., Mandal S., and Hurst J. R., Prevalence, severity and mortality associated with COPD and smoking in patients with COVID-19: a rapid systematic review and meta-analysis, PLoS One. (2020) 15, no. 5, e0233147, https://doi.org/10.1371/journal.pone.0233147.
10.1371/journal.pone.0233147
CAS PubMed Web of Science® Google Scholar
7 Higgins M. W., Keller J. B., and Metzner H. L., Smoking, socioeconomic status, and chronic respiratory Disease1,2, American Review of Respiratory Disease. (1977) 116, no. 3, 403–410, https://doi.org/10.1164/arrd.1977.116.3.403, 2-s2.0-0017655902.
10.1164/arrd.1977.116.3.403
CAS PubMed Web of Science® Google Scholar
8 Park J.-E., Jung S., Kim A., and Park J.-E., MERS transmission and risk factors: a systematic review, BMC Public Health. (2018) 18, no. 1, https://doi.org/10.1186/s12889-018-5484-8, 2-s2.0-85046262643.
10.1186/s12889-018-5484-8
Web of Science® Google Scholar
9 Castillo-Garsow C., Jordan-Salivia G., and Herrera A. R., Mathematical models for the dynamics of tobacco use, recovery and relapse, 1997, Cornell Uneversity, Ithaca NY, USA, Technical Report Series; BU-1505-M.
Google Scholar
10 Shoromi O. and Gumel A. B., Curtailing smoking dynamics, a mathematical modeling approach, Applied Mathematics and Computation. (2008) 195, no. 2, 475–499.
10.1016/j.amc.2007.05.012
Web of Science® Google Scholar
11 Lahrouz A., Omari L., Kiouach D., and Belmaâti A., Deterministic and stochastic stability of a mathematical model of smoking, Statistics & Probability Letters. (2011) 81, no. 8, 1276–1284, https://doi.org/10.1016/j.spl.2011.03.029, 2-s2.0-79956207923.
10.1016/j.spl.2011.03.029
Web of Science® Google Scholar
12 ur Rahman G., Agarwal R. P., Din Q., and Din Q., Mathematical analysis of giving up smoking model via harmonic mean type incidence rate, Applied Mathematics and Computation. (2019) 354, no. C, 128–148, https://doi.org/10.1016/j.amc.2019.01.053, 2-s2.0-85062062745.
10.1016/j.amc.2019.01.053
Web of Science® Google Scholar
13 Zeb A., Zaman G., and Momani S., Square-root dynamics of a giving up smoking model, Applied Mathematical Modelling. (2013) 37, no. 7, 5326–5334, https://doi.org/10.1016/j.apm.2012.10.005, 2-s2.0-84872598848.
10.1016/j.apm.2012.10.005
Web of Science® Google Scholar
14 Huo H. F. and Zhu C. C., Influence of relapse in a giving up smoking model, Abst Appl Anal Hindawi January. (2013) 2013, 12, 525461, https://doi.org/10.1155/2013/525461, 2-s2.0-84874524804.
10.1155/2013/525461
Google Scholar
15 Elhia M., Balatif O., Boujallal L., and Rachik M., Optimal control problem for a tuberculosis model with multiple infectious compartments and time delays, An International Journal of Optimization and Control: Theories & Applications. (2021) 11, no. 1, 75–91, https://doi.org/10.11121/ijocta.01.2021.00885.
10.11121/ijocta.01.2021.00885
Google Scholar
16 Moussouni N. and Aliane M., Optimal control of COVID-19, An International Journal of Optimization and Control: Theories & Applications. (2021) 11, no. 1, 114–122, https://doi.org/10.11121/ijocta.01.2021.00974.
10.11121/ijocta.01.2021.00974
Google Scholar
17 Eroglu B. B. I, Avci D., and Özdemir N., Optimal control problem for a conformable fractional heat conduction equation, Acta Physica Polonica A. (2017) 132, no. 3, 658–662.
10.12693/APhysPolA.132.658
CAS Web of Science® Google Scholar
18 Uçar E., Uçar S., Evirgen F., and Özdemir N., Investigation of E-cigarette smoking model with mittag-leffler kernel, Foundations of Computing and Decision Sciences. (2021) 46, no. 1, 97–109, https://doi.org/10.2478/fcds-2021-0007.
10.2478/fcds-2021-0007
Web of Science® Google Scholar
19 Uçar S., Uçar E., Özdemir N., and Hammouch Z., Mathematical analysis and numerical simulation for a smoking model with Atangana-Baleanu derivative, Chaos, Solitons & Fractals. (2019) 118, 300–306, https://doi.org/10.1016/j.chaos.2018.12.003, 2-s2.0-85058047670.
10.1016/j.chaos.2018.12.003
Web of Science® Google Scholar
20 Singh J., Kumar D., Qurashi M. A., and Baleanu D., A new fractional model for giving up smoking dynamics, Advances in Difference Equations. (2017) 2017, no. 1, 1–16, https://doi.org/10.1186/s13662-017-1139-9, 2-s2.0-85016157209.
10.1186/s13662-017-1139-9
Web of Science® Google Scholar
21 Singh H., Baleanu D., Singh J., and Dutta H., Computational study of fractional order smoking model, Chaos, Solitons & Fractals. (2021) 142, 110440, https://doi.org/10.1016/j.chaos.2020.110440.
10.1016/j.chaos.2020.110440
Web of Science® Google Scholar
22 Alrabaiah H., Zeb A., Alzahrani E., and Shah K., Dynamical analysis of fractional-order tobacco smoking model containing snuffing class, Alexandria Engineering Journal. (2021) 60, no. 4, 3669–3678, https://doi.org/10.1016/j.aej.2021.02.005.
10.1016/j.aej.2021.02.005
Web of Science® Google Scholar
23 Morales-Delgadoa V. F., Gomez-Aguilar J. F., Taneco-Hernandez M. A., Escobar-Jimenezc R. F., and Olivares-Peregrino V. H., Mathematical modeling of the smoking dynamics using fractional differential equations with local and nonlocal kernel, The Journal of Nonlinear Science and Applications. (2018) 11, no. 8, 994–1014, https://doi.org/10.22436/jnsa.011.08.06.
10.22436/jnsa.011.08.06
Google Scholar
24 Hale J. K., Lunel S. M. V., and Verduyn L. S., Introduction to functional differential equations, Springer Sci Business Media. (1993) 99, https://doi.org/10.1007/978-1-4612-4342-7.
10.1007/978-1-4612-4342-7
Google Scholar
25 Diekmann O., Heesterbeek J. A. P., and Roberts M. G., The construction of next-generation matrices for compartmental epidemic models, Journal of The Royal Society Interface. (2010) 7, no. 47, 873–885, https://doi.org/10.1098/rsif.2009.0386, 2-s2.0-77953160649.
10.1098/rsif.2009.0386
CAS PubMed Web of Science® Google Scholar
26 Göllmann L., Kern D., and Maurer H., Optimal control problems with delays in state and control variables subject to mixed control-state constraints, Optimal Control Applications and Methods. (2009) 30, no. 4, 341–365, https://doi.org/10.1002/oca.843, 2-s2.0-67749137297.
10.1002/oca.843
Web of Science® Google Scholar
27 Pang L., Zhao Z., Liu S., and Zhang X., A mathematical model approach for tobacco control in China, Applied Mathematics and Computation. (2015) 259, 497–509, https://doi.org/10.1016/j.amc.2015.02.078, 2-s2.0-84925424204.
10.1016/j.amc.2015.02.078
Web of Science® Google Scholar
28 Gumel A. B., Shivakumar P. N., and Sahai B. M., A mathematical model for the dynamics of HIV-1 during the typical course of infection, Nonlinear Analysis: Theory, Methods & Applications. (2001) 47, no. 3, 1773–1783, https://doi.org/10.1016/s0362-546x(01)00309-1, 2-s2.0-0035425119.
10.1016/S0362-546X(01)00309-1
Web of Science® Google Scholar
29 Laarabi H., Abta A., and Hattaf K., Optimal control of a delayed SIRS epidemic model with vaccination and treatment, Acta Biotheoretica. (2015) 63, no. 2, 87–97, https://doi.org/10.1007/s10441-015-9244-1, 2-s2.0-84930081376.
10.1007/s10441-015-9244-1
PubMed Web of Science® Google Scholar
30 Danane J., Meskaf A., and Allali K., Optimal control of a delayed hepatitis B viral infection model with HBV DNA-containing capsids and CTL immune response, Optimal Control Applications and Methods. (2018) 39, no. 3, 1262–1272, https://doi.org/10.1002/oca.2407, 2-s2.0-85048036803.
10.1002/oca.2407
Web of Science® Google Scholar

Citing Literature

All articles

Mathematical Analysis and Optimal Control of Giving up the Smoking Model

Abstract

1. Introduction