In this paper, the efficient combined method based on the homotopy perturbation Sadik transform method (HPSTM) is applied to solve the physical and functional equations containing the Caputo–Prabhakar fractional derivative. The mathematical model of this equation of order μ ∈ (0,1] with λ ∈ ℤ⁺, θ, σ ∈ ℝ⁺ is presented as follows: where for λ = 1, θ = 1, σ = 1s and λ = 2, θ = 3, σ = 1, equations are changed into the equal width and modified equal width equations, respectively. The analytical method which we have used for solving this equation is based on a combination of the homotopy perturbation method and Sadik transform. The convergence and error analysis are discussed in this article. Plots of the analytical results with three examples are presented to show the applicability of this numerical method. Comparison between the obtained absolute errors by the suggested method and other methods is demonstrated.

1. Introduction

The integrals and derivatives of fractional order in fractional calculus play an important role in many branches such as mathematics, engineering, and physics [1–6]. The differential systems of fractional order are regarded as an extension of the differential systems of integer order and have important application in expressing nonlinear phenomena in many scopes such as applied sciences [7, 8], engineering [9, 10], and physics [11, 12]. One of the most important nonlinear differential equations used in many fields of mathematics, engineering, and physics is the equal width (EW) differential equation of fractional order where the equation is a partial differential equation that describes physical behaviors such as water transfer in soils [13], crystal growth [14], and shallow water waves [15]. The main reason for choosing these types of equations is due to their application in mathematics and physics, plasma waves, fluid mechanics, solid-state physics, and chemical physics [16, 17]. In this paper, we state the time-fractional comprehensive EW equation containing Caputo–Prabhakar fractional derivative as follows [18–20]:

(1)

where 0 < μ ≤ 1, θ ≥ 0, σ ≥ 0, and λ ∈ ℤ⁺ is an integer. For equation (1), we consider two cases as follows:

(1)
If λ = 1, θ = 1, σ = 1 are considered, then equation (1) becomes the nonlinear equal width equation of fractional order μ. This type of equation is one of the most important equations that examine the nonlinear behaviors of physical phenomena such as hydromagnetic waves [21], optics [22], and biological systems [23].
(2)
If λ = 2, θ = 3, σ = 1 are considered, then equation (1) becomes the nonlinear modified equal width equation (MEW) of fractional order μ.

Moreover, in equation (1), function u(x, t) is the probability density function, x is the spatial coordinate, and t is the temporal coordinate. To find the solutions of these types of equations, the homotopy perturbation Sadik transform method is used, which is a generalization of the homotopy perturbation and Sumudu transform methods. The method presented in this article is similar to the methods discussed in [24–31]. In equation (1),

is the Caputo–Prabhakar fractional derivative of order μ which is defined by

(2)

where

is the Prabhakar fractional integral and is defined by [32]

(3)

where u(x, t) ∈ L¹([0, b] × [0, b]), b ∈ ℝ and

that W^m,1 is the Sobolev space. Also,

is the three-parameter Mittag-Leffler function which is defined by [32]

(4)

and (γ)_n is the Pochhammer symbol which is given by [33]

(5)

The main reason for choosing the three-parameter Mittag-Leffler function in this paper is related to its application in many models such as disordered materials and heterogeneous models [34], Havriliak–Negami models [35, 36], viscoelasticity models [37], stochastic models [38], probability models [39], spherical stellar models [40], Poisson models [41], and fractional models or integral models [42–45]. Many research studies have been conducted in numerical fields to obtain numerical solutions of fractional differential equations such as the Adomian decomposition method [46], the q-homotopy analysis transform method (q-HATM) [47], the Laplace transform method [48], the method based on the implementation of an iterative perturbation method [49], the numerical method based on the Petrov–Galerkin method [50], the Petrov–Galerkin finite element scheme [51], the local discontinuous Galerkin method [52], and other methods [24, 27, 30, 53]. Recently, a new integral transform named the Sadik transform was introduced by Sadikali Latif Shaikh in 2018 (see [54, 55]). The Sadik transform is nothing but an unification of the Laplace transform, Sumudu transform, Elzaki transform, and all those integral transforms whose kernels are of exponential type or similar to the kernel of the Laplace transform. The Sadik transform is a very powerful integral transform. In this paper, we apply the HPSTM to solve the nonlinear time-fractional EW equation, MEW equation, and VMEW equation. The key intention of the present work is to extend the utilization of the HPSTM to derive analytical and approximate solutions of the time-fractional EW equation, time-fractional MEW equation, and time-fractional VMEW equation.

This paper is organized as follows. Some definitions and mathematical preliminaries of the fractional calculus are presented in Section 2. In Section 3, we introduce an analytical method based on the HPSTM to the nonlinear nonhomogeneous partial differential equation. In Section 4, to show the validity of the suggested method in Section 3, three examples are simulated.

2. Important Notations

In this section, we express theorems and lemmas which are used in the next parts.where ℜ(μ) > 0, ℜ(ρ) > 0 and ρ, μ, ω, γ ∈ ℂ.

Lemma 1. The Laplace transformation of function (4) is given by [33, 56]

(6)

Lemma 2 (see [3].)The following relation holds:

(7)

where ℜ(μ) > 0, ℜ(ρ) > 0 and ρ, μ, ω, γ ∈ ℂ.

Lemma 3 (see [57].)Suppose Φ₁(υ, α, β) is a Sadik transform of φ₁(t) and Φ₂(υ, α, β) is a Sadik transform of φ₂(t). Then, Sadik transform of (φ₁∗φ₂)(t) is given by

(8)

where ∗ is a convolution. Also,

and

Theorem 1 (see [57].)Suppose and φ(t), φ′(t), …, φ^m−1(t), m ∈ ℕ, are continuous. Then,

(9)

Also, the Sadik transform of integration of φ(t) is defined by

(10)

Theorem 2. The Sadik transform of the Caputo–Prabhakar fractional derivative of order μ for m = 1 is obtained by

(11)

where

and ρ, μ, ω, γ ∈ ℂ, ℜ(μ) > 0, ℜ(ρ) > 0.

Proof. By applying equations (2), (6), (8), and (9), we obtain

(12)

The proof is proven.

3. The Proposed Scheme

This section focuses on an analytical method based on the homotopy perturbation and Sadik transform method for finding the solutions of the following fractional differential equations:

(13)

where Au(x, t) is a linear differential operator, Nu(x, t) is a nonlinear differential operator, and g(x, t) is an indicated source term. Using equation (11) and taking the Sadik transform on both sides of equation (13), we get

(14)

Now applying Sadik inverse transform on equation (14), we obtain

(15)

To get the solution of equation (15), we can state the solutions of equation (15) by the following infinite series:

(16)

where u_n(x, t), n = 0,1,2, …, are known. Also, the nonlinear term Nu(x, t) can be displayed as the following infinite series:

(17)

where

are the Adomian polynomials which were introduced in [46]. Now, substituting equations (16) and (17) into (15), we get

(18)

where

. Therefore, we put the coefficients on powers of ϱ on both sides of relation (18) equally, which results in

(19)

Then, the analytical solution of equation (13) can be obtained as

(20)

Theorem 3. Let u(x, t) be the exact solution of equation (13) and u_n(x, t) be the approximate solution of equation (13) so that ‖u_n+1(x, t)‖ ≤ ϖ‖u_n(x, t)‖, ϖ ∈ (0,1), n ∈ ℕ. Then, the series defined by (20) converges.

Proof. From ‖u_n+1(x, t)‖ ≤ ϖ‖u_n(x, t)‖, we obtain

(21)

Then,

(22)

Therefore,

(23)

Because ϖ ∈ (0,1), ‖u − u_n‖⟶0 as n⟶∞. The proof is proven.

Theorem 4. Let u(x, t) be the exact solution of equation (1) and (u(x, t))_N be the best approximate solution of equation (1) so that . Then, the following relation for the error holds:

(24)

Proof. Since u(x, t) is the exact solution of equation (1) and (u(x, t))_N is the best approximate solution of equation (1), then we have

(25)

Using Lemma 2, equation (3), and , for , we get

(26)

and by using the Lipschitz condition with constant 0 < k₁ < 1 for derivative of the first order with respect to the variable t, we have

(27)

By using the Lipschitz condition with constant 0 < k₂ < 1 for derivative of the first order with respect to the variable x and theorem assumptions, from equation (25), we obtain

(28)

and according to Theorem 2 introduced in [58], we have

(29)

where u(x, t), (u(x, t))_N ∈ ℌ^σ(0,1), σ ≥ 0, ξ > 0, that ℌ^σ(0,1), σ ≥ 0, given [58].

4. Numerical Results

In this section, we show the approximate solution obtained by the proposed method which is named the homotopy perturbation Sadik transform method with three examples to express its performance. In this section, we consider the absolute error as follows:

(30)

where u(x, t) is the exact solution of equation (1) and u_n(x, t) is the numerical solution of equation (1).

4.1. Example 1

We consider the following fractional EW equation with λ = 1, θ = 1, σ = 1:

(31)

when γ = 0, and the exact solution is u(x, t) = 3 sec h²(x − 15 − t/2). By applying the proposed method given in Section 3, we solve equation (31); then,

(32)

where H_n(u(x, t)) is the nonlinear uu_x. The polynomials H_n(u(x, t)) are calculated as follows:

(33)

Comparing coefficients of same powers of p in equation (32), we obtain

(34)

Then, the approximate solution of u(x, t) is obtained as

(35)

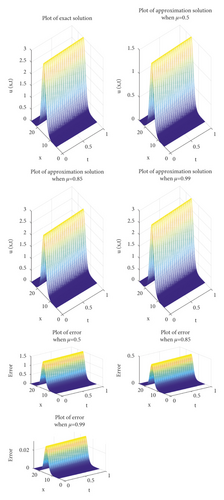
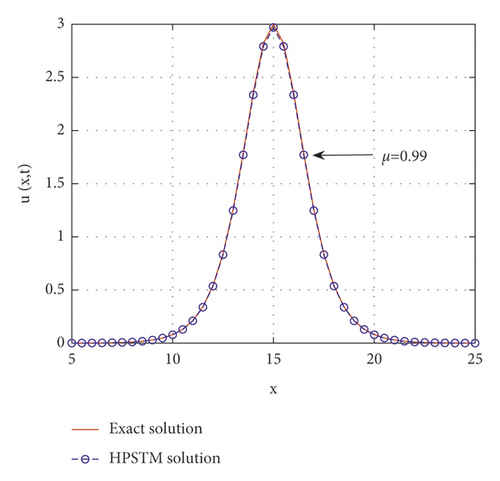
The comparison between the exact and the approximate solutions and the absolute error are expressed in Figure 1 for different values of μ when μ = 0.5, 0.85, 0.99, 1. Also, in Figure 2, the exact and the numerical solutions at t = 0.0001 are given. In Table 1, a comparison between the absolute error in [2] and the absolute error for HPSTM with different values of μ is given.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Graphs of approximate solution and the exact solution and absolute error for different values of μ when μ = 0.5, 0.85, 0.99, 1 and ρ = ω = γ = 1 for example 1.

Table 1. Comparison between the absolute error in [2] and the absolute error for homotopy perturbation Sadik transform method with different values of μ for example 1.

x	\|u − u_n\|		\|u − u_n\|
x	μ = 0.5	μ = 0.85	μ = 0.99	Method [2]
10	1.4006135487E − 09	1.4210717446E − 09	1.4412222851E − 09	7.242560880E − 06
11	1.4804436993E − 09	1.4994344786E − 09	1.5179577058E − 09	1.610108943E − 05
12	1.5534369379E − 09	1.5703105528E − 09	1.5865522230E − 09	2.246615682E − 05
13	1.16169787676E − 09	1.6310851118E − 09	1.6444028957E − 09	2.494373852E − 05
14	1.16685291313E − 09	1.6792699469E − 09	1.6890873673E − 09	1.482055499E − 04
15	1.17271757893E − 09	1.7298751108E − 09	1.7314989455E − 09	7.000000000E − 09
16	1.7315032733E − 09	1.7298837530E − 09	1.7271887190E − 09	1.482115835E − 04
17	1.7186088774E − 09	1.7127505267E − 09	1.7058693781E − 09	2.493848058E − 05
18	1.16891247436E − 09	1.6793110759E − 09	1.6685738938E − 09	2.247007139E − 05
19	1.6444545342E − 09	1.6311399784E − 09	1.6170367143E − 09	1.610299997E − 05
20	1.5866158664E − 09	1.5703768054E − 09	1.5535056371E − 09	7.243321962E − 06

4.2. Example 2

Consider the following MEW equation with λ = 2, θ = 3, σ = 1:

(36)

for γ = 0, and the exact solution is u(x, t) = 1/4sec h(x − 30 − t/4). Applying the HPSTM on equation (36), we obtain

(37)

where the polynomials H_n(u(x, t)) are represented as the nonlinear terms which are denoted as

(38)

The polynomials H_n(u(x, t)) are calculated as follows:

(39)

Comparing coefficients of same powers of p in equation (37), we obtain

(40)

Finally, the approximate solution of u(x, t) is given by

(41)

The comparison between exact solution and the approximate solution and absolute error are expressed in Figure 3 for different values of μ when μ = 0.5, 0.85, 0.99, 1. Figure 4 shows the comparison of exact solution with homotopy perturbation Sadik transform method solution at t = 0.0001. In Table 2, a comparison between the absolute error in [2] and the absolute error for HPSTM with different values of μ is given.

Table 2. Comparison between the absolute error in [2] and the absolute error for homotopy perturbation Sadik transform method with different values of μ for example 2.

x	\|u − u_n\|		\|u − u_n\|
x	μ = 0.5	μ = 0.85	μ = 0.99	Method [2]
25	4.9233966126E − 09	4.8905216623E − 09	4.8523133049E − 09	8.419085488E − 07
26	4.7611171679E − 09	4.7088017083E − 09	4.6524848045E − 09	2.284567360E − 06
27	4.5293288600E − 09	4.4632329663E − 09	4.3946122324E − 09	6.130812328E − 06
28	4.2511941226E − 09	4.1770584430E − 09	4.1017168885E − 09	1.516464963E − 05
29	3.9485345529E − 09	3.8712015990E − 09	3.7936781419E − 09	2.113002231E − 05
30	3.6388500689E − 09	3.5618921913E − 09	3.4854390699E − 09	7.800000000E − 09
31	3.3345479504E − 09	3.2603221763E − 09	3.1870278987E − 09	2.113176846E − 05
32	3.04351478950E − 09	2.9734094032E − 09	2.9044644353E − 09	1.516821359E − 05
33	2.7701849765E − 09	2.7048973756E − 09	2.6408655090E − 09	6.132358065E − 06
34	2.5166006751E − 09	2.4563726541E − 09	2.3974113232E − 09	2.285133776E − 06
35	2.2832615675E − 09	2.2280532855E − 09	2.1740726737E − 09	8.421208912E − 07

In the example 2, we study the solution of a variant of fractional modified equal width equation (VMEW) which is obtained by the proposed method.

4.3. Example 3

Consider the following VMEW equation:

(42)

and the exact solution is u(x, t) = cosh^5/2(5(x − t)/6) when γ = 0. Applying the homotopy perturbation and Sadik transform method on equation (42), we have

(43)

where H_n(u(x, t)) are obtained as

(44)

and H₀(u(x, t)), …, H_n(u(x, t)) are calculated as follows:

(45)

Comparing coefficients of same powers of p in equation (43), we obtain

(46)

So, the approximate solution of u(x, t) is calculated as

(47)

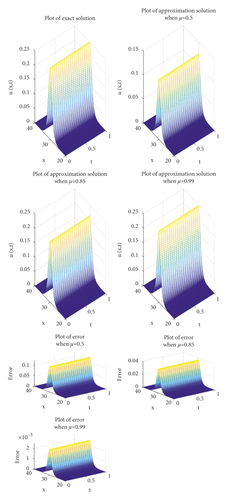
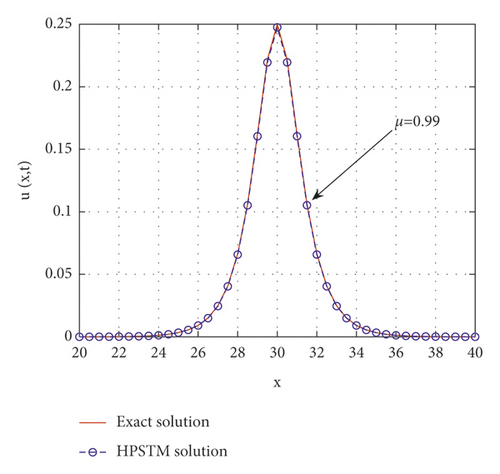
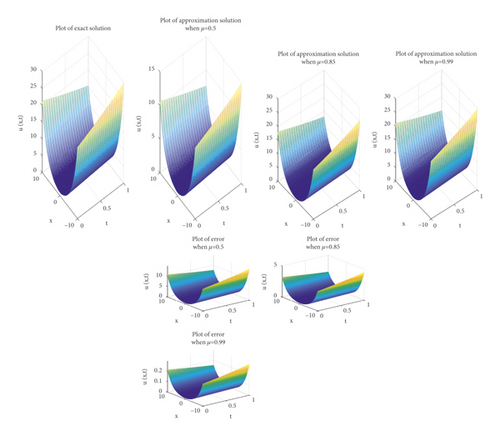
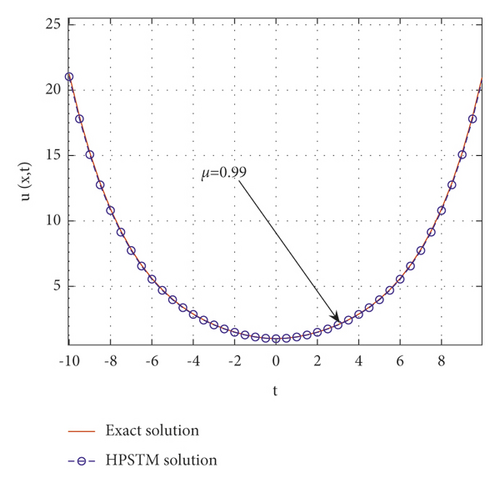
Comparison between the exact and the approximate solutions and the absolute error are shown in Figure 5 for different values of μ when μ = 0.5, 0.85, 0.99, 1. Also, in Figure 6, comparison of the exact solution and the approximate solution at t = 0.0001 is illustrated. In Table 3, a comparison between the absolute error in [2] and the absolute error for homotopy perturbation Sadik transform method with different values of μ is given.

Table 3. Comparison between the absolute error in [2] and the absolute error for homotopy perturbation Sadik transform method with different values of μ for example 3.

x	\|u − u_n\|		\|u − u_n\|
x	μ = 0.5	μ = 0.85	μ = 0.99	Method [2]
0	4.5709477859E − 09	4.5330148328E − 09	4.4953966746E − 09	1.000000000E − 09
1	4.4210943150E − 09	4.3844049537E − 09	4.3480200672E − 09	2.563406968E − 05
2	4.2761536328E − 09	4.2406670942E − 09	4.2054750487E − 09	4.601380631E − 05
3	4.1359646818E − 09	4.1016415335E − 09	4.0676032238E − 09	6.668778565E − 05
4	4.0003716853E − 09	3.9671737878E − 09	3.9342513912E − 09	9.224742588E − 05
5	3.8692239749E − 09	3.8371144396E − 09	3.8052713736E − 09	1.244701205E − 04
6	3.7423758233E − 09	3.7113189714E − 09	3.6805198536E − 09	1.615598280E − 04
7	3.6196862832E − 09	3.5896476064E − 09	3.5598582149E − 09	1.923074240E − 04
8	3.5010190312E − 09	3.4719651533E − 09	3.4431523893E − 09	1.781977647E − 04
9	3.3862422172E − 09	3.3581408576E − 09	3.3302727086E − 09	3.522674800E − 06
10	3.2752283194E − 09	3.2480482574E − 09	3.2210937625E − 09	6.615336660E − 04

5. Conclusion

This paper describes a numerical method based on the homotopy perturbation Sadik transform method for solving the equations such as EW, MEW, and VMEW. The fractional derivatives are used in this paper in the Caputo–Prabhakar sense. This paper demonstrates that the HPSTM is sufficient, easy, and suitable for various other nonlinear models. It can be seen that as x increases, it leads to variation in u(x, t) for waves in plasma at specific value of t. All tables and figures show that the proposed method produces numerical solutions with more accuracy. Comparison between the obtained absolute errors by the suggested method and method presented in [2] is demonstrated. Discussion on the convergence and error analysis of the proposed method is presented. Three numerical examples are given to show the applicability of the suggested method.

Conflicts of Interest

The author declares that there are no conflicts of interest.

Open Research

Data Availability

No data were used to support this study.

References

1 Diethelm K., Baleanu D., and Scalas E., Fractional Calculus: Models and Numerical Methods, 2012, World Scientific, Singapore.
Google Scholar
2 Goswami A., Singh J., Kumar D., and Sushila, An efficient analytical approach for fractional equal width equations describing hydro-magnetic waves in cold plasma, Physica A: Statistical Mechanics and its Applications. (2019) 524, 563–575, https://doi.org/10.1016/j.physa.2019.04.058, 2-s2.0-85064965457.
10.1016/j.physa.2019.04.058
Web of Science® Google Scholar
3 Kilbas A. A., Saigo M., and Saxena R. K., Generalized Mittag-Leffler function and generalized fractional calculus operators, Integral Transforms and Special Functions. (2004) 15, no. 1, 31–49, https://doi.org/10.1080/10652460310001600717, 2-s2.0-0842346737.
10.1080/10652460310001600717
Web of Science® Google Scholar
4 Ma C.-Y., Shiri B., Wu G.-C., and Baleanu D., New fractional signal smoothing equations with short memory and variable order, Optik. (2020) 218, 164507, https://doi.org/10.1016/j.ijleo.2020.164507.
10.1016/j.ijleo.2020.164507
Web of Science® Google Scholar
5 Podlubny I., Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and Some of their Applications, 1998, Elsevier, Amsterdam, Netherlands.
Google Scholar
6 Yang G., Shiri B., Kong H., and Wu G. C., Intermediate value problems for fractional differential equations, Computational and Applied Mathematics. (2021) 40, no. 6, 1–20, https://doi.org/10.1007/s40314-021-01590-8.
10.1007/s40314-021-01590-8
Web of Science® Google Scholar
7 Kako M., Nonlinear wave modulation in cold magnetized plasmas, Journal of the Physical Society of Japan. (1972) 33, no. 6, 1678–1687, https://doi.org/10.1143/jpsj.33.1678, 2-s2.0-0015473891.
10.1143/JPSJ.33.1678
Web of Science® Google Scholar
8 Shiri B., Wu G.-C., and Baleanu D., Collocation methods for terminal value problems of tempered fractional differential equations, Applied Numerical Mathematics. (2020) 156, 385–395, https://doi.org/10.1016/j.apnum.2020.05.007.
10.1016/j.apnum.2020.05.007
Web of Science® Google Scholar
9 Shiri B., Wu G. C., and Baleanu D., Terminal value problems for the nonlinear systems of fractional differential equations, Applied Numerical Mathematics. (2021) 170, 162–178, https://doi.org/10.1016/j.apnum.2021.06.015.
10.1016/j.apnum.2021.06.015
Web of Science® Google Scholar
10 Xiong T., Lv Y., and Yi W., Nonlinear vibration and control of underwater supercavitating vehicles, IEEE Access. (2018) 6, 62503–62513, https://doi.org/10.1109/access.2018.2876596, 2-s2.0-85055045989.
10.1109/ACCESS.2018.2876596
Web of Science® Google Scholar
11 Lu D., Seadawy A. R., and Arshad M., Bright-dark solitary wave and elliptic function solutions of unstable nonlinear Schrödinger equation and their applications, Optical and Quantum Electronics. (2018) 50, no. 1, https://doi.org/10.1007/s11082-017-1294-y, 2-s2.0-85039044218.
10.1007/s11082-017-1294-y
PubMed Web of Science® Google Scholar
12 Shchepetil’inikov V. A., Starodubtsev P. A., Traskovskii V. I., Senchenko A. G., and Alifanov R. N., Method of the finding the nonlinear phenomenas in ocean from moving undersea object and their theoretical explanation, Journal of Siberian Federal University. Mathematics & Physics. (2010) 3, no. 2, 267–75.
Google Scholar
13 Parlange J. Y., Water transport in soils, Annual Review of Fluid Mechanics. (1980) 12, no. 1, 77–102, https://doi.org/10.1146/annurev.fl.12.010180.000453.
10.1146/annurev.fl.12.010180.000453
Web of Science® Google Scholar
14 Pimpinelli A and Villain J, Physics of Crystal Growth, 1998, Cambridge University Press, Cambridge, UK.
10.1017/CBO9780511622526
Google Scholar
15 Ankiewicz A, Bokaeeyan M, and Akhmediev N, Shallow-water rogue waves: an approach based on complex solutions of the Korteweg–de Vries equation, Physical Review E. (2019) 99, no. 5, 050201, https://doi.org/10.1103/physreve.99.050201, 2-s2.0-85066450783.
10.1103/PhysRevE.99.050201
CAS PubMed Web of Science® Google Scholar
16 Singh J., Kumar D., and Kumar S., A new fractional model of nonlinear shock wave equation arising in flow of gases, Nonlinear Engineering. (2014) 3, no. 1, 43–50, https://doi.org/10.1515/nleng-2013-0022.
10.1515/nleng-2013-0022
CAS Google Scholar
17 Yang X.-J. and Machado J. T., A new fractional operator of variable order: application in the description of anomalous diffusion, Physica A: Statistical Mechanics and its Applications. (2017) 481, 276–83, https://doi.org/10.1016/j.physa.2017.04.054, 2-s2.0-85018442228.
10.1016/j.physa.2017.04.054
Web of Science® Google Scholar
18 Arora R, Siddiqui M. J., and Singh V. P., Solution of modified equal width wave equation, its variant and non-homogeneous Burgers’ equation by RDT method, American Journal of Computational and Applied Mathematics. (2011) 1, no. 2, 53–56.
10.5923/j.ajcam.20110102.10
Google Scholar
19 Gardner L. R. T. and Gardner G. A., Solitary waves of the equal width wave equation, Journal of Computational Physics. (1992) 101, no. 1, 218–223, https://doi.org/10.1016/0021-9991(92)90054-3, 2-s2.0-0001204872.
10.1016/0021-9991(92)90054-3
Web of Science® Google Scholar
20 Raslan K. R., Collocation method using quartic B-spline for the equal width (EW) equation, Applied Mathematics and Computation. (2005) 168, no. 2, 795–805, https://doi.org/10.1016/j.amc.2004.09.019, 2-s2.0-26044431920.
10.1016/j.amc.2004.09.019
Web of Science® Google Scholar
21 Hamabata H. and Namikawa T., Propagation of hydromagnetic waves in a cold plasma mixed with hot ions, Journal of Plasma Physics. (1985) 33, no. 3, 443–453, https://doi.org/10.1017/s0022377800002610, 2-s2.0-0022082152.
10.1017/S0022377800002610
Web of Science® Google Scholar
22 Zhou Q., Sonmezoglu A., Ekici M., and Mirzazadeh M., Optical solitons of some fractional differential equations in nonlinear optics, Journal of Modern Optics. (2017) 64, no. 21, 2345–2349, https://doi.org/10.1080/09500340.2017.1357856, 2-s2.0-85026353198.
10.1080/09500340.2017.1357856
Web of Science® Google Scholar
23 Khater M., Attia R. A., and Lu D., Modified auxiliary equation method versus three nonlinear fractional biological models in present explicit wave solutions, Mathematical and Computational Applications. (2019) 24, no. 1.
Web of Science® Google Scholar
24 Anjum N. and He J.-H., Laplace transform: making the variational iteration method easier, Applied Mathematics Letters. (2019) 92, 134–138, https://doi.org/10.1016/j.aml.2019.01.016, 2-s2.0-85060526016.
10.1016/j.aml.2019.01.016
Web of Science® Google Scholar
25 Daftardar-Gejji V. and Jafari H., An iterative method for solving nonlinear functional equations, Journal of Mathematical Analysis and Applications. (2006) 316, no. 2, 753–763, https://doi.org/10.1016/j.jmaa.2005.05.009, 2-s2.0-29844442304.
10.1016/j.jmaa.2005.05.009
Web of Science® Google Scholar
26 Jafari H., Iterative methods for solving system of fractional differential equations, 2006, Pune University, Pune City, India, Doctoral dissertation, Ph. D. Thesis.
Google Scholar
27 Prakash A., Goyal M., and Gupta S., Fractional variational iteration method for solving time-fractional Newell-Whitehead-Segel equation, Nonlinear Engineering. (2019) 8, no. 1, 164–171, https://doi.org/10.1515/nleng-2018-0001, 2-s2.0-85049516170.
10.1515/nleng-2018-0001
Google Scholar
28 Prakash A. and Kaur H., A new numerical method for a fractional model of non-linear Zakharov-Kuznetsov equations via Sumudu transform, Methods of Mathematical Modelling. (2019) 189, https://doi.org/10.1201/9780429274114-11.
10.1201/9780429274114-11
Google Scholar
29 Pasha S. A., Nawaz Y., and Arif M. S., The modified homotopy perturbation method with an auxiliary term for the nonlinear oscillator with discontinuity, Journal of Low Frequency Noise, Vibration and Active Control. (2019) 38, no. 3-4, 1363–1373, https://doi.org/10.1177/0962144x18820454, 2-s2.0-85059674844.
10.1177/0962144X18820454
Web of Science® Google Scholar
30 Yépez-Martínez H. and Gómez-Aguilar J. F., A new modified definition of Caputo-Fabrizio fractional-order derivative and their applications to the multi step homotopy analysis method (MHAM), Journal of Computational and Applied Mathematics. (2019) 346, 247–60, https://doi.org/10.1016/j.cam.2018.07.023, 2-s2.0-85050717363.
10.1016/j.cam.2018.07.023
Web of Science® Google Scholar
31 Yu D. N., He J. H., and Garcıa A. G., Homotopy perturbation method with an auxiliary parameter for nonlinear oscillators, Journal of Low Frequency Noise, Vibration and Active Control. (2019) 38, no. 3-4, 1540–54, https://doi.org/10.1177/1461348418811028, 2-s2.0-85059689590.
10.1177/1461348418811028
Web of Science® Google Scholar
32 Prabhakar T. R., A Singular Integral Equation with a Generalized Mittag Leffler Function in the Kernel, 1969, University of Delhi, New Delhi, India.
Google Scholar
33 Gorenflo R., Kilbas A. A., Mainardi F., and Rogosin S. V., Mittag-Leffler Functions, Related Topics and Applications, 2014, Springer, Berlin, Germany.
10.1007/978-3-662-43930-2
Google Scholar
34 Miskinis P., The Havriliak-Negami susceptibility as a nonlinear and nonlocal process, Physica Scripta. (2009) T136, no. T136, 014019, https://doi.org/10.1088/0031-8949/2009/t136/014019, 2-s2.0-77952792419.
10.1088/0031-8949/2009/T136/014019
Web of Science® Google Scholar
35 Garrappa R., Mainardi F., and Guido M., Models of dielectric relaxation based on completely monotone functions, Fractional Calculus and Applied Analysis. (2016) 19, no. 5, 1105–1160, https://doi.org/10.1515/fca-2016-0060, 2-s2.0-84995544887.
10.1515/fca-2016-0060
Web of Science® Google Scholar
36 Stanislavsky A. and Weron K., Atypical case of the dielectric relaxation responses and its fractional kinetic equation, Fractional Calculus and Applied Analysis. (2016) 19, no. 1, 212–228, https://doi.org/10.1515/fca-2016-0012, 2-s2.0-84962144671.
10.1515/fca-2016-0012
Web of Science® Google Scholar
37 Giusti A. and Colombaro I., Prabhakar-like fractional viscoelasticity, Communications in Nonlinear Science and Numerical Simulation. (2018) 56, 138–143, https://doi.org/10.1016/j.cnsns.2017.08.002, 2-s2.0-85026868213.
10.1016/j.cnsns.2017.08.002
Web of Science® Google Scholar
38 D’Ovidio M. and Polito F., Fractional diffusion–telegraph equations and their associated stochastic solutions, Theory of Probability & Its Applications. (2018) 62, no. 4, 552–74.
10.1137/S0040585X97T988812
Web of Science® Google Scholar
39 Górska K., Horzela A., Bratek L., Penson K. A., and Dattoli G., The probability density function for the Havriliak-Negami relaxation, 2016, https://arxiv.org/abs/1611.06433.
Google Scholar
40 An J., Van Hese E., and Baes M., Phase-space consistency of stellar dynamical models determined by separable augmented densities, Monthly Notices of the Royal Astronomical Society. (2012) 422, no. 1, 652–664, https://doi.org/10.1111/j.1365-2966.2012.20642.x, 2-s2.0-84859817427.
10.1111/j.1365-2966.2012.20642.x
Web of Science® Google Scholar
41 Beghin L. and Orsingher E., Fractional poisson processes and related planar random motions, Electronic Journal of Probability. (2009) 14, 1790–826, https://doi.org/10.1214/ejp.v14-675, 2-s2.0-70349472846.
10.1214/EJP.v14-675
Web of Science® Google Scholar
42 Derakhshan M. H. and Ansari A., On Hyers-Ulam stability of fractional differential equations with Prabhakar derivatives, Analysis. (2018) 38, no. 1, 37–46, https://doi.org/10.1515/anly-2017-0029, 2-s2.0-85042048096.
10.1515/anly-2017-0029
Google Scholar
43 Derakhshan M. H. and Ansari A., Numerical approximation to Prabhakar fractional Sturm-Liouville problem, Computational and Applied Mathematics. (2019) 38, no. 2, https://doi.org/10.1007/s40314-019-0826-4, 2-s2.0-85063288109.
10.1007/s40314-019-0826-4
Web of Science® Google Scholar
44 Derakhshan M. H., Ahmadi Darani M., Ansari A., and Khoshsiar Ghaziani R., On asymptotic stability of Prabhakar fractional differential systems, Computational Methods for Differential Equations. (2016) 4, no. 4, 276–84.
Google Scholar
45 Liemert A., Sandev T., and Kantz H., Generalized Langevin equation with tempered memory kernel, Physica A: Statistical Mechanics and its Applications. (2017) 466, 356–369, https://doi.org/10.1016/j.physa.2016.09.018, 2-s2.0-84990032083.
10.1016/j.physa.2016.09.018
Web of Science® Google Scholar
46 Ghorbani A., Beyond adomian polynomials: he polynomials, Chaos, Solitons & Fractals. (2009) 39, no. 3, 1486–1492, https://doi.org/10.1016/j.chaos.2007.06.034, 2-s2.0-62949242120.
10.1016/j.chaos.2007.06.034
Web of Science® Google Scholar
47 Veeresha P., Prakasha D. G., and Kumar D., An efficient technique for nonlinear time-fractional Klein-Fock-Gordon equation, Applied Mathematics and Computation. (2020) 364, 124637, https://doi.org/10.1016/j.amc.2019.124637.
10.1016/j.amc.2019.124637
Web of Science® Google Scholar
48 Sadabad M. K., Akbarfam A. J., and Shiri B., A numerical study of eigenvalues and eigenfunctions of fractional Sturm-Liouville problems via Laplace transform, Indian Journal of Pure and Applied Mathematics. (2020) 51, no. 3, 857–868, https://doi.org/10.1007/s13226-020-0436-2.
10.1007/s13226-020-0436-2
Web of Science® Google Scholar
49 Khalid M., Khan F. S., and Sultana M., A highly accurate numerical method for solving nonlinear time-fractional differential difference equation, Mathematical Methods in the Applied Sciences. (2019) 44, no. 10, 8243–8253, https://doi.org/10.1002/mma.5883, 2-s2.0-85071122711.
10.1002/mma.5883
Google Scholar
50 Bhowmik S. K. and Karakoc S. B., Numerical solutions of the generalized equal width wave equation using the Petrov–Galerkin method, Applicable Analysis. (2019) 100, no. 4, 714–734, https://doi.org/10.1080/00036811.2019.1616696, 2-s2.0-85066081626.
10.1080/00036811.2019.1616696
Web of Science® Google Scholar
51 GaziKarakoc S. B. and Ali K. K., Analytical and computational approaches on solitary wave solutions of the generalized equal width equation, Applied Mathematics and Computation. (2020) 371, 124933, https://doi.org/10.1016/j.amc.2019.124933.
10.1016/j.amc.2019.124933
Web of Science® Google Scholar
52 Eshaghi J., Kazem S., and Adibi H., The local discontinuous Galerkin method for 2D nonlinear time-fractional advection-diffusion equations, Engineering with Computers. (2019) 35, no. 4, 1317–1332, https://doi.org/10.1007/s00366-018-0665-8, 2-s2.0-85058044776.
10.1007/s00366-018-0665-8
Web of Science® Google Scholar
53 Jarad F., Abdeljawad T., and Hammouch Z., On a class of ordinary differential equations in the frame of Atangana-Baleanu fractional derivative, Chaos, Solitons & Fractals. (2018) 117, 16–20, https://doi.org/10.1016/j.chaos.2018.10.006, 2-s2.0-85054432146.
10.1016/j.chaos.2018.10.006
Web of Science® Google Scholar
54 Shaikh S. L., Introducing a new integral transform: Sadik transform, American International Journal of Research in Science, Technology, Engineering & Mathematics. (2018) 22, no. 1, 100–102.
Google Scholar
55 Shaikh SL, Sadik transform in control theory, International Journal of Innovative Sciences and Research Technology. (2018) 3, no. 5, 396–398.
Google Scholar
56 Garra R., Gorenflo R., Polito F., and Tomovski Ž., Hilfer-Prabhakar derivatives and some applications, Applied mathematics and computation. (2014) 242, 576–589, https://doi.org/10.1016/j.amc.2014.05.129, 2-s2.0-84903555141.
10.1016/j.amc.2014.05.129
Web of Science® Google Scholar
57 Redhwan S. S., Shaikh S. L., and Abdo M. S., Some properties of Sadik transform and its applications of fractional-order dynamical systems in control theory, Advances in the Theory of Nonlinear Analysis and its Application. (2019) 4, no. 1, 51–66.
10.31197/atnaa.647503
Google Scholar
58 Mashayekhi S., Ordokhani Y., and Razzaghi M., A hybrid functions approach for the Duffing equation, Physica Scripta. (2013) 88, no. 2, 025002, https://doi.org/10.1088/0031-8949/88/02/025002, 2-s2.0-84881435472.
10.1088/0031-8949/88/02/025002
CAS Web of Science® Google Scholar

Citing Literature

All articles

Analytical Solutions for the Equal Width Equations Containing Generalized Fractional Derivative Using the Efficient Combined Method

Abstract

1. Introduction

2. Important Notations

3. The Proposed Scheme