International Journal of Mathematics and Mathematical Sciences
Volume 2021, Issue 1 6687527
Research Article
Open Access

Derivations of a Sullivan Model and the Rationalized G-Sequence

Oteng Maphane, 

Corresponding Author

Oteng Maphane

Department of Mathematics and Statistical Sciences, Faculty of Science, Botswana International University of Science and Technology, Palapye, Botswana biust.ac.bw

Search for more papers by this author
First published: 01 February 2021
https://doi.org/10.1155/2021/6687527
Citations: 1
Academic Editor: Sumit Chandok

Abstract

Let Gk,n(ℂ) for 2 ≤ k < n denote the Grassmann manifold of k-dimensional vector subspaces of ℂn. In this paper, we compute, in terms of the Sullivan models, the rational evaluation subgroups and, more generally, the G-sequence of the inclusion G2,n(ℂ)↣G2,n+r(ℂ) for r ≥ 1.

1. Introduction

Throughout this paper, we rely on the theory of minimal Sullivan models in rational homotopy theory for which [1] is our standard reference. Let X be a based CW-complex; the nth Gottlieb group of X (or the nth evaluation subgroup [2] of πn(X)), denoted by Gn(X), consists of those elements a ∈ πn(X) for which there is a continuous map H : X × Sn⟶X such that the following diagram commutes:

image

(1)
where h : Sn⟶X is a representative of a and ▽ is the folding map. Let f : X⟶Y be a based map of simply connected finite CW-complexes. In [3], the evaluation at the base point of X gives the evaluation map ω : (Map)(X, Y; f)⟶Y, where (Map)(X, Y; f) is the component of f in the space of mappings from X to Y. The image of the homomorphism induced in homotopy groups
(2)
is called the nth evaluation subgroup of p, and it is denoted by Gn(Y, X; f). Moreover, if f = idX, the space (Map)(X, Y; f) is the monoid aut1(X) of self-equivalences of X homotopic to the identity of X; then, ev : aut1(X)⟶X is the evaluation map, and the image of the induced homomorphism
(3)
is Gn(X), i.e., the nth Gottlieb group. Moreover, in [4], Woo and Lee studied the relative evaluation subgroups and proved that they fit in a sequence
(4)
called the G-sequence of f. Finally, in [3], Smith and Lupton identify the homomorphism induced on rational homotopy groups by the evaluation map ω : (Map(X, Y; f))⟶Y, in terms of a map of complexes of derivations constructed directly from the Sullivan minimal model of f. In [5], the authors use a map of complexes of derivations of minimal Sullivan models of mapping spaces to compute rational relative Gottlieb groups of the inclusion G2,n(ℂ)↣G2,n+1(ℂ) between complex Grassmannians. In this paper, we generalize their work to compute rational relative Gottlieb groups of the inclusion Gk,n(ℂ)↣Gk,n+r(ℂ), r ≥ 1 between complex Grassmannians for 2 ≤ k < n.

2. Preliminaries

Here, we fix terminology and recall some standard facts on differential graded algebras. All vector spaces and algebras are taken over a field ℚ of rational numbers.

Definition 1. A graded algebra A is a sum A = ⊕n≥0An, where An is a vector space, together with an associative multiplication Ai ⊗ Aj⟶Ai+j, x ⊗ y ↦ xy, and has 1 ∈ A0. It is graded commutative if, for any homogeneous elements x and y,

(5)
where |x| = i for x ∈ Ai. If A is a graded algebra equipped with a linear differential map d : An⟶An+1 such that d°d = 0 and
(6)
then (A, d) is called a differential-graded algebra and d is called a differential. Moreover, if A is also a graded commutative algebra, then (A, d) is a commutative differential graded algebra (cdga). It is said to be connected if A0≅ℚ.

Definition 2. Let V = ⊕i≥0Vi with Veven : = ⊕i≥0V2i and Vodd : = ⊕i≥1V2i−1. A commutative-graded algebra A is called free commutative if A = ∧V = S(Veven) ⊗ E(Vodd), where S(Veven) is the symmetric algebra on Veven and E(Vodd) is the exterior algebra on Vodd.

Definition 3. A Sullivan algebra is a commutative differential-graded algebra (∧V, d), where V = ∪k≥0V(k) and V(0) ⊂ V(1)⋯ such that dV(0) = 0 and dV(k) ⊂ ∧V(k − 1). It is called minimal if dV  ⊂ ∧≥2V.

If (A, d) is a cdga whose cohomology is connected and finite dimensional in each degree, then there always exists a quasi-isomorphism from a Sullivan algebra (∧V, d) to (A, d) [1]. To each simply connected space, Sullivan associates a cdga APL(X) of rational polynomial differential forms on X that uniquely determines the rational homotopy type of X [6]. A minimal Sullivan model of X is a minimal Sullivan model of APL(X). More precisely, H∗(∧V, d)≅H∗(X; ℚ) as graded algebras and V≅π∗(X) ⊗ ℚ as graded vector spaces.

3. Derivations of a Sullivan Model and the G-Sequence

Let (A, d) be a commutative differential-graded algebra. A derivation θ of degree k is a linear mapping θ : An⟶An−k such that θ(ab) = θ(a)b + (−1)k|a|aθ(b). Denote by DerkA the vector space of all derivation of degree k and DerA = ⊕kDerkA. The commutator bracket induces a graded Lie algebra structure on DerA. Moreover, (DerA, δ) is a differential graded Lie algebra [6], with the differential δ defined in the usual way by
(7)

Let (∧V, d) be a Sullivan algebra, where V is spanned by {v1, …, vk}. Then, Der∧V is spanned by θ1, …, θk, where θi is the unique derivation of ∧V defined by θi(vj) = δij. The derivation θi will be denoted by (vi, 1). Moreover, an element v ∈ V≅π∗(X) ⊗ ℚ is a Gottlieb element of π∗(X) ⊗ ℚ if and only if there is a derivation θ of ∧V satisfying θ(v) = 1 and such that δθ = 0,see page 392 in [1].

Let ϕ : (A, d)⟶(B, d) be a morphism of cdga’s. A ϕ-derivation of degree k is a linear mapping θ : An⟶Bn−k for which θ(ab) = θ(a)ϕ(b) + (−1)k|a|ϕ(a)θ(b).

We consider only derivations of positive degree. Denote by Dern(A, B; ϕ) the vector space of ϕ-derivations of degree n for n > 0 and by Der(A, B; ϕ) = ⊕nDern(A, B; ϕ) the ℤ-graded vector space of all ϕ-derivations. The differential-graded vector space of ϕ-derivations is denoted by (Der(A, B; ϕ), ∂), where the differential ∂ is defined by ∂θ = dB°θ + (−1)k+1θ°dA. In case A = B and ϕ = 1B, then (Der(B, B; 1), ∂) is just the usual differential-graded Lie algebra of derivations on the cdga B [3]. Whenever A = (∧V, d) is a Sullivan algebra, we note that there is an isomorphism of graded vector spaces:
(8)
If {vi} is a basis of V, then the vector space Der(A, B; ϕ) is spanned by the unique ϕ-derivation θ denoted by (vi, bi) such that θi(vi) = bi, where bi ∈ B and θi(vj) = 0 for i ≠ j. Moreover, in [3], precomposition with ϕ gives a chain complex map ϕ∗ : Der(B, B; 1)⟶Der(A, B; ϕ) and postcomposition with the augmentation ε : B⟶ℚ gives a chain complex map ε∗ : Der(A, B; ϕ)⟶Der(A, ℚ; ε). The evaluation subgroup of ϕ is defined as follows:
(9)
In case A = B and ϕ = 1B, we get the Gottlieb group of (B, d) defined as follows:
(10)

In particular, Gn(B)≅Gn(Xℚ), if B is the minimal Sullivan model of a simply connected space X (see Proposition 29.8 in [1]).

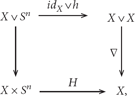
Definition 4. (see [3, 7]). Let ϕ : A⟶B be a map of differential-graded vector spaces. A differential-graded vector space, Rel∗(ϕ), called the mapping cone of ϕ is defined as follows. Reln(ϕ) = An−1 ⊕ Bn with the differential δ(a, b) = (−dA(a), ϕ(a) + dB(b)). There are inclusion and projection chain maps J : Bn⟶Reln(ϕ) and P : Reln(ϕ)⟶An−1 defined by J(w) = (0, w) and P(a, b) = a. These yields a short exact sequence of chain complexes

(11)
and a long exact homology sequence of ϕ
(12)
whose connecting homomorphism is H(ϕ).

Following [3], we consider a commutative diagram of differential-graded vector spaces:

image

(13)
where ε is the augmentation of either A or B, which leads to the following homology ladder for n ≥ 2:

image

(14)
The nth relative evaluation subgroup of ϕ is defined as follows:
(15)
The G-sequence of the map ϕ : A⟶B is given by
(16)
which ends in G2(A, B; ϕ). Moreover, Theorem 3.5 in [3] can be applied to the Sullivan model ϕ : (∧V, d)⟶(B, d) of the map f : X⟶Y.

4. The Inclusion Gk,n(ℂ)↣Gk,n+1(ℂ)

The complex Grassmannian Gk,n(ℂ) is a simply connected homogeneous space as Gk,n(ℂ)≅U(n)/(U(k) × U(n − k)) for 1 ≤ k < n, where U(n) is the unitary group. It is a symplectic manifold of dimension 2m, where m = k(n − k). As the complex Grassmannian Gk,n(ℂ) is simply connected, so we may associate a minimal Sullivan model.

The method to compute a Sullivan model of the homogeneous space Gk,n(ℂ) is given in detail in [8, 9].

Following [9], a Sullivan model of Gk,n(ℂ) for 1 ≤ k < n is given by
(17)
with
(18)

Lemma 1. The minimal Sullivan model of Gk,n(ℂ) for 2 ≤ k < n is given by

(19)
where dbi = 0 and dy2(n − k)+1 ∈ ∧(b2, …, b2k).

Proof. Consider the Sullivan model

(20)
of Gk,n(ℂ) for 2 ≤ k < n:
(21)

The model is not minimal as the linear part is not zero. To find its minimal Sullivan model, we make a change of variable t2 = b2 + x2 and replace x2 by t2 − b2 wherever it appears in the differential. This gives an isomorphic Sullivan algebra

(22)
where
(23)

As the ideal generated by y1 and t2 is acyclic, the above Sullivan algebra is quasi-isomorphic to

(24)
where
(25)

One continues in this fashion and makes another change of variable and replaces x4 by wherever it appears in the differential and does so until they reach a change of variable of the form

(26)
where α ∈ ∧(b2, …, b2(k − 1)), β ∈ ∧(b2, …, b2k) and replace
(27)
wherever it appears in the differential. This gives an isomorphic Sullivan algebra:
(28)
where
(29)

As the ideal generated by t2(n − k) and y2(n − k)−1 is acyclic, we get the minimal Sullivan model:

(30)
with dbi = 0 and dy2(n − k)+1 ∈ ∧(b2, …, b2k).

In the same way, by Lemma 1, the minimal Sullivan model of Gk,n+r(ℂ) for 2 ≤ k < n + r and r ≥ 1 is given by

(31)
where dai = 0 and dz2(n + r − k)+1 ∈ ∧(a2, …, a2k). We establish the following results.

Theorem 1. Let B = (∧(b2, …, b2k, y2(n − k)+1, …, y2n−1), d). Then,

Proof. Let (y2(n − t)+1, 1) denote the derivation θ2(n − t)+1 for t ∈ {1, …, k} such that θ2(n − t)+1(y2(n − t)+1) = 1 and zero on other generators. Then,

(32)

Moreover, the generators θ2(n − t)+1 cannot be boundaries for degree reasons. Therefore, [θ2(n − t)+1] are nonzero homology classes in H∗(Der(B, B; 1)). Furthermore,

As Gk,n(ℂ) is a simply connected finite CW-complex, then Geven(B) = 0 (see Proposition 28.8 in [1]. Thus,

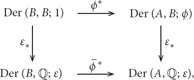
Theorem 2. Given the inclusion Gk,n(ℂ)↣Gk,n+r(ℂ), r ≥ 1 for 2 ≤ k < n and ϕ : (∧V, d)⟶(B, d) for its Sullivan model, then

Proof. The vector space Der(∧V, B; ϕ) is generated by the derivations θ2(n + r − t)+1 = (z2(n + r − t)+1, 1) for t ∈ {1, …, k}. The differential is given by

(33)

Hence, [θ2(n + r − t)+1] are the nonzero homology classes in H∗(Der(∧V, B; ϕ)). Moreover, , where Thus,

Theorem 3. Given the inclusion Gk,n(ℂ)↣Gk,n+r(ℂ), r ≥ 1 for 2 ≤ k < n and ϕ : (∧V, d)⟶(B, d) for its Sullivan model, then

Proof. Define the derivations α2(n − t)+1 = (y2(n − t)+1, 1) for t ∈ {1, …, k} in Der(B, B; 1) and θ2(n + r − t)+1 = (z2(n + r − t)+1, 1) in Der(∧V, B; ϕ). Then,

(34)
such that
(35)
and D(0, θ2(n + r − t)+1) = (0,0). Thus, [(α2(n − t)+1, 0)] if 2(n − t) + 1 ≠ 2(n + r − t) + 1 and [(0, θ2(n + r − t)+1)] are the nonzero homology classes in H∗(Rel(ϕ∗)). Moreover, , for 2(n − t) + 1 ≠ 2(n + r − t) + 1, and in the same way, A straightforward calculation shows that for 2(n − t) + 1 ≠ 2(n + r − t) + 1 and span H(ε∗, ε∗).

The G-sequence reduces to

(36)
and it is exact.

Conflicts of Interest

The author declares no conflicts of interest.

Acknowledgments

This work was completed with the support of the Botswana International University of Science and Technology (BIUST).

    Data Availability

    No data were used to support this study.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.