Earth Pressure of Three-Dimensional Stress States under Different Strength Criteria and Its Application
Abstract
To solve the Earth pressure problems in practical engineering, such as retaining walls and foundation pits, we derive active and passive Earth pressure formulas in accordance with the relationship between intermediate principal stress and excavation under three-dimensional stress states. The formulas are derived on the basis of the Mohr–Coulomb, spatially mobilized plane (SMP), SMP, Lade–Duncan, axisymmetric compression- (AC-) SMP strength, and generalized Mises (Gen-Mises) criteria and then extended to clay. We also compare the calculated Earth pressure with the measured data. Results indicate that the Earth pressure considering medium principal stress contribution under a three-dimensional stress state is consistent with the actual engineering. The calculated active Earth pressure in the Mohr–Coulomb strength criterion is larger, and the passive Earth pressure is smaller than the practical one because the intermediate principal stress effect is not considered. The calculated results of the SMP, SMP, Lade–Duncan, AC-SMP strength, and Gen-Mises criteria are close to the measured data, among which the result of the Gen-Mises criterion is closer. The Earth pressure calculated using the Lade–Duncan criterion is no longer appropriate to describe the Earth pressure under medium principal stress condition in this study. The results of this study have theoretical significance for retaining structure design under a three-dimensional stress state.
1. Introduction
In practical engineering, the Earth pressure problems of retaining walls and vertical excavation of foundation pits are usually in a three-dimensional stress state. The classical Rankine Earth pressure theory is based on the Mohr–Coulomb strength criterion, only considering the influence of large and small principal stresses on strength and ignoring the contribution of intermediate principal stress. This limitation leads to underrating Earth pressure, which has been confirmed by many experimental results [1]. To obtain the real Earth pressure, numerous studies, such as on the passive Earth pressure under seismic load, have been conducted [2–5]. However, most research focuses on the Earth pressure under static load, which can be divided into two categories. The first one regards the retaining structure as a plane strain problem, the intermediate principal stress condition is obtained on the basis of a specific strength criterion in accordance with the deformation conditions and elastic-plastic theory [6–9], and the general stress state strength theory is introduced into the Earth pressure calculation. Otherwise, the formula of the intermediate principal stress, obtained in accordance with the generalized Hooke’s law and the strain conditions in the plane strain direction [10], is substituted into the strength criterion to determine the Earth pressure. The second one obtains the Earth pressure under a specific strength criterion in accordance with the empirical or assumed intermediate principal stress conditions under three-dimensional stress states [11–15]. Overall, the study of the Earth pressure is still based on certain strength criterion and the corresponding intermediate principal stress condition. A systematic study of Earth pressure theory under different strength criteria and its comparative analysis should be conducted.
Therefore, a calculation method for Earth pressure in a three-dimensional stress state, considering the contribution of intermediate principal stress and revealing the differences of the results based on various strength criteria, should be established, and its applicability should be studied. In this paper, we propose the design formulas of active and passive Earth pressures for cohesionless and cohesive soils under three-dimensional stress states. The calculated results are compared with the measured data of sand and clay soil to verify the precision and applicability of the formulas.
2. Several Common Strength Criteria for Soils
The soil strength criterion reflects the relationship among the shear stress, normal stress, and characteristic parameters of soil on a specific shear plane when destroyed. The state of principal stress can be expressed as F(σij, kf) = 0. The strength criteria for soils are Mohr–Coulomb, spatially mobilized plane (SMP), Lade–Duncan, generalized Mises (Gen-Mises), axisymmetric compression- (AC-) SMP [16], and SMP [17], which can be expressed as follows.
2.1. Mohr–Coulomb Strength Criterion
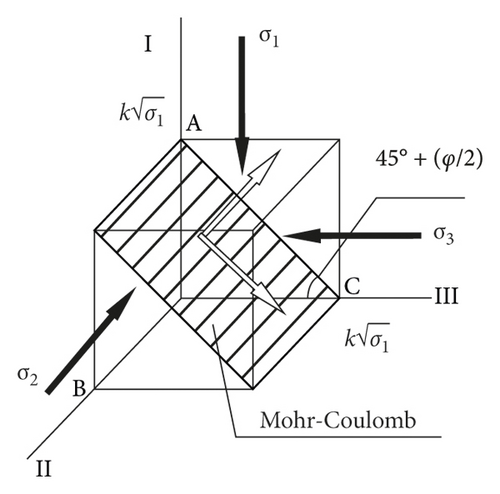
The Mohr–Coulomb criterion does not consider the effect of intermediate principal stress; thus, the mobilized plane is 45° + φ/2, as shown in Figure 1.
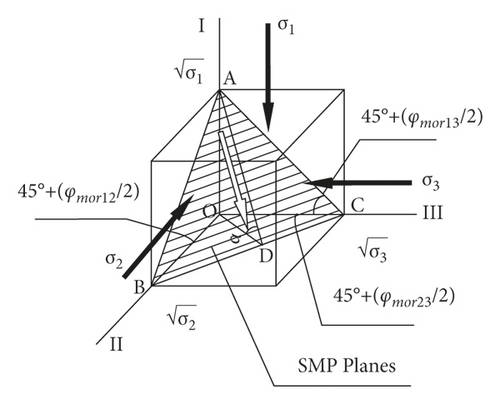
2.2. SMP Strength Criterion
2.3. Lade–Duncan Strength Criterion
2.4. Gen-Mises Strength Criterion
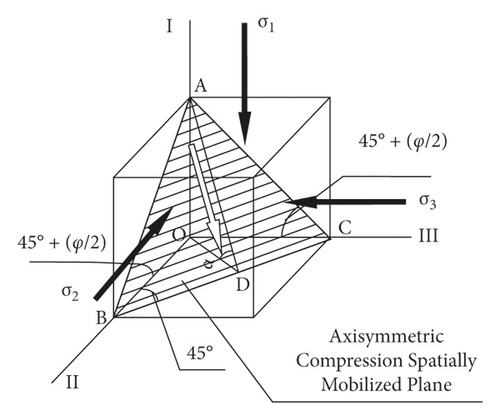
2.5. AC-SMP Strength Criterion
2.6. SMP Criterion
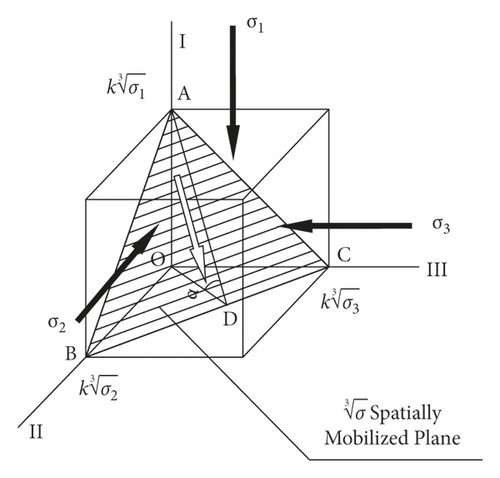
The failure shear planes of each criterion are different, and the shear and normal stresses are irrelevant to the intermediate principal stress in the Mohr–Coulomb criterion. For the other criteria, the shear and normal stresses include the intermediate principal stress. Thus, the soil strength described by different criteria differs. To describe the soil strength defined by each strength criterion clearly, we plot the failure lines of each strength criterion when the internal friction angle is 35° on the π plane in the principal stress space (Figure 6).
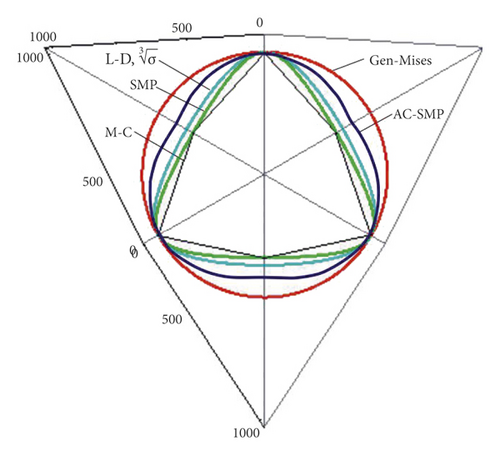
From Figure 6, the criteria are arranged in descending order on the basis of described soil strength: Gen-Mises, AC-SMP, Lade–Duncan and SMP, SMP, and Mohr–Coulomb. The strength of Lade–Duncan and SMP are the same. Previous studies have also indicated the SMP of the Lade–Duncan strength criterion and SMP criterion [17]. The soil strength differs greatly based on different strength criteria because of the different intermediate principal stresses in each strength criterion. When the soil is damaged, the higher the degree of the intermediate principal stress, the greater the soil strength will be. Previous research results [18–21] indicate that the strength criterion considering the effect of intermediate principal stress can better exert the strength characteristics of the rock and soil. For the practical project, proper strength criterion will exert the maximum resistance of soil and therefore be more economical.
3. Active and Passive Soil Pressures of Cohesive Soils with Various Strength Criteria under a Three-Dimensional Stress State
The classical Rankine Earth pressure theory is based on the Mohr–Coulomb strength criterion, disregarding the contribution of intermediate principal stress. In practice, soil is generally in a three-dimensional stress state σ1 > σ2 > σ3, and the soil pressure calculated using the Mohr–Coulomb strength criterion is inconsistent with the real one. Therefore, the analysis of the calculation method for Earth pressure with the consideration of intermediate principal stress is of great importance. From equations (2)–(6), the development of intermediate principal stress directly determines the soil strength described by the strength criteria and then affects the calculated value. The intermediate principal stress of soil should be determined to acquire the Earth pressure under a three-dimensional stress state. Then, the result should be integrated into the strength criteria of each three-dimensional stress state, and the relationship between large and small principal stresses of the failure soil can be obtained.
When calculating the active Earth pressure, σ1 = γz and σ2 = k2γz (γ is the soil unit weight, and z is the depth) are integrated into each strength criterion and Pa = σ3 and Pp = σ1 can be obtained. Then, we can derive the active and passive Earth pressure expressions based on each strength criterion.
3.1. Earth Pressure Based on the Mohr–Coulomb Strength Criterion
3.2. Earth Pressure Based on the SMP Strength Criterion
3.3. Earth Pressure Based on the Lade–Duncan Strength Criterion
3.4. Earth Pressure Based on the Gen-Mises Strength Criterion
3.5. Earth Pressure Based on the AC-SMP Strength Criterion
3.6. Earth Pressure Based on the SMP Criterion
4. Analysis of the Active and Passive Earth Pressure Coefficients of Cohesionless Soil Based on Each Strength Criterion
The core of Earth pressure theory is the determination of Earth pressure coefficient, and the key of Earth pressure problem in three-dimensional stress state is the influence of intermediate principal stress on the Earth pressure coefficient. The relative difference value of the Earth pressure coefficient calculated based on each strength criterion essentially reflects the contribution of intermediate principal stress to strength and also clearly reflects the influence of each strength criterion on Earth pressure. For test parameters fitting, R2 (the correlation coefficient) is usually applied to describe the correlation of parameters [25–27]. For the theoretical analysis in this paper, we assumed the same soil parameters and the calculation results of each strength criterion and the Mohr–Coulomb strength criterion could reflect the difference clearly. Equations (25) and (26) are used to conduct the coefficient of Earth pressure based on each strength criterion.
In accordance with the expression of active Earth pressure coefficient Ka obtained using different strength criteria, the active Earth pressure coefficient under different strength criteria can be obtained by putting in the internal friction angle φ. In accordance with Earth pressure theory, the active Earth pressure coefficient Ka should be less than 1. From the failure line on the π plane (Figure 6), the more the Earth strength described by the criterion is, the less the active Earth pressure when soil breaks will be. The active Earth pressure coefficient in the order of small to large is obtained using the Gen-Mises, AC-SMP, Lade–Duncan, SMP, SMP, and Mohr–Coulomb strength criteria. The active Earth pressure coefficient based on each criterion should satisfy two conditions. The active Earth pressure coefficient is calculated when φ is in the range of 0°< φ ≤ 50°. The results show that when 15°≤ φ, the Gen-Mises, AC-SMP, SMP, SMP, and Mohr–Coulomb strength criteria meet the above two conditions, which could reflect the Earth pressure on the retaining structure well. The Lade–Duncan strength criterion could not meet the condition with any range of friction angle and is no longer applicable to describe the Earth pressure under the condition of medium principal stress. Therefore, the Lade–Duncan criterion will not be involved in the subsequent discussion.
4.1. Analysis of the Active Earth Pressure Coefficient
The variation in the active Earth pressure coefficient Ka with internal friction angle φ based on each strength criterion is shown in Figure 7.
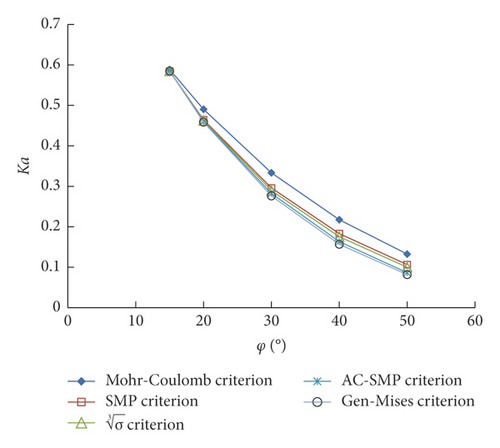
From Figure 7, the active Earth pressure coefficients decrease nonlinearly with the increase in internal friction angle. The larger the internal friction angle is, the greater the difference will be. The value of the active Earth pressure coefficients is less than that calculated using the Mohr–Coulomb strength criterion. The active Earth pressure coefficient in the order of large to small is obtained using the Mohr–Coulomb, SMP, , AC-SMP, and Gen-Mises strength criteria, consistent with the Earth strength described by the strength criteria. When the contribution of intermediate principal stress to strength is considered, the soil strength can be further developed and the soil can bear increased deformation and maintain stability with active unloading.
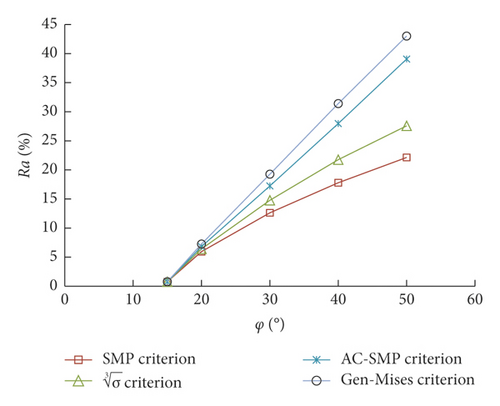
From Figure 8, the relative difference between the active Earth pressure coefficient and the Mohr–Coulomb strength criterion increases rapidly with the increase in the internal friction angle. When φ < 50°, the maximum value of relative difference of active Earth pressure coefficients is less than 40%, indicating that active Earth pressure can be well calculated using each strength criterion.
4.2. Analysis of the Passive Earth Pressure Coefficient
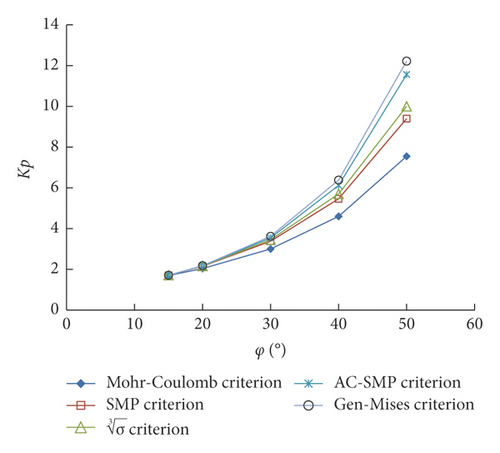

From Figure 9, the passive Earth pressure coefficient increases nonlinearly with the increase in the internal friction angle. The larger the internal friction angle is, the greater the difference in the passive Earth pressure coefficient will be. When φ > 40°, the difference in passive Earth pressure coefficient increases rapidly but can reflect the passive Earth pressure well.
As shown in Figure 10, the relative difference in passive Earth pressure coefficient also increases nonlinearly with the increase in internal friction angle. The larger the internal friction angle is, the larger the relative difference in passive Earth pressure coefficient will be. When φ > 50°, the relative differences of the Gen-Mises and AC-SMP strength criteria exceed 40% and the rationality of the calculation results should be verified.
From the active and passive Earth pressure coefficients in Figures 7–10, the active Earth pressure coefficient based on the Mohr–Coulomb strength criterion is large, whereas the passive Earth pressure coefficient is small because the contribution of intermediate principal stress is disregarded and the results are conservative. Different from the axisymmetrical state, the intermediate principal stress is always greater than the small principal stress under the three-dimensional stress state. This strengthens the constraint in the direction of the intermediate principal stress, which plays a positive role in improving the soil strength. Therefore, the active Earth pressure coefficient is smaller and the passive Earth pressure coefficient is larger. The three-dimensional stress-state strength criteria can exert the Earth strength entirely. Under a three-dimensional stress state, when φ > 15°, the calculation results of each strength criterion can describe the Earth pressure of the retaining structure well. When φ > 50°, the calculation errors of the Gen-Mises and AC-SMP strength criteria are relatively large. The soil internal friction angle is generally less than 50°; hence, the calculation results based on the strength criteria can be used to describe the value of Earth pressure in a three-dimensional stress state. The selection of reasonable strength criterion calculation results for different soil properties and engineering problems could enhance the Earth strength, reduce the support strength, and make projects considerably economical.
5. Active and Passive Soil Pressures of Cohesive Soil Based on Various Strength Criteria under a Three-Dimensional Stress State
5.1. Earth Pressure of Cohesive Soil Based on the Mohr–Coulomb Strength Criterion
The large and small principal stresses of cohesionless soil based on the Mohr–Coulomb strength criterion are replaced with , and the expression of Earth pressure for cohesive soil can be obtained as follows.
5.2. Earth Pressure of Cohesive Soil Based on the SMP Strength Criterion
In accordance with equation (27), the expression of Earth pressure based on the SMP strength criterion can be obtained as follows.
5.3. Earth Pressure of Cohesive Soil Based on the Lade–Duncan Strength Criterion
In accordance with equation (27), the expression of Earth pressure based on the Lade–Duncan strength criterion can be obtained as follows.
5.4. Earth Pressure of Cohesive Soil Based on the Gen-Mises Strength Criterion
In accordance with equation (27), the expression of Earth pressure based on the Gen-Mises strength criterion can be obtained as follows.
5.5. Earth Pressure of Cohesive Soil Based on the AC-SMP Strength Criterion
In accordance with equation (27), the expression of Earth pressure based on the AC-SMP strength criterion can be obtained as follows.
5.6. Earth Pressure of Cohesive Soil Based on Strength Criterion
In accordance with equation (27), the expression of Earth pressure based on strength criterion can be obtained as follows.
6. Theoretical Calculation and Analysis of Earth Pressure
6.1. Verification of Earth Pressure in Cohesionless Soil
The cohesionless sand used in the test [28] has an internal friction angle φ of 34° and a volume weight γ of 19.56 kN/m3. The retaining wall is made of mixed wooden planks and is 5 cm thick, 1 m high, and 1 m wide. It is reinforced to meet the stiffness requirements. The active Earth pressure measured during the test is shown in Figure 11, where H is the height of the wall and Pa is the active Earth pressure. The sand property parameters are substituted into the active Earth pressure expression based on each strength criterion, and the active Earth pressure values in a three-dimensional stress state at different depths of the retaining wall can be calculated. A comparison between the calculated and measured results is shown in Figure 11.
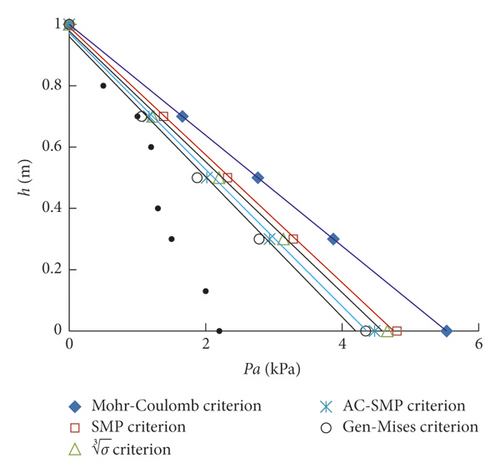
From Figure 11, the active Earth pressure in a three-dimensional stress state calculated in accordance with the strength criteria increases approximately linearly with the increase in depth. The active Earth pressures in the order of large to small are obtained using the Mohr–Coulomb, SMP, SMP, AC-SMP, and Gen-Mises strength criteria. The measured active Earth pressure is remarkably less than the calculated value based on the Mohr–Coulomb strength criterion, implying that the calculation result of the Mohr–Coulomb strength criterion is excessively conservative. In engineering construction, the support strength can be appropriately reduced to improve the economy.
The difference in active Earth pressure based on the strength criteria is increased with increasing excavation depth. The active Earth pressures based on the SMP, SMP, AC-SMP, and Gen-Mises strength criteria reflect the contribution of intermediate principal stress to Earth strength, which could reveal the Earth pressure on the retaining wall well. The calculation result based on the Gen-Mises strength criterion is closer to the measured Earth pressure value than others.
6.2. Verification of Earth Pressure in Cohesive Soil
6.2.1. Analysis of Homogeneous Cohesive Soil
In a deep foundation pit project, the excavation depth is 14 m, the continuous retaining wall is 5 m into the bottom, and the soil is homogeneous clay. The parameters are as follows: c = 20 kPa, φ = 20o, and γ = 19kN/m3. The calculation diagram is shown in Figure 12. When the soil in the pit is excavated, the soil behind the pit will shift to the free face because of the horizontal discharge and the active Earth pressure will be generated at the continuous retaining wall. At the same time, the soil at the bottom of the pit, compressed by the wall embedded in the pit bottom, exerts passive Earth pressure.
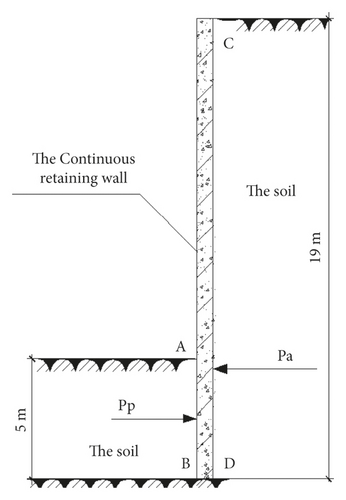
In accordance with equations (28)–(39), the active and passive Earth pressure values of the continuous retaining wall at different depths under the condition of three-dimensional stress state can be calculated on the basis of different strength criteria. The values are shown in Table 1.
| Strength criterion | PpA (kPa) | PpB (kPa) | PaC (kPa) | PaD (kPa) |
|---|---|---|---|---|
| Mohr–Coulomb criterion | 57.13 | 250.89 | −28.01 | 148.99 |
| SMP criterion | 58.7 | 263.29 | −27.26 | 140.37 |
| criterion | 58.83 | 264.3 | −27.19 | 139.71 |
| AC-SMP criterion | 58.94 | 265.2 | −27.15 | 139.12 |
| Gen-Mises criterion | 59.06 | 266.19 | −27.09 | 138.49 |
Table 1 presents that the active and passive Earth pressures at various depths calculated in accordance with the strength criteria are different. The maximum active Earth pressure on the retaining wall is calculated using the Mohr–Coulomb strength criterion, and the minimum is obtained using the Gen-Mises strength criterion. The calculation results of passive Earth pressure are opposite. The three-dimensional stress-state Earth pressure calculation results of each strength criterion can well describe the Earth pressure on the homogeneous clay-retaining structure. This result indicates that the intermediate principal stress has an evident contribution to the improvement of soil strength by helping the excavated soil withstand great passive Earth pressure and small active Earth pressure, which could develop the strength of soil to resist the external load and reduce the support strength.
6.2.2. Analysis of Layered Cohesive Soil
A deep foundation pit with a depth of 7.1 m is supported by 800 mm cantilever piles with a length of 12.70 m. The distribution of soil layers in the pit depth and the soil properties of each soil layer are shown in Figure 13 [12].

In accordance with the formula of the active Earth pressure of cohesive soil and the soil parameters of each layer, the active Earth pressure at different depths based on each strength criterion can be calculated, as shown in Table 2. A comparison of calculated and measured Earth pressure values at the upper and lower interfaces is shown in Figure 14.
| Strength criterion | Pa (kPa) 0 m | Pa (kPa) above 0.8 m | Pa (kPa) below 0.8 m | Pa (kPa) above 3.8 m | Pa (kPa) below 3.8 m | Pa (kPa) above 6.3 m | Pa (kPa) below 6.3 m | Pa (kPa) 7.1 m |
|---|---|---|---|---|---|---|---|---|
| Mohr–Coulomb criterion | −23.02 | −13.98 | 0.38 | 27.31 | 11.69 | 31.73 | 35.82 | 41.48 |
| SMP criterion | −22.94 | −13.95 | 0.16 | 25.46 | 9.97 | 28.32 | 31.71 | 36.78 |
| criterion | −22.94 | −13.96 | 0.14 | 25.29 | 9.59 | 27.56 | 31 | 35.97 |
| AC-SMP criterion | −22.94 | −13.96 | 0.12 | 25.15 | 9.53 | 27.46 | 30.3 | 35.2 |
| Gen-Mises criterion | −22.94 | −13.96 | 0.1 | 25 | 9.33 | 27 | 29.7 | 34.5 |
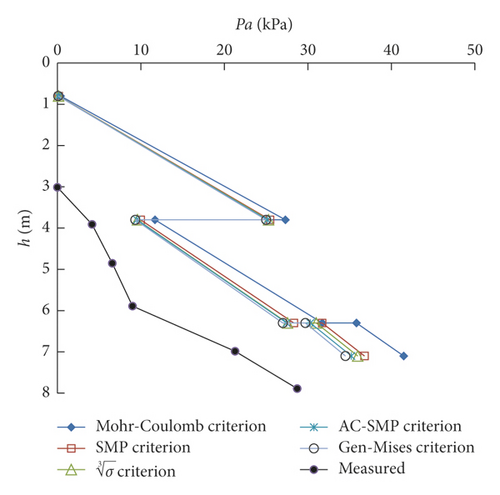
Table 2 and Figure 14 demonstrate that the variation in active Earth pressure of layered cohesive soil is consistent with that of cohesionless soil and homogeneous cohesive soil calculated on the basis of each strength criterion. The calculation results of each strength criterion show that positive active Earth pressure begins to be generated when the foundation pit is excavated to approximately 0.8 m. This result means that the depth of the foundation pit that can be excavated without support is 0.8 m theoretically. The measured results show that positive active Earth pressure develops until the foundation pit is excavated to 3 m, indicating the complexity of Earth pressure in actual engineering. When the excavation depth is less than 3.8 m, the calculated results of Earth pressure in accordance with the strength criteria differ greatly from the measured values. However, the failure of the foundation pit is generally at the middle and bottom, and the difference in calculation results of soil pressure on the top of the foundation pit will not affect the safety. When the excavation depth is greater than 3.8 m, the Earth pressure calculation results of each strength criterion basically reflect the variation law of Earth pressure, but all of them are conservative. The preceding analysis indicates that for layered soil sites under a three-dimensional stress state, the Earth pressure calculation results based on each strength criterion can describe the value of Earth pressure well on the retaining structure. The calculated results presented in this paper are closer to the measured values than those of the Mohr–Coulomb strength criterion, and the result of the Gen-Mises strength criterion is the most accurate. On the premise of safety, when calculating Earth pressure under the condition of three-dimensional stress state, the theory in this paper can fully consider the contribution of intermediate principal stress to Earth strength, which is consistent with actual engineering.
7. Conclusions
- (1)
Under the condition of three-dimensional stress state, large and small principal stresses based on different strength criteria are obtained in accordance with the equation of the Earth pressure coefficient in the direction of intermediate principal stress and excavation depth. The active and passive Earth pressures in a three-dimensional stress state are deduced on the basis of each strength criterion and extended to cohesive soil.
- (2)
Under the condition of three-dimensional stress state, when 15°≤φ, the Earth pressure coefficient based on each strength criterion can be used to calculate the active and passive Earth pressures. When φ > 50°, the errors of the Earth pressure calculation based on AC-SMP and Gen-Mises criteria are larger than those of the Mohr–Coulomb criterion.
- (3)
Under the condition of three-dimensional stress state, the calculation results of active and passive Earth pressures of cohesionless and cohesive soils based on each strength criterion show that the calculated active Earth pressure is small and the passive Earth pressure is large after considering the effect of intermediate principal stress. This finding is closer to actual engineering.
- (4)
Under the condition of three-dimensional stress state, the comparison analysis between the measured Earth pressure data and the calculation results of cohesionless and cohesive soils shows that the Mohr–Coulomb strength criterion tends to be conservative in retaining the structure design because it does not consider the contribution of intermediate principal stress. The Lade–Duncan strength criterion is unsuitable for calculating the Earth pressure on the retaining wall under the condition of principal stress in this paper. The calculated results of the SMP, SMP, AC-SMP, and Gen-Mises strength criteria can be used to show the Earth pressure on the retaining structure in actual engineering. The calculation result of the Gen-Mises strength criterion is the most accurate.
Conflicts of Interest
The authors declare no conflicts of interest.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (nos. 11802218 and 42007257), Science and Technology Plan Project of Shaanxi Province (no. 2019JQ-349), Shaanxi Key Laboratory of Loess Mechanics and Engineering (no. LME201801), and Natural Science Foundation of Shaanxi Provincial Department of Education (no. 20JK0670).
Open Research
Data Availability
The data used to support the findings of this study are available from the corresponding author upon request.




