The brittleness of rock is an important parameter that influences and controls the evolution mechanism of the fracture and formation of a fracture net. The existing methods of brittle characterization are describing the brittleness of rock mass as a whole. They lack reliability descriptions to guide the fracture strike and improve the volume of the reservoir. It is considered that the macroscopic brittle fracture of a rock is the process of continuous initiation and propagation of local fractures in the rock mass under the action of external loads. The macroscopic fracture is the appearance caused by a local rupture to a certain extent, and the local rupture is the root cause of macroscopic fracture. The study of the local brittleness of a rock can reveal the intrinsic nature of its fracture behavior and can reflect the evolution mechanism of fracture more directly and accurately. In this paper, coring sampling in field outcrop is first carried out, and the break evolution law of core is described by a CT scanner. The mineral compositions in the core are determined by a mineral analysis diffractometer. The regulation of the rock local brittleness with different mineral contents is analyzed. And a new method for local brittle region division and characterization of rock has been developed. This method gives the connotation relation of the rock brittle fracture as a whole induced by a local brittle fracture. And it provides a new approach to study the law of a rock fracture.

1. Introduction

With the shortening of the proven oil and gas reserves, unconventional oil and gas exploitation is the inevitable development trend in the future to ensure the sustained and stable oil and gas production. As a new type of clean energy, unconventional oil and gas has the advantages of wide resource distribution, abundant reserves, and long exploitation life. It has become a hot spot in global oil and gas exploration and development.

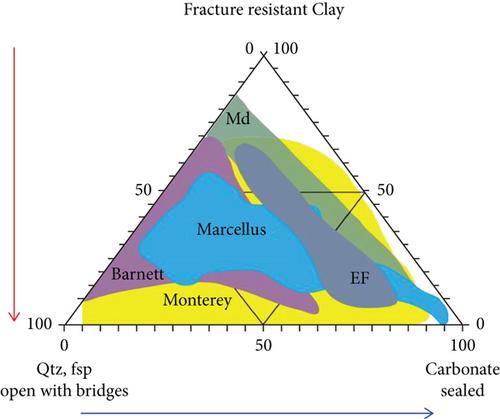
For unconventional oil and gas reservoir development, the large-scale volume fracturing method is often used to reform. This method is efficient and economical, and the effect of improving reservoir permeability is outstanding. The study shows that the brittleness of a rock can significantly affect the reservoir fracturing effect and wellbore stability [1]. Therefore, the evaluation of brittleness characteristics has become the primary factor to be considered in fracturing well selection and scheme design [2]. Statistical analysis shows that there are more than 30 methods to characterize brittleness [3–23]. Most of these methods are put forward to specific problems, applicable to different disciplines, each with its own advantages and limitations. During this period, Zhaoping and Suping [24] applied the methods of X-ray diffraction, fluorescence spectrum analysis, and mechanical test to study the mineral composition and chemical composition characteristics of coal-bearing mudstone. They established a qualitative and quantitative relationship between the mechanical properties (including uniaxial compressive strength and elastic modulus) of mudstone and its chemical composition (including SiO₂ and FeO) and found that the uniaxial compressive strength and modulus of elasticity of mudstone increased with the increase of SiO₂ content. Burnaman and other scholars [25, 26] consider that mineral composition is the internal reason for controlling rock brittleness and causing a difference in the fracture net fracturing effect and makes a three-terminal element diagram of a rock brittle to evaluate the brittleness qualitatively according to the relative content of minerals in shale. Wen-Long’s [27] analysis shows that the rock with high contents of quartz, feldspar, and carbonate is brittle. This kind of rock is easy to form natural fractures and induced fractures under the action of external forces, and its development degree is generally positively correlated with the content of brittle minerals. Liu et al. [28] found that the mineral content, composition distribution, and fracture development characteristics are important internal controlling factors affecting the brittleness of rock mass. In the same year, Gale et al. [29] found a negative correlation between the clay mineral content and natural fracture development characteristics, as shown in Figure 1. Lin et al. [30] established a nonlinear viscoplastic element on the basis of time-dependent shear strength by connecting the plastic element representing shear strength with the viscous element in parallel and studied effectively the mechanical properties of rock from the point of difference of shear strength. Zhang et al. [31] are using the discrete element numerical method to establish five different numerical models of regular sawtooth joints, study the shear mechanical characteristics of joints under creep condition, and analyze the influence of creep on the mechanical characteristics of joints. Xiangyuan et al. [32] obtained that reservoir brittleness controlled the development characteristics and degree of natural fractures based on the analysis of Chang 7 tight reservoir in Longdong Area. The larger the reservoir brittleness is, the more likely the fracture will occur under the action of tectonic stress, which will lead to the increase of fracture development. That is, the higher the content of brittle minerals (quartz, calcite, dolomite, and feldspar) in shale, the more developed the natural fractures in the area and the larger the brittleness. And the higher the content of clay minerals, the less developed the natural fractures in the area and the larger the toughness, as shown in Figure 2.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Mineral composition and fracture development diagram.

At present, the following two methods are widely used to calculate the rock brittleness in the industry. One is the rock mineral analysis method proposed by Jravie et al. [33] in 2009. In this method, quartz is regarded as a brittle mineral. And the contents of quartz, carbonate rock, and clay are measured, so as to calculate the rock brittleness, as shown in formula (1).

(1)

where BRIT is the rock brittleness index and V is the mineral volume.

Another commonly used method for calculating rock brittleness is the elastic parameter method proposed by Xue et al. [34] in 2007, as shown in formula (2). According to this method, the higher the elastic modulus of rock is, the lower Poisson’s ratio is, and the larger the rock brittleness is, as shown in Figure 3. The brittleness index of the rock is defined by the method of mechanics parameters, which is generally accepted and adopted in the field.

(2)

where E_max is the maximum elastic modulus of the rock, E_min is the minimum elastic modulus of te rock, ν_max is maximum Poisson’s ratio of the rock, and ν_min is minimum Poisson’s ratio of the rock.

Both of these methods can accurately characterize the brittleness of reservoir rocks to a certain extent. However, the brittleness description is based on the analysis of the overall brittleness of the research object, and the influence of natural fracture development on rock brittleness in reservoir cannot be described. In 2015, Bing et al. [36] analyzed the acoustic emission signal of the fracturing test and found that the peak of AE accumulation events occurred before the pump pressure reached the peak rupture pressure. This phenomenon shows that before the macrofracture of the rock mass, many microfractures have appeared in it, and the accumulation of microfracture finally leads to the fracture of the core as a whole. Wang et al. [37] proposed a new index for the brittleness evaluation of rock mass based on catastrophe theory and found that the softening modulus and brittleness index changed in polynomial with the increase of confining pressure.

Therefore, it is considered in this paper that the macrobrittle fracture of the rock is a process of local fracture initiation, propagation, microfracture, and gradual deterioration of rock matrix under external loads. The study of the local brittleness characteristics of the rock mass can reveal the intrinsic essence of the rock microfracture behavior and can more directly and accurately reflect the fracturing capacity and fracture evolution mechanism. Firstly, the law of local fracture propagation and fracture in shale during compression test is analyzed by CT scanning. And a method for characterizing local brittleness of shale is established by means of diffraction analysis of the core mineral composition and stepwise regression method. Finally, the local brittle fracture law of an artificial fracture is analyzed by a hydraulic fracturing test.

2. Analysis of Shale Core Compressive Fracture Law by CT Scanning

In this paper, the SkyScan 1172 high-resolution CT machine is used for the CT scanning test, as shown in Figure 4. This machine is a product of SkyScan company in Belgium. It uses the principle of microfocus X-ray imaging to perform ultrahigh-resolution three-dimensional imaging, which can obtain high-precision three-dimensional images without damaging the core. It is small in size, high in resolution, and can observe very fine structure without sample preparation, dyeing, and slicing. The test cores are taken from layer B in block A in Liaohe Oilfield, as shown in Figure 5. The core is scanned by CT, and the fracture distribution of the sample after CT scanning is obtained in 30 s, 90 s, 120 s, and 180 s, as shown in Figure 6 [38].

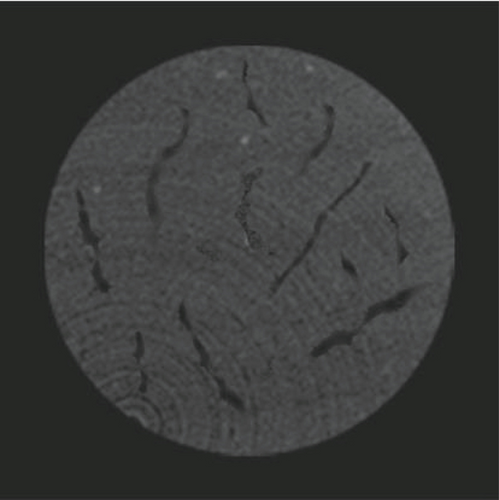
The CT scan results show that the process of shale rupture begins with the formation of local short microfractures in the core between 0 and 30 s. With time between 30 s and 90 s, local microfractures grow longer and new ones form elsewhere. When the time reaches 120 s, the microfractures intersect and connect with others to form larger microfractures, which cause core instability and fracture at 180 s. Therefore, the macrofracture of shale is the phenomenon caused by local fracture to a certain extent, and the local fracture is the fundamental cause of macrofracture.

3. Establishment of Rock Local Brittleness Characterization Method

Because the macrofracture of a rock is caused by the local brittle fracture and expansion, how to characterize the rock local brittleness has become an important research content in this paper. It is impossible to analyze the rock brittle distribution from the microscopic field by means of rock mechanical parameters or stress-strain tests. The mineral component analysis method is used to describe the rock brittle distribution in this paper. The mineral analysis method proposed by Rickman only considers the rock mineral composition itself, without considering the influence of rock heterogeneity, reservoir environmental factors, and the development of natural fractures. Therefore, this method is improved and perfected.

In this paper, the rock local brittleness distribution is analyzed based on reservoir heterogeneity. And the stepwise regression analysis is used to screen the main controlling factors to study the influence of different mineral components on the elastic modulus and Poisson’s ratio of rock. This method means that when a phenomenon is affected by multiple factors at the same time, the inversion compact transformation method and bidirectional test method are used to gradually analyze the contribution of influencing factors to the explained variables. If the factor is discriminated, it will be introduced into the stepwise regression model. According to the F test, the significance analysis of the introduced parameters is conducted to determine whether the relevant parameters in the regression model need to be eliminated because of the change of contribution. After repeated screening and elimination, the optimal regression equation is established. The stepwise regression analysis can include many explanatory variables. The explanatory variables of this method are the rock elastic modulus and Poisson’s ratio, and the explained variables are the content determination values of quartz, potassium feldspar, plagioclase, calcite, dolomite, analcite, siderite, pyrite, and clay minerals. The general form of the established regression model is

(3)

where β_j(j = 0, 1, 2, ⋯, 9) are regression coefficients,

are explained variables including the rock elastic modulus and Poisson’s ratio, and Z_j (j = quartz, potassium, ⋯, clay minerals) are the experimental values of 9 explanatory variables that have significant influence on

Because of the experimental data with n periods, the correlation coefficients between explanatory variables and explained variables are calculated based on these data, as shown in formula (4). The initial correlation coefficient matrix of regression analysis is established according to the correlation coefficient between different parameters, as shown in formula (5).

(4)

(5)

where X_i and Y_i are the experimental values of parameters,

and

are the average values of parameters’ experimental data, r_XY are the correlation coefficients between parameters X and Y, and R is to obtain the initial correlation coefficient matrix by one-to-one correspondence calculation of the research parameters.

According to the initial correlation coefficient matrix, the partial regression square sum u_i between explanatory variables and explained variables which represents the contribution of different parameters in regression equation, as shown in formula (6).

(6)

The parameter which has a maximum partial regression square sum is selected as the introduction parameter and tested by the F test method. When the test result is larger than the empirical threshold, this parameter can be introduced into the regression equation as a regression parameter. Conversely, the parameter cannot be introduced into the regression equation and need to be eliminated. Its F test method is shown in formula (7). The critical threshold is determined by referring to the F distribution table.

(7)

where F_in is the F test value when the parameter is quoted; f₁ is the number of independent variables introduced this time, usually 1 is appropriate; f₂ = n − m − 1, in which n is the number of experimental groups and m is the number of independent variables introduced into the regression equation.

When the parameter is quoted successfully, it is required to use it as the primary element. The contribution of this parameter should be eliminated by the inversion compact transformation method, and the new correlation coefficient matrix should be calculated. Through the new correlation coefficient matrix, the contribution degree of residual parameters can be calculated by partial regression square sum of research parameters, and then, the parameters of the newly introduced regression equation can be determined by F test. At the same time, due to the introduction of new parameters, the contribution of parameters in the regression equation needs to be redistributed, and the selected parameters need to be tested by F test in reverse to eliminate the parameters that cannot pass, as shown in formula (8).

(8)

where F_out is the F test value when the parameter is eliminated.

Repeatedly quoting and eliminating parameters until the regression equation cannot quote and eliminate any variables. In this case, all the selected parameters are independent variables for the regression equation.

After choosing the influencing parameters of the regression equation, the regression coefficients of each parameter can be calculated by formula (9). The regression coefficients of the unselected variables are all 0. After the calculation, the average value of the experimental data is substituted into the regression equation to calculate the regression coefficient β₀, as shown in formula (10).

(9)

(10)

where σ_i is the variance of the experimental data of parameter i, σ_Y is the variance of the experimental data of explained variable Y,

is the average value of the experimental data of parameter i, and

is the average value of the experimental data of explained variable Y.

After establishing a complete regression equation, the accuracy of the regression equation can be verified by significance analysis, and the calculation process is shown in formula (11). When the calculation result is larger than the critical threshold value, it shows that the regression equation is significant and the linear relationship is accurate, which can be used as an effective result.

(11)

where F_significant is the significant analysis result of regression equation and k is the principal element of the correlation coefficient matrix.

The regression equations of the rock elastic modulus and Poisson’s ratio calculated by the stepwise regression analysis method are and , respectively. So for a new core sample, it can be discretized into infinitesimal units, as shown in Figure 7.

At this time, each core unit can be represented by (o, p, q) in azimuth. The corresponding modulus of elasticity

and Poisson’s ratio

are calculated according to the regression equation after the mineral composition content of each unit is determined. By substituting the results into the elastic parameter method in formula (2), the rock local brittleness expression formula can be obtained as follows:

(12)

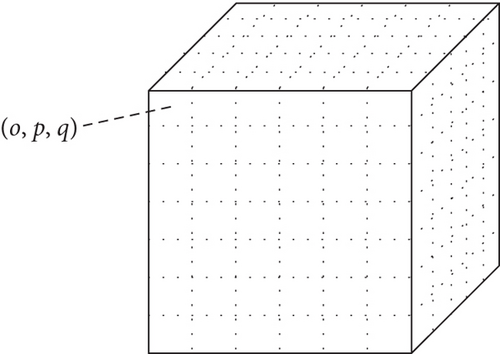
Formula (12) is the expression of rock local brittleness. This formula combines the study of reservoir environment to analyze and quantify the influence of mineral composition on the rock brittleness. The results are scientific and representative. And the local brittleness change low can be accurately characterized according to the heterogeneity of reservoir.

4. Case Verification

In this paper, the microarea mineral composition diffraction test is carried out by D8-ADVANCE X-ray diffractometer, as shown in Figure 8. This machine is produced by BRUKED-AXS Co. Ltd. of Germany, which is one of the most advanced X-ray diffractometer systems in the world. Its high-precision goniometer can satisfy the error of measuring peak position of any diffraction peaks in the whole spectrum range with the standard peak position not exceeding 0.01 degrees. The test cores are taken from layer B in block A in Liaohe Oilfield, with a total of 22 cores, as shown in Figure 9.

Firstly, mechanical parameters such as the elastic modulus and Poisson’s ratio of test cores are measured by simulating the actual stress of the formation through the triaxial compressive test, and the mineral compositions of test cores are analyzed by an X-ray diffractometer. The specific data obtained are shown in Table 1.

Table 1. The determination result of core mineral compositions and mechanical parameters.

Serial number	The type and content of minerals								Clay minerals	Elastic modulus (GPa)	Poisson’s ratio
Serial number	Quartz	Potassium feldspar	Plagioclase	Calcite	Dolomite	Analcite	Siderite	Pyrite	Clay minerals	Elastic modulus (GPa)	Poisson’s ratio
1	0.203	0.031	0.168	0.033	0.202	0.132	0.021	0.025	0.185	29.23	0.285
2	0.197	0.036	0.073	0.089	0.095	0.291	0.018	0.019	0.182	31.79	0.278
3	0.148	0.038	0.166	0.044	0.217	0.121	0.014	0.028	0.224	24.65	0.307
4	0.289	0.032	0.138	0	0.248	0.089	0	0	0.204	26.98	0.271
5	0.211	0.04	0.159	0.052	0.151	0.136	0.015	0.02	0.216	26.74	0.283
6	0.195	0.037	0.165	0.011	0.214	0.14	0	0	0.238	24.88	0.288
7	0.177	0.054	0.273	0	0.153	0.033	0	0.015	0.295	21.56	0.281
8	0.096	0.043	0.125	0	0.116	0.341	0.075	0.032	0.172	22.56	0.274
9	0.106	0.07	0.117	0.02	0.267	0.16	0.03	0.018	0.212	26.27	0.274
10	0.12	0.073	0.242	0.11	0.18	0.05	0.013	0.024	0.188	21.93	0.297
11	0.203	0.071	0.169	0.024	0.073	0.182	0.056	0	0.222	22.1	0.28
12	0.218	0.027	0.114	0.011	0.313	0.109	0.101	0	0.107	29.53	0.271
13	0.251	0.103	0.164	0	0.189	0.04	0.087	0.03	0.136	31.63	0.268
14	0.196	0.065	0.096	0.02	0.139	0.309	0	0	0.175	30	0.271
15	0.124	0.058	0.063	0.017	0.054	0.429	0.019	0	0.236	28.84	0.279
16	0.131	0.148	0.21	0.039	0.256	0.028	0.017	0.042	0.129	29.53	0.281
17	0.068	0.144	0.316	0.037	0.245	0	0.022	0.015	0.153	26.28	0.289
18	0.122	0.067	0.375	0.019	0.177	0.048	0.031	0	0.161	28.6	0.273
19	0.095	0.101	0.113	0.036	0.359	0.045	0.016	0.027	0.208	23.49	0.312
20	0.125	0.12	0.192	0.144	0.141	0.095	0.013	0.046	0.124	25.21	0.272
21	0.198	0.059	0.103	0.15	0.108	0.168	0.048	0	0.166	21.42	0.274
22	0.061	0.084	0.458	0.034	0.137	0.017	0.049	0	0.16	22.53	0.284

According to the data analysis, the core samples taken in block A of Liaohe Oilfield are mainly composed of quartz, potassium feldspar, plagioclase, dolomite, and clay minerals. Some cores contain calcite, analcite, siderite and pyrite, and others are too low to be considered in this paper. The core elastic modulus is in the range of [21.42, 31.79] and the Poisson’s ratio is in the range of [0.268, 0.312].

Through stepwise regression analysis, the initial correlation coefficient matrix R among elastic modulus, Poisson’s ratio, and mineral contents are calculated as shown in Table 2.

Table 2. The initial correlation coefficient matrix R.

R =	1	-0.50037	-0.45817	-0.13212	-0.05214	0.09481	0.05809	-0.24719	0.08393	0.35372	-0.39678
	-0.50037	1	0.36313	0.19435	0.19137	-0.45001	-0.03055	0.44192	-0.41878	0.00199	0.090176
	-0.45817	0.36313	1	-0.05867	0.01911	-0.65828	-0.02337	-0.07040	-0.12159	-0.27625	0.110721
	-0.13212	0.19435	-0.05867	1	-0.24949	-0.04570	-0.15995	0.27187	-0.27396	-0.23883	0.098718
	-0.05214	0.19137	0.01911	-0.24949	1	-0.57396	-0.00198	0.19780	-0.19621	0.11737	0.3602
	0.09481	-0.45001	-0.65828	-0.04570	-0.57396	1	0.02244	-0.20717	0.20291	0.19098	-0.27216
	0.05809	-0.03055	-0.02337	-0.15995	-0.00198	0.02244	1	-0.05565	-0.52406	0.06922	-0.36284
	-0.24719	0.44192	-0.07040	0.27187	0.19780	-0.20717	-0.05565	1	-0.24243	0.05379	0.230505
	0.08393	-0.41878	-0.12159	-0.27396	-0.19621	0.20291	-0.52406	-0.24243	1	-0.39416	0.357259
	0.35372	0.00199	-0.27625	-0.23883	0.11737	0.19098	0.06922	0.05379	-0.39416	1	/
	-0.39678	0.090176	0.110721	0.098718	0.3602	-0.27216	-0.36284	0.230505	0.357259	/	1

The critical threshold of the model is mainly related to reliability and free degree, so the screening limit should not be too large; otherwise, the introduction of fewer variables will make the model impractical. In this paper, four parameters are introduced to establish the regression model, and the critical threshold is . From the F distribution table, we can see that .

According to the stepwise regression analysis, the process of quoted and eliminating parameters of core elasticity modulus and Poisson’s ratio by inversion compact transformation method and bidirectional test method is shown in Table 3.

Table 3. Flow table for introducing the elastic modulus and Poisson’s ratio parameters.

Introduced variables	Elastic modulus E					Poisson’s ratio ν
Introduced variables	u_max	F_in	u_min	F_out	Results	u_max	F_in	u_min	F_out	Results
First variable	0.155	3.679			Clay minerals in	0.157	3.737			Quartz in
Second variable	0.151	4.126			Quartz in	0.154	4.237			Clay minerals in
Third variable	0.101	3.081	0.181	4.954	Calcite in	0.179	6..334	0.183	5.059	Dolomite in
Fourth variable	0.121	4.377	0.122	3.708	Siderite in	0.098	4.043	0.170	6.011	Calcite in
Fifth variable	0.099	4.253	0.143	5.144	Analcite in	0..008	0.314	0.135	5.572	End of regression
Sixth variable	0.013	0.530	0.126	4.467	End of regression

After the influence parameters of the core elastic modulus and Poisson’s ratio are quoted and eliminated for many times, the regression coefficients of the elastic modulus and Poisson’s ratio are calculated by formulas (10) and (11), as shown in Table 4.

Table 4. Stepwise regression analysis results.

Regression coefficient	Elastic modulus E	Poisson’s ratio ν
Initial coefficient	37.6374	0.2472
Quartz	20.1992	-0.0714
Potassium feldspar	0	0
Plagioclase	0	0
Calcite	-38.5568	0.0911
Dolomite	0	0.0813
Analcite	9.5781	0
Siderite	-60.0874	0
Pyrite	0	0
Clay minerals	-68.1563	0.154

By substituting the results of the stepwise regression analysis into formula (3), the regression model between the core elastic modulus, Poisson’s ratio, and mineral compositions can be obtained as follows:

(13)

(14)

According to the stepwise regression analysis, the main factors affecting the rock elastic modulus under simulated confining pressure include the contents of quartz, calcite, analcite, siderite, and clay minerals. And the main factors affecting rock Poisson’s ratio include the contents of quartz, calcite, dolomite, and clay minerals. Among them, the content of quartz and analcite is positively correlated with the rock elastic modulus and the content of calcite, siderite, and clay minerals is negatively correlated with the rock elastic modulus. The content of calcite, dolomite, and clay minerals is positively correlated with rock Poisson’s ratio, and the content of quartz is negatively correlated with rock Poisson’s ratio.

The regression equations are tested and analyzed by significance test and R². The calculation by formula (12) shows that and . And the R² of the elastic modulus and Poisson’s ratio are 0.913 and 0.936. This shows that the regression equations of the rock elastic modulus and Poisson’s ratio are significant, and the linear relationships between rock mechanical parameters and mineral compositions are highly accurate, which can be used as an effective result.

According to the relationship between the elastic modulus, Poisson’s ratio, and rock mineral composition, the elastic parameter method is introduced to analyze rock brittleness, and the following formula is obtained after substitution:

(15)

Formula (15) is the rock local brittleness evaluation model in Block A of Liaohe Oilfield. This model quantitatively establishes the relationship between the mineral composition in rock and the local brittleness, taking into account the actual reservoir environment and the influence of different mineral components on the development of natural fractures.

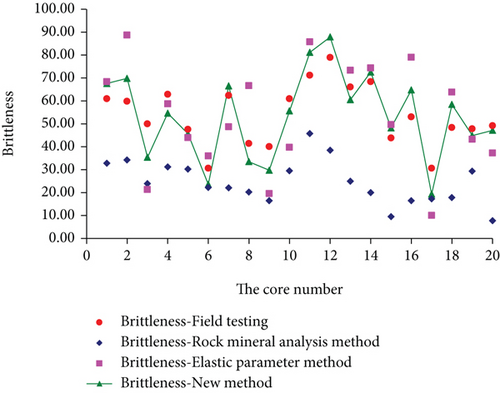
As shown in Figure 10, it can be found that the brittleness trend of different calculation methods is basically the same, which compared the rock brittleness calculated by mineral composition analysis method, elastic parameter method, and the new method. However, the rock mineral analysis method lacks quantitative characterization of mineral composition, and its calculated brittleness index is seriously low, which is quite different from the actual situation in the field. The difference of brittleness variation calculated by the elastic parameter method is large, which leads to great calculation errors. In this paper, the trend of the brittleness index of the new calculation method is the same as that of the elastic parameter method. However, considering the effect of different mineral compositions on reservoir brittleness, the calculation results are more precise and the calculation error of elastic parameter method is reduced. The calculation results are more in line with the actual situation of the study block.

5. Conclusion

(1)
In this paper, the fracture states of the shale core at different times are observed by CT scanning tests. The results show that with the increase of time, local microfractures are first formed in the core. While the microfractures grow longer, new microfractures are formed elsewhere. Until a large number of microfractures intersect and communicate with each other, eventually leading to core instability and fracture. Therefore, it can be seen that the rock macrofractures are the appearance of local fractures after reaching a certain degree, and the local fractures are the fundamental cause of macrofractures
(2)
The stepwise regression analysis method is used to quantitatively analyze the relationships between the rock elastic modulus, Poisson’s ratio, and rock mineral compositions combined with the environment of the Liaohe Oilfield actual reservoir, which is the basis of establishing the characterization method of local shale brittleness. A new method for characterizing shale brittleness by rock mineral compositions is established in combination with the elastic parameter method, thus realizing the characterization of local brittleness of the discrete core. This method is scientific and representative and can describe the change rule of rock local brittleness accurately
(3)
The results show that quartz, calcite, siderite, analcite, and clay minerals are the main influencing factors of the rock elastic modulus. Dolomite, calcite, quartz, and clay minerals are the main influencing factors of Poisson’s ratio. Among them, quartz and analcite have a positive correlation with the elastic modulus, and calcite, dolomite, and clay minerals have a positive correlation with Poisson’s ratio. Other minerals have negative correlations
(4)
It can be seen from the comparative analysis that the new method of the local brittleness index characterizes the change rule of rock brittleness from the microcosmic point of view, and the results are the same as those of the elastic parameter method. It can precisely quantify the influence of different mineral components on the reservoir brittleness, reduce the calculation errors of elastic parameter method, and avoid the low calculation results of the rock mineral analysis method. The results are more in line with the actual situation of the study block

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This research was supported by the Talented Reserves of Heilongjiang Province Science Foundation for Distinguished Young Scholars of Northeast Petroleum University (SJQHB201802), National Natural Science Foundation of China (Grant Nos. 51404073 and 51574088), Natural Science Foundation of Heilongjiang Province of China (Young Scientists) (Grant No. QC2017043), 9th special China Postdoctoral Science Foundation projects (Grant No. 2016T90268), Heilongjiang Postdoctoral Foundation (LBH-TZ-0503), China Postdoctoral Science Foundation (Grant No. 2018M630335), Heilongjiang General Undergraduate Colleges and Universities Young Innovative Talents Training Plan (Grant No. UNPYSCT-2016084), and Key Young Project of Northeast Petroleum University “National Foundation” Cultivating foundation (Science) 2017.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Qinghui L., Mian C., Fred P. W., Yan J., and Zhimeng L., Influences of engineering factors on shale gas production-take the Haynesville shale gas reservoir in North America for example, Journal of Natural Gas Industry. (2012) 32, no. 4, 54–59.
Google Scholar
2 Meng F., Zhou H., Zhang C., Xu R., and Lu J., Evaluation methodology of brittleness of rock based on post-peak stress-strain curves, Rock Mechanics and Rock Engineering. (2015) 48, no. 5, 1787–1805, https://doi.org/10.1007/s00603-014-0694-6, 2-s2.0-84939566407.
10.1007/s00603-014-0694-6
Web of Science® Google Scholar
3 Honda H. and Sanada Y., Hardness of coal, Fuel. (1956) 35.
Web of Science® Google Scholar
4 Protodyakonov M. M., Mechanical properties and drill-ability of rocks, Proceedings of the 5th Symposium on Rock Mechanics, 1963, Twin Cities, USA, 103–118.
Google Scholar
5 Bishop A. W., Progressive failure with special reference to the mechanism causing it, Proceedings of the Geotechnical Conference, 1967, Oslo, 142–150.
Google Scholar
6 Hucka V. and Das B., Brittleness determination of rocks by different methods, International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts. (1974) 11, no. 10, 389–392, https://doi.org/10.1016/0148-9062(74)91109-7, 2-s2.0-0016118633.
10.1016/0148-9062(74)91109-7
Web of Science® Google Scholar
7 Lawn B. R. and Marshall D. B., Hardness, Toughness, and brittleness: an indentation analysis, Journal of American Ceramic Society. (1979) 62, no. 7-8, 347–350, https://doi.org/10.1111/j.1151-2916.1979.tb19075.x, 2-s2.0-84979434138.
10.1111/j.1151-2916.1979.tb19075.x
CAS Web of Science® Google Scholar
8 Andreev G. E., Brittle Failure of Rock Materials: Test Results and Constitutive Models, 1995, A. A. Balkema Press, Netherlands.
Google Scholar
9 Quinn J. B. and Quinn G. D., Indentation brittleness of ceramics: a fresh approach, Journal of Materials Science. (1997) 32, no. 16, 4331–4346, https://doi.org/10.1023/A:1018671823059, 2-s2.0-0031207278.
10.1023/A:1018671823059
CAS Web of Science® Google Scholar
10 Hajiabdolmajid V. and Kaiser P., Brittleness of rock and stability assessment in hard rock tunneling, Tunneling and Underground Space Technology. (2003) 18, no. 1, 35–48, https://doi.org/10.1016/S0886-7798(02)00100-1, 2-s2.0-0037225150.
10.1016/S0886-7798(02)00100-1
Web of Science® Google Scholar
11 Altindag R., The correlation of specific energy with rock brittleness concept on rock cutting, Journal of the South African Institute of Mining and Metallurgy. (2003) 103, no. 3, 163–171.
Google Scholar
12 Copur H., Bilgin N., Tuncdemir H., and Balci C., A set of indices based on indentation test for assessment of rock cutting performance and rock properties, Journal of the South African Institute of Mining and Metallurgy. (2003) 103, no. 9, 589–600.
Google Scholar
13 Yagiz S., An investigation on the relationship between rock strength and brittleness, Proceedings of the 59th Geological Congress of Turkey, 2006, Ankara, Turkey.
Google Scholar
14 Rickman R., Mullen M. J., Petre J. E., Grieser W. V., and Kundert D., A practical use of shale petro- physics for stimulation design optimization: all shale plays are not clones of the Barnett Shale, SPE annual technical conference and exhibition, 2008, Denver, Colorado, USA, 1–22.
Google Scholar
15 Feng T., Xie X. B., Wang W. X., and Pan C. L., Brittleness of rocks and brittleness indexes for describing rockburst proneness, Mining and Metallurgical Engineering. (2000) 20, no. 4, 18–19.
Google Scholar
16 Hu C., Wang F., and Ai C., An Improved New Convolutional Neural Network Method for Inverting the Pore Pressure in Oil Reservoir by Surface Vertical Deformation, Lithosphere. (2021) 2021, no. 1.
10.2113/2021/5597238
Web of Science® Google Scholar
17 Enlong L. and Shen Z., Study on brittleness of geomaterials, Chinese Journal of Rock Mechanics and Engineering. (2005) 24, no. 19, 3449–3453.
Google Scholar
18 Sondergeld C. H., Newsham K. E., Comisky J. T., Rice M. C., and Rai C. S., Petrophysical considerations in evaluating and producing shale gas resources, SPE unconventional gas conference, 2010, Pittsburgh, Pennsylvania, USA, 1–17.
Google Scholar
19 Li Q. H., Chen M., Jin Y., Wang F. P., Hou B., and Zhang B. W., Indoor evaluation method for shale brittleness and improvement, Chinese Journal of Rock Mechanics and Engineering. (2012) 31, no. 8, 1680–1685.
Google Scholar
20 Diao H. Y., Rock mechanical properties and brittleness evaluation of shale reservoir, Acta Petrologica Sinica. (2013) 29, no. 9, 3300–3306.
Web of Science® Google Scholar
21 Zhou H., Meng F. Z., Zhang C. Q., Xu R. C., and Lu J. J., Quantitative evaluation of rock brittleness based on stress-strain curve, Chinese Journal of Rock Mechanics and Engineering. (2014) 6, 1114–1122.
Google Scholar
22 Yun C., Yan J., and Mian C., A rock brittleness evaluation method based on energy dissipation, Chinese Journal of Theoretical and Applied Mechanics. (2015) 47, no. 6, 984–993.
Google Scholar
23 Wu T., The Study on the Influencing Factors and Evaluation Method of Rock Brittleness in Shale Gas Reservoir, 2015, The Southwest Petroleum University.
Google Scholar
24 Zhaoping M. and Suping P., Mudstone composition of coal measures and its influence on the mechanical properties, Coal Geology & Exploration. (2004) 32, no. 2, 14–16.
Google Scholar
25 Burnaman M. D., Xia W., and Shelton J., Shale gas play screening and evaluation criteria, China Petroleum Exploration. (2009) 14, no. 3, 51–64.
CAS Google Scholar
26 Hofmann A., Rigollet C., Portier E., and Burns S., Gas shale characterization - results of the mineralogical, lithological and geochemical analysis of cuttings samples from radioactive Silurian shales of a Paleozoic Basin, North Africa Technical Conference and Exhibition, 2013, Cairo, Egypt, 1–12.
Google Scholar
27 Wen-Long D. I., Chao L., Chun-Yan L. I., Chang-Chun H. U., Kai J., and Wei-Te C. E., Dominant factor of fracture development in shale and its relationship to gas accu-mulation, Earth Science Fronties. (2012) 19, no. 2, 212–220.
Google Scholar
28 Liu B., Lü Y. F., Ran Q., Dai C. L., Li M., and Wang M., Geological conditions and exploration potential of shale oil in Qingshankou Formation, Northern Songliao Basin, Oil & Gas Geology. (2014) 35, no. 2, 280–285.
CAS Google Scholar
29 Gale J. F., Laubach S. E., Olson J. E., Eichhuble P., and Fall A., Natural fractures in shale: a review and new observations, AAPG Bulletin. (2014) 98, no. 11, 2165–2216, https://doi.org/10.1306/08121413151, 2-s2.0-84911906694.
10.1306/08121413151
Web of Science® Google Scholar
30 Lin H., Zhang X., Cao R., and Wen Z., Improved nonlinear burgers shear creep model based on the time-dependent shear strength for rock, Environmental Earth Sciences. (2020) 79, no. 6, 1–9.
10.1007/s12665-020-8896-6
Web of Science® Google Scholar
31 Zhang X., Lin H., Wang Y., Yong R., Zhao Y., and Du S., Damage evolution characteristics of saw-tooth joint under shear creep condition, International Journal of Damage Mechanics. (2021) 30, no. 3, 453–480.
10.1177/1056789520974420
Web of Science® Google Scholar
32 Zhao X., Zeng L., Zu K., Hu X., and Shi J., Brittleness characteristics and its control on natural fractures in tight reservoirs: a case study from Chang 7 tight reservoir in Longdong area of the Ordos Basin, Oil & Gas Geology. (2016) 37, no. 1, 62–71.
Google Scholar
33 Jarvie D. M., Hill R. J., Ruble T. E., and Pollastro R. M., Unconventional shale-gas systems: the Mississippian Barnett Shale of north-central Texas as one model for thermogenic shale-gas assessment, AAPG Bulletin. (2009) 91, no. 4, 475–479.
10.1306/12190606068
Web of Science® Google Scholar
34 Xue Y., Liu J., Ranjith P. G., Liang X., and Wang S., Investigation of the influence of gas fracturing on fracturing characteristics of coal mass and gas extraction efficiency based on a multi-physical field model, Journal of Petroleum Science and Engineering. (2021) 206, article 109018, https://doi.org/10.1016/j.petrol.2021.109018.
10.1016/j.petrol.2021.109018
Web of Science® Google Scholar
35 Rickman R., Mullen M. J., Petre J. E., Grieser W. V., and Kundert D., A practical use of shale petrophysics for stimulation design optimization all shale plays are not clones of the Barnett shale, SPE annual technical conference and exhibition, 2008, Denver, Colorado, USA, 1–13.
Google Scholar
36 Bing H., Mian C., Tan P., and Li D., Monitoring of hydraulic fracture network by acoustic emission method in simulated tri-axial fracturing system of shale gas reservoirs, Journal of China University of Petroleum. (2015) 39, no. 1, 66–71.
Google Scholar
37 Wang T., Zhang T., Ranjith P. G., Li Y., Song Z., Wang S., and Zhao W., A new approach to the evaluation of rock mass rupture and brittleness under triaxial stress condition, Journal of Petroleum Science and Engineering. (2020) 184, article 106482.
10.1007/978-3-030-51423-5
Web of Science® Google Scholar
38 Wang T., Evolution Mode on Shale Fracture with Acoustic Emission Behavior, 2017, The Northeast Petroleum University.
Google Scholar

All articles

Study on Fracture Distribution and Local Brittleness Characteristics Based on Stepwise Regression Method

Abstract

1. Introduction

2. Analysis of Shale Core Compressive Fracture Law by CT Scanning

3. Establishment of Rock Local Brittleness Characterization Method

4. Case Verification

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Study on Fracture Distribution and Local Brittleness Characteristics Based on Stepwise Regression Method

Abstract

1. Introduction

2. Analysis of Shale Core Compressive Fracture Law by CT Scanning

3. Establishment of Rock Local Brittleness Characterization Method

4. Case Verification

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Related

Information