Volume 2021, Issue 1 3771640

Research Article

Open Access

Analyzing Accident Injury Severity via an Extreme Gradient Boosting (XGBoost) Model

Shubo Wu,

Shubo Wu

orcid.org/0000-0002-2207-7290

Merchant Marine College, Shanghai Maritime University, Shanghai 201306, China shmtu.edu.cn

Search for more papers by this author

Quan Yuan,

Corresponding Author

Quan Yuan

[email protected]

orcid.org/0000-0002-2326-4856

State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing 100084, China tsinghua.edu.cn

Search for more papers by this author

Zhongwei Yan,

Zhongwei Yan

orcid.org/0000-0001-6370-7941

Merchant Marine College, Shanghai Maritime University, Shanghai 201306, China shmtu.edu.cn

Search for more papers by this author

Qing Xu,

Qing Xu

State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing 100084, China tsinghua.edu.cn

Search for more papers by this author

Shubo Wu,

Shubo Wu

orcid.org/0000-0002-2207-7290

Merchant Marine College, Shanghai Maritime University, Shanghai 201306, China shmtu.edu.cn

Search for more papers by this author

Quan Yuan,

Corresponding Author

Quan Yuan

[email protected]

orcid.org/0000-0002-2326-4856

State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing 100084, China tsinghua.edu.cn

Search for more papers by this author

Zhongwei Yan,

Zhongwei Yan

orcid.org/0000-0001-6370-7941

Merchant Marine College, Shanghai Maritime University, Shanghai 201306, China shmtu.edu.cn

Search for more papers by this author

Qing Xu,

Qing Xu

State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing 100084, China tsinghua.edu.cn

Search for more papers by this author

First published: 27 September 2021

https://doi.org/10.1155/2021/3771640

Citations: 17

Academic Editor: Long Truong

Share a link

Email
Wechat
Bluesky

Abstract

Vehicle to vulnerable road user (VRU) crashes occupy a large proportion of traffic crashes in China, and crash injury severity analysis can support traffic managers to understand the implicit rules behind the crashes. Therefore, 554 VRUs-involved crashes are collected from January, 2017, to February, 2021, in a city in northern China, including 322 vehicle-pedestrian crashes and 232 vehicle-bicycle crashes. First, a descriptive statistical analysis is conducted to investigate the characteristics of VRUs-involved crashes. Second, the extreme gradient boosting (XGBoost) model is introduced to identify the importance of risk factors (i.e., time of day, day of week, rushing hour, crash position, weather, and crash involvements) of VRUs-involved crashes. The statistical analysis demonstrates that the risk factors are closely related to VRUs-involved crash injury severity. Moreover, the results of XGBoost reveal that time of day has the greatest impact on VRUs-involved crashes, and crash position shows the minimum importance among these risk factors.

1. Introduction

Crash injury severity analysis plays a crucial role in traffic crash analysis, which can assist traffic management [1–4]. Crash injury severity is defined as the degree of injury and property damage caused by a crash event. The crash injury severity analysis aims to explore the correlation between crash injury severity and various contributing factors, such as road-users-related factors, temporal-related factors, environmental conditions, and crash types. The universal rules support traffic managers to better understand the contributions of factors on crash injury severity and further reduce the crash severity and improve traffic safety by developing countermeasures [5–7].

Currently, the research approaches on crash injury severity can be divided into two categories, which are statistical models and machine learning-based models. The statistical models assume that the contributing factors affecting crash injury severity follow a particular distribution, which needs to be defined carefully for better capturing the relationship between crash injury severity and explanatory variables. The commonly used models contain multivariate Poisson regression model [8, 9], ordered probit model [10, 11], bivariate binary/ordered probit model [12, 13], random parameter probit model [14], etc. Wang et al. focused on mountainous expressways and proposed a partial proportional odds model to determine the determinants of truck-involved crash injury severity [15]. Xu et al. attempted to investigate pedestrian-involved crash injury severity by using geographically and temporally weighted regression model taking into account spatial-temporal correlation [16]. The statistical models could demonstrate and explain clearly the correlation between crash severity and related variables with the help of explainable and logical theoretical deductions. However, due to the nonlinear relationship between crash injury severity and contributing factors, these statistical models difficultly capture the inner and intrinsic correlations [17–19].

Machine-learning-based models have a powerful internal inferential capability, which makes them more flexible by learning without or little prior assumptions of related factors to describe the complex characteristics of crash events. Previous researches employed logistic models (e.g., random parameter logit model, and mixed/ordered logit model) [20, 21], support vector machine (SVM) [22, 23], random forest (RF) [24, 25], Bayesian-related models [26, 27], etc., to explore the complex relationship between crash injury severity and contributing factors and further identify the risk factors on crash injury severity. For comprehensive accounting of the observed heterogeneity, Behnood et al. introduced a random parameter multinomial logit model for comparing the contribution of risk factors to crash injury severity under bicycle-vehicle crashes [28]. Liu et al. introduced an ordinal logistic regression model to examine the risk factors on pedestrian-motor vehicle collisions, taking into account the spatial-temporal correlation [29]. Li et al. introduced SVM model to investigate the potential correlation between external factors and crash injury severity, but the performance was suppressed due to multiclass classification problems [30]. Li et al. analyzed the key factors affecting electric bicycle-related crash injury severity with the help of random forest model [31].

Beyond that, Bayesian approaches, as a classical machine learning model, have been widely used in crash injury severity modelling, which were regarded as Bayesian-related models. For instance, Bayesian binomial logistic model [32, 33], Bayesian multivariate regression model [34, 35], Bayesian spatial model [36, 37], and Bayesian mixed logit model [38] have successfully demonstrated their applicability in crash injury severity-involved correlation issues. Yuan et al. divided crash severity into two categories (property damage only and injury/fatality) and integrated bivariate probit model and Bayesian approach to identify the contributing factors associated with crash injury severity [39]. Haq et al. developed binary logistic model with Bayesian inference approach to investigate the effects on truck-involved crashes, especially on occupant injury severity considering comprehensive factors [40]. Guo et al. proposed a novel random parameter, that is, multivariate Tobit model, to identify risk factors on crash severity under different crash types [41]. Zhang et al. utilized a Bayesian multinomial logit model with conditional autoregression prior to examining the hazardous factors that contributed to freeway crash injury severity [42].

In sum, previous researches focused on identifying risk factors towards traffic injury severity by various statistical models and machine learning-based models, and satisfying results were obtained. However, decision tree ensemble-based models, also a type of machine leaning model, including adaptive boosting (AdaBoost), gradient boost decision tree (GBDT), light gradient boosting machine (LightGBM), and extreme gradient boosting (XGBoost), are less utilized for crash injury severity analysis. Additionally, vulnerable road users (VRUs), as the vulnerable groups of the traffic participants, are prone to fatal injuries in crashes [43]. As the most common VRUs, the pedestrians and bicyclists have been paid much attention to, but decision tree ensembles-based models are rarely utilized to investigate the potential universal rules behind the VRUs-involved crashes. Hence, this paper attempts to describe the characteristics of VRUs-involved crashes and identify the contributing factors associated with crash injury severity. Based on this purpose, 554 VRU-vehicle crashes (contains 232 bicycle-vehicle crashes and 322 pedestrian-vehicle crashes) were collected. Moreover, XGBoost is introduced for crash injury severity modelling and ranking the importance of risk factors on crash injury severity. The contribution of this paper is twofold:

(1)
Conduct a descriptive statistical analysis to investigate the characteristics of VRUs-involved crashes from the perspective of six risk factors (i.e., time of day, day of week, rush hour, crash position, weather, and crash involvements), and further transform into universal rules to support traffic management
(2)
XGBoost is adopted to identify the risk factors contributing to VRUs-involved crash injury severity with the help of VRUs-involved crashes dataset from policy records, which further determine the real causes to enhance traffic safety

The rest of this paper is organized as follows. Section 2 introduces the data details and candidate variables analyzed in this paper. Section 3 describes the details of XGBoost model. Section 4 provides the experimental results, which consist of crash severity characteristics and identified risk factors. Section 5 briefly concludes the study.

2. Data Description

2.1. Data Source

For exploring the characteristic of VRUs-involved crashes, 554 crash samples were collected from police records on crashes, which have occurred in a city in northern China within about four years. The dataset contains various information, such as crash time, position, involvements, and injury severity, and six factors are extracted to explain the characteristics of VRUs-involved crashes. Vehicles and bicycles or pedestrians were involved in one crash, and bicyclists and pedestrians were defined as VRUs. The crashes dataset contains 323 vehicle-bicycle crashes and 322 vehicle-pedestrian crashes. The property-damage-only crashes are excluded because the vehicle-bicycle or vehicle-pedestrian crashes are prone to injury or death, which belong to injury or fatal accidents. Additionally, the crashes dataset consists of 385 injury crashes and 169 fatal crashes, which caused 517 injuries and 173 deaths.

2.2. Candidate Variables

Generally, if fatal or injured occupants are involved in a crash, it can be regarded as a severe accident. Considering that the dataset only contains fatal accidents and injury accidents, but without property-damage-only accidents, the crash injury severity is divided into two categories: injury accident (only injured occupant involved in the crash), which is coded as 0, and fatal accident (at least one fatality occupant involved in the crash), which is coded as 1. Figure 1 describes the extracted factors related to crashes from the dataset, which are time of day, day of week, rush hour, weather, crash position, and crash involvements. These six factors are extracted to investigate the characteristics of VRUs-involved crashes, divided into two typical injury categories (see Table 1).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Selected factors related to crashes.

Table 1. Data list of main variables related to crashes.

Variable	Categories	Value	Fatal (n = 169)	Injury (n = 385)
Time of day	Day (7:00–19:00)	1	92 (54.4%)	263 (68.3%)
Time of day	Night (19:00–7:00)	0	77 (45.6%)	122 (31.7%)
Day of week	Weekday	1	118 (69.8%)	294 (76.4%)
Day of week	Weekend/holiday	0	51 (30.2%)	91 (23.6%)
Rush hour	Rush hour (7:00–9:00, 17:00–20:00)	1	49 (29.0%)	126 (32.7%)
Rush hour	Off-peak hour	0	120 (71.0%)	259 (67.3%)
Weather	Good (sunny, cloudy)	1	138 (81.7%)	320 (83.1%)
Weather	Adverse (rainy, snowy, etc.)	0	31 (18.3%)	65 (16.9%)
Crash position	Road section	1	110 (65.1%)	266 (69.1%)
Crash position	Intersection	0	59 (34.9%)	119 (30.9%)
Crash involvements	Vehicle-bicycle	1	53 (31.4%)	179 (46.5%)
Crash involvements	Vehicle-pedestrian	0	116 (68.6%)	206 (53.5%)

To some extent, time of day reflects the lighting conditions laterally, which is a crucial factor for traveling. Considering that, the crash position is complex, which mainly contains road section and intersection, but less sidewalk, roundabout. For better modelling, the crashes happened on sidewalk were regarded as road section. The weather information is collected from the related website (see http://www.tianqihoubao.com/lishi) based on the date and time of crashes [26]. Noting that this website provides the weather information only in two periods, that is daytime and night, it is not detailed enough to the specific hours. Additionally, due to the various types of weather, some of them have similar impact on traveling environment, for instance, sunny and cloudy, rainy and snowy. Therefore, the weather was divided into two categories: good and adverse.

3. Methodology

Extreme gradient boosting (XGBoost), as a typical decision tree ensemble-based model, was proposed by Chen in 2016 [44]. XGBoost is optimized from GBDT, which introduced second-order derivatives into optimization process. It outperforms with advantages of parallel learning, high flexibility, built-in cross-validation, etc. Previous studies have proved the successful use in traffic crash severity analysis and risk prediction [45, 46].

3.1. Objective Function

Given training data T = {(x₁, y₁), (x₂, y₂), …, (x_n, y_n)}, the objective function is described as

(1)

where

is the training loss, which measures the fitting performance of the model to training data, and Ω(f_k) denotes the regularization term, which controls the model complexity for preventing overfitting. n is the volume of training dataset, and K denotes the number of trees. Generally, for classification problems, the logistic loss is adopted as loss function, and the expression is given in

(2)

where y_i is the truth value, and

is the predictive value. In XGBoost model, the predictive value is the sum of the score for each tree and the

can be defined as

(3)

where ℱ denotes the functional space and f_k is the function of k-th tree.

3.2. Additive Training

In the training process, it is intractable to learn all trees simultaneously. Instead, XGBoost introduces an additive strategy, which corrects what we have learned and adds one new tree at a time. The details of additive strategy are provided as

(4)

where

and f_t(x_i) denote the predictive value and the added predictive function (i.e., new tree) at step t, respectively. For obtaining the best tree at each step, the objective function at step t is defined as

(5)

where

is a constant. For the training loss function, Taylor formula is introduced in loss function and its second-order expansion is expressed as

(6)

where g_i and h_i are the first-order and second-order partial derivative on loss function and can be expressed as

(7)

Generally, the constant terms in the objective function are ignored, and the simplified objective function can be obtained as

(8)

3.3. Model Complexity

For defining the complexity of tree, we refine the tree f(x) as (9). It contains the vector of weight on leaves ω and mapping function q, which maps each data sample to the corresponding leaf.

(9)

Here, T is the number of leaves. Then, the complexity can be defined as (10). γ is the coefficient of leaf, and λ denotes the coefficient of L2 regularization term.

(10)

We define I_j = {i|q(x_i) = j}, which denotes the set of data samples assigned to j-th leaf. Then, we introduce (10) into (9), and the objective function of t-th tree can be rewritten as

(11)

represents the sum of first-order partial derivative on jth leaf.

denotes the sum of second-order partial derivative on jth leaf. We take partial derivation with respect to

, and the best ω_j and objective value can be obtained as

(12)

(13)

To measure how good a tree is and find the best tree structure, a greedy algorithm is introduced. It starts from a single leaf and attempts to split each leaf into two leaves and then calculates the information gain in this split process (see equation (14)).

(14)

where G_L, H_L and G_R, H_R are the derivative values of left and right after split. Gain denotes the gain for loss function in the split. If Gain > 0, the result of split will be considered.

4. Results

Based on the 544 crashes data, the time-related information, crash position, weather, and crash involvements are investigated. In the section, six risk factors are extracted to explore the characteristics of VRUs-involved crashes and further determine the risk factors contributing to crash injury severity.

4.1. Descriptive Statistical Analysis

4.1.1. Temporal Characteristics

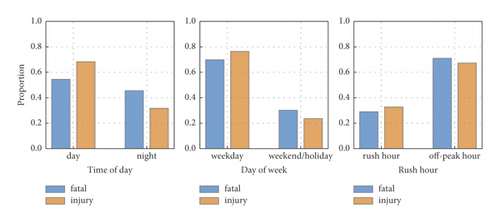
Figure 2 illustrates the proportion of different accident types under three time-related factors. From the perspective of the time of day, the VRUs-involved crashes are probable to occur in the daytime, while the proportion of fatal crashes at night is relatively higher than those in the daytime, with values of 38.7% and 25.9% (see Table 2). Maybe most people intend to travel during the daytime, which is prone to cause crashes. But at night, due to the terrible travel environment (i.e., poor light visible condition), the crashes are easy to cause deaths. Additionally, the proportion of crashes on weekdays is larger than that on weekends/holidays, but the fatality rate is the opposite and the values of weekday and weekend/holiday are 28.6% and 35.9%, respectively. The reason may be that people keep a relatively low safety alert when traveling on weekends/holidays than on weekdays. Moreover, the VRUs-involved crashes are prone to happen in off-peak hours than in rush hours due to the longer period of off-peak hours. Similarly, the fatality rate of off-peak hours is higher than those of rush hours (the values are 31.7% and 28.0%, respectively).

Table 2. Statistical information of time-related factors for injury severity.

	Time of day		Day of week		Rush hour
	Day	Night	Weekday	Weekend/Holiday	Rush hour	Off-peak hour
Fatal	92 (25.9%)	77 (38.7%)	118 (28.6%)	51 (35.9%)	49 (28.0%)	120 (31.7%)
Injury	263 (74.1%)	122 (61.3%)	294 (71.4%)	91 (64.1%)	126 (72.0%)	259 (68.3%)
Total	355	199	412	142	175	379

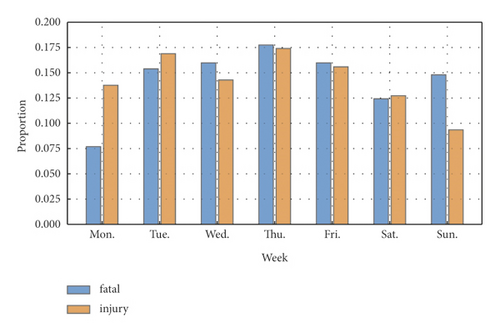
The variation tendency of VRUs-involved crashes counted by different days of the week is shown in Figure 3, and Table 3 provides the crash injury severity information under each day of the week. It illustrates that the largest number of crashes appears on Thursday, while Sunday occupies the least number. The main reason possible is that Thursday is the day near the weekend, the busiest day for most people as well as for the traffic, and yet Sunday is the final of a weekend when people are more likely to take a rest at home. However, the fatality rate is higher on Sunday (the value is 41.0%) because of the low safety awareness of people during leisure travel. Additionally, Monday takes up the minimum fatality rate with a value of 19.7%. The reason may be that Monday is the first day of weekday, and people will maintain a relatively high-security alert while commuting to work.

Table 3. Statistical information of different days of the week for injury severity.

	Monday	Tuesday	Wednesday	Thursday	Friday	Saturday	Sunday
Fatal	13 (19.7%)	26 (28.6%)	27 (32.9%)	30 (30.9%)	27 (31.0%)	21 (30.0%)	25 (41.0%)
Injury	53 (80.3%)	65 (71.4%)	55 (67.1%)	67 (69.1%)	60 (69.0%)	49 (70.0%)	36 (59.0%)
Total	66	91	82	97	87	70	61

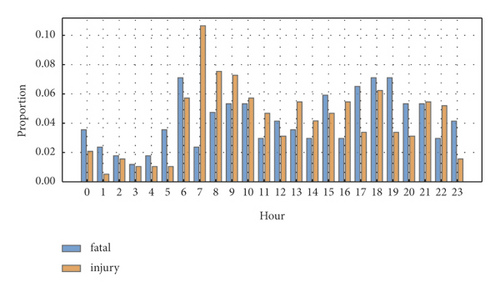
The statistical information of VRUs-involved crashes for injury severity is shown in Table 4, and Figure 4 illustrates the variation tendency of crashes counted by hours of the day. It indicates that crashes are prone to appear in rush hour (i.e., 7:00–9:00, 17:00–20:00), especially in the rush hours of the morning, with the highest peak existing in 7:00–8:00 (the total number of crashes is 45). It is because that this period is the time to go to work when the traffic is busy, likely to cause crashes. Moreover, most of the crashes happened at 6:00–23:00, which is the time for human activities, while few crashes occur within 23:00–6:00, which is the sleeping time. Overall, we found that the mortality at night is relatively higher than that in the daytime.

Table 4. Statistical information of hours of the day for injury severity.

Hour	Fatal	Injury	Total
0	6 (42.9%)	8 (57.1%)	14
1	4 (66.7%)	2 (33.3%)	6
2	3 (33.3%)	6 (66.7%)	9
3	2 (33.3%)	4 (66.7%)	6
4	3 (42.9%)	4 (57.1%)	7
5	6 (60.0%)	4 (40.0%)	10
6	12 (35.3%)	22 (64.7%)	34
7	4 (8.9%)	41 (91.1%)	45
8	8 (21.6%)	29 (78.4%)	37
9	9 (24.3%)	28 (75.7%)	37
10	9 (29.0%)	22 (71.0%)	31
11	5 (21.7%)	18 (78.3%)	23
12	7 (36.8%)	12 (63.2%)	19
13	6 (22.2%)	21 (77.8%)	27
14	5 (23.8%)	16 (76.2%)	21
15	10 (35.7%)	18 (64.3%)	28
16	5 (19.2%)	21 (80.8%)	26
17	11 (45.8%)	13 (54.2%)	24
18	12 (33.3%)	24 (66.7%)	36
19	12 (48.0%)	13 (52.0%)	25
20	9 (42.9%)	12 (57.1%)	21
21	9 (30.0%)	21 (70.0%)	30
22	5 (20.0%)	20 (80.0%)	25
23	7 (53.8%)	6 (46.2%)	13

4.1.2. Spatial Characteristics

In the raw crash dataset, the crash position is complex, which makes the spatial characteristics hard to be described. Hence, we reorganized the complicated crashes environment into two types: road section and intersection. Table 5 provides the statistical information of crashes under two types of positions. There are 169 fatalities involved in crashes, including 110 on road sections and 59 at intersections. Moreover, the crashes that occurred on road sections take a higher proportion than intersections, and the mortality of crashes on road sections and at intersections are 0.293 and 0.331, respectively. Additionally, the proportion of fatal crashes that happened at intersections is higher than that of injury crashes, with values of 34.9% and 30.9%. Therefore, we can obtain that the crashes are more likely to happen on road sections, but the crashes happening at intersections have higher fatalities.

Table 5. Statistical information of crash position for injury severity.

Position	Fatal accident	Injury accident	Total	Mortality
Road section	110 (65.1%)	266 (69.1%)	376 (67.9%)	0.293
Intersection	59 (34.9%)	119 (30.9%)	178 (32.1%)	0.331
Total	169	385	554	0.305

4.1.3. Weather Characteristics

There are various types of weather, so that it is hard to describe the weather characteristics associated with crash injury severity. Hence, the weather is divided into good (including sunny and cloudy) and adverse weather (including rainy, snowy, etc.). Table 6 shows the statistical information of injury severity in all weathers. Most VRUs-involved crashes happened in good weather, taking up 82.7%. That is because people prefer to travel in good weather compared to adverse weather. However, the mortality of crashes in adverse weather is higher than that in good weather, with values of 0.323 and 0.301, respectively. Similarly, the crashes that happened in adverse of fatal accidents account for a high proportion than injury accidents; the values are 18.3% and 16.9%, respectively. The results illustrate that VRUs-involved crash rarely happens in adverse weather. But once it happens, it may cause fatality.

Table 6. Statistical information of weather for injury severity.

Weather	Fatal accident	Injury accident	Total	Mortality
Good	138 (81.7%)	320 (83.1%)	458 (82.7%)	0.301
Adverse	31 (18.3%)	65 (16.9%)	96 (17.3%)	0.323
Total	169	385	554	0.305

4.1.4. Crash Involvements’ Characteristics

In the crash dataset, the simultaneous participants in the crashes are vehicle and bicycle or vehicle and pedestrian; thus, the crash involvements are divided into vehicle-bicycle and vehicle-pedestrian. It can be seen that vehicle-pedestrian crashes take up a relatively high proportion not only in fatal accidents but also in injury accidents (see Table 7), and the proportion of fatal crashes is higher than that of injury crashes, with values of 68.6% and 53.5%, respectively. Additionally, the mortality of vehicle-pedestrian crashes is higher than vehicle-bicycle crashes, with values of 0.360 and 0.228. In sum, we can infer that vehicle-pedestrian crashes more easily result in death compared to vehicle-bicycle crashes, and most of these crashes may happen in intersections and crosswalks. It is probably because that the targets of bicycles are larger than pedestrians, more likely to attract the attention of vehicle drivers. And the reaction distance of cyclists is longer than pedestrians, which can reduce the injury severity in crashes.

Table 7. Statistical information of crash involvements for injury severity.

Crash involvements	Fatal accident	Injury accident	Total	Mortality
Vehicle-bicycle	53 (31.4%)	179 (46.5%)	232 (41.9%)	0.228
Vehicle-pedestrian	116 (68.6%)	206 (53.5%)	322 (58.1%)	0.360
Total	169	385	554	0.305

4.2. Importance Identification for Risk Factors

4.2.1. Parameters Optimization

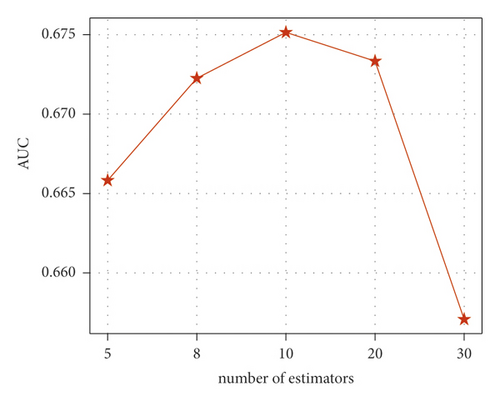
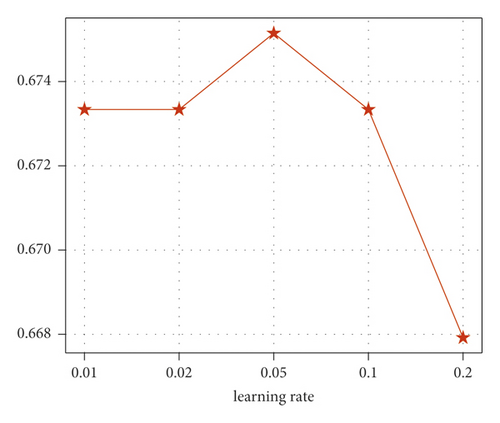
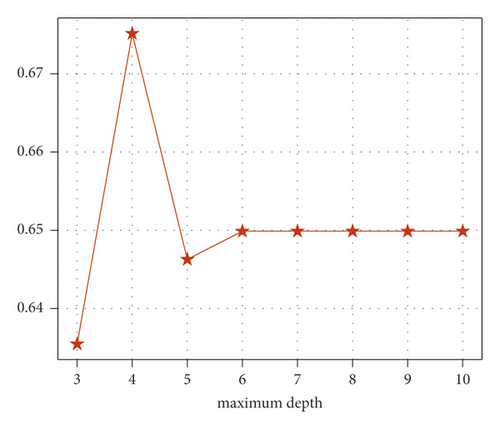
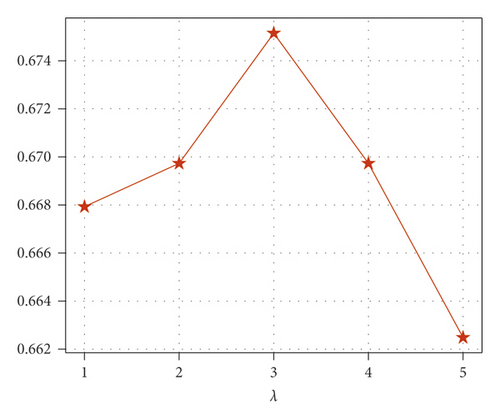
In this section, XGBoost is utilized to identify the contributing factors influencing crash injury severity. It is noted that the parameters of XGBoost are crucial for the model performance, and the grid search algorithm is introduced to obtain the optimal parameters. For binary classification problem in this study, the logistic loss and area under receiver operating characteristic curve are defined as objective loss function and evaluation metric, respectively. Moreover, four parameters, including number of estimators (n_estimators), learning rate, maximum depth, and coefficient of regularization (λ), are selected to optimize by grid search algorithm, and the candidate values are given in Table 8. The number of estimators refers to the number of iterations (i.e., the number of decision tree), learning rate controls the step size in weight updating, and maximum depth denotes the maximum depth of a tree. All these parameters contribute to preventing overfitting.

Table 8. The candidate values of four parameters for grid search algorithm.

Parameter	Number of estimators	Learning rate	Maximum depth	λ
Value	5, 8, 10, 20, 30	0.01, 0.02, 0.05, 0.1, 0.2	3, 4, 5, 6, 7, 8, 9, 10	1, 2, 3, 4, 5

Based on the grid search results, we found that the optimal parameters model can be obtained, when the number of estimators is set as 10, learning rate as 0.05, maximum depth as 4, and λ as 3, and the scores of AUC and accuracy are 0.675 and 0.706, respectively. Figure 5 provides the AUC variation trends under different parameter settings. From Figure 5(a), the AUC scores show a up and down trend, and the maximum scores is 0.675 when number of estimators is set as 10, which indicates the optimal value of number of estimators is 10. The optimal values of learning rate, max depth, and λ are 0.05, 4, and 3, respectively. It is noted that the other three parameters are set as optimal values (i.e., learning rate is set as 0.05, max depth as 4, and λ as 3) in Figure 5(a), and other cases follow this rule.

4.2.2. Risk Factors’ Analysis

The XGBoost model with optimal parameters can be obtained after the parameters optimization procedure by using grid search algorithm. Then, the contributing factors were identified such that which factors show greater impact on VRUs-involved crashes injury severity. Figure 6 shows the importance of various risk factors from XGBoost model based on information gain, which is defined as the average gain for objective function optimization across all splits the feature (i.e., factor) is used in. The time of day occupies the most important role in VURs-involved crash injury severity, with the information gain score as 4.56. It reveals that time of day (day/night), which can use lighting conditions (good/adverse) instead, has a greater impact on VRUs-involved crashes, maybe because that the crashes are prone to happen in the daytime (or good lighting condition), while the crashes that occurred at night (or adverse conditions) are more likely to cause deaths.

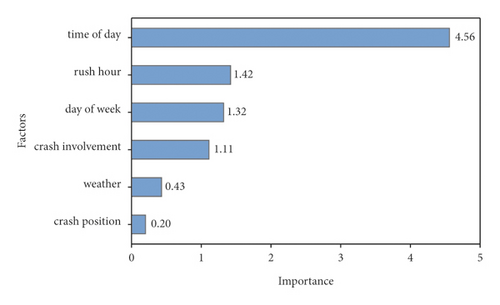
Moreover, rush hour, day of week, and crash involvements show relatively similar importance, with the information gain scores as 1.42, 1.32, and 1.11, respectively. The reason may be that the categories of rush hour (i.e., rush hour and off-peak hour) show a minor difference of influence on VRUs-involved crashes, and day of week (i.e., weekday and weekend/holiday) and crash involvements (i.e., vehicle-bicycle and vehicle-pedestrian) are similar. The weather and crash position represent the least importance to VRUs-involved crash injury severity, and the information gain values are 0.43 and 0.20. Therefore, we infer that the people who travel in good or adverse weather show a similar impact on crash injury severity, which is consistent with the result of Section 4.1.3 (the mortalities are close in Table 6). This may be because people do not like to travel in adverse weather and they keep a relatively high safety awareness when traveling. Additionally, the VRUs-involved crashes that happened in different position (i.e., road section and intersection) show semblable result.

5. Conclusions

VRUs-involved crash injury severity analysis transforms the relationship behind the crashes into universal rules and further supports traffic management. This paper demonstrates a descriptive statistical analysis of the characteristics of VRUs-involved crashes based on 554 crashes data collected in a city of northern China and further utilizes XGBoost to identify the risk factors affecting crash injury severity. The important conclusions are summarized as follows. (1) The risk factors (i.e., time of day, day of week, rush hour, crash position, weather, and crash involvements) are closely related to VRUs-involved crash injury severity. More specifically, vehicle-bicycle and vehicle-pedestrian crashes are prone to involve fatalities at intersections on the weekend night in adverse weather. (2) The time of day plays a more important role in VRUs-involved crash injury severity compared with other factors, which reveals that VRUs-involved crashes that happened at night are prone to cause deaths. Additionally, the weather has little effect on VRUs-involved crash injury severity. (3) Compared to vehicle-bicycle crashes, vehicle-pedestrian crashes are prone to happen at intersections (especially at the crosswalk near the intersection), and these crashes readily cause deaths.

Although few factors were analyzed, the AUC and accuracy of XGBoost are 0.675 and 0.706, respectively, and the results still can be accepted and meet the current study. To obtain more accurate and detailed characteristics of VRU-vehicle crash injury severity, several research directions are proposed. (1) More risk factors (e.g., lighting condition, drivers’ age, gender, crash pattern, and crash location related factors) can be considered to better explain the characteristics of VRU-vehicle crash injury severity and further identify the crucial risk factors. The characteristics of VRU-vehicle crash injury severity are not perfectly and accurately exploited due to the limitation of the risk factors. However, abundant risk factors may cause unfaithful characteristics to be described. To this topic, how to extract an appropriate number and precise risk factors is a crucial challenge. (2) Risk factors identified mechanism can be developed with high accuracy and robustness on crash injury severity analysis, such as random forest (RF) and nonparametric Bayesian approach, to better explain the characteristics and determine the real causes of crashes. The XGBoost model facilitates the investigation of crash injury severity issues, but the accuracy is limited due to the small sample size. Therefore, how to develop risk factors identified approach with a small sample size is a hot point. In addition, how to consider the spatial-temporal correlations in modelling process is a crucial challenge.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

This paper was supported by the National Natural Science Foundation of China (nos. 52102397 and 52072214) and the National Key R&D Program of China (no. 2019YFB1600605).

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Yuan Y., Yang M., Guo Y., Rasouli S., Gan Z., and Ren Y., Risk factors associated with truck-involved fatal crash severity: analyzing their impact for different groups of truck drivers, Journal of Safety Research. (2021) 76, 154–165, https://doi.org/10.1016/j.jsr.2020.12.012.
10.1016/j.jsr.2020.12.012
PubMed Web of Science® Google Scholar
2 Liu P. and Fan W., Analysis of head-on crash injury severity using a partial proportional odds model, Journal of Transportation Safety & Security. (2019) 13, no. 7, 714–734, https://doi.org/10.1080/19439962.2019.1667933, 2-s2.0-85073835648.
10.1080/19439962.2019.1667933
Web of Science® Google Scholar
3 Li D., Ranjitkar P., Zhao Y., Yi H., and Rashidi S., Analyzing pedestrian crash injury severity under different weather conditions, Traffic Injury Prevention. (2017) 18, no. 4, 427–430, https://doi.org/10.1080/15389588.2016.1207762, 2-s2.0-84994673257.
10.1080/15389588.2016.1207762
PubMed Web of Science® Google Scholar
4 Chen X., Li Z., Yang Y., Qi L., and Ke R., High-resolution vehicle trajectory extraction and denoising from aerial videos, IEEE Transactions on Intelligent Transportation Systems. (2020) 22, no. 5, 3190–3202, https://doi.org/10.1109/tits.2020.3003782.
10.1109/TITS.2020.3003782
Web of Science® Google Scholar
5 Lee C. and Abdel-Aty M., Comprehensive analysis of vehicle-pedestrian crashes at intersections in Florida, Accident Analysis & Prevention. (2005) 37, no. 4, 775–786, https://doi.org/10.1016/j.aap.2005.03.019, 2-s2.0-19944416633.
10.1016/j.aap.2005.03.019
PubMed Web of Science® Google Scholar
6 Mohamed M. G., Saunier N., Miranda-Moreno L. F., and Ukkusuri S. V., A clustering regression approach: a comprehensive injury severity analysis of pedestrian-vehicle crashes in New York, US and Montreal, Canada, Safety Science. (2013) 54, 27–37, https://doi.org/10.1016/j.ssci.2012.11.001, 2-s2.0-84871374921.
10.1016/j.ssci.2012.11.001
Web of Science® Google Scholar
7 Chen X., Wang S., Shi C., Wu H., Zhao J., and Fu J., Robust ship tracking via multi-view learning and sparse representation, Journal of Navigation. (2019) 72, no. 1, 176–192, https://doi.org/10.1017/s0373463318000504, 2-s2.0-85053663012.
10.1017/S0373463318000504
Web of Science® Google Scholar
8 Ma J., Kockelman K. M., and Damien P., A multivariate Poisson-lognormal regression model for prediction of crash counts by severity, using Bayesian methods, Accident Analysis & Prevention. (2008) 40, no. 3, 964–975, https://doi.org/10.1016/j.aap.2007.11.002, 2-s2.0-42749088635.
10.1016/j.aap.2007.11.002
PubMed Web of Science® Google Scholar
9 El-Basyouny K., Barua S., and Islam M. T., Investigation of time and weather effects on crash types using full Bayesian multivariate Poisson lognormal models, Accident Analysis & Prevention. (2014) 73, 91–99, https://doi.org/10.1016/j.aap.2014.08.014, 2-s2.0-84907349852.
10.1016/j.aap.2014.08.014
PubMed Web of Science® Google Scholar
10 Anarkooli A. J., Hosseinpour M., and Kardar A., Investigation of factors affecting the injury severity of single-vehicle rollover crashes: a random-effects generalized ordered probit model, Accident Analysis & Prevention. (2017) 106, 399–410, https://doi.org/10.1016/j.aap.2017.07.008, 2-s2.0-85024363762.
10.1016/j.aap.2017.07.008
PubMed Web of Science® Google Scholar
11 Fountas G. and Anastasopoulos P. C., Analysis of accident injury-severity outcomes: the zero-inflated hierarchical ordered probit model with correlated disturbances, Analytic Methods in Accident Research. (2018) 20, 30–45, https://doi.org/10.1016/j.amar.2018.09.002, 2-s2.0-85054162498.
10.1016/j.amar.2018.09.002
Web of Science® Google Scholar
12 Guo Y., Zhou J., Wu Y., and Chen J., Evaluation of factors affecting e-bike involved crash and e-bike license plate use in China using a bivariate probit model, Journal of Advanced Transportation. (2017) 2017, 12, 2142659, https://doi.org/10.1155/2017/2142659, 2-s2.0-85039071930.
10.1155/2017/2142659
Google Scholar
13 Chen F., Song M., and Ma X., Investigation on the injury severity of drivers in rear-end collisions between cars using a random parameters bivariate ordered probit model, International Journal of Environmental Research and Public Health. (2019) 16, no. 14, https://doi.org/10.3390/ijerph16142632, 2-s2.0-85070533219.
10.3390/ijerph16142632
Web of Science® Google Scholar
14 Darban Khales S., Kunt M. M., and Dimitrijevic B., Analysis of the impacts of risk factors on teenage and older driver injury severity using random-parameter ordered probit, Canadian Journal of Civil Engineering. (2020) 47, no. 11, 1249–1257, https://doi.org/10.1139/cjce-2019-0394.
10.1139/cjce-2019-0394
Web of Science® Google Scholar
15 Wang Y. and Prato C. G., Determinants of injury severity for truck crashes on mountain expressways in China: a case-study with a partial proportional odds model, Safety Science. (2019) 117, no. April, 100–107, https://doi.org/10.1016/j.ssci.2019.04.011, 2-s2.0-85064249477.
10.1016/j.ssci.2019.04.011
Web of Science® Google Scholar
16 Xu X., Luo X., Ma C., and Xiao D., Spatial-temporal analysis of pedestrian injury severity with geographically and temporally weighted regression model in Hong Kong, Transportation Research Part F: Traffic Psychology and Behaviour. (2020) 69, 286–300, https://doi.org/10.1016/j.trf.2020.02.003.
10.1016/j.trf.2020.02.003
Web of Science® Google Scholar
17 Mannering F. L. and Bhat C. R., Analytic methods in accident research: methodological frontier and future directions, Analytic Methods in Accident Research. (2014) 1, 1–22, https://doi.org/10.1016/j.amar.2013.09.001, 2-s2.0-84893489445.
10.1016/j.amar.2013.09.001
Google Scholar
18 Chen X., Lu J., Zhao J., Qu Z., Yang Y., and Xian J., Traffic flow prediction at varied time scales via ensemble empirical mode decomposition and artificial neural network, Sustainability. (2020) 12, no. 9, https://doi.org/10.3390/su12093678.
10.3390/su12093678
Web of Science® Google Scholar
19 Chen X., Qi L., Yang Y., Luo Q., Postolache O., Tang J., and Wu H., Video-based detection infrastructure enhancement for automated ship recognition and behavior analysis, Journal of Advanced Transportation. (2020) 2020, 12, 7194342, https://doi.org/10.1155/2020/7194342.
10.1155/2020/7194342
Web of Science® Google Scholar
20 Yuan Q., Yang H., Huang J., Kou S., Li Y., and Theofilatos A., What factors impact injury severity of vehicle to electric bike crashes in China?, Advances in Mechanical Engineering. (2017) 9, no. 8, https://doi.org/10.1177/1687814017700546, 2-s2.0-85028355692.
10.1177/1687814017700546
Web of Science® Google Scholar
21 Haleem K. and Gan A., Effect of driver’s age and side of impact on crash severity along urban freeways: a mixed logit approach, Journal of Safety Research. (2013) 46, 67–76, https://doi.org/10.1016/j.jsr.2013.04.002, 2-s2.0-84879115868.
10.1016/j.jsr.2013.04.002
PubMed Web of Science® Google Scholar
22 Iranitalab A. and Khattak A., Comparison of four statistical and machine learning methods for crash severity prediction, Accident Analysis & Prevention. (2017) 108, no. August, 27–36, https://doi.org/10.1016/j.aap.2017.08.008, 2-s2.0-85027874583.
10.1016/j.aap.2017.08.008
PubMed Web of Science® Google Scholar
23 Tang J., Liang J., Han C., Li Z., and Huang H., Crash injury severity analysis using a two-layer Stacking framework, Accident Analysis & Prevention. (2019) 122, no. May, 226–238, https://doi.org/10.1016/j.aap.2018.10.016, 2-s2.0-85055733159.
10.1016/j.aap.2018.10.016
PubMed Web of Science® Google Scholar
24 Zhou X., Lu P., Zheng Z., Tolliver D., and Keramati A., Accident prediction accuracy assessment for highway-rail grade crossings using random forest algorithm compared with decision tree, Reliability Engineering & System Safety. (2020) 200, no. July, 106931, https://doi.org/10.1016/j.ress.2020.106931.
10.1016/j.ress.2020.106931
Web of Science® Google Scholar
25 Li L., Prato C. G., and Wang Y., Ranking contributors to traffic crashes on mountainous freeways from an incomplete dataset: a sequential approach of multivariate imputation by chained equations and random forest classifier, Accident Analysis & Prevention. (2020) 146, no. January, 105744, https://doi.org/10.1016/j.aap.2020.105744.
10.1016/j.aap.2020.105744
PubMed Web of Science® Google Scholar
26 Yuan Q., Liang Z., Hao W., and Li Y., Investigating severity and main weather factors in tricycle crashes in Beijing, Proceedings of the 18th COTA International Conference of Transportation, July 2018, Beijing, China, 1710–1719.
Google Scholar
27 Guo Y., Li Z., Wu Y., and Xu C., Exploring unobserved heterogeneity in bicyclists’ red-light running behaviors at different crossing facilities, Accident Analysis & Prevention. (2018) 115, no. November, 118–127, https://doi.org/10.1016/j.aap.2018.03.006, 2-s2.0-85043754624.
10.1016/j.aap.2018.03.006
PubMed Web of Science® Google Scholar
28 Behnood A. and Mannering F., Determinants of bicyclist injury severities in bicycle-vehicle crashes: a random parameters approach with heterogeneity in means and variances, Analytic Methods in Accident Research. (2017) 16, 35–47, https://doi.org/10.1016/j.amar.2017.08.001, 2-s2.0-85027543181.
10.1016/j.amar.2017.08.001
Web of Science® Google Scholar
29 Liu J., Hainen A., Li X., Nie Q., and Nambisan S., Pedestrian injury severity in motor vehicle crashes: an integrated spatio-temporal modeling approach, Accident Analysis & Prevention. (2019) 132, no. August, https://doi.org/10.1016/j.aap.2019.105272, 2-s2.0-85071093672.
10.1016/j.aap.2019.105272
PubMed Web of Science® Google Scholar
30 Li Z., Liu P., Wang W., and Xu C., Using support vector machine models for crash injury severity analysis, Accident Analysis & Prevention. (2012) 45, 478–486, https://doi.org/10.1016/j.aap.2011.08.016, 2-s2.0-84856080826.
10.1016/j.aap.2011.08.016
PubMed Web of Science® Google Scholar
31 Li Y. S., Zhang X., Wang W. J., and Ju X. F., Factors affecting electric bicycle rider injury in accident based on random forest model, Journal of Transportation Systems Engineering and Information Technology. (2021) 21, no. 1, 196–200, https://doi.org/10.16097/j.cnki.1009-6744.2021.01.030.
10.16097/j.cnki.1009-6744.2021.01.030
Google Scholar
32 Guo Y., Li Z., Wu Y., and Xu C., Evaluating factors affecting electric bike users’ registration of license plate in China using Bayesian approach, Transportation Research Part F: Traffic Psychology and Behaviour. (2018) 59, 212–221, https://doi.org/10.1016/j.trf.2018.09.008, 2-s2.0-85053907614.
10.1016/j.trf.2018.09.008
Web of Science® Google Scholar
33 Yu R., Wang X., Yang K., and Abdel-Aty M., Crash risk analysis for Shanghai urban expressways: a Bayesian semi-parametric modeling approach, Accident Analysis & Prevention. (2016) 95, 495–502, https://doi.org/10.1016/j.aap.2015.11.029, 2-s2.0-84956646625.
10.1016/j.aap.2015.11.029
PubMed Web of Science® Google Scholar
34 Heydari S., Fu L., Joseph L., and Miranda-Moreno L. F., Bayesian nonparametric modeling in transportation safety studies: applications in univariate and multivariate settings, Analytic Methods in Accident Research. (2016) 12, no. September, 18–34, https://doi.org/10.1016/j.amar.2016.09.001, 2-s2.0-84991585664.
10.1016/j.amar.2016.09.001
Web of Science® Google Scholar
35 Zeng Q., Gu W., Zhang X., Wen H., Lee J., and Hao W., Analyzing freeway crash severity using a Bayesian spatial generalized ordered logit model with conditional autoregressive priors, Accident Analysis & Prevention. (2019) 127, no. February, 87–95, https://doi.org/10.1016/j.aap.2019.02.029, 2-s2.0-85062407330.
10.1016/j.aap.2019.02.029
PubMed Web of Science® Google Scholar
36 Xu X., Xie S., Wong S. C., Xu P., Huang H., and Pei X., Severity of pedestrian injuries due to traffic crashes at signalized intersections in Hong Kong: a Bayesian spatial logit model, Journal of Advanced Transportation. (2016) 50, no. 8, 2015–2028, https://doi.org/10.1002/atr.1442, 2-s2.0-85012894252.
10.1002/atr.1442
Web of Science® Google Scholar
37 Zeng Q., Wen H., Huang H., and Abdel-Aty M., A Bayesian spatial random parameters Tobit model for analyzing crash rates on roadway segments, Accident Analysis & Prevention. (2017) 100, 37–43, https://doi.org/10.1016/j.aap.2016.12.023, 2-s2.0-85011883183.
10.1016/j.aap.2016.12.023
PubMed Web of Science® Google Scholar
38 Khattak Z. H. and Fontaine M. D., A Bayesian modeling framework for crash severity effects of active traffic management systems, Accident Analysis & Prevention. (2020) 145, 105544, https://doi.org/10.1016/j.aap.2020.105544.
10.1016/j.aap.2020.105544
PubMed Web of Science® Google Scholar
39 Yuan Q., Xu X., Xu M., Zhao J., and Li Y., The role of striking and struck vehicles in side crashes between vehicles: bayesian bivariate probit analysis in China, Accident Analysis & Prevention. (2020) 134, no. October, 105324, https://doi.org/10.1016/j.aap.2019.105324.
10.1016/j.aap.2019.105324
PubMed Web of Science® Google Scholar
40 Haq M. T., Zlatkovic M., and Ksaibati K., Investigating occupant injury severity of truck-involved crashes based on vehicle types on a mountainous freeway: a hierarchical Bayesian random intercept approach, Accident Analysis & Prevention. (2020) 144, 105654, https://doi.org/10.1016/j.aap.2020.105654.
10.1016/j.aap.2020.105654
PubMed Google Scholar
41 Guo Y., Li Z., Liu P., and Wu Y., Modeling correlation and heterogeneity in crash rates by collision types using full bayesian random parameters multivariate Tobit model, Accident Analysis & Prevention. (2019) 128, 164–174, https://doi.org/10.1016/j.aap.2019.04.013, 2-s2.0-85064608828.
10.1016/j.aap.2019.04.013
PubMed Web of Science® Google Scholar
42 Zhang X., Wen H., Yamamoto T., and Zeng Q., Investigating hazardous factors affecting freeway crash injury severity incorporating real-time weather data: using a Bayesian multinomial logit model with conditional autoregressive priors, Journal of Safety Research. (2021) 76, 248–255, https://doi.org/10.1016/j.jsr.2020.12.014.
10.1016/j.jsr.2020.12.014
PubMed Web of Science® Google Scholar
43 Yuan Q. and Chen H., Factor comparison of passenger-vehicle to vulnerable road user crashes in Beijing, China, International Journal of Crashworthiness. (2017) 22, no. 3, 260–270, https://doi.org/10.1080/13588265.2016.1248226, 2-s2.0-84992486766.
10.1080/13588265.2016.1248226
Web of Science® Google Scholar
44 Chen T. and Guestrin C., XGBoost, Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. (2016) 13-17, 785–794, https://doi.org/10.1145/2939672.2939785, 2-s2.0-84984950690.
10.1145/2939672.2939785
Google Scholar
45 Shi X., Wong Y. D., Li M. Z.-F., Palanisamy C., and Chai C., A feature learning approach based on XGBoost for driving assessment and risk prediction, Accident Analysis & Prevention. (2019) 129, no. March, 170–179, https://doi.org/10.1016/j.aap.2019.05.005, 2-s2.0-85066065544.
10.1016/j.aap.2019.05.005
PubMed Web of Science® Google Scholar
46 Guo M., Yuan Z., Janson B., Peng Y., Yang Y., and Wang W., Older pedestrian traffic crashes severity analysis based on an emerging machine learning xgboost, Sustainability. (2021) 13, no. 2, 926–26, https://doi.org/10.3390/su13020926.
10.3390/su13020926
Web of Science® Google Scholar

Citing Literature

All articles

Analyzing Accident Injury Severity via an Extreme Gradient Boosting (XGBoost) Model

Abstract

1. Introduction