Graded crushed stone (GCS), as a cheap and essential component, is of great importance in road construction. The irregularity and variability of particle shape is known to affect the packing characteristics of GCS, such as compactness and void ratio. In this study, the realistic particle outline is first automatically extracted based on digital image processing and deep learning algorithms. Then, the elongation (EI), roundness (Rd), and roughness (Rg) of GCS are quantified by shape evaluation algorithms. Moreover, based on the establishment of the GCS shape library, the gravity deposition with various elongations is simulated using the discrete element method to study the packing features of GCS. The elongation effects on the macroscopic and microscopic quantities are explored. Finally, the shear behavior of GCS is studied. The results illustrate that elongation has a significant effect on the packing of GCS.

1. Introduction

With the development of the highway industry and the deepening of engineering practice, the asphalt pavement structure used in China has been diversified from the single semirigid asphalt base, and the graded crushed stone flexible base asphalt pavement has become one of the main pavement structure forms in China. As a mixture composed of aggregates of different sizes, the graded crushed stone (GCS) is widely applied between the asphalt surface and semirigid base and can effectively weaken the cracks in the top of the semirigid base and the stress concentration effect. Additionally, GCS can also reduce the temperature shrinkage and dry shrinkage stress caused by the change of temperature and humidity of the semirigid base [1, 2].

Due to the great significance of GCS to highway construction, it is particularly essential to study its mechanical properties, deformation, and failure mechanism. However, it is difficult to analyze its mechanical properties quantitatively and qualitatively by conventional methods because of its granular structural characteristics and nonlinear mechanical properties [3]. On the one hand, the conventional laboratory test for GCS is complex and costly, which makes it difficult to reveal the macro-meso mechanical characteristics of GCS under load. On the other hand, the granular material such as GCS has great variability and the data results of different specimens in the same group are relatively low in correlation, which makes experimental data unreliable [4]. Hence, it is very necessary to use the numerical test method to study the mechanical properties of GCS from the microscopic point of view, to make up for the lack of laboratory tests and provide a powerful means for the in-depth understanding of GCS [5, 6].

As a basic road material, the shape of crushed stone particles has a significant effect on its mechanical properties. Scholars have done much research on the mechanical properties of GCS influenced by GCS shape. An [7] carried out a quantitative analysis on the particle shape of GCS to explore the relationship between the real particle shape and particle accumulation porosity. Le Pen et al. [8] set out methods for evaluating form and roundness (aspects of shape) and proposed a new measure for evaluating roundness, termed ellipses for crushed stone. Zhang et al. [9] simulated the geometric anisotropy of the GCS using randomly generated models. The results showed that the changes of both friction and anisotropy had a similar trend with the particle size enlarging in the dense assembly, which maintains stability when the size is less than 3.0 mm.

Numerical simulation methods are often used in exploring the properties of GCS. Jiang et al. [10] used PFC^2D to establish a numerical test method for California bearing ratio (CBR) and found that CBR values increase with the friction coefficient at the contact and shear modulus of the rocks, while the influence of Poisson’s ratio on the CBR values is insignificant. Ren et al. [11] proposed a random calculation model for GCS and studied the Direct Shear Tests (DST) of GCS by PFC^2D. Xu et al. [12] proposed Plastic Deformation Index (PDI) as the evaluation indicator and founded that the PDI should be less than or equal to 1900 mm number for expressway and first-grade highway. Jiang et al. [13] established a numerical model of dynamic triaxial test of GCS based on PFC^2D and founded that the size of the specimen has a slight influence on the simulated value of axial strain when specimen height is greater than 40 cm and diameter is greater than 20 cm.

In this study, the particle outlines are firstly extracted based on deep learning algorithms. The U-NET model is trained for contour extraction. Then, the shape evaluation indexes including elongation, roundness, and roughness are quantified. In addition, the gravity deposition with a distinct EI value is simulated by the discrete element method to explore the elongation effects on the macroscopic and microscopic quantities. Finally, the shear behavior of GCS is studied. Overall, this study lays a foundation for future research about GCS.

2. Materials and Equipment

In construction projects, GCS are transported by large-scale transport equipment. To simulate the real conveyance cases, a conveyor belt is used to carry GCS obtained from the laboratory of civil engineering materials in Shenzhen University. The GCS is first screened and the stone with a particle size of 4.75 mm∼25 mm is selected for preparation. Then, in order to obtain the data set with images of GCS in batches, the equipment shown in Figure 1(a) is used. The specific components are illustrated as follows:

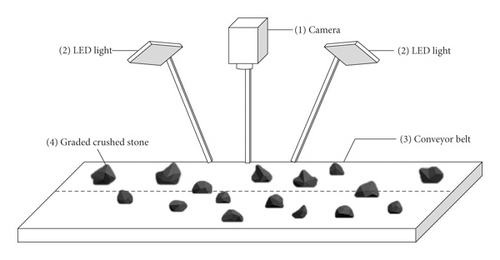
Component (1): A Fujinon X-T20 camera as shown in Figure 1(b) with a resolution of 24 million pixels (6000 × 4000 pixels) and two lenses: Fujinon XF60 mm F2.4 R Macro and Fujinon XF35 mm F2 R WR. At least 90 pixels are used to represent the smallest diameter of the particle.
Component (2): A conveyor belt as shown in Figure 1(c) used to carry GCS to simulate the real transport of GCS.
Component (3): Two lamps composed of 256 LEDs as shown in Figure 1(d) provide controllable lighting conditions. The light is scattered uniformly so the lamps have good color rendering. The LED lamp arm is installed on the copy stand and is perpendicular to the plane of each LED lamp. In addition, the lamp is placed 45 cm above the transparent plastic plate. Besides, the side of the lamp is parallel to the side of the base of the copy stand. The color temperature is 5600 K at the maximum brightness value.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Materials and equipment for GCS images capture. (a) The equipment to photograph GCS. (b) Fujinon camera. (c) Conveyor belt. (d) LED light.

3. Automated Extraction of GCS Contours

3.1. Implementation of Algorithms

For image processing, convolutional neural network (CNN) and full convolutional network (FCN) are the main frames for image segmentation. However, CNN has two obvious drawbacks: (1) slow training process because of too much redundancy and (2) asynchronism between obtaining sensing field and positioning accuracy. Mostly, CNN is used for image classification at the image level. By contrast, FCN can classify images at pixel level with good training results. In order to avoid these defects as much as possible, in this study, according to Liang et al. [14] a lightweight U-NET [15] method of a fully convolutional neural network is adopted for image segmentation.

3.1.1. Lightweight U-NET and Operation

In this study, a U-NET deep neural network is introduced. Firstly, the lightweight U-NET particle image is converted into a 3D matrix W × C × h as the input data, where W and h are the width and height of the input image, respectively; C is the number of color channels of input images, where C = 3 represents RGB image and C = 1 represents gray/binary image. The gray images are input data, and binary images are output data. Then, the network generates a mask by a matrix with a size of W × h × 1 to record the pixels on the projection of GCS. For clarity, three parts of the operation of lightweight U-NET are briefly explained: convolution, Maxpool, and deconvolution.

The kernel of convolution used in this study is defined as a square matrix. And the overwritten elements in the input matrix are transformed into feature mapping elements (y_ij) by multiplying elements:

(1)

where k_n is the size of the kernel matrix; x_mn is the element at position (m, n) of the input matrix; w_mn is the element of the nuclear matrix overlapping with x_mn; b is the bias term of the output feature graph, and AF(·) is the activation function. During the training process, both parameters w_mn and b are the targets of training. According to the recommended values [16], the default value of k_n is 3 and the default activation function is ReLu (AF(x) = Max(0, x)) in this study. The principle of convolution is shown in Figure 2.

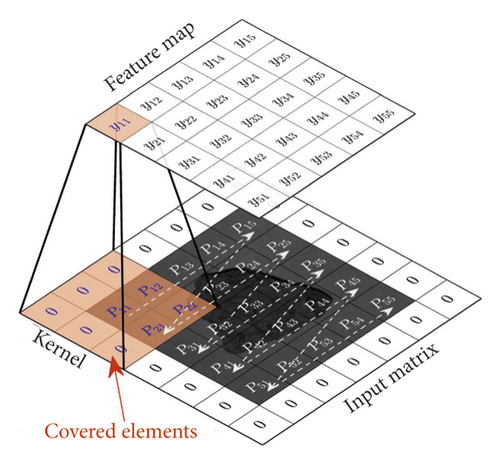
The Maxpool and Upconv operations use different kernels and computations to downsample and upsample the input matrix, respectively. But they are both executed by sliding Windows, just like convolution operations. The Maxpool operation can be regarded as a special convolution operation, with k_n = 2 and S = 2, and the function of formula y_ij which outputs the maximum element covered by the kernel. Deconvolution, as opposed to convolution, has different interpretations like upsampling or transposed convolution. In this study, we used a UpSampling2D built-in Keras to implement the upsampling operation.

3.1.2. Model Optimization

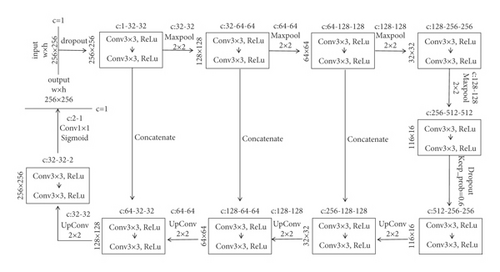
Considering the limited size and computing power of the model, the size of the network was reduced by half; thus, the number of channels (c) of all operations was reduced to half of the original number except for the number of channels at the end and the beginning. At the same time, in order to prevent overfitting, part of neural network units are temporarily dropped from the network according to a certain probability, which is equivalent to finding a thinner network from the original network. Dropout [17] should be performed after the fourth Maxpool operation with the parameter keep_prob_(the probability of which part of the network would not be dropped) set to 0.6. It is a parameter of the dropout method. The overall structure of U-NET is shown in Figure 3.

The commonly used optimization method Adam of deep learning is used to dynamically adjust the learning rate of each parameter by using the first-order moment estimation and second-order moment estimation of the gradient. For the loss function, cross-entropy was used in this study.

3.2. Training of the Model

3.2.1. Data Set Preparation

For the collected pictures, the “labelme” image marking tool was used to manually mark the GCS. A total of 400 pictures is collected as the training set. Meanwhile, 50 pictures are collected as the validation set.

3.2.2. Data Enhancement

Image enhancement is a widely used training sample expansion method. In order to improve the diversity of training samples and enhance the antinoise performance of the model, image enhancement technology was used to expand the obtained samples. A total of 4 categories and 8 image enhancement technologies were used, including (1) image rotation; (2) image flipping; (3) random brightness transformation; and (4) random pepper and salt noise, as shown in Figures 4.

3.2.3. Recognition Effect

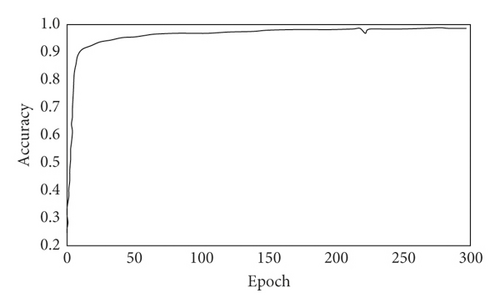
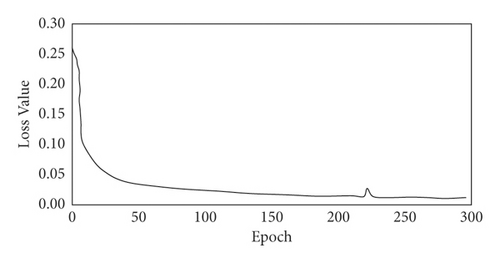
Parameters are adjusted manually. Through multiple experiments of different parameter setting, the best parameter is chosen. By adjusting the parameters, the learning rate was set to 1 × 10⁻⁴, the scale of the U-NET network was reduced, and the effect of the data set was enhanced. The performance of U-NET model is validated by the validation data set. After each iteration of 30 times and 300 rounds of epochs training, the accuracy of the validation set reached a value of 96%, which shows a strong generalization ability of this U-NET model. The loss function reached a value of about 0.01. The curves of accuracy and loss value of the trained model are shown in Figures 5 and 6, respectively.

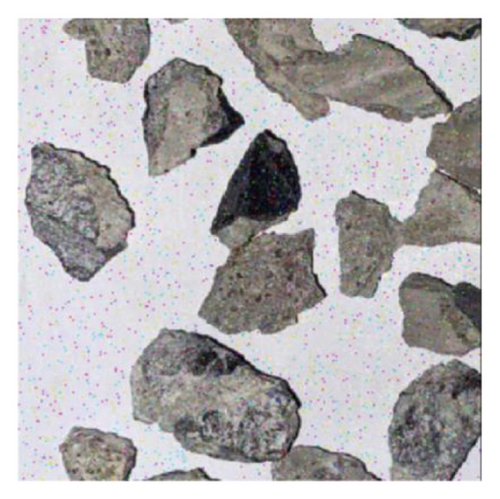
The particle identification effect is shown in Figure 7.

3.3. Segmentation of GCS

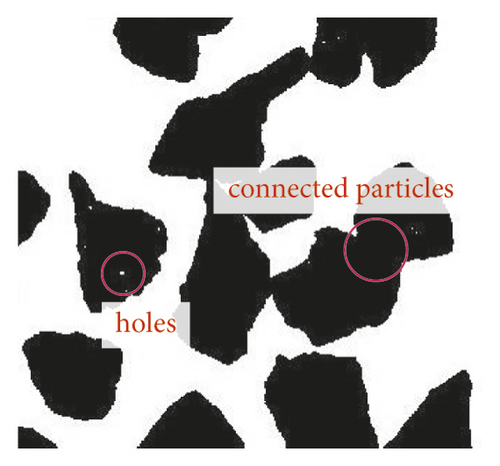
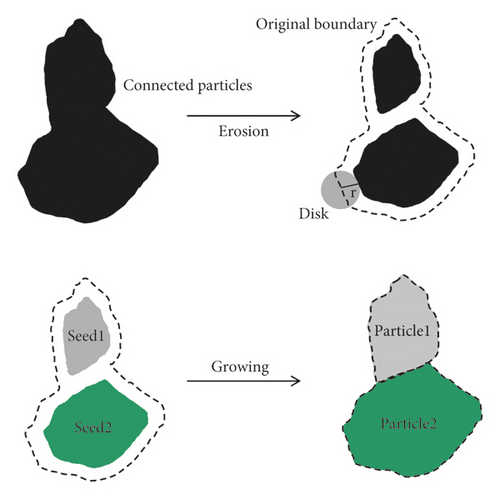
Generally, images obtained through the trained network still have some defects. The red marked area in Figure 8 shows the adhesion between particles, which affects further morphological analysis and calculation.

The binary image output by the neural network often contains some defects, and postprocessing technology is needed to improve the accuracy. Among all the defects, the two most obvious problems are as follows: (1) there are holes in the particles. (2) There are interconnected particles. To solve the problem of holes, a relatively mature pore filling algorithm can be used [18]. For the segmentation of connected particles, algorithms based on image morphology, such as the watershed method [19] and the corrosion-flooding method [20] are mostly adopted. Among them, the classic corrosion-flooding method used by Liu et al. [20] has a simple concept and has a good effect on the segmentation of objects with small contact sizes. The main steps are shown in Figure 9.

(1)
The corrosion algorithm is used to separate the connected particles into several independent parts, and each part is labeled as the expanded seed of the flooding method.
(2)
The seed is taken as the base point and expanded outward in the way of coloring. When the pixel meets the boundary of other seeds or particles, freeze the pixel and stop the expansion of this part.
(3)
When the expansion of all seed pixels stops, the segmented particles are obtained.

The radius r_ero of the corrosion mask is a decisive parameter in the corrosion operation, and a fixed value is often used in the existing research. Liu et al. [20] suggested the value of r_ero as follows:

(2)

4. Quantitatively Analysis of GCS Shapes

4.1. Methods for Quantifying the Particle Shape Indexes

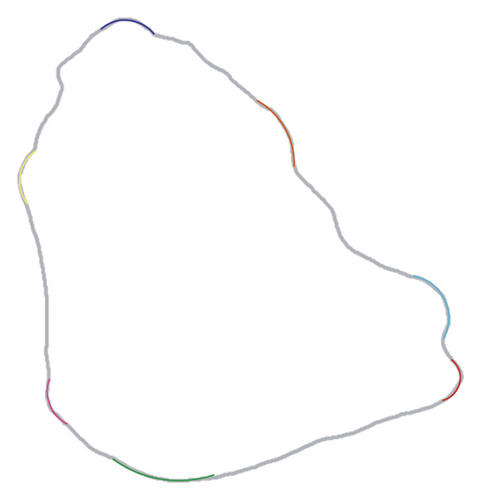
4.1.1. Quantification of Elongation

To reflect the particle contour, elongation (EI) is often used:

(3)

where D_minor is the width along the minor principal axis and D_major is the length along the major principal axis. Apparently, a smaller EI value represents the greater slenderness of the particle. Through a second-order tensor matrix based on the normal vector of particle contour, the two principal axes can be determined by

(4)

where

is the component of the unit normal vector T^k and the k_th micro arc in i direction and

is the counterpart in j direction; L^k is the length of the kth micro arc; L_P is the circumference of the particle contour, which is the sum of lengths of n micro arcs; and λ_a and λ_b are eigenvalues of matrix C, λ_a ≥ λ_b. The value of λ_b is the minimum percentage of the arc length in particle contour circumference along the major principal axis direction of Ω_ij. The value of λ_a is the maximum percentage along the minor principal axis direction of Ω_ij. After having two principle axis directions, D_minor and D_major can be calculated in a rectangular boundary containing the particle contour (Figure 10).

4.1.2. Quantification of Roundness

Roundness (Rd) reflects the sharpness and smoothness of the particle corners. Rd can be calculated by the ratio between the mean curvature of particle corner and the radius of the maximum inscribed circle of particle contour, as shown below:

(5)

where N is the number of corners; r_i is the curvature radius of the ith corner, and R_insc is the radius of the maximum inscribed circle of the particle contour.

Wadell [21] presented that a point belongs to the corner region when the curvature radius of the point is less than R_insc. Thus, the curvature radius of all contour points should be calculated to classify the corner region. For Fourier-presented contour curve, the curvature radius of the contour point can be calculated as

(6)

where r(θ) is the curvature radius.

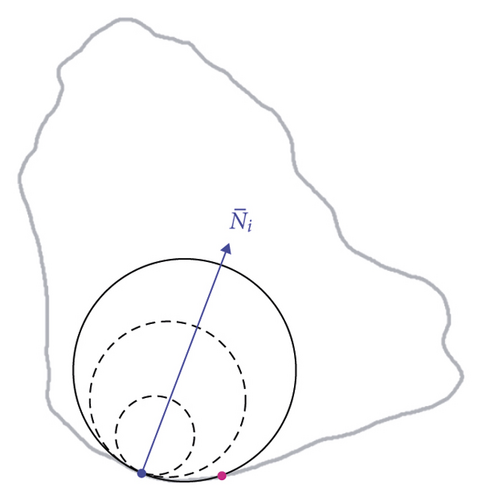
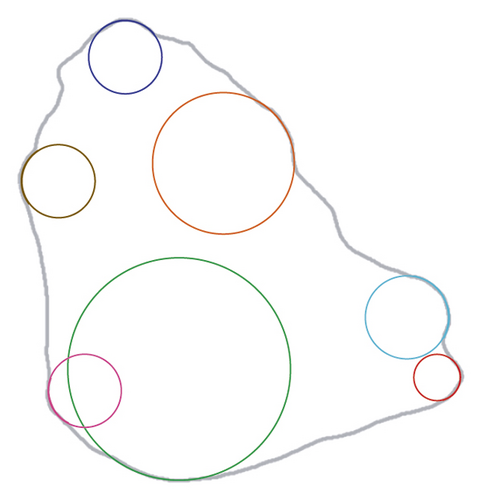
The contour point P(θ, r(θ)) can be seen as a corner point when r(θ) < R_insc. Thus, the corner region is the contour of all corner points (Figure 11(a)). The ODEC algorithm [22] can be used to calculate the radius of the inscribed circle of corner points, as shown in Figure 11(b). To be specific, the inner normal vector of the ith corner point is first calculated. Then, the inscribed circle along the direction of is determined, by starting from the ith corner point with a radius of ∆r. After that, whether the inscribed circle is tangent to any other contour point is determined. If not, the radius ∆r is increased and the last two steps are repeated; otherwise, terminate the process and take ∆r as the radius of the inscribed circle of the ith corner point.

The optimal inscribed circle of the corner can be determined by having the inscribed circles of all corner points. To value the fit performance of the inscribed circle of a corner point relative to other corner points, e_fit is defined:

(7)

where n_cp is the number of corner points; (x_i, y_i) are the coordinates of the ith corner point; (x_c, y_c) are the center coordinates of the inscribed circle; and r_c is the radius of inscribed circle radius. Particularly, the minimum value of e_fit represents the optimal inscribed circle of the corner. Through the optimal inscribed circles of all corners shown in Figure 11(c), the curvature radius of each corner and Rd can be calculated.

4.1.3. Quantification of Roughness

Roughness is a shape index that evaluates the concavity of the particle contour and it can show the shape difference between the real contour and the smoothed contour of particles. Fourier transform can be used to calculate the smoothed contour of a particle. The larger Fourier series (N) corresponds to a higher similarity between the real contour and the smoothed contour [23]. In this study, the Fourier series N is set to 16 to calculate the smoothed contour. The deviation between the smoothed contour and the real contour is shown in Figure 12.

Next, the deviation regions and the geometric types are extracted and determined. For nonintersecting parts between smoothed contour and real contour, the deviation region can be calculated as a quadrilateral area. For intersecting parts, the deviation region is simplified to two triangles. At the ith microunit, the deviation distance (△d_i) is the ratio of the deviation area to the corresponding length. Based on the average deviation distance of all microunits, Rg can be expressed as

(8)

where

is the average deviation distance, N_d is the number of all microunits, A_p is the area of the particle contour, A_i is the deviation area, l_i is the corresponding arc length, and L_p is the perimeter of the particle contour.

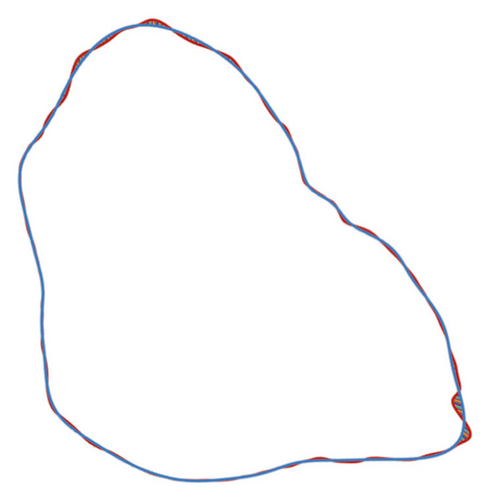
4.2. Statistics of Shape Indexes

Through the quantification algorithms introduced above, the elongation (EI), roundness (Ed), and roughness (Rg) of 1200 GCS were calculated. The fitting results are shown in Table 1.

Table 1. Fitting function and related parameters.

Shape index	Fitting function	Mean value	Goodness of fit R²	Range
EI	Normal distribution	0.68	0.98	From 0.25 to 1
Rd	Normal distribution	0.33	0.98	From 0.2 to 0.6
Rg	Normal distribution	0.0039	0.97	From 0.002 to 0.006

Normal distribution tests were implemented on the probability density of the three shape indexes. The results showed that all three indexes satisfied normal distribution appropriately. Within the results, the width of the distribution of elongation is the maximum and the width of the distribution of roundness is the minimum, with ranges from 0.4 to 1 and from 0.2 to 0.5, respectively. Furthermore, the mean values of the three shape indexes EI, Rd, and Rg are 0.68, 0.33, and 0.0039, respectively.

4.3. Establish Shape Library

To facilitate retrieval and sample preparation, the shape indicators of the GCS are stored together with the coordinates, with the storage format [number, outline, slender length, elongation, roundness, roughness].

The steps for sample preparation from the particle library are as follows:

(1)
The required shape parameter range is input
(2)
According to the range of these values, the two-dimensional contour that meets the requirements can be searched automatically
(3)
The visualized two-dimensional contour is selected and is output to the “dxf” file

After establishing the particle library, it will be very convenient to select the two-dimensional contours of GCS that meet specific requirements, so as to facilitate the discrete element modeling of GCS. Moreover, it lays the foundation for further study on the relationship between the geometric information and mechanical properties of GCS.

5. Application to DEM Simulation of GCS Packing

5.1. Simulation of Gravity Deposition

The mechanical parameters of GCS like shear strength and deformation modulus can be affected by the packing characteristics. The shape index EI is set as the DEM [24] simulation variable to explore the influence of particle shape on packing properties, as shown in Figure 13(a). Considering the elongation variable, the GCS were selected and divided into 7 groups where EI is set from 0.4 to 1.0. In this study, the particles in DEM are not generated randomly; on the contrary, real GCS were used as samples to enhance the reliability of the simulations.

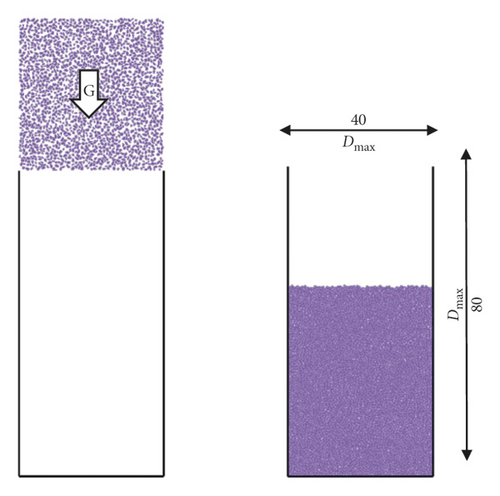
Stratified gravity deposition simulation of the natural packing process of particles is the common way to generate particle models. In the model, DEM particles fall naturally with gravity. After completing the previous layer deposition, a new layer of particles is generated and the deposition process is repeated until the whole simulation is completed, as shown in Figure 13(b) [25]. The gravity deposition process is simulated by PFC^2D, and the interparticle contact and the wall-particle contact are both linear contacts. The parameters of the model are shown in Table 2.

Table 2. Particle number and model parameters.

Parameter	Value
Particle number	1000 × 3
Particle density (kg/m³)	2650
Interparticle frictional coefficient	0.5
Wall-particle frictional coefficient	0
Effective modulus (Pa)	1 × 10⁸
Stiffness ratio	4/3
Damping factor	0.7

5.2. Analysis of Macro-Meso Parameter

Macro-meso parameters reflect the particle packing properties, such as void ratio, compactness, and coordination number. In this section, the effect on EI is considered.

5.2.1. Macro Parameter

The degree of density of particles can be described by a macro parameter, void ratio (e), which is affected by particle shape.

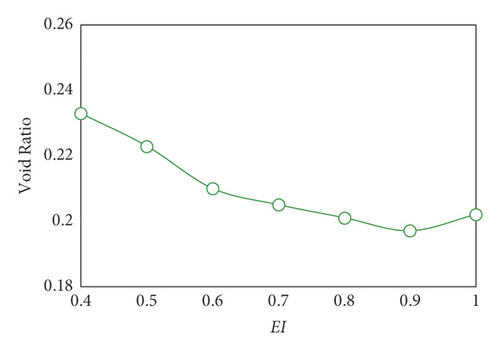
The change curves of the void ratio with respect to EI are shown in Figure 14. Void ratio e decreases with the growth of EI, indicating that the particle packing gets closer with EI increasing. Then, the void ratio reaches a bottom value of 0.187 and starts to soar at the point where EI is 0.9.

5.2.2. Micro Parameter

The degree of particle contact can be measured by a micro parameter, the mean coordination number (C_mean), which can reflect the internal structure of particle packing [26]:

(9)

where N_p is the number of particles and C_i is the contact particle number of the ith particle.

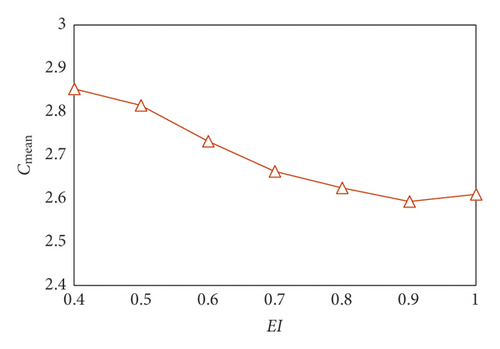
In the change curve of the mean coordination number with respect to EI shown in Figure 15, a reflection point also appears at the point where EI is 0.9. Similar to the curve of void ratio, C_mean exhibits a decreasing trend with EI increasing. After reaching the bottom of the curve, C_mean stays stable and has a slight increase.

5.2.3. Fabric Anisotropy

The fabric anisotropy is the anisotropy between the spatial distribution of particle contacts and the length of branch vectors. The branch vector is the vector connecting the mass centers of two particles. Fabric anisotropy coefficients can be used to quantify the fabric anisotropy properties, including coefficient of contact (a_c), coefficient of normal contact forces (a_n), coefficient of tangential contact forces (a_t), and coefficient of branch vectors (a_d). The anisotropy coefficients can be calculated as

(10)

where a∗ is the anisotropy coefficients (a_c, a_n, a_t, and a_d) and

is the tensors (

, and

) indicating the directional distribution of a_c, a_n, a_t, and a_d. The tensors can be calculated as

(11)

where

is the average normal contact force,

is the average length of the branch vector,

is the partial tensor of

, and

is the partial tensor of

, and

can be calculated as

(12)

where

and

are the ith and jth components of the unit normal vector of contact c, respectively, and

, and

are the normal contact force, tangential contact force and normal branch vector of contact c, respectively.

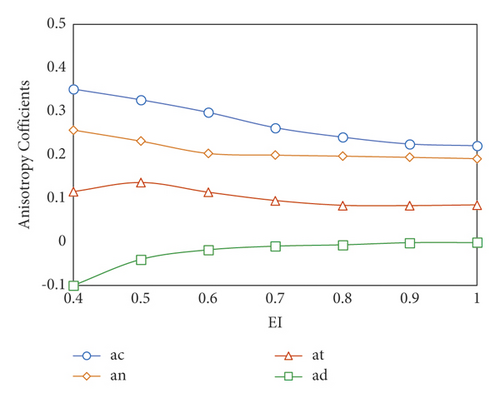
Figure 16 shows the change curves of the fabric anisotropy coefficients with respect to EI. Among all coefficients, a_c, a_n, and a_t slightly decrease with the increase of EI, that is, the anisotropy degree of the normal contact force and tangential contact force decreases with EI collapsing. On the contrary, a_d shows a positive correlation with EI, indicating that the anisotropy degree of branch vector declines with EI increasing. Furthermore, a_d slightly stabilizes to 0 with EI increasing from 0.4 to 1.0, showing that the anisotropy of branch vector almost disappears. Thus, the degree of fabric anisotropy decreases with EI decreasing. Note that when EI ≥ 0.8, the fabric anisotropy coefficients stay relatively stable; thus, the degree of fabric anisotropy is not affected by EI.

6. Application to DEM Simulation of GCS Shear Behavior

6.1. Simulation of Biaxial Compression Test

First, five samples with different elongation (EI = 0.4, 0.5, 0.6, 0.7, 0.9) were constructed. Each sample has an initial size of 9 m ∗ 18 m and contains approximately 5000 GCS particles. The linear elastic model is used as the contact law between particles. The samples are compressed by shifting the four rigid boundaries, and the boundary has a force at 100 kPa (stress boundary condition controlled by numerical servo). During the shearing process, in order to make the state of samples quasistatic (to make the loading process of the sample quasistatic loading), the rate of shear strain is supposed to be relatively small. Thus, the inertial parameters are introduced as follows:

(13)

where

is the loading strain rate, d is mean particle size, ρ is material density, σ₀ is the consolidation stress. Previous studies have shown that the value of the Inertia parameter should be less than 2.5 × 10⁻³. Thus, the shifting speed of the rigid wall is fixed to 0.05 m/s. The inertia parameter is less than 10⁻⁴ throughout the tests’ negative correlation.

6.2. Analysis of Macro-Meso Parameter

6.2.1. Analysis of Stress Ratio

The mean stress p and deviator stress q are calculated to explore the sample shear strength. In the two-dimensional biaxial shear test, the valid average stress p′ and deviator stress q are shown as follows:

(14)

(15)

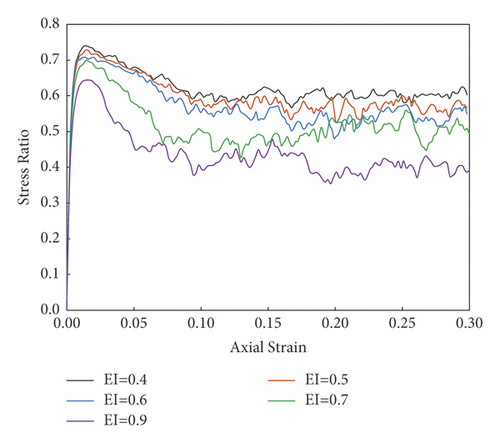
For different EI values of samples, Figure 17 shows the variation of the stress ratio q/p′ with the axial strain ε₁. In the initial stage, as the axial strain increases, the stress ratio of all samples rises significantly. After increasing to a peak value, the stress ratio slightly descends and tends to stabilize.

6.2.2. Analysis of Volumetric Deformation

In this section, the evolution of volumetric deformation is analyzed. Regarding the boundaries of the simulation being rigid walls, the axial strain and volume strain can be calculated as

(16)

where h₀ and h are the original height and the current height of the sample, respectively; v₀ and v are the original volume and the current volume of the sample, respectively; negative volume strain indicates volume expansion. In order to study the critical state characteristics of the stabilized sample, all samples were sheared to the axial strain ε₁ = 30%. Under this deformation, the typical conditions of the critical state are basically satisfied (i.e., the stress and volume remain constant with strain).

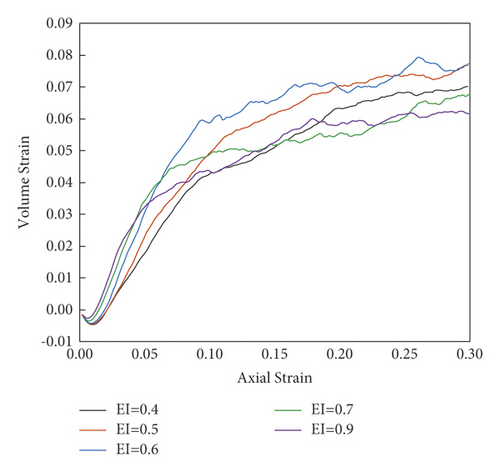
As shown in Figure 18, in the initial stage, the volume strain descends with the ascent of the axial strain. After the axial strain reaches about 1%, the volume strain reverses. As the axial strain increases to a range of 20% to 30% which is a critical state, the volume deformation of the sample remains constant, which indicates that all samples show shear-induced dilatancy deformation with strain softening. Moreover, as the sample gets a steady state, the volume strain shows a negative correlation with the EI value. Therefore, a sample with a smaller EI value has stronger dilatancy.

6.2.3. Analysis of Mean Coordination Number

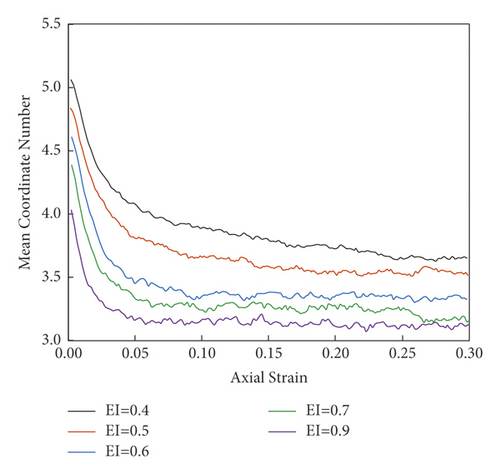
In this section, we focus on the mean coordination number (MCN), which can reflect the microscopic packing structure of the simulated GCS. The evolution of MCN versus axial strain is illustrated in Figure 19 for samples with various values. In the beginning stage of shear, the MCN of samples decreases significantly with axial strain. Then, MCN declines with a lower speed when the axial strain is greater than 2%. When the axial strain is greater than 10%, the MCN is roughly steady. Then, as the EI value rises from 0.4 to 0.9, the MCN collapses from 5.0 to 4.0; thus, a negative correlation with the EI value can be found.

6.2.4. Analysis of Sliding Contact Percentage

The Mohr–Coulomb law conducts the percentage of sliding contact. The sliding coefficient is shown as follows:

(17)

where

is the tangential contact force of contact c,

is the normal contact force of contact c, and μ is the friction factor. When S_C > 0.9999, it is considered that a contact slip has occurred. The percentage of sliding contact in the particle system is as follows:

(18)

where N_SC indicates the number of sliding contacts in the particle system and N_C is the total number of contacts. Figure 20 shows the variation of S_P of each sample with axial strain. The variation of S_P with an axial strain of all samples is basically the same. As ε₁ increases, S_P rapidly increases to a peak value and then gradually decreases to a stable value. Figure 20 also indicates that the contact slip rate descends with EI climbing. As the EI value rises from 0.4 to 0.9, the maximum value and the stability value of S_P descends from 0.36 to about 0.16, and from 11% to approximately 5%, respectively.

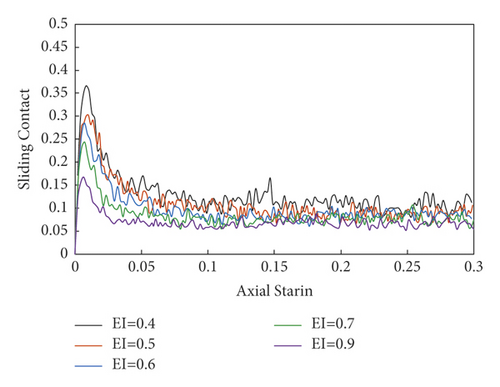
7. Conclusion

Graded crushed stone (GCS) is of great significance in road construction as an essential material used in the base or transition layer. The packing properties like compactness and void ratio can be affected by the irregularity and variability of particle shape. In this study, the particle outlines are firstly extracted based on deep learning algorithms. Then, the shape evaluation indexes are quantified. In addition, the gravity deposition with distinct EI value is simulated by the discrete element method. Finally, the shear behavior of GCS is studied. The specific results are as follows:

(1)
The realistic particle contour is first automatically extracted based on digital image processing and deep learning algorithms. The lightweight U-NET model is trained and the results show the accuracy of the training set reached a value of 97% and the loss value is about 0.01.
(2)
The elongation (EI), roundness (Rd), and roughness (Rg) of GCS are quantified by shape evaluation algorithms.
(3)
Based on the establishment of the GCS shape library, the gravity deposition with various elongation is simulated using the discrete element method to study the packing properties of GCS. The elongation effects on the macroscopic and microscopic quantities are explored. The results illustrate that the void ratio decreases with increasing elongation before a reflection point where EI value is 0.9. Similar to the void ratio, the mean coordinate number C_mean exhibits a decreasing trend with EI increasing. After reaching the bottom of the curve, C_mean stays stable and has a slight increase.
(4)
The shear behavior of GCS is studied by simulation of the biaxial compression test. The stress ratio of all samples increases rapidly, and then reaches the peak stage, after which the stress ratio gradually decreases and tends to stabilize. The volume strain decreases with the increase of the axial strain, and when the axial strain reaches about 1%, the volume strain reverses. Then, in the range of 20% to 30%, the volume strain stays constant, indicating a shear-induced dilatancy deformation accompanied by strain softening. The mean coordinate number of all samples increases with axial strain at the beginning; then, after the value of axial strain reaching 2%, the MCN reaches its peak and decreases to be stable when the axial strain is greater than 10%. The variation of the percentage of sliding contact S_P with the axial strain of all samples is basically the same. As ε₁ increases, S_P rapidly increases to a peak value and then gradually decreases to a stable value.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This research was funded by the Ministry of Transport of China (Grant no. 2020-MS5-145) and the State Archives Bureau of China (Grant no. 2021-X-45).

Open Research

Data Availability

The data used in the paper are including in the article.

References

1 Long W., Xiaoguang X., and Hai L., Influence of laboratory compaction methods on shear performance of graded crushed stone, Journal of Materials in Civil Engineering. (2011) 23, no. 10, 1483–1487, https://doi.org/10.1061/(asce)mt.1943-5533.0000323, 2-s2.0-80155171741.
10.1061/(ASCE)MT.1943-5533.0000323
Web of Science® Google Scholar
2 Li J., Zheng J., Yao Y. et al., Numerical method of flexible pavement considering moisture and stress sensitivity of subgrade soils, Advances in Civil Engineering. (2019) 2019, 10, 7091210, https://doi.org/10.1155/2019/7091210, 2-s2.0-85067106124.
10.1155/2019/7091210
Web of Science® Google Scholar
3 Yi J., Liang C., Qian J. et al., Laboratory evaluation and design of construction and demolition wastes for granular base, Advances in Civil Engineering. (2020) 2020, 1–10, https://doi.org/10.1155/2020/8827715.
10.1155/2020/8827715
Web of Science® Google Scholar
4 Li J., Zhang J., Qian G., Zheng J., and Zhang Y., Three-dimensional simulation of aggregate and asphalt mixture using parameterized shape and size gradation, Journal of Materials in Civil Engineering. (2019) 31, no. 3, 04019004, https://doi.org/10.1061/(asce)mt.1943-5533.0002623, 2-s2.0-85059624792.
10.1061/(ASCE)MT.1943-5533.0002623
CAS Web of Science® Google Scholar
5 Hui W., Li J., Wang F., Zheng J., Tao Y., and Zhang Y., Numerical investigation on fracture evolution of asphalt mixture compared with acoustic emission, International Journal of Pavement Engineering. (2021) 1–11, https://doi.org/10.1080/10298436.2021.1902524.
10.1080/10298436.2021.1902524
Web of Science® Google Scholar
6 Qian G., Hu K., Li J., Bai X., and Li N., Compaction process tracking for asphalt mixture using discrete element method, Construction and Building Materials. (2020) 235, 117478, https://doi.org/10.1016/j.conbuildmat.2019.117478.
10.1016/j.conbuildmat.2019.117478
Web of Science® Google Scholar
7 Wang Y., Shao S., and Wang Z., Effect of particle breakage and shape on the mechanical behaviors of granular materials, Advances in Civil Engineering. (2019) 2019, no. S2, 1–15, https://doi.org/10.1155/2019/7248427.
10.1155/2019/7248427
CAS Web of Science® Google Scholar
8 Le Pen L. M., Powrie W., Zervos A., Ahmed S., and Aingaran S., Dependence of shape on particle size for a crushed rock railway ballast, Granular Matter. (2013) 15, no. 6, 849–861, https://doi.org/10.1007/s10035-013-0437-5, 2-s2.0-84888128323.
10.1007/s10035-013-0437-5
Web of Science® Google Scholar
9 Zhang J., Li J., Yao Y., Zheng J., and Gu F., Geometric anisotropy modeling and shear behavior evaluation of graded crushed rocks, Construction and Building Materials. (2018) 183, 346–355, https://doi.org/10.1016/j.conbuildmat.2018.06.188, 2-s2.0-85049110437.
10.1016/j.conbuildmat.2018.06.188
Web of Science® Google Scholar
10 Jiang Y., Wong L. N. Y., and Ren J., A numerical test method of California bearing ratio on graded crushed rocks using particle flow modeling, Journal of Traffic and Transportation Engineering. (2015) 2, no. 2, 107–115, https://doi.org/10.1016/j.jtte.2015.02.004, 2-s2.0-84997161477.
10.1016/j.jtte.2015.02.004
Google Scholar
11 Ren L., Xiao Z., and Hu X., Micromechanical analysis for direct shear tests of grade crushed stones, Highways. (2008) 5, 152–156.
Google Scholar
12 Xu G., Chen Z., Li X., Lu G., Dong D., and Liu Z., Establishment of control standard for plastic deformation performance of graded crushed stone, Construction and Building Materials. (2019) 211, 383–394, https://doi.org/10.1016/j.conbuildmat.2019.03.254, 2-s2.0-85063317172.
10.1016/j.conbuildmat.2019.03.254
Web of Science® Google Scholar
13 Jiang Y., Li S., and Wang T., Numerical method of dynamic triaxial test on graded crushed rock, Journal of Southeast University (Natural Science Edition). (2013) 43, no. 3, 604–609.
Google Scholar
14 Liang Z., Nie Z., An A., Gong J., and Wang X., A particle shape extraction and evaluation method using a deep convolutional neural network and digital image processing, Powder Technology. (2019) 353, 156–170, https://doi.org/10.1016/j.powtec.2019.05.025, 2-s2.0-85065731199.
10.1016/j.powtec.2019.05.025
CAS Web of Science® Google Scholar
15 Ronneberger O., Fischer P., and Brox T., U-net: convolutional networks for biomedical image segmentation, Proceedings of International Conference on Medical Image Computing and Computer-Assisted Intervention, 2015, Munich, Germany, Springer, 234–241, https://doi.org/10.1007/978-3-319-24574-4_28, 2-s2.0-84951834022.
10.1007/978-3-319-24574-4_28
Google Scholar
16 Yang J., Runyang Y. U., and Lianghui F., Early Smoke Segmentation Method Based on U-Net Convolutional Network, 2019, Fire Safety ence.
Google Scholar
17 Srivastava N., Hinton G., Krizhevsky A. et al., Dropout: a simple way to prevent neural networks from overfitting, Journal of Machine Learning Research. (2014) 15, no. 1, 1929–1958.
Web of Science® Google Scholar
18 Soille P., Morphological Image Analysis: Principles and Applications, 2013, Springer Science & Business Media, Berlin, Germany.
Google Scholar
19 Zheng J. and Hryciw R. D., Segmentation of contacting soil particles in images by modified watershed analysis, Computers and Geotechnics. (2016) 73, 142–152, https://doi.org/10.1016/j.compgeo.2015.11.025, 2-s2.0-84955286563.
10.1016/j.compgeo.2015.11.025
Web of Science® Google Scholar
20 Liu C., Shi B., Zhou J., and Tang C., Quantification and characterization of microporosity by image processing, geometric measurement and statistical methods: application on SEM images of clay materials, Applied Clay Science. (2011) 54, no. 1, 97–106, https://doi.org/10.1016/j.clay.2011.07.022, 2-s2.0-80053298470.
10.1016/j.clay.2011.07.022
CAS Web of Science® Google Scholar
21 Wadell H., Sphericity and roundness of rock particles, The Journal of Geology. (1933) 41, no. 3, 310–331, https://doi.org/10.1086/624040.
10.1086/624040
Web of Science® Google Scholar
22 Garcia X., Latham J.-P., Xiang J., and Harrison J. P., A clustered overlapping sphere algorithm to represent real particles in discrete element modelling, Géotechnique. (2009) 59, no. 9, 779–784, https://doi.org/10.1680/geot.8.t.037, 2-s2.0-77949702642.
10.1680/geot.8.T.037
Web of Science® Google Scholar
23 Nie Z.-H., Wang X., Huang D.-L., and Zhao L.-H., Fourier-shape-based reconstruction of rock joint profile with realistic unevenness and waviness features, Journal of Central South University. (2019) 26, no. 11, 3103–3113, https://doi.org/10.1007/s11771-019-4239-8.
10.1007/s11771-019-4239-8
Web of Science® Google Scholar
24 Zhao H. and Chen J., A numerical study of railway ballast subjected to direct shearing using the discrete element method, Advances in Materials Science and Engineering. (2020) 2020, 1–13, https://doi.org/10.1155/2020/3404208.
10.1155/2020/3404208
Web of Science® Google Scholar
25 Zhu Y., Nie Z., and Gong J., Influence of the rolling-resistance-based shape of coarse particles on the shear responses of granular mixtures, Particuology. (2020) 52, 67–82, https://doi.org/10.1016/j.partic.2019.12.004.
10.1016/j.partic.2019.12.004
Web of Science® Google Scholar
26 Jia X. and Williams R. A., A packing algorithm for particles of arbitrary shapes, Powder Technology. (2001) 120, no. 3, 175–186, https://doi.org/10.1016/s0032-5910(01)00268-6, 2-s2.0-0035935222.
10.1016/S0032-5910(01)00268-6
CAS Web of Science® Google Scholar

Citing Literature

All articles

Automated Shape Analysis and DEM Study on Graded Crushed Stone

Abstract

1. Introduction

2. Materials and Equipment

3. Automated Extraction of GCS Contours

3.1. Implementation of Algorithms

3.1.1. Lightweight U-NET and Operation

3.1.2. Model Optimization

3.2. Training of the Model

3.2.1. Data Set Preparation

3.2.2. Data Enhancement

3.2.3. Recognition Effect

3.3. Segmentation of GCS

4. Quantitatively Analysis of GCS Shapes

4.1. Methods for Quantifying the Particle Shape Indexes

4.1.1. Quantification of Elongation

4.1.2. Quantification of Roundness

4.1.3. Quantification of Roughness

4.2. Statistics of Shape Indexes

4.3. Establish Shape Library

5. Application to DEM Simulation of GCS Packing

5.1. Simulation of Gravity Deposition

5.2. Analysis of Macro-Meso Parameter

5.2.1. Macro Parameter

5.2.2. Micro Parameter

5.2.3. Fabric Anisotropy

6. Application to DEM Simulation of GCS Shear Behavior

6.1. Simulation of Biaxial Compression Test

6.2. Analysis of Macro-Meso Parameter

6.2.1. Analysis of Stress Ratio

6.2.2. Analysis of Volumetric Deformation

6.2.3. Analysis of Mean Coordination Number

6.2.4. Analysis of Sliding Contact Percentage

7. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information