For a simple graph G with a vertex set V(G) and an edge set E(G), a labeling f : V(G)∪E(G)⟶{1,2, ⋯, k} is called a vertex irregular total k − labeling of G if for any two different vertices x and y in V(G) we have wt(x) ≠ wt(y) where wt(x) = f(x) + ∑_u∈V(G)f(xu). The smallest positive integer k such that G has a vertex irregular total k − labeling is called the total vertex irregularity strength of G, denoted by tvs(G). The lower bound of tvs(G) for any graph G have been found by Baca et. al. In this paper, we determined the exact value of the total vertex irregularity strength of the hexagonal cluster graph on n cluster for n ≥ 2. Moreover, we show that the total vertex irregularity strength of the hexagonal cluster graph on n cluster is (3n² + 1)/2.

1. Introduction

A graph labeling is an assignment of integers from 1 to n, for the vertices, edges, or both. Graph labelings have been used in many applications like communication network addressing, software testing, information security, technology and sports tournament scheduling, and coding theory problems including the design of good radar location codes, missile guidance codes, and convolution codes.

We consider the finite undirected graph G without loops and multiple edges with vertex set V(G) and edge set E(G). The degree of a vertex x is the number of edges that have x as an endpoint, and the set of neighbors of x is denoted by N(x). If the domain of the labeling function f(x) is the vertex set or the edge set, the labeling is called, respectively, vertex labeling or edge labeling. If the domain is V(G)∪E(G), then we call the labeling a total labeling.

A labeling f : E(G)⟶{1, 2, 3, ⋯, k} is called an edge k − labeling of G. The associated vertex weight of a vertex x ∈ V(G) under an edge k − labelingf is defined as wt(x) = ∑_v∈N(x)f(xv). Chartrand et al. [1] introduced an edge k − labeling of a graph G such that wt(x) ≠ wt(y) for all vertices x, y ∈ V(G) with x ≠ y. Such labelings were called irregular assignments, and the irregularity strength s(G) of a graph G is known as the minimum k for which G has an irregular assignment using labels at most k. The irregularity strength s(G) can be interpreted as the smallest integer k for which G can be turned into a multigraph G′ by replacing each edge by a set of at most k parallel edges, such that the degrees of the vertices in G′ are all different.

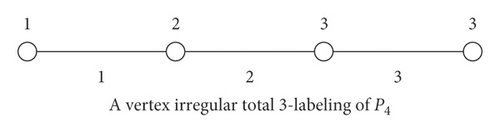
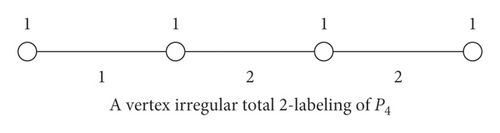
In this paper, we consider for a total k − labeling of G, that is, f : V(G)∪E(G)⟶{1, 2, 3, ⋯, k}. The associated vertex weight of a vertex x ∈ V(G) under a total k − labelingf is defined as wt(x) = f(x) + ∑_v∈N(x)f(xv). A total k − labelingf is defined to be a vertex irregular total k − labeling of G if for every two different vertices x and y of G, wt(x) ≠ wt(y). The minimum positive integer k for which G has a vertex irregular total k − labeling is called the total vertex irregularity strength of G, denoted by tvs(G). In Figure 1, there are a two total labeling of P₄, one of is a vertex irregular total 3-labeling of P₄ and the other is a vertex irregular total 2-labeling of P₄. However, P₄ does not have a vertex irregular total vertex 1-labeling. Such that the minimum positive integer k for which P₄ has a vertex irregular total k − labeling is 2, or the total vertex irregularity strength of P₄ is 2.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

A vertex irregular total k-labeling of P₄ for k = 2 and k = 3.

Baca et al. [2] in 2007 started to investigate the total vertex irregularity strength of a graph, an invariant analogous to the irregularity strength for total labelings. There are not many graphs for which the exact values of their total vertex irregularity strength are known. Baca et al. [2] have determined the total vertex irregularity strengths for some classes of graphs, namely, cycles, stars, and prisms. Nurdin et al. have determined the total vertex irregularity strengths of a disjoint union of t copies of a path [3], tree graphs [4], and caterpillar graph [5]. Nurdin and Kim have determined the total vertex irregularity strength of splitting graphs of stars [6].

In this paper, we determine exact value of the total vertex irregularity strength of the hexagonal cluster graph with n cluster for n ≠ 2.

2. Hexagonal Cluster Graph

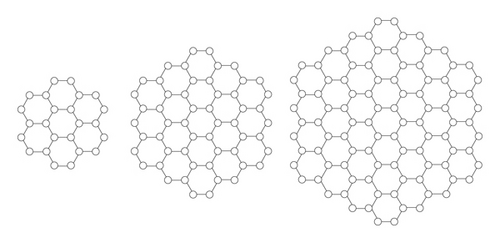
In this section, we give the definition of hexagonal cluster graphs. The hexagonal cluster graph with n ≥ 2 cluster, denoted by HC(n), where HC(1) isomorphs to C₆, is obtained by adding as many as 6(n − 1) cycle C₆ on the outer path of HC(n − 1). Figure 2 demonstrates hexagonal cluster graphs HC(2), HC(3), and HC(4).

Some interconnection networks are designed, and some are borrowed from nature. For example, hypercubes, complete binary trees, butterflies, and torus networks are some of the designed architectures. Grids, hexagonal networks, honeycomb networks, and diamond networks, for instance, bear resemblance to atomic or molecular lattice structures. They are called natural architectures. The advancement of large scale integrated circuit technology has enabled the construction of complex interconnection networks. Besides that, the hexagonal cluster graphs have been studied as models of organic compounds build up entirely from benzene rings, social networks, and wireless sensor networks. Graph theory provides a fundamental tool for designing and analyzing such networks [7–11].

In [2], Baca et al. studied the lower bound of tvs(G) for any graph G as follows.

Theorem 1. If p is the number of vertices of any graph G, δ is the minimum degree of vertex, and Δ is the maximum degree of vertex of G, then

(1)

3. Results and Discussion

In this paper, we have proved that the total vertex irregularity strength of the hexagonal cluster graph (network) with n cluster is equal to its lower bound in Theorem 1.

Theorem 2. For n ≥ 2, we have

(2)

Proof. Since the number of vertices of HC(n) is 6n², the minimum degree of vertex is 2 and the maximum degree of vertex is 3; by using (1) in Theorem 1, we found that

(3)

To find that tvs(HC(n)) ≤ (3n² + 1)/2, we have to construct a vertex irregular total k − labeling on HC(n) where k = (3n² + 1)/2 as follows.

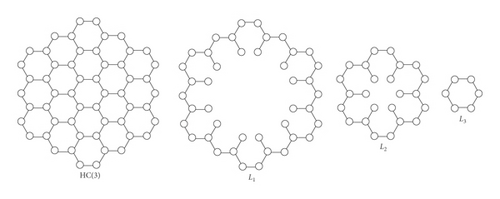
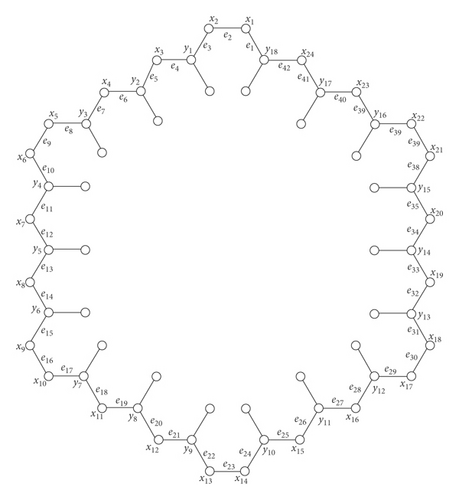
Note that there are n layers in HC(n). Layer i is denoted by L_i. For illustration, in Figure 3, there are 3 layers in HC(3).

In L₁, there is an outer cycle C_12n−6 of HC(n) which consists of 6n vertices of degree 2 denoted by x_i(i = 1, 2, ⋯, 6n), 6(n − 1) vertices of degree 3 denoted by y_j(j = 1, 2, ⋯, 6(n − 1)), and 12n − 6 edges denoted by e_t(t = 1, 2, ⋯, 12n − 6).

Now, consider all vertices and all edges in the outer cycle C_12n−6 of HC(n) sequentially.

To label some of vertices and all edges in L₁, we use Algorithm 1 as follows.

To label all of edges in L_t for 2 ≤ t ≤ n − 1 and for 3 ≤ i ≤ 2n − 3 define

(4)

(5)

and use Algorithm 2 as follows.

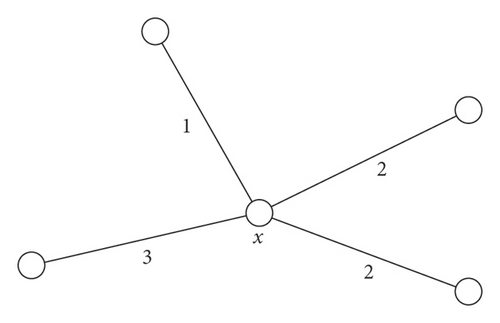
All of edges of HC(n) are already labeled, but vertices have not labeled yet. Next, label all of vertices using the following method. The temporary weight of a vertex x is the number of label of all edges incident tox, denoted by w(x). For example, the temporary weight of a vertex x in Figure 4 is 8.

Order the temporary weight of all vertices and rename them by such that For i = 2, 3, ⋯, 6n, define

(6)

where wt(z₁) = 3 is the total weight of vertex z₁.

Based on equation (6), we have that

(7)

Besides that, from Algorithms 1 and 2, we can see that

(8)

Based on Statements (7) and (8), we conclude that the function construction with Algorithms 1 and 2 is a total vertex irregular k − labeling on HC(n) where k = (3n² + 1)/2. This shown as follows:

(9)

Based on equations (3) and (9), we find equation (2), i.e., tvs(HC(n)) = (3n² + 1)/2.

As illustration, we shall use Algorithms 1 and 2 to construct a total vertex irregular 25-labeling on HC(4). The first step, all the vertices and all the edges on the outer cyrcle C₄₂ of HC(4) are named sequentially as in Figure 5.

Now, we use Algorithm 3 to label some of vertices and all edges in L₁ as follows.

For 3 ≤ I ≤ 5, using equations (4) and (5), we have S₃ = 24.3–(3/2)(3² − 1) = 60, S₄ = 24.4–(3/2)4² = 72, and S₅ = 24.5 − (3/2)(5² − 1) = 84.

Then, use Algorithm 4 to label all edges in L₂ and L₃, as follows.

Algorithm 1: Algorithm for labeling all edges of the outer cycle of L1.

Step 1. For i = 1 + 3(k − 1) where k = 1, 2, ⋯, 2n, label e^′, e^″, and x_i with (i + 2)/3 where e^′ and e^″ are edges incident to vertex x_i
Step 2. For i = 1 + 3(k − 1) where k = 1, 2, ⋯, 2n, label edges between x_i and x_i+1by f(x_i) + 1 except for the labeling edges in Step 1
Step 3. Label all edges between x₁ and x_6n−2 by f(x_6n−2) + 1 = 2n + 1
Step 4. Label the remaining edges of L₁ by 4n − 3

Algorithm 2: Algorithm for labeling all other edges in HC(n).

K_2t−1=(S_2t−1+2−K_2t−2)/3,
Step A. Label all of edges of the outer cycle in L_t for 2 ≤ t ≤ n − 1 by where K₂ = 4n − 3
Step B. Label all of the remaining edges from L_t for 2 ≤ t ≤ n − 2 by K_2t = (S_2t + 2 − 2K_2t−1)/2
Step C. Label all of the remaining edges in HC(n) by (3n² + 1)/2

Algorithm 3: Algorithm for labeling all edges of the outer cycle of L1 of HC(4).

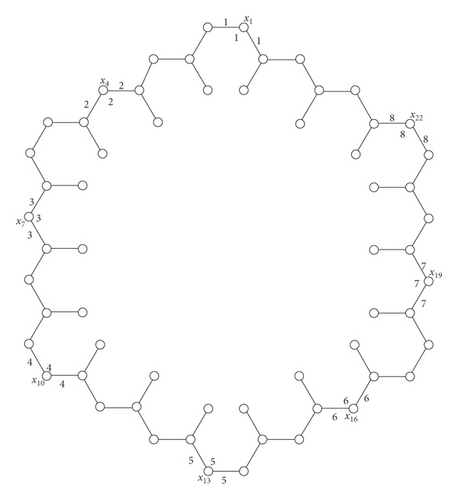
Step 1. For i = 1 + 3(k − 1) where k = 1, 2, 3, 4, 5, 6, 7, 8, label e^′, e^″, and x_i with (i + 2)/3 where e^′ and e^″ are edges incident to vertex x_i (see Figure 6)
Step 2. For i = 1 + 3(k − 1) where k = 1, 2, 3, 4, 5, 6, 7, 8, label edges between x_i and x_i+1 by f(x_i) + 1 except for the labeling edges in Step 1
Step 3. Label all edges between x₁ and x₂₂ by f(x₂₄) + 1 = 9 except for the labeling edges in Step 1 (see Figure 7)
Step 4. Label the remaining edges of L₁ by 13 (see Figure 8)

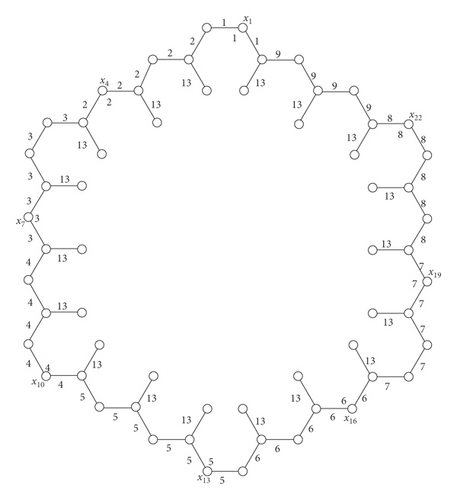
Algorithm 4: Algorithm for labeling all other edges in HC(4).

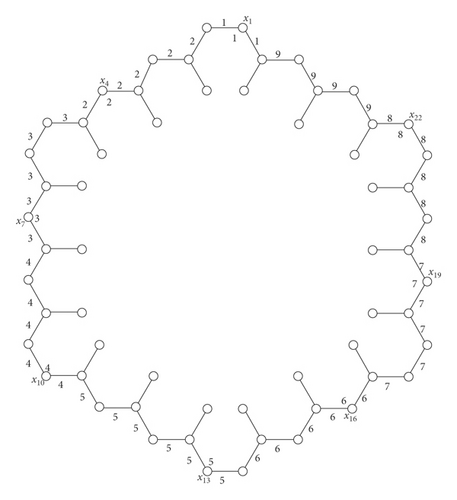
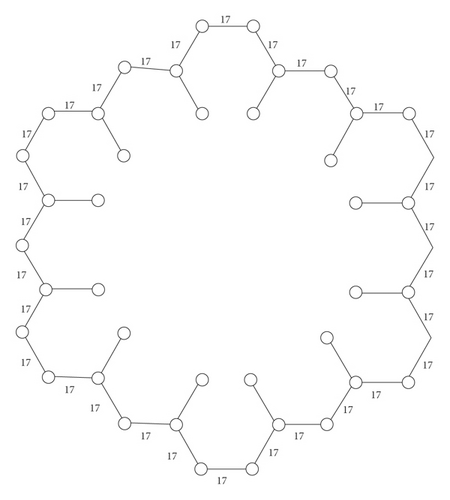
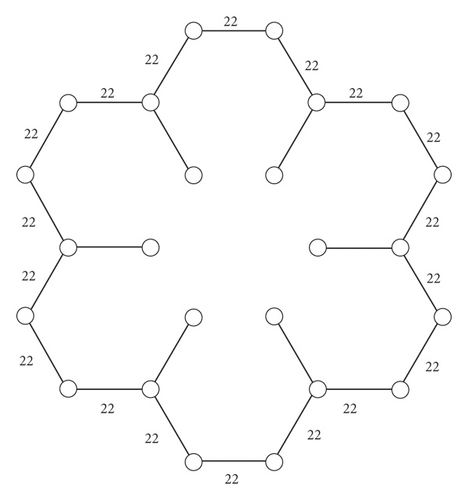
Step A. Label all edges of the outer cycle in L₂ by using Algorithm 2, i.e., K₃ = (S₃ + 2 − K₂)/3 where K₂ = 13, i.e., K₃ = (60 + 2 − 13)/3 = 17 (see Figure 9) and all edges of the outer cycle in L₃ by K₅ = (S₅ + 2 − K₄)/3 = (84 + 2 − 20)/3 = 22 (see Figure 10)
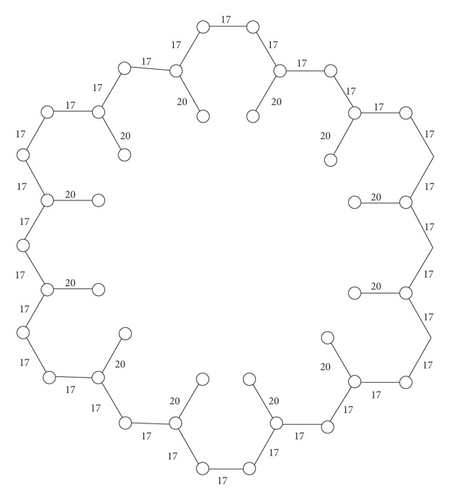
Step B. Label all of the remaining edges from L₂ by using Algorithm 2, i.e., K₄ = (S₄ + 2 − 2K₃)/2 = (72 + 2 − 2.17)/2 = 20 (see Figure 11)
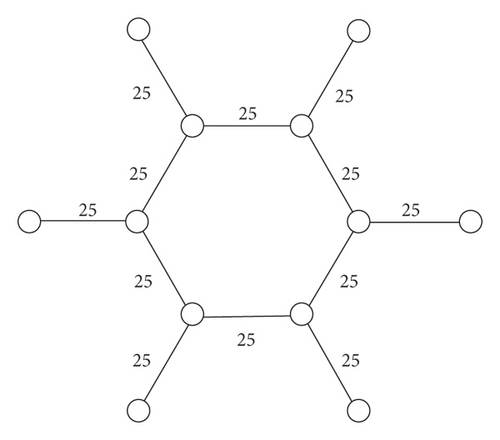
Step C. Label all of the remaining edges in HC(4) by (3.4² + 1)/2 = 25 (see Figure 12)

4. Conclusions

In this paper, we obtained the precise values for the total vertex irregularity strength of the hexagonal cluster graphs HC(n), for all n ≥ 2. Furthermore, we show that the hexagonal cluster graphs HC(n) is an example that the lower bound in \cite{BJMR07} is sharp. In the future, we are interested in computing the exact value for the total vertex (or edge) irregularity strength of grids, hexagonal networks, and honeycombs networks.

Conflicts of Interest

The author(s) declare that they have no conflicts of interest regarding the publication of this paper.

Acknowledgments

This research was supported by the Basic Science Research Program, National Research Foundation of Korea, Ministry of Education, (NRF-2018R1D1A1B07049584) and Basic Research Superior College, Directorate of Research and Community Service, Ministry of Research, Technology and Higher Education, Republic of Indonesia (007/SP2H/AMD/LT/DRPM/2020).

Open Research

Data Availability

The data used to support the findings of this study are included within the article.

References

1 Chartrand G., Jacobson M. S., Lehel J. et al., Irregular networks, Congressus Numerantium. (1988) 81, 113–119.
Google Scholar
2 Baca M., Jendrol S., Miller M., and Ryan J., On irregular total labellings, Discrete Mathematics. (2007) 307, 1378–1388.
10.1016/j.disc.2005.11.075
Web of Science® Google Scholar
3 Nurdin, Salman A. N. M., Gaos N. N., and Baskoro E. T., On the total vertex-irregular strength of a disjoint union of tcopies of a path, Journal of Combinatorial Mathematics and Combinatorial Computing. (2009) 71, 227–233.
Google Scholar
4 Nurdin E. T. B., Salman A. N. M., and Gaos N. N., On the total vertex irregularity strength of trees, Discrete Mathematics. (2010) 71, 227–233.
Google Scholar
5 Nurdin, Zakir M., and Firman, Vertex-irregular labeling and vertex-irregular total labeling on caterpillar graph, International Journal of Applied Mathematics and Statistics. (2013) 40, no. 10, 99–105.
Google Scholar
6 Nurdin and Kim H. K., Irregular labeling on transportation network of splitting graphs of stars, Proceedings of the Jangjeon Mathematical Society. (2019) 22, no. 1, 103–108.
Google Scholar
7 Al-Mushayt O. and Ahmad A., On the total edge irregularity strength of hexagonal grid graphs, Australasian Journal of Combinatorics. (2012) 53, 263–271.
Google Scholar
8 Rajasingh I. and Arockiamary S. T., Total edge irregularity strength of honeycomb torus networks, Global Journal of Pure and Applied Mathematics. (2017) 13, no. 4, 1135–1142.
Google Scholar
9 Sedlacek J., Problem 27 in thoery of graphs and its applications, Proceedings of the Symposium Smolenice. (1963) 163–167.
Google Scholar
10 Stojmenovic I., Honeycomb networks: topological properties and communication algorithms, IEEE Transactions on Parallel and Distributed Systems. (1997) 8, no. 10, 1036–1042, https://doi.org/10.1109/71.629486, 2-s2.0-0031248377.
10.1109/71.629486
Web of Science® Google Scholar
11 Tarawneh I., Hasni R., and Ahmad A., On the edge irregularity strength of grid graphs, AKCE International Journal of Graphs and Combinatorics. (2020) 17, no. 1, 414–418, https://doi.org/10.1016/j.akcej.2018.06.011, 2-s2.0-85049632388.
10.1016/j.akcej.2018.06.011
Web of Science® Google Scholar

Citing Literature

All articles

On Total Vertex Irregularity Strength of Hexagonal Cluster Graphs

Abstract

1. Introduction

2. Hexagonal Cluster Graph

3. Results and Discussion

4. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

On Total Vertex Irregularity Strength of Hexagonal Cluster Graphs

Abstract

1. Introduction

2. Hexagonal Cluster Graph

3. Results and Discussion

4. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information