For the dynamic adjustment strategy of intelligent rail guide vehicle, the dynamic planning model has been built with the longest working time in the paper. In solving this problem, the longest target of the rail guide vehicles’ running time is converted to find the optimal moving path of the rail guide vehicles. Drawing on the shortest path idea, the model uses the Floyd algorithm and the simulated annealing algorithm. The longest running time of the rail guide vehicles in the model is the innovation point in the paper. When the rail guide vehicles path is optimal, when the rail guide vehicles is the busiest, the system is the most efficient.

1. Introduction

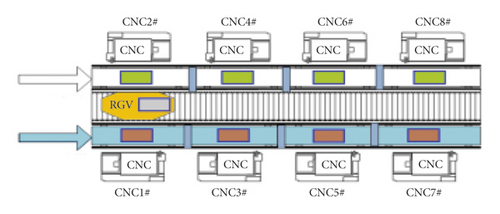
In Figure 1, the intermediate equipment is a rail guide vehicle with a cleaning groove and a manipulator. Rail guide vehicle is abbreviated as RGV. A cleaning groove washes only a material at a time. There are two claws at the front of the manipulator; through rotation, it can grab one material each to complete the loading and unloading operation. Computer number controllers are arranged on both sides [1–3]. Computer number controller is abbreviated as CNC. A material conveyor belt is installed in front of each CNC. The loading conveyor belt is on the right and is responsible for delivering unprocessed material to the CNC. The unloading conveyor belt is on the left and is responsible for sending the processed and cleaned material out of the system [4, 5]. Other auxiliary equipment is designed to ensure the normal operation of the system [6–8].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Workshop layout diagram of RGV—CNC.

RGV is an abbreviation for rail guide vehicles. With the rapid development of the industrial age, the mechanization of industry becomes more and more frequent. According to the demand of different industrial processing, RGV can be designed to run the track rail for the longest time [9–11]. In the process of industrial operation, the reduction of personnel improves the safety, is not affected by the special circumstances such as time and space, effectively improves the efficiency of industrial processing, promotes industrial production, and maximizes the profits obtained by industrial manufacturers [12–14]. These are inseparable from intelligent processing systems. At the same time, intelligent machinery also needs to be improved artificially [4, 5]. RGV has an intelligent control capability to receive and send command signals [15–18].

Figure 2 shows the schematic figure about intelligent machining system of rail guide vehicle. There are eight computer number controllers (CNCs), a rail guide vehicle(RGV), and two conveyor belts for materials. The rail guide vehicle is an intelligent machine. It does not need to be run by people [19–21]. It can run freely on a fixed track. According to the instruction, it can automatically control the moving direction and distance. There are one mechanical arm, two mechanical claws, and a material cleaning tank in a rail guide vehicle. It can finish some tasks like loading, unloading, and cleaning material [22–25].

2. Material Processing in a Process

First of all, only one-process material processing situation is considered, and a model that can make RGV work more efficiently is established. To make RGV work most efficiently, we assume that RGV is moving all the time for eight hours of a shift, and when multiple CNCs send a demand signal to the RGV, the RGV chooses to work on the nearest CNC to it. From this, we transform the time problem into the displacement problem, which can simplify the RGV dynamic scheduling model and the corresponding solution algorithm to the problem of finding the longest running time of the rail guide vehicle. The cyclic dynamic programming model is established firstly. Then, the MATLAB software is used to program and solve the problem. Finally, the MATLAB software is used to find out the path that makes the RGV work most efficiently.

2.1. Cyclic Dynamic Programming Model

(1)
Four phases: the first stage comprises the first CNC and the second CNC. The second stage comprises the third CNC and fourth CNC. The third stage comprises the fifth CNC and sixth CNC. The fourth stage comprises the seventh CNC and eighth CNC.
(2)
Selecting state S_k:
(1)
(3)
Determining strategies μ_k(s_k): RGV units of movement are represented for 1, 2, 3 or −1, −2, −3.
(4)
Decision value ν_k(S_k): working hours of RGV = movement time of RGV + loading, cleaning, and discharging time of CNC#k and CNC#k + 1.
(5)
Writing the state transition equation:
(2)
(6)
Establishing index function f_1k(S_k): RGV working times from the initial moment to the end of this phase.
(7)
Establishing objective function:

(3)

After eight hours, it eventually stops at a certain stage.

2.2. Floyd Algorithm

Through the Floyd algorithm, the shortest path time of each vertex is calculated in the graph G = (V, E). If w(i, j) is represented for the realizable distance between i and j, w(i, j) is represented for the shortest distance between i and j. For, for any i, j, k, there is w(i, j) ≤ w(i, k) + w(k, j). The algorithm is represented by matrix and calculated systematically. By iteration, the situation by which the above theorem is not satisfied is eliminated. Each n-n matrix E and matrix R in order for a graph can be calculated with a given edge length d_ij at n ports. d_ij in the matrix W is represented for the distance from the i vertex to the j vertex. d_ij in the matrix P is represented for the distance from the i vertex to the j vertex (vertex represented by recorded values b_ij), i.e., a transfer route.

The steps are as follows:

Step 1. F₀:
(4)
Step 2. F₁: if we know W^{(k − 1)}and R⁽ⁿ⁾, we may solve as follows.
(5)
Step 3. F₂: if k ＜ n, repeat F₁. If k = n, end.

If can shorten the length of the road, is changed and noted in the R matrix. Finally, we can obtain W⁽ⁿ⁾and R⁽ⁿ⁾. The shortest path length and transfer route are obtained.

2.3. Solution of Floyd Algorithm

(1)
A matrix sequence B₁, …, B_k, …, B₈ is recursively generated. Line i, column j elements of the matrix A_{k(i, j)} represent the shortest path length in which the number of vertex passing through the path is not greater than k from vertex v_i to vertex v_j. The iteration formula used in the calculation is as follows.
(6)
(2)
When k = n, B_n is the ordinal number of passing vertices through the shortest path between vertices.

Step 1. The two matrices are initialized, and matrix W is obtained as shown in Table 1 and matrix P is obtained as shown in Table 2.
Step 2. By the iterative formula (1), the number of iterations is 8 by using the MATLAB equation.
Step 3. It can be concluded that when only one-process material processing operation is considered, B₈(number of iterations is 8) is the serial number of the vertices passing through the shortest path between the vertices.

Table 1. Matrix W: the distance between two CNCs in RGV motion.

	CNC1	CNC2	CNC3	CNC4	CNC5	CNC6	CNC7	CNC8
CNC1	ν₁₁	ν₁₂	ν₁₃	ν₁₄	ν₁₅	ν₁₆	ν₁₇	ν₁₈
CNC2	ν₂₁	ν₂₂	ν₂₃	ν₂₄	ν₂₅	ν₂₆	ν₂₇	ν₂₈
CNC3	ν₃₁	ν₃₂	ν₃₃	ν₃₄	ν₃₅	ν₃₆	ν₃₇	ν₃₈
CNC4	ν₄₁	ν₄₂	ν₄₃	ν₄₄	ν₄₅	ν₄₆	ν₄₇	ν₄₈
CNC5	ν₅₁	ν₅₂	ν₅₃	ν₅₄	ν₅₅	ν₅₆	ν₅₇	ν₅₈
CNC6	ν₆₁	ν₆₂	ν₆₃	ν₆₄	ν₆₅	ν₆₆	ν₆₇	ν₆₈
CNC7	ν₇₁	ν₇₂	ν₇₃	ν₇₄	ν₇₅	ν₇₆	ν₇₇	ν₇₈
CNC8	ν₈₁	ν₈₂	ν₈₃	ν₈₄	ν₈₅	ν₈₆	ν₈₇	ν₈₈

Table 2. Matrix P: passing vertices between two CNCs.

	CNC2	CNC3	CNC4	CNC5	CNC6	CNC7	CNC8
CNC1	1	2	3	4	5	6	7
CNC2	1	2	3	4	5	6	7
CNC3	1	2	3	4	5	6	7
CNC4	1	2	3	4	5	6	7
CNC5	1	2	3	4	5	6	7
CNC6	1	2	3	4	5	6	7
CNC7	1	2	3	4	5	6	7
CNC8	1	2	3	4	5	6	7

2.4. Testing the Practicability of the Model and the Effectiveness of the Algorithm

The intelligent processing system is used to obtain three sets of data of operation parameters as shown in Table 3.

Table 3. Three sets of data of operation parameters of the intelligent processing system (unit of time is seconds).

System operation parameters	Group 1	Group 2	Group 3
RGV time required to move 1 unit	20	23	18
RGV time required to move 2 units	33	41	32
RGV time required to move 3 units	46	59	46
CNC material requirement time to finish a process	560	580	545
RGV time required for one loading and discharging to CNC1#, CNC3#, CNC5#, CNC7#	28	30	27
RGV time required for one loading and discharging to CNC2#, CNC4#, CNC6#, CNC8#	31	35	32
RGV time required to complete a material cleaning operation	25	30	25

On the basis of the established cyclic dynamic programming model, three groups of data in Table 3 are put into the program by Floyd algorithm and MATLB software, respectively. RGV scheduling strategy and work efficiency tables for one process to 3 groups can be obtained as shown in Table 4.

Table 4. RGV scheduling strategy and work efficiency for one process for 3 groups.

Group	RGV scheduling strategy	Number of processed materials	Work efficiency
Group 1	4—6—5—8—7—1—2—3	405	50.62
Group 2	5—4—3—1—2—8—7—6	390	48.75
Group 3	1—2—3—4—5—6—7—8	417	52.12

2.5. Consideration of Occurring Failures

During processing, CNC may fail. According to statistics, the probability of failure is about 1%. Unfinished materials are scrapped if handled manually. The time for each troubleshooting is between 10 and 20 minutes. Operation sequence is immediately run after troubleshooting.

2.5.1. Circular Dynamic Programming Model

(1)
Four phases: the first stage comprises the first CNC and the second CNC. The second stage comprises the third CNC and fourth CNC. The third stage comprises the fifth CNC and sixth CNC. The fourth stage comprises the seventh CNC and eighth CNC.
(2)
Selecting state S_k:
(7)
(3)
Determining strategies μ_k(s_k): RGV units of movement are represented for 1, 2, 3 or −1, −2, −3.
(4)
Decision value ν_k(S_k): working hours of RGV = movement time of RGV + loading, cleaning, and discharging time of CNC#k and CNC#k + 1.
(5)
Writing the state transition equation:
(8)
(6)
Establishing index function f_1k(S_k): RGV working hours from the initial moment to the end of this phase.
(7)
Establishing objective function:

(9)

After eight hours of constraint, it eventually stops at a certain stage.

2.5.2. Solution of the Model

From the establishment of the model, it can be found that the model is the same when the fault occurs and when the fault does not occur, but the algorithm should be changed when the MATLAB software is used to calculate.

The specific approach is as follows.

A random number producer is set up, which is assigned to each machining table according to equal probability. When the RGV rotates to the faulty machining table, only the RGV motion time is considered, not the time of feeding, discharging, and cleaning RGV.

Through the Floyd algorithm and the MATLB software, the three groups of data in Table 3 are substituted into the program. We can get three sets of data on material processing failures. In one process, the first set of data on material processing failures is shown in Table 5.

Table 5. The first set of data on material processing failures.

Material serial number	CNC number	Start time	Closing time
53	7	3720	0
61	7	0	4874
266	6	19117	0
274	6	0	20271
362	6	26041	0
370	6	0	27195
380	8	27324	0
388	8	0	28478

3. Material Processing in Two Processes

Each material’s first and second processes are processed by two different CNCs in turn. According to the problem analysis of the material processing operation of only one working procedure, the RGV dynamic scheduling model and the corresponding algorithm problem are obtained, which include the material processing operation of two working procedures. The dynamic scheduling model with the highest working efficiency is established. If the process of material requires two processes, it is necessary to have different CNCs to install different tools to complete the processing; the tool cannot be replaced during processing. The first and second processes need to be processed in turn on different CNCs, and the completion time is different. Each CNC can only complete one of them. Through analysis, it is decided to use odd-number CNC to process the first process and even-number CNC to process the second process. The two-dimensional dynamic programming model is established by the method of partition processing under the condition that only one working procedure is considered.

3.1. Setting Up a Two-Dimensional Dynamic Programming Model considering the Material Processing in Two Processes

(1)
First of all, it is assumed that CNC#m(m = 1,2,3,4,5,6,7,8) is installed as follows. CNC#m(m = 1,3,5,7) was installed as the first procedure. CNC#m(m = 1,3,5,7) was installed as the second procedure.
(2)
k phase variables are set, k = 1,2,3,4,5,6,7,8.
(3)
The state variable is set to CNC#k state. The state variable is set to CNC#k + 1 state.
(4)
Policy variables are and . means that the RGV unit of movement is 1, 2, 3. means that the RGV unit of movement is −1, −2, −3.
(5)
Decision variables are and . RGV working hours = RGV movement time+CNC#k and CNC#k + 1 feeding, cleaning, and discharging time.
(6)
State transfer equation:
(10)
(7)
Setting up the index function : represents RGV working hours from inception to the end of the phase.
(8)
Establishing objective function:

(11)

3.2. Establishing a Simulated Annealing Algorithm by considering the Processing of Two Materials

(1)
Assuming the energy of the material is E(i) under state i, then the material entering from state i to state j follows the following rule.
- If E(j) ≤ E(i), we accept that the state is converted.
- If E(j) > E(i), the probability of the acceptance of the state is e^{(E(i)−E(j)/KT)}.
(2)
Probabilities in state i satisfy the Boltzmann distribution.

(12)

Obviously,

(13)

This suggests that all states have the same probability at high temperatures. When the temperature drops, there is

(14)

The above formula shows that when the temperature drops to very low, the material enters the minimum energy state with a high probability. The problem to be solved is an optimization problem seeking a minimal path, so the simulated annealing optimization method is obtained by applying the path optimization problem in physics to the simulated annealing optimization problem in this problem.

3.3. Solving Simulated Annealing Algorithm by considering the Material Processing Situation of Two Processes

(1)
First, an initial journey T₀ and an initial solution x(0) to the optimization problem are given. x(0) generate the next solution x^′(x^′ ∈ N[x(0)]). When it gets satisfied on the following probability, x^′ is a new solution x(1):
(15)
(2)
For a certain journey T_i and a solution x(k) to the optimization problem, x^′ can be generated. When it satisfy on the following probability, x^′ is a new solution x(k + 1):

(16)

Under the journey T_i, after many transfers, we found the journey T_i+1 < T_i. Under the conditions T_i+1, the above process is repeated. We constantly find the new solution and the alternate process of the last journey. Finally, the optimal solution is obtained with the shortest distance within 8 hours of continuous operation in each shift.

3.4. Solution of Material Processing Model in Two Processes

According to the simulated annealing algorithm model, by replacing the three groups of data in Table 3 with the MATLB software, we can obtain the working time of the material processing as shown in Table 6.

Table 6. The working time of the material processing.

Material serial number	CNC number in process 1	Starting time	Closing time	CNC number in process 2	Starting time	Closing time
197	1	27685	28250	2	28285	28850
198	3	27768	28333	4	28398	28963
199	5	27881	28446	6	28511	29076
200	7	27994	28559	8	28624	29189
201	1	28250	28815	2	28850
202	3	28333	28898	4	28963
203	5	28446	29011	6	29076
204	7	28559	29124	8	29189
205	1	28815
206	3	28898
207	5	29011
208	7	29124

Using the annealing algorithm, RGV scheduling strategy can be obtained as shown in Table 7 and work efficiency can be obtained as shown in Table 8 for 3 groups for two processes.

Table 7. RGV scheduling for 3 groups for two processes.

Group	RGV scheduling strategy in process 1	RGV scheduling strategy in process 2
Group 1	1—3—5—7	2—4—6—8
Group 2	1—3—5—7	2—4—6—8
Group 3	5—7—1—3	2—4—6—8

Table 8. Work efficiency for 3 groups for two processes.

Group	Number of processed materials	Work efficiency
Group 1	197	24.625
Group 2	198	24.75
Group 3	198	24.75

It is seen from Table 4 and 8 that within one working day, the number of two processing processes is reduced by about half, but the work efficiency tends to be stable, and the material processing situation of the three groups of data is maintained at about 24 times per hour.

4. Considering Only the Failure of One-Process Material Processing

4.1. Establishing a Fault Model during Material Processing

(1)
Four stages: the first stage comprises the first CNC and the second CNC. The second stage comprises the third CNC and fourth CNC. The third stage comprises the fifth CNC and sixth CNC. The fourth stage comprises the seventh CNC and eighth CNC.
(2)
Selecting state S_k:
(17)
(3)
Determining strategies μ_k(s_k): RGV units of movement are represented for 1, 2, 3 or −1, −2, −3.
(4)
Decision value ν_k(S_k): working hours of RGV = movement time of RGV + loading, cleaning, and discharging time of CNC#k and CNC#k + 1
(5)
Writing the state transition equation:
(18)
(6)
Establishing index function f_1k(S_k): RGV working hours from the initial moment to the end of this phase.
(7)
Establishing objective function:

(19)

After eight hours of constraint, it eventually stops at a certain stage.

4.2. Material Processing Fault Model of One Process for Solution

From the establishment of the model, the model is the same as that without failure, but the algorithm should be changed when using MATLAB software.

Specific practice is to set up a random number producer, assigned to each processing table by equal probability. When the RGV turns to the faulty processing table, consider only the RGV movement time, not the RGV loading, unloading, and cleaning material time. For example, 1% probability is generated by the number of intervals setting [1,100]. Assuming a number like 50, you can specify which CNC fails.

According to the established cyclic dynamic planning model, the Floyd algorithm uses MATLB software, and the obtained data are given in Table 9.

Table 9. Material processing failure in one process.

Material serial number during a failure	CNC number during a failure	Starting time during a failure	End of the time during a failure
53	7	3720	0
61	7	0	4874
266	6	19117	0
274	6	0	20271
362	6	26041	0
370	6	0	27195
380	8	27324	0
388	8	0	28478

Table 9 shows that there are four failed CNCs during processing one material process.

5. Material Processing Fault Model for Two Processes

5.1. Establishing a Material Processing Fault Model for Two Processes

(1)
First of all, it is assumed that CNC#m(m = 1,2,3,4,5,6,7,8) is installed as follows. CNC#m(m = 1,3,5,7) was installed as the first procedure. CNC#m(m = 1,3,5,7) was installed as the second procedure.
(2)
We set k phase variables, k = 1,2,3,4,5,6,7,8.
(3)
The state variable is set to CNC#k state. The state variable is set to CNC#k + 1 state.
(4)
Policy variables are and . means that the RGV unit of movement is 1,2,3. means that the RGV unit of movement is −1, −2, −3.
(5)
Decision variables are and .
RGV working hours = RGV movement time+CNC#k and CNC#k + 1 feeding, cleaning, and discharging time.
(7)
State transfer equation:
(20)
(8)
Setting up the index function : represents RGV working hours from inception to the end of the phase.
(9)
Establishing objective function:

(21)

5.2. Solution of the Material Processing Fault Model for the Two Processes

According to the established cyclic dynamic planning model and calculated using MATLB software by the Floyd algorithm, the results are given in Table 10.

Table 10. Material processing failure in the two processes.

Material serial number during a failure	CNC number during a failure	Starting time during a failure	End of the time during a failure
90	3	10180	0
94	3	0	0
98	3	0	11557
211	5	24060	0
215	5	0	0
219	5	0	25437
86	4	10239	0
90	4	0	0
94	4	0	11616
207	6	24119	0
211	6	0	0
215	6	0	25496

According to the table, when processing two material processes, there are four failed CNCs, each with three CNC numbers.

6. Summary

The cyclic dynamic planning model with the longest running time and the dynamic planning model are established in the paper. Using the most short circuit idea, the longest running time is transformed to find the optimal moving path of the track car.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

No data were used to support this study.

References

1 Wu Y., Liu Y., Zhang D., and Han Z., Study on the dynamic scheduling of RGV based on genetic algorithms, Lift Transport Machinery. (2012) 6, 20–23.
Google Scholar
2 Liu Y., Study on the Dynamic Scheduling of RGV Based on Genetic Algorithms, 2012, Hefei University of Technology, Hefei, China.
Google Scholar
3 Chen H. and Sun Q., Study on the linear reciprocating 2-RGV system scheduling based on the TS algorithm, Industrial Engineering and Management. (2015) 20, no. 05, 80–88.
Google Scholar
4 Chen H., Model and algorithm for 2-RGV scheduling problems based on the partition method, Industrial Engineering and Management. (2014) 19, no. 6, 70–77.
Google Scholar
5 Zha Z., Li J., and Sheng R., Application of intelligent translation rail guide vehicle, Robotics Technology and Application. (2017) 5, 42–43.
Google Scholar
6 Gu H., Zou P., and Xu W., Self-learning algorithm for optimizing the scheduling problem of the circular shuttle vehicle, The Theory and Practice of System Engineering. (2013) 33, no. 12, 3223–3230.
Google Scholar
7 Shi A., Li L., Xue S., and Shao B., Research on the dynamic scheduling problem of intelligent RGV-CNC, Computer and Digital Engineering. (2021) 49, no. 04, 760–765.
Google Scholar
8 Wang S., The RGV dynamic scheduling model based on the Memetic algorithm, Journal of Shanxi Datong University (Natural Science Edition). (2021) 37, no. 01, 37–40.
Google Scholar
9 Jing B., Dynamic scheduling strategy for smart RGV, Electronic Testing. (2020) 21, 64–65.
Google Scholar
10 Wei W., Yang Z., Xie H., and Hu Y., Intelligent RGV dynamic scheduling of the multi-objective planning model, Computer Applications and Software. (2020) 37, no. 04, 178–185.
Google Scholar
11 Zhou L., Zeng Y., Xie G., and Li J., Intelligent RGV dynamic scheduling strategy based on multi-objective optimization, Automation Applications. (2020) 6, 55–58.
Google Scholar
12 Li Y., Cai L., Jia R., Zhang Y., and Zhu X., Intelligent RGV dynamic scheduling strategy based on the DP-FCFS algorithm, Journal of Chengdu Institute of Technology. (2020) 23, no. 02, 48–53.
CAS Google Scholar
13 Niu Y., Study on the intelligent RGV scheduling strategy for two processes, Modern Trade Industry. (2020) 41, no. 17, 194–196.
Google Scholar
14 Wei D., Hao E., and Wu Y., Two-process processing policies for smart RGV, Electronic Devices and Information Technology. (2020) 4, no. 03, 78–79.
Google Scholar
15 Li S., Dynamic scheduling strategy for intelligent RGV based on a greedy algorithm, Scientific and Technological Innovation and Application. (2020) 6, 16–17.
CAS Google Scholar
16 Li J., Intelligent RGV dynamic scheduling policy for the FMS two-process system considering random failures, Industrial Control Computers. (2020) 33, no. 02, 117–120.
Google Scholar
17 Du Y., Feng M., Li J., and Fang R., Dynamic scheduling strategy for smart RGV, Shantou University Journal (Natural Science Edition). (2020) 35, no. 01, 54–65.
Google Scholar
18 Yao X., Liu Y., and Liu J., Dynamic scheduling strategy based on a single-process intelligent processing system, Ordnance Automation. (2020) 39, no. 01, 35–39.
Google Scholar
19 Qiao X., Dynamic scheduling strategy for smart RGV, Journal of Nanning Normal University (Natural Science Edition). (2019) 36, no. 04, 40–44.
Google Scholar
20 Zeng Q. and Qi F., RGV dynamic scheduling policy based on computer simulation failure, Engineering Construction and Design. (2019) 19, 165–166.
Google Scholar
21 Yuan M., Yang I., Sun R., and Lv P., Dynamic scheduling strategy for RGV in a circular intelligent processing system, Value Engineering. (2019) 38, no. 27, 43–45.
Google Scholar
22 Zhang M., Chen M., Wang X., and Zhuang L., Research on intelligent RGV dynamic scheduling strategy for multi-objective optimization and simulation, China New Communications. (2019) 21, no. 18.
Google Scholar
23 Yao T. and Xu N., Dynamic scheduling strategy for smart RGV, Computer Knowledge and Technology. (2019) 15, no. 22, 270–273.
Google Scholar
24 Zhou Y., Li Y., Zuo M., and Li Y., Research on the dynamic scheduling strategies of intelligent RGV, Journal of Qiqihar University (Natural Science Edition). (2019) 35, no. 05, 72–77.
Google Scholar
25 Zhu Z. and Meng X., Modeling and optimization of RGV dynamic scheduling based on particle group algorithm and simulation technology, Mechanical and Electronic Information. (2019) 18, 98–101.
Google Scholar

Citing Literature

All articles

Dynamic Adjustment Strategy of Rail Guide Vehicle

Abstract

1. Introduction

2. Material Processing in a Process

2.1. Cyclic Dynamic Programming Model

2.2. Floyd Algorithm

2.3. Solution of Floyd Algorithm

2.4. Testing the Practicability of the Model and the Effectiveness of the Algorithm

2.5. Consideration of Occurring Failures

2.5.1. Circular Dynamic Programming Model

2.5.2. Solution of the Model

3. Material Processing in Two Processes

3.1. Setting Up a Two-Dimensional Dynamic Programming Model considering the Material Processing in Two Processes

3.2. Establishing a Simulated Annealing Algorithm by considering the Processing of Two Materials

3.3. Solving Simulated Annealing Algorithm by considering the Material Processing Situation of Two Processes

3.4. Solution of Material Processing Model in Two Processes

4. Considering Only the Failure of One-Process Material Processing

4.1. Establishing a Fault Model during Material Processing

4.2. Material Processing Fault Model of One Process for Solution

5. Material Processing Fault Model for Two Processes

5.1. Establishing a Material Processing Fault Model for Two Processes

5.2. Solution of the Material Processing Fault Model for the Two Processes

6. Summary

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Dynamic Adjustment Strategy of Rail Guide Vehicle

Abstract

1. Introduction

2. Material Processing in a Process

2.1. Cyclic Dynamic Programming Model

2.2. Floyd Algorithm

2.3. Solution of Floyd Algorithm

2.4. Testing the Practicability of the Model and the Effectiveness of the Algorithm

2.5. Consideration of Occurring Failures

2.5.1. Circular Dynamic Programming Model

2.5.2. Solution of the Model

3. Material Processing in Two Processes

3.1. Setting Up a Two-Dimensional Dynamic Programming Model considering the Material Processing in Two Processes

3.2. Establishing a Simulated Annealing Algorithm by considering the Processing of Two Materials

3.3. Solving Simulated Annealing Algorithm by considering the Material Processing Situation of Two Processes

3.4. Solution of Material Processing Model in Two Processes

4. Considering Only the Failure of One-Process Material Processing

4.1. Establishing a Fault Model during Material Processing

4.2. Material Processing Fault Model of One Process for Solution

5. Material Processing Fault Model for Two Processes

5.1. Establishing a Material Processing Fault Model for Two Processes

5.2. Solution of the Material Processing Fault Model for the Two Processes

6. Summary

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information