With the proliferation of wireless communication and mobile devices, various location-based services are emerging. For the growth of the location-based services, more accurate and various types of personal location data are required. However, concerns about privacy violations are a significant obstacle to obtain personal location data. In this paper, we propose a local differential privacy scheme in an environment where there is no trusted third party to implement privacy protection techniques and incentive mechanisms to motivate users to provide more accurate location data. The proposed local differential privacy scheme allows a user to set a personalized safe region that he/she can disclose and then perturb the user’s location within the safe region. It is the way to satisfy the user’s various privacy requirements and improve data utility. The proposed incentive mechanism has two models, and both models pay the incentive differently according to the user’s safe region size to motivate to set a more precise safe region. We verify the proposed local differential privacy algorithm and incentive mechanism can satisfy the privacy protection level while achieving the desirable utility through the experiment.

1. Introduction

With the development of wireless communication technology and widespread of mobile devices, various location-based services are emerging. For example, Dark Sky [1] offers hyperlocal forecasts for an exact address, with down-to-the-minute notifications about changing weather conditions. Curbside [2] is the shopping app using the customer’s location information. When the user uses the curbside service, the user gets a notification that the order is ready, and the retailer/restaurant gets an alert when the customer arrives.

There are various techniques [3–8] researched for the proliferation of LBS, and acquiring the good quality of personal location data is one of the essential elements in the LBS. However, there is a risk that personal location data may cause serious privacy violations such as lifestyle exposure or stalking. Users who are threatened by privacy violations do not want to provide their accurate location data. It is one of the biggest obstacles to use more accurate personal location information. Many research studies have been carried out to solve this privacy violation [9–23], and differential privacy, which is accepted as a de facto standard among the privacy protection techniques, is being studied to protect the privacy of personal location data.

Existing differential privacy is based on the assumption that a trustworthy third party performs the perturbation process. However, it is not suitable for real-world applications because the trusted third party is an overly strong assumption. Therefore, local differential privacy (LDP), in which data owners randomly perturb their data to guarantee the plausible deniability without the trusted data curator, has been proposed. However, LDP has a disadvantage that the data utility is lower than the central DP (CDP). Thus, this limitation should be solved to apply LDP in the real world.

In this paper, we propose a local differential privacy scheme to protect the data owner’s location data in an environment where there is no trustworthy third party to perform privacy protection. The proposed local differential privacy scheme allows a data owner to set a publicly available region and apply differential privacy to the data owner’s location data within the region. For example, a certain data owner does not mind to disclose the information that he/she is located in New York. In this case, the goal of differential privacy is to ensure that the data owner’s exact location cannot be distinguished from any other location within New York. We call the region that the data owner set to be publicly open as a safe region, and the differential privacy is applied only for the location within the safe region (Figure 1).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The example of a safe region. In this map, users A, B, C, and D have different sizes of safe region.

In addition, we propose an incentive mechanism that motivates the data owner to provide more accurate location data. In terms of the proposed LDP scheme with the safe region, how to set the safe region size is a major factor in the privacy protection level and data utility. Thus, the data consumer pays the incentive to motivate the data owner to set a safe region as accurate as possible to maximize their profit. We propose the two types of incentive mechanisms to determine the incentive and safe region size. One is the incentive mechanism that maximizes the data consumer’s profit, and the other is to optimize the profit of both the data owner and consumer.

The contributions of this paper are as follows:

(1)
Personalized local differential privacy based on the safe region: in the proposed local differential privacy scheme, each data owner sets a safe region to reflect their own privacy sensitivity and the incentive. The safe region size is set differently for each data owner. Thus, personalized privacy protection is possible.
(2)
Adaptive grid size considering population density: we suggest an adaptive size grid configuration technique considering population density in the area to minimize the unnecessary error. By this scheme, we can improve the data utility while satisfying the privacy protection requirements.
(3)
Incentive mechanism for profit optimization: we propose an incentive mechanism that can determine the safe region size considering the profit between the data owner and the data consumer. The proposed incentive mechanism has two types: a principal-agent model that maximizes a data consumer’s profit, and the Stackelberg model that negotiates the incentive to maximize a data owner and consumer’s profit.

The structure of the paper is as follows. In Section 2, we describe the related works and the existing work’s limitation. In Section 3, we introduce the proposed local differential privacy scheme and incentive mechanism. In Section 4, we verify the proposed method through experiments. In Section 5, we discuss the conclusions and future research studies.

2. Related Works

2.1. Differential Privacy

Differential privacy is a privacy protection mechanism that prevents private information exposure, which is proposed by Dwork [9]. Dwork defined a mathematical model to prevent information exposure, which ensures privacy protection at a specified level ε. Given two neighboring databases, D₁ and D_2, which differ by only one record, a randomized function K provides ε-differential privacy if all datasets with D₁ and D₂ differ by one element only and all O Range (K), i.e.,

(1)

This description of differential privacy means that specific individuals in the statistical database cannot be deduced correctly by keeping the probability of a change in query results by inserting/deleting one data to be less than e^ε.

According to the definition, the value of ε which is called the privacy budget affects the amount of added noise. As ε decreases, the privacy protection is enhanced. Conversely, as ε increases, the degree of privacy protection decreases.

The most widely used technique for inserting noise to satisfy differential privacy is the Laplace mechanism using the Laplace distribution. Let ƒ (D) denote a function of database D. An ε-differentially private Laplace noise mechanism is defined as L (D) = ƒ (D)+X, where X is a random variable drawn from the Laplace distribution and standard deviation = √2Δƒ/ε. The Laplace distribution is as follows:

(2)

Δf is the sensitivity of the function, which means that the maximum value of the change in the query results due to insertion/deletion of a specific individual, that is, the higher the sensitivity and the smaller ε are, the greater the probability that a larger noise is inserted.

One of the main properties of differential privacy [9] is that it allows composing of queries. Suppose that the algorithms K₁ and K₂ satisfy ε₁-DP and ε₂-DP, respectively. Then, K₁ and K₂ also satisfy the following properties:

Sequential composition: for any database D, the algorithm that performs K₁(D) and K₂(D) satisfies (ε₁ + ε₂)-DP.
Parallel composition: let A and B be the partition of any database D (A ∪ B = D, A∩B = ∅). Then, the algorithm that performs K₁(A) and K₂(B) satisfies the max (ε₁, ε₂)-DP.

2.2. Differentially Private Location Data

The research for differentially private location data has mainly been studied to protect the count estimation of users for cell-based locations. The utility of these studies is evaluated by the difference between the differentially count estimation in each cell and real count estimation for range query Q.

The study of [10] applied differential privacy by dividing the entire area into hierarchical grids. In this study, they propose two spatial decomposition techniques: kd-tree, which divides the area in consideration of the density, and quad-tree, which divides the region regardless of density. The study of [11] argues that the existing differential privacy mechanism is not suitable for location data because of the problem of excessive sensitivity when considering all the points of interest. They divide the entire location data into smaller local problems using a local quad-tree with differential privacy to provide better accuracy at the same differential privacy level. Qardaji et al. [12] proposed a uniform grid method (UG) and an adaptive grid approach (AG) to determine the optimal size of the grid cell that divides the region. In the UG scheme, each cell has the same size, but in the AG scheme, the size of each cell differs depending on the data distribution. Li et al. [13] proposed a range query method that determines the optimum size for partitioning the data domain considering the data distribution and calculates the count of each region considering the query workload. Li et al. [13] have verified that the proposed method is suitable for two-dimensional data through the experiment. Chen [14] is the first study to apply differential privacy to location data in a local setting. Chen [14] has defined a safe region taxonomically where the user feels safe to disclose and provide location perturbation method, which satisfies local differential privacy.

As we have seen, the application of differential privacy to location data has mainly focused on studies in the central setting. However, existing research cannot be applied to a local setting environment where there is no trustworthy data curator to carry out differential privacy. Although the local setting has a more realistic premise than the central setting, it is important to improve the utility in the local setting because it has the disadvantage of being less useful than the central setting in terms of data utility.

In this paper, we try to improve the utility in a local setting by determining the adaptive grid size considering the population density in each area. In addition to that, we propose an incentive mechanism that can motivate users to provide more accurate location data by paying an incentive.

2.3. Variation of Differential Privacy

Apple, Google, and Microsoft have introduced local differential privacy algorithms [15–17], and several studies try to apply existing CDP algorithms to local settings. The definition of local differential privacy is as follows.

Definition 1 (local differential privacy, see [18]). A randomized algorithm K satisfies ε-local differential privacy if, for any pair of values d and d’∈D and for any O ⊆ Range (K),

(3)

where the probability space is over the coin flips of K.

LDP has the advantage of not having a trusted third party that performs the DP, but it has the disadvantage of significantly reducing data utility compared to CDP. Especially, as the data domain size increases in LDP, the data utility is deteriorated because of the probability of reporting a noncorrect value by the randomization algorithm increases. For example, in the case of location data, if a country level is set as the data domain, data utility is much lower than for a city. Several techniques are proposed to avoid this problem in LDP, such as domain size reduction or fixed domain size using a hash function.

Another variation of DP is a personal DP (PDP). In general, DP applies the parameter ε, which determines the level of privacy protection to all personal data. PDP is a variation of DP that each data owner can personally set ε on the premise that each individual has a different privacy sensitivity. Ebadi et al. [19] defined the PDP that generalizes the definition of DP and proposed an interactive query system called ProPer to implement PDP. Jorgensen et al. [20] proposed a PDP technique that improved data utility while satisfying each user’s privacy requirements using the exponential mechanism. Chen [14] proposed a personalized LDP in which the user can select the size of the safe region that each individual allows disclosing the area where his or her is located.

PDP is proposed under the realistic assumption that each individual’s privacy sensitivity is different. Although PDP has the advantage of being able to meet each person’s privacy requirements while providing better data utility compared to existing DP, PDP needs to consider how to make criteria to determine each user’s privacy parameter. In this paper, we define the personalized LPD in which each user can set different safe regions according to each individual’s privacy sensitivity and propose an incentive mechanism to motivate the user to set the smaller safe region. Our Personalized LDP definition is as follows.

Definition 2 (personalized local differential privacy). Given the personalized privacy specification (τ, ε) of a data owner u and τ is the data owner u’s safe region size, a randomized algorithm K satisfies (τ, ε)-personalized local differential privacy (or (τ, ε)-PLDP) for u if, for any two locations l and l′ ∈ τ and any O ⊆ Range (K),

(4)

where the probability space is over the coin flips of K.

2.4. Pricing Mechanism

Along with the study of differential privacy itself, research has studied data pricing in consideration of the privacy protection level [24–30]. Jorgensen et al. [20] proposed a pricing function considering arbitrage-free and discount-free when the buyer queries the data. Ghosh and Roth [25] proposed a compensation mechanism in which data owner is rewarded based on data accuracy when they provide data with differential privacy. In the previous research, a data pricing mechanism sets the price according to the predefined query type or proceeds auction. However, these methods have limitations in determining price only from the data consumer’s perspective. Anke et al. and Rachana et al. [26, 31] suggested a mechanism to adjust the balance between privacy and cost in the data market environment. They consider the owner’s benefit, but it is still at an early stage.

The existing pricing mechanism focuses on data pricing according to ε value. In addition to the existing pricing mechanism for ε value, we propose an incentive mechanism based on safe regions to satisfy the PLDP definition. We propose the two incentive mechanisms in terms of the participant’s profit: one is the principal-agent model to maximize the data consumer’s profit; the other is the Stackelberg model which optimizes both the data owner and consumer’s profit.

3. Differentially Private Location Data in Local Setting and Pricing Mechanism

3.1. Overview

As described above, the proposed local differential privacy scheme determines the adaptive grid size by considering the density information of the area and satisfies PLDP definition by applying perturbation within a personal safe region, which is set by the user. To perform the proposed scheme, we need a user’s privacy sensitivity, density information, and incentive incentive_i,j. Unlike CDP, user’s privacy sensitivity and density information should be collected in the LDP environment. To this end, we design the proposed scheme in two phases to collect the necessary information from the user. An overview of the entire process is shown in Figure 2.

Step 1:
the data consumer divides the entire area into a uniform size grid and then sends the grid map to each user.
Step 2:
users perturb their location using a uniform size grid map and send perturbed location data to the data consumer.
Step 3:
the data consumer aggregates perturbed location data and then divides each uniform grid area into an adaptive grid size using the aggregated perturbed data. The data consumer sends the adaptive grid map, density information, and suggested incentive incentive_i,j to each user.
Step 4:
each user determines the safe region size using the adaptive grid map, density information, and incentive_i,j and sends the perturbed data within a safe region to the data consumer.
Step 5:
the data consumer estimates the total count estimation using the perturbed location information.

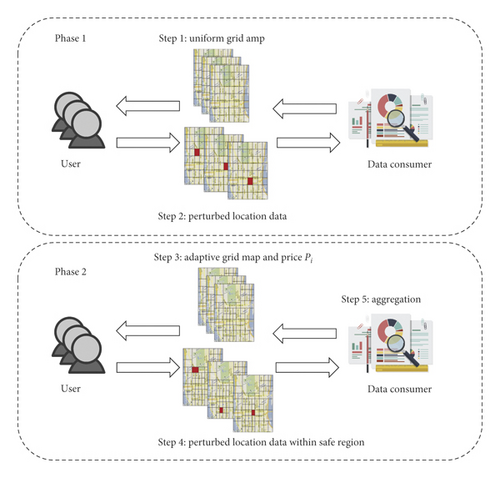
In the following sections, we describe each step in more detail. Section 3.2 describes the local differential privacy schemes, and Section 3.3 describes the proposed incentive mechanism. The notation used in this paper is as follows (Table 1).

Table 1. Key notation.

Key notations
C_i	i^th data consumer
P_j	j^th user
S_j	j^th user safe region
	i^th data consumer profit
	j^th user profit
incentive_i,j	Incentive by the i^th data consumer to the j^th user
util_i	i^th data consumer’s utility for j^th user data
θ_j	j^th user privacy sensitivity
p_cost_j	j^th user privacy cost
c_cost_j	j^th user communication cost
S_maxandS_min	Maximum/minimum size of safe region

3.2. Differentially Private Location Data in a Local Setting

3.2.1. Phase 1: Density Estimation for the Entire Area

The first step in the proposed local differential privacy scheme is to obtain the entire area’s density information. In the central setting, it is not necessary to collect the density information because it is already known. However, in the local setting, we should collect density information to determine the adaptive grid size. We split the entire budget to ε₁ and ε₂ and use ε₁ to collect the entire area’s density information and ε₂ to perturb user’s location within the safe region.

First, we divide the entire area into a uniform grid size. When we divide the area into the grid and apply the DP to location information, we should consider two types of error. The first one is caused by noise insertion for DP, and the other is a nonuniformity error that is caused by dividing the area into the grid. If the density of all areas is uniform, the nonuniformity error is 0, but if the density is skewed, this error increases, that is, if the size of the grid increases, the nonuniformity error increases. On the contrary, the error for DP reduces as the grid size increases because of the number of the grid in which noise is inserted by DP decreases. Thus, we need to set an appropriate grid size to minimize the sum of the two types of errors. In this paper, we follow Guideline 1, which is validated by Qardaji et al. [12] to minimize the sum of errors.

Guideline 1. In order to minimize the error in uniform grid size, the grid should be partitioned into m₁ × m₁ cells, where m₁ is computed as follows:

(5)

where N is the number of users in the entire area, ε₁ is the total privacy budget, and c is the small constant (usually c = 10) depending on the dataset.

After the data consumer sends the grid map to the user, users send the perturbed location using a uniform size grid map to the data consumer. We use the Hadamard count-min sketch data structure for the user’s location perturbation. The count-min sketch is the probabilistic data structure [30], which is mainly used for frequency estimation in data streaming environments where only a small fraction of elements have a high-frequency value. Our intuition is that the count-min sketch is suitable because location data is generally skewed in a specific area.

Hadamard transform is [32] a useful tool for reducing the communication cost and error. The Hadamard matrix H is defined recursively as follows:

(6)

where H₁ = [1] and i is power of two.

Note that the columns of H_i are orthogonal and .

Our randomizer takes as input an m-bit string represented as , and m could be any value that is large enough to satisfy the Johnson–Lindenstrauss Lemma (JL-Lemma).

Theorem 1 (Johnson–Lindenstrauss lemma). Given 0< η < 1, a set of V of m points in R^D, and a number n > 8 ln(m)/η², there is a linear map f: R^D⟶ R^d such that

(7)

for all u, v ∈ V.

The local randomizer and count estimation algorithm are given in Algorithm 1.

This local randomizer [25] guarantees the local differential privacy. We use this local randomizer in Algorithm 2.

Algorithm 2 is based on succinct histogram protocol [25], and we describe Algorithm 2. Firstly, the server calculates the number of grid d and divides the entire area into a uniform grid size (line 1). Secondly, the server generates the k × m sketch matrix M^h(line 5), and each user maps their location’s grid to j hash function value, randomizes this hash function using local randomizer LR, and sends it to the server (lines 7–14). The server decodes the perturbed Hadamard code, estimates the count-min sketch (lines 15–19), and returns the count-min sketch structure M^h. The server determines the user i^th location l_i’s count estimation as .

Algorithm 1: Local randomizer LR.

Input: m-bit string , the privacy budget ε, and user’s hashed location l_i,j
Output: sanitized bit z^j
(1)
Generate the standard basis vector e_l ∈ {0,1}^d
(2)
x_l = X^Te_l
(3)
Randomize j-bit x_j of the input
(4)
(5)
where c_ε = (e^ε + 1/e^ε − 1)
(6)
return z^j

Algorithm 2: Hadamard count-min sketch LDP algorithm.

Input: user’s location l_i, number of user n, confidence parameter 0 < β < 1, and user’s privacy specification ε₁
Output: user location count
(1)
Server calculates the number of grid
(2)
Server calculates
(3)
Server calculates m m⟵(log(d + 1)log(2/β)/γ²)
(4)
Server generates a random matrix
(5)
Server initializes M^h ∈ {0}^k×m
(6)
Server initializes z and f
(7)
for each user u_ido
(8)
for each hash h_jdo
(9)
server randomly generates k from {1, …, m}
(10)
server sends kth row φ_k to u_i
(11)
u_i returns z_i,j = LR(ϕ_k, h_j(l_i), ε₁) to server
(12)
server adds z_i,j to kth bit of
(13)
end for
(14)
end for
(15)
for each hash h_jdo
(16)
for each hashed location h_j(l_i)do
(17)
server sets ‘s ith element of c to 〈φ_i, z〉
(18)
end for
(19)
end for
(20)
return

3.2.2. Phase 2: Count Estimation Using the Safe Region

The data consumer estimates the density of the entire area using information gathered in phase 1 and then divides the entire area into adaptive grid sizes. We follow the adaptive grid size guideline [12].

Guideline 2. Given a cell with a noisy count of N’, to minimize the errors, the grid should be partitioned into m₂ × m₂ cells, where m₂ is computed as follows:

(8)

where c₂ = c/2 and c is the same constant as in Guideline 1.

The major benefit of the adaptive grid over the existing recursive partition-based method [8] is the data utility enhancement. In the case of the existing partition-based method without considering the population density, noise is inserted into an unnecessary area where users do not exist (sparsity problem). It causes serious data utility degradation. On the contrary, in the case of an adaptive grid considering the population density, the grid size is determined according to the density of each cell. It mitigates the data utility deterioration.

In addition to that, we apply PLDP within the safe region. By using the safe region, we can reduce the data domain to improve the data utility and meet each user’s realistic privacy requirements.

After the adaptive grid size determination, the data consumer distributes an adaptive grid map and the incentive incentive_i,j to each user. Each user sets a safe region based on the adaptive grid map, incentive_i,j, and their own privacy sensitivity θ_j.

Definition 3 (safe region). The safe region is an area where each user j allows to be exposed in public. The safe region size is calculated as follows:

(9)

where S_max is set by the data consumer.

If the proposed incentive incentive_i,j becomes larger, the safe region size becomes smaller. If privacy sensitivity becomes larger, the size of the safe region also becomes larger. Each user perturbs his/her location data within a safe region using an adaptive grid and sends it to the data consumer. We use ε₂ for the location perturbation and modify the succinct histogram method [33] for the local environment to perturb the user’s location. The data consumer aggregates the perturbed location and performs the final count estimation.

3.3. Incentive Mechanism for Optimization

In the proposed technique, the data utility is affected by ε value and safe region size S_i. We assume that the ε value determines the existing incentive mechanism. Thus, data consumers have the motivation to pay a reasonable incentive to encourage the user to set a safe region size as accurate as possible. We propose the two incentive models: a principle-agent model that maximizes a data consumer’s profit, and the Stackelberg model to maximize a profit of both data consumer and data owner.

3.3.1. Principal-Agent Model

If a data consumer knows the user’s privacy sensitivity, the data consumer can set an incentive to maximize his/her own profit. This incentive must be larger than the user’s cost. The equation is expressed as follows:

(10)

The profit of the consumer is calculated by the profit that consumer gains using the data minus the cost that the consumer pays. The consumer’s profit is affected by the safe region size S_i, data utility util_i, and payment incentive_i,j for the data.

The safe region size is determined by each user’s privacy sensitivity θ_j and incentive_i,j paid by the consumer i (Figure 3).

The higher the privacy sensitivity θ, the larger the S_i, and the higher the incentive_i,j, the smaller the S_i. The data consumer and user’s profit function U(incentive_i,j) is as follows:

(11)

(12)

where

is the user j’s privacy cost.

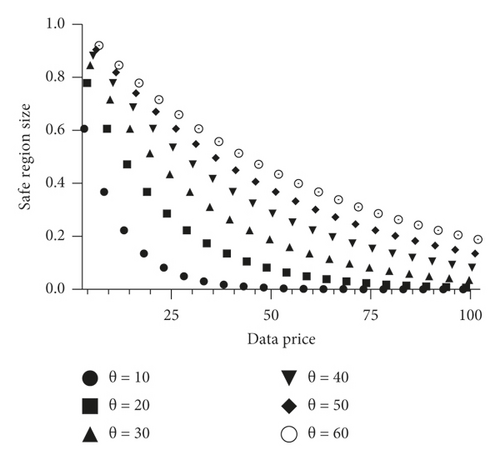
Since the util_i and θ_j are constants, which are set by the consumer and user, the profit is determined by S_i, which is affected by the incentive_i,j paid by the consumer. Thus, we should find a incentive_i,j to maximize equation (11).

The first-order derivate of the function is . We obtain optimal , where because the second-order derivate of the function is .

Then, the data consumer pays for the user who is able to maximize their profits.

3.3.2. Stackelberg Game Model

If the data consumer does not know the user’s privacy sensitivity, the principal-agent model cannot be used. In this case, we use the Stackelberg model for incentive mechanisms. The Stackelberg game [34] is a type of game theory in which one participant becomes a leader with more information than the other participants, predicting their reaction to their strategy and making decisions. The remaining participants become followers of the leader and take the action that is most profitable to himself/herself. The follower does not have information about the leader’s decision, but the leader has information about the follower’s decision-making process. Therefore, the leader can predict the reaction that the follower will react to the leader’s decision. The leader puts his followers’ responses to his choices in advance and decides his optimal strategy. The follower observes the leader’s strategy and chooses his/her best strategy.

We define the incentive problem of safe region size as a Stackelberg game situation. The data consumer is acting as the leader, and the user is the follower. They try to maximize their own profit as follows:

(13)

Backward induction is applied to solve the problem. First, given incentive_i,j, the user determines S_i to optimize . Based on the user’s decision on safe region size, the data consumer decides on incentive_i,j to optimize their profit .

4. Experimental Results

4.1. Experimental Environments

We perform the following experiments to verify the proposed scheme:

(1)
Hadamard count-min sketch local DP performance
(2)
Impact of privacy sensitivity based on safe region size
(3)
Comparison of the principle-agent model and Stackelberg model
(4)
Comparison of the proposed PLDP and existing methods

The data used in the experiment are Yelp [35] and California datasets [36]. Yelp data is a check-in data consisting of user’s location data, about 5 million data, and California data is location data of the point of interest in California, which has 85,920 data. We sampled this data in our experiments.

The parameters used in the experiments and the default values are given in Table 2.

Table 2. The parameter and default value.

Parameter	Value
Number of sample N	10,000, 15,000, and 20,000
Epsilon value ε	1, 2, and 3
Number of hash h	2, 3, and 4
Sketch vector size w	16, 32, and 64
θ_j	20, 40, and 60
P_cost_j	40
util_i	40
Price_i,j	40

The values in bold are the default parameter values. The size of the grid was determined by using Guidelines 1 and 2, and the ratio of ε₁ to epsilon ε₂ is 7 : 3 because ε₁ splits to the hash function which is used in sketch structure. We use the RMSE as the evaluation criteria for measuring the performance.

We use Super Micro Computer, Inc.’s SuperServer 7049P-TR (64-bit), consisting of CPU Intel Xeon Silver 4110 and 64 GB memory, and the operating system is Ubuntu 16.04.2 LTS. The proposed technique is implemented in Python 2.7.12.

4.2. Hadamard Count-Min Sketch Local DP Performance

The proposed PLDP scheme uses the succinct histogram method proposed in [33] using a count-min sketch and Hadamard transform. As the number of hash h and sketch vector size w become larger, the error due to collision decreases. However, if the w becomes larger, the domain size increases and data utility decreases due to the perturbation. If h increases, ε₁ should split by the sequential composition property. We experimented with changing the number of sample N, h, and w.

Experimental results show that the accuracy increases when h and w increases (Figure 4). However, as the h and w increases, the accuracy enhancement ratio decreases. We find that if the epsilon value was sufficient, the accuracy enhancement ratio is sustained. This is the result of interference between the sketch structure and succinct histogram protocol.

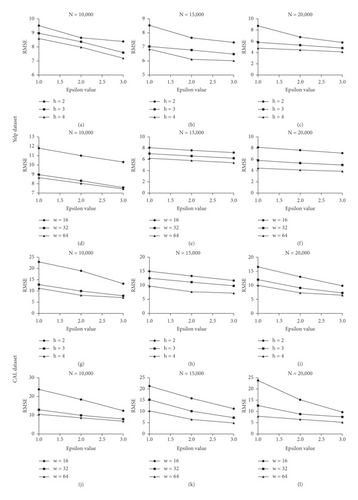
4.3. Impact of Privacy Sensitivity Based on Safe Region Size

In the proposed scheme, each user has their own privacy sensitivity θ_j, which is a factor determining the safe region size with incentive_i,j.

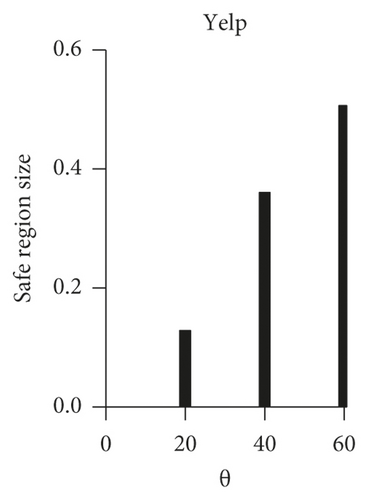
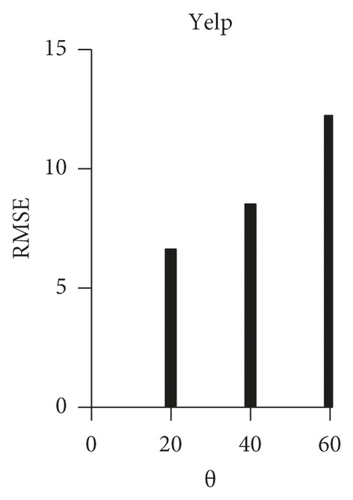
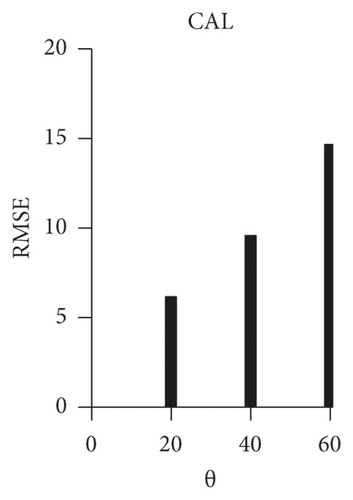
We measured the mean value of the safe region size according to the distribution of the users’ θ_j and the RMSE value when the price_i,j is fixed. First, we classify the users into three groups: (θ = 20: θ = 40: θ = 60)=(10 : 20 : 70), (θ = 20: θ = 40: θ = 60)=(30 : 40 : 30), and (θ = 20: θ = 40: θ = 60)=(70 : 20 : 10), that is, we classify the users into high-sensitivity group, normal sensitivity group, and low-sensitivity group. incentive_i,j is fixed at 40, and the other parameter is set equal to the default setting.

When S_max is set as the entire area, the experimental results show that safe region size is changed according to the privacy sensitivity (Figure 5). These results confirm that the group with higher privacy sensitivity set a larger safe region and the group with smaller privacy settings had a smaller safe region. Moreover, the RMSE score was changed in proportion to the safe region size.

4.4. Comparison in the Principle-Agent Model and Stackelberg Model

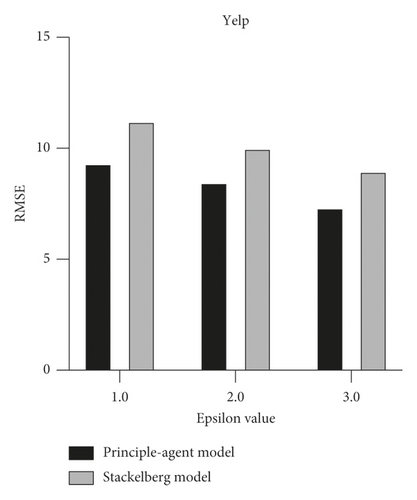
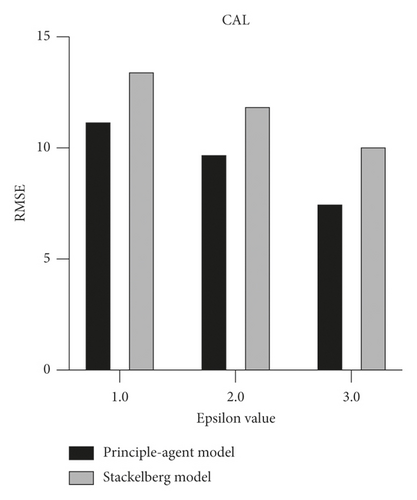
We compared the profits of data consumers and users when determining incentive_i,j using the proposed incentive models, the principal-agent model and Stackelberg model. We fixed the privacy sensitivity to a normal group and compared the profit and performance of both models. The consumer’s total budget was limited to 100,000. As shown in the results, the principal-agent model has a higher profit for the data consumer, and the RMSE is also lower (Table 3, Figure 6). This is because the Stackelberg model basically supposes the decentralized environment, which does not have a trusted third party. However, as can be seen from the safe region size, the Stackelberg model is a more fair model for the user than the principal-agent model.

Table 3. Parameter and default values.

	Model	Total profit	Average profit	Average safe region size	RMSE
Yelp	Principal-agent model	54,030	5.783	0.156	8.485
Yelp	Stackelberg model	39,141	4.189	0.193	10.021
CAL	Principal-agent model	39,128	4.169	0.192	9.764
CAL	Stackelberg model	27,812	2.877	0.237	11.932

4.5. Comparison in the Proposed PLDP and Existing Methods

We compared the performance of the proposed PLDP and existing methods [13, 14]. We select [13] as a comparative group because it proposes a local differential privacy scheme using a safe region in the same way as the proposed technique. However, they use a uniform grid size and static tree-structure taxonomy for the safe region. The study [13] is used as a comparative group in many research studies because it shows a fine performance for differentially private location data. It [13] is not a local differential privacy scheme, but it can adapt to the local differential privacy easily. In the experiment, we set the default parameter value, but for [13], we set the average safe region size in the proposed technique. The experiment was carried out by changing the epsilon value from 1 to 3.

The experimental result shows that the proposed technique has the lowest RMSE value (Figure 7). In the case of the proposed technique and [10], it shows higher performance than [13] because noise is only inserted into the safe region’s grid. The proposed technique shows higher performance than [14] because the proposed technique adjusts the grid size in consideration of the population density. In the local differential scheme, inserting noise into unnecessary grid deteriorates the data utility and the experimental result shows that the proposed technique successfully reduces unnecessary noise.

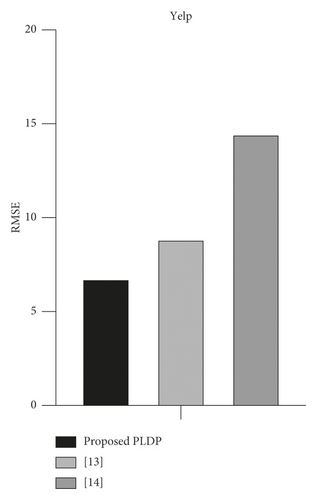
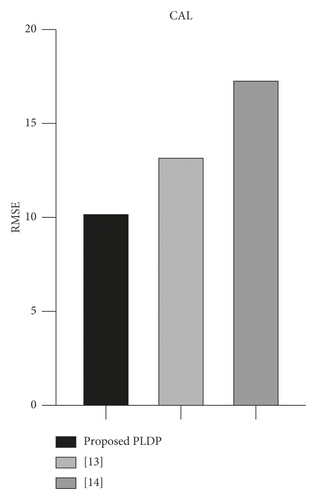
However, the proposed technique has a problem that it spends privacy budget twice to collect the population density information for grid size adaption. If we can use the publicly available data, such as [37], we can enhance the proposed technique’s performance.

5. Conclusion

As the demand for valuable personal data increases, the privacy violation also increases. The personal location data is directly related to individual privacy. Thus, it needs to be protected more strictly. In this paper, we propose a personalized differentially private location data scheme in the local setting and an incentive mechanism in which users receive reasonable compensation for their data, while the data consumer optimizes their profit. The proposed scheme aims to satisfy both privacy protection and utility more realistically by introducing the concept of a safe region. In future work, we will study the pricing mechanism that considers epsilon values with safe region size.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (no. NRF-2019R1A2C1088126).

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Dark Sky, https://darksky.net/forecast/40.7127,-74.0059/us12/en.
Google Scholar
2 Curbside, https://curbside.com/.
Google Scholar
3 Liu W., Tang Y., Yang F., Dou Y., and Wang J., A multi-objective decision-making approach for the optimal location of electric vehicle charging facilities, Computers, Materials & Continua. (2019) 60, no. 2, 813–834, https://doi.org/10.32604/cmc.2019.06754.
10.32604/cmc.2019.06754
Web of Science® Google Scholar
4 Li W., Chen Z., Gao X., Liu W., and Wang J., Multimodel framework for indoor localization under mobile edge computing environment, IEEE Internet of Things Journal. (2019) 6, no. 3, 4844–4853, https://doi.org/10.1109/jiot.2018.2872133, 2-s2.0-85054253163.
10.1109/JIOT.2018.2872133
Web of Science® Google Scholar
5 Yin C. et al., Mobile marketing recommendation method based on user location feedback, Human-centric Computing and Information Sciences. (2019) 9, no. 1, 1–17, https://doi.org/10.1186/s13673-019-0177-6, 2-s2.0-85065149487.
10.1186/s13673-019-0177-6
Web of Science® Google Scholar
6 Liu M. et al., Indoor Acoustic Localization: A Survey, Human-centric Computing and Information Sciences. (2020) 10, no. 1, 1–24.
10.1186/s13673-019-0207-4
Web of Science® Google Scholar
7 Zhang J., Personalized product recommendation model based on user interest, Computer Systems Science and Engineering. (2019) 34, no. 4, 231–236.
10.32604/csse.2019.34.231
CAS Web of Science® Google Scholar
8 Hussain A. et al., Accurate location prediction of social-users using mHMM”, Intelligent Automation and Soft Computing. (2019) 25, no. 3, 473–486.
Web of Science® Google Scholar
9 Dwork C. and Roth A., The algorithmic foundations of differential privacy, Foundations and Trends® in Theoretical Computer Science. (2014) 9, no. 3-4, 211–407.
10.1561/0400000042
Google Scholar
10 Cormode G. et al., Differentially private spatial decompositions, Proceedings of International Conference on Data Engineering, April 2012, Arlington, VA, USA, 20–31.
Google Scholar
11 Ho S. and Ruan S., Differential privacy for location pattern mining, Proceedings of the ACM SIGSPATIAL International Workshop on Security and Privacy in GIS and LBS, November 2011, Chicago, Illinois, 17–24.
Google Scholar
12 Qardaji W., Yang W., and Li N., Differentially private grids for geospatial data, Proceedings of the International Conference on Data Engineering, April 2013, Arlington, VA, USA, 757–768.
Google Scholar
13 Li C., Hay M., Miklau G., and Wang Y., A data- and workload-aware algorithm for range queries under differential privacy, Proceedings of the VLDB Endowment. (2014) 7, no. 5, 341–352, https://doi.org/10.14778/2732269.2732271, 2-s2.0-84891766947.
10.14778/2732269.2732271
Google Scholar
14 Chen R. et al., Private spatial data aggregation in the local setting, Proceedings of the International Conference on Data Engineering, March 2016, Arlington, VA, USA, 289–300.
Google Scholar
15 Erlingsson Ú., Pihur V., and Korolova A., Rappor RaRandomized aggregatable privacy-preserving ordinal respons, Proceedings of International Conference on Computer and Communications Security, November 2014, Scottsdale, Arizona, USA, 1054–1067.
Google Scholar
16 Cormode G. et al., Privacy at Scale: Local Differential Privacy in Practice, Proceedings of the International Conference on Management of Data, June 2018, Houston, TX, USA, 1655–1658.
Google Scholar
17 Thông T. N., Xiaokui X., Yin Y. et al., Collecting and analyzing data from smart device users with local differential privacy, 2016, https://arxiv.org/abs/1606.05053.
Google Scholar
18 Kasiviswanathan S. P. et al., What can we learn privately, SIAM Journal on Computing. (2011) 40, no. 3, 7903–8826, https://doi.org/10.1137/090756090, 2-s2.0-79960379430.
10.1137/090756090
Web of Science® Google Scholar
19 Ebadi H., Sands D., and Schneider G., Differential privacy, ACM Sigplan Notices. (2015) 50, no. 1, 69–81, https://doi.org/10.1145/2775051.2677005.
10.1145/2775051.2677005
Google Scholar
20 Jorgensen Z., Yu T., and Cormode G., Conservative or liberal? Personalized differential privacy, Proceedings of the International Conference on Data Engineering, April 2015, Arlington, VA, USA, 1023–1034.
Google Scholar
21 Yin C. et al., Location recommendation privacy protection method based on location sensitivity division, EURASIP Journal on Wireless Communications and Networking. (2019) 2019, no. 1, 1–13, https://doi.org/10.1186/s13638-019-1606-y.
10.1186/s13638-019-1606-y
Web of Science® Google Scholar
22 Wang Y., Sun Y., Su S. et al., Location privacy in device-dependent location-based services: challenges and solution, Computers, Materials & Continua. (2019) 59, no. 3, 983–993, https://doi.org/10.32604/cmc.2019.05547, 2-s2.0-85069600853.
10.32604/cmc.2019.05547
Web of Science® Google Scholar
23 Centonze P. et al., Security and privacy frameworks for access control big data systems, Computers, Materials & Continua. (2019) 59, no. 2, 361–374, https://doi.org/10.32604/cmc.2019.06223, 2-s2.0-85069577651.
10.32604/cmc.2019.06223
Web of Science® Google Scholar
24 Koutris P. et al., Query-based data pricing, Journal of the ACM (JACM). (2015) 62, no. 5, 43–86, https://doi.org/10.1145/2770870, 2-s2.0-84946601316.
10.1145/2770870
Web of Science® Google Scholar
25 Ghosh A. and Roth A., Selling privacy at auction, Games and Economic Behavior. (2015) 91, no. 1, 334–346, https://doi.org/10.1016/j.geb.2013.06.013, 2-s2.0-84937975357.
10.1016/j.geb.2013.06.013
Web of Science® Google Scholar
26 Anke H., Spector L. B., and Yoshikawa M., Evidence for an acetyl-enzyme intermediate in the action of acetyl-CoA synthetase, Biochemical and Biophysical Research Communications. (1975) 67, no. 2.
10.1016/0006-291X(75)90879-7
PubMed Web of Science® Google Scholar
27 Hsu J. et al., Differential privacy: an economic method for choosing epsilon, Proceedings of the IEEE Computer Security Foundations Symposium, July 2014, Vienna, Austria, 1–29.
Google Scholar
28 Roth A., Buying private data at auction, ACM SIGecom Exchanges. (2012) 11, no. 1, 1–8, https://doi.org/10.1145/2325713.2325714.
10.1145/2325713.2325714
Google Scholar
29 Fleischer L. K. and Lyu Y. H., Approximately optimal auctions for selling privacy when costs are correlated with data, Proceedings of the ACM Conference on Electronic Commerce, June 2012, Valencia Spain, 568–585.
Google Scholar
30 Aperjis C. and Huberman B. A., A market for unbiased private data: paying individuals according to their privacy attitudes, 2012, https://arxiv.org/abs/1205.0030.
Google Scholar
31 Rachana N., Yang C., and Masatoshi Y., How to balance privacy and money through pricing mechanism in personal data market, 2017, 767–773, https://arxiv.org/pdf/1705.02982.pdf.
Google Scholar
32 Cormode G., Count-min sketch, Encyclopedia of Database Systems. (2009) 511–516.
10.1007/978-0-387-39940-9_87
Google Scholar
33 Ritter T., 1996, Walsh-hadamard transforms: a literature survey. Research Comments from Cipers by Ritter, http://www.ciphersbyritter.com/RES/.
Google Scholar
34 Bassily R. and Smith A., Local, private, efficient protocols for succinct histograms, Proceedings of the Annual ACM Symposium on Theory of Computing, June 2015, Portland, OR, USA, 127–135.
Google Scholar
35 Simaan M. and Cruz J. B., On the Stackelberg strategy in nonzero-sum games, Journal of Optimization Theory and Applications. (1973) 11, no. 5, 533–555, https://doi.org/10.1007/bf00935665, 2-s2.0-0001461528.
10.1007/BF00935665
Web of Science® Google Scholar
36 Yelp, https://www.yelp.com/dataset/challenge.
Google Scholar
37 Feifei L. et al., On trip planning queries in spatial databases, Proceedings of the Advances in Spatial and Temporal Databases, August 2005, Brazil, South America, 273–290.
Google Scholar

All articles

An Adaptive Grid and Incentive Mechanism for Personalized Differentially Private Location Data in the Local Setting

Abstract

1. Introduction

2. Related Works

2.1. Differential Privacy

2.2. Differentially Private Location Data

2.3. Variation of Differential Privacy

2.4. Pricing Mechanism

3. Differentially Private Location Data in Local Setting and Pricing Mechanism

3.1. Overview

3.2. Differentially Private Location Data in a Local Setting

3.2.1. Phase 1: Density Estimation for the Entire Area

3.2.2. Phase 2: Count Estimation Using the Safe Region

3.3. Incentive Mechanism for Optimization

3.3.1. Principal-Agent Model

3.3.2. Stackelberg Game Model

4. Experimental Results

4.1. Experimental Environments

4.2. Hadamard Count-Min Sketch Local DP Performance

4.3. Impact of Privacy Sensitivity Based on Safe Region Size

4.4. Comparison in the Principle-Agent Model and Stackelberg Model

4.5. Comparison in the Proposed PLDP and Existing Methods

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley