Upon the teenagers’ failure to obtain the plenty of physical exercises at the growth and development stage, the related central nervous system is prone to degeneration and the physical fitness starts to decline gradually. In fact, through monitoring the exercise process real-timely and quantifying the exercise data, the adolescent physical training can be effectively conducted. For such process, it involves two issues, i.e., the real-time data monitoring and data quantification evaluation. Therefore, this paper proposes a novel method based on Reinforcement Learning (RL) and Markov model to monitor and evaluate the physical training effect. Meanwhile, the RL is used to optimize the adaptive bit rate of surveillance video and help the real-time data monitoring; the Markov model is employed to evaluate the health condition on the physical training. Finally, we develop a real-time monitoring system on exercise data and compare with the state-of-the-art mechanisms based on this system platform. The experimental results indicate that the proposed performance optimization mechanism can be more efficient to conduct the physical training. Particularly the average evaluation deviation rate based on Markov model is controlled within 0.16%.

1. Introduction

The physical fitness of teenagers has attracted the global attention for a long time because it has the considerably important influence on the rise and fall of each country. In fact, the related central nervous system gradually starts to degenerate, and the physical fitness also will decline with it, when the teenagers fail to obtain the plenty of physical exercises at the growth and development stage. Furthermore, according to what one hears and sees as well as the reliable news, the sudden death events among high school and college students happen frequently, which makes people turn their attention to the fitness problem during the process of physical training [1]. To put it crudely, the adolescent physical training is of great importance while the exercise (including public/private, individual/population) must be done properly.

The researches show that the generated physical training data not only reflects the real trajectories of exercisers but also implies the abundant and valuable information related to the whole exercise process [2]. To be specific, the information includes time, speed, acceleration, steps, and energy consumption. Among them, the energy consumption is an important metric and it can release two key signals, i.e., the amount of exercise and the exercise intensity. Given this, the amount of exercise and exercise intensity information can be obtained easily via monitoring the consumed energy, and then the physical training can be conducted and adjusted, which can be regarded as the healthy and reasonable exercise. In addition, according to the monitored energy consumption, the unforeseen circumstances due to the overtraining can be discovered in a timely manner, avoiding the worse tragedies as much as possible.

According to the above statements, we can observe that the video surveillance pays the nonnegligible role during the process of monitoring the physical training data. However, the traditional video surveillance shows some limitations. On the one hand, the development of computation speed is unable to keep pace with the increasing of application data; on the other hand, the inherent transmission overhead is very large, and the provided network bandwidth and the transmission of sliced segments are also not always matched [3]. Therefore, it is very necessary to optimize the Adaptive Bit Rate (ABR) [4] and guarantee obtaining the real-time monitoring data.

The typical ABR algorithm includes caching stage and stable stage [5]. At the first stage, the ABR algorithm usually tends to fill up the cache as quickly as possible; at the second stage, the ABR algorithm usually tries the best to improve the quality of video segment and prevent the cache overflow. At present, there have been some ABR optimization algorithms, including the traditional ones and the Artificial Intelligence- (AI-) based ones. To the best of our knowledge, the traditional ABR optimization algorithms cannot obtain the real-time network status to adapt to the dynamic network environment. On the contrary, the AI-based ABR optimization algorithms can adaptively adjust the network parameters and obtain the relatively optimal video transmission [6]. In terms of AI, the Reinforcement Learning (RL) [7] is the most popular representative. For RL, it can retrieve the demanded data by information exchanging between the intelligent agents and the external environment, without preparing the additional training datasets before training. Compared with the other RL-based ABR optimization algorithms, the Q-learning-based ABR optimization algorithms have better experience quality. However, the current Q-learning-based ABR optimization algorithms fail to encode for the continuous state values and cannot complete the fast convergence in terms of the large state space. As a conclusion, this paper improve the Q-learning to optimize the ABR algorithm.

In addition to the data monitoring, the quantification evaluation for the physical training data is also very significant. Specifically, the physical training features can be extracted by analyzing the monitored exercise data [8]; on this basis, the embedded laws on the physical training can be explored and the corresponding physical fitness evaluation model can be built, such as exercise effect, exercise tolerance, and improvement situation. Based on the evaluation model, the differentiated physical training educations can be effectively developed.

With the above considerations, this paper proposes a novel method based on RL and Markov model to monitor and evaluate the adolescent physical training effect. The major contributions are summarized as follows. (i) The Q-learning-based RL is exploited to optimize the ABR of surveillance video by combining the nearest neighbor algorithm. (ii) The Markov model is used to evaluate the health condition on the physical training by considering the energy consumption metric. (iii) The real-time monitoring system on exercise data is implemented, and the performance optimization effect on the adolescent physical training is demonstrated based on the system platform.

The rest of the paper is organized as follows. Section 2 reviews the related work. The improved Q-learning-based ABR optimization is proposed in Section 3. Section 4 gives the physical fitness evaluation model. The experimental results are shown in Section 5. Section 6 concludes this paper.

2. Related Work

The physical training has always been concerned and some most cutting-edge works have been developed. Buckinx et al. evaluated the effect of citrulline supplementation combined with high-intensity interval training on physical performance in healthy older adults [9]. Ana et al. proposed the multicomponent exercise training method by combining with the nutritional counselling to improve the physical education [10]. Konstantinos et al. presented a study to compare the effectiveness of virtual and physical training for teaching a bimanual assembly task and in a novel approach, where the task complexity was introduced as an indicator of assembly errors during final assembly [11]. Roland Van Den et al. studied the training order of explosive strength and plyometrics training on different physical abilities in adolescent handball players [12]. Rodrigo et al. investigated the plyometric training on the soccer players’ physical fitness by considering muscle power, speed, and change-of-direction speed tasks [13]. Simpson et al. enhanced the physical performance in professional rugby league players via the optimised force-velocity training [14]. Unquestionably, the above references showed the professional research on the physical training. In spite of this, they did not provide the networked physical training mode, i.e., regardless of the transmission of data generated from the video surveillance. To this end, Sun and Zou concentrated on the video transmission and improved the performance of extended training by using mobile edge computing [3]. However, [3, 9–14] still did not pay attention to the ABR optimization during the transmission process of physical training data.

The ABR optimization plays an important role in the networked physical training mode. The traditional optimization algorithms usually are heuristics. Cicco et al. announced two policies to optimize ABR, i.e., gradual increasing, but accelerate decreasing for the bit rate [15]. The heuristic ABR optimization existed the suboptimal problem and the shock problem of transmission quality, which had the considerable influence on the experience quality. As a result, Mok et al. paid attention to the improvement of quality of experience [16], which could guarantee that the transmission quality kept the stable level. Furthermore, the traditional ABR optimization algorithms also had a limitation, i.e., could not build the predictable and describable mathematical models for the concrete problems. For such purpose, some researchers used the control theory to optimize the ABR, where the controller was responsible for handling the input parameters. For example, Xiong et al. proposed the adaptive control model based on fuzzy logic, which could effectively meet the dynamic network change [17]. Besides, Vergados et al. used the fuzzy logic to design the adaptive policy by inputting the varying information on caching [18], preventing the cache overflow. Although [17, 18] achieved the good effect on the ABR optimization, they could not obtain the real-time network status to adapt to the dynamic network environment. To this end, some AI-based ABR optimization algorithms were proposed. For example, Chien et al. mapped the feature values related to network bandwidth to the bit rate of video by using the random forest classification decision tree [19]. Basso et al. [20] trained the classification model and estimated the bit rate based on the classification model. In fact, these ABR optimization algorithms like [19, 20] needed the ready-made dataset used for training. Instead, the RL-based ABR optimization algorithms could easily obtain the physical training data without preparing the additional datasets. Among them, the Q-learning-based ABR optimization algorithms could obtain the relatively best experience quality [21]. In spite of this, it was very difficult for the current Q-learning-based ABR optimization algorithms to encode for the continuous state values and realize the fast convergence in case of the large state space.

The evaluation model building of physical training data is very significant because it can effectively conduct and adjust the physical training. ElSamahy et al. presented a computer-based system for safe physical fitness evaluation for subjects undergoing aerobic physical stress, in which a proportional-integral fuzzy controller was applied to control the applied physical stress to ensure not exceeding the predefined target heart rate to satisfy safety [22]. Zhong and Hu designed a WebGIS-based interactive platform to collect and analyze national physical fitness-related indicators, including realizing the seven functional modules [23]. Heldens et al. studied the care data evaluation model to address the association between performance parameters of physical fitness and postoperative outcomes in patients undergoing colorectal surgery [24]. Ma proposed a kind of multilevel estimation and fuzzy evaluation of physical fitness and health effect of college students in regular institutions of higher learning based on classification and regression tree algorithm [25]. Qu et al. considered the physical fitness evaluation in children with congenital heart diseases versus healthy population [26]. Although the above references built the evaluation models for the physical fitness, they did not address the adolescent physical training. Regarding this, Guo et al. proposed a machine learning-based physical fitness evaluation model oriented to wearable running monitoring for teenagers, in which a variant of the gradient boosting machine combined with advanced feature selection and Bayesian hyperparameter optimization was employed to build a physical fitness evaluation model [27]. In spite of this, [27] did not concentrate the ABR optimization, which cannot complete the optimal performance optimization for the adolescent physical training.

3. Q-Learning-Based RL for ABR Optimization

The RL-based ABR optimization algorithms show the tradeoff between state space division and convergence speed. To be specific, if the state space is divided in the more fine-grained way, the more adequate states are generated and further the system behaviors can be more precisely described, while this causes the slow convergence problem. On the contrary, if the division granularity is relatively large, the number of states becomes small with it, while the convergence speed can be accelerated. Besides, these states in the ABR optimization problem are usually continuous, and the current Q-learning-based ABR optimization algorithms only make the simple discrete processing for these states. Therefore, this section plans to combine the nearest neighbor algorithm to address the abovementioned problems.

3.1. ABR Decision Model

Suppose that each code rate involves N video segments, denoted by seg₁, seg₂, …, seg_N, respectively. The client can select the corresponding segment from some code rate according to the network status information, such as network bandwidth, caching condition, and so on. In fact, the video segment selection can be regarded as the sequential decision process, and the decision objective is to guarantee the stable video display with the high code rate on the condition where the network bandwidth keeps the dynamic change. Given this, this paper assumes that there is an intelligent agent to determine how to download the video segment. Mathematically, for any seg_i, we can observe the information like network bandwidth (denoted by BD_i), caching state (denoted by CH_i), and the previous segment’s quality (denoted by q_i−1), and the corresponding environment state is defined as s_i = (BD_i, CH_i, q_i−1).

The intelligent agent selects the specific video segment from different code rates according to the perceived information. For the selection behavior regarding seg_i, it can be called as an intelligent action, denoted by a_i. After a_i is completed, CH_i will be updated by referring to BD_i and the selected code rate (denoted by br(a_i)). Let T_i denote the duration time of seg_i, and the corresponding download time is defined as follows:

(1)

Furthermore, for seg_i+1, its corresponding cache is defined as follows:

(2)

which suggests that the segment lag time equals the caching consumption time. To the best of our knowledge, the strategy conducted by the intelligent agent usually is not optimal. Thus, we give the reward function (denoted by R_i) to conduct the intelligent agent reaching the optimal level. In spite of this, the design of reward function should follow the requirements of service quality, which mainly includes the following three factors: the quality of video segment, the quality varying value between two frames, and the risk coefficient with respect to the cache overflow. Therein, the higher evaluation on service quality comes from the higher first factor and the smaller second/third factor. With the above three factors consideration, R_i is defined as follows:

(3)

where γ is a regulatory parameter to adjust the difference between q_i and q_i+1; φ_i is used to measure the risk coefficient with respect to the cache overflow, which has two functions: guaranteeing that the caching keeps the safe level and avoiding such actions that cause the low caching since they trigger the duplicate caching events easily. As a result, φ_i is defined as follows:

(4)

where the two parts of the right-hand side of equation (4) represent safe caching level and duplicate caching event, respectively; α and β are two regulatory parameters to, respectively, determine whether safe caching level and duplicate caching event are considered.

In fact, the ABR optimization problem based on the sequential segment selections by the intelligent agent can be built as the Markov decision model [28], which is expressed by four attributes, i.e., state space, action space, conditional transition probability, and instant reward function, denoted by S, A, P, and R, respectively. As mentioned earlier, the state space includes network bandwidth, caching state, and the previous segment’s quality. The action space is the set of all available code rates. Particularly, the strategy conducted by the intelligent agent is the mapping relationship from state space to action space, i.e., F : S⟶A. Furthermore, the corresponding s_i will change with it and be converted into s_i+1 when a_i is finished, and the situation is called the conditional transition probability, denoted by P(s_i+1|s_i, a_i). Moreover, the intelligent agent’s decision objective is to obtain the optimal long-term benefits according to some strategy (F), and the long-term benefits function is defined as follows:

(5)

where s₀ is the initial state; λ is the discount parameter and is between 0 and 1. When λ = 0, it means the action only pays attention to the current benefits irrespective of the expected benefits. With the increasing of λ, the action starts to pay attention to the expected benefits. Suppose that F^∗ is the optimal strategy while guaranteeing that the long-term benefits are the maximal, and we have

(6)

3.2. Nearest Neighbor Algorithm for Q-Learning

3.2.1. K-Nearest Neighbor Proposal

In order to obtain the optimal strategy of formula (6), the long-term benefits function is modified with the recursive form, as follows

(7)

As we know, formula (7) can be solved by the dynamic linear programming algorithm to obtain the optimal strategy. However, the dynamic linear programming has high computation complexity, and thus Kröse [29] uses the Q-learning method to obtain the optimal strategy with the relatively low computation complexity. In terms of Q-learning, it maintains one Q-table which includes the entries on mapping from the state to the action. As above mentioned, the Q-learning has two limitations; thus, this paper prepares to use K-nearest neighbor algorithm to optimize it.

The K-nearest neighbor algorithm is first proposed by Cover and Hart [30] in 1968, and it belongs to the instance-based learning method. In the K-nearest neighbor algorithm, the Euclidean distance between two samples is usually used to measure the similarity, where the larger Euclidean distance means the lower similarity. For example, suppose that X = {x₁, x₂, …, x_m} and Y = {y₁, y₂, …, y_m} are two data samples in terms of m-dimensional space, and the Euclidean distance between X and Y is defined as

(8)

3.2.2. ABR Optimization

We employ the Q-learning based on K-nearest neighbor algorithm to optimize the ABR, and the corresponding state division is shown in Figure 1. We can observe that when and only when the middle value of each interval is determined, the state is found. Under such condition, the state’s Q-value can be obtained by referring to the neighbouring Q-value(s). Suppose that d_i is the Euclidean distance between two states, and it is defined as follows:

(9)

where

, and

are the Euclidean distances regarding two network bandwidths, two cache states, and two previous segment’s qualities respectively, and their computations are similar to formula (8). After obtaining these Euclidean distances between s_i and the state in each Q-table, the first K-nearest distances are selected and their corresponding Q-values are used to compute the array of Q-values for s_i, defined as follows:

(10)

here,

is the neighbouring state with s_i; w_i is the Q-value proportion of

. If the corresponding d_i is larger, w_i is set to be smaller. Given an intermediate variable ρ_i = 1/d_i, w_i is defined as follows:

(11)

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The state division in terms of the Q-learning based on K-nearest neighbor algorithm.

Furthermore, after the action is finished, it requires to update the Q-table according to the returned instant reward and the new state. If the current state is found in the state division table, i.e., s_i ∈ S, the updating of Q-value is defined as follows:

(12)

On the contrary, if the current state cannot be found in the state division table, i.e., s_i ∉ S, the updating of Q-value is defined as follows:

(13)

(14)

where ϒ is an intermediate variable; ξ is a regularity parameter;

is the next K state after

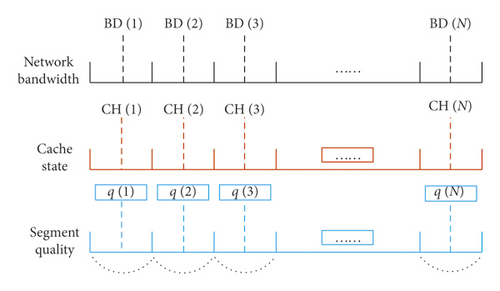
According to the above statements, the pseudocode of ABR optimization based on Q-learning with consideration of K-nearest neighbor algorithm is described in Algorithm 1.

Algorithm 1: ABR optimization algorithm.

Input: State space and action space
Output: Q-value
Initialize Q-table;
for each state, do
Compute Q(s_i, :) with formula (10);
Confirm br(a_i) by Q(s_i, :);
Request to download seg_i;
Update CH_i with formula (2);
Compute R(i) with formula (3);
ifs_i ∈ S, then
Update Q-value with formula (12);
else
Update Q-value with formula (13);
endfor

4. Physical Fitness Evaluation

The quantification evaluation for the physical training data is also very significant. In fact, the physical training process is intricate and has the strong randomness, which leads to the difficulty of quantification evaluation. The traditional physical evaluation models (e.g., [22–26]) usually consider the relatively simple factors with the subjectivity, which have a few limitations. Thus, it is required to find a proper model to evaluate the physical training.

4.1. Thought Incubation

The physical training process has the feature of randomness, that is, the subsequent exercise state only depends on the current exercise state and has no connection with the history exercise states. This conforms to the Markov process; thus, this paper uses the Markov model to simulate the physical training process and further present the related evaluation models, including individual exercise modelling and population exercise modelling. The main ideas are summarized as follows:

(i)
Individual Exercise Modelling. (i) The generated physical training data is given a rank; (ii) the matrix of transition probability is obtained by the varying data rank; (iii) the vector of stability probability is computed by referring to the stability of Markov process, to predict the stable state; and (iv) the subsequent physical training is conducted based on the exercise limit.
(ii)
Population Exercise Modelling. The first two steps are similar to those in the individual exercise modelling. The third step is to compare the generated population data and adjust the improvement degree to adapt to the whole physical training effect.

Furthermore, the generated energy during the physical training process usually reflects the situation of physical fitness; thus, this paper regards the energy consumption as the evaluation metric. Particularly for the adolescent physical training, the consumed energy gradually increases at the initial stage. After reaching the relatively stable level, it begins to decrease rapidly until the teenagers lose their strength. In terms of the individual exercise modelling, we adopt the energy consumption rate as the evaluation metric, which is defined as follows:

(15)

Among them, t ∈ [1, t_max] is the time period used for data collection and t_max is the maximal number of periods; EE_t is the consumed energy of the tth data collection; and ET_t is the spent time to complete EE_t. In terms of the population exercise modelling, we adopt the improvement degree with respect to the energy consumption transition as the evaluation metric, which is defined as follows:

(16)

Among them, ep_ij is the transition probability; ed_ij is the energy consumption span difference, and it can be computed by formula (8); and c is the regularity parameter.

4.2. Modelling for Two Situations

4.2.1. Individual Modelling

Based on the Markov model and the ABR optimization algorithm (see Section 3), the consumed energy data can be monitored and computed easily. After that, the sequence on energy consumption rates can be obtained by formula (15). For the sequence, the individual evaluation model based on the Markov process is described as follows:

(i)
State Space Division. The maximal value and the minimal value in the sequence are found, denoted by cr_max and cr_min, respectively. Suppose that there are θ divided state intervals, and the length of interval is defined as

(17)

On this basis, the divided intervals are [cr_min, cr_min + Δcr), …, [cr_min + (θ − 1)Δcr, cr_max].
(ii)
Transition Probability Matrix Computation. For the continuous time periods, their transition probabilities are computed, and one matrix used to record these transition probabilities can be obtained and denoted by eP.
(iii)
Stable-State Vector Determination. When t_max energy consumption rates are completed, we give an initial state vector denoted by to satisfy

(18)

According to the stability of Markov chain, we can obtain a state vector eS^∗ = {es₁, es₂, …, es_θ} to satisfy , where eS^∗ is called the stable-state vector.
(iv)
Limited Energy Consumption Rate Computation. For θ state intervals, their maximal values are selected, where denotes the maximal value of the ith interval, and the limited energy consumption rate is defined as

(19)

To sum up, if cr_i is larger than cr^lim, it means that the current physical training is dangerous and the system will notify the teenagers to slow down the physical training.

4.2.2. Population Modelling

Suppose that one population includes Nump teenager individuals, and the average energy consumption for the population is defined as follows:

(20)

where Ei_i is the consumed energy by the arbitrary teenager individual in the population. In a similar way, the sequence on the average energy consumptions can be obtained by formula (20), denoted by

; that is, there are t_max collection periods. For the sequence, the population evaluation model based on the Markov process is described as follows:

(i)
State Space Division. The maximal value and the minimal value in the sequence are found, denoted by and , respectively. Suppose that there are θ divided state intervals, and the length of interval is defined as

(21)

Then, the divided intervals are .
(ii)
Transition Probability Matrix Computation. It is similar to the operation in the individual evaluation model.
(iii)
Transition Improvement Degree Computation. It can be obtained by formula (16).

In total, if eK_ij is larger than ∑eK_ij/(θ − 1), it means that the physical training effect has been improved and the system will notify the population to enhance the physical training.

5. Simulation Results

In this section, we pay attention to the simulation experiments. At first, we develop the data monitoring system. Then, we test the physical training evaluation models. Finally, the whole performance optimization on the adolescent physical training is verified. Meanwhile, the last two parts are based on the developed system platform. In particular, regarding the simulation settings, we make the different simulations and find one proper combination.

5.1. System Implementation

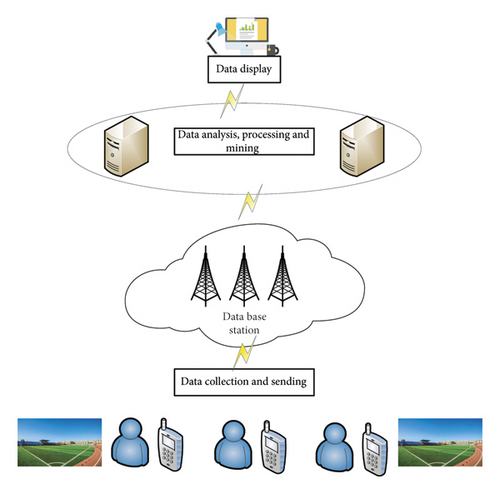
The real-time data monitoring system depends on computer technology, communication technology, and sports science, which provides the real-time exercise monitoring services according to collecting the data information with respect to the physical training. In terms of the adolescent physical training, the data monitoring system platform architecture is shown in Figure 2. We observe that the system platform includes four modules, i.e., data collection, data receiving and data sending, data analysis and handling, and data display. Among them, the last module can provide the reference for the adolescent physical training directly according to the monitored data.

5.2. Model Evaluation

This section will evaluate two models, i.e., individual evaluation model and population evaluation model. The involved parameters are set as follows: c = 3, t_max = 300, θ = 24, and time period for 30 s. In addition, we use the deviation rate to measure whether the evaluation models can be acceptable. For the individual evaluation model, we test 1000 teenagers for 12 times experiments, where the frequency is once a day. The experimental results on the conducted physical training conditions are shown in Table 1. For the population evaluation model, we also test 1000 populations for 12 times experiments, where one population includes 20 teenagers and the frequency is once a day. The corresponding results on the population physical training conditions are shown in Table 2. Among them, the deviation rate is defined as the ratio of the number of improper conducts and the total number of experiments.

Table 1. The experimental results on the individual physical training conditions.

Experiment no.	1	2	3	4	5	6	7	8	9	10	11	12
#Correct conduct	998	1000	997	999	999	998	999	999	999	997	998	1000
#Improper conduct	2	0	3	1	1	2	1	1	1	3	2	0
Deviation rate (%)	0.2	0	0.3	0.1	0.1	0.2	0.1	0.1	0.1	0.3	0.2	0

Table 2. The experimental results on the population physical training conditions.

Experiment no.	1	2	3	4	5	6	7	8	9	10	11	12
#Correct conduct	1000	998	999	1000	997	1000	999	999	1000	999	1000	998
#Improper conduct	0	2	1	0	3	0	1	1	0	1	0	2
Deviation rate (%)	0	0.2	0.1	0	0.3	0	0.1	0.1	0	0.1	0	0.2

As seen from Tables 1 and 2, the deviation rate for each group experiment is always smaller than 0.3%. To be specific, the average deviation rate in terms of the individual evaluation model is 0.158% and that for the population evaluation model is 0.092%, and the two values can be controlled within the 0.16%, which implies that it is efficient to use the Markov model to evaluate the adolescent physical training. Furthermore, it implies that the Markov model has better evaluation effect in terms of the population physical training situation because 0.158% < 0.092%.

5.3. Performance Verification

This section will verify the optimization preformation of adolescent physical training by comparing with two benchmarks, i.e., [3, 27] published by Internet Technology Letters (ITL) and Computer Networks (CN), respectively. Meanwhile, the whole transmission time and packet loss rate are adopted as two performance verification metrics. The involved parameters are set as follows: γ = 0.45, α = 0.6, β = 0.4, λ = 0.9, K = 6, η = 0.35, and ξ = 0.4. In addition, the number of simulations is set as 10. The experimental results on the whole transmission time and packet loss rate are shown in Tables 3 and 4, respectively.

Table 3. The experimental results on the whole transmission time (ms).

Experiment no.	1	2	3	4	5	6	7	8	9	10
This paper	43.26	44.61	43.97	45.67	43.09	44.56	44.13	45.02	43.86	42.61
ITL	56.67	55.37	58.64	57.26	55.97	56.43	59.06	58.34	53.49	55.73
CN	83.18	82.67	84.62	85.64	85.31	84.64	83.59	84.22	82.98	84.55

Table 4. The experimental results on the packet loss rate (%).

Experiment no.	1	2	3	4	5	6	7	8	9	10
This paper	0.156	0.173	0.146	0.152	0.139	0.109	0.154	0.167	0.141	0.121
ITL	0.648	0.694	0.703	0.625	0.713	0.633	0.687	0.701	0.692	0.681
CN	0.355	0.386	0.321	0.364	0.339	0.309	0.359	0.316	0.356	0.392

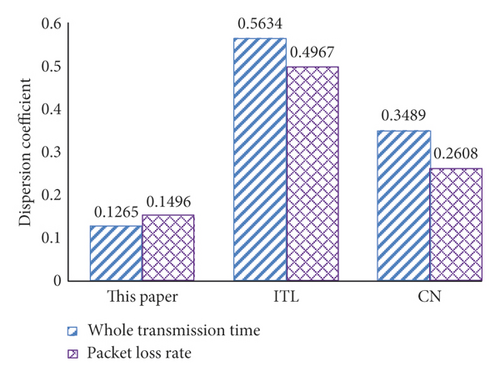
It can be seen from Tables 3 and 4 that this paper always consumes the smallest whole transmission time and the lowest packet loss rate. This implies that this paper has the optimal optimization performance for the adolescent physical training. This is because this paper uses RL to obtain the relatively optimal solution and uses the Markov model to obtain the relatively accurate training effect. In addition, regarding the two metrics, we show the corresponding dispersion coefficients to evaluate the stability, as shown in Figure 3. We observe that this paper always has the smallest dispersion coefficient due to the stability guarantee of using RL, which implies that the performance mechanism is the most stable.

6. Conclusions

The physical fitness of teenagers has attracted the global attention for a long time because it has a considerably important influence on the rise and fall of each country. This paper proposes to optimize the adolescent physical training based on RL and Markov model. Because the RL-based ABR optimization algorithms shows the tradeoff between state space division and convergence speed, this paper improves the Q-learning by using the K-nearest neighbor algorithm. In addition, we also present the evaluation models on the physical fitness, including individual exercise modelling and population exercise modelling, based on the Markov model. Moreover, we make the simulation experiments based on the developed data monitoring system platform, and the results have demonstrated that this paper has always the optimal optimization performance for the adolescent physical training with the most stable state. In the future, we will deploy more functions in our system platform, such as adaptive recognition and falling warning. Besides, we also make the large-scale experiments based on the real testbed instead of the system platform.

Conflicts of Interest

The authors declare that they have no conflicts of interest regarding the publication of this paper.

Acknowledgments

The work was supported by the Special Funds Project for Basic Scientific Research in Central Universities (no. 451170306081) and the Research Project on the Realization PATH of High-Quality Development of School Competitive Sports in Jilin Province (no. 2020C088). In addition, the authors also thank Yuanshuang Li who is an expert in the field of video transmission to provide the great help for ABR knowledge.

Open Research

Data Availability

No data were used to support this study.

References

1 Jin Y. and Wang X., Study on safety mode of dragon boat sports physical fitness training based on machine learning, Safety Science. (2019) 120, 1–5, https://doi.org/10.1016/j.ssci.2019.06.028, 2-s2.0-85067841601.
10.1016/j.ssci.2019.06.028
Web of Science® Google Scholar
2 Andrienko G., Andrienko N., Bak P., Keim D., Kisilevich S., and Wrobel S., A conceptual framework and taxonomy of techniques for analyzing movement, Journal of Visual Languages & Computing. (2011) 22, no. 3, 213–232, https://doi.org/10.1016/j.jvlc.2011.02.003, 2-s2.0-79957934163.
10.1016/j.jvlc.2011.02.003
Web of Science® Google Scholar
3 Sun L. and Zou Y., Mobile edge computing based video surveillance model for improving the performance of extended training, Internet Technology Letters. (2020) https://doi.org/10.1002/itl2.236.
10.1002/itl2.236
Web of Science® Google Scholar
4 Yang A., Wu X., Qiao Y., and Sun Y.-n., Bit-rate adaptive optical performance monitoring method for fiber communication systems, Optics Communications. (2011) 284, no. 1, 436–440, https://doi.org/10.1016/j.optcom.2010.08.029, 2-s2.0-78649670799.
10.1016/j.optcom.2010.08.029
CAS Web of Science® Google Scholar
5 Rao A., Lim Y., Barakat C. et al., Network characteristics of video streaming traffic, Proceedings of the Seventh Conference on Emerging Networking EXperiments and Technologies, December 2011, Tokyo Japan, 1–12, https://doi.org/10.23919/tma.2019.8784688, 2-s2.0-85071185665.
10.23919/tma.2019.8784688
Google Scholar
6 Mohanta B. K., Jena D., Ramasubbareddy S., Daneshmand M., and Gandomi A. H., Addressing security and privacy issues of IoT using blockchain technology, IEEE Internet of Things Journal. (2020) 111, 1–17, https://doi.org/10.1109/jiot.2020.3008906.
10.1109/jiot.2020.3008906
Google Scholar
7 Kaelbling L. P., Littman M. L., and Moore A. W., An Introduction to Reinforcement Learning, 2005, IEEE Press, Hoboken, NJ, USA.
Google Scholar
8 Yuan H., Wang J., Liu J., and Li S., Research of zigbee and big data analysis based pulse monitoring system for efficient physical training, Procedia Computer Science. (2016) 80, 2357–2361, https://doi.org/10.1016/j.procs.2016.05.442, 2-s2.0-84978513089.
10.1016/j.procs.2016.05.442
Google Scholar
9 Buckinx F., Carvalho L. P., and Marcangeli V., High intensity interval training combined with L-citrulline supplementation: effects on physical performance in healthy older adults, Experimental Gerontology. (2020) 140, https://doi.org/10.1016/j.exger.2020.111036.
10.1016/j.exger.2020.111036
Web of Science® Google Scholar
10 Ana C., Beatriz P., Paula G. et al., Multicomponent exercise training combined with nutritional counselling improves physical function, biochemical and anthropometric profiles in obese children: a pilot study, Nutrients. (2020) 12, no. 9, 1–15, https://doi.org/10.3390/nu12092723.
10.3390/nu12092723
Web of Science® Google Scholar
11 Konstantinos K., Francesco C., Panagiotis M., and Simon K., Effectiveness of virtual versus physical training: the case of assembly tasks, trainer’s verbal assistance, and task complexity, IEEE Computer Graphics and Applications. (2020) 40, no. 5, 41–56, https://doi.org/10.1109/mcg.2020.3006330.
10.1109/MCG.2020.3006330
PubMed Web of Science® Google Scholar
12 Roland Van Den T., Truls Valland R., and Dustin O., Comparison of effects of training order of explosive strength and plyometrics training on different physical abilities in adolescent handball players, Biology of Sport. (2020) 37, no. 3, 239–246, https://doi.org/10.5114/biolsport.2020.95634.
10.5114/biolsport.2020.95634
PubMed Web of Science® Google Scholar
13 Rodrigo R., Cristian A., Felipe G. et al., Effects of combined surfaces vs. single-surface plyometric training on soccer players’ physical fitness, Journal of Strength and Conditioning Research. (2020) 34, no. 9, 2644–2653, https://doi.org/10.1519/jsc.0000000000002929.
10.1519/JSC.0000000000002929
PubMed Web of Science® Google Scholar
14 Simpson A., Waldron M., Cushion E. et al., Optimised force-velocity training during pre-season enhances physical performance in professional rugby league players, Journal of Sports Sciences. (2020) https://doi.org/10.1080/02640414.2020.1805850.
10.1080/02640414.2020.1805850
Web of Science® Google Scholar
15 Cicco L. D., Mascolo S., and Palmisano V., Feedback control for adaptive live video streaming, Proceedings of the Second Annual ACM Conference on Multimedia Systems, February 2011, San Jose, CA, USA, 145–156, https://doi.org/10.1145/1943552.1943573, 2-s2.0-79952858984.
10.1145/1943552.1943573
Google Scholar
16 Mok R. K. P., Luo X., Chan E., and Chang R. K. C., QDASH: a QoE-aware DASH system, Proceedings of the 3rd Annual ACM Conference on Multimedia Systems, February 2012, Chapel Hill, NC, USA, 11–22, https://doi.org/10.1145/2155555.2155558, 2-s2.0-84858768981.
10.1145/2155555.2155558
Google Scholar
17 Xiong P., Shen J., Wang Q. et al., NBS: a network-bandwidth-aware streaming version switcher for mobile streaming applications under fuzzy logic control, Proceedings of the IEEE First International Conference on Mobile Services, June 2012, Honolulu, HI, USA, 48–55, https://doi.org/10.1109/mobserv.2012.10, 2-s2.0-84866415702.
10.1109/mobserv.2012.10
Google Scholar
18 Vergados D. J., Michalas A., Sgora A. et al., A control-based algorithm for rate adaption in MPEG-DASH, Proceedings of the 5th International Conference on Information, Intelligence, Systems and Applications, July 2014, Chania, Greece, 1–5, https://doi.org/10.1109/iisa.2014.6878834, 2-s2.0-84906774927.
10.1109/iisa.2014.6878834
Google Scholar
19 Chien Y., Lin C., and Chen M., Machine learning based rate adaptation with elastic feature selection for HTTP-based streaming, Proceedings of the IEEE International Conference on Multimedia and Expo, June 2015, Turin, Italy, 1–6, https://doi.org/10.1109/icme.2015.7177418, 2-s2.0-84946100473.
10.1109/icme.2015.7177418
Google Scholar
20 Basso S., Servetti A., Masala E. et al., Measuring DASH streaming performance from the end users perspective using neubot, Proceedings of the 5th Annual ACM Conference on Multimedia Systems, March 2014, Singapore, 1–6, https://doi.org/10.1145/2557642.2563671, 2-s2.0-84898977675.
10.1145/2557642.2563671
Google Scholar
21 Watkins C. J. C. H. and Dayan P., Technical note: Q-learning, Machine Learning. (1992) 8, no. 3-4, 279–292, https://doi.org/10.1007/bf00992698.
10.1007/BF00992698
Web of Science® Google Scholar
22 ElSamahy E., Genedy A., Abbass M. A. et al., A computer-based system for safe physical fitness evaluation, Proceedings of the 4th International Conference on Biomedical Engineering and Informatics, October 2011, Shanghai, China, 1443–1447, https://doi.org/10.1109/bmei.2011.6098567, 2-s2.0-84855782743.
10.1109/bmei.2011.6098567
Google Scholar
23 Zhong Y. and Hu W., The research on WebGIS-based information integration and data analysis platform for China’s Physical Fitness and the National Fitness Program, Proceedings of the 2nd IEEE International Conference on Computer and Communications, October 2016, Chengdu, China, 135–139, https://doi.org/10.1109/compcomm.2016.7924680, 2-s2.0-85020233832.
10.1109/compcomm.2016.7924680
Google Scholar
24 Heldens A. F. J. M., Bongers B. C., Lenssen A. F., Stassen L. P. S., Buhre W. F., and van Meeteren N. L. U., The association between performance parameters of physical fitness and postoperative outcomes in patients undergoing colorectal surgery: an evaluation of care data, European Journal of Surgical Oncology. (2017) 43, no. 11, 2084–2092, https://doi.org/10.1016/j.ejso.2017.08.012, 2-s2.0-85029628600.
10.1016/j.ejso.2017.08.012
CAS PubMed Web of Science® Google Scholar
25 Ma L., Multi-level estimation and fuzzy evaluation of physical fitness and health effect of college students in regular institutions of higher learning based on classification and regression tree algorithm, Proceedings of the 2018 International Conference on Virtual Reality and Intelligent Systems, August 2018, Changsha, China, 201–205, https://doi.org/10.1109/icvris.2018.00056, 2-s2.0-85058304783.
10.1109/icvris.2018.00056
Google Scholar
26 Qu J., Shi H., Chen X. et al., Evaluation of physical fitness in children with congenital heart diseases versus healthy population, Seminars in Thoracic and Cardiovascular Surgery. (2020) https://doi.org/10.1053/j.semtcvs.2020.05.014.
10.1053/j.semtcvs.2020.05.014
PubMed Web of Science® Google Scholar
27 Guo J., Yang L., Bie R. et al., An XGBoost-based physical fitness evaluation model using advanced feature selection and Bayesian hyper-parameter optimization for wearable running monitoring, Computer Networks. (2019) 151, 166–180, https://doi.org/10.1016/j.comnet.2019.01.026, 2-s2.0-85060858783.
10.1016/j.comnet.2019.01.026
Web of Science® Google Scholar
28 Kalnoor G. and Subrahmanyam G., A review on applications of Markov decision process model and energy efficiency in wireless sensor networks, Procedia Computer Science. (2020) 167, 2308–2317, https://doi.org/10.1016/j.procs.2020.03.283.
10.1016/j.procs.2020.03.283
Google Scholar
29 Kröse B. J. A., Learning from delayed rewards, Robotics and Autonomous Systems. (1995) 15, no. 4, 233–235, https://doi.org/10.1016/0921-8890(95)00026-c, 2-s2.0-0011669655.
10.1016/0921-8890(95)00026-C
Web of Science® Google Scholar
30 Chirici G., Mura M., McInerney D. et al., A meta-analysis and review of the literature on the k-nearest neighbors technique for forestry applications that use remotely sensed data, Remote Sensing of Environment. (2016) 176, 282–294, https://doi.org/10.1016/j.rse.2016.02.001, 2-s2.0-84957681049.
10.1016/j.rse.2016.02.001
Web of Science® Google Scholar

Citing Literature

All articles

Performance Optimization Mechanism of Adolescent Physical Training Based on Reinforcement Learning and Markov Model

Abstract

1. Introduction

2. Related Work

3. Q-Learning-Based RL for ABR Optimization

3.1. ABR Decision Model

3.2. Nearest Neighbor Algorithm for Q-Learning

3.2.1. K-Nearest Neighbor Proposal

3.2.2. ABR Optimization

4. Physical Fitness Evaluation

4.1. Thought Incubation

4.2. Modelling for Two Situations

4.2.1. Individual Modelling

4.2.2. Population Modelling

5. Simulation Results

5.1. System Implementation

5.2. Model Evaluation

5.3. Performance Verification

6. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley