Volume 2020, Issue 1 7096276

Research Article

Open Access

An Empirical Model of Angle-of-Arrival Variance for a Gaussian Wave Propagation through Non-Kolmogorov Turbulence

Chao Gao

orcid.org/0000-0002-4917-324X

The 54th Research Institute of China Electronics Technology Group Corporation, Shijiazhuang 050081, China

Science and Technology on Information Transmission and Dissemination in Communication Networks Laboratory, Shijiazhuang 050081, China

School of Astronautics and Aeronautic, University of Electronic Science and Technology of China, Chengdu 611731, China uestc.edu.cn

Search for more papers by this author

Libin Jiao,

Libin Jiao

The 54th Research Institute of China Electronics Technology Group Corporation, Shijiazhuang 050081, China

Science and Technology on Information Transmission and Dissemination in Communication Networks Laboratory, Shijiazhuang 050081, China

Search for more papers by this author

Xiaofeng Li,

Corresponding Author

Xiaofeng Li

[email protected]

orcid.org/0000-0002-0490-1717

School of Astronautics and Aeronautic, University of Electronic Science and Technology of China, Chengdu 611731, China uestc.edu.cn

Search for more papers by this author

Chao Gao,

Chao Gao

orcid.org/0000-0002-4917-324X

The 54th Research Institute of China Electronics Technology Group Corporation, Shijiazhuang 050081, China

Science and Technology on Information Transmission and Dissemination in Communication Networks Laboratory, Shijiazhuang 050081, China

School of Astronautics and Aeronautic, University of Electronic Science and Technology of China, Chengdu 611731, China uestc.edu.cn

Search for more papers by this author

Libin Jiao,

Libin Jiao

The 54th Research Institute of China Electronics Technology Group Corporation, Shijiazhuang 050081, China

Science and Technology on Information Transmission and Dissemination in Communication Networks Laboratory, Shijiazhuang 050081, China

Search for more papers by this author

Xiaofeng Li,

Corresponding Author

Xiaofeng Li

[email protected]

orcid.org/0000-0002-0490-1717

School of Astronautics and Aeronautic, University of Electronic Science and Technology of China, Chengdu 611731, China uestc.edu.cn

Search for more papers by this author

First published: 26 May 2020

https://doi.org/10.1155/2020/7096276

Citations: 2

Academic Editor: Sulaiman W. Harun

Share a link

Email
Wechat
Bluesky

Abstract

This paper proposes an empirical model of the angle-of-arrival (AOA) variance for a Gaussian wave propagating through the weak non-Kolmogorov turbulence. The proposed model is approximately expressed as the linear weighted average between the AOA variances of the plane and spherical waves. The Monte Carlo method is applied to validate the proposed model. The numerical simulations indicate that, under the geometrical optics approximation, the AOA variance for a Gaussian wave is insensitive to the change of the diffraction parameter and can be closely approximated by a simple linear relationship in the refraction parameter. These two properties ensure the validity of the empirical model.

1. Introduction

Optical wireless communication technology has attracted widespread attention during the past few decades. It adopts unguided laser beam propagating in random media to carry the digital signal for data transmission with high data rates. The random media, however, may contain numerous invisible turbulent eddies, which fluctuate the refractive index inside the random media and distort the equiphase wavefront of the laser beam. Considering that the equiphase wavefront in the vacuum is undistorted and uniform, AOA can be defined as the angle between the normal vectors of the distorted and undistorted equiphase wavefront. It is generally accepted that AOA could hardly degenerate the quality of the imaging spot, but will lead the focus position to deviate from the optimal point. This phenomenon is equivalent to the geometric misalignment between the receiving and transmitting antennas [1–3].

AOA stochastically fluctuates with the changes in both temporal and spatial dimensions, and the degree of the AOA fluctuation is conventionally described by its variance. In recent years, theoretical models of the AOA variances for plane and spherical waves have been fully analyzed based on different turbulent power spectrums [4–15]. However, the research on the AOA variance for a Gaussian wave still needs further discussion. Gao et al. [16] proposed a heuristic model of the AOA variance for a Gaussian wave propagation through non-Kolmogorov turbulence, but lacked adequate evidence to ensure the validity of the expressions. Regarded as an increment to the previous literature studies, this paper not only investigates the similar scenario but also conducts simulations for experimental verification. The rest of the paper is organized as follows. Section 2 presents the theoretical models of the AOA variances for different types of laser beams. In Section 3, numerical simulations are performed, followed by conclusions in Section 4.

2. Theoretical Models

2.1. AOA Variances for Plane and Spherical Waves

The AOA variance for either plane or spherical wave can be calculated by

(1)

where d is the aperture diameter of the collecting lens, k = 2π/λ is the angular wavenumber with the wavelength λ, and

(2)

is the phase structure function [1]. In equation (2), ρ is the scalar separation between two observation points, L is the propagation optical path length, ξ is the normalized path coordinate, and κ is the scalar spatial wavenumber which regularized the scale of the turbulence eddy. Φ_n(κ) and f(κ, ξ) in equation (2) represent the turbulent power spectrum and the weight function, respectively. This paper applies the benchmark non-Kolmogorov model:

(3)

as the turbulent power spectrum, where α ∈ (3,4) is the general spectral power law value, A(α) = Γ(α − 1)/4π²cosαπ/2 is a function related to α,

is the gamma function, and

is the scalar generalized atmospheric structure parameter [14]. The weight function for the plane wave f_p(κ, ξ) and for the spherical wave f_s(κ, ξ) are defined as

(4)

where

is the Bessel function of the first kind with zero order.

To achieve the closed-form expression of equation (1), this paper invokes the geometrical optics approximation (GOA) to reduce equation (2). For terrestrial horizontal wireless optical communication link, the Fresnel length

is usually in the order of magnitude of centimeter, whereas d is designed in the order of magnitude of decimeter, i.e., d > l_F is almost satisfied. For ρ > l_F, the lens effect of the turbulent eddy can be dealt with GOA, which yields Lκ²/k ≪ 1. Consequently, equation (4) leads to

(5)

Based on the equation for −3 < p < −1 and a > 0 [17]:

(6)

the double integrals in equation (2) can be reduced to

(7)

Thus, based on GOA, the AOA variances for plane and spherical wave can be rewritten as

(8)

It is found that under GOA, the AOA variances are independent to λ. This property has been confirmed under various situations [15, 16, 18].

2.2. AOA Variances for a Gaussian Wave

The Gaussian beam is a representative type of the electromagnetic wave, with normally distributed transverse electric field and intensity [19]. The mathematical description of a Gaussian wave usually depends on the wavelength λ and the waist radius w₀. For the optical wireless communication, more parameters are necessary to determine the location of both the transmitter and the receiver. The curvature parameter Θ₀ = 1 − L/R₀ and the Fresnel ratio , two nondimensional scalars, are related to the transmitter, where R₀ is the radius of curvature of the phase wavefront at the transmitter and W₀ is the radius where the intensity reduces to 1/e² of the axial values at the transmitter. Similarly, there are also three nondimensional scalars, the refraction parameter , the complementary parameter , and the diffraction parameter Λ = λL/πW², related to the receiver, where is the beam radius in a vacuum at the receiver.

It is known that both plane and spherical waves are particular types of the Gaussian waves; therefore, their AOA variances should take the form as follows:

(9)

For the given Gaussian wave with arbitrary values of Λ and Θ, it is difficult to achieve the analytic formulae of

. As an alternative,

may be approximatively expressed by

and

. On the one hand, according to the definition of Λ, it follows that

(10)

On another hand, equation (8) implies that, under GOA, both

and

are independent to λ. Thus, a heuristic inference can be made that

may be insensitive to the change of Λ when d > l_F, i.e.,

(11)

Furthermore,

may be closely approximated by a simple linear relationship in Θ, i.e.,

(12)

Equation (12) is inspired by [20], which investigated the on-axis scintillation index for a Gaussian wave in the saturation regime.

3. Numerical Simulations

This section adopts the Monte Carlo method to validate equations (11) and (12), respectively. In our simulations, the distorted equiphase wavefront is generated by the stochastic phase screen with the first 496 terms of the Zernike polynomials, whose theoretical formulae are presented in Section 4.1. Afterwards, over 50 points are stochastically sampled on the surface of the distorted equiphase wavefront, and the corresponding AOA can be computed by their normal vectors. For each combination of optical parameters, the simulations are repeated 100 times, and the AOA variance can be statistically estimated by the empirical data. Other default settings are listed as follows: α ∈ {3.2, 3.5, 3.8}, , λ = 1.55 × 10⁻⁶ m, k ≈ 4.05 × 10⁶rad/m, L = 4000 m, and d = 0.1 m > l_F = 0.078 m.

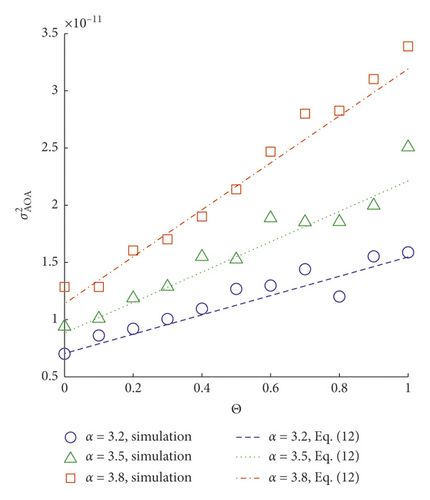
To validate equation (12), Λ is fixed at 0, whereas Θ is assigned to 11 points linearly spaced between and including 0 and 1. Particularly, Θ = 1 refers to the plane wave, and Θ = 0 refers to the spherical wave. The simulation results are depicted in Figure 1, where the dots stand for the experimental values, and the lines stand for the theoretical values. It can be identified that there is linear relationship between and Θ. Thus, equation (12) is valid within the range of the allowable error.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Validation of equation (12).

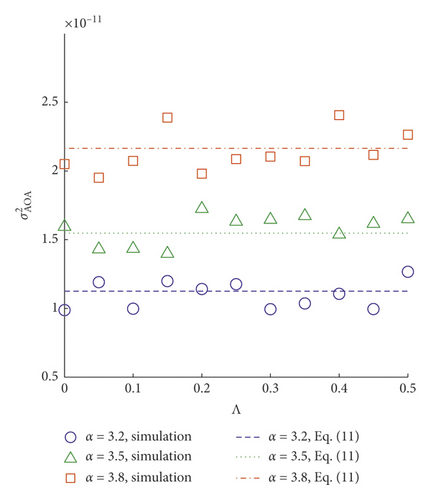
To validate equation (11), Θ is fixed at 0.5. Considering that the optical wireless communication systems usually adopt the collimators to parallel the outgoing beam at the transmitting antenna, Λ is assigned to 11 points linearly spaced between and including 0 and 0.5. Figure 2 illustrates the simulation results. It is evident that due to the observational errors, the experimental values of fluctuate around the theoretical values of , and the margin of the relative error is less than 15%. Thus, equation (11) is valid for d > l_F. This phenomenon can be explained physically. The validity of equation (11) is associated with the validity of equation (10). The condition “d > l_F” ensures the validity of GOA, which implies that diffraction effects are negligible and can be generally characterized by the limiting case with λ⟶0. Hence, equation (10) is valid under GOA.

4. Conclusions

This paper investigates the AOA variance for a Gaussian wave propagating through the weak non-Kolmogorov turbulence along a horizontal link. An empirical model is deduced from the results of plane and spherical waves under the GOA. The stochastic phase screens based on the Zernike terms are generated to validate the proposed model. The numerical simulations indicate that, under the GOA:

(1)
The AOA variance for a Gaussian wave is insensitive to the change of the diffraction parameter
(2)
The AOA variance for a Gaussian wave can be closely approximated by a simple linear relationship in the refraction parameter

These two points ensure the validity of our proposed model.

It should be pointed out that the phase screen based on the Zernike terms is capable of characterizing the low-frequency component, but is insufficient to describe the high-frequency component. However, the high-frequency component, associated with the small-scale turbulent eddies, makes little contribution to the phase fluctuation of laser beam. Considering that AOA is directly connected with the phase fluctuation, the forementioned weakness could hardly invalidate the conclusions.

4.1. Stochastic Phase Screen with Zernike Polynomials

The Zernike polynomials are a set of binary functions orthogonal on the unit disk, whose expressions in the polar coordinate system take the form [21]:

(13)

where j = (n, m) is the index ordered by Noll’s sequence, ρ is the radius, and θ is the azimuth. R_n,m(ρ) is the radial component:

(14)

and A_m(θ) is the angular component:

(15)

Let Ψ be the distorted equiphase wavefront. It can be decomposed as [22, 23]

(16)

where c_j are undetermined coefficients. To generate the stochastic phase screen, the covariance between c_j1 and c_j2 should be

(17)

where j1 = (n1, m1), j2 = (n2, m2), r₀ is the Fried coherent length, and

(18)

N_n1,n2 is the factor related to the radial degrees:

(19)

and M_m1,m2 is the logical Kronecker symbol related to the azimuthal frequencies:

(20)

The covariance matrix C about {c_j} is real and symmetrical, so there must be a unitary matrix U such that S = UCU^T is diagonal. U can be obtained by the singular value decomposition. R is a Gaussian random variable, with zero mean and variance given by S. The components of the vector U^TR are the desired Zernike coefficients c_j.

The influences of Θ and Λ on the stochastic phase screen can be delivered by r₀. In the weak fluctuation region [24],

(21)

where

(22)

4.2. Tangent Plane and Normal Vector

The equiphase wavefront generated by the stochastic phase screen can be regarded as a surface S in the three-dimensional space. Mathematically, S can be described by the implicit function

(23)

If these partial derivatives ∂F/∂x, ∂F/∂y and ∂F/∂z are continuous over S, and

(24)

S is called smooth.

For arbitrary point P₀ = (x₀, y₀, z₀) ∈ S, its tangent plane is

(25)

and the corresponding normal line takes the form as follows:

(26)

The normal vector

is orthogonal to the tangent plane.

For the stochastic phase screen with the Zernike polynomials, the equiphase wavefront takes the form as

(27)

with the normal vector

. Particularly,

is the normal vector of the undistorted equiphase wavefront.

Since AOA can be defined as the angle between the normal vector of the distorted and undistorted equiphase wavefront, it follows that

(28)

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

The authors want to thank Lingling SU from Chengdu CORPRO Technology Co., Ltd., Lingjun LI from Chengdu Technology University, and Yueting ZHOU from Patent Examination Cooperation Jiangsu Center of the Patent Office, CNIPA.

Open Research

Data Availability

The data used to support the findings of this study are available within the article.

References

1 Andrews L. C. and Phillips R. L., Laser Beam Propagation through Random Media, 2005, 2nd edition, SPIE Press, Bellingham, WA, USA.
10.1117/3.626196
Google Scholar
2 Mansour A., Mesleh R., and Abaza M., New challenges in wireless and free space optical communications, Optics and Lasers in Engineering. (2017) 89, no. 1, 95–108, https://doi.org/10.1016/j.optlaseng.2016.03.027, 2-s2.0-84966589434.
10.1016/j.optlaseng.2016.03.027
Web of Science® Google Scholar
3 Kaushal H. and Kaddoum G., Optical communication in space: challenges and mitigation techniques, IEEE Communications Surveys & Tutorials. (2017) 19, no. 1, 57–96, https://doi.org/10.1109/comst.2016.2603518, 2-s2.0-85027695956.
10.1109/COMST.2016.2603518
Web of Science® Google Scholar
4 Cui L. and Cao L., Angle of arrival fluctuations of optical waves considering finite turbulence outer scale under anisotropic turbulence, Optik. (2016) 127, no. 8, 3820–3827, https://doi.org/10.1016/j.ijleo.2016.01.090, 2-s2.0-84959018343.
10.1016/j.ijleo.2016.01.090
Web of Science® Google Scholar
5 Du W., Yang J., Gong Q. et al., Angle of arrival fluctuations for optical waves propagating through joint moderate to strong atmospheric turbulence, Journal of Russian Laser Research. (2016) 37, no. 1, 82–90, https://doi.org/10.1007/s10946-016-9547-y, 2-s2.0-84959452093.
10.1007/s10946-016-9547-y
Web of Science® Google Scholar
6 Cui L., Xue B., and Zhou F., Generalized anisotropic turbulence spectra and applications in the optical waves’ propagation through anisotropic turbulence, Optics Express. (2015) 23, no. 23, 30088–30103, https://doi.org/10.1364/oe.23.030088, 2-s2.0-84956977732.
10.1364/OE.23.030088
PubMed Web of Science® Google Scholar
7 Cui L. and Xue B., Influence of asymmetry turbulence cells on the angle of arrival fluctuations of optical waves in anisotropic non-Kolmogorov turbulence, Journal of the Optical Society of America A. (2015) 32, no. 9, 1691–1699, https://doi.org/10.1364/josaa.32.001691, 2-s2.0-84943424494.
10.1364/JOSAA.32.001691
Google Scholar
8 Cui L., Xue B., Cao X., and Zhou F., Angle of arrival fluctuations considering turbulence outer scale for optical waves’ propagation through moderate-to-strong non-Kolmogorov turbulence, Journal of the Optical Society of America A. (2014) 31, no. 4, 829–835, https://doi.org/10.1364/josaa.31.000829, 2-s2.0-84898068769.
10.1364/JOSAA.31.000829
CAS Google Scholar
9 Cui L., Cao X., Xue B., and Cao L., Analysis of angle-of-arrival fluctuations for optical waves propagating through weak non-Kolmogorov turbulence, Optics Communications. (2013) 305, no. 5, 36–41, https://doi.org/10.1016/j.optcom.2013.04.057, 2-s2.0-84878548279.
10.1016/j.optcom.2013.04.057
CAS Web of Science® Google Scholar
10 Cao B., Cui L., Xue W., Bai X., and Zhou F., Theoretical expressions of the angle-of-arrival variance for optical waves propagating through non-Kolmogorov turbulence, Optics Express. (2011) 19, no. 9, 8433–8443, https://doi.org/10.1364/oe.19.008433, 2-s2.0-79955415583.
10.1364/OE.19.008433
PubMed Web of Science® Google Scholar
11 Toselli I., Agrawal B., and Restaino S., Light propagation through anisotropic turbulence, Journal of the Optical Society of America A. (2011) 28, no. 3, 483–488, https://doi.org/10.1364/josaa.28.000483, 2-s2.0-79952347438.
10.1364/JOSAA.28.000483
Google Scholar
12 Tan L., Du W., and Ma J., Effect of the outer scale on the angle of arrival variance for free-space-laser beam corrugated by non-Kolmogorov turbulence, Journal of Russian Laser Research. (2009) 30, no. 6, 552–559, https://doi.org/10.1007/s10946-009-9111-0, 2-s2.0-74449092289.
10.1007/s10946-009-9111-0
Web of Science® Google Scholar
13 Du W., Yu S., Tan L., Ma J., Jiang Y., and Xie W., Angle-of-arrival fluctuations for wave propagation through non-Kolmogorov turbulence, Optics Communications. (2009) 282, no. 5, 705–708, https://doi.org/10.1016/j.optcom.2008.11.006, 2-s2.0-58249130912.
10.1016/j.optcom.2008.11.006
CAS Web of Science® Google Scholar
14 Xie I., Andrews L. C., Phillips R. L., and Ferrero V., Free space optical system performance for a Gaussian beam propagating through non-Kolmogorov weak turbulence, IEEE Transactions on Antennas and Propagation. (2009) 57, no. 6, 1783–1788, https://doi.org/10.1109/tap.2009.2019871, 2-s2.0-67649407560.
10.1109/TAP.2009.2019871
Web of Science® Google Scholar
15 Toselli I., Andrews L. C., and Phillips R. L., Angle of arrival fluctuations for free space laser beam propagation through non-Kolmogorov turbulence, Proceedings of SPIE—The International Society for Optical Engineering, May 2007, Orlando, FL, USA.
Google Scholar
16 Gao C., Li Y., Miao M., Liang H., and Li X., A heuristic model of aperture-averaged angle-of-arrival variance for a Gaussian wave through anisotropic non-Kolmogorov turbulence, Proceedings of SPIE Fourth International Conference on Optical and Photonics Engineering, April 2016, Belgium, China.
Google Scholar
17 Gradshteyn I. S. and Ryzhik I. M., Table of Integrals, Series, and Products, 2014, 8th edition, Academic Press, Waltham, MA, USA.
Google Scholar
18 Cheon Y. and Muschinski A., Closed-form approximations for the angle-of-arrival variance of plane and spherical waves propagating through homogeneous and isotropic turbulence, Journal of the Optical Society of America A. (2007) 24, no. 2, 415–422, https://doi.org/10.1364/josaa.24.000415, 2-s2.0-33847336017.
10.1364/JOSAA.24.000415
Google Scholar
19 Gao C. and Li X., Effects of inner and outer scale on beam spreading for a Gaussian wave propagating through anisotropic non-Kolmogorov turbulence, Optica Applicata. (2017) 47, no. 1, 63–74.
Web of Science® Google Scholar
20 Andrews L. C., Al-Habash M. A., Hopen C. Y., and Phillips R. L., Theory of optical scintillation: Gaussian beam wave model, Waves in Random Media. (2001) 11, no. 3, 271–291, https://doi.org/10.1088/0959-7174/11/3/306.
10.1080/13616670109409785
Google Scholar
21 Noll R. J., Zernike polynomials and atmospheric turbulence∗, Journal of the Optical Society of America. (1976) 66, no. 3, 207–211, https://doi.org/10.1364/josa.66.000207, 2-s2.0-0016932959.
10.1364/JOSA.66.000207
Web of Science® Google Scholar
22 Li Y., Zhu W., and Rao R., Simulation of random phase screen of non-Kolmogorov atmospheric turbulence, Infrared and Laser Engineering. (2016) 45, no. 12, 162–169, https://doi.org/10.3788/irla20164512.1211001.
10.3788/irla20164512.1211001
Google Scholar
23 Roddier N. A., Atmospheric wavefront simulation using Zernike polynomials, Optical Engineering. (1990) 29, no. 10, 1174–1180, https://doi.org/10.1117/12.55712, 2-s2.0-0025503438.
10.1117/12.55712
Web of Science® Google Scholar
24 Kotiang S. and Choi J., Wave structure function and long-exposure MTF for laser beam propagation through non-Kolmogorov turbulence, Optics & Laser Technology. (2015) 74, no. 1, 87–92, https://doi.org/10.1016/j.optlastec.2015.05.011, 2-s2.0-84935924744.
10.1016/j.optlastec.2015.05.011
Web of Science® Google Scholar

Citing Literature

All articles

An Empirical Model of Angle-of-Arrival Variance for a Gaussian Wave Propagation through Non-Kolmogorov Turbulence

Abstract

1. Introduction

2. Theoretical Models

2.1. AOA Variances for Plane and Spherical Waves

2.2. AOA Variances for a Gaussian Wave

3. Numerical Simulations

4. Conclusions

4.1. Stochastic Phase Screen with Zernike Polynomials

4.2. Tangent Plane and Normal Vector

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

An Empirical Model of Angle-of-Arrival Variance for a Gaussian Wave Propagation through Non-Kolmogorov Turbulence

Abstract

1. Introduction

2. Theoretical Models

2.1. AOA Variances for Plane and Spherical Waves

2.2. AOA Variances for a Gaussian Wave

3. Numerical Simulations

4. Conclusions

4.1. Stochastic Phase Screen with Zernike Polynomials

4.2. Tangent Plane and Normal Vector

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information