In order to promote mutual trust and win-win cooperation between the users and the providers, we propose a trust-game-based access control model for cloud service in the paper. First, we construct a trust evaluation model based on multiple factors, such as the direct trust, feedback trust, reward punishment, and trust risk and further propose a weight method by maximum discrete degree and information entropy theory; second, we combine trust evaluation with the payoff matrix for game analysis and calculate the mixed Nash equilibrium strategy for the users and service providers; third, we give the game control condition based on trust level prediction and payment matrix to encourage participants to make honest strategy. Experimental results show that our research has good effect in terms of acceptance probability, deception probability, accuracy of trust evaluation, and cooperation rate in the cloud service.

1. Introduction

Cloud computing is a very popular technology in the field of information technology and is highly valued by the government, academia, and industry [1, 2]. For example, Apple and Amazon have launched cloud computing services, which allow personals and organizations to use dynamic computing infrastructure based on needs. Convenient and fast services are the core advantages of cloud computing, but cloud computing services have a lot of security problems, which have attracted widespread attention in the industry [3]. So, it is necessary to choose a good solution for requirement of customer in terms of service quality and cost.

1.1. Motivation

With the development in information technology, many fraud incidents have damaged the interests of transaction entities and brought crisis to cloud services [4]. In cloud computing, each entity will choose favorable action strategies according to the actual environment and benefits, and these strategies will eventually reach a mutually constrained equilibrium state.

The process of trust is a bargaining game process. Applying game theory to trust construction provides a new way for cloud computing services. Because the decision-making strategies of different trust levels are different, the control strategy depends on the game analysis of both sides, rather than their own unilateral inference. However, trust is a complex process based on multifactor decision-making, which involves interactive history, and direct and recommend trust management [5]. Because of the coexistence of trust and risk, it is very one-sided and dangerous to rely on trust level alone in decision-making. Therefore, it is necessary to combine behavioral trust and game analysis to analyze the payment matrix of both sides and calculate the mixed Nash equilibrium strategy based on the attribute of user’s behavior.

Access control is also an important security mechanism to prevent malicious users from illegally accessing [5–7]. However, due to the large number of dynamic users and services, how to authenticate the access security and mutual trust of outsourcing data is a problem [8, 9]. Game theory provides many mathematical frameworks for analysis and decision process of network security, trust, and privacy problems. In fact, service providers and users play different roles of complexity, which need further detailed analysis from three disciplines: access control, trust evaluation, and game theory [8, 10–12].

1.2. Contributions

In this paper, we propose a trust-game-based access control model for cloud service, which is one of the types of dynamic models, each access is modeled as a game between the subjects and objects, and the result of the game services is used as the basis for authorization decision. The main contributions of our article are as follows:

(1)
We construct a trust model based on multiple factors, such as the direct trust, reward punishment, feedback trust, and trust risk, and the weight factor is determined by maximum discrete degree and information entropy.
(2)
We combine the trust evaluation results with the payoff matrix for game analysis and calculate the mixed Nash equilibrium strategy for the users and service providers.
(3)
We give the game control condition based on trust prediction and payment matrix to encourage subjects for honest access.

The rest of this paper is structured as follows. In Section 2, we review some related research in access control, game theory, and trust management in cloud services. In Section 3, we propose a method of trust evaluation in the cloud environments. In Section 4, in order to motivate both sides to behave in an honest manner, we make use of trust-game-based access control model to calculate the mixed strategy Nash equilibrium for users and service providers. In Section 5, we design several related experiments. Simulation results show the superiority of our research in the cloud service. Finally, in Section 6, we conclude the current research and discuss some future work.

2. Related Work

In the basic idea of access control based on game theory, service providers decide whether to open information to users according to income matrix to maximize their own benefit, which is suitable for dynamic and complex cloud service environment [8, 9].

Many researchers have applied access control, trust, and risk assessment to deal with security and privacy problems in dynamic environments [6, 9]. Chunyong et al. [7] studied the hybrid recommendation algorithm for large data based on optimization and constructed some trust models, and the results showed that the error was reduced compared with the traditional method. Considering the practical existence and involvement of permission risk, Helil et al. [12] constructed a non-zero-sum game model that chose trust, risk, and cost as metrics in the payoff functions of player and analyzed the Pareto efficient strategy from the application system and the user. Based on game theory, Furuncu and Sogukpinar [13] proposed an extensible security risk assessment model in cloud environment, which can assess whether the risk should be determined by the cloud provider or tenant.

Njilla and Pissinou [14] proposed a game theoretic framework in cyberspace, which can optimize the trust between the user and the provider. Baranwal and Vidyarth [15] proposed a new license control framework based on game theory in the cloud computing, and the results showed that there were a dominant strategy and Nash equilibrium in pure strategy. He and Sun [16] used the game theory model to study the impact of the adversary’s strategy and the accuracy requirements on defense performance.

Mehdi et al. [17] proposed a method of identifying and confronting malicious nodes. The outcome was determined by the game matrix that contained the cost values of the possible action combination. Kamhoua et al. [18] proposed a zero-sum game model to help online social network users determine the best strategy for sharing data. It is difficult for peer-to-peer network to identify random jammer attacks. Garnaev et al. [19] proposed an attack model based on Bayesian game and proved the convergence of the algorithm. LTE networks are vulnerable to denial of service and service loss attacks. Aziz et al. [20] proposed a strategy algorithm based on repeated game learning, which can recover most of the performance loss.

Considering the social effects represented by the average population, Salhab and Malhamé [21] proposed a collective dynamic choice model and proved that the dispersion strategy of the optimal tracking trajectory was an approximate Nash equilibrium. Wang and Cai [22] proposed a trust measurement model of a social network based on game theory and solved the free-rider problem by the punishment mechanism. From the perspective of noncooperative game theory, Hu et al. [23] studied the multiattribute cloud resource allocation and proposed both ESI (equilibrium solution iterative) and NPB (near-equalization price bidding) algorithms to obtain Nash equilibrium solution.

Cardellini and Di Valerio [24] proposed a game theory approach to the service and pricing strategy of cloud systems. Furthermore, they proposed SSPM (Same Spot Price Model) and MSPM (Multiple Spot Prices Model) strategies for IAAS suppliers. Based on contextual feedback from different sources, Varalakshmi and Judgi [25] proposed a reliable method to select service providers, which can filter unfair feedback nodes to improve transaction success rate and help customers to select suppliers more accurately. Gao and Zheng [26] studied the acceptance of reputation-based access control system, which was constructed by applying a compensation mechanism to improve the utility and punishment mechanism of users in the cloud computing.

3. Trust Computation

Trust computing needs multiple factors, and we introduce the direct trust, feedback trust, reward punishment, trust risk, and so on. In addition, the weight of the trust factor is determined by information entropy and maximum dispersion; in order to the convenience of reading this paper, some symbols are given in Table 1.

Table 1. Meanings of symbols.

Symbols	Meanings
D₁, D₂, …, D_Z ∈ D(S)	Z entities of system
Y₁, Y₂, Y₃, Y₄, Y₅	Trust function
ω_m	Weight of trust function
TG(D_i, D_j, S, t)	Trust between D_i and D_j
TS = (T₁, T₂, …, T_i, …, T_N)	N level trust level
ψ(TG(D_i, D_j))	Trust decision
T⁽ⁱ⁾	Decay time factor
R(D_i, D_j)	Risk function
S = {s₁, s₂, …, s_P}	Service level
Level	The level of a trust tree
ρ(F_k)	Feedback weight factor
F(D_i) = {F₁, F₂ … F_n}	Feedback entities of D_i
PT_i	Predicted probability of T_i
e_t	Evaluation error at time t

3.1. Trust Decision

In a trust decision system, authorization is determined by the trust map relationship. If D₁, D₂, …, D_Z ∈ D(S) denotes Z entities in the system, according to the different roles, they are divided into 2 types: service provider and user. If total trust evaluation functions have (Y₁(D_i, D_j), Y₂(D_i, D_j), …, Y_m(D_i, D_j)) between D_i and D_j, (D_j ∈ D(S)), the decision sets are expressed by the Y = (Y₁, Y₂, …, Y_M), 0 ≤ Y_m(D_i, D_j) ≤ 1, (m = 1,2, …, M). Let ω_m express weight factor of Y_m(D_i, D_j), the constraint condition is expressed as follows:

()

TG(D_i, D_j, S, t) represents the total trust evaluation value between entity D_i and entity D_j, and it can be expressed as follows:

()

where S is the service provided by D_j, the quality of service can be determined by trust evaluation, the value of TG(D_i, D_j, S, t) is higher, the quality of service is better, and t is the interactive time stamp.

Assume that TG(D_i, D_j) can be divided N level TS = (T₁, T₂, …, T_i, …, T_N), 0 ≤ T_i ≤ 1(i = 1,2, …, N). TS is an order division of space, service provider can provide service set S = {s₁, s₂, …, s_P}, S is an order division space, and the ψ(TG(D_i, D_j)) between S = {s₁, s₂, …, s_P} and TG(D_i, D_j) is defined as follows:

()

TS = (T₁, T₂, …, T_i, …, T_N) is determined by the application requirement in the network environment, and permission is determined by the trust value. For example, a cloud application system provides 3 levels of services, S = (s₁, s₂, s₃): s₁ represents denial of service, s₂ represents the reading services, and s₃ represents both reading and writing services. The corresponding decision space is TS = {T₁, T₂} = {0.3, 0.5}, the trust decision function can be expressed as follows: . If the trust value of D_i is TG(D_i, D_j) = 0.2, then the decision result is ψ(TG(D_i, D_j)) = ψ(0.2) = s₁ = deny.

3.2. Fuzzy Trust Level

Discrete trust level is conducive to the normalization and quantification of the trust evaluation, and we introduce the concept of fuzzy [27]. We set the fuzzy center value of adjacent trust values to 1 : 1.3 (Table 2), and some overlap is used to represent the trust evaluation.

Table 2. Trust level description.

Trust level	Description	Trust value
T₅	Distrust	(0, 0.26, 0.34)
T₄	Doubt	(0.26, 0.34, 0.44)
T₃	Common trust	(0.34, 0.44, 0.57)
T₂	Middle trust	(0.44, 0.57, 0.74)
T₁	Very trust	(0.57, 0.74, 1)

If the trust level of TG(u) is T₅, according to the principle of fuzzy function, in order to describe the trust level, the probability of the T₅ is expressed as follows:

()

In formula (4), TG(u) represents the total trust value of the node u; furthermore, when TG(u) is in [0,0.26], the probability of T₅ is PT₅, PT₅ = (0.26 − TG(u))/(0.26 − 0) = (0.26 − TG(u))/0.26; when the trust value of TG(u) is in [0.26, 0.34], PT₅ = (0.34 − TG(u))/(0.34 − 0.26) = (0.34 − TG(u))/0.08. If level of TG(u) is T₄, T₃, T₂, or T₁, the probability of the trust level can be calculated by formula (4).

3.3. Direct Trust

Direct trust is usually made up of multiple factors, and the relevant attributes can be selected from the interaction history.

3.3.1. Weight Calculation

In order to quantify the multiple indicators, we use the maximum entropy method to determine the factor weight. There are m users and n attributes of direct trust evaluation, matrix E(D) is as presented in formula (5), and e_ij is the evaluation score of the ith user to the jth attribute:

()

Entropy weight method:

()

The jth attribute weight:

()

3.3.2. Time Decay Factor

In this section, t_i is the time span of the ith transaction,

is the start time of the ith transaction,

is the end time of the ith transaction, t₀ is the time of user successful registration, and n is the number of interaction times between the service provider and user, so the decay time factor T⁽ⁱ⁾ is expressed as follows:

()

3.3.3. Calculation of Direct Trust

According to formulae (6)–(8), Y₁(D_i, D_j) is the direct trust evaluation between D_i and D_j, n is the number of interactive times, and it is as follows:

()

3.4. Feedback Trust

Feedback trust is based on the transfer content of entity, such as D_i trusts D_j, and D_j trusts D_k, so D_i also trusts D_k. Assume that D_i is a parent entity, all the neighbors are child nodes, a neighbor also has neighbor, so we can construct a multilevel weighted direction trust tree (WDT, a sample is shown in Figure 1), which is expressed as follows:

()

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

An example WDT of computation feedback trust.

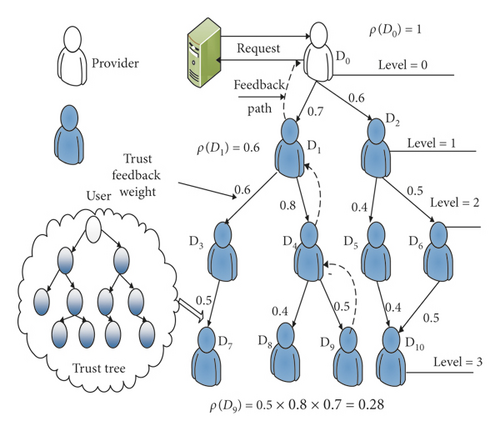
D(S) is a set of entity; DTR represents the direct trust relationship among entities; and Y₁ is the direct trust value. In the WDT, the level of the root entity is level = 0, the level of the direct neighbor of the root entity is level = 1, the level of neighbor’s neighbor is level = 2, and the rest of nodes can follow the arrangement in turn.

There are many recommendation paths in the procession of feedback trust, so how to select and aggregate path is a problem. Because the effects of each layer are different, we introduce feedback weight factor to adjust the polymerization accuracy. In an interaction, the entity D_j needs to evaluate the feedback trust value of the entity D_i, {F₁, F₂, …, F_l} is a feedback entity set, and F_k is a feedback entity, so the feedback trust function is defined as follows:

()

where l is the number of feedback entities; ρ(F_k) is the weight factor of feedback trust, in order to improve the speed of feedback trust computing, according to the “Six Degrees of Separation” [28], and it is expressed as follows:

()

Y₁(D_m, D_n) represents the direct trust value from D_m to D_n, according to formula (10), and level is the level of the feedback trust. Such as an interesting illusion example in Figure 1, level = 1, ρ(D₁) = 0.6; level = 2, ρ(D₃) = 0.7 × 0.6 = 0.42; level = 3, ρ(D₉) = 0.8 × 0.7 × 0.5 = 0.28. If the entity D₀ needs the feedback trust of the entity D₁₀ and there are two entities D₅ and D₆ interacting with D₁₀, the direct trust value is Y₁(D₅, D₁₀) = 0.4, Y₁(D₆, D₁₀) = 0.5. According to formula (12), ρ(D₅) = 0.4 × 0.6 = 0.24 and ρ(D₆) = 0.5 × 0.6 = 0.30. According to both formula (11) and formula (12), Y₂(D₀, D₁₀) = (0.24^∗0.4 + 0.3^∗0.5)/(0.24 + 0.3) ≈ 0.45.

3.5. Reward Punishment

In the process of trust evaluation, the honest entities should be rewarded; the malicious entities must be punished. Therefore, we introduce reward punishment function to encourage participants to take honest actions, which is expressed by using the following formula:

()

where ∑_BF(D_i, D_j) represents the number of failure times and B is the number of transaction times.

3.6. Trust Risk

Trust and risk are closely related; according to the perspective of service [5], risk function can be expressed as follows:

()

where s_j represents the quality of service provider of D_j. The value of s_j is greater, and the risk is greater, so the risk is positive proportional to the s_j. Trust risk function refers to the cognition between service providers and users, which can be expressed as follows:

()

According to formulas (14) and (15), risk and service have an inverse proportional relationship between Y₄(D_i, D_j) and R(D_i, D_j).

3.7. Weight of Trust Attribute

The effect of multiple attributes is different, and we propose a weight method to determine the weight based on maximum discrete degree. Let W = (ω₁, ω₂, …, ω_m) be weight factor vector of trust attribute function, according to literature [29], “Or metric method” is represented as

; the discrete degree is expressed by the

, which reflects the participation degree of each attribute, further deduction, 0 ≤ Disp(W) ≤ ln m. In a word, W = (ω₁, ω₂, …, ω_m) meets the following three conditions:

()

From formula (16) and the maximum dispersion principle [29], we can obtain these following formulas:

()

In the practical application, we can set a series of reasonable values of α and calculate ω₁, ω_i, and ω_m by formulas (18)–(20). Next, according to these above descriptions, we introduce Algorithm 1 to determine the values of different trust attributes.

Algorithm 1: Weight of the trust attribute.

(1)
if 0 < m ≤ 2
(2)
then ω₁ = a,
(3)
ω₂ = 1 − a;
(4)
if m > 2
(5)
then ,
(6)
ω_m = ((m − 1)α − m)ω₁ + 1/(m − 1)a + 1 − mω₁;
(7)
for i = 2 to m − 1 do
(8)
;
(9)
when ω₁ = ω₂ = ⋯ = ω_m = 1/m
(10)
⟹disp(W) = ln m, a = 0.5;
(11)
End.

In Algorithm 1, the classification weight vector is mainly determined by m and α. m is a certain value, and the key is how to reasonably determine the value of the α. According to Table 3, if α = 0, then ω₁ = 1, ω₂ = ω₃ = ⋯ = ω_m = 0; if α = 1, then ω_m = 1, and ω₁ = ω₂ = ⋯ω_i = ⋯ = ω_m−1 = 0; if α = 0.5, then ω₁ = ω₂ = ⋯ = ω_i = ⋯ = ω_m = 1/m, when 0 < α < 1, a ≠ 0.5, we get different values of ω_i.

Table 3. (ω₁, ω₂, ω₃, ω₄) for different values of a.

Weight	a = 0	a = 0.1	a = 0.2	a = 0.3	a = 0.4	a = 0.5	a = 0.6	a = 0.7	a = 0.8	a = 0.9	a = 1.0
ω₁	0.00	0.0104	0.0145	0.0983	0.1647	0.2500	0.3474	0.4612	0.5965	0.7646	1.00
ω₂	0.00	0.0434	0.1065	0.2756	0.2133	0.2500	0.2722	0.2757	0.2757	0.1818	0.00
ω₃	0.00	0.1821	0.2520	0.4614	0.2722	0.2500	0.2133	0.1647	0.1647	0.0433	0.00
ω₄	1.00	0.7641	0.5965	0.1647	0.3474	0.2500	0.1647	0.0451	0.0451	0.0103	0.00

3.8. Total Trust

Total trust reflects the overall subjective judgment of the object in the network environment, according to requirement of the trust evaluation model, we introduce Algorithm 2 to compute the total trust value.

Algorithm 2: Total trust value.

Input: Y₁, Y₂, Y₃, Y₄, and ω_m
Output: total trust value
(1)
Calculate direct trust function Y₁, feedback trust function Y₂, reward punishment function Y₃, and trust risk function Y₄,
(2)
Calculate the weight ω_m of the trust attribute function (Algorithm 1);
(3)
Calculate total trust TG(D_i, D_j, S, t).

4. Trust-Game-Based Access Control

Essentially, access control can be regarded as a game between the users and the service providers in the cloud computing environment. From the perspective of the service provider, access authorization is the payoff, and long-term protection services can be rewarded [14], and these meanings of different related game parameters are described in Table 4.

Table 4. Symbols of game parameter.

Symbol	Definition
	The average loss of the service provider in accepting the user’s deception access
	The average benefit of the service provider in accepting the user’s honest access
	The average loss of the service provider in rejecting an honest access of the user
	The user’s extra benefit of deception access
	The average benefit of user of honest access
Ucost	The cost of deception for a user
Upunish	The punishment of user for deception
A_i	Payment matrix of service provider
B_i	Payment matrix of user
γ_k ∈ [0,1], (k = 1, …, 6)	Parameter factor of the game
y^∗	Deception probability of user
x^∗	Acceptation probability of provider

4.1. Game Theory

Game theory describes the decision scenario where each player chooses an action to obtain the best benefit [22, 24]. A game includes several basic elements [30]:

(1)
Player: it is a basic entity in a game that is responsible for making choices for certain behaviors. A player can represent a person, a machine, or a group of individuals in a game.
(2)
Strategy: it is the action plan that player can take during the game.
(3)
Order: it is the sequences of strategy chosen by the player.
(4)
Payoff: it is a positive or negative reward for player ‘s specific action in the game.
(5)
Nash equilibrium: it is a solution for a game involving two or more players in which each player is assumed to know the equilibrium strategy of the other players and no player can gain benefit by changing his or her strategy [25].

4.2. Game Analysis

In a dynamic game, strategy and trust are closely related, which can reach the equilibrium by continuous amendment. If the service providers accept the honest access of users, both the service provider and the user can obtain win-win benefits which are and , respectively; if the service provider accepts the deception access of user, then it has no benefit and only losses ; in addition to , the user can also get by deception behavior. Obviously, users can suffer losses because of deception behaviors, the cost is Ucost, and Upunish is punishment for users. If the service provider rejects the user’s access request, he/she has no income and no loss; if user has the intent to cheat, he/she also must pay Ucost.

Because the user’s trust level is different, the payment matrix is different. We divide the trust from high to low level and set the user trust level i, (i = 1,2, …, N); then, the payment matrix of service provider and user are A_i and B_i, respectively, and can get the following formulas:

()

γ_k ∈ [0,1], (k = 1,2, …, 6) mainly depends on the trust level of division size and security and privacy requirements, and it can be adjusted according to the requirement of decision maker.

By the simple line drawing method, there is no pure strategy equilibrium in the game model, but a mixed strategy Nash equilibrium P₁ = (x, 1 − x) is established. Assume that the service provider chooses the acceptance probability x and reject probability 1 − x, and the service provider’s mixed strategy is P₁ = (x, 1 − x).

If the user chooses to deception probability y and honesty probability 1 − y, the mixed strategy is P₂ = (y, 1 − y), then the user’s expected payoff is formula (23). Taking the partial derivative of formula (23) with respect to y, the first-order optimal condition of the service provider is the following formula (24), making it equal to 0, and the acceptance probability x^∗ is formula (25):

()

In formula (25), the acceptance probability of the service provider is related to the payment of the user. Because 0 < x^∗ < 1 is true, further ; if , then x^∗ > 1, but that is not true. In addition, according to formula (25), in order to improve the acceptance probability, when the cost is constant, service providers can increase the average normal benefit and punishment of deception and reduce the benefits of user deception.

The advantage of the mixed strategy Nash equilibrium is that users can only get an uncertain game result. Although users know the payment matrix and decision probability of service providers, they do not know how to make decisions. In this game, the acceptance probability and reject the probability of service provider are x^∗ and 1 − x^∗, respectively, which can reduce the control cost of the service provider. Even if denial access is uncertain, the high probability of rejection threatens the user’s deception. If the rejection probability is less than 1 − x^∗, because the user is rational, according to formula (24), the best choice of user is deception strategy.

On the contrary, if reject probability is greater than 1 − x^∗, the optimal selection of user is honest access. In a word, if the reject probability of service provider is too low or too high, users can have the pure strategy choice; under the mixed strategy Nash equilibrium, the acceptance probability of service provider is x^∗, and reject probability is 1 − x^∗, there is no difference between the user’s choice of deception and honesty, and service providers do not provide users with any speculative opportunity. Next, we introduce Lemma 1 to express the relationship between trust level and payment.

Lemma 1. Both gain and loss of the service provider and the user are positively proportional to the user’s trust value.

Proof. In Section 4, the gain and loss of the service provider and the user are , , , , and . Assume that the trust levels of users U_i and U_j are T_i, T_j, i < j, i − j = Δ < 0 and γⁱ⁻¹/γ^j−1 = γ^{(i − 1)−(j − 1)} = γ^Δ, when γ ∈ [0,1], then γ^Δ > 1, so the ratio of the same payment value between user U_i and U_j is constant greater than 1, so their relationship is actively proportional. This Lemma 1 can be understood from the actual network application, the trust value of user is higher, and service providers and users can be in more in-depth cooperation.

The mixed strategy Nash equilibrium of the service provider has been calculated, but each specific evaluation is not determined, which also depends on the trust level of user and the probability of the other user′s decision. Because the evaluation strategies of users with different trust levels are different and the control strategy depends on the game result, this is not just one side inference, which is also the connotation of game theory [20, 22, 31]. Next, we give Lemma 2 to show the game control condition based on trust prediction and payment matrix.

Lemma 2. Assume that the prediction probability PT_i of the user trust level and the payment matrix of the service provider have been known, formula (26) is the control condition that the service provider accepts access:

()

Proof. Because the payment matrix of users of trust levels is different, PT_i can be predicted by fuzzy membership formula and trust evaluation model; furthermore, participants can judge the total revenue according to the strategy choice. Assume that the users and service providers are rational, they seek to play game in the most favorable way of payment and know that the mixed strategy Nash equilibrium is the optimal choice for both sides to ensure the maximum benefit of mutual transaction. The expected payment matrix function of the service provider can be expressed as follows:

()

We can derive the partial derivative of formula (27) for x, and the first-order optimization condition for the user is expressed as follows:

()

Further deduction, we can obtain the following formula of deception probability y^∗:

()

Here, (y^∗, 1 − y^∗) is the user’s Nash equilibrium of mixed strategy, and the payment matrix of the service provider is expressed as follows:

()

In fact, when the service provider’s acceptance probability is 1, these user’s choices are deception probability y^∗ and honest probability 1 − y^∗, respectively. According to formula (30), the first line represents that provider choose to accept access of user, the first column represents deception choice of user, and the second column represents honesty choice, so the benefit of service provider can be expressed as

()

Formula (31) is the benefit of service provider when the trust level of user is T_i. Because the trust level is uncertain, in order to obtain the total benefit of the user, and then determine whether the decision is or not, it needs a weighted sum of each trust level, and the total benefit of the provider is expressed as follows:

()

Solving formula (32), if this value is greater than zero, and the service provider′s benefit is greater than zero, then request is accepted; otherwise, access is denied.

5. Experiment and Analysis

Experiment hardware environment: 2 core CPU, clock 2.2 GHz, 8 GB memories, storage 500 GB; soft environment: Windows 10, 64 Bit. In addition, in order to objectivity, these experiments are divided into two parts: the synthetic data and real data.

5.1. Evaluation of Synthetic Data

Based on the parameters of trust and game model, we design relevant experiments by MATLAB 2015a, and specific numerical details are listed in Table 5.

Table 5. Values of parameters.

Trust level						Ucost	Upunish
T₁	1000	300	300	800	1000	200	350
T₂	550	250	250	700	900	200	300
T₃	250	200	200	580	800	200	240
T₄	180	150	150	450	700	200	200
T₅	130	100	100	300	600	200	150

5.1.1. Acceptance Probability

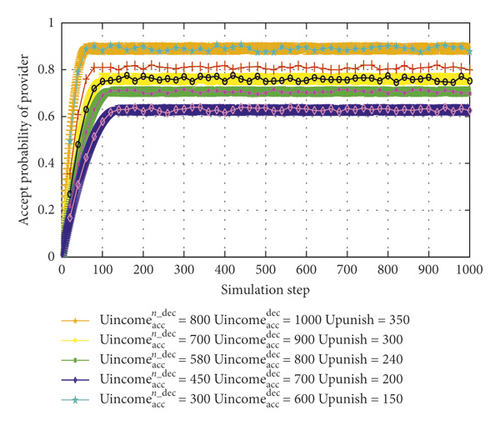
There are γ₃ = 0.7, γ₄ = 0.65, γ₅ = 0.7, and Ucost = 100; these values of , , and Upunish can be adapted by the trust level. According to formula (25), if sum between deception cost and normal average benefit is lower than the deception benefit, the user can choose deception action.

In Figure 2, with the , , and Upunish, the acceptance probability rises from 0.62 to 0.71, 0.76, 0.81, and 0.89.

5.1.2. Deception Probability

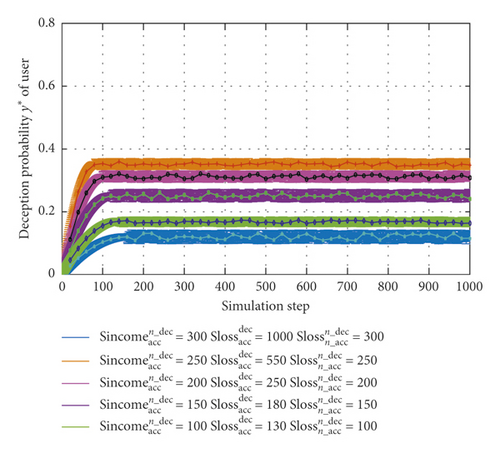
According to formulas (27) and (28) and Lemma 1, parameters can be set as γ₁ = 0.9, γ₂ = 0.3, and γ₆ = 0.3 and the value of , , can be adapted with the trust level. As can be seen from Figure 3, deception probability reduces from 0.35 to 0.29, 0.25, 0.17, and 0.12. These higher values of , , and are corresponded to lower deception probability.

5.1.3. Transaction Success Rate

In this section, successful transaction is that the users choose the honest access, and the service party accepts access.

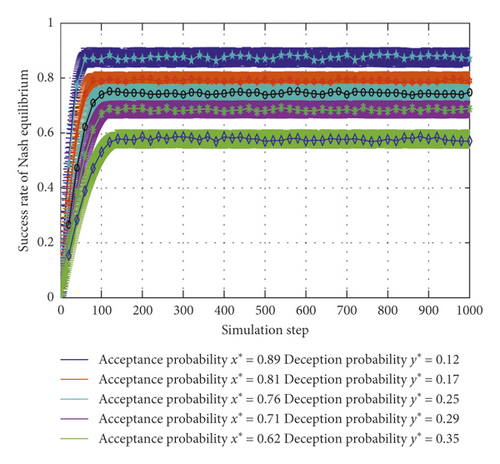
In Figure 4, according to the acceptance probability and deception probability in Figures 2 and 3, after the transaction is carried out to a certain stage, the success rates of five curves are about 0.88, 0.80, 0.70, 0.64, and 0.58, respectively; on further analysis, both a higher acceptation probability and a lower deception probability are corresponded to a better success rate.

5.1.4. Average Payoff of Participant

In the process of trust game, according to payment matrix formulas (23) and (27), it is necessary to compare benefits of game participants, according to values of parameters in Table 5 and Figures 2–4, and the specific results are shown in Figures 5 and 6.

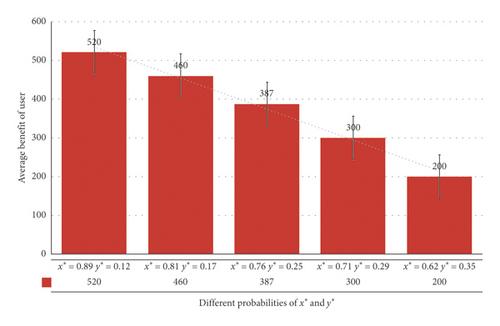
In Figure 5, the average benefit of user is 520, 460, 387, 300, and 200. On further analysis, when the deception probability becomes smaller, the acceptance probability becomes larger, and the user’s income also increases. This result validates Lemma 1 very well.

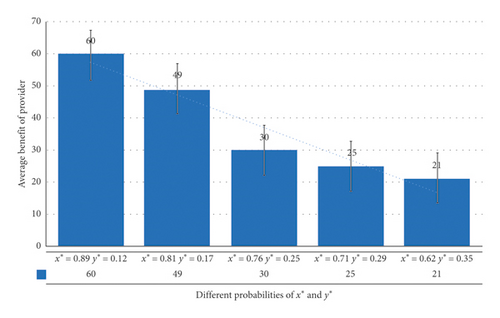
In Figure 6, the average benefit of provider is 60, 49, 30, 25, and 21. It is like Figure 5, when the deception probability of users becomes smaller, the acceptance probability becomes larger, and the benefit of service providers also increases. Same as Figure 5, this result validates Lemma 2 very well.

According to Figures 5 and 6, users get more benefit than service providers during the game process. Because service providers are market-oriented, which can provide many services to more users, thereby gain more revenue, this indirectly proves the effectiveness in promoting good faith and orderly transactions.

5.2. Evaluation of QWS Dataset

In this section, we design several experiments to compare TGAC (A Trust-Game-Based Access Control Model for Cloud Services) with RCST (an improved recommendation algorithm for big data cloud service based on the trust in sociology) [7] and FFCT (identifying fake feedback in cloud trust systems using feedback evaluation component and Bayesian game model) [19].

For the sake of fairness and credibility of experiments, these three models are evaluated by CloudSim 4.0; furthermore, we consider the QWS dataset on the http://www.uoguelph.ca/qmahmoud/qws/, which contains 5000 real services (Table 6).

Table 6. Attributes of QWS.

Attribute	Value
Cost	(0, 2000)
Response time (ms)	(0, 400)
Reputation	(1, 10)
Success rate	(0, 100)
Reliability	(0, 100)
Location	{Shanghai, Beijing, London}
Privacy	{Visible to anyone, visible to network, not visible}
Number of concurrent	(0, 1000)
Availability	(0, 100)

5.2.1. Cooperation Rate

In this section, we define honest access of user and real service provided by a service provider as a cooperation. The formula of cooperation rate between service providers and users is as follows:

()

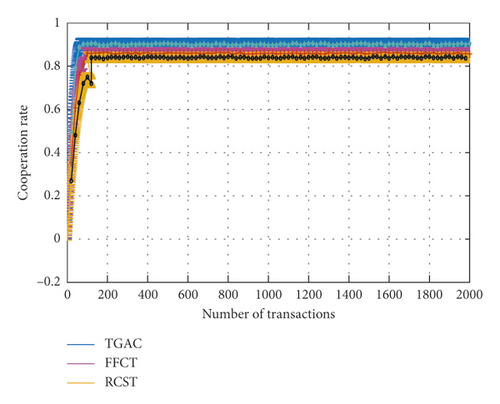
In Figure 7, the cooperation rate of TGAC, FFCT, and RCST is 0.902, 0.861, and 0.853, respectively. In the RCST, quantification of trust is relatively simple, which is difficult to deal with the complex situation, and thus affects mutual trust and transaction between the two sides in the cloud computing. Although FFCT plays a prominent role in identifying error feedback nodes, the lack of attribute weight model will result in accurately determining the role of trust attributes, which can lead to the reduction of mutual trust, and thus affects the cooperative transactions between the two sides. TGAC not only can make use of multiattribute trust algorithms but also can adjust the related parameters by feedback weight, reward punishment, and risk factors; furthermore, it can improve the cooperation rate by adjusting the relevance of honesty probability and deception parameters.

5.2.2. Accuracy Evaluation

Accuracy is used to check whether the proposed scheme algorithms can accurately and consistently provide trust calculation, which is often measured by the error. The smaller the error, the higher the accuracy. Assuming that A_t+1 is the actual trust value, TG_t+1 is the prediction trust value at time t + 1, and there are three methods for the accuracy of the trust evaluation.

MAD (mean absolute deviation) is used to measure the degree of deviation of evaluation results; thus, the closer its value is to 0, the higher the evaluation accuracy. It is expressed as follows:

()

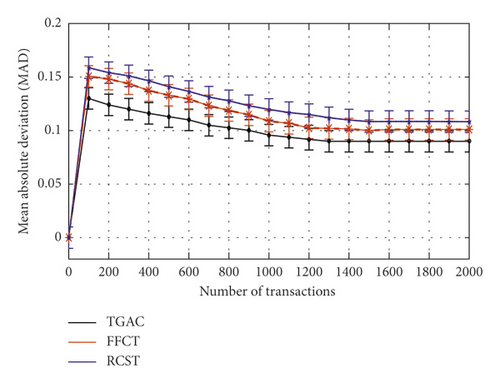
According to Figure 8, the average MAD of TGAC, RCST, and FFCT is stable at 0.090, 0.1081, and 0.1019, respectively. When the number of transactions is more than 1200, the curve of TGAC changes more smoothly than do those of FFCT and RCST, which indicates that fewer transactions enable our model to achieve a better accuracy level.

RMSE (root mean square error) is the variance of the arithmetic square root, which is used to measure the deviation between the evaluation value and the true value. If the RMSE is smaller, the performance of the algorithm is better. It is shown as follows:

()

According to Figure 9, the average RMSE of TGAC, RCST, and FFCT is stable at 0.0918, 0.1087, and 0.1025, respectively. When the number of transactions is more than 1200, the curve of TGAC changes more smoothly than those of FFCT and RCST, which indicates that fewer transactions enable our model to achieve a better accuracy value.

MAPE (mean absolute percentage error) is a measure method of error, which usually expresses accuracy as a percentage and can reflect the assuredness of the evaluation model. It is expressed by the following formula:

()

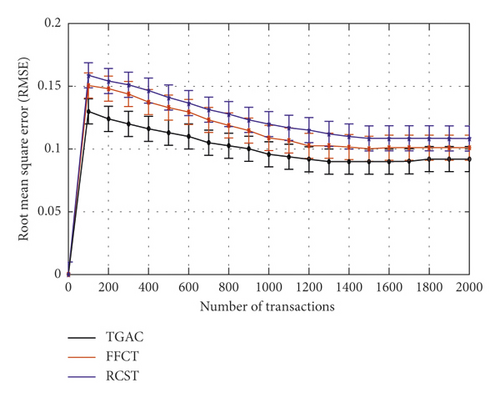
As can be seen in Figure 10, the average MAPE of TGAC, FFCT, and RCST is stable at 10.51%, 12.11%, and 12.75%, respectively. When the number of transactions is more than 1200, the MAPE fitting curve of TGAC changes more smoothly than the other two models, which indicate that fewer transactions can generate unbiased trust prediction. Based on comprehensive comparative analysis between Figures 8–10, TGAC has better accuracy than FFCT and RCST.

5.3. Application Example

According to the trust value of participant and the corresponding payoff matrix of the game model, we can forecast the probability of honesty access of user and acceptance of provider and thus adjust the corresponding parameters to achieve an equilibrium state.

5.3.1. Parameters

In this section, according to Section 3, trust is divided into very trust, trust, medium trust, doubt, and distrust, the probability PT_i is corresponded to five trust levels 0.1, 0.65, 0.1, 0.1, and 0.05, and the value of is 0.7, 0.95, 0.9, 0.85, 0.87, and 0.95, and these parameters , , , , , Ucost, and Upunish are shown in the second column to the eighth column of Table 7. These above parameters are put into formulas (21) and (25), the acceptance probability x^∗ of service provider and the deception probability y^∗ of user can be obtained under the mixed strategy Nash equilibrium, and specific results are shown in Table 7 from the ninth to the tenth column. PT_i, r_i, , , and x^∗ are put into formula (26), and the benefit of provider is calculated.

Table 7. Parameter initial value and calculation result.

Trust level						Ucost	Upunish	x^∗	y^∗
T₁	1000	100	100	300	850	200	800	82	18
T₂	700	95	95	273	734	200	730	78	22
T₃	600	90	90	240	667	200	640	73	25
T₄	400	85	85	226	538	200	503	69	31
T₅	300	80	80	207	446	200	382	63	36

5.3.2. Discussion and Analysis

In this paper, according to Figures 7–10, our scheme is superior to the RCST and FFCT, there are several following factors:

(1)
TGAC not only can make use of multiattribute trust algorithms but also can adjust the related parameters by risk and reward punishment factors; especially, it uses feedback weight factors to filter out unnecessary nodes by the “Six Degrees of Separation,” and this can ensure the accuracy of trust evaluation and reduce the computational burden.
(2)
The prediction probability of trust level is combined with the decision-making in the paper, which is appropriate to make use of game theory to analyze the gains and losses, and the results of the statistical data of example are shown in Figure 11.

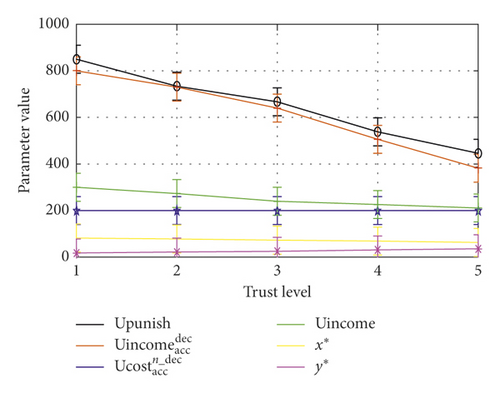
In Figure 11, we can see that the value of and Upunish increases as well as the trust level. When the user deception cost is fixed, with the decrease in trust level, the acceptance probability x^∗ of service provider increases, and the deception probability y^∗ of user reduces, which is consistent with the conclusion of the paper. Note: in order to see the trend of the computed results in the same drawing, the percentage of the drawings is magnified by 100 times.

6. Conclusion

Trust has a great influence on making decisions in the open and dynamic network environment, and we construct a trust evaluation scheme based on multiple factors and propose a weight method of trust attribute. Furthermore, from the perspective of game theory, we design the mixed strategy Nash equilibrium mechanism and give the game control condition based on trust prediction and payment matrix to encourage the participant to continue honest strategy. The experimental results show that our research is feasible and effective in cloud services. Furthermore, compared with other two models (RCST and FFCT), our model shows considerable advantages in terms of trust evaluation accuracy and cooperation rate.

In the future, we will use trust-game-based access control in a more complex scenario, develop more advanced technology, and design more experiments to further improve the effectiveness in mobile cloud environments [26, 31, 32].

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was financially supported by the National Development and Reform Commission, Information Security Special Project, Development and Reform Office, under No. 1424 (2012).

Open Research

Data Availability

The data used to support the findings of this study are included within the article.

References

1 Cloud Security Alliance, Security Guidance for Critical Areas of Focus in Cloud Computing V4.0, 2017, Cloud Security Alliance, Seattle, DC, USA.
Google Scholar
2 Sun P. J., Privacy protection and data security in cloud computing: a survey, challenges, and solutions, IEEE Access. (2019) 7, 147420–147452, https://doi.org/10.1109/ACCESS.2019.2946185.
10.1109/ACCESS.2019.2946185
Web of Science® Google Scholar
3 Krishna Kalluri R., Addressing the security, privacy and trust challenges of cloud computing, International Journal of Computer Science and Information Technologies. (2014) 5, no. 5, 6094–6609.
Google Scholar
4 Li L. and Wang Y., The roadmap of trust and trust evaluation in web applications and web services, Advanced Web Services, 2014, Springer, New York, NY, USA.
10.1007/978-1-4614-7535-4_4
Google Scholar
5 Mahmud K. and Usman M., Trust establishment and estimation in cloud services: a systematic literature review, Journal of Network and Systems Management. (2018) 27, no. 2, 489–540, https://doi.org/10.1007/s10922-018-9475-y, 2-s2.0-85054547220.
10.1007/s10922-018-9475-y
Web of Science® Google Scholar
6 Sun P. J., Research on the tradeoff between privacy and trust in cloud computing, IEEE Access. (2019) 7, 10428–10441, https://doi.org/10.1109/ACCESS.2019.2891589, 2-s2.0-85061199056.
10.1109/ACCESS.2019.2891589
Web of Science® Google Scholar
7 Chunyong Y., Wang J., and Park J. H., An improved recommendation algorithm for big data cloud service based on the trust in sociology, Neurocomputing. (2017) 256, 49–55, https://doi.org/10.1016/j.neucom.2016.07.079, 2-s2.0-85019355915.
10.1016/j.neucom.2016.07.079
Web of Science® Google Scholar
8 Aluvalu R. K. and Muddana L., A survey on access control models in cloud computing, Emerging ICT for Bridging the Future, 2015, Springer, Berlin, Germany.
10.1007/978-3-319-13728-5_73
Google Scholar
9 Shynu P. G. and Singh K. J., A comprehensive survey and analysis on access control schemes in cloud environment, Cybernetics and Information Technologies. (2016) 16, no. 1, 19–38, https://doi.org/10.1515/cait-2016-0002, 2-s2.0-84962910532.
10.1515/cait-2016-0002
Google Scholar
10 Neumann V., Theory of Games and Economic Beavior, 1972, Princeton University Press, Princeton, NJ, USA.
Google Scholar
11 Manshaei M. H., Zhu Q., and Alpcan T., Game theory meets network security and privacy, ACM Computing Surveys. (2013) 45, no. 3, 1–39, https://doi.org/10.1145/2480741.2480742, 2-s2.0-84874284297.
10.1145/2480741.2480742
Web of Science® Google Scholar
12 Helil N., Halik A., and Rahman K., Non-zero-sum cooperative access control game model with user trust and permission risk, Applied Mathematics and Computation. (2017) 307, 299–310, https://doi.org/10.1016/j.amc.2017.03.006, 2-s2.0-85016144501.
10.1016/j.amc.2017.03.006
Web of Science® Google Scholar
13 Furuncu E. and Sogukpinar I., Scalable riskassessment method for cloud computing using game theory, Computer Standards & Interfaces. (2015) 38, https://doi.org/10.1016/j.csi.2014.08.007, 2-s2.0-84913580411.
10.1016/j.csi.2014.08.007
Web of Science® Google Scholar
14 Njilla L. Y., Pissinou N., and Makki K., Game theoretic modeling of security and trust relationship in cyberspace, International Journal of Communication Systems. (2016) 29, no. 9, 1500–1512, https://doi.org/10.1002/dac.3115, 2-s2.0-84975717704.
10.1002/dac.3115
Web of Science® Google Scholar
15 Baranwal G. and Vidyarthi D. P., Admission control in cloud computing using game theory, The Journal of Supercomputing. (2016) 72, no. 1, 317–346, https://doi.org/10.1007/s11227-015-1565-y, 2-s2.0-84957438084.
10.1007/s11227-015-1565-y
Web of Science® Google Scholar
16 He Y. and Sun L., A game theory-based analysis of data privacy in vehicular sensor networks, International Journal of Distributed Sensor Networks. (2014) 10, no. 1, https://doi.org/10.1155/2014/838391, 2-s2.0-84893861103.
10.1155/2014/838391
Google Scholar
17 Mehdi M. M., Raza I., and Hussain S. A., A game theory based trust model for vehicular Ad hoc Networks (VANETs), Computer Networks. (2017) 121, 152–172, https://doi.org/10.1016/j.comnet.2017.04.024, 2-s2.0-85018476885.
10.1016/j.comnet.2017.04.024
Web of Science® Google Scholar
18 Kamhoua C., Kwiat L., Kwiat K., Park J., and Zhao M., Game theory modeling of security and inter dependency in a public cloud, Proceedings of the IEEE 7th International Conference on Cloud Computing, June 2014, Anchorage, AK, USA, https://doi.org/10.1109/cloud.2014.75, 2-s2.0-84919784577.
10.1109/cloud.2014.75
Google Scholar
19 Garnaev A., Liu Y., and Trappe W., Anti-jamming strategy versus a low-power jamming attack when intelligence of adversary’s attack type is unknown, IEEE Transactions on Signal and Information Processing Over Networks. (2016) 2, no. 1, 49–56, https://doi.org/10.1109/tsipn.2015.2506038, 2-s2.0-85031986809.
10.1109/TSIPN.2015.2506038
Web of Science® Google Scholar
20 Aziz F. M., Shamma J. S., and Stuber G. L., Resilience of LTE networks against smart jamming attacks, Proceedings of the IEEE Global Communications Conference (GLOBECOM), December 2014, Austin, TX, USA, 734–739, https://doi.org/10.1109/glocom.2014.7036895, 2-s2.0-84949487311.
10.1109/glocom.2014.7036895
Google Scholar
21 Salhab R., Malhamé R. P., and Ny J. L., A dynamic game model of collective choice in multi-agent systems, IEEE Transactions on Automatic Control. (2016) 63, no. 3, 1–15.
Web of Science® Google Scholar
22 Wang Y. and Cai Z., A game theory-based trust measurement model for social networks, Computional Social Networks. (2016) 3, https://doi.org/10.1186/s40649-016-0027-x, 2-s2.0-85021430374.
10.1186/s40649-016-0027-x
PubMed Google Scholar
23 Hu J., Li K., Liu C., and Li K., A game based Price bidding algorithm for multi-attribute cloud resource provision, IEEE Transactions on Services Computing. (2019) 11, https://doi.org/10.1109/tsc.2018.2860022, 2-s2.0-85050625354.
10.1109/tsc.2018.2860022
Google Scholar
24 Cardellini V. and Di Valerio V., Game theoretic resource pricing and provisioning strategies in cloud systems, IEEE Transactions on Services Computing. (2016) 13, no. 1, 86–98, https://doi.org/10.1109/TSC.2016.2633266, 2-s2.0-85053165963.
10.1109/TSC.2016.2633266
Google Scholar
25 Varalakshmi P. and Judgi T., Multifaceted trust management framework based on a trust level agreement in a collaborative cloud, Computers & Electrical Engineering. (2017) 59, 110–125, https://doi.org/10.1016/j.compeleceng.2016.10.002, 2-s2.0-85002189018.
10.1016/j.compeleceng.2016.10.002
Web of Science® Google Scholar
26 Gao L. and Zheng Y., Game theoretical analysis on acceptance of a cloud data access control system based on reputation, IEEE Transactions on Cloud Computing. (2016) 12, https://doi.org/10.1109/tcc.2016.2632110.
10.1109/tcc.2016.2632110
Google Scholar
27 Zhang C. and Lam H.K., A new design of membership function dependent controller for TS fuzzy systems under imperfect premise matching, IEEE Transactions on Fuzzy Systems. (2019) 27, no. 7, 1428–1440, https://doi.org/10.1109/tfuzz.2018.2880424, 2-s2.0-85056362502.
10.1109/TFUZZ.2018.2880424
Web of Science® Google Scholar
28 Leonesi S., The mystery of the six degrees of separation, Lettera Matematica. (2015) 3, no. 4, 215–220, https://doi.org/10.1007/s40329-015-0096-y.
10.1007/s40329-015-0096-y
Google Scholar
29 Fullér R. and Majlender P., An analytic approach for obtaining maximal entropy OWA operator weights, Fuzzy Sets and Systems. (2001) 124, no. 1, 53–57, https://doi.org/10.1016/s0165-0114(01)00007-0, 2-s2.0-0035900270.
10.1016/S0165-0114(01)00007-0
Web of Science® Google Scholar
30 Matsumoto A., Repeated and dynamic games, Game Theory and Its Applications, 2016, Springer, Tokyo, Japan.
10.1007/978-4-431-54786-0_9
Google Scholar
31 Andiraja N., Optimal control feedback Nash in the scalar infinite non-cooperative dynamic game with discount factor, Global Journal of Pure and Applied Mathematics. (2016) 12, no. 4.
Google Scholar
32 Rusk J. D., Trust and decision making in the privacy paradox?, Proceedings of the Southern Association for Information Systems Conference, March 2014, Macon, GA, USA.
Google Scholar

Citing Literature

All articles