Volume 2019, Issue 1 9402539

Research Article

Open Access

A Method for Analyzing Hand-Transmitted Vibration Characteristics in the Hand-Arm Parts When Operating the Portable Pneumatic Extinguisher

Jian Wen,

Jian Wen

orcid.org/0000-0002-4606-1875

School of Technology, Beijing Forestry University, Beijing 100083, China bjfu.edu.cn

Key Lab of State Forestry and Grassland Administration for Forestry Equipment and Automation, Beijing 100083, China

Search for more papers by this author

Wenkai Ma,

Wenkai Ma

orcid.org/0000-0001-7566-8126

School of Technology, Beijing Forestry University, Beijing 100083, China bjfu.edu.cn

Key Lab of State Forestry and Grassland Administration for Forestry Equipment and Automation, Beijing 100083, China

Search for more papers by this author

Wenbin Li,

Corresponding Author

Wenbin Li

[email protected]

orcid.org/0000-0001-8821-8992

School of Technology, Beijing Forestry University, Beijing 100083, China bjfu.edu.cn

Key Lab of State Forestry and Grassland Administration for Forestry Equipment and Automation, Beijing 100083, China

Search for more papers by this author

Jian Wen,

Jian Wen

orcid.org/0000-0002-4606-1875

School of Technology, Beijing Forestry University, Beijing 100083, China bjfu.edu.cn

Key Lab of State Forestry and Grassland Administration for Forestry Equipment and Automation, Beijing 100083, China

Search for more papers by this author

Wenkai Ma,

Wenkai Ma

orcid.org/0000-0001-7566-8126

School of Technology, Beijing Forestry University, Beijing 100083, China bjfu.edu.cn

Key Lab of State Forestry and Grassland Administration for Forestry Equipment and Automation, Beijing 100083, China

Search for more papers by this author

Wenbin Li,

Corresponding Author

Wenbin Li

[email protected]

orcid.org/0000-0001-8821-8992

School of Technology, Beijing Forestry University, Beijing 100083, China bjfu.edu.cn

Key Lab of State Forestry and Grassland Administration for Forestry Equipment and Automation, Beijing 100083, China

Search for more papers by this author

First published: 2019

https://doi.org/10.1155/2019/9402539

Citations: 7

Guest Editor: Franco Concli

Share a link

Email
Wechat
Bluesky

Abstract

This study presents the vibration transfer characteristics and the vibration absorption power distribution of the specific working condition of a portable pneumatic extinguisher. A hand-transmitted vibration biomechanical model of the hand-arm system was developed. Using a vibration test platform, the model parameters were derived simultaneously, and the driving-point mechanical impedance and distributed vibration transmissibility were measured. The vibration transmissibility of the wrist, forearm, and upper arm measured by the model was compared with the measured data of a 6MF-30 portable pneumatic extinguisher. The vibration power absorption distributions were estimated by the model and were compared with the actual vibration power absorption distributions at 3400 r/min, 5000 r/min, and 7000 r/min, respectively. The results showed that the predicted response of the model agreed well with the measured data in distribution, total impedance, and phase and can accurately fit the response curve of hand-transmitted vibration. This study discussed the vibration response of the hand-arm in the operation of the portable pneumatic extinguisher from the view of biomechanics. The analyses confirmed that the proposed model can be used as an effective tool for predicting the vibration responses of the hand-arm during the operation of a portable pneumatic extinguisher.

1. Introduction

A portable pneumatic extinguisher is a typical low-intensity fire extinguishing equipment for the forest fire in China, which is widely equipped in forest firefighting forces and forestry bureaus [1, 2]. A blower drives the wind wheel to produce high-speed steam flow through a two-stroke gasoline engine, and then flames were blown out [3]. The flame retardant gas, such as carbon dioxide, is expanded by the gasoline combustion and is moved toward the object with the wind, which achieves the effect of separating oxygen and extinguishing fire. Hand-transmitted vibration (HTV) is a phenomenon that vibration is transmitted to the hand or arm system through the handle of a device, which is commonly found in the operation of small handheld vibration devices, such as portable pneumatic extinguisher. Epidemiological studies have shown that prolonged occupational exposure to HTV resulted in the hand-arm vibration syndrome (HAVS), such as vibration-induced white fingers (VWF) [4, 5].

The biomechanical response of HTV is greatly different due to the influence of posture and hand forces, which poses a challenge to the development of the mechanical equivalent model of HTV. These differences are influenced by the body shape and experimental conditions. Extensive experimental studies on HTV have been further called upon to enhance our knowledge on the assessment of vibration exposure. Existing international guidelines (ISO 5349-1 [6]) neglect the effect of posture and hand forces and could not adequately predict the biomechanical response of HTV. Extensive experimental studies on HTV have been published, but analytical models of the hand-arm have mostly been limited to lump parameter models [7] due to the complexity of the hand-arm system, which is a nonuniform, nonlinear, anisotropic, and composite system.

The grip forces of the handle and the posture of the operating equipment had a great influence on the driving-point mechanical impedance (DPMI) of the arm system [8]. The perceived intensity produced by the vibration applied to the hand is tied to the magnitude, frequency, and direction of the vibration [9]. The majority of the reported lumped-parameter hand-arm models [10–12] were derived from DPMI responses and considered the fingers, palm, and hand-arm posture, but the body structure and anthropometric data were neglectful. Dong et al. [12] developed a five-degrees-of-freedom model for analyzing the vibration power flow and the distribution of vibration power absorption in the human arm system exposed to hand-transmitted vibration. In order to identify the model parameters, four different hand force combinations were used to measure the mechanical impedance data of the two driving points on the finger and palm. The model took into account the quality of the main structure while ignored the angle of rotation of the human arm. In addition, Knez et al. [13] established a detailed mechanical model based on biodynamic finger measurements to simulate the accurate response of a single finger, and the sequentially measured responses of the different finger parts were used to identify the parameters of a multibody mechanical model of the index finger.

Due to the observed discrepancy between epidemiological studies and hand-arm injury assessment based on ISO 5349-1 (2001) guidelines, vibration power absorption (VPA) distribution has been proposed. VPA distribution in the hand and arm substructures and VPA-based frequency weightings for different hand-arm substructures can be obtained by the hand-arm model. Dong et al. [12] analyzed the vibration power flow and the VPA distribution in the major parts of the system exposed to HTV, including the fingers, palm-hand-wrist, forearm, upper arm, and shoulder. Marchetti et al. [14] investigated the vibration transmissibility (VT) of the elbow along the forearm direction as a function of hand grip force, confirmed that the hand grip force has a large influence on the elbow vibration response, and also found that there is significant resonance in the two frequency ranges along the forearm direction. Adewusi et al. [15] presented distributed VPA of different hand-arm substructures in the bent arm and extended arm postures due to z_h-axis broadband random and typical power tool excitations. The VPA distribution analysis could provide more effective means for predicting various vibration-induced disorders. VPA is very important for predicting damage risk of vibration to arm system, but the measurement of VPA is very complex. The force of handheld vibration equipment is sometimes difficult to measure because it is constantly changing, but the vibration of the handle can be easily simulated in the laboratory [11]. Although the VPA can be obtained indirectly from the impedance response of the driving point, the mechanical equivalent model of the arm system is needed to determine the VPA of the arm system with different substructures, and different types of arm models show great differences. Some national standards have no clear requirements for the posture of operating equipment. It is necessary to use ergonomics to determine the posture of operating equipment and to utilize the human arm model established to evaluate the vibration energy absorbed during the operation of wind fire extinguishers.

This study analyses the mechanical characteristics of the hand-arm system based on the force relationship and presents the balance equation of the hand-arm system according to the biodynamic characteristics and the dynamic balance state of the hand-arm during the vibration. The equivalent mechanical model of the hand-arm with five degrees of freedom is developed, and the vibration testing platform is set up to measure the vibration acceleration data. The parameters of the model are identified through parameter identification. The response of driving-point impedance and VT is obtained, and the VPA distribution of different hand-arm parts is estimated, which provides a basis for the measurement of distributed vibration energy absorption.

2. Modeling

2.1. Model of the Hand-Arm System

The methods for constructing the model of a system generally include the forward dynamic approach, the inverse dynamic approach, and the hybrid forward and reverse approach in engineering. The forward dynamic approach is generally applicable to the dynamic properties of the system that can be directly measured and used in the model to predict dynamic responses. The inverse dynamic approach, or hybrid forward and reverse approach, is usually applied to the study which is difficult to directly measure the biodynamic properties of living human subjects [16–18]. Considering the difficulty of direct measurement, this study used the inverse dynamics approach based on frequency response function to develop the human hand-arm model in order to estimate the biodynamic characteristics of the model. A number of studies have proposed a set of standards to guide the development of human vibration models [18]. This study utilized the standard to guide the development of the model.

Portable pneumatic extinguisher operators take a posture with a 90° elbow angle and 0 abduction angle. Therefore, it is necessary to establish a hand-arm system biomechanical model with a bent arm, in order to study the biodynamic characteristics of the hand-transmitted vibration when operating a portable pneumatic extinguisher. The hand-arm system biomechanical model for the common operational posture of the portable pneumatic extinguisher is shown in Figure 1. It is a five-degrees-of-freedom model consisting of masses, springs, and dampers. The structures of the forearm and upper arm (Figure 1(b)) of the model adopt the biomechanical model of the hand-arm system with a 90° elbow angle [19]. The strong coupling between the hand-arm and whole-body vibrations is not regarded due to the relatively static condition of the shoulder joint during the operation of the portable pneumatic extinguisher. The palm structure of the model uses the palm structure (Figure 1(a)) [10], in order to describe the vibration power absorption characteristics of the palm. This model consists of six mass elements: m₁ for the fingers’ bone, m₂ for the palm bone, m₃ for the fingers’ skin, m₄ for the wrist skin, m₅ for the forearm, and m₆ for the upper arm. Dampers (c₁, c₂, c₃, c₄, c₅, c₆, C₁, and C₂) and springs (k₁, k₂, k₃, k₄, k₅, k₆, K₁, and K₂) are used to simulate the connection between masses. c_i (i = 1, 2, 3, 4, 5, 6) represents the damping constant, C_i (i = 1, 2) represents the rotational damping constant, k_i (i = 1, 2, 3, 4, 5, 6) represents the linear stiffness, and K_i (i = 1, 2) represents the rotational linear stiffness. In the study, rotational linear stiffness and rotational damping constant of the wrist joint are ignored. Besides, l_i (i = 1, 2, 3, 4) represents the length of each part of the hand-arm system model.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The hand-arm system biomechanical model with elbow bending.

The model is assumed to be a linear system within a certain vibration range. With the linear hypothesis, the motion equations of the model are as follows:

\begin{matrix} [\begin{matrix} m_{1} & 0 & 0 & 0 & 0 \\ 0 & m_{2} & 0 & 0 & 0 \\ 0 & 0 & m_{5} & 0 & 0 \\ 0 & 0 & 0 & m_{6} & 0 \\ 0 & 0 & 0 & 0 & J_{1} \end{matrix}] \cdot [\begin{matrix} {\ddot{z}}_{1} \\ {\ddot{z}}_{2} \\ {\ddot{z}}_{3} \\ {\ddot{z}}_{4} \\ {\ddot{θ}}_{1} \end{matrix}] + [\begin{matrix} c_{1} + c_{3} & - c_{3} & 0 & 0 & 0 \\ - c_{3} & c_{2} + c_{3} + c_{4} & - c_{4} & 0 & 0 \\ 0 & - c_{4} & c_{4} + c_{3} & - c_{5} & c_{5} \cdot l_{1} \\ 0 & 0 & - c_{5} & c_{5} + c_{6} & c_{6} \cdot l_{2} - c_{5} \cdot l_{1} \\ 0 & 0 & - c_{5} \cdot l_{1} & c_{6} \cdot l_{2} + c_{5} \cdot l_{1} & C_{1} + C_{2} + c_{6} \cdot l_{2}^{2} - c_{5} \cdot l_{1}^{2} \end{matrix}] \cdot [\begin{matrix} {\dot{z}}_{1} \\ {\dot{z}}_{2} \\ {\dot{z}}_{3} \\ {\dot{z}}_{4} \\ {\dot{θ}}_{1} \end{matrix}] \\ + [\begin{matrix} k_{1} + k_{3} & - k_{3} & 0 & 0 & 0 \\ - k_{3} & k_{2} + k_{3} + k_{4} & - k_{4} & 0 & 0 \\ 0 & - k_{4} & k_{4} + k_{3} & - k_{5} & k_{5} \cdot l_{1} \\ 0 & 0 & - k_{5} & k_{5} + k_{6} & k_{6} \cdot l_{2} - k_{5} \cdot l_{1} \\ 0 & 0 & - k_{5} \cdot l_{1} & k_{6} \cdot l_{2} + k_{5} \cdot l_{1} & K_{1} + K_{2} + k_{6} \cdot l_{2}^{2} - k_{6} \cdot l_{1}^{2} \end{matrix}] \cdot [\begin{matrix} z_{1} \\ z_{2} \\ z_{3} \\ z_{4} \\ θ_{1} \end{matrix}] = [\begin{matrix} k_{1} \cdot z_{h h} + c_{1} \cdot {\dot{z}}_{h h} \\ k_{2} \cdot z_{h h} + c_{2} \cdot {\dot{z}}_{h h} \\ 0 \\ 0 \\ 0 \end{matrix}] . \end{matrix}

(1)

Equation (1) is simplified as follows:

\begin{matrix} [M] \{\ddot{z}\} + [C] \{\dot{z}\} + [K] \{z\} = \{F_{z}\}, \end{matrix}

(2)

where [M], [C], and [K] are the (5 × 5) mass, damping, and stiffness matrices, respectively, and {F_z} is the (5 × 1) force vector.

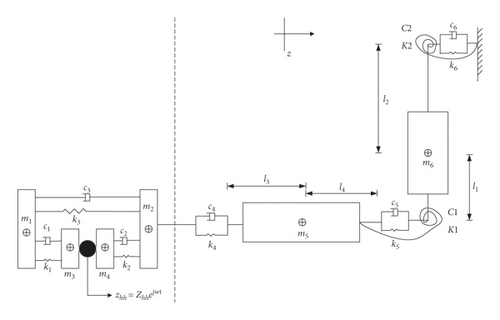
2.2. Biodynamic Response Analyses of the Models

VT is a parameter that the attenuation characteristics of the hand-arm joint part are relative to the vibration source. Vibration acceleration data at the wrist, forearm, and upper arm are collected in the experiment. Based on the data, the VT of different joints can be obtained. The VT of the different joints is expressed as

\begin{matrix} T (j ω) = \frac{Z (j ω)}{Z_{h h} (j ω)}, \end{matrix}

(3)

where Z(jω) is the displacement amplitude value of different joint parts of the hand-arm and Z_hh(jω) is the displacement amplitude value of the vibration source.

The driving-point mechanical impedance (DPMI) is the parameter that characterizes the obstruction and absorption of vibration by mechanical structures. At the same frequency, the driving-point impedance can be expressed as

\begin{matrix} DPMI (j ω) = \frac{F (j ω)}{V (j ω)}, \end{matrix}

(4)

where F(jω) is the vibration source and V(jω) is the complex number of vibration velocity. The magnitude of the DPMI depends on the amplitude of F(jω), V(jω), and their mutual phase relationship. When F(jω) and V(jω) are in phase, the impedance value is the largest. The value of the impedance consists of the real part and the imaginary part. When the phase relationship is known, accurate amplitude values and phase values can be given.

The DPMI is generally generated on the fingers and palm sides of the handle. The DPMI at the fingers can be expressed as DPMI₁(jω):

\begin{matrix} {DPMI}_{1} (j ω) = \frac{F_{1} (j ω)}{j ω Z_{h h}} = \frac{- ω^{2} Z_{h h} m_{3} + (k_{1} + j ω c_{1}) (Z_{h h} - Z_{1} (j ω))}{j ω Z_{h h}} = j ω m_{3} + \frac{(k_{1} + j ω c_{1}) (Z_{h h} - Z_{1} (j ω))}{j ω Z_{h h}} . \end{matrix}

(5)

The DPMI at the palm sides of the handle can be expressed as DPMI₂(jω):

\begin{matrix} {DPMI}_{2} (j ω) = \frac{F_{2} (j ω)}{j ω Z_{h h}} = \frac{- ω^{2} Z_{h h} m_{4} + (k_{2} + j ω c_{2}) (Z_{h h} - Z_{2} (j ω))}{j ω Z_{h h}} = j ω m_{4} + \frac{(k_{2} + j ω c_{2}) (Z_{h h} - Z_{2} (j ω))}{j ω Z_{h h}} . \end{matrix}

(6)

The total impedance of the hand-arm system is the sum of DPMI₁(jω) and DPMI₂(jω):

\begin{matrix} DPMI (j ω) = {DPMI}_{1} (j ω) + {DPMI}_{2} (j ω) = j ω (m_{3} + m_{4}) + \frac{(k_{1} + j ω c_{1}) (Z_{h h} - Z_{1} (j ω)) + (k_{2} + j ω c_{2}) (Z_{h h} - Z_{2} (j ω))}{j ω Z_{h h}} . \end{matrix}

(7)

Distributed VPA refers to the vibration power absorption at each joint of the hand-arm during the operation of handheld vibration equipment, which is generated by the vibration source. The distributed VPA can be obtained according to the force F(jω) at the handle and the vibration speed V(jω). Because DPMI has a mathematical relationship with F(jω) and V(jω), the distributed VPA can be obtained from DPMI and V(jω), which is expressed as [15]

\begin{matrix} P (f) = Re [DPMI (f)] \cdot {|v (f)|}^{2}, \end{matrix}

(8)

where f is the frequency in Hz.

In addition, the energy absorbed by each of the substructure damping elements can be used to estimate the arm system VPA [15] because other components do not absorb energy. It is expressed as

\begin{matrix} P_{k} (f) = c_{k} {[Δ v_{k} (f)]}^{2} + C_{k} {[Δ Ω_{k} (f)]}^{2}, \end{matrix}

(9)

\begin{matrix} P (f) = \sum_{k = 1}^{6} P_{k} (f), \end{matrix}

(10)

where f is the vibration frequency, Δv_k(f) and ΔΩ(f) are relative translational and rotational rms velocities across the damping element at joint k, respectively, and c_k and C_k are the linear and rotational damping coefficients at joint k.

3. Experimental

3.1. Test Platform Experiment

The experiments were carried out indoors for the quiet and suitable experimental conditions. An electrodynamic exciter was used to simulate a random broadband white noise signal with a fixed frequency band range. In the experiment, the subjects were asked to simulate the posture of firefighting task. The metal handle of a portable pneumatic extinguisher was simulated with the cylindrical aluminum handle [19]. Two accelerometers for measuring the grip force were installed inside the handle, and the other two accelerometers for measuring the push force were installed between the handle bracket and the exciter. The subjects’ elbow joint were required to be controlled around 90° (80°–100°) elbow angle. During the experiments, their arms could not touch their body to ensure the accuracy of the experimental data. When using the portable pneumatic extinguisher, the 30 N grip force and 50 N push force are the most comfortable hand forces. Thus in the experiment the hand force of the subjects should be kept as constant as possible. The force detection software was used to detect the current change of the force. The grip force and the push force of the subjects were displayed on the computer to keep the force close to the expected value range. PCB 356B08 is an instrument for measuring triaxis vibration acceleration. Triaxis accelerometers were fixed in the upper arm, forearm, and wrist to measure the acceleration of three parts. NEC Sanei Instruments’ Omniace II RA1100 (NEC RA1100) is an instrument that accurately measures voltage, vibration, frequency, temperature, and logic signals directly. It is connected to a three-axis accelerometer for data collection. The experiment of each subject was conducted three times. Simultaneously, the subjects were advised to keep identical posture and hand force during each experiment for the sake of reducing errors. Figure 2 illustrates the operating posture of the experiment.

The vibration test platform was built to identify the parameters of the model. Six young healthy male subjects participated in this experiment. None of the subjects had a history of muscular or arm bone injuries and diseases. None of them was engaged in exposure to vibration-related work. Before participating in this experiment, each subject signed informed consent. Table 1 summarizes the anthropometric data of six subjects.

Table Table1. The anthropometric data of subjects.

Parameter	Data range	Data mean
Age (year)	23–27	24.7
Height (cm)	172–181	176.5
Weight (kg)	61–75	66.5
Right palm length (mm)	18–22	20.2
Right forearm length (mm)	21–27	23.5
Right upper arm length (mm)	28–33	30

3.2. The 6MF-30 Portable Pneumatic Extinguisher Experiment

The 6MF-30 portable pneumatic extinguisher is widely employed in Chinese forest firefighting. The rotating speed range of the two-stroke gasoline engine is in the range of 3400–13000 r/min. Laboratory experiments were performed with a 6MF-30 portable pneumatic extinguisher, as shown in Figure 3. The effects of operational posture and hand force on hand-transmitted vibration transmission characteristics were studied in the experiments. PCB 356B08 triaxis accelerometers were attached on the front handle, rear handle, and midpoint of air duct, in order to measure the vibration along the axis. NEC RA1100 was utilized to collect data. The sampling frequency was 1000 Hz, and the sampling time was 8 s each time [20]. The measurements were obtained for three rotary speed designated as 3400 r/min, 5000 r/min, and 7000 r/min. The force level of 30 N grip force and 50 N push force was applied by the subjects, while maintaining around 90° (80°–100°) elbow angle. The subjects held the 6MF-30 portable pneumatic extinguisher with feet the same width as shoulders. Simulated fire source 1 meter ahead of the subjects was assigned. The data were begun to record when the rotary speed was stable. Six young healthy male subjects were called upon to repeat the test to ensure the accuracy of the experimental data.

4. Determination of the Model Parameters

4.1. Parameter Identification Method and Results

The equivalent mechanical model of hand-arm for hand-transmitted vibration corresponding to the bent arm postures involves identification of 16 parameters. The parameter vectors {χ} for the bent-arm models, comprising mass and viscoelastic parameters, are given by

\begin{matrix} \{χ\} = \{c_{1} c_{2} c_{3} c_{4} c_{5} c_{6} C_{1} C_{2} k_{1} k_{2} k_{3} k_{4} k_{5} k_{6} K_{1} K_{2}\} . \end{matrix}

(11)

GB10000 [21] provides the relevant weight and upper arm and forearm length of adult males. The size of the arm segment is estimated based on the reported anthropometric data [22]. In GB10000, the weight of most adult males is 78 kg, and the length of the forearm and upper arm were 26.9 cm and 35.0 cm, respectively. The average body weight of 0.65%, 1.9%, and 3.3% is the estimated mass of the hand m_h, forearm m₅, and upper arm m₆, respectively [18]. Table 2 summarizes the standard anthropometric parameters.

Table 2. Standard anthropometric parameters.

Substructure	Anthropometric measurements
Forearm mass m₅	1.48 kg
Forearm length l_f	26.9 cm
Forearm centroid to wrist length l₃	15.3 cm
Forearm centroid to elbow length l₄	11.6 cm
Upper arm mass m₆	2.57 kg
Upper arm length l_u	35.0 cm
Upper arm centroid to elbow length l₁	15.2 cm
Upper arm centroid to shoulder length l₂	19.8 cm

The method to identify the parameters in the model is to use MATLAB to constrain multiobjective optimization of a large amount of data measured by using the vibration experimental test platform. In the system identification, the force and posture of the hand-arm have a significant impact on the biomechanical response of the vibration. In order to determine the model parameters, VT was measured under experimental conditions. The model parameters are given in the difference between the measured data and the model response. The parameter is as indicated in equation (9). Error E(χ) is expressed as [19]

\begin{matrix} E (χ) = α_{1} [\sum_{p = 1}^{3} E_{z p}] + α_{2} [E_{DPMI}], \end{matrix}

(12)

where α₁ is the weighting function of the transmission rate error function and α₂ is the weighting constant of the impedance error function. E_zp is the squared error of the transfer rate of the wrist, forearm, and upper arm, and E_DPMI is the squared error of the DPMI.

Finally, E(χ) is expressed as

\begin{matrix} E (χ) = α_{1} \{\begin{matrix} {[T_{11} (ω_{r}) - T_{1} (ω_{r})]}^{2} + {[T_{22} (ω_{r}) - T_{2} (ω_{r})]}^{2} + {[T_{33} (ω_{r}) - T_{3} (ω_{r})]}^{2} \\ + {[ϕ_{11} (ω_{r}) - ϕ_{1} (ω_{r})]}^{2} + {[ϕ_{22} (ω_{r}) - ϕ_{2} (ω_{r})]}^{2} + {[ϕ_{33} (ω_{r}) - ϕ_{3} (ω_{r})]}^{2} \end{matrix}\} \\ + α_{2} \{{[{DPMI}_{1} (ω_{r}) - DPMI (ω_{r})]}^{2} + {[φ_{1} (ω_{r}) - φ (ω_{r})]}^{2}\} . \end{matrix}

(13)

In the above objective function, the wrist, forearm, and the upper arm of measuring the VT of amplitude and phase are represented by T₁(ω_r), ϕ₁(ω_r), T₂(ω_r), ϕ₂(ω_r), T₃(ω_r), and ϕ₃(ω_r). The wrist, forearm, and upper arm according to the model to calculate the VT of the amplitude and phase are represented by T₁₁(ω_r), ϕ₁₁(ω_r), T₂₂(ω_r), ϕ₂₂(ω_r), T₃₃(ω_r), and ϕ₃₃(ω_r). The measured DPMI amplitude and phase are represented by DPMI(ω_r) and φ(ω_r), and DPMI₁(ω_r) and φ₁(ω_r) represent the DPMI amplitude and phase calculated from the model, respectively.

The parameters are summarized in Table 3.

Table 3. The parameter identification result.

Parameters	Identification value
c₁(Ns/m)	80.10
c₂(Ns/m)	20.08
c₃(Ns/m)	2.09
c₄(Ns/m)	199.99
c₅(Ns/m)	100.00
c₆(Ns/m)	20.04
C₁(Nms/rad)	2.24
C₂(Nms/rad)	2.65
k₁(N/m)	94741.41
k₂(N/m)	89251.97
k₃(N/m)	6478
k₄(N/m)	55712.2
k₅(N/m)	6115.51
k₆(N/m)	0.002
K₁(Nms/rad)	35098.88
K₂(Nms/rad)	605.30

4.2. Feasibility of Identification Results

The comparisons between the measured hand-arm responses from the test platform (designated “Measured”) and the model-obtained responses (designated “Modeled”) are shown in Figure 4. Figure 4 presents the VT for different sets of measurements (wrist, forearm, and upper arm). The frequency range of the majority of handheld tools is below 500 Hz [18], and the low frequency of the portable pneumatic extinguisher is about 2.5 Hz. Therefore, this study only analyzes the frequency range from 2.5 to 500 Hz.

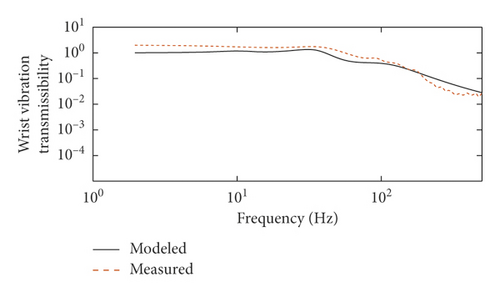
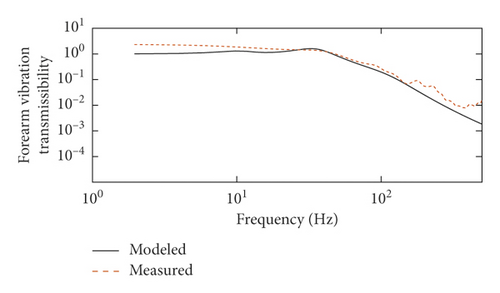
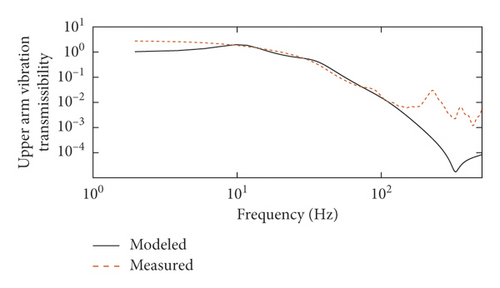
The comparison results show that the modeled VTs of the wrist, forearm, and upper arm agree well with the measured VTs when the frequency is less than 100 Hz, but the measured VTs have many fluctuations above 100 Hz, while the modeled VTs are smooth. As shown in Table 3, the value of the parameter k₆ identified by minimizing an error function is very small. Figure 4 suggests that the cutting frequency is very low by analyzing the vibration transmissibility at the upper arm. These situations may be caused by the fact that the human body is equated to a fixation point and the sway of the trunk is ignored in the establishment of the five-degree-of-freedom model. As a whole, the VT data obtained by the established arm model are very close to the target responses. Therefore, it is possible to identify the model parameters from the vibration acceleration data measured by using the platform.

The goodness of fit [23, 24] can be used to quantitatively evaluate the fit of the arm model to the hand-transmitted VT data. The calculation formula is shown as

\begin{matrix} ε = 1 - \frac{\sqrt{\sum ({(τ_{m} - τ_{c})}^{2} / (n - 2))}}{\sum (τ_{m} / n)}, \end{matrix}

(14)

where ε (goodness of fit) represents how much the two curves overlap, τ_m represents the VT data of “Measured,” τ_c represents the VT data of “Modeled,” and n represents the number of samples. The closer ε to 100%, the better the fit of the two curves.

The goodness of fit of different sets between the Measured and the Modeled are listed in Table 4. The goodness of fit of VT curves between the Measured and the Modeled at the wrist and forearm are near 95%, indicating that the trend of the curves is more consistent. The goodness of fit of VT curves between the Measured and the Modeled at the upper arm is close to 80%, demonstrating that the curve trend is good. The results show that the biomechanical model of hand-transmitted vibration is reasonable in the frequency range of 2.5–500 Hz.

Table 4. The goodness of fit at different sets between the Measured and the Modeled.

Frequency	The wrist	The forearm	The upper arm
2.5–500 Hz	95.36%	93.57%	78.56%

5. Results and Discussion

5.1. Vibration Transmissibility Comparison

The comparisons between the measured hand-arm responses from the 6MF-30 portable pneumatic extinguisher (designated “6MF-30 Measured”) and the model-obtained responses (designated “Modeled”) are shown in Figure 5. Figure 5 shows the comparison results of VT of the wrist, forearm, and upper arm under 5000 r/min operating mode.

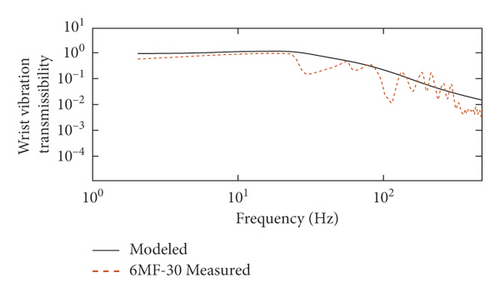
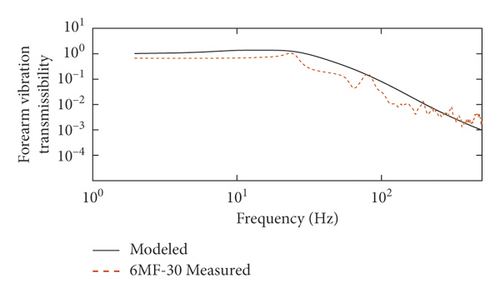
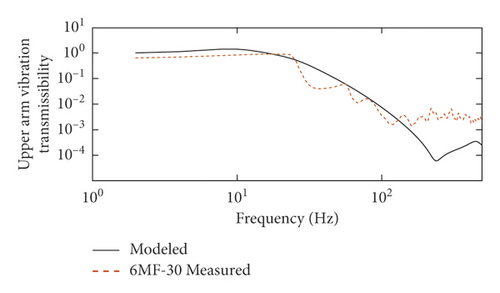
As shown in Figure 6, the VT curves of the model change smoothly, and the measured data of the 6MF-30 portable pneumatic extinguisher fluctuate in a high-frequency band. At the wrist, forearm, and upper arm, the Modeled and the 6MF-30 Measured curves peak around 20 Hz, while the peak curves of the 6MF-30 Measured has a certain attenuation. As can be seen from Table 5, at the wrist and forearm, the goodness of fit of curves is close to 90% and the goodness of fit of curves is close to 80% at the upper arm. In summary, the VT obtained by the model is consistent with the trend by the portable pneumatic extinguisher. The model is reasonable and has a good evaluation effect on the hand-transmitted vibration of portable wind fire extinguishers in the frequency range of 2.5–500 Hz.

Table 5. The goodness of fit at different sets between the 6MF-30 Measured and the Modeled.

Frequency	The wrist	The forearm	The upper arm
2.5–500 Hz	91.01%	90.99%	80.63%

5.2. Vibration Power Absorption Comparison

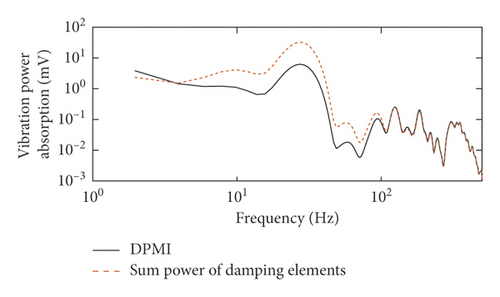
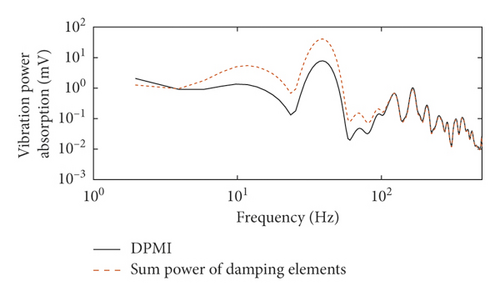
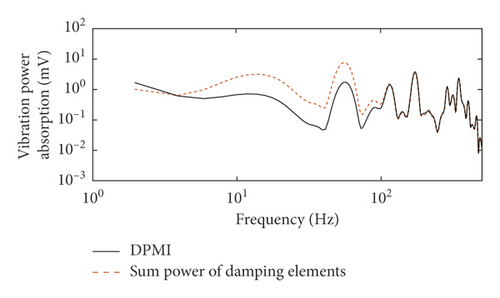
In the vibration situation of the 6MF-30 portable pneumatic extinguisher, the actual VPA can be calculated by DPMI when it runs at 3400 r/min, 5000 r/min, and 7000 r/min, respectively. The mass and linear stiffness do not absorb energy, while only the damping constant absorbs energy. Therefore, the total energy absorbed during the operation of the portable pneumatic extinguisher can be calculated according to the damping coefficient, as shown in Figure 6.

Table 6 shows the goodness of fit between the measured VPA and the modeled VPA. The range of the goodness of fit is from 82% to 85%. The results show that the calculated VPA distribution of the model agrees well with the VPA distributions of the portable pneumatic extinguisher. In summary, the calculated VPA distribution has good consistency with the measured VPA distribution, while there are still large errors in the low-frequency part.

Table 6. The goodness of fit of VPA at different speeds.

Frequency	3400 r/min	5000 r/min	7000 r/min
2.5–500 Hz	82.40%	84.07%	85.05%

6. Conclusions

The hand-transmitted vibration biomechanical model of the human hand-arm was developed using the inverse dynamics approach, considering the conventional operating posture of the 6MF-30 portable pneumatic extinguisher. Experiments and analyses were conducted to evaluate the developed model. The parameters of the model were derived by the vibration acceleration data of the wrist, forearm, and upper arm measured by using the standard vibration test platform, in terms of combined impedance and transmissibility responses.

By calculating the goodness of fit, the coincidence of the vibration transmission curve between the hand-arm model and the measured one by using the 6MF-30 portable pneumatic extinguisher at the wrist, forearm, and upper arm is from 80% to 90%, which indicates that the trend of the vibration transmission curve was more consistent. The VPA distribution of different hand-arm joints was estimated using the hand-transmitted vibration biomechanical model of the hand-arm system in the bent-arm posture, derived from impedance and transmissibility responses. And the VPA distribution of the hand-arm when using the 6MF-30 portable pneumatic extinguisher was also estimated. The results showed that the hand-arm model resulted a very good agreement with the model and the measured responses. The results showed that the developed hand-transmitted vibration biomechanical model was accurate and reasonable in the frequency range of 2.5–500 Hz and can be used to predict the hand-transmitted vibration of the 6MF-30 portable pneumatic extinguisher.

These observations suggest that the developed model was acceptable at least for the prediction of the basic trends of the hand-arm system responses. Therefore, this model can be used to explore and evaluate engineering methods for vibration exposure during the operation of the 6MF-30 portable pneumatic extinguisher.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

This work was supported by the Fundamental Research Funds for the Central Universities (grant no. 2017ZY27) and Doctoral Fund of Ministry of Education of China (grant no. 20120014110012).

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

Supporting Information

References

1 Zhang S. Q. and Yu G. S., Research and development of portable pneumatic extinguishers, Forestry Machinery & Woodworking Equipment. (2012) 40, no. 6, 8–10.
Google Scholar
2 Wang L. H., Sun Y., Yu W. N. et al., Portable wind extinguisher automatic testing platform, Journal of Forestry Engineering. (2016) 1, no. 1, 105–110.
Google Scholar
3 Wang L., Li W., and Chen J., Ergonomic evaluation of the operating characteristics of the 6MF-30 portable pneumatic extinguisher, Applied Ergonomics. (2015) 51, 39–43, https://doi.org/10.1016/j.apergo.2015.04.009, 2-s2.0-84937398970.
10.1016/j.apergo.2015.04.009
CAS PubMed Web of Science® Google Scholar
4 Su A. T., Darus A., Bulgiba A., Maeda S., and Miyashita K., The clinical features of hand-arm vibration syndrome in a warm environment: a review of the literature, Journal of Occupational Health. (2012) 54, no. 5, 349–360, https://doi.org/10.1539/joh.12-0089-ra, 2-s2.0-84872559073.
10.1539/joh.12-0089-RA
PubMed Web of Science® Google Scholar
5 Nilsson T., Wahlström J., and Burström L., Hand-arm vibration and the risk of vascular and neurological diseases—a systematic review and meta-analysis, PLoS One. (2017) 12, no. 7, e0180795, https://doi.org/10.1371/journal.pone.0180795, 2-s2.0-85023628910.
10.1371/journal.pone.0180795
PubMed Web of Science® Google Scholar
6 ISO-5349, Mechanical Vibration-Measurement and Evaluation of Human Exposure to Hand-Transmitted Vibration: Part 1: General Requirements, 2001, International Standard, Geneva, Switzerland.
Google Scholar
7 Rakheja S., Wu J. Z., Dong R. G., Schopper A. W., and Boileau P.-É., A comparison of biodynamic models of the human hand-arm system for applications to hand-held power tools, Journal of Sound and Vibration. (2002) 249, no. 1, 55–82, https://doi.org/10.1006/jsvi.2001.3831, 2-s2.0-0037012054.
10.1006/jsvi.2001.3831
Web of Science® Google Scholar
8 Besa A. J., Valero F. J., Suñer J. L., and Carballeira J., Characterisation of the mechanical impedance of the human hand-arm system: the influence of vibration direction, hand-arm posture and muscle tension, International Journal of Industrial Ergonomics. (2007) 37, no. 3, 225–231, https://doi.org/10.1016/j.ergon.2006.10.019, 2-s2.0-33846839263.
10.1016/j.ergon.2006.10.019
Web of Science® Google Scholar
9 Morioka M. and Griffin M. J., Magnitude-dependence of equivalent comfort contours for fore-and-aft, lateral and vertical whole-body vibration, Journal of Sound and Vibration. (2006) 298, no. 3, 755–772, https://doi.org/10.1016/j.jsv.2006.06.011, 2-s2.0-33748423061.
10.1016/j.jsv.2006.06.011
Web of Science® Google Scholar
10 Xu X. S., Dong R. G., Welcome D. E., Warren C., McDowell T. W., and Wu J. Z., Vibrations transmitted from human hands to upper arm, shoulder, back, neck, and head, International Journal of Industrial Ergonomics. (2017) 62, 1–12, https://doi.org/10.1016/j.ergon.2016.07.001, 2-s2.0-84979026031.
10.1016/j.ergon.2016.07.001
Web of Science® Google Scholar
11 Dong R. G., Welcome D. E., Xu X. et al., A model for simulating vibration responses of grinding machine-workpiece-hand-arm systems, Journal of Sound and Vibration. (2018) 431, 276–294, https://doi.org/10.1016/j.jsv.2018.06.008, 2-s2.0-85048445806.
10.1016/j.jsv.2018.06.008
Web of Science® Google Scholar
12 Dong J. H., Dong R. G., Rakheja S., Welcome D. E., McDowell T. W., and Wu J. Z., A method for analyzing absorbed power distribution in the hand and arm substructures when operating vibrating tools, Journal of Sound and Vibration. (2008) 311, no. 3–5, 1286–1304, https://doi.org/10.1016/j.jsv.2007.10.031, 2-s2.0-38749092905.
10.1016/j.jsv.2007.10.031
Web of Science® Google Scholar
13 Knez L., Slavic J., and Boltežar M., A sequential approach to the biodynamic modeling of a human finger, Shock and Vibration. (2017) 2017, 1–12, https://doi.org/10.1155/2017/8791406, 2-s2.0-85042757268.
10.1155/2017/8791406
Web of Science® Google Scholar
14 Marchetti E., Sisto R., Lunghi A. et al., An investigation on the vibration transmissibility of the human elbow subjected to hand-transmitted vibration, International Journal of Industrial Ergonomics. (2017) 62, 82–89, https://doi.org/10.1016/j.ergon.2017.04.001, 2-s2.0-85017424847.
10.1016/j.ergon.2017.04.001
Web of Science® Google Scholar
15 Adewusi S., Rakheja S., Marcotte P., and Thomas M., Distributed vibration power absorption of the human hand-arm system in different postures coupled with vibrating handle and power tools, International Journal of Industrial Ergonomics. (2013) 43, no. 4, 363–374, https://doi.org/10.1016/j.ergon.2013.04.004, 2-s2.0-84882606959.
10.1016/j.ergon.2013.04.004
Web of Science® Google Scholar
16 Kim T.-H., Kim Y.-T., and Yoon Y.-S., Development of a biomechanical model of the human body in a sitting posture with vibration transmissibility in the vertical direction, International Journal of Industrial Ergonomics. (2005) 35, no. 9, 817–829, https://doi.org/10.1016/j.ergon.2005.01.013, 2-s2.0-23644459480.
10.1016/j.ergon.2005.01.013
Web of Science® Google Scholar
17 Wu J. Z., Dong R. G., Welcome D. E., and Xu X. S., A method for analyzing vibration power absorption density in human fingertip, Journal of Sound and Vibration. (2010) 329, no. 26, 5600–5614, https://doi.org/10.1016/j.jsv.2010.07.022, 2-s2.0-77958058824.
10.1016/j.jsv.2010.07.022
Web of Science® Google Scholar
18 Dong R. G., Welcome D. E., McDowell T. W., and Wu J. Z., Fundamental theory, methods, and criteria for calibrating the human vibration models using frequency response functions, Journal of Sound & Vibration. (2015) 356, 95–216, https://doi.org/10.1016/j.jsv.2015.06.047, 2-s2.0-84938745231.
10.1016/j.jsv.2015.06.047
Web of Science® Google Scholar
19 Adewusi S., Rakheja S., and Marcotte P., Biomechanical models of the human hand-arm to simulate distributed biodynamic responses for different postures, International Journal of Industrial Ergonomics. (2012) 42, no. 2, 249–260, https://doi.org/10.1016/j.ergon.2012.01.005, 2-s2.0-84857410436.
10.1016/j.ergon.2012.01.005
Web of Science® Google Scholar
20 Wang L. J., Li W. B., and Zhou Q. H., Ergonomics evaluation of portable pneumatic extinguisher, Journal of Beijing Forestry University. (2015) 37, no. 2, 148–152.
Google Scholar
21 GB-10000, Human Dimensions of Chinese Adults, 1988, GB standards, China.
Google Scholar
22 Bunch R. W., Occupational Biomechanics, 2006, 4th edition, Professional Safety, Park Ridge, IL, USA.
Google Scholar
23 Griffin M. J., Measurement, evaluation, and assessment of occupational exposures to hand-transmitted vibration, Occupational and Environmental Medicine. (1997) 54, no. 2, 73–89, https://doi.org/10.1136/oem.54.2.73, 2-s2.0-0031059086.
10.1136/oem.54.2.73
CAS PubMed Web of Science® Google Scholar
24 Liang C.-C. and Chiang C.-F., A study on biodynamic models of seated human subjects exposed to vertical vibration, International Journal of Industrial Ergonomics. (2006) 36, no. 10, 869–890, https://doi.org/10.1016/j.ergon.2006.06.008, 2-s2.0-33748980402.
10.1016/j.ergon.2006.06.008
Web of Science® Google Scholar

Citing Literature

All articles

A Method for Analyzing Hand-Transmitted Vibration Characteristics in the Hand-Arm Parts When Operating the Portable Pneumatic Extinguisher

Abstract

1. Introduction

2. Modeling

2.1. Model of the Hand-Arm System

2.2. Biodynamic Response Analyses of the Models

3. Experimental

3.1. Test Platform Experiment

3.2. The 6MF-30 Portable Pneumatic Extinguisher Experiment

4. Determination of the Model Parameters

4.1. Parameter Identification Method and Results

4.2. Feasibility of Identification Results

5. Results and Discussion

5.1. Vibration Transmissibility Comparison

5.2. Vibration Power Absorption Comparison

6. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

Supporting Information

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Method for Analyzing Hand-Transmitted Vibration Characteristics in the Hand-Arm Parts When Operating the Portable Pneumatic Extinguisher

Abstract

1. Introduction

2. Modeling

2.1. Model of the Hand-Arm System

2.2. Biodynamic Response Analyses of the Models

3. Experimental

3.1. Test Platform Experiment

3.2. The 6MF-30 Portable Pneumatic Extinguisher Experiment

4. Determination of the Model Parameters

4.1. Parameter Identification Method and Results

4.2. Feasibility of Identification Results

5. Results and Discussion

5.1. Vibration Transmissibility Comparison

5.2. Vibration Power Absorption Comparison

6. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

Supporting Information

References

Citing Literature

Figures

References

Related

Information