1. Introduction

With the fast growth related to cellular networks and WiFi network-aware transmission techniques, several wireless facilities to support smart devices are becoming more widespread trend. Massive connections and huge multimedia streaming are adapted to satisfy an explosive growth in the wireless data traffic transmission. As a widely recognized key technology for the fifth-generation (5G) mobile communication systems, nonorthogonal multiple access (NOMA) paradigm is proposed to support the tremendous demands on data traffic. NOMA recently investigated and the related novel architectures for NOMA have drawn great considerations in both academy and industry [1–3]. In the conventional orthogonal multiple access (OMA) schemes, in which at signal domains (i.e., frequency, time, or space), the different orthogonal channels are allocated for accommodated users. In contrast, NOMA assigns the same channel for such users. More specifically, different power levels are nominated to different data flows with assistance of the superposition coding (SC) at the transmitter. At the receiver, the successive interference cancellation (SIC) is deployed to detach separated signals. As a result, main advantages including massive connections, reduced communication latency, and increased spectral efficiency can be achieved by the deployment of NOMA [1, 2].

More recent works have considered the integration of cooperative relaying transmission with energy harvesting in systems [4–8] and with NOMA systems in [9–11]. The crucial advantage of the combined model is that users need the help of the dedicated relays cooperative in NOMA systems to further expand both transmission reliability and energy efficiency [12–20]. Specifically, users with strong channel conditions proceeded as relays to assist the users with weak channel conditions in a cooperative NOMA (C-NOMA) scheme proposed in NOMA-based cellular network [10]. Other trends are applications for wireless power transfer to NOMA as interesting investigation in [6, 8]; that is, simultaneous wireless information and power transfer (SWIPT) technique was used in relaying systems, in which trade-offs between outage performance and energy harvesting coefficients are examined. Additionally, the overlay cognitive radio (CR) networks can require C-NOMA, where a secondary transmitter [12] or a secondary receiver [13] helps as a relay and supports transmitting the primary messages, and hence, the primary network assigned the same frequency band can be able to deliver multiple access capabilities. To expand the performance, a dedicated relay can be employed in NOMA systems [14–20]. In [14, 15], the classical three-node cooperative relaying system (CRS) was applied in NOMA, where the source transfers two symbols with dissimilar power levels possessing superposition coding to a dedicated half-duplex relay so that the acquired symbols corresponding to two time slots are forwarded to the destination. In [16, 17], to increase the performance of the user with the poor channel condition, two-user NOMA systems were measured in two scenarios, including deploying a dedicated half-duplex relay [16] and deploying a dedicated full-duplex relay [17]. Additionally, a variable gain relay was presented to simplify the transmission between the source and NOMA users to serve multiusers in NOMA systems in the case of nonexistence of direct link transmissions as in [18]. System performance such as exact and asymptotic high signal-to-noise ratio (SNR) expressions were presented to illustrate the superiority of NOMA over orthogonal multiple access (OMA) with respect to applied Nakagami-m fading channels [20]. While a fixed gain relay and direct link transmissions were considered to examine performance in concerned NOMA-based relaying networks [18, 19]. With regard to wireless power transfer, a SWIPT-based decode-and-forward (DF) relay was considered in NOMA-based relaying network [21].

Recently, due to its potential to double the spectral efficiency, full-duplex (FD) wireless communication has attracted substantial attentions by permitting concurrent downlink (DL) and uplink (UL) transmission in the same frequency band [22–24]. The two-way communication links in a two-user FD scheme were inspected in terms of the rate region and the achievable sum rate [25, 26], respectively. Most of the researches on NOMA schemes rely on the Rayleigh fading channel model. Nevertheless, Rayleigh fading is considered as the special case of fading channels. Alternately, it is the most effective way to consider influences of Nakagami-m fading channels in the outage performance evaluation of NOMA with regard to the line of sight (LoS) transmission. To our best knowledge, the wide-ranging topic-related wireless analysis, i.e., Nakagami-m fading channels in relaying-aware NOMA, has not been well considered yet in the previous literature. In [18], the closed form and lower and upper bounds on the ergodic sum rate together with the outage probability have been provided in amplify-and-forward (AF) relaying over Nakagami-m fading channels, whereas the achievable rates over Rayleigh fading channels in the decode-and-forward (DF) scheme have been explored in [27]. Contrasting with the case single of antenna equipped in all nodes as recent works [18, 27], the outage performance analysis over Rayleigh fading channels deploying multiple antennas has been assigned for the source and all destinations in [28]. Furthermore, by resolving the combined power allocation and relay beamforming scheme, the maximum sum rate has been attained in the case of multiple antennas equipped in the relay, while the single antenna is equipped in source and all destinations [29]. In [30], the authors studied the performance of the cooperative relay scheme with a single relay over Nakagami-m fading channels in terms of downlink in NOMA, in which both DF and AF protocols are examined. To determine the decoding order of cell-edge users’ data, they adopt statistical channel state information (CSI) for such system and the closed form of the ergodic sum rate and outage probability are derived. In a similar trend, the authors in [19] developed new closed-form expressions of both precise and approximate outage probabilities of fixed gain AF relaying in NOMA.

The remaining of this paper is organized as follows. The overall system model and assumptions are introduced in Section 2. In addition, Sections 3 and 4 represent the detail analytical derivations of the outage probability for FD and HD transmission mode, respectively. In Section 5 provides simulation results, and Section 6 provides a conclusion for this research.

2. System and Signal Model

2.1. Network Topology and Channel Assumptions

2.1.1. Network Topology

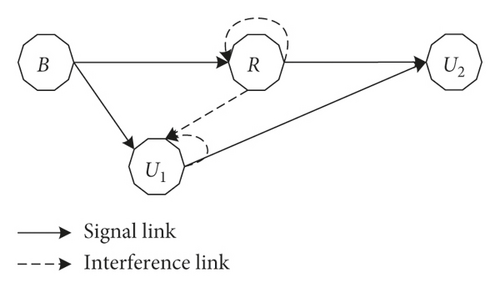
The considered FD cooperative relaying NOMA network is depicted in Figure 1, where a base station assigned with single antenna, denoted by B, transfers the information toward two single antenna equipment users, U₁ and U₂, by exploiting the power domain division technique, namely, NOMA. In such a model, it is assumed that existence of the B⟶U₁ link can be seen due to nearer distance, while the connection of B⟶U₂ link is nonexistence. Hence, B directly transmits messages to U₁ and indirectly sends to U₂ with help of the intermediate relay node which is denoted by ℛ. Specially, in order to enhance the spectral efficiency, ℛ is designed to operate in the full-duplex mode and thus ℛ facilitates two antennas as assumed in [9, 17]. It is worth noting that the multiple antenna relay node can further mitigate the self-interference power; however, this approach leads system to be more complex [31]. Thus, we assume the single antenna for transmitting and receiving at terminals in this work. It can refer as a typical situation of a multiantenna scheme as investigated in [9, 17].

2.1.2. Outdated Channel Model

In practice, because of estimation errors, it is highly difficult to estimate the perfect channel state information (CSI) of wireless network. Thus, the outdated channel coefficient is modelled as follows [32, 33]:

$$ (1)

where $$ represents the outdated CSI at the transceiver with variance $$, whereas z is the perfect channel coefficient, and Δ_z denotes the estimated channel error which can be approximated as a Gaussian random variable with zero mean and variance δ_z, and $$ [33], respectively. In fact, the known channel factor at the transmitter is a feedback from receiver after estimating the period; hence, the CSI at the transmitter is outdated.

2.1.3. Channel Statistic Distribution

In this work, all estimated channel coefficients are modelled under Nakagami-m fading condition. Although the Rician fading environment is more suitable to examine the self-interference (SI) link due to the short distance between antennas, its complicated distribution functions prevent to give the analytical expressions. Fortunately, the Nakagami-m fading distribution provides an alternate approximation to the Rician distribution. Inspired by this, and to simplify the analysis, we have adopted the Nakagami-m fading to model the SI channel as in this paper and recent works [6, 22]. Thus, the probability density function (PDF) and cumulative distribution function (CDF) of their gains follow gamma distributions with mean λ_z and integer severity factor m and, respectively, formulated as

$$ (2)

$$ (3)

where m_z and λ_z present the fading severity factor and mean, respectively. In this paper, we also assume m_z is an integer number and m_z ≥ 1. When m_z = 1, the channel environment returns to the Rayleigh fading channel. It implies that the considered Nakagami-m fading channels are more general than the previous Rayleigh fading condition. The equality in (3) is achieved by applying an equivalent relationship in Eq. 8.352.6 of [34].

Additionally, the channel coefficients are denoted as follows: the channels from B to U₁ and from B to ℛ are h₁ and h_r, respectively. The connection between ℛ (or U₁) and U₂ be g₂ (or g₁), while the self-interference link at ℛ and interference of ℛ⟶U₁ link are symbolized as f_r and f₁, respectively. In general, the channel gain |x|² follows the gamma distribution with parameter m_x and λ_x with x ∈ {h₁, h_r, g₂, g₁, f_r, f₁}.

Remark 1. It is noted that, although the considered system in this study is as same as in [9, 17], the channel conditions investigated in our system undergo imperfect knowledge of the Nakagami-m fading environment. Since such channel condition is more general than the Rayleigh fading environment in [9], and this research can be considered as a generalized version of previous work in [17] when considering nonideal interference cancellation hardware for both co-channel interference at U₁ and self-interference at ℛ, taking imperfect CSI noise into account.

Remark 2. In this paper, the severity fading parameter, i.e., m, is strictly supposed as an integer value. Thus, the analytical expression is only true for such considerations. The general case of noninterger values of m is beyond the scope of this study.

3. Outage Probability Consideration on Full-Duplex Relaying NOMA

4. A Comparison Study on Half-Duplex Relaying NOMA

For the comparison purpose, the HD NOMA relaying is represented as a benchmark. Some results for the HD cooperative NOMA system can be addressed in [16]. Unlike the FD NOMA relaying architecture, the HD ones divide a data transmission period into two slots. In the first phase, the source B transmits message to U₁ and ℛ based on the superposed signal in (4); thus the SINR at U₁ for retrieving U₂ data and its own data are, respectively, given by $$ and $$ while the SINR at ℛ to detect U₂ symbol can be expressed as $$ with $$ and $$.

In the second phase, we consider two scenarios of implementation as in the FD transmission mode, such as conventional and proposed user-aided relaying for the HD cooperative NOMA system. Firstly, for the conventional cooperative NOMA network, the relay ℛ regenerates and forwards signal to U₂ while the source and U₁ remain silent. Thus, the SNR at user U₂ from ℛ in the latter time slot is given by $$. Secondly, in the case of user U₁-aided relaying scheme, the SINR at U₂ from U₁ is $$ with $$ and $$. Similarly, by exploiting selection combining technique at the far user, the received SINR is given by $$. It is noted that the SINR of U₁ and U₂ for the proposed user-aided relaying HD scheme is similar to that for the conventional HD cooperative scheme except that transmitting power is replaced by the corresponding proposed power, i.e., $$, $$, and $$. In what follows, we will study the outage probability of considered HD networks.

5. Numerical Results

In this section, the effectiveness channel factor to the NOMA relaying system is simulated. In the simulation, the noise is normalized, i.e., N₀ = 1. The final results are averaged over 10⁶ realization runs. For fairness in comparison, we assume the total power budget to equal ρ, the transmitted power is set up for conventional cooperative NOMA scheme ρ_B = ρ_ℛ≜ρ/2 and that for the user-aided relaying scheme $$. Unless other stated, the target rates of U₁ and U₂ are set R₁ = 0.5 and R₂ = 1, respectively. The allocated power fraction be a₁ = 0.2 so that a₂ = 0.8. We also set the fading severity parameter as $$.

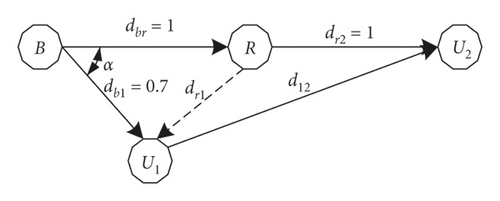
The system model is conducted as Figure 2. The distances between nodes x and y are denoted d_xy with (x, y) ∈ {(b, r), (r, 2), (b, 1), (r, 1), (1,2)}. We normalize d_br = d_r2 = 1 and d_b1 = 0.7. The angle between B⟶ℛ link and B⟶U₁ link is α. Hence, the space form relay to U₁ is $$ and distance between U₁ and U₂ is $$. In order to invoke large-scale fading, the channel power mean parameters are set as the following function of distance, such as $$, $$, $$, and $$. $$. The power mean of self-interference links at relay and U₁ after precancellation is set $$, where κ is the imperfect CSI level, n is the exponential loss factor, and ε represents the interference mitigation level. Unless other stated, we set α = π/4, n = 3, and ε = 0.01.

Figures 3 and 4 plot the impact of the fading parameter m on the outage performance with varying total transmitted power. It is experimentally illustrated that the fading parameters of the transmission links have a great influence on the outage performance. The outage performance with a higher m outperforms the ones with the lower m. This is because a higher m implies a stronger received SNR at destination. Furthermore, the main reason is that a larger fading parameter leads to a higher diversity order for the user, resulting in a lower outage probability [18]. As shown in Figures 3 and 4, analysis results match very well with the Monte Carlo simulation curves.

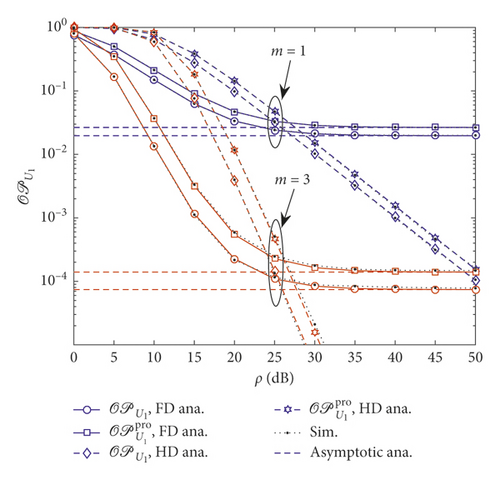
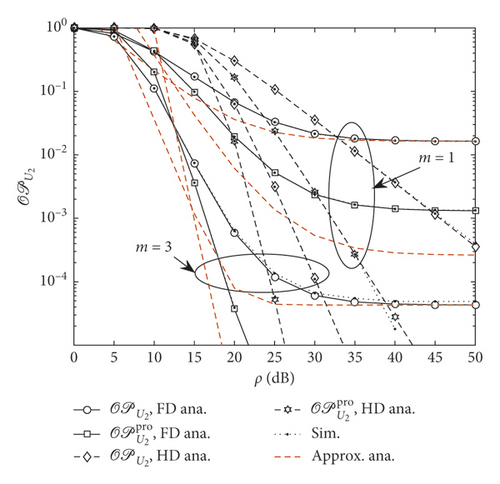
Performance gap can be seen among three cases of outage probability related to users U₁ and U₂. Furthermore, there exists a saturation for the outage probability in the higher transmit power region. One can also observe from Figure 4 that the fading parameters of all links (m = 5) have crucial impact on the outage performance.

Figures 5 and 6 investigate the impact of imperfect CSI level on the outage performance of the system.

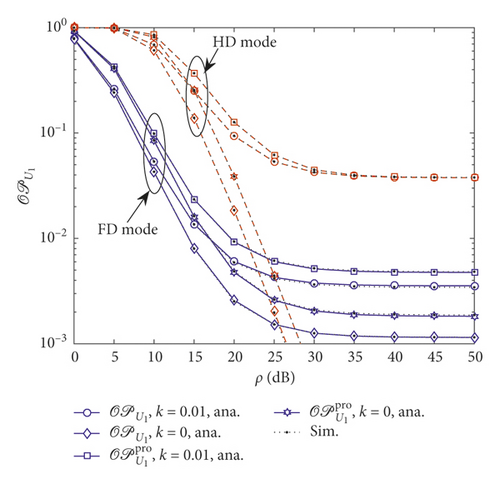
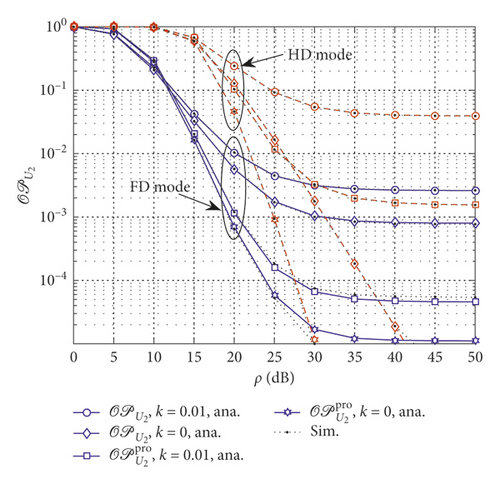
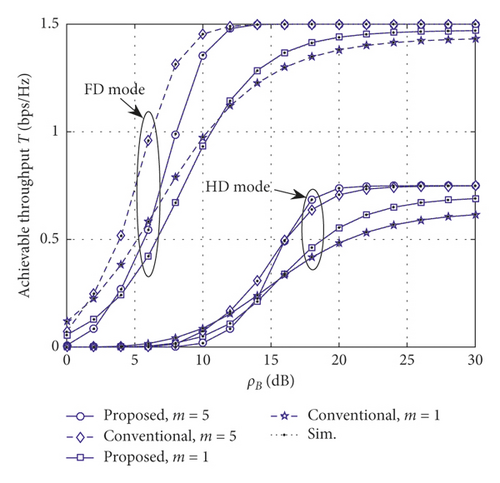
Figure 7 provides a comparison of the achievable throughput by considering two concerned modes at relay. Note that the considered system also gains benefit of the FD scheme and achieves a higher throughput as increasing the fading parameters. However, performance gap as varying fading parameters can be seen clearly in transmitting power ranging from 10 dB to 20 dB for the FD scheme and ranging from 15 dB to 25 dB for the HD scheme. It is worth noting that throughput performance of the HD scheme for the one time slot is lower than the remaining schemes. To sum up, the better channel condition leads to higher throughput can be obtained and such throughput reaches the limited value at a high level of transmitting power at B. Such observations verify the accuracy of our derived expressions.

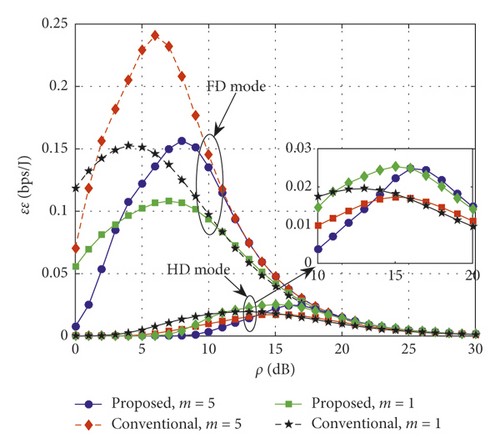
From Figure 8, we can see that the NOMA using the FD mode always outperforms the NOMA using the HD mode in terms of the optimal energy efficiency. Interestingly, optimal energy efficiency can be achieved at the FD mode and HD mode during the first time slot, but such values can only be found by using the numerical method. Moreover, the low energy efficiency can be seen at high transmitting power of B. The reason is that putting more power at B reduces energy efficiency of the considered system.

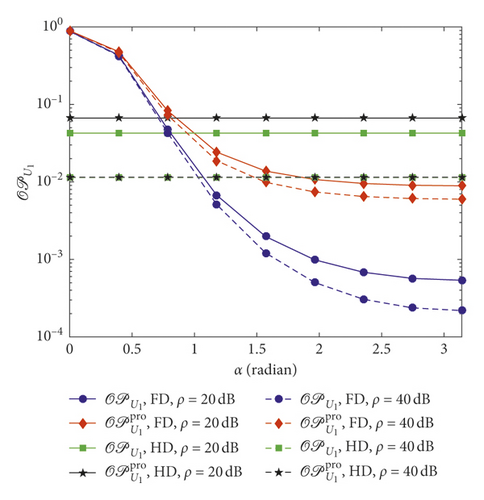
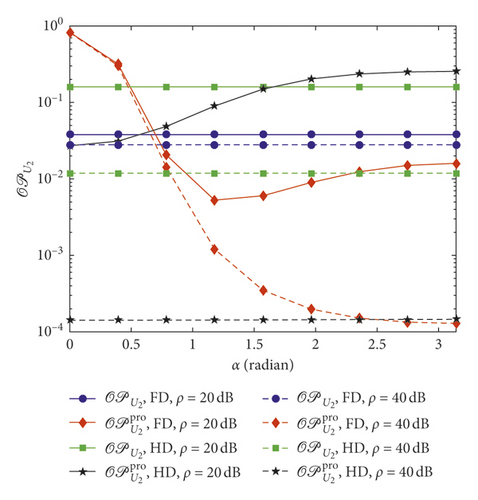
Figures 9 and 10 show the variation of outage performance of U₁ and U₂ under impact of angle α with κ = 0.01, m = 3, and ε = 0.1. As can be seen from Figure 9, the outage probability of FD network decreases when α increases from 0 to π. This is due to the decline of interference from relay to U₁ since the distance between these nodes grow. However, performance of the HD scheme does not suffer from this variation. From Figure 10, there are some fluctuations of U₂ outage. Outage performance of the proposed user-aided relaying FD scheme outperforms than that of the conventional scheme when α ≥ π/4. This can be explained that since space between relay and user U₁ is large enough, it leads to the small interference between nodes and improves the proposed user-aided relying.

6. Conclusion

In this paper, the system performance of cooperative NOMA networks over imperfect Nakagami-m fading environments has been studied. We have derived the closed-form expressions of the outage probability and delay-limited throughput and energy efficiency for both conventional relaying and near user-aided relaying for the cooperative NOMA system. The numerical simulations have been conduced to verify the exactness of analytical expressions. The results show that the system performance can further be enhanced by improving either severity parameter m or exactness of the channel as imperfect CSI is raised. In addition, the simulation results also reveal that the near user-based relaying for the cooperative NOMA scheme can improve far user performance; however, it degrades that of near user.

Conflicts of Interest

The authors declare that they have no conflicts of interest.