Over the last decades, the advancements in networking technology and new multimedia devices have motivated the research on efficient video streaming mechanisms under wireless. We consider combing soft real-time video streaming scheduling with threshold to minimize the ineffective preemption. Based on the value density and urgency of soft real-time task, the dynamic scheduling with preemption threshold strategy (DSPT) is proposed in the paper. By analyzing the response time and preemption relationship of tasks, the preemption thresholds are assigned. Simulation results show that the DSPT strategy achieves improvements about success rate, delay time, and benefit of the system.

1. Introduction

With the advancements in networking technology and new multimedia devices, video streaming mechanisms under various network and devices have attracted more and more attention. Nowadays, multimedia communications over the internet especially wireless network are the necessarily part of modern life. Many researchers have studied on video streaming management over wireless, including video coding [1–4], network coding [5–8], and wireless communication [9–11]. In wireless networks, video streaming applications are almost the largest consumer of mobile wireless data, so scheduling video streaming in wireless networks is very important.

Video streaming scheduling in wireless networks has been developed for recent years, such as given quality on service mechanisms [12–16] and real-time adaptive [17–19]. Many of video streaming scheduling studies are about hard real-time [20–22] that requires all the packets complete before the deadline; otherwise the packets will be considered invalid and dropped. However, for some actual video streaming media application, the packets of the transmission with delay can still bring a certain service and these packets can be forwarded and represented by soft real-time tasks. The soft real-time task model with value function is also applicable to video streaming with delay [23, 24]. For soft real-time scheduling, task executing under delay-constrained can bring goodput and benefit.

Generally, real-time scheduling can be divided into preemptive scheduling and non-preemptive scheduling according to whether the task can preempt each other or not. In a dynamic network, the preemptive method is more applicable. However, arbitrary preemption between tasks will affect the scheduling performance. Therefore, considering the drawbacks of the two methods, a compromise approach is utilized to limit the arbitrary or invalid preemption by setting preemption threshold. Furthermore, the limited preemption scheduling strategy is a correct choice for improving the performance.

Soft real-time task model is conducted for the video streaming under wireless. We propose a soft real-time threshold preemption scheduling strategy by combining value density and urgency for video streaming in the paper. Simulation results show that the strategy can improve the goodput, reduce the delay, and increase the benefit comparing with the EDF and LSF methods.

In this paper, we only consider the CPU in the system scheduling and ignore the time caused by context switching. We study the video streaming transmission problem of gateway devices in wireless network at the specific level of packets of transport tiers.

Organization. The structure of the paper is organized as follows: Section 2 describes the related work. Section 3 designs the structure of DSPT strategy. Section 4 defines the task model and problem analysis in detail. Section 5 is priority and preemption thresholds description. The details of scheduling based on preemption threshold are introduced in Section 6. The simulation setup and results are given in Section 7. Finally, the conclusions and future work are discussed.

2. Related Work

In wireless networks, the scheduling strategy should ensure high quality. For this purpose, lots of studies were proposed. The works in [1, 2] enabled high-quality HTTP streaming, in which video pre-encoded into segments that can only start to play if all the packet have received. However, much packet lost for video application in the above work. The literature [3] optimized the dynamic HTTP live streaming service by segment adaption. Some literatures proposed video streaming scheduling using video coding with network coding. For example, the literatures [5, 6] optimized video streaming by combining video coding and network coding for P2P network and distributed network, respectively. However, it might suffer from bandwidth inefficiencies because of unrecoverable packets. The work [7] proposed streaming scheduling for multiple server by Markov decision processes, but it had high computational complexity. In [9], the authors designed a crosslayer optimization scheme for dynamic wireless video streaming. However, these methods cannot contain the packet urgency for streaming control.

With the emergence of various networks, the research on heterogeneous wireless networks had been motivated. The literatures [11, 19] studied the concurrent multipath transfer of the capacity-limited heterogeneous wireless platform. Another work [17] proposed a real-time adaptive video streaming deliver method over multiple wireless networks. In [23, 24], delay-constrained video transmission with multiple interface in heterogeneous network was proposed.

Some researchers considered video streaming as hard real-time; that is, the streaming packet missing the deadline will be considered invalid. For example, the literature [20] proposed a feedback-based control approach under hard real-time workload to improve admission rate. In literatures [18, 21], the author studied in hard real-time video stream allocation to improve the utilization of video decoding. Nevertheless, most video streaming data meets the characteristics of soft real-time task, so delay-constrained of video is considered acceptable in applications.

3. DSPT Detail Design

We consider video streaming deliver over wireless networks as soft real-time scheduling. The streaming packet is expressed as task, and its quality and urgency are the metrics in scheduling. The task’s delay will affect the quality. Therefore, we introduced the value to measure the quality. Response time analysis (RTA) is used to test the schedulability of real-time task, and the preemption threshold-based scheduling approach is to reduce invalid preemption among tasks. The scheduling algorithm can effectively reduce the delay and improve the success rate and benefit. The flow diagram of DSPT strategy is shown in Figure 1. In this paper, we assume that the value function V_i(t) of the soft real-time task T_i keeps unchanged in the interval [a_i, d_i) and decreases linearly in the interval. While executing in the interval [d_i, cr_i), the task T_i is not allowed to be preempted in order to protect the execution of the task.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The flow diagram of DSPT strategy.

Contribution 1. We construct the priority assignment function combining value density and urgency, improving the success and quality of task soft real-time scheduling.

Contribution 2. We propose the task scheduling strategy DSPT based on preemption threshold, which can obtain better performance.

4. Task Model and Analysis

Considering video streaming with delay-constrained under wireless, we conduct soft real-time task model in this section.

4.1. Soft Real-Time Task Model

We refer to a task as an aperiodic task model, and the task is soft real-time. This section provides the definitions of soft real-time task model used in the paper.

Task T_i: An aperiodic task T_i is defined as a triple T_i : = {a_i, et_i, d_i, cr_i}, where a_i,et_i,d_i, and cr_i are the arrival time, the estimated execution time, the relative deadline, and the critical time of task T_i.

Having executed time ht_i: ht_i denotes that the task has been executing ht_i units at time t₀.

Required execution time rt_i: rt_i denotes the remaining execution time of task T_i. Thus, it meets rt_i = et_i − ht_i.

Executable time lt_i: lt_i is the executable time of the task T_i prior to its deadline d_i, where at the time t₀(t₀ < d_i).

Soft Executable time slt_i: When missed deadline d_i, task can continue to execute until cr_i. slt_i is the executable time prior to the critical time cr_i, that is, slt_i = cr_i − t₀.

Slack time st_i: The slack time st_i denotes that the time unit after finish execution until deadline d_i, thus, st_i = lt_i − rt_i. st_i remains stable when the task T_i is in execution, and st_i decreases when the task T_i is preempted. Once st_i < 0, the task T_i cannot finish before d_i.

Delay Time dt_i: The delay time dt_i denotes the finish time of task T_i after d_i. At the time t₀(d_i < t₀ ≤ cr_i), it meets dt_i = t₀ − d_i.

Priority pr_i: pr_i is defined as the priority of task T_i. The larger pr_i’s value, the higher T_i’s priority.

Threshold θ_i: θ_i is the preemption threshold of task T_i, where θ_i ≥ pr_i.

Value function V_i(t): V_i(t) defines the value of the system for executing T_i at time t, where t ∈ [a_i, cr_i). The task T_i ’s value will change when T_i keeps executing, and the function V_i(t) is dynamic. V_i(t) will be analyzed in detail in Section 4.

Value density function VD_i(t): VD_i(t) is the ratio between V_i(t) and required execution time rt_i, that is, VD_i(t) = V_i(t)/rt_i. Obviously, VD_i(t) is growing with the decreasing of rt_i.

4.2. Value and Value Density Function of Soft Real-Time Task

According to assumption, the value function V_i(t) of the soft real-time task T_i at time t is defined as

(1)

From (1), we can see that when t < d_i, V_i(t) is stable at V_i; however when d_i ≤ t < cr_i, V_i(t) is linearly diminishing until 0.

Value density function VD_i(t) is denoted as

(2)

We can see that VD_i(t) is not only concerned with V_i(t) but also related to rt_i. According to the definition, rt_i = et_i − ht_i. As we known, when the task T_i is executing, rt_i decreases with the growing of the time t. And when the task T_i is blocked, the rt_i remains unchanged. The discussion of VD_i(t) is as follows:

(1)
t < d_i. Within this interval, VD_i(t) = V_i/rt_i. When T_i is executing, VD_i(t) grows with the decreasing of rt_i. While T_i is blocked, VD_i(t) remains unchanged.
(2)
d_i ≤ t < cr_i. In this interval, VD_i(t) can be derived as follows: VD_i(t) = (V_i/rt_i) × ((cr_i − t)/(cr_i − d_i))
From the above expression, the affect part of the VD_i(t) is
(3)
Because the task in scheduler can finish without any interference of any other task, (cr_i − t)/rt_i > 1. In this case, if the task T_i keeps executing, the molecular part and the denominator part of (3) decrease at the same time. Further analysis is needed:
- (1)
  At t₀ time, (3) is recorded as: (cr_i − t₀)/rt_i. When task T_i has executed Δt from t₀, (3) is formulated to (cr_i − (t₀ + Δt))/(rt_i − Δt). Because slt_i/rt_i > 1, then (cr_i − (t₀ + Δt))/(rt_i − Δt) > (cr_i − t₀)/rt_i, where Δt > 0. That is, when task T_i is executing, VD_i(t) grows with the decreasing of rt_i.
- (2)
  When the task T_i is blocked, the molecular part of (3) decreases with the growth of t, while the denominator rt_i is kept unchanged. Thus, (3) decreases with the growth of t. Therefore, Theorem 1 can be obtained.

Theorem 1. While the task keeps executing in the progress, it increases with time t.

4.3. Analysis of the Task’s Urgency

The more urgency of the task is, the sooner execution is required.

Definition 2. At any t, the urgency Ug_i(t) of task T_i is defined as .

Ug_i(t) is affected by st_i, the discussion is as follows:

(1)
When T_i remains in execution, st_i does not change with the growing of the time t and then Ug_i(t) remains unchanged.
(2)
When T_i is blocked, st_i decreases with the growth of t, which makes Ug_i(t) increase.

5. Priority and Preemption Thresholds for Soft Real-Time Tasks

Task scheduling is driven by priority, while task priority function combines value density with urgency.

5.1. The Construction of Task’s Priority Function

Considering the urgency and the benefits of task, task scheduling is based on priority. Only the completed task can gain value, so relative to the value density, the urgency is more important. In system scheduling, the first consideration is system success rate and then is value brought by tasks. It means that urgency is given much greater weight than value density in priority function. Therefore, we use exponential weighting to the urgency while using logarithmic weighting to the value density. The function of priority assignment can be rewritten to

(4)

Based on the above analysis of value density VD_i(t) and urgency Ug_i(t), we can conclude that

(1)
When T_i executes at interval [a_i, d_i), pr_i satisfies
(5)
Further analysis is needed:
- (1)
  According to Theorem 1, when T_i keeps running, ln⁡[1 + V_i/rt_i] increases. Because st_i remain unchanged with time t growing. Therefore, (5) keeps increasing.
- (2)
  Once T_i is preempted, augments as time t grows, while ln⁡[1 + V_i/rt_i] remain unchanged, then (5) keeps increasing. Based on above, pr_i increases as time t at interval [a_i, d_i).
(2)
When T_i executes at [d_i, cr_i), its slack time is slt_i and satisfies
(6)
- (1)
  In the process of running T_i, with the growing of the time t, ((cr_i − t)/(cr_i − d_i)) × (V_i/rt_i) increases while slt_i remains unchanged and then (6) keeps increasing.
- (2)
  When T_i has been preempted, with the growing of time t, slt_i decreases and augments accordingly while ((cr_i − t)/(cr_i − d_i)) × (V_i/rt_i) reduces. Further discussion of Eq. (6) is needed. At moment t, slt_i = cr_i − t − rt_i < cr_i − d_i. After task T_i has been executed with Δt, there is , where cr_i − t − rt_i − Δt > 0. And is exponential growth, in which growth rate is faster than ln[1 + ((cr_i − t − Δt)/(cr_i − d_i)) × (V_i/rt_i)]’s logarithmic descent rate significantly. Therefore, pr_i(Δt) increases when Δt grows.

5.2. Preemption Threshold Selection for Task

The selection of preemption thresholds directly affects the scheduling algorithm. We select preemption threshold by analyzing the task’s response time.

Definition 3. Task T_i’s Effect Job Set is denoted as EJS_i. During the execution of task T_i, all task of the sets can preempt T_i, which are defined as Effect Job Set (EJS_i), satisfying EJS_i = T_m∣(pri_m > pri_i∧(D_m > A_i)∧(A_m < D_i).

Response time Rt_i of task T_i contains two parts: estimated execution time et_i and sum of the remaining execution time of the effect job sets EJS_i:

(7)

By analyzing the response time of T_i, its threshold θ_i can be obtained under the condition which can be scheduled. The procedure of preemption threshold selection is shown in Algorithm 1, where T_max is the highest priority task.

Algorithm 1: Compute θ_i.

1: Calculate θ_i using (7);
2: θ_i = pr_i;
3: WHILE (Rt_i ≤ cr_i) DO
4: IF (θ_i > pr_max)
5: return not scheduled;
6: ELSE
7: IF T_i is executing and st_i < st_max
8: θ_i : = pr_max;
9: return θ_i;
10: ELSE
11: Calculate Rt_i using (7)
12: END IF
13: END IF
14: END WHILE
15: return θ_i

Obviously, the computational complexity of Algorithm 1 is O(n).

6. Task Scheduling Strategy Based on Preemption Threshold

We propose a limited preemption scheduling strategy DSPT based on preemption threshold, which reduces the blocking time of the tasks by restricting preemption.

Definition 4. Sufficient and necessary conditions of pr_i > θ_j is that task T_i can preempt task T_j.

By Definition 4, if task T_i preempts task T_j, there must be pr_i > pr_j.

Theorem 5. If task T_i and task T_j are not preempted, the following should be satisfied: (pr_i ≤ θ_j)∧(pr_j ≤ θ_i).

Proof. Supposing that there are two tasks, T_p and T_q, which do not preempt each other, ⌝((pr_p ≤ θ_q)∧(((pr_q ≤ θ_p))))⇒(pr_p > θ_q)∨(pr_q > θ_p) is satisfied.

There are two possible cases:

(1)
If pr_p > θ_q, task T_p can preempt task T_q,
(2)
If pr_q > θ_p, task T_p may be preempted by task T_q.

Obviously, tasks T_p and T_q can preempt each other, in contradiction with Definition 4. Therefore, Theorem 5 can be proved.

6.1. Scheduling Algorithm Based On Preemption Threshold

The soft real-time dynamic task scheduling based on preemption threshold (DSPT) called Algorithm 1 is to calculate the threshold and determines the scheduling queue dynamically as shown in Algorithm 2.

Algorithm 2: Task scheduling.

θ_i: preemption threshold of T_i;
pr_i: priority of T_i;
S_j: ready tasks queue. 1 ≤ j ≤ num,
num is the number of tasks in the queue;
T_arr: task just arriving;
T_exe: task in executing;
T_max: the highest priority task of S_j;
1: T_arr arrive;
2: IF num = 0;
3: T_exe : = T_arr;
4: EXECUTE T_exe;
5: ELSE
6: Compute pr_arr using (7);
7: FOR i = 1 to num DO
8: Compute pr_i using (5);
9: Compute θ_i;
10: SORT task in S_j by pr_j Desc;
11: END IF
12: IF pr_arr > θ_max
13: T_exe : = T_arr;
14: IF T_in in S_j can’t Finish
15: ABORT T_in;
16: ELSE
17: T_exe : = T_max;
18: ADD T_arr to S_j;
19: num + +;
20: END IF
21: EXECUTE T_exe;
22: END IF

6.2. Algorithm Complexity

There is only one loop in Algorithm 2, that is, the 7th step is the loop of the length that is equal to the number of tasks in the ready queue. Thus, the computational complexity of the Algorithm 2 is O(n × m), and the computational complexity of the whole scheduling algorithm is O(n × m).

7. Simulations and Analysis

7.1. Simulation Experiments

The experiment platform’s CPU is Intel dual-core 2.8 GHZ processor, and the memory is 8 GB. The operating system is Ubuntu Linux, and the source code is implemented by C language.

In the experiment, we consider the aperiodic soft real-time task. Any task T_i’s arrival time a_i obeys Poisson distribution (λ = 4) and the estimated execution time et_i is subject to [3.0,5.0] average distribution. Therefore, its relative deadline d_i is [1.2,1.5] × et_i average distribution, its critical time cr_i is [1.2,1.5] × d_i, and its value V_i is randomly selected between [10,50].

Performance indicators are included as follows:

(1)
Systematic success rate (SSR):
(8)
where N_s denotes as the number of successful tasks and N represents the number of system overages.
(2)
Average task latency rate ATDR:
(9)
where TS denotes the successful task set and el_i and et_i denote execution latency and execution time of the success task T_i.
(3)
Effective utilization Rate (EUR):
(10)
where CT_s denotes as the CPU time for successful tasks and CT represents the total CPU time in scheduling.
(4)
Cumulative Value (CV):
(11)
where TS denotes the successful task set and represents the value of the task T_i.

7.2. Performance Analysis

Under soft real-time environment, the preemptive threshold scheduling strategy is compared with Earliest Deadline First (EDF) method and Least Slack First (LSF) method, and the simulation results and performance are analyzed as follows.

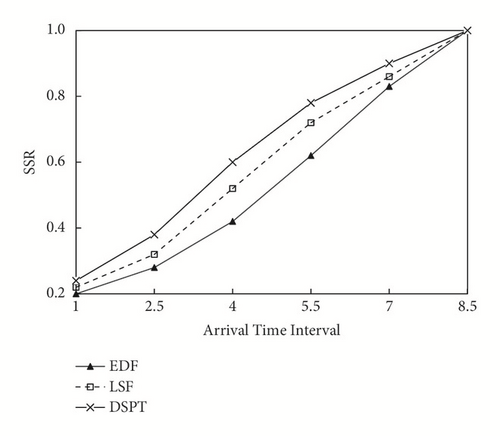
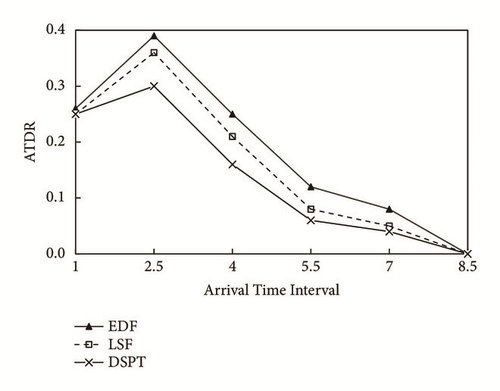
(1) Figure 2 shows simulation results for SSR scheduled by DSPT, EDF and LSF. The task’s arrival interval is represented on the horizontal axis, and the vertical axis is SSR. When the arrival interval of the task is very short, the preemption among the tasks causes the SSR to be low. With the increasing of arrival interval, the preemption among tasks decreases and the SSR arguments. From Figure 2, SSR is sorted in descending order followed by DSPT, LSF, and EDF. This is due to the EDF algorithm chooses task with earliest deadline but not most urgent, which can lead to many tasks fail. While the LSF algorithm always chose the task with the shortest slack time dynamically, its unrestricted preemption causes the thrashing which can make lots of task fail. The DSPT can adapt to the system environment dynamically, and its preemption threshold can avoid the invalid preemption among tasks. (2) The simulation results of ATDR are shown in Figure 3, in which the ATDR is on the vertical axis and arrival interval is on the horizontal axis. It can be seen from Figure 3, the ATDR decreases since the arrival interval grows from 2.5, while ATDR is lower because the intervals among tasks are so short that many of these are dropped to 1.0. Moreover, EDF algorithm leads to the highest ATDR, while the DSPT method produces the lowest ATDR. Because the EDF algorithm always chooses the task with earliest deadline of slack time to execute, many tasks miss the deadline and delay. Relative to the EDF method, the LSF algorithm assigns the most urgency task to execute in time. But its unconstrained preemption may cause serious thrashing among tasks under system overload and this increases the ATDR. The DSPT approach chooses the most urgency task to execute, and limits the preemption among the tasks by the threshold, thereby reduces the delay of the task effectively.

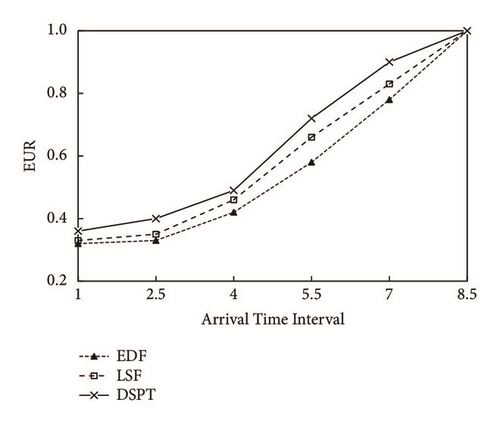
(3) The simulation results for EUR scheduled by EDF, LSF, and DSPT are shown in Figure 4, where the horizontal axis is task’s arrival interval and the vertical axis is EUR. The short arrival interval means intense preemption among tasks, which causes the EUR low. While the arrival interval becomes longer, there are EUR arguments as the tasks’ preemption decreases. From Figure 4, DSPT obtains the best EUR and EDF has the least EUR. Because the EDF algorithm always execute the task with earliest deadline, which causes more invalid CPU utilization than LSF along with the task failure. The DSPT using preemption threshold can improve the EUR through reducing invalid preemption of tasks.

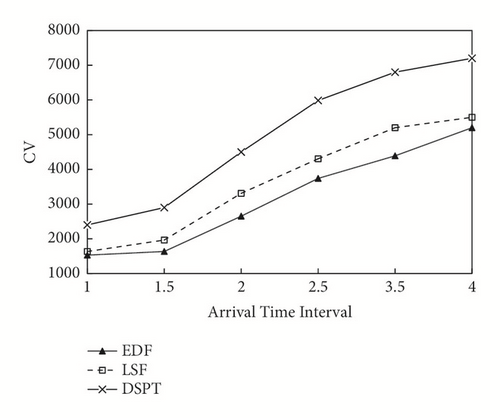
(4) Figure 5 plots the system’s CV as arrival interval grows. It can be seen from Figure 5, the CV increases when the arrival interval of tasks increases. DSPT obtains the highest CV, because it assigns higher executing priority of the task with high value density. The LSF method produces better CV than EDF method, because under the same system load, that more tasks finish augments CV obtained with the formal approach.

8. Conclusions and Future Works

In this paper, we consider video streaming scheduling in wireless networks as soft real-time scheduling. The soft real-time task model has been constructed to express streaming packet and its quality, measure as value, and urgency metric are explored in scheduling. Response time analysis (RTA) approach has been used to test the task’s schedulability, and preemption threshold has been added to the schedule to release the invalid preemption. The scheduling schema DSPT can constrain the delay and improve the success ratio and benefit effectively.

In future works, we want to apply our scheduling method to practical wireless networks, like 5G net, to test its practical effect. Moreover, the stream scheduling of mixed hard real-time and soft real-time characterizes are also a study work in the next step.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (NSFC) (Grant nos. 61562044, 41661083) and the Science and Technology Research Project of Jiangxi Provincial Department of Education (Grant nos. GJJ170234, GJJ160781).

Open Research

Data Availability

The data, including task’s properties and performance indicators in the experiments, used to support the findings of this study are available from the corresponding author upon request.

References

1 De Cicco L. and Mascolo S., An adaptive video streaming control system: Modeling, validation, and performance evaluation, IEEE/ACM Transactions on Networking. (2014) 22, no. 2, 526–539, 2-s2.0-84899505546, https://doi.org/10.1109/TNET.2013.2253797.
10.1109/TNET.2013.2253797
Web of Science® Google Scholar
2 Oyman O. and Singh S., Quality of experience for HTTP adaptive streaming services, IEEE Communications Magazine. (2012) 50, no. 4, 20–27, 2-s2.0-84859805464, https://doi.org/10.1109/MCOM.2012.6178830.
10.1109/MCOM.2012.6178830
Web of Science® Google Scholar
3 Thang T. C., Le H. T., Pham A. T., and Ro Y. M., An evaluation of bitrate adaptation methods for HTTP live streaming, IEEE Journal on Selected Areas in Communications. (2014) 32, no. 4, 693–705, 2-s2.0-84897129982, https://doi.org/10.1109/JSAC.2014.140403.
10.1109/JSAC.2014.140403
Web of Science® Google Scholar
4 He L. and Li F., Content and buffer status aware packet scheduling and resource management framework for video streaming over LTE system, Eurasip Journal on Image and Video Processing. (2017) 2017, no. 1, 2-s2.0-85034741220.
10.1186/s13640-017-0222-1
Google Scholar
5 Sheikh A. M., Fiandrotti A., and Magli E., Distributed scheduling for scalable P2P video streaming with network coding, Proceedings of the 32nd IEEE Conference on Computer Communications (IEEE INFOCOM ′13), April 2013, 11–12, https://doi.org/10.1109/infcom.2013.6566721, 2-s2.0-84883100610.
10.1109/infcom.2013.6566721
Google Scholar
6 Sheikh A. M., Fiandrotti A., and Magli E., Distributed scheduling for low-delay and loss-resilient media streaming with network coding, IEEE Transactions on Multimedia. (2014) 16, no. 8, 2294–2306, 2-s2.0-84912101056, https://doi.org/10.1109/TMM.2014.2357716.
10.1109/TMM.2014.2357716
Web of Science® Google Scholar
7 Thomos N., Kurdoglu E., Frossard P., and Van Der Schaar M., Adaptive prioritized random linear coding and scheduling for layered data delivery from multiple servers, IEEE Transactions on Multimedia. (2015) 17, no. 6, 893–906, 2-s2.0-84929315113, https://doi.org/10.1109/TMM.2015.2425228.
10.1109/TMM.2015.2425228
Web of Science® Google Scholar
8 Huang S., Izquierdo E., and Hao P., Adaptive packet scheduling for scalable video streaming with network coding, Journal of Visual Communication and Image Representation. (2017) 43, 10–20, 2-s2.0-85007389269, https://doi.org/10.1016/j.jvcir.2016.11.014.
10.1016/j.jvcir.2016.11.014
Web of Science® Google Scholar
9 Zhao M., Gong X., Liang J., Wang W., Que X., and Cheng S., QoE-driven cross-layer optimization for wireless dynamic adaptive streaming of scalable videos over HTTP, IEEE Transactions on Circuits and Systems for Video Technology. (2015) 25, no. 3, 451–465, 2-s2.0-84924364320, https://doi.org/10.1109/TCSVT.2014.2357094.
10.1109/TCSVT.2014.2357094
Web of Science® Google Scholar
10 Chen D.-R., A real-time streaming control for quality-of-service coexisting wireless body area networks, Applied Soft Computing. (2017) 2-s2.0-85029628675.
Google Scholar
11 Cao Y., Liu Q., Zuo Y., Luo G., Wang H., and Huang M., Receiver-assisted cellular/wifi handover management for efficient multipath multimedia delivery in heterogeneous wireless networks, EURASIP Journal on Wireless Communications and Networking. (2016) 2016, no. 1, https://doi.org/10.1186/s13638-016-0728-8.
10.1186/s13638-016-0728-8
Google Scholar
12 Sieber C., Hosfeld T., Zinner T., Tran-Gia P., and Timmerer C., Implementation and user-centric comparison of a novel adaptation logic for DASH with SVC, Proceedings of the 2013 IFIP/IEEE International Symposium on Integrated Network Management, IM 2013, May 2013, Belgium, 1318–1323, 2-s2.0-84883479200.
Google Scholar
13 Hosseini S. A., Fund F., and Panwar S. S., (Not) yet another policy for scalable video delivery to mobile users, Proceedings of the 7th ACM Workshop on Mobile Video, MoVid 2015, March 2015, USA, 17–22, 2-s2.0-84942522174.
Google Scholar
14 Hosseini S. A. and Panwar S. S., Restless streaming bandits: Scheduling scalable video in wireless networks, Proceedings of the 2017 55th Annual Allerton Conference on Communication, Control, and Computing (Allerton), October 2017, Monticello, IL, USA, 620–628, https://doi.org/10.1109/ALLERTON.2017.8262794.
10.1109/ALLERTON.2017.8262794
Google Scholar
15 Yeh Y.-H., Lai Y.-C., Chen Y.-H., and Lai C.-N., A bandwidth allocation algorithm with channel quality and QoS aware for IEEE 802.16 base stations, International Journal of Communication Systems. (2014) 27, no. 10, 1601–1615, 2-s2.0-84911365574, https://doi.org/10.1002/dac.2422.
10.1002/dac.2422
Web of Science® Google Scholar
16 Kim J. and Ryu E.-S., QoS optimal real-time video streaming in distributed wireless image-sensing platforms, Journal of Real-Time Image Processing. (2017) 13, no. 3, 547–556, 2-s2.0-84981223731, https://doi.org/10.1007/s11554-016-0629-4.
10.1007/s11554-016-0629-4
Web of Science® Google Scholar
17 Xing M., Xiang S., and Cai L., A real-time adaptive algorithm for video streaming over multiple wireless access networks, IEEE Journal on Selected Areas in Communications. (2014) 32, no. 4, 795–805, 2-s2.0-84897133407, https://doi.org/10.1109/JSAC.2014.140411.
10.1109/JSAC.2014.140411
Web of Science® Google Scholar
18 Mendis H. R., Audsley N. C., and Indrusiak L. S., Task allocation for decoding multiple hard real-time video streams on homogeneous NoCs, Proceedings of the 13th International Conference on Industrial Informatics, INDIN 2015, July 2015, UK, 246–251, 2-s2.0-84949520736.
Google Scholar
19 Cao Y., Song F., Liu Q., Huang M., Wang H., and You I., A LDDoS-Aware energy-efficient multipathing scheme for mobile cloud computing systems, IEEE Access. (2017) 5, 21862–21872, 2-s2.0-85028928637, https://doi.org/10.1109/ACCESS.2017.2731899.
10.1109/ACCESS.2017.2731899
Web of Science® Google Scholar
20 Dziurzanski P., Singh A. K., and Indrusiak L. S., Feedback-based admission control for hard real-time task allocation under dynamic workload on many-core systems, Architecture of computing systems---{ARCS} 2016, 2016, 9637, Springer, [Cham], 157–169, Lecture Notes in Comput. Sci., https://doi.org/10.1007/978-3-319-30695-7_12, MR3515451.
10.1007/978-3-319-30695-7_12
Google Scholar
21 Wang W., Cao Y., Gong J., and Li Z., CP-TPS: A Real-Time Transaction Processing Strategy Supporting Compensatory Task, Proceedings of the 20th IEEE International Conference on Computational Science and Engineering and 15th IEEE/IFIP International Conference on Embedded and Ubiquitous Computing, CSE and EUC 2017, July 2017, China, 475–482, 2-s2.0-85034654044.
Google Scholar
22 Mendis H., Audsley N., Indrusiak L. et al., Dynamic and static task allocation for hard real-time video stream decoding on NoCs, Leibniz Transactions on Embedded Systems. (2017) 4, no. 2, 01–25.
Google Scholar
23 Wu J., Yuen C., Cheung N.-M., and Chen J., Delay-Constrained High Definition Video Transmission in Heterogeneous Wireless Networks with Multi-Homed Terminals, IEEE Transactions on Mobile Computing. (2016) 15, no. 3, 641–655, 2-s2.0-84962127927, https://doi.org/10.1109/TMC.2015.2426710.
10.1109/TMC.2015.2426710
Web of Science® Google Scholar
24 Wu J., Yuen C., Cheng B., Wang M., and Chen J., Adaptive Flow Assignment and Packet Scheduling for Delay-Constrained Traffic over Heterogeneous Wireless Networks, IEEE Transactions on Vehicular Technology. (2016) 65, no. 10, 8781–8787, 2-s2.0-85027003093, https://doi.org/10.1109/TVT.2015.2504455.
10.1109/TVT.2015.2504455
Web of Science® Google Scholar

Citing Literature

All articles

Dynamic Soft Real-Time Scheduling with Preemption Threshold for Streaming Media

Abstract

1. Introduction

2. Related Work

3. DSPT Detail Design

4. Task Model and Analysis

4.1. Soft Real-Time Task Model

4.2. Value and Value Density Function of Soft Real-Time Task

4.3. Analysis of the Task’s Urgency

5. Priority and Preemption Thresholds for Soft Real-Time Tasks

5.1. The Construction of Task’s Priority Function

5.2. Preemption Threshold Selection for Task

6. Task Scheduling Strategy Based on Preemption Threshold

6.1. Scheduling Algorithm Based On Preemption Threshold

6.2. Algorithm Complexity

7. Simulations and Analysis

7.1. Simulation Experiments

7.2. Performance Analysis

8. Conclusions and Future Works

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley