For the free-floating space manipulator with free-swinging joint failure, motions among its active joints, passive joints, free-floating base, and end-effector are coupled. It is significant to make clear all motion coupling relationships, which are defined as “kinematic coupling relationships” and “dynamic coupling relationships,” inside the system. With the help of conservation of system momentum, the kinematic model is established, and velocity mapping relation between active joints and passive joints, velocity mapping relation between active joints and base, velocity mapping relation between active joints and end-effector. We establish the dynamic model based on the Lagrange equation, and the system inertia matrix is partitioned according to the distribution of active joints, passive joints, and the base. Then, kinematic and dynamic coupling relationships are explicitly derived, and coupling indexes are defined to depict coupling degree. Motions of a space manipulator with free-swinging joint failure simultaneously satisfy the first-order nonholonomic constraint (kinematic coupling relationships) and the second-order nonholonomic constraint (dynamic coupling relationships), and the manipulator can perform tasks through motion planning and control. Finally, simulation experiments are carried out to verify the existence and correctness of the first-order and second-order nonholonomic constraints and display task execution effects of the space manipulator. This research analyzes the kinematic and dynamic characteristics of the free-floating space manipulator with free-swinging joint failure for the first time. It is the theoretical basis of free-swinging joint failure treatment for a space manipulator.

1. Introduction

The application of a space manipulator can not only improve execution efficiency of space tasks but also decrease risks of an astronaut’s EVA. Therefore, space manipulators play an important role in space exploration [1, 2]. However, space manipulators are exposed to hazardous space environment with high temperature difference and intense radiation and usually execute many heavy tasks, like carrying a load whose mass reaches up to 8-25 tons, so parts in joints suffer from severe abrasion, and joints are prone to fail during the long-term service [3]. Subjected to hazardous environment, maintaining fault joints in orbit is accompanied with high costs and risks, so we hope to design a failure treatment strategy to keep using space manipulators after joint failure [4, 5].

Wu et al. [6] divided joint failure of space manipulators into two types: a fail-on type with infinite torque and a fail-off type with zero torque, according to joint failure cases in Canadarm1. Afterwards, these two failure types are explicitly defined as locked joint failure and free-swinging joint failure [7, 8]. Locked joint failure means the fault joint is rigidly locked so long as the abnormal operation is detected. Reconfiguring the kinematic and dynamic models, the space manipulator with locked joints is degraded into a new manipulator with less degrees of freedom (DOF) to be used [9, 10]. Free-swinging joints cannot support torque at all, so they swing freely. It is usually caused by motor excitation loss, gear engagement separation, or cracking of the transmission shaft in alternant speed-up and speed-down. However, there are few researches on free-swinging joint failure treatment for space manipulators [11].

For the space manipulator with free-swinging joint failure, its DOF is larger than the number of actuated joints, so it is an underactuated system. Referring to the service experience of underactuated manipulators on the ground, we conclude that free-swinging joint failure treatment methods mainly include the following: (1) direct control of underactuated manipulators to execute tasks [12]; (2) with the help of the kinematic and dynamic coupling relationships between active joints and passive joints, free-swinging joints are passively regulated to target angles and are locked. Then, the manipulator with locked joints comes into use [13]. Because free-swinging joints can only be regulated passively, they are called as “passive joints,” and the healthy joints regulating passive joints are called “active joints.” The free-swinging joint failure treatment methods above either depend on motion planning or depend on the control method. No matter which method is used, it is significant to establish kinematic and dynamic models of underactuated manipulators and analyze kinematic and dynamic characteristics to make clear all coupling relationships inside the system at the beginning.

Kinematic and dynamic characteristic analysis has been extensively studied around underactuated manipulators on the ground. Aiming at a 2 DOF planar manipulator whose second joint is passive, Nakamura et al. [14] established its dynamic model based on the Hamiltonian function in phase space. Introducing periodic motion into an active joint, he drew Poincaré mapping figures to show the displacement relation between an active joint and a passive joint. Arai et al. [15] derived the unintegrable acceleration coupling relationship between active joints and a passive joint of a 3 DOF underactuated planar manipulator. The acceleration coupling relationship was called as “dynamic coupling relationship,” and it was the second-order nonholonomic constraint inside system. Lai et al. analyzed the dynamic coupling relationships of 2 DOF [16, 17], 3 DOF [18], 4 DOF [19], and n DOF [20] underactuated planar manipulators with the passive first joint and pointed out that when the first joint is passive, the second-order nonholonomic constraint could be integrated into the first-order nonholonomic constraint, so velocities of active joints and a passive joint were coupled. The researches above tell us that for underactuated planar manipulators, if only the first joint is passive, the underactuated system is with the first-order nonholonomic constraint, which represents that velocities of active joints and passive joints are coupled. Otherwise, the second-order nonholonomic constraint exists, and accelerations of active joints and passive joints are coupled.

The researches above used many geometric constraints of planar mechanism to simplify the analysis procedure, so they are only appropriate for underactuated planar manipulators. High DOF manipulators have three-dimensional geometric structure, so their kinematic and dynamic characteristic analysis is more complicated. Considering balance of gravity, English and Maciejewski [21] established the velocity mapping relation between joints and end-effector for n DOF underactuated manipulators. Bergerman and Xu [22] derived the second-order nonholonomic constraint which contained centrifugal force, Coriolis force, and gravitational torque and defined the local and global dynamic coupling indexes to depict acceleration transmission efficiency from active joints to passive joints, namely, dynamic coupling degree. Analysis of high DOF underactuated manipulators on the ground must consider gravity effects. However, the space manipulator is free from gravity. Mukherjee and Chen [23] established a dynamic model of the space manipulator with free-swinging joints through the Lagrange equation and derived dynamic coupling relationship between active joints and passive joints based on the Hamiltonian operator. Aiming at the case that active joints are more than passive joints, He et al. [24] pointed out that “passive redundancy” existed when regulating passive joints. Then, they designed a sliding-mode controller with end-effector position/attitude correction, to minimize end-effector disturbance when regulating passive joints. Chen et al. [25] analyzed dynamic coupling relationship between an adjacent active joint and a passive joint for a space manipulator with single free-swinging joint failure and proposed a passive joint regulation strategy based on iteration control. The researches above treated the space manipulator base as fixed. In practice, space manipulators are installed on a free-floating base and motions between joints and the base are coupled. This coupled motion will act on kinematic and dynamic modelling. If it is neglected, we cannot establish valid kinematic and dynamic models and cannot reveal kinematic and dynamic coupling relationships of the space manipulator with free-swinging joint failure.

For the free-floating space manipulator, motion between the base and joints satisfies the first-order nonholonomic constraint originally because of momentum conservation without external force [26]. Moreover, according to existing researches about kinematic and dynamic modelling for underactuated manipulators, the second-order nonholonomic constraint also exists in accelerations among active joints, passive joints, and the base. Therefore, the free-floating space manipulator with free-swinging joint failure simultaneously contains the first-order nonholonomic constraint (kinematic coupling relationships) and the second-order nonholonomic constraint (dynamic coupling relationships), and they are independent. However, for underactuated manipulators on the ground, either the first-order nonholonomic constraint or the second-order nonholonomic constraint exists inside systems. Therefore, the kinematic and dynamic characteristic analysis of the free-floating space manipulator with free-swinging joint failure is more complicated than conventional underactuated manipulators, and all kinematic and dynamic coupling relationships need to be studied.

Aiming at the free-floating space manipulator with free-swinging joint failure, we establish the kinematic model based on the momentum conservation. Then, the partitioned dynamic equation corresponding to the distribution of active joints, passive joints, and the base are derived based on the Lagrange equation. Then, the kinematic and dynamic coupling relationships among active joints, passive joints, the base and end-effector are derived, and local and global coupling indexes are defined to evaluate the coupling degree. Finally, we briefly introduce motion planning and a control method for the space manipulator with free-swinging joint failure, as the reference of free-swinging joint failure treatment. The traits of this paper mainly include the following:

(1)
The general kinematic and dynamic modelling procedure of the free-floating space manipulator with free-swinging joint failure is proposed for the first time
(2)
We point out that the free-floating space manipulator with free-swinging joint failure simultaneously contains the first-order and second-order nonholonomic constraints, and we explicitly reveal all kinematic and dynamic coupling relationships among active joints, passive joints, free-floating base, and end-effector
(3)
We simply design motion planning and the control method based on the kinematic and dynamic coupling relationships for the free-floating space manipulator with free-swinging joint failure, and many tasks can be completed successfully

The remainder of this paper is as follows: Section II is the kinematic modelling of the free-floating space manipulator with free-swinging joint failure, and the velocity mapping relations between active joints, passive joints, base, and end-effector are derived. Then, we establish the partitioned dynamic model based on the Lagrange equation in Section III. In Section IV, all kinematic and dynamic coupling relationships inside the system are derived, and the local and global coupling indexes are defined. Then, motion planning and control methods for the free-floating space manipulator with free-swinging joint failure to execute tasks are designed. In Section V, simulation experiments are carried out to verify the existence and correctness of the first-order and second-order nonholonomic constraints and to display the execution effects of many tasks of the free-floating space manipulator with free-swinging joint failure. The conclusion is in Section VI.

2. Kinematic Modelling of the Free-Floating Space Manipulator with Free-Swinging Joint Failure

In this section, the kinematic model of the free-floating space manipulator with free-swinging joint failure is established and the expression of the conservation of system momentum is derived. Then, the velocity mapping relations between active joints, passive joints, the base, and end-effector are obtained.

2.1. Kinematic Modelling

An n DOF space manipulator with free-swinging joint failure is in Figure 1. In this paper, vectors and matrixes with subscript in the upper left corner are with respect to the corresponding coordinate frame and others with no subscript in the upper left corner are with respect to the inertial coordinate frame. Definitions of frequently used variables are as follow:

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Kinematic model of the n-DOF space manipulator with free-swinging joint failure.

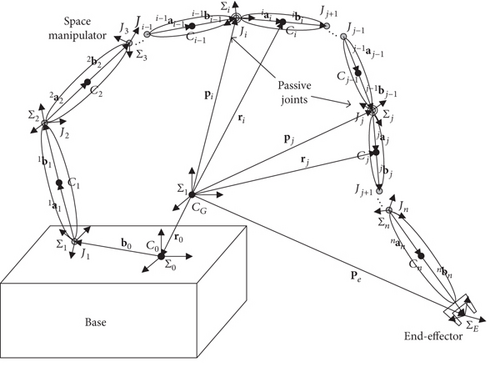
C₀: base centroid,

C_i: centroid of the i-th link,

C_G: centroid of the whole system,

J_i: i-th joint, i = 1, 2, ⋯, n,

∑_I: inertial coordinate frame built at C_G,

∑₀: base coordinate frame built at C₀,

∑_i: i-th link coordinate frame built at C_i,

∑_E: end-effector coordinate frame,

m₀: base mass,

m_i: mass of the i-th link,

M: mass of the whole system,

I₀ ∈ R^3×3: base inertia matrix with respect to C₀,

I_i ∈ R^3×3: inertia matrix of the i-th link with respect to C_i,

p_i ∈ R^3×1: position vector of J_i, i = 1, 2, ⋯, n,

: position vector of end-effector,

: attitude vector of end-effector,

r_i ∈ R^3×1: position vector of C_i, i = 1, 2, ⋯, n,

r_g ∈ R^3×1: position vector of C_G (if ∑_I is built at C_G, r_g ≡ 0),

r₀ ∈ R^3×1: position vector of C₀,

Ψ₀ ∈ R^3×1: attitude vector of base,

b₀ ∈ R^3×1: position vector from C₀ to J₁,

: joint angle vector,

: joint velocity vector,

: joint acceleration vector,

: state variable of system ( and are velocity and acceleration, respectively),

: attitude transformation matrix from ∑_j to ∑_i,

: position vector from J_i to C_i (a_i is its norm, i = 1, 2, ⋯, n),

: position vector from C_i to J_i+1 (b_i is its norm, i = 1, 2, ⋯, n),

z_i ∈ R^3×1: unit vector of the i-th joint axis, i = 1, 2, ⋯, n,

v₀, ω₀ ∈ R^3×1: velocity of C₀/base angular velocity,

v_i, ω_i ∈ R^3×1: velocity of C_i/angular velocity of the i-th link,

v_e, ω_e ∈ R^3×1: end-effector velocity/end-effector angular velocity.

For a free-floating space manipulator, linear/angular velocities of i-th link and end-effector are

(1)

(2)

where J_Li = [z₁ × (r_i − p₁), z₂ × (r_i − p₂), ⋯, z_i × (r_i − p_i), 0, ⋯, 0] ∈ R^3×n, J_Le = [z₁ × (p_e − p₁), z₂ × (p_e − p₂), ⋯, z_i × (p_e − p_i), ⋯, z_n × (p_e − p_n)] ∈ R^3×n, J_Ai = [z₁, z₂, ⋯, z_i, 0, ⋯, 0] ∈ R^3×n, and J_Ae = [z₁, z₂, ⋯, z_i, ⋯, z_n] ∈ R^3×n.and where p_0e = p_e − r₀ and r_0i = r_i − r₀ and

and

are the antisymmetric matrixes of p_0e and r_0i, respectively. E₃ ∈ R^3×3 is a unit matrix, and O₃ ∈ R^3×3 is a zero matrix. J_b ∈ R^6×6 denotes base Jacobian matrixes representing the transmission from

. J_mi ∈ R^6×n and J_m ∈ R^6×n denote manipulator Jacobian matrixes representing the transmission from

J_m consists of n column vectors: J_m = [j_m1, j_m2, ⋯, j_mn] ∈ R^6×n. So

can be expressed as

(3)

As can be seen from equation (3), j_mi depicts the contribution of i-th joint velocity

. If selecting the rest of the healthy joints as active joints, we can obtain a serial number set of passive joints as S_P = {s_Pi|∀ s_Pi ∈ {1, 2, ⋯, n}, i = 1, 2, ⋯, p} and serial number set of active joints as S_A = {s_Aj|∀ s_Aj ∈ {1, 2, ⋯, n}, j = 1, 2, ⋯, a}. So the passive joint velocity is

, and the active joint velocity is

. With the help of the commutative law of addition, we express equation (3) as

(4)

where

is the column vectors corresponding to passive joints, and they make up J_mP ∈ R^6×p which represents transmission from

is the column vectors corresponding to active joints, and they make up J_mA ∈ R^6×a which represents transmission from

. If making

, equation (2) becomes

(5)

If we know the desired , we can acquire , , and from equation (5). However, the base and passive joints cannot actively supply and because of lacking actuators. All motions of passive joints, base, and end-effector can only be actuated by active joints. In the next subsection, we are going to derive specific velocity mapping relations among active joints, passive joints, base, and end-effector based on conservation of system momentum.

2.2. Velocity Mapping Relations between Active Joints, Passive Joints, Base, and End-Effector Based on Momentum Conservation

Linear momentum and angular momentum of the whole system are

(6)

(7)

where

represents the contribution of

to linear momentum P and

represents the contribution of

to angular momentum L. J_LM and J_AM can be expressed as J_LM = [j_LM1, j_LM2, ⋯, j_LMn] and J_AM = [j_AM1, j_AM2, ⋯, j_AMn], respectively, and we can find column vectors corresponding to passive joints and active joints to make up matrixes

(8)

Equations (6) and (7) can be expressed in matrix form

(9)

where

. Without the external force, system momentum is conservative. Setting the initial momentum is zero, so

(10)

From equation (10), we know that

, and

are coupled with each other, but we care more about the transmission from

and

. From equation (10), we have

(11)

Making

(12)

Equation (11) becomes

(13)

Then, we can obtain transmission from

and

(14)

represents the Jacobian matrix from

and

is the null space of H_bP, and ξ is an arbitrary vector. Because 6 < 6 + p, when H_bP is full rank, the null space exists. In particular, making ξ = 0, we can obtain transmission from

and from

(15)

J_bA ∈ R^6×a is the first six rows of vectors of J_bPA, and J_PA ∈ R^p×a is the last p rows of vectors of J_bPA. Substituting equation (15) into equation (5), we obtain the transmission from

(16)

where

, and J_eA = J_bPJ_bPA + J_mA ∈ R^6×a is the Jacobian matrix representing transmission from

. Equations (15) and (16) can be reduced to the following constraints:

(17)

Obviously, for space manipulators, there is no definite relation between θ_A and θ_P, θ_b, p_e, Ψ_e, which means we cannot find constraints like h₁₀(θ_P, θ_A, t) = 0, h₂₀(θ_b, θ_A, t) = 0, and h₃₀(p_e, Ψ_e, θ_A, t) = 0 making h₁ = dh₁₀/dt, h₂ = dh₂₀/dt, and h₃ = dh₃₀/dt, so constraints in equation (17) are nonholonomic. Because equation (17) includes constraints among the first-order derivatives of θ_b, θ_A, θ_P, p_e, Ψ_e, it is called as the first-order nonholonomic constraint. The first-order nonholonomic constraint is unique for the free-floating space manipulator with free-swinging joint failure because its momentum is conservative.

3. Dynamic Modelling of the Free-Floating Space Manipulator with Free-Swinging Joint Failure

Establishment of a dynamic model is the basis of dynamic coupling relationship analysis and controller design, so the dynamic model of the space manipulator with free-swinging joint failure is established in this section.

3.1. Kinetic Energy of System

The Lagrange function of the space manipulator with free-swinging joint failure is as follows:

(18)

where K is system kinetic energy and E is the system potential energy. The space manipulator is free from gravity, and we take no account of joint and link flexibility, so E = 0. The Lagrange function equals to total kinetic energy:

(19)

where

(20)

M_b denotes the base inertia matrix. M_m denotes the manipulator inertia matrix. M_bm and M_mb are the coupling inertia matrixes between base and manipulator. M is the inertia matrix of the whole system. Expanding equation (19), we have

(21)

We can know that M_bm, M_mb, and M_m are relative to joint velocity, so we can utilize commutative law of addition to divide these matrixes into

(22)

The row vector m_{mb_rowi} of M_mb, the column vector m_{bm_coli} of M_bm, and the element m_mij of M_m represent the contribution of the corresponding joint velocity to kinetic energy. Then, equation (21) can be expressed as

(23)

where

(24)

M becomes

(25)

And the Lagrange function of the system is

(26)

3.2. Lagrange Equation of the System

The Lagrange equation is

(27)

Substituting equation (26) into equation (27), and calculating derivatives, we have

(28)

Making , , and . And , , and .

, and

are centrifugal forces and Coriolis forces acting on the base, passive joints, and active joints. So equation (28) becomes

(29)

where

(30)

Passive joints and base cannot supply torque, so τ_b ≡ 0 and τ_P ≡ 0. If we know the motions of active joints, passive joints, and the base, the required active joint torque τ_A can be calculated to actuate the space manipulator to arrive at the target state.

4. The Analysis of Kinematic and Dynamic Coupling Relationships

Based on kinematic and dynamic models of the free-floating space manipulator with free-swinging joint failure, the kinematic and dynamic coupling relationships inside system are derived, and coupling indexes are defined to depict the coupling degree.

4.1. Kinematic Coupling Relationships and Coupling Indexes

For the space manipulator with free-swinging joint failure, passive joints, base, and end-effector can only be passively actuated by active joints, so we call them as “passive units” [27]. Combining them with equations (15) and (16), we have

(31)

v_t ∈ R^{(6 + p + 6)×1} denotes the vector consisting of all passive unit velocities, and J_t ∈ R^{(6 + p + 6)×a} is the total Jacobian matrix of the system. Equation (31) reflects the kinematic coupling relationships between active joints and all passive units. For a specific task, it requires no more than a part of the passive units to move as the desired velocities in v_t, so v_t is the velocity of the entire task space. From equation (31), we can acquire nonhomogeneous linear equations:

(32)

j_tri, i = 1, 2, ⋯, 12 + p, of J_t represents the contribution of

to v_ti. The necessary and sufficient condition for the existence of a solution of equation (32) is rank(J_t) = rank([J_t, v_t]) ≤ a, which is equivalent to

(33)

It tells us that if active joints are more than passive units, and J_t is full rank, we can find at least one set of solutions of

, which means active joints can actuate all passive units at the same time. For the desired v_t, we can calculate

(34)

In particular, if a > 12 + p, the system is redundant, and equation (34) has the general solution

(35)

where φ ∈ R^a×1 is an arbitrary vector. Equation (35) means there are infinite solutions of

corresponding to the same v_t because of the arbitrariness of φ. Generally speaking, redundancy empowers the space manipulator with free-swinging joint failure to perform secondary tasks, such as obstacle-avoidance, singularity-avoidance, and dexterity-optimization, as long as we find an analytical expression of φ according to secondary task requirements.

If conditions in equation (33) are unsatisfactory, the row vectors of J_t are linearly dependent and some velocities in v_t cannot be actuated by

. In other words, the transmission efficiency from

to v_t is insufficient, corresponding to insufficiency of kinematic coupling degree. The kinematic coupling degree depends on the degree of closeness of J_t to singularity, which can be represented by the minimum singular value, condition number, and manipulability. Because manipulability can reflect the general closeness to singularity, which means it can reflect the comprehensive transmission capacity from active joint motion/torque to passive units’ motion. We define the kinematic coupling index based on the manipulability of J_t to evaluate kinematic coupling degree.

(36)

where σ_t1 ≥ σ_t2≥⋯≥σ_{t(6 + p + 6)} ≥ 0 are singular values of J_t. When w_t is close to zeros, the transmission efficiency from

to v_t is inefficient, which means v_t is kinematically uncontrollable for

. Because w_t = w_t(q), in motion planning, we should continually calculate w_t according to current state q.

However, assuming at least one joint fails, so 12 + p ≥ 13. If we hope all passive units are controllable, the manipulator must have 14 joints at least. It is unrealistic for real space manipulators because of complicated structure and high difficulty in design. Fortunately, many space tasks only require active joints to actuate a part of passive units. We are going to discuss some typical tasks in the following.

4.1.1. End-Effector Trajectory Tracking Task

This task requires the end-effector to move along the predefined trajectory to arrive at the desired positon/attitude, so the task velocity vector is

. The transmission from

to v_eA depends on J_eA. When a ≥ 6, the end-effector could be effectively actuated by active joints. The kinematic coupling index is defined as the manipulability of J_eA:

(37)

If w_eA(q) is close to zero, v_eA is uncontrollable for and the end-effector trajectory tracking task is unrealizable. If w_eA(q) is big enough, we should interpolate to track the predefined trajectory and calculate . The manipulator can complete the task successfully with the obtained .

4.1.2. Passive Joint Regulating Task

This task requires active joints to regulate passive joints to target angles based on the first-order nonholonomic constraint between

and

. The task velocity vector is

, and the transmission from

depends on J_PA. When a ≥ p, passive joints could be actuated by active joints. The kinematic coupling index is defined as the manipulability of J_PA:

(38)

If w_PA(q) is close to zero, v_PA is uncontrollable for and the passive joint regulating task is unrealizable. If w_PA(q) is big enough, we should interpolate according to the task requirement and calculate .

4.1.3. Base Position/Attitude Controlling Task

This task requires the base to move to the desired positon/attitude relying on the first-order nonholonomic constraint between

and

, so the task velocity vector is

. The transmission from

to v_bA depends on J_bA. When a ≥ 6, the base can be actuated. The kinematic coupling index is defined as the manipulability of J_bA:

(39)

If w_bA(q) is close to zero, v_bA is uncontrollable for so the task is unrealizable. If w_bA(q) is big enough, we should interpolate as the requirement and calculate .

4.1.4. The Combination Tasks

The space manipulator with free-swinging joint failure usually executes some combination tasks, like the task that requires active joints to actuate the end-effector to the desired position and passive joints to target angles at the same time. For this task, we select the task velocity vector as

and the Jacobian matrix is

(40)

where J_{eA_v} is the first three rows of J_eA. The kinematic coupling index is the manipulability of J_vePA. For the task to eliminate the base attitude deflection when regulating passive joints, we select the task velocity vector as

and the Jacobian matrix is

(41)

where J_{bA_ω} is the last three row vectors of J_bA. The kinematic coupling index is the manipulability of J_ωbPA. To eliminate base attitude disturbance, we keep ω₀ ≡ 0 [28].

For general space tasks, we should select

according to controlled passive units for current task requirements. f is the dimensionality of v_task. Then, the corresponding row vectors from J_t need to be taken out to construct the Jacobian matrix:

(42)

and the kinematic coupling index is

(43)

If a ≥ f and

, we can interpolate v_task as requested and calculate

; for a > f, the space manipulator with free-swinging joint failure is redundant for the current task, and the general solution of

exists as

(44)

The analysis above depends on the conservation of system momentum. Space manipulators are usually installed on the base with large mass and inertia, such as a space station or space laboratory. The partition of Jacobian matrix is equivalent to move all passive joints to the base, so passive joints and the base make up a large combination, and all active joints make up a small combination. If system momentum is conservative, it is difficult to use a small combination to regulate a large combination. So when the base mass and inertia is large, as well as the kinematic coupling degree between active joints and passive joints, the base will be seriously inefficient. Passive joint regulation and base control tasks cannot be performed relying on motion planning.

4.2. Dynamic Coupling Relationships and Coupling Indexes

Expanding equation (29):

(45)

(46)

(47)

Dynamic coupling relationships inside the system can be derived from equations (45), (46), and (47).

4.2.1. Dynamic Coupling Relationship between Active Joints and Passive Joints

Eliminating

in equations (45) and (46), we have

(48)

(49)

where

is the coupling inertia matrix between active joints and passive joints and

is the nonlinear item. The first term in the right of equation (49) reflects the transmission from

, and it is the dynamic coupling relationship between active joints and passive joints. We can obtain nonhomogeneous linear equations

. If p ≤ a and rank(M_PA) = p, we have the solution of

. Therefore, referring to [29], the dynamic coupling index is defined as the manipulability of M_PA to evaluate the transmission efficiency from

(50)

where ε_PA1 ≥ ε_PA2≥⋯≥ε_PAp ≥ 0 are singular values of M_PA. When η_PA(q) is close to zero, the dynamic coupling degree between passive joints and active joints is inefficient and

is dynamically uncontrollable for

. When η_PA(q) is big enough, we can design the control law for

, and

which actuates the manipulator to complete the passive joint regulating task can be obtained by

4.2.2. Dynamic Coupling Relationship between Active Joints and Base

Eliminating

in equations (45) and (46), we have

(51)

(52)

where

is the coupling inertia matrix between active joints and the base.

is the nonlinear item. The first term in the right of equation (52) is the dynamic coupling relationship between active joints and the base. The dynamic coupling index is defined as the manipulability of M_bA to evaluate the transmission efficiency from

(53)

If η_bA(q) is close to zero, is uncontrollable for . On the contrary, we can design the control law for to calculate .

In particular, we can get transmission from

by combining equations (49) and (52):

(54)

If we calculate the derivative of equation (22), we have

(55)

Equation (55) has a similar form with equation (54), but obviously, J_PA ≠ M_PA, J_bA ≠ M_bA, , and , so equations (22) and (54) are different.

Equation (54) can also be derived from equations (45) and (46):

(56)

Substituting equation (56) into equation (47), we have

(57)

where

(58)

represents the mapping relation between

and τ_A and

(59)

is the nonlinear item. Equation (57) establishes the direct relation between

and τ_A. After designing the control law of

, we can calculate

, and then we can obtain the torque τ_A that actuates the manipulator. We can further find the transmission from τ_A to

(60)

where

, and

. So we can directly calculate τ_A from equation (60) corresponding to the desired

. Dynamic coupling indexes are defined to evaluate transmission efficiency from τ_A to

(61)

4.2.3. Dynamic Coupling Relationship between Active Joints and End-Effector

Because

does not appear in the Lagrange equation, we cannot find a mapping relation between

and

in equation (29), but we can find the dynamic coupling relationship between active joints and the end-effector from another perspective [12]. Calculating derivative of equation (16), we have

(62)

Multiplying equation (57) by

, we have

(63)

where

is the coupling inertia matrix representing the transmission from τ_A to

and

is the nonlinear item. Equation (63) is the dynamic coupling relationship between active joints and the end-effector. The dynamic coupling index between active joints and the end-effector is the manipulability of M_eτ:

(64)

If η_eτ(q) is close to zero,

is uncontrollable for τ_A. On the contrary, we can design the control law for

to calculate

(65)

Equations (60) and (63) can be reduced to the following constraints:

(66)

Theorem. The constraints in equation (70) are also nonholonomic.

Proof. Taking equation (49) as an example, we have

(67)

making

. Assuming there exists the first-order constraint

whose derivative with respect to time is

(68)

Assuming constraint in equation (66) is holonomic, we have

(69)

Considering

, we can obtain the general solution of

(70)

s(q) is relative to the state variable q. C is a constant vector. The derivative of equation (70) is

(71)

Substituting c_b and c_P into equation (71), and comparing it with equation (67), we obtain

(72)

where

and

. To satisfy the above equality, we have

(73)

s(q) is only relative to q instead of , so the first equality is not satisfied. The second equality is also not satisfied because θ_P and θ_b are not cyclic coordinates in Μ. Therefore, does not exist and the constraints in equation (66) are nonholonomic. Because equation (66) is the constraints among the second-order derivatives of θ_b, θ_A, θ_P, p_e, Ψ_e, they are called as the second-order nonholonomic constraint.

The free-floating space manipulator with free-swinging joint failure simultaneously contains the first-order nonholonomic constraint and the second-order nonholonomic constraint, and they are independent with each other. From a mathematical viewpoint, equations (17) and (66) belong to differential equations, and they have the same solution. In fact, because null space exists in equation (14), we can find the same solution to these two differential equations. Therefore, motions of the free-floating space manipulator with free-swinging joint failure simultaneously satisfy the first-order and second-order nonholonomic constraints.

The analysis above is not based on conservation of system momentum, so even if base mass and inertia are very large, the degree of dynamic coupling may be large enough to enable active joints to actuate passive units through the control method.

In summary, dynamic coupling relationship between active joints and all passive units is

(74)

a_t ∈ R^{(p + 12)×1} is the acceleration of the entire task space.

(75)

is the coupling inertia matrix representing the transmission from

, and

(76)

is the coupling inertia matrix representing the transmission from τ_A to a_t.

(77)

are nonlinear items. Based on dynamic coupling relationships, active joints can actuate the manipulator to execute tasks as the same as motion planning. For general tasks, we should select the task acceleration vector a_task ∈ R^f×1 according to task requirements and construct

and

. Then, we design the control law for a_task to guarantee that the selected passive units will converge to the equilibrium point, and τ_A is obtained. If a > f, the space manipulator is redundant and the solutions of

and τ_A are

(78)

is an arbitrary vector. Appropriately designing ς, the manipulator can perform primary and secondary tasks at the same time.

4.3. Global Kinematic and Dynamic Coupling Indexes

The kinematic and dynamic coupling indexes defined above are with respect to system state variables q. If their values are large, it only indicates that motion transmission efficiency from active joints to passive units is high only at the current q, so the indexes above are called as local indexes for kinematic and dynamic coupling in state space. However, before structure design, motion planning, and controller design, the system state is unknown, so the local coupling indexes are not appropriate at this moment. We care more about the global coupling degree in the entire state space, and global kinematic and dynamic coupling indexes are defined as

(79)

w_∗ and correspond to local and global manipulability of a Jacobian matrix J_∗, respectively. η_∗ and correspond to local and global manipulability of an inertia matrix M_∗, respectively. If kinematic and dynamic parameters are determined, global indexes can be calculated. The higher the values of global indexes, the higher the motion transmission efficiency from active joints to passive units whatever state the manipulator is in. If selecting different healthy joints as active joints, different values of global indexes will be obtained. There exists the case that values of global indexes are close whether we select some healthy joins. It indicates that these joints are incapable to actuate passive units, so we should not select them as active joints.

5. Simulation Experiments

In simulation, we plan motions for the space manipulator with free-swing joint failure to perform some tasks to verify the existence and correctness of the first-order nonholonomic constraint. Then, we give a study case for calculating kinematic and dynamic indexes and discuss the variation of and with the increasing base mass and inertia. In particular, aiming at the case where a passive regulating task cannot be completed through motion planning with large base mass and inertia, we design the control law based on PD controller for , and the task is completed based on the second-order nonholonomic constraint. The practicability of the coupling index and correctness of the second-order nonholonomic constraint are verified.

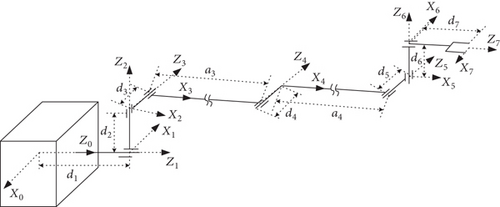
Simulation experiments are carried out surrounding SSRMS-type 7 DOF space manipulator in Figure 2. Its kinematic and dynamic parameters are in Tables 1 and 2.

Table 1. Kinematic parameters of SSRMS-type 7 DOF space manipulator.

Joint no.	Torsion angle α_i−1 (°)	Link length a_i−1 (m)	Joint angle θ_i (°)	Link offset d_i (m)
1	0	0	180	1.1
2	−90	0	−90	0.5
3	−90	0	0	0.5
4	0	5	0	0.5
5	0	5	0	0.5
6	90	0	90	0.5
7	90	0	180	1.1

Table 2. Dynamic parameters of SSRMS-type 7 DOF space manipulator.

Joint no.	Link mass m_i (kg)	Link inertia mdiag[I_xxi, I_yyi, I_zzi] (kg·m²)	Link centroid position P_cii (m)
0	10⁶	Diag[10⁶, 10⁶, 10⁶]	[0, 0, 0] ^T
1	42.5	Diag[0.8854, 0.0531, 0.8854]	[0, 0.25, 0] ^T
2	42.5	Diag[0.8854, 0.0531, 0.8854]	[0, 0.25, 0] ^T
3	70	Diag[0.0875, 145.8333, 145.8333]	[2.5, 0, 0] ^T
4	70	Diag[0.0875, 145.8333, 145.8333]	[2.5, 0, 0] ^T
5	42.5	Diag[0.8854, 0.8854, 0.0531]	[0, 0, 0.25] ^T
6	42.5	Diag[0.8854, 0.8854, 0.0531]	[0, 0, 0.25] ^T
7	42.5	Diag[1.2750, 1.2750, 0.0531]	[0, 0, 0.55] ^T

5.1. Motion Planning for the Space Manipulator with Free-Swinging Joint Failure

Aiming at the end-effector trajectory tracking and passive joint regulating tasks and the combination tasks that track end-effector trajectory and limit base attitude deflection when regulating passive joints, we plan motions for the space manipulator based on the first-order nonholonomic constraint. The existence of the first-order nonholonomic constraint is verified, and the motion planning based on kinematic coupling relationships is applied.

5.1.1. End-Effector Trajectory Tracking Task

For the SSRMS-type space manipulator with the single joint failure, it has 6 healthy joints. Selecting all healthy joints as active joints, the end-effector trajectory tracking task can be performed. Assuming the first joint fails, the setting initial manipulator configuration is θ_ini = [−50°,−170°,150°,−60°,130°,170°,0°]^T and the initial base position/attitude is θ_{b_ini} = [0, 0, 0, 0, 0, 0]^T. The task requires the end-effector to move along an arc trajectory to position/attitude

and pass the middle point x_{e_mid} = [4 m, 3 m, 5.5 m]^T. Task execution time is 40 s. We interpolate the velocity of the end-effector with the quartic polynomial

(80)

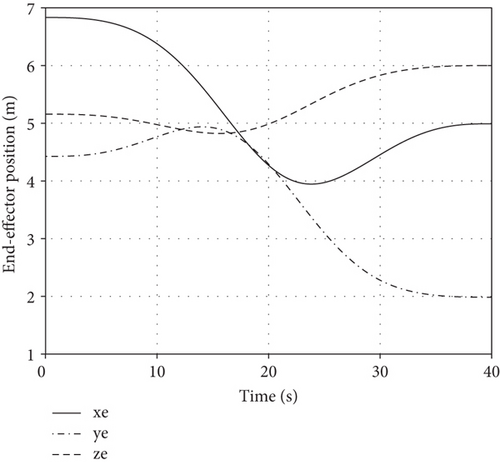
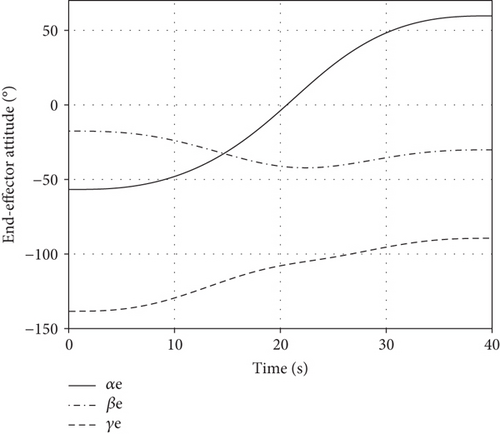
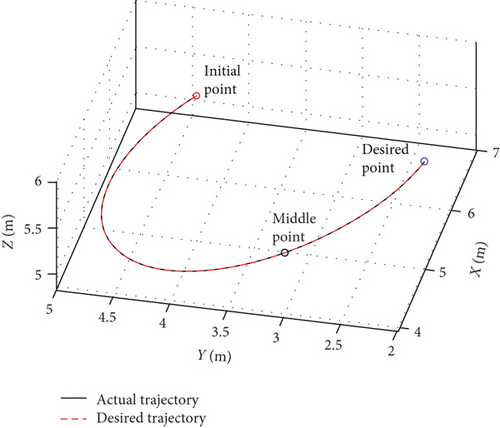
The variation of is in Figure 3, and the comparison between the actual and the desired end-effector trajectory is in Figure 4.

The joint motion is shown in Figure 5.

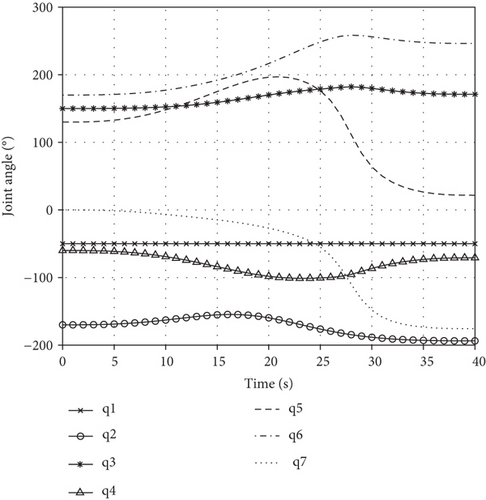
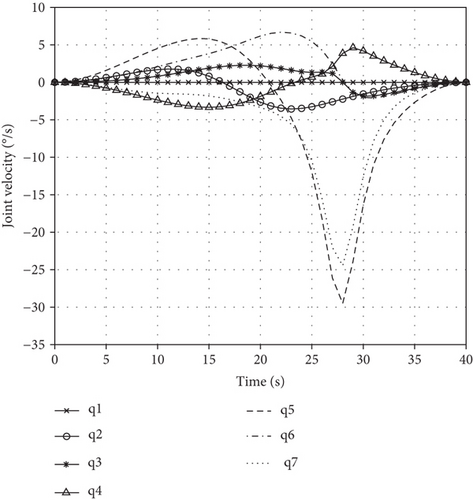
As can be seen from Figures 3–5, end-effector moves along the desired trajectory to arrive at the desired position/attitude, and the joint motion is smooth, so the end-effector trajectory tracking task is accomplished based on motion planning. Velocity of the passive first joint is calculated from equation (15), and its angle is obtained by integral.

5.1.2. Passive Joint Regulating Task

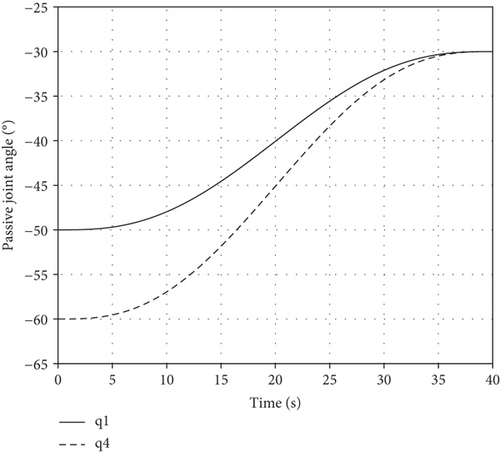
If the number of passive joints is less than or equal to 3, there will be at least 4 healthy joints and the manipulator can perform passive joint regulating task. Assuming the first and fourth joints fail, the initial configuration is θ_ini = [−50°,−170°,150°,−60°,130°,170°,0°]^T and the initial base position/attitude is θ_{b_ini} = [0, 0, 0, 0, 0, 0]^T. The task requires all passive joints to be regulated to θ_{P_des} = [−30°,−30°]^T in 40 s. However, for the base mass and inertia in Table 2, active joints cannot regulate passive joints because the kinematic coupling degree is seriously insufficient. Therefore, we reset the base mass as m₀ = 100 kg and inertia as I₀ = diag[100 kg · m², 100 kg · m², 100 kg · m²]. Interpolating with the quartic polynomial, variations of θ_P and are shown in Figure 6.

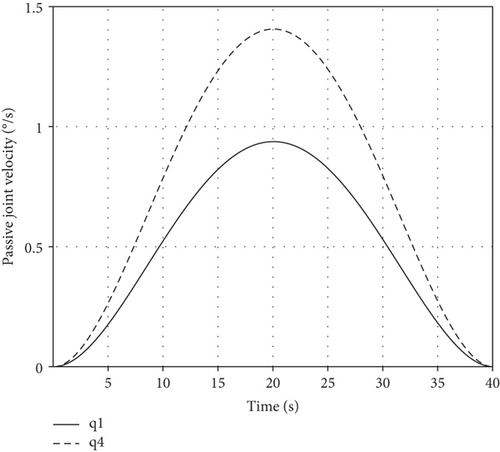
Variations of θ_A and are shown in Figure 7.

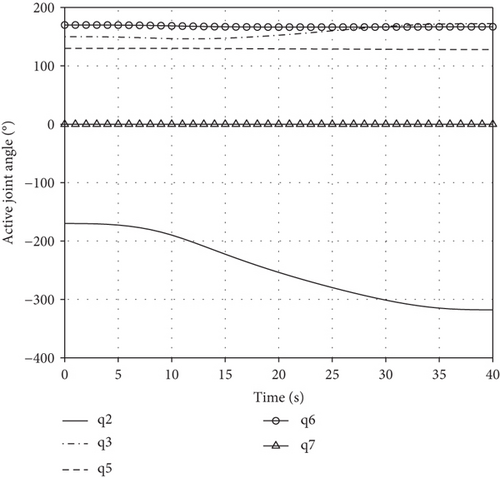
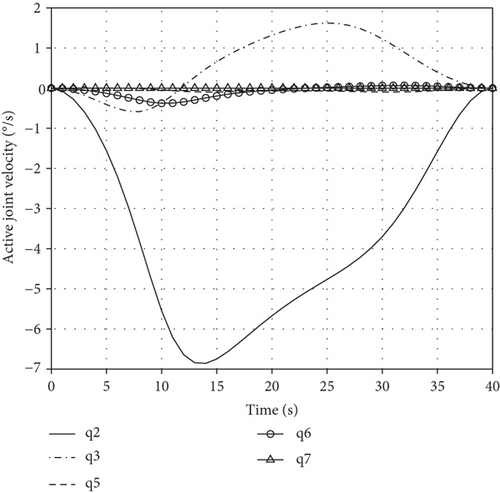
It can be seen that two passive joints are regulated to −30° in 40 s and the motion of active joints is smooth, so the passive joint regulating task is accomplished.

5.1.3. Tracking End-Effector Trajectory When Regulating Passive Joints

If the number of passive joints is less than or equal to 2, there will be at least 5 healthy joints, and active joints can actuate the end-effector to the desired position and regulate passive joints to target angles simultaneously. Assuming the first joint fails, the initial configuration is θ_ini = [−50°,−170°,150°,−60°,130°,170°,0°]^T and initial base position/attitude is θ_{b_ini} = [0, 0, 0, 0, 0, 0]^T. The task requires the end-effector to track a straight trajectory to the desired position x_{e_des} = [4 m, 2 m, 3 m]^T and the passive joints to be regulated to θ_{P_des} = 0^° in 40 s. Base mass and inertia are the same with the passive regulating task. Variations of x_e and θ_P are in Figure 8. The comparison between the actual and the desired trajectory is in Figure 9.

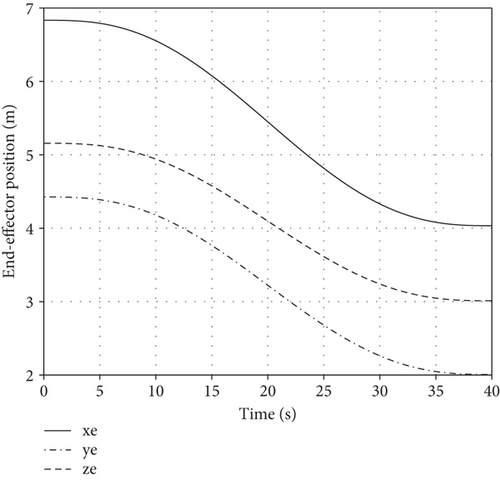
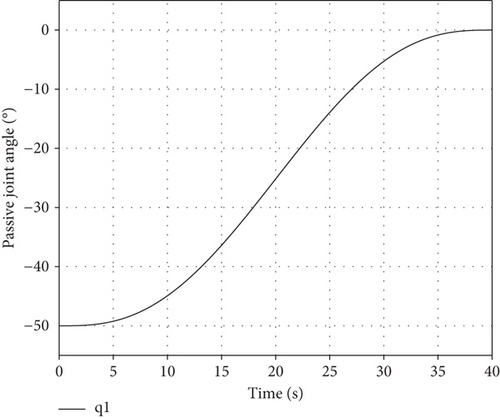
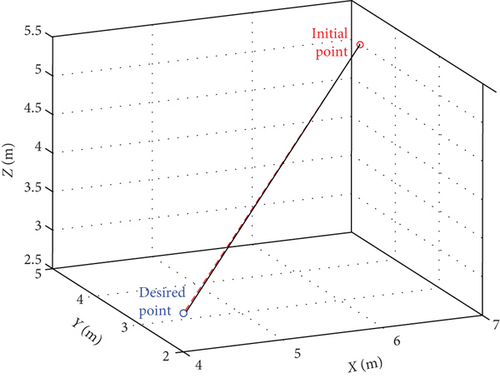
The end-effector arrives at the desired position, and the passive joint is regulated to the target angle in 40 s, so the combination task is accomplished.

5.1.4. Limiting Base Attitude Deflection When Regulating Passive Joints

If the number of passive joints is less than or equal to 2, active joints can eliminate base attitude deflection when regulating passive joints. Assuming the first joint fails, the initial configuration is θ_ini = [−50°,−170°,150°,−60°,130°,170°,0°]^T and the initial base position/attitude is θ_{b_ini} = [0, 0, 0, 0, 0, 0]^T. The task requires the passive joint to be regulated to θ_{P_des} = 0^°, and base attitude is not disturbed. Base mass and inertia are also the same with the passive regulating task. Variations of θ_P and θ_b are in Figure 10.

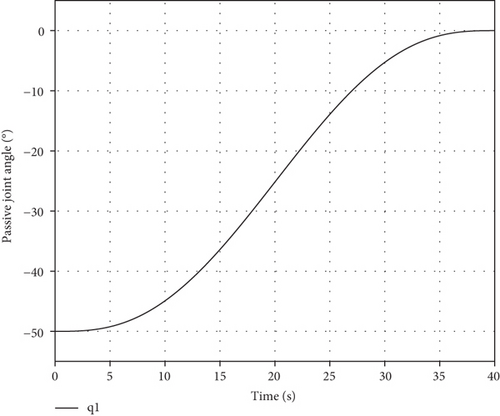
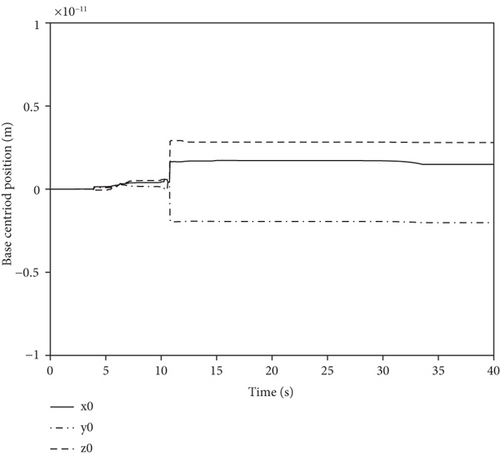
Figure 10 shows that the passive joint converges to 0^° in 40 s and the order of magnitudes of base attitude deflection is only 10^−11°, so the combination task is accomplished.

During task execution, the values of kinematic coupling indexes are large enough, or else the tasks cannot be accomplished. The simulation results above tell us the space manipulator can execute many typical tasks based on motion planning, which verifies the existence and correctness of the first-order nonholonomic constraint inside the system.

5.2. Calculation and Application Example for Kinematic and Dynamic Coupling Indexes

Aiming at the space manipulator in Figure 2 with free-swinging first joint failure, we give an example for calculating local and global kinematic and dynamic coupling indexes and discuss the differences of values of coupling indexes when selecting different healthy joints as active joints. Then, we analyze the variations of and with the increasing base mass and inertia in particular and point out that when the base mass and inertia are large, passive joint regulation and base deflection limitation cannot be realized through motion planning. In particular, aiming at the passive joint regulating task, we design the control law for based on PD controller and calculate τ_A to actuate the manipulator to complete the task.

5.2.1. Calculation of Coupling Indexes

Setting the configuration as θ = [−50°,−170°,150°,−60°,130°,170°,0°]^T, the base position/attitude is θ_b = [0, 0, 0, 0, 0, 0]^T, the base mass is m₀ = 100 kg, and the base inertia is I₀ = diag[100 kg · m², 100 kg · m², 100 kg · m²]. Assuming that the rotation range of every joint is [θ_{i_min}, θ_{i_max}] = [−180^°, 180^°], i = 1, 2, ⋯, 7, the base position deflection limitation is [x_{0j_min}, x_{0j_max}] = [−1 m, 1 m], j = 1, 2, 3 and the attitude deflection limitation is [Ψ_{0k_min}, Ψ_{0k_max}] = [−20^°, 20^°], k = 1, 2, 3. For the space manipulator with free-swinging first joint failure in Figure 2, selecting all healthy joints as active joints, we calculate the kinematic and dynamic coupling indexes in Table 3.

Table 3. Kinematic and dynamic coupling indexes.

	Single	Maximum	Minimum	Global value
	Local value			Global value
w_eA	0.0016	1.9130	1.0320 × 10⁻⁷	0.0085
w_PA	0.1475	1.6794	0.0082	0.1962
w_bA	8.8645 × 10⁻¹⁰	8.8645 × 10⁻⁶	7.4366 × 10⁻¹⁶	3.4419 × 10⁻¹⁶
η_PA	0.6014	210.9814	0.0165	9.8958
η_bA	0	2.1145 × 10⁻³⁵	0	0
η_Pτ	0.0079	1.6818 × 10³	2.1660 × 10⁻⁴	15.9581
η_bτ	0	2.1145 × 10⁻³¹	0	0
η_eτ	6.8770 × 10⁻¹¹	1.7706 × 10⁻⁵	2.5938 × 10⁻¹⁶	4.2568 × 10⁻¹⁵

In Table 3, we make the value which is less than 10⁻⁴⁰ equal to zero. Thus, the dynamic coupling degree between active joints and the base is insufficient. In particular, if we lock the fourth and seventh joints, and select other healthy joints as active joints, kinematic and dynamic coupling indexes turn into what is found in Table 4.

Table 4. Kinematic and dynamic coupling indexes with the fourth and seventh joints locked.

Single	Maximum	Minimum	Global value
Local value			Global value
3.2168 × 10⁻¹⁸	8.4015 × 10⁻¹⁶	0	7.4488 × 10⁻³⁵
0.1338	2.0813	0.0025	0.1471
6.4487 × 10⁻²¹	7.3665 × 10⁻¹⁸	0	3.7389 × 10⁻⁴⁰
0.5825	145.4495	0.0072	8.0662
0	1.2862 × 10⁻³⁶	0	0
0.0078	968.7484	1.2646 × 10⁻⁴	13.3688
0	1.0415 × 10⁻³¹	0	0
3.9886 × 10⁻²⁶	1.1401 × 10⁻¹⁴	5.7742 × 10⁻³⁰	6.0911 × 10⁻³⁴

As can be seen from Table 4, active joints without the fourth and seventh joints are incapable of actuating the end-effector or controlling the base because the number of active joints is less than the DOF of the end-effector and base. However, values of w_PA, η_PA, and η_Pτ in Tables 3 and 4 are similar, especially for global indexes, so active joints without the fourth and seventh joints can still regulate passive joints.

The global indexes can not only depict the motion transmission efficiency from active joints to passive units but also serve as the reference to reducing the number of active joints. Users can select the fewest active joints with enough coupling degree to actuate the manipulator.

5.2.2. Effect of Base Mass and Inertia on and

Making base mass and inertia are

(81)

m_c is the equivalent mass of the base [30]. We set the values of m_c as m_c ∈ {10¹, 10², 10³, 10⁴, 10⁵, 10⁶, 10⁷}kg. Assuming the first joint fails and selecting all healthy joints as active joints and taking lgm_c as the x-axis, we draw the figures to exhibit the variation of and with m_c in Figure 11.

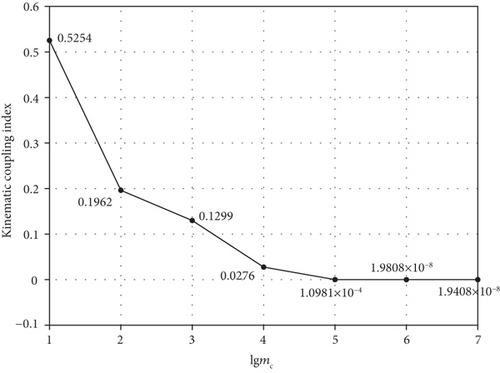
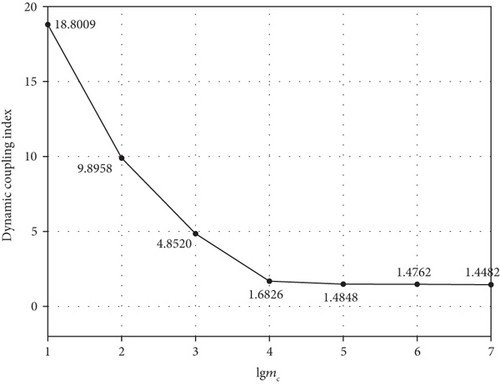
With increase of the base mass and inertia, and decrease continually. When m_c > 10⁶, the value of reduces to 10⁻⁸ and the magnitudes of change in reach up to 10⁷. But value of stabilizes around 1.4, and the magnitudes of change in are only 10¹. Thus, active joints cannot effectively regulate passive joints based on motion planning, but can regulate passive joints based on the control method at this moment.

We design the control method to regulate passive joints based on the second-order nonholonomic constraint. We make θ_{P_des} = −30^°,

, and

as the desired states of passive joints and design the PD controller for

(82)

Making e = θ_{P_des} − θ_P, we have . According to the characteristic of the second-order homogeneous differential equation, e exponentially converges to zero. Taking K_D = 0.5 and K_P = 0.1, and θ_P are in Figure 12 and θ_A, , and τ_A are in Figure 13.

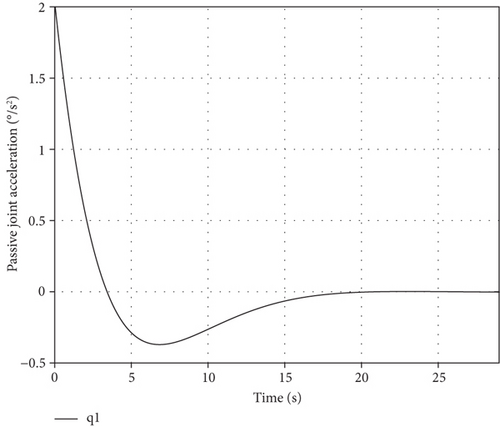
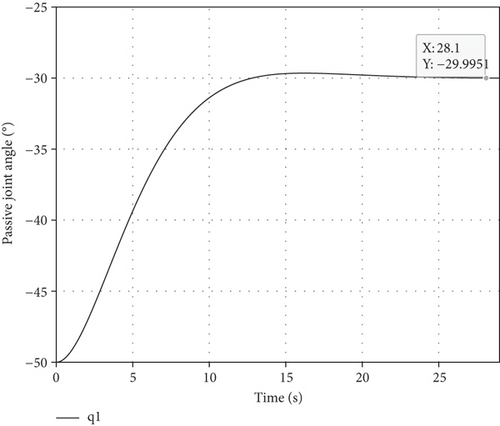
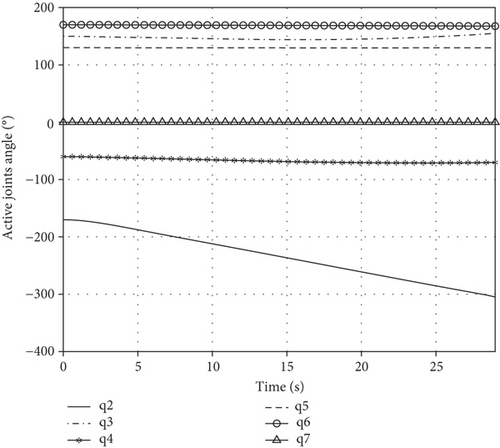
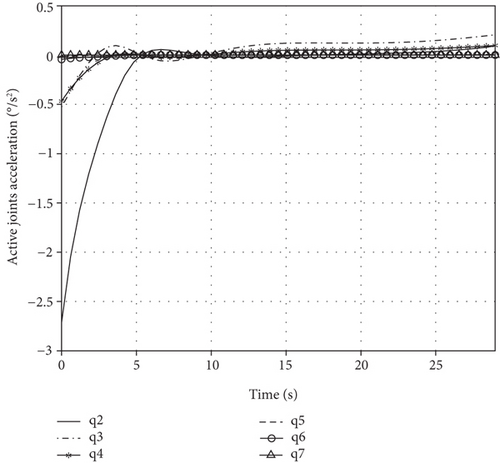
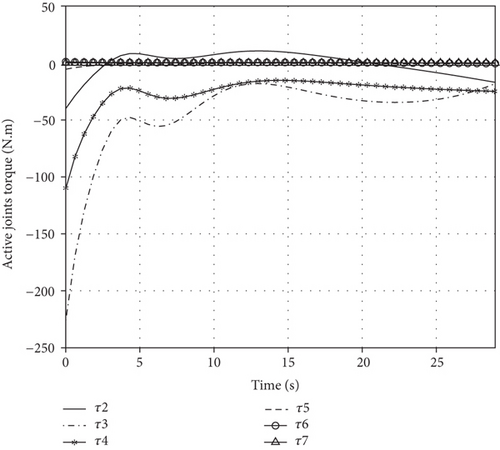
Figure 12 shows that the passive joint is regulated to the desired angle at 28.1 s, and the active joint’s motion and torque are smooth in Figure 13. Thus, the passive joint regulating task is accomplished based on the control method. The PD controller above is only appropriate to the space manipulator with an accurate dynamic model. Considering model uncertainty and external disturbance, a robust control system needs to be designed. But in this paper, we mainly analyze the kinematic and dynamic characteristics of the space manipulator with free-swinging joint failure, instead of a robust controller design. In the future study, we will combine the sliding mode and fuzzy control method to design a controller robust to the bounded unknown disturbance and unmodeled uncertainty for the space manipulator with free-swinging joint failure.

The simulation above verifies the following theories:

(1)
The first-order nonholonomic constraint and the second-order nonholonomic constraint do simultaneously exist inside the system of the space manipulator with free-swinging joint failure
(2)
The kinematic and dynamic coupling indexes proposed in this paper can objectively evaluate kinematic and dynamic coupling degrees from active joints to passive units
(3)
Many space tasks are either based on motion planning with the first-order nonholonomic constraint or based on a controller design with the second-order nonholonomic constraint

6. Conclusions

We analyze kinematic and dynamic characteristics of the free-floating space manipulators with free-swinging joint failure in this paper. Based on momentum conservation and the Lagrange equation, the kinematic and dynamic models are established. On this basis, the kinematic and dynamic coupling relationships are derived and we point out that the first-order nonholonomic constraint and the second-order nonholonomic constraint simultaneously exist in the system. Local and global kinematic and dynamic coupling indexes are correspondingly defined. Finally, simulation experiments surrounding the SSRMS-type space manipulator are designed to verify the existence and correctness of the first-order and second-order nonholonomic constraints and display the execution effect of many tasks based on motion planning and the control method. The main contributions in this paper include the following:

(1)
We explicitly propose kinematic and dynamic modelling methods for the space manipulator with free-swinging joint failure for the first time
(2)
All kinematic coupling relationships (the first-order nonholonomic constraint) and dynamic coupling relationships (the second-order nonholonomic constraint) inside the system of the space manipulator with free-swinging joint failure are derived
(3)
For general tasks, we propose the motion planning method based on the first-order nonholonomic constraint and design a control strategy based on the second-order nonholonomic constraint. This is the basis of treatment of free-swinging joint failure

In future research, we will pay more attention to task optimization to make the space manipulator with free-swinging joint failure perform primary and secondary tasks in the meantime. And we further design the control system to be robust to model uncertainty and external disturbance.

Conflicts of Interest

All authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (61403038, 61573066) and Fundamental Research Funds for the Central Universities (2019PTB-012).

Open Research

Data Availability

The data and codes in MATLAB used to support the findings of this study are available from the corresponding author upon request.

References

1 Hu B., Chen F., Han L., Chen H., and Yu H., Design and ground verification of space station manipulator control method for orbital replacement unit changeout, International Journal of Aerospace Engineering, 2018, 2018, 18, 4271035, https://doi.org/10.1155/2018/4271035, 2-s2.0-85062638307.
10.1155/2018/4271035
Google Scholar
2 Huang P., Chen L., Zhang B., Meng Z., and Liu Z., Autonomous rendezvous and docking with nonfull field of view for tethered space robot, International Journal of Aerospace Engineering. (2017) 2017, 11, 3162349, https://doi.org/10.1155/2017/3162349, 2-s2.0-85014367307.
10.1155/2017/3162349
Web of Science® Google Scholar
3 Chen G., Yuan B., Jia Q., Sun H., and Guo W., Failure tolerance strategy of space manipulator for large load carrying tasks, Acta Astronautica. (2018) 148, 186–204, https://doi.org/10.1016/j.actaastro.2018.04.052, 2-s2.0-85046842100.
10.1016/j.actaastro.2018.04.052
Web of Science® Google Scholar
4 Jamisola R. S., Maciejewski A. A., and Roberts R. G., Failure-tolerant path planning for kinematically redundant manipulators anticipating locked-joint failures, IEEE Transactions on Robotics. (2006) 22, no. 4, 603–612, https://doi.org/10.1109/TRO.2006.878959, 2-s2.0-33747609108.
10.1109/TRO.2006.878959
Web of Science® Google Scholar
5 Abdi H., Nahavandi S., Frayman Y., and Maciejewski A. A., Optimal mapping of joint faults into healthy joint velocity space for fault-tolerant redundant manipulators, Robotica. (2012) 30, no. 4, 635–648, https://doi.org/10.1017/S0263574711000671, 2-s2.0-84862014169.
10.1017/S0263574711000671
Web of Science® Google Scholar
6 Wu E. C., Hwang J. C., and Chladek J. T., Fault-tolerant joint development for the space shuttle remote manipulator system: analysis and experiment, IEEE Transactions on Robotics and Automation. (1993) 9, no. 5, 675–684, https://doi.org/10.1109/70.258058, 2-s2.0-0027678262.
10.1109/70.258058
Web of Science® Google Scholar
7 De Luca A. and Mattone R., Actuator failure detection and isolation using generalized momenta, 2003 IEEE International Conference on Robotics and Automation (Cat. No.03CH37422), September 2003, Taipei, Taiwan, 634–639, https://doi.org/10.1109/ROBOT.2003.1241665.
10.1109/ROBOT.2003.1241665
Google Scholar
8 Guo W., Development of fault-tolerant motion control system for space manipulator with joint failure, 2018, Master Thesis, Beijing University of Posts and Telecommunications, Beijing, China.
Google Scholar
9 She Y., Xu W., Su H., Liang B., and Shi H., Fault-tolerant analysis and control of SSRMS-type manipulators with single-joint failure, Acta Astronautica. (2016) 120, 270–286, https://doi.org/10.1016/j.actaastro.2015.12.012, 2-s2.0-84952801768.
10.1016/j.actaastro.2015.12.012
Web of Science® Google Scholar
10 Jia Q., Li T., Chen G., Sun H., and Zhang J., Trajectory optimization for velocity jumps reduction considering the unexpectedness characteristics of space manipulator joint-locked failure, International Journal of Aerospace Engineering. (2016) 2016, 14, 7819540, https://doi.org/10.1155/2016/7819540, 2-s2.0-84960969572.
10.1155/2016/7819540
Web of Science® Google Scholar
11 Hattori M. and Yabuno H., Reachable area of an underactuated space manipulator subjected to simple spinning, Nonlinear Dynamics. (2008) 51, no. 1-2, 345–353, https://doi.org/10.1007/s11071-007-9215-4, 2-s2.0-35448997418.
10.1007/s11071-007-9215-4
Web of Science® Google Scholar
12 Shin J. and Lee J., Dynamic control of underactuated manipulators with free-swinging passive joints in Cartesian space, Proceedings of International Conference on Robotics and Automation, April 1997, Albuquerque, NM, USA, 3294–3299, https://doi.org/10.1109/ROBOT.1997.606791.
10.1109/ROBOT.1997.606791
Google Scholar
13 Roberts R. G., The dexterity and singularities of an underactuated robot, Journal of Robotic Systems. (2001) 18, no. 4, 159–169, https://doi.org/10.1002/rob.1013, 2-s2.0-0035309429.
10.1002/rob.1013
Web of Science® Google Scholar
14 Nakamura Y., Suzuki T., and Koinuma M., Nonlinear behavior and control of a nonholonomic free-joint manipulator, IEEE Transactions on Robotics and Automation. (1997) 13, no. 6, 853–862, https://doi.org/10.1109/70.650164, 2-s2.0-0031363035.
10.1109/70.650164
Web of Science® Google Scholar
15 Arai H., Tanie K., and Shiroma N., Nonholonomic control of a three-DOF planar underactuated manipulator, IEEE Transactions on Robotics and Automation. (1998) 14, no. 5, 681–695, https://doi.org/10.1109/70.720345, 2-s2.0-0032186778.
10.1109/70.720345
Web of Science® Google Scholar
16 Lai X.-Z., She J. H., Cao W. H., and Yang S. X., Stabilization of underactuated planar acrobot based on motion-state constraints, International Journal of Non-Linear Mechanics. (2015) 77, 342–347, https://doi.org/10.1016/j.ijnonlinmec.2015.09.006, 2-s2.0-84944196264.
10.1016/j.ijnonlinmec.2015.09.006
Web of Science® Google Scholar
17 Liu D., Lai X., Wang Y., Wan X., and Wu M., Position control for planar four-link underactuated manipulator with a passive third joint, ISA Transactions. (2019) 87, 46–54, https://doi.org/10.1016/j.isatra.2018.11.030, 2-s2.0-85057531480, 30522815.
10.1016/j.isatra.2018.11.030
CAS PubMed Web of Science® Google Scholar
18 Lai X. Z., Pan C. Z., Wu M., Yang S. X., and Cao W. H., Control of an underactuated three-link passive–active–active manipulator based on three stages and stability analysis, Journal of Dynamic Systems, Measurement, and Control. (2015) 137, no. 2, article 021007, https://doi.org/10.1115/1.4028051, 2-s2.0-84907708064.
10.1115/1.4028051
PubMed Web of Science® Google Scholar
19 Lai X., Zhang P., Wang Y., and Wu M., Position-posture control of a planar four-link underactuated manipulator based on genetic algorithm, IEEE Transactions on Industrial Electronics. (2017) 64, no. 6, 4781–4791, https://doi.org/10.1109/TIE.2017.2668979, 2-s2.0-85028731928.
10.1109/TIE.2017.2668979
Web of Science® Google Scholar
20 Wang Y., Lai X., Chen L., Ding H., and Wu M., A quick control strategy based on hybrid intelligent optimization algorithm for planar n-link underactuated manipulators, Information Sciences. (2017) 420, 148–158, https://doi.org/10.1016/j.ins.2017.08.052, 2-s2.0-85027852350.
10.1016/j.ins.2017.08.052
Web of Science® Google Scholar
21 English J. D. and Maciejewski A. A., Measuring and reducing the Euclidean-space effects of robotic joint failures, IEEE Transactions on Robotics and Automation. (2000) 16, no. 1, 20–28, https://doi.org/10.1109/70.833184, 2-s2.0-0033903862.
10.1109/70.833184
Google Scholar
22 Bergerman M. and Xu Y., Optimal control of manipulators with any number of passive joints, Journal of Robotic Systems. (1998) 15, no. 3, 115–129, https://doi.org/10.1002/(SICI)1097-4563(199803)15:3<115::AID-ROB1>3.0.CO;2-T.
10.1002/(SICI)1097-4563(199803)15:3<115::AID-ROB1>3.0.CO;2-T
Google Scholar
23 Mukherjee R. and Degang Chen, Control of free-flying underactuated space manipulators to equilibrium manifolds, IEEE Transactions on Robotics and Automation. (1993) 9, no. 5, 561–570, https://doi.org/10.1109/70.258049, 2-s2.0-0027684011.
10.1109/70.258049
Web of Science® Google Scholar
24 He G. P., Lu Z., and Wang F. X., Optimal control of under-actuated redundant space-robot system, Control Theory & Applications. (2004) 21, no. 2, 305–310.
Google Scholar
25 Chen G., Guo W., Jia Q., Wang X., and Fu Y., Failure treatment strategy and fault-tolerant path planning of a space manipulator with free-swinging joint failure, Chinese Journal of Aeronautics. (2018) 31, no. 12, 2290–2305, https://doi.org/10.1016/j.cja.2018.04.008, 2-s2.0-85046702022.
10.1016/j.cja.2018.04.008
Web of Science® Google Scholar
26 Huang X. H., Jia Y. H., and Xu S. J., Path planning of a free-floating space robot based on the degree of controllability, Science China Technological Sciences. (2017) 60, no. 2, 251–263, https://doi.org/10.1007/s11431-016-6069-3, 2-s2.0-84976321560.
10.1007/s11431-016-6069-3
Web of Science® Google Scholar
27 Liang B., Xu Y., and Bergerman M., Mapping a space manipulator to a dynamically equivalent manipulator, Journal of Dynamic Systems Measurement and Control. (1998) 120, no. 1, 1–7, https://doi.org/10.1115/1.2801316, 2-s2.0-1442308784.
10.1115/1.2801316
Web of Science® Google Scholar
28 Xie Y., Wu X., Inamori T., Shi Z., Sun X., and Cui H., Compensation of base disturbance using optimal trajectory planning of dual-manipulators in a space robot, Advances in Space Research. (2019) 63, no. 3, 1147–1160, https://doi.org/10.1016/j.asr.2018.10.034, 2-s2.0-85056379262.
10.1016/j.asr.2018.10.034
Web of Science® Google Scholar
29 Maciel B. C. O., Terra M. H., and Bergerman M., Optimal robust control of underactuated manipulators via actuation redundancy, Journal of Robotic Systems. (2003) 20, no. 11, 635–648, https://doi.org/10.1002/rob.10113, 2-s2.0-0344740727.
10.1002/rob.10113
Web of Science® Google Scholar
30 Jia Q., Liu Y., Chen G., Sun H., and Peng J., Analysis of load-carrying capacity for redundant free-floating space manipulators in trajectory tracking task, Mathematical Problems in Engineering. (2014) 2014, 12, 125940, https://doi.org/10.1155/2014/125940, 2-s2.0-84919722778.
10.1155/2014/125940
Web of Science® Google Scholar

Citing Literature

All articles

Kinematic and Dynamic Characteristics of the Free-Floating Space Manipulator with Free-Swinging Joint Failure

Abstract

1. Introduction

2. Kinematic Modelling of the Free-Floating Space Manipulator with Free-Swinging Joint Failure

2.1. Kinematic Modelling

2.2. Velocity Mapping Relations between Active Joints, Passive Joints, Base, and End-Effector Based on Momentum Conservation

3. Dynamic Modelling of the Free-Floating Space Manipulator with Free-Swinging Joint Failure

3.1. Kinetic Energy of System

3.2. Lagrange Equation of the System

4. The Analysis of Kinematic and Dynamic Coupling Relationships

4.1. Kinematic Coupling Relationships and Coupling Indexes

4.1.1. End-Effector Trajectory Tracking Task

4.1.2. Passive Joint Regulating Task

4.1.3. Base Position/Attitude Controlling Task

4.1.4. The Combination Tasks

4.2. Dynamic Coupling Relationships and Coupling Indexes

4.2.1. Dynamic Coupling Relationship between Active Joints and Passive Joints

4.2.2. Dynamic Coupling Relationship between Active Joints and Base

4.2.3. Dynamic Coupling Relationship between Active Joints and End-Effector

4.3. Global Kinematic and Dynamic Coupling Indexes

5. Simulation Experiments

5.1. Motion Planning for the Space Manipulator with Free-Swinging Joint Failure

5.1.1. End-Effector Trajectory Tracking Task

5.1.2. Passive Joint Regulating Task

5.1.3. Tracking End-Effector Trajectory When Regulating Passive Joints

5.1.4. Limiting Base Attitude Deflection When Regulating Passive Joints

5.2. Calculation and Application Example for Kinematic and Dynamic Coupling Indexes

5.2.1. Calculation of Coupling Indexes

5.2.2. Effect of Base Mass and Inertia on and

6. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information