Volume 2019, Issue 1 1843205

Research Article

Open Access

Sensing and Quantifying a New Mechanism for Vehicle Brake Creep Groan

Dejian Meng,

Dejian Meng

orcid.org/0000-0003-4153-8109

School of Automotive Studies, Tongji University, Shanghai 201804, China tongji.edu.cn

Search for more papers by this author

Lijun Zhang,

Corresponding Author

Lijun Zhang

[email protected]

orcid.org/0000-0002-6944-1918

School of Automotive Studies, Tongji University, Shanghai 201804, China tongji.edu.cn

Search for more papers by this author

Xiaotian Xu,

Xiaotian Xu

College of IT & and Engineering, Marshall University, Huntington 25755, WV, USA marshall.edu

Search for more papers by this author

Yousef Sardahi,

Yousef Sardahi

College of IT & and Engineering, Marshall University, Huntington 25755, WV, USA marshall.edu

Search for more papers by this author

Gang S. Chen,

Gang S. Chen

orcid.org/0000-0002-0344-6476

College of IT & and Engineering, Marshall University, Huntington 25755, WV, USA marshall.edu

Search for more papers by this author

Dejian Meng,

Dejian Meng

orcid.org/0000-0003-4153-8109

School of Automotive Studies, Tongji University, Shanghai 201804, China tongji.edu.cn

Search for more papers by this author

Lijun Zhang,

Corresponding Author

Lijun Zhang

[email protected]

orcid.org/0000-0002-6944-1918

School of Automotive Studies, Tongji University, Shanghai 201804, China tongji.edu.cn

Search for more papers by this author

Xiaotian Xu,

Xiaotian Xu

College of IT & and Engineering, Marshall University, Huntington 25755, WV, USA marshall.edu

Search for more papers by this author

Yousef Sardahi,

Yousef Sardahi

College of IT & and Engineering, Marshall University, Huntington 25755, WV, USA marshall.edu

Search for more papers by this author

Gang S. Chen,

Gang S. Chen

orcid.org/0000-0002-0344-6476

College of IT & and Engineering, Marshall University, Huntington 25755, WV, USA marshall.edu

Search for more papers by this author

First published: 2019

https://doi.org/10.1155/2019/1843205

Citations: 8

Academic Editor: Adam Glowacz

Share a link

Email
Wechat
Bluesky

Abstract

This paper investigates the creep groan of a vehicle’s brake experimentally, analytically, and numerically. Experimentally, the effects of acceleration on caliper and strut, noise, brake pressure, and tension are measured. The results show that the measured signals and their relevant spectra broadly capture the complex vibrations of creep groan. This includes the simple stick-slip, severe stick-slip vibrations/resonances, multiple harmonics, half-order harmonics; stick-slip-induced impulsive vibrations, steady/unstable vibrations, and their transitions. Analytically, a new mathematical model is presented to capture the unique features of half-order harmonics and the connections to fundamental stick-slip/resonant frequency and multiple harmonics. The analytical solution and the experimental results show that the vibro-impact of the brake pad-disc system can be triggered by severe stick-slip vibrations and is associated with instable, impulsive stick-slip vibration with wideband. The induced stick-slip vibro-impact can evolve into a steady and strong state with half-order, stick-slip fundamental, and multiple-order components. This new mechanism is different from all previously proposed mechanisms of creep groan in that we also view some type of creep groan as a stick-slip vibration-induced vibro-impact phenomenon in addition to conventional stick-slip phenomena. The new mechanism comprehensively explains the complex experimental phenomena reported in the literature. Numerically, the salient features of phase diagrams of instable stick-slip and vibro-impact are examined by using a seven-degree-of-freedom brake system model, which shows that the phase diagrams of the dynamics of creep groan with and without vibro-impact are substantially different. The phase diagram of the dynamics with vibro-impact is closer to the experimental results. In contrast to existing mechanisms, the proposed new mechanism encompasses the instable stick-slip nature of creep groan and elaborates the inherent connections and transition of the spectrogram. The new knowledge can be used to attain critical improvements to brake noise and vibration analysis and design. By applying the proposed new model in addition to existing models, all experimental phenomena in creep groan are elaborated and quantified.

1. Introduction

Noise, vibration, and harshness (NVH) are important factors for customers’ rating of vehicles. In vehicle brake NVH problems, creep groan is a specific brake noise that usually occurs at low wheel speed and low brake pressure [1–5]. The range of the vibratory frequency of the creep groan is usually 50 to 500 Hz. Due to the dramatic increase in the number of complaints about brake creep groan, much attention has recently been paid to this problem in the automotive industry. To understand the mechanism and find the countermeasures of brake creep groan, much research has been conducted on vehicles [3–5], brake dynamometers [6–8], tribometers [9–12], and chassis dynamometers [13]. Creep groan-related vibrations from the caliper/knuckle could be transferred to the lower arm and then to the frame front and the rear MTG to body, or be transferred to the strut and then to the body, giving rise to an uncomfortable structurally borne noise. In addition to the brake system, both the suspension system and driveline system have effects on the occurrences and features of creep groan [4, 8, 9, 13].

Experimentally, researchers have studied varied creep groan phenomena and the effects of structural parameters on creep groan, such as sliding stick-slip [7, 12, 14], torsional stick-slip of torque [15], tangential or torsional stiffness [9, 10], and variations of caliper, suspension, chassis, and drivelines [12, 13]. The tribological parameters of pad-disc interface are also characterized in terms of varied friction models such as LuGre and the bristle friction law in addition to the Coulomb and Stribeck model with varied slopes, magnitudes, and gap of static and dynamic friction coefficients [16–23].

Analytically and numerically, different models have been developed to characterize creep groan. Conventionally, friction oscillator models with a single degree of freedom (DOF) and two DOFs have been used as a caliper model with a contact sliding interface to quantify vibrations [17–19]. Usually, two major subsystems are included in groan analytical models. The nonrotating substructure includes the brake, mounting brackets, and suspension systems. The rotating structure is the drive train side, including the rotor, wheel, and tire. In general, all suspension-type modes could exhibit resonances in the creep groan range. By considering the components of the brake and driveline, and even the tire and vehicle mass, three, four, five, and seven-DOFs models have been used to investigate varied aspects of brake friction vibrations [20–22, 24–26]. The multibody dynamic models of the chassis corner have also been used [27]. Moreover, finite element (FE) models of the disc brake for creep groan analysis have been proposed to quantify creep groan [28–30]. FEA models have advantages in the calculation of the interface contact, as well as multiple elastic subsystems, including pad, caliper, suspension, and driveline systems. However, FE models of creep groan have not been successfully used to elaborate the complex mechanisms of creep groan, except for evaluating the effects of structural design change on vibrations. In fact, for this kind of problem of elastic bulky components connected by relatively compliant parts such as springs, finite element analysis may not be the most suitable tool for simulating problems due to their weakness dealing with “weak connections” among different components. Possible ill conditioning due to large differences in the stiffness of varied components and interconnections can degrade the accuracy of the results. Moreover, the modeling of interacting components in low-frequency events in an elastic model with huge numbers of elements and nodes is far from efficient, and the data interpretation is very difficult. As such, theoretical models with varied DOFs have been used to classify varied mechanisms and resources of low-frequency vibrations [31–33].

The sensing and evaluation of “creep groan” noise has been a challenge for the NVH community. The creep groan is usually not a purely tonal sound, although ultimately it could generate a tonal subjective perception of users [34]. The vibrations resulting in creep groan noise have conventionally been considered friction-induced vibrations of the stick-slip mode, characterized by simple phase diagrams of velocity and displacement of caliper motions. However, the recorded vibration usually does not exhibit simple stick-slip periodic vibration but rather exhibits complex properties with multiple frequencies, time-varying frequencies, and their transitions. The real creep groan has been found to exhibit complex motions in addition to typical stick-slip motions, which include single stick-slip, continuous stick-slip, resonance, varied complex motions, and transitions [7, 9, 11, 15, 20, 30]. Basically, stick-slip is a sustained “attach-detach” vibration process that arises via specific friction properties, specific system elastic properties, and relative motion [31, 35]. In particular, negative slopes of friction-velocity curves yield equivalently negative damping to system dynamic motion and could cause system instability and a self-excited vibration, which are likely locked in certain natural frequencies or resonances. The spectral content of the creep groan usually shows a response at multiples of a certain fundamental frequency of stick-slip or its induced resonance. The stick-slip vibrations may occur at the 1st, 2nd, or 3rd order of the fundamental frequency corresponding to the sustained “stick-slip” cycle. The stick-slip motions mainly depend on the properties of the mechanical system and are also related to different characteristics of the interface friction [36–38]. However, existing theories and models are unable to explain these phenomena comprehensively and consistently. For example, in the event of creep groan, there could be half-order components in addition to fundamental components corresponding to the stick-slip repetition frequency and the multiple components [16, 21, 24, 30]. The root causes of the half-order components and their transitions with other components have not been explained. The inherent connections among fundamental stick-slip, multiple harmonics, half-order component, resonance, impulsive components of wideband, and transitions have not been explained consistently.

In this study, a vehicle road test of creep groan under the downhill condition is conducted, and the varied complicated types of vibrations in creep groans are comprehensively recorded, which consist of simple stick-slip motion, continuous/discontinuous stick-slip motions, and sliding/impulsive motions with varied spectrum signatures from half-order, fundamental order, multiple orders, time-varying spectrum transition, and wideband components. A new mechanism of severe stick-slip motion-induced vibro-impact is proposed to interpret the occurrence and the transition of the half-order vibrations, and a theoretical vibro-impact model with transient pad-disc separation is applied for the analysis.

Conventionally, the phase diagram of brake vibration with limit cycles has been used as experimental evidence of the stick-slip mechanism in creep groan. In this study, the phase diagram of experimentally recorded brake vibrations is found to exhibit a complex unsymmetrical pattern. To characterize this, a seven-DOFs model with and without vibro-impact effect were used for simulations to derive phase diagrams, which showed that only the model with the vibro-impact effect gives rise to an unsymmetrical phase diagram.

Creep groan has been investigated widely, and many mechanisms have been proposed in the last two decades. In contrast to all of these existing mechanisms, the proposed new mechanism can encompass the transient vibro-impact nature of a braking process, which is different from conventional excitation resources such as periodic torque, stick-slip, negative friction-velocity gradient, and resonance. The severe stick-slip vibration-induced interface separation gives rise to unique vibrational features of vibro-impact, such as half-order components. This mechanism is different from all previously proposed mechanisms in that we also view severe creep groan as a stick-slip-caused vibro-impact phenomenon in addition to conventional stick-slip phenomena. This research offers some insights to guide the analysis of brake creep groan.

2. Vehicle Brake System and Experiments

2.1. Experimental Test Setup

Based on our existing understanding, when creep groan occurs, the vehicle-driving force does not necessarily come from the engine. This may come from the inertia force when the vehicle is downhill. In most existing research, the vehicle tests were conducted on horizontal road when the engine was running. The engine could induce some extra vibration in the suspension, which aggravates the complexity of creep groan motion. To reduce the effect of the engine, in this study, a vehicle road test of creep groan was conducted under a downhill vehicle condition. In the experiment, an A-class car is used, which is equipped with six-speed automatic transmission and has McPherson suspension in front and torsion beam suspension in the rear. The total mass of the vehicle is 1431 kg, including two passengers in the front seats.

The vehicle is put on a ramp road with a slope of 10%. The driver presses the brake pedal and starts the engine, releases the handbrake and hangs in the N gear, and finally releases brake pedal slowly until the vehicle starts to move. When creep groan occurs, the brake pressure is maintained to prevent creep groan from occurring, if possible.

2.2. Measurement Instrumentation

Two triaxial accelerometers are mounted at the piston side of the caliper and suspension strut, respectively. To induce the effect of added mass by vibration transducer and its attachment the mass of one vibration transducer is less than 5 g, and each vibration transducer is stuck to the surface of the caliper and strut using a 454 instant adhesive. The X, Y, and Z directions of the accelerometer on the caliper are aligned to be the tangential, radial, and axial directions of the disc, respectively. An oil pressure sensor connecting the brake tube with a hose is used to measure the brake pressure. These sensors are arranged in the front left chassis corner of the car, as shown in Figure 1. The sampling frequency of the vibration signal is 5120 Hz.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Sensors used to test brake creep groan: (a) accelerometer at strut and oil pressure sensor; (b) accelerometer at caliper; (c) tension sensor.

2.3. Experimental Results

Existing research has found that the specific stick-slip vibrations of brake calipers are the index of the occurrence of groan and have a good correlation with the subjective rating of creep groan noise. In this study, all kinds of caliper vibrations associated with creep groan noise are recorded in the test and analyzed using advanced methods. Figure 2 shows the time history of typical oil pressure and the vibration accelerations and spectrograms of calipers recorded while severe creep groan occurs. Before severe creep groan occurs, simple stick-slip motions were recorded, which are quasi-harmonic vibrations. The accelerations in all directions are consistent, except that acceleration in the X direction is larger than that in the other two directions. The result of short-time Fourier-transform or spectrogram of clipper acceleration in the X direction is shown in Figure 2(e). Because the interior noise of creep groan occurs within 500 Hz, the vibration frequency is analyzed up to 500 Hz in Figure 2(e). As shown in Figure 2, when the brake pressure drops to 8 bar, creep groan lasts for approximately 18 s. According to the characteristics of acceleration in the X direction, the whole process is divided into seven stages, which are respectively named A to G in Figures 2(b)–2(d). As seen, the characteristics of caliper acceleration in amplitude and frequency evolve complexly with time when creep groan occurs.

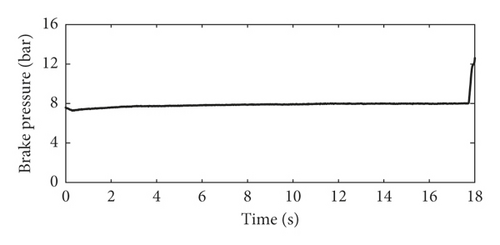
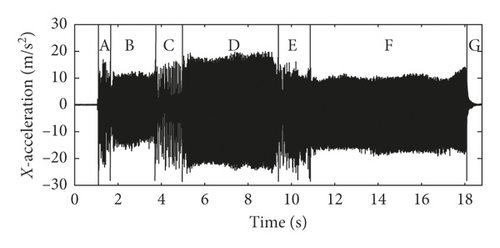
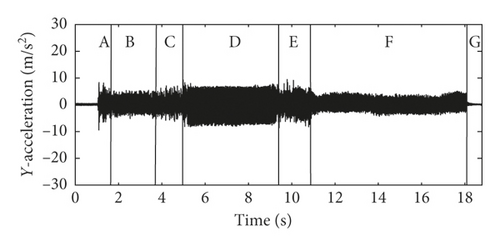
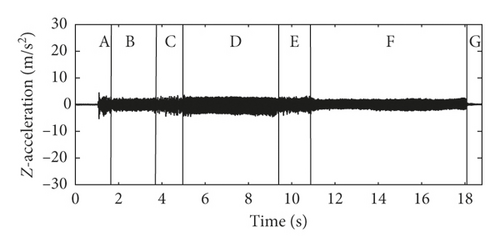
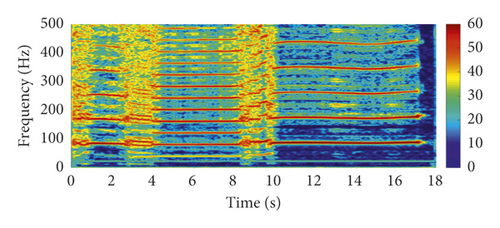
The accelerations in stages B and F have smaller amplitudes than the other stages (A, C, D, and E) and exhibit simple and clear harmonics that correspond to fundamental periodic stick-slip motions (approximately 90 Hz) and multiple harmonic components. This type of regular stick-slip has been widely studied and reported in existing research. This kind of severe vibration is likely to be a systemsʼ resonance in which the stick-slip frequency is close or equal to the specific natural frequency of the system.

The accelerations in stages A, C, and E have relatively larger amplitudes and are half-order of the fundamental periodic stick-slip motions (approximately 45 Hz), wideband components and transitions, in addition to the fundamental components (approximately 90 Hz) and multiple components. This indicates that stick-slip motions have evolved into unstable motions and triggered impulsive effects.

The accelerations in stage D have the largest amplitudes and clearly have half-order fundamental periodic stick-slip motions (approximately 45 Hz), fundamental components (approximately 90 Hz), and their multiple components. This suggests that steady, strong, and periodic impulsive vibrations were formed by the severe stick-slip motion.

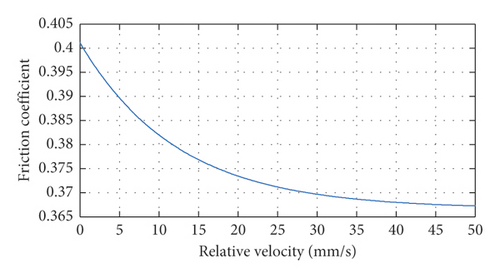
Table 1 shows the recorded tension in the experiments. When creep groan occurs, the tension varies obviously. The maximum and minimum of the tension variation, respectively, correspond to the maximum static friction force and dynamic friction force. Based on the radius of the piston, equivalent brake radius, level arm, and recorded tension, the friction coefficients are calculated and shown in Figure 3.

Table 1. Friction coefficient under 8 bar oil pressure.

Times	1	2	3	4	5	6	Average	Standard deviation
Oil pressure (bar)	7.67	7.67	7.65	7.66	7.65	7.65	7.66	0.0095
Maximum of tension (N)	388.29	391.04	382.42	393.20	387.95	398.53	390.24	5.45
Minimum of tension (N)	351.41	356.03	359.30	360.47	354.13	358.50	356.64	3.44
Static friction coefficient	0.3987	0.4014	0.3936	0.4041	0.3991	0.4102	0.4012	0.0056
Dynamic friction coefficient	0.3608	0.3654	0.3698	0.3705	0.3643	0.3690	0.3666	0.0038

3. New Model of Vibro-Impact for Mechanism of Instable Stick-Slip in Creep Groan

Various stick-slip vibration models of brake creep groan have been developed, and these models can generally be classified into two categories: one is the tangential vibration model, and the other is the torsional vibration model. Some research has also considered both the tangential and torsional vibrations of the brake system in creep groan. This work quantified the influence of system parameters such as speed and friction properties on tangential and torsional stick-slip vibrations. The existing models for characterizing creep groan have been focused on the sliding motion between the pad and disc and the associated vibrations of suspension and driveline systems [20, 21, 30]. However, the instable stick-slips and complex features such as half-order harmonics observed in the last decade have not been explained using existing models [16, 21, 24, 30]. To interpret the system complex motions in creep groan recorded in stages A, C, D, and E in Figure 2, we propose the following mechanism, noting that during the whole creep groan process, the oil pressure and speed remain constant or change slightly. In stages B and F, the strong system stick-slip vibrations and possibly the resonance of some suspension subsystems are steadily established and are characterized by the fundamental frequency approximately 90 Hz and their multiple harmonics (e.g., approximately 180 Hz or 270 Hz). The similar phenomena of severe stick-slip vibrations/resonance have been reported in many existing reports. This critical state of both severe vibrations and low oil pressure on the pad is likely to further cause the transient separation of the pad-disc interface, which leads to vibro-impact vibrations in stage C (similarly A and E). The triggered vibro-impacts exaggerate the vibrations and possess a half-order component of 45 Hz and multiple components. At the same time, the interface separation/close and vibro-impact cause unstable impulsive excitation of the system, leading to the vibrations with a wideband spectrum.

This composite effect allows vibrations in stage C that are stronger than those in stage B. The system’s stick-slip vibrations and the induced instable vibro-impact gradually evolve into a steady state denoted as stage D, which has clearer periodic signature and larger amplitudes. Since the whole process is unstable, the vibration instability or slight changes in oil pressure or speed could allow the system to further evolve into stage E (similar to stage C) and finally change to stage F (similar to stage B).

To further quantify this mechanism, we propose the following analytical model. Figure 4 shows the schematic model of the pad-disc interface of an idealized brake. In contrast to all existing studies focusing on sliding and torsional vibrations, we consider the critical vibrations vertical to the sliding surface, which are likely triggered when the system enters the severe stick-slip vibrations/resonance with specific fundamental stick-slip/resonance frequency ω (stage B, ω = 90 Hz).

Consider the idealized vertical vibration equation of the pad/disk for the contact/separation event or vibro-impact effect due to severe stick-slip vibration with specific fundamental stick-slip/resonant frequency ω,

\begin{matrix} m \ddot{y} + (k + k_{c}) y = F \cos ω t, y < y_{c}, \\ m \ddot{y} + k y = F \cos ω t, y \geq y_{c}, \end{matrix}

(1)

in which ω could be specific stick-slip fundamental frequency or some stick-slip-induced resonant frequency of subsystems such as suspension; y is the pad displacement in the direction perpendicular to the disc; y_c could be assumed to be the root mean square of the roughness of interface; k is the stiffness of the pad-caliper system; k_c is the contact stiffness of the pad-disk interface, which consists of solid body stiffness and surface roughness stiffness characterized by elasticity and the Hertz contact model; and m is the mass of the pad. The vibro-impact could occur after severe stick-slip is established. The simple and severe stick-slips in the brake system have been widely characterized in existing research and will not be proceeded here. The stick-slip fundamental frequency of the system is the specific excitation frequency to vibro-impact motion. Equation (1) is a strong nonlinear equation, and the solutions can be derived as follows:

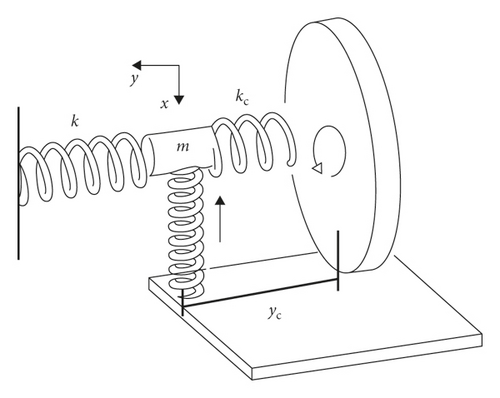
(a)
Primary resonant solutions:
$\begin{matrix} y = [\frac{2 F}{(ω_{2}^{2} - ω_{1}^{2}) m (21 Δ +)} + \frac{3 F}{4 ω^{2} m {(21 Δ +)}^{2}}] sin ω t - \frac{π F}{2 ω^{2} m (21 Δ +)} cos ω t + \frac{F}{π ω^{2} m (21 Δ +)} \sum_{n = 1,3,5}^{\infty} \frac{\cos (n - 1) ω t - \cos (n + 1) ω t}{n} - \frac{F (ω t - π)}{π ω^{2} m (21 Δ +)} \sum_{n = 1,3,5}^{\infty} \frac{\sin (n - 1) ω t + \sin (n + 1) ω t}{n}, \end{matrix}$ (2)
in which $ω_{1} = \sqrt{k / m}$ , $ω_{2} = \sqrt{(k + k_{c}) / m}$ , ω₀ = 2ω₁ω₂/(ω₁ + ω₂), α₀ = πω₀/(2ω₁), β₀ = π(1 − (ω₂/ω₁))/2, and $Δ = (ω_{1}^{2} - ω^{2}) / (ω_{2}^{2} - ω_{1}^{2})$ .
(b)
Superharmonic solutions:
When the system natural frequency is close to the multiple times for the specific excitation frequency, multiple harmonics are excited:
$\begin{matrix} y = \frac{F (2 n^{2} ω^{2} - ω^{2} - ω_{1}^{2})}{m {(n^{2} - 1)}^{2} ω^{4}} sin ω t + \frac{2 F (ω_{2}^{2} - ω_{1}^{2})}{π m {(n^{2} - 1)}^{2} (ω_{1}^{2} - n^{2} ω^{2}) ω^{2}} cos ω t - \sum_{n = 2,3,4}^{\infty} \frac{2 F (ω_{2}^{2} - ω_{1}^{2})}{π m {(n^{2} - 1)}^{2} (ω_{1}^{2} - n^{2} ω^{2}) ω^{2}} cos n ω t . \end{matrix}$ (3)
This could be attributed to the periodic effect of stick-slip excitation, which in principle can be developed into multiple harmonics by using the Fourier series concept.
(c)
Subharmonic solutions:
When a certain system natural frequency is close to half the specific excitation frequency, the half-order component (frequency is half of the specific excitation frequency) can be excited:
$\begin{matrix} y = \frac{4 l F}{π^{2} m ω_{1} (l^{2} - 1) (ω - l ω_{1})} \sum_{n = 1,3,5}^{\infty} \frac{\cos [((n + 1) ω t) / l] - \cos [((n - 1) ω t) / l]}{n}, l = 246,,, \dots . \end{matrix}$ (4)

This solution consists of a dominant component, which is a half-order component with frequency equal to half of the specific stick-slip fundamental frequency, ω/2. Notably, this kind of specific response also contains multiple harmonics of the half-order.

The above analysis suggests that if systems’ vertical natural frequency is close to the specific excitation frequency (from stick-slip motion) or close to the multiple order or half order of the specific excitation frequency, the system will experience larger vibrations, which correspond to primary, superharmonic, or subharmonic resonance. Notably, all existing stick-slip models of creep groan including the most recently developed ones with a varied friction model are unable to predict this half-order feature.

This analytical result also explains the generation and transition between half order and fundamental order and multiple orders. The vibrations associated with the half order in vibro-impact exaggerate the severe stick-slip vibrations. When the severe stick-slips are high enough and close to a certain threshold, the vibro-impacts could be triggered, making the vibrations more severe. The triggered vibro-impact could evolve from an unstable state into a steady state, or deteriorate back to pure-type stick-slip motion without interface separation.

Moreover, the unstable vibro-impact tends to impart random impulsive excitations to the system, which allows system vibrations to exhibit wideband spectrum features.

By integrating the above theoretical observations including stick-slip vibration/system resonance, the induced vibro-impact vibrations, and the relevant impulsive effects, the major spectral signatures and transitions in Figure 2(c) can be fully understood and explained.

4. Characterization of Phase Diagrams of Creep Groan with and without Vibro-Impact

Creep groan is generally caused by stick-slip motion between the disc and pads as a self-excited vibration of the brake assembly. The phase diagrams are widely used to characterize creep groan. The phase diagram of caliper acceleration with a limit cycle has been considered the first experimental evidence of creep groan and stick-slip/friction-induced vibrations. This section will further quantify the phase diagrams of creep groan dynamics based on experiments and numerical analysis of a system model with and without vibro-impact. To this end, a multiple-DOFs model is used, and real measured friction data are used in the simulation to minimize the effects from other factors.

Creep groan is generally caused by the stick-slip motion between discs. The phase diagrams with the limit cycles of brake calipers have been used as the first experimental evidence of the stick-slip mechanism of creep groan. In this section, we employ the experimental data for friction to simulate a seven-DOF model, as shown in Figure 5, with and without vibro-impacts.

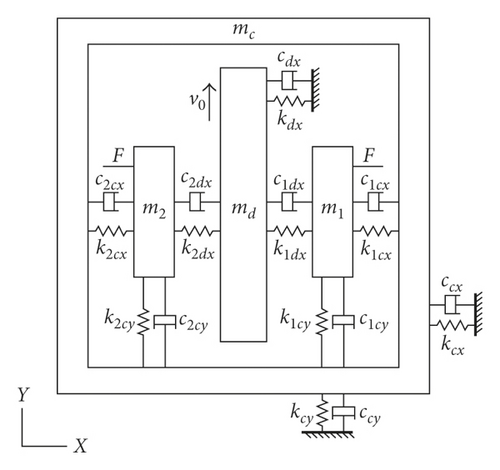
The parameters are summarized in Table 2, which is slightly different from the previous seven-DOF model [26]:

Table 2. Parameters used in system model of fixed-caliper disc brake.

Mass	Value (kg)	Stiffness	Value (N·m⁻¹)	Damping	Value (N·s·m⁻¹)
m₁	0.35	k₁	1.5 × 10⁵	c₁	6.5
m₂	0.35	k₂	7.5 × 10⁵	c₂	30
m_c	5.56	k₃	7.5 × 10⁵	c₃	19.5
m_d	7.04	k₄	1.0 × 10⁶	c₄	40
		k₅	1.5 × 10⁶	c₅	50
		k₆	1.5 × 10⁶	c₆	50

\begin{matrix} k_{1} = k_{1 d x} = k_{2 d x}, \\ c_{1} = c_{1 d x} = c_{2 d x}, \\ k_{2} = k_{1 c y} = k_{2 c y}, \\ c_{2} = c_{1 c y} = c_{2 c y}, \\ k_{3} = k_{1 c x} = k_{2 c x}, \\ c_{3} = c_{1 x} = c_{2 x}, \\ k_{4} = k_{d x}, \\ c_{4} = c_{d x}, \\ k_{5} = k_{c x}, \\ c_{5} = c_{c x}, \\ c_{6} = c_{c y}, \\ F = 1000 N, \\ F_{f 1} = F_{f 2} = μ_{s} F . \end{matrix}

(5)

In the following analysis, a nonlinear vibro-impact, or the separation effect between the disc and pad in a brake, is considered. In the dynamic model, a spring and a damper are modeled between the mass of the disc and two pads. When each part in the brake model starts to oscillate, there is a severe condition in which the surfaces of disc and pads lose contact and separate. The motion equation of the system is given as follows:

\begin{matrix} m_{c} {\ddot{x}}_{c} = - c_{c x} {\dot{x}}_{c} + c_{2 c x} ({\dot{x}}_{2} - {\dot{x}}_{c}) - c_{1 c x} ({\dot{x}}_{c} - {\dot{x}}_{1}) - k_{c x} x_{c} + k_{2 c x} (x_{2} - x_{c}) - k_{1 c x} (x_{c} - x_{1}), \\ m_{c} {\ddot{y}}_{c} = - c_{c y} {\dot{y}}_{c} + c_{2 c y} ({\dot{y}}_{2} - {\dot{y}}_{c}) - c_{1 c y} ({\dot{y}}_{1} - y_{c}) - k_{c y} y_{c} + k_{2 c y} (y_{2} - y_{c}) - k_{1 c y} (y_{1} - y_{c}), \\ m_{d} {\ddot{x}}_{d} = - c_{d} {\dot{x}}_{d} + S (δ x_{2}) c_{2 d x} ({\dot{x}}_{2} - {\dot{x}}_{d}) - S (δ x_{1}) c_{1 d x} ({\dot{x}}_{d} - {\dot{x}}_{1}) - k_{d} x_{d} + S (δ x_{2}) k_{2 d x} (x_{2} - x_{d}) - S (δ x_{1}) k_{1 d x} (x_{d} - x_{1}), \\ m_{1} {\ddot{x}}_{1} = - F + S (δ x_{1}) c_{1 d x} ({\dot{x}}_{d} - {\dot{x}}_{1}) + c_{1 c x} ({\dot{x}}_{c} - {\dot{x}}_{1}) + S (δ x_{1}) k_{1 d x} (x_{d} - x_{1}) + k_{1 c x} (x_{c} - x_{1}), \\ m_{1} {\ddot{y}}_{1} = - S (δ x_{1}) F_{f 1} - c_{1 c y} ({\dot{y}}_{1} - {\dot{y}}_{c}) - k_{1 c y} (y_{1} - y_{c}), \\ m_{2} {\ddot{x}}_{2} = F - S (δ x_{2}) c_{2 d x} ({\dot{x}}_{2} - {\dot{x}}_{d}) - c_{2 c x} ({\dot{x}}_{2} - {\dot{x}}_{c}) - S (δ x_{2}) k_{2 d x} (x_{2} - x_{d}) - k_{2 c x} (x_{2} - x_{c}), \\ m_{2} {\ddot{y}}_{2} = S (δ x_{2}) F_{f 2} - c_{2 c y} ({\dot{y}}_{2} - {\dot{y}}_{c}) - k_{2 c y} (y_{2} - y_{c}), \end{matrix}

(6)

in which S(δx_i)(i = 1, 2) is a piecewise linear function. This piecewise linear function defines the contact loss between the brake disc and pad as follows:

\begin{matrix} S (δ x_{i}) = \{\begin{cases} 1, & δ x_{i} < L_{i}, \\ 0, & δ x_{i} > L_{i}, \end{cases} \end{matrix}

(7)

in which L_i represents the free length of the equilibrium spring between disc and pad. Since S(δx_i) is a discontinuous function, we need a smooth function to approximate it perfectly. Thus, we employ a continuous function with a smooth factor σ:

\begin{matrix} S (δ x_{i}) = \frac{1}{2} - \tanh \frac{(σ (|δ x_{i}| - L_{i}))}{2}, \end{matrix}

(8)

where σ is often a large positive number. Figure 6 shows the effects of a smooth function with different values of σ.

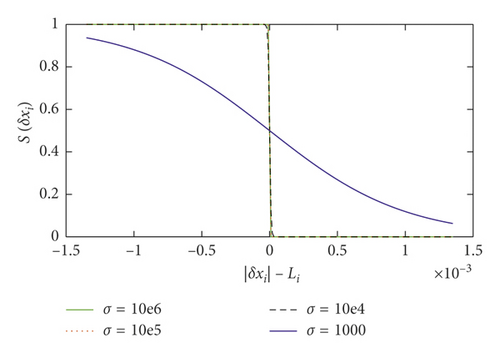
As seen in Figure 6, the approximation tends to converge when σ = 1000. Because the results are sensitive to the interface separation approximation, we use a value of σ = 10⁶ for the simulation.

Figure 7 shows the phase diagrams from simulations and experiments. Figure 7(a) shows simulation results for the brake model without contact loss. Figure 7(b) shows the simulation results for the brake model with contact loss. Figure 7(c) is the phase diagram evaluated from measured vibration data in stage C in Figure 2(b).

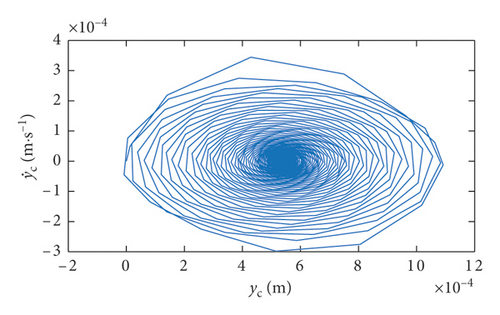
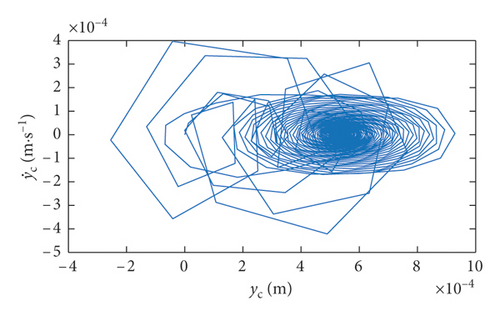
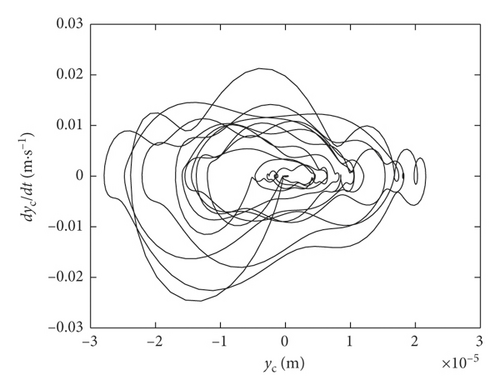
Phase diagrams have been used to judge whether the behaviors of the dynamical system are cyclic. Generally, if the phase plane trajectory is a limit cycle, the system is cyclic; if the phase plane trajectory forms a ring belt area, the system is quasi-periodic, and if the phase diagram is distributed within an area of the phase plane and not clear, the system behaviors could be random or even chaotic.

As seen in Figure 7, the simulation results of the brake model with interface separation or vibro-impact (Figure 7(b)) exhibit a much more irregular trend than the case without vibro-impact (Figure 7(a)). This suggests that the irregularity is increased by vibro-impact effects. Moreover, compared with Figures 7(a) and 7(b) more closely resembles the experimental results shown in Figure 7(c), which exhibits the unsymmetrical “fingerprints” in the phase diagram.

The phase diagram of the system with vibro-impact (Figure 7(b)) exhibits random close loops with multiple sharp corners and exhibits transition from the half order to integer order with an unsymmetrical signature, which are closer to the measured results (Figure 7(c)). Pure stick-slip vibrations, in contrast, exhibit a fixed phase diagram with relatively fixed signature.

5. Conclusions

Through experimental, analytical, and numerical investigations of creep groan vibrations of vehicle brake, we can draw the following conclusions:

(1)
The experimental results comprehensively exhibit varied vibrations in creep groan phenomena, which include simple stick-slip, stick-slip resonance, instable/sliding/impulsive stick-slip, stick-slip-induced vibro-impacts, and their back-and-forth transitions.
(2)
In contrast to conventional theories of creep groan, which comprehensively characterized the simple stick-slip, sliding stick-slip, stick-slip-induced resonances of suspension systems, we develop a new mechanism and analytical model of creep groan, and stick-slip-induced vibro-impacts, which quantitatively explain the existence of half-order harmonics and its transitions to a stick-slip fundamental frequency.
(3)
The severe stick-slip vibration-induced vibro-impact vibrations are unstable and could be triggered when stable stick-slip vibration is strong enough and could deteriorate back to pure, stable stick-slip vibrations without vibro-impact. The transitions have inherent connections with clear trend patterns of increase or decrease in specific frequencies in the spectrogram, which are also accompanied by a wideband spectrum due to the random impulsive effect in the unstable transition. The varied vibrations associated with creep groan are not irrelevant but rather have regularity and internal relationships.
(4)
Based on numerical simulations, the phase diagrams of the dynamics of brake creep groan have different patterns for cases with and without vibro-impacts. The irregularity of the phase diagram is increased by the vibro-impact effect, which is more similar to the experimental phase diagram.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (grant numbers 51575395, 51705366, and U1564207).

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Abdelhamid M. K., Creep groan of disc brakes, 1995, SAE Technical Paper Serieshttps://doi.org/10.4271/951282, 2-s2.0-84881194346.
10.4271/951282
Google Scholar
2 Gouya M. and Nishiwaki M., Study on disc brake groan, 1990, SAE Technical Paper Serieshttps://doi.org/10.4271/900007, 2-s2.0-84877189213.
10.4271/900007
Google Scholar
3 Brecht J., Hoffrichter W., and Dohle A., Mechanisms of brake creep groan, 1997, SAE Technical Paper Serieshttps://doi.org/10.4271/973026, 2-s2.0-84877206913.
10.4271/973026
Google Scholar
4 Vadari V. and Jackson M., An experimental investigation of disk brake creep-groan in vehicles and brake dynamometer correlation, 1999, SAE Technical Paper Serieshttps://doi.org/10.4271/1999-01-3408, 2-s2.0-84877195604.
10.4271/1999-01-3408
Google Scholar
5 Bettella M., Harrison M. F., and Sharp R. S., Investigation of automotive creep groan noise with a distributed-source excitation technique, Journal of Sound and Vibration. (2002) 255, no. 3, 531–547, https://doi.org/10.1006/jsvi.2001.4178, 2-s2.0-0037104821.
10.1006/jsvi.2001.4178
Web of Science® Google Scholar
6 Jang H., Lee J. S., and Fash J. W., Compositional effects of the brake friction material on creep groan phenomena, Wear. (2001) 251, no. 1–12, 1477–1483, https://doi.org/10.1016/s0043-1648(01)00786-4, 2-s2.0-0035482631.
10.1016/S0043-1648(01)00786-4
Web of Science® Google Scholar
7 Zhao X., Gräbner N., and Von Wagner U., Theoretical and experimental investigations of the bifurcation behavior of creep groan of automotive disk brakes, Journal of Theoretical and Applied Mechanics. (2018) 56, no. 2, 351–364, https://doi.org/10.15632/jtam-pl.56.2.351, 2-s2.0-85047065169.
10.15632/jtam-pl.56.2.351
Web of Science® Google Scholar
8 Gonzalez M., Díez R., and Canibano E., Comparative analysis of vented brake discs in groan noise test on dynamometer, 2004, SAE Technical Paper Serieshttps://doi.org/10.4271/2004-01-2789.
10.4271/2004-01-2789
Google Scholar
9 Fuadi Z., Adachi K., Ikeda H., Naito H., and Kato K., Effect of contact stiffness on creep-groan occurrence on a simple caliper-slider experimental model, Tribology Letters. (2009) 33, no. 3, 169–178, https://doi.org/10.1007/s11249-008-9404-4, 2-s2.0-60349102850.
10.1007/s11249-008-9404-4
Web of Science® Google Scholar
10 Yoon S. W., Shin M. W., Lee W. G., and Jang H., Effect of surface contact conditions on the stick-slip behavior of brake friction material, Wear. (2012) 294-295, 305–312, https://doi.org/10.1016/j.wear.2012.07.011, 2-s2.0-84866841565.
10.1016/j.wear.2012.07.011
CAS Web of Science® Google Scholar
11 Neis P. D., Ferreira N. F., Poletto J. C., Matozo L. T., and Masotti D., Quantification of brake creep groan in vehicle tests and its relation with stick-slip obtained in laboratory tests, Journal of Sound and Vibration. (2016) 369, 63–76, https://doi.org/10.1016/j.jsv.2016.01.036, 2-s2.0-84956633640.
10.1016/j.jsv.2016.01.036
Web of Science® Google Scholar
12 Zhao X., Gräbner N., and von Wagner U., Avoiding creep groan: investigation on active suppression of stick-slip limit cycle vibrations in an automotive disk brake via piezoceramic actuators, Journal of Sound and Vibration. (2019) 441, 174–186, https://doi.org/10.1016/j.jsv.2018.10.049.
10.1016/j.jsv.2018.10.049
Web of Science® Google Scholar
13 Joo K., Jeon H., Sung W., and Cho M. H., Transfer path analysis of brake creep noise, SAE International Journal of Passenger Cars-Mechanical Systems. (2013) 6, no. 3, 1408–1417, https://doi.org/10.4271/2013-01-2036, 2-s2.0-84886602824.
10.4271/2013-01-2036
Google Scholar
14 Cantoni C., Cesarini R., Mastinu G., Rocca G., and Sicigliano R., Brake comfort-a review, Vehicle System Dynamics. (2009) 47, no. 8, 901–947, https://doi.org/10.1080/00423110903100432, 2-s2.0-73349111908.
10.1080/00423110903100432
Web of Science® Google Scholar
15 Ashraf N., Bryant D., and Fieldhouse J. D., Investigation of stick-slip vibration in a commercial vehicle brake assembly, International Journal of Acoustics and Vibration. (2017) 22, no. 3, 326–333, https://doi.org/10.20855/ijav.2017.22.3478, 2-s2.0-85031691133.
10.20855/ijav.2017.22.3478
Web of Science® Google Scholar
16 Fuadi Z., Maegawa S., Nakano K., and Adachi K., Map of low-frequency stick-slip of a creep groan, Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology. (2010) 224, no. 12, 1235–1246, https://doi.org/10.1243/13506501jet834, 2-s2.0-79955416815.
10.1243/13506501JET834
Web of Science® Google Scholar
17 Brecht J. and Schiffner K., Influence of friction law on brake creep-groan, 2001, SAE Technical Paper Serieshttps://doi.org/10.4271/2001-01-3138, 2-s2.0-84877190789.
10.4271/2001-01-3138
Google Scholar
18 Hetzler H., Schwarzer D., and Seemann W., Analytical investigation of steady-state stability and hopf-bifurcations occurring in sliding friction oscillators with application to low-frequency disc brake noise, Communications in Nonlinear Science and Numerical Simulation. (2007) 12, no. 1, 83–99, https://doi.org/10.1016/j.cnsns.2006.01.007, 2-s2.0-33745266408.
10.1016/j.cnsns.2006.01.007
Web of Science® Google Scholar
19 Hetzler H., Schwarzer D., and Seemann W., Steady-state stability and bifurcations of friction oscillators due to velocity-dependent friction characteristics, Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics. (2007) 221, no. 3, 401–412, https://doi.org/10.1243/14644193jmbd80, 2-s2.0-34848928101.
10.1243/14644193JMBD80
Web of Science® Google Scholar
20 Crowther A. R. and Singh R., Analytical investigation of stick-slip motions in coupled brake-driveline systems, Nonlinear Dynamics. (2007) 50, no. 3, 463–481, https://doi.org/10.1007/s11071-006-9187-9, 2-s2.0-35148823506.
10.1007/s11071-006-9187-9
Web of Science® Google Scholar
21 Crowther A. R. and Singh R., Identification and quantification of stick-slip induced brake groan events using experimental and analytical investigations, Noise Control Engineering Journal. (2008) 56, no. 4, 235–255, https://doi.org/10.3397/1.2955772, 2-s2.0-53549103047.
10.3397/1.2955772
Web of Science® Google Scholar
22 Wei D., Ruan J., Zhu W., and Kang Z., Properties of stability, bifurcation, and chaos of the tangential motion disk brake, Journal of Sound and Vibration. (2016) 375, 353–365, https://doi.org/10.1016/j.jsv.2016.04.022, 2-s2.0-84992302750.
10.1016/j.jsv.2016.04.022
Web of Science® Google Scholar
23 Zhao X., Gräbner N., and von Wagner U., Experimental and theoretical investigation of creep groan of brakes through minimal models, Pamm. (2016) 16, no. 1, 295–296, https://doi.org/10.1002/pamm.201610136.
10.1002/pamm.201610136
Google Scholar
24 Fuadi Z., Adachi K., Ikeda H., Naito H., and Kato K., Experimental model for creep groan analysis, Lubrication Science. (2009) 21, no. 1, 27–40, https://doi.org/10.1002/ls.70, 2-s2.0-63449132846.
10.1002/ls.70
Web of Science® Google Scholar
25 Zhang L., Zhang P., and Meng D., Tests and theoretical analysis of creep groan in vehicle disc brake, Automotive Engineering. (2016) 38, no. 9, 1132–1139.
Google Scholar
26 Hu S. and Liu Y., Disc brake vibration model based on Stribeck effect and its characteristics under different braking conditions, Mathematical Problems in Engineering. (2017) 2017, 1–13, https://doi.org/10.1155/2017/6023809, 2-s2.0-85021663007.
10.1155/2017/6023809
Web of Science® Google Scholar
27 Donley M. and Riesland D., Brake groan simulation for a mcpherson strut type suspension, 2003, SAE Technical Paper Serieshttps://doi.org/10.4271/2003-01-1627, 2-s2.0-84877167942.
10.4271/2003-01-1627
Google Scholar
28 Uchiyama K. and Shishido Y., Study of creep groan simulation by implicit dynamic analysis method of FEA (Part 2), 2014, SAE Technical Paper Serieshttps://doi.org/10.4271/2014-01-2516, 2-s2.0-84937459394.
10.4271/2014-01-2516
Google Scholar
29 Uchiyama K. and Shishido Y., Study of creep groan simulation by implicit dynamic analysis method of FEA (Part 3), 2015, SAE Technical Paper Serieshttps://doi.org/10.4271/2015-01-2689, 2-s2.0-84959421511.
10.4271/2015-01-2689
Google Scholar
30 Meng D., Zhang L., Xu J., and Yu Z., A transient dynamic model of brake corner and subsystems for brake creep groan analysis, Shock and Vibration. (2017) 2017, 18, 8020797, https://doi.org/10.1155/2017/8020797, 2-s2.0-85042792012.
10.1155/2017/8020797
Web of Science® Google Scholar
31 Li Z., Ouyang H., and Guan Z., Friction-induced vibration of an elastic disc and a moving slider with separation and reattachment, Nonlinear Dynamics. (2017) 87, no. 2, 1045–1067, https://doi.org/10.1007/s11071-016-3097-2, 2-s2.0-84989874838.
10.1007/s11071-016-3097-2
Web of Science® Google Scholar
32 Stender M., Tiedemann M., Hoffmann N., and Oberst S., Impact of an irregular friction formulation on dynamics of a minimal model for brake squeal, Mechanical Systems and Signal Processing. (2018) 107, 439–451, https://doi.org/10.1016/j.ymssp.2018.01.032, 2-s2.0-85042112229.
10.1016/j.ymssp.2018.01.032
Web of Science® Google Scholar
33 Mercier A., Jezequel L., Besset S., Hamdi A., and Diebold J.-F., Nonlinear analysis of the friction-induced vibrations of a rotor-stator system, Journal of Sound and Vibration. (2019) 443, 483–501, https://doi.org/10.1016/j.jsv.2018.12.005.
10.1016/j.jsv.2018.12.005
Web of Science® Google Scholar
34 Abdelhamid M. and Bray W., Braking systems creep groan noise: detection and evaluation, 2009, SAE Technical Paper Serieshttps://doi.org/10.4271/2009-01-2103, 2-s2.0-84877178060.
10.4271/2009-01-2103
Google Scholar
35 Sui X. and Ding Q., Instability and stochastic analyses of a pad-on-disc frictional system in moving interactions, Nonlinear Dynamics. (2018) 93, no. 3, 1619–1634, https://doi.org/10.1007/s11071-018-4280-4, 2-s2.0-85045907010.
10.1007/s11071-018-4280-4
Web of Science® Google Scholar
36 Gaus N., Proppe C., and Zaccardi C., Modeling of dynamical systems with friction between randomly rough surfaces, Probabilistic Engineering Mechanics. (2018) 54, 82–86, https://doi.org/10.1016/j.probengmech.2017.07.004, 2-s2.0-85026803316.
10.1016/j.probengmech.2017.07.004
Web of Science® Google Scholar
37 Tonazzi D., Massi F., Baillet L., Brunetti J., and Berthier Y., Interaction between contact behaviour and vibrational response for dry contact system, Mechanical Systems and Signal Processing. (2018) 110, 110–121, https://doi.org/10.1016/j.ymssp.2018.03.020, 2-s2.0-85044135196.
10.1016/j.ymssp.2018.03.020
Web of Science® Google Scholar
38 Lacerra G., Di Bartolomeo M., Milana S., Baillet L., Chatelet E., and Massi F., Validation of a new frictional law for simulating friction-induced vibrations of rough surfaces, Tribology International. (2018) 121, 468–480, https://doi.org/10.1016/j.triboint.2018.01.052, 2-s2.0-85042276407.
10.1016/j.triboint.2018.01.052
Web of Science® Google Scholar

Citing Literature

All articles

Sensing and Quantifying a New Mechanism for Vehicle Brake Creep Groan

Abstract

1. Introduction