Advances in Materials Science and Engineering

Volume 2018, Issue 1 9254865

Research Article

Open Access

Entire Process Simulation of Corrosion due to the Ingress of Chloride Ions and CO₂ in Concrete

Xingji Zhu,

Xingji Zhu

Department of Civil Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, China hit.edu.cn

Search for more papers by this author

Zhaozheng Meng,

Zhaozheng Meng

Department of Civil Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, China hit.edu.cn

Search for more papers by this author

Yang Liu,

Yang Liu

Department of Civil Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, China hit.edu.cn

Search for more papers by this author

Longjun Xu,

Longjun Xu

Department of Civil Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, China hit.edu.cn

Cooperative Innovation Center of Engineering Construction and Safety in Shandong Blue Economic Zone, Qingdao, China

Search for more papers by this author

Zaixian Chen,

Corresponding Author

Zaixian Chen

[email protected]

orcid.org/0000-0002-4864-7175

Department of Civil Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, China hit.edu.cn

Search for more papers by this author

Xingji Zhu,

Xingji Zhu

Department of Civil Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, China hit.edu.cn

Search for more papers by this author

Zhaozheng Meng,

Zhaozheng Meng

Department of Civil Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, China hit.edu.cn

Search for more papers by this author

Yang Liu,

Yang Liu

Department of Civil Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, China hit.edu.cn

Search for more papers by this author

Longjun Xu,

Longjun Xu

Department of Civil Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, China hit.edu.cn

Cooperative Innovation Center of Engineering Construction and Safety in Shandong Blue Economic Zone, Qingdao, China

Search for more papers by this author

Zaixian Chen,

Corresponding Author

Zaixian Chen

[email protected]

orcid.org/0000-0002-4864-7175

Department of Civil Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, China hit.edu.cn

Search for more papers by this author

First published: 13 August 2018

https://doi.org/10.1155/2018/9254865

Citations: 9

Academic Editor: Shimin Liu

Share a link

Email
Wechat
Bluesky

Abstract

A comprehensive mathematical model which can simulate the entire corrosion process of reinforcement in concrete is proposed in this paper. The combined effect of carbonation and chloride ingress is also discussed in the mass transport module. Nonuniform corrosion distribution is employed for the study of mechanical damage in concrete. The link of ABAQUS with MATLAB is adopted for the numerical implementation of the developed model. The numerical results of an illustrative example indicate that the depassivation time of reinforcement, corrosion rate and expansion displacement, and cracking pattern of concrete all can be accurately predicted.

1. Introduction

Reinforced concrete (RC) structure is widely applied in the modern building construction area because of its advantages in structural stability. With the promotion of sustainable development strategy, great concern has been attached to the durability and longevity of reinforced concrete. Due to the alkaline environment of concrete, a spontaneous process called passivation can initiate. When the pH value ranges from 12 to 13 [1, 2], a protection oxide layer on the surface of steel reinforcement is gradually formed. This oxide layer can prevent the RC structure from corrosion. However, because concrete is a porous material, the protective layer can be damaged by the penetration of aggressive agents. In addition, through the air in pores, carbon dioxide can also diffuse in concrete. They both can reduce the service life and cause deterioration of the RC structure severely.

The main factors causing chloride-induced corrosion are the prevalent usage of deicing salt and marine moisture containing aggressive agents. And the carbonation process also appears in concrete because of the diffusion of carbon dioxide. In most cases, carbonation occurs with the chloride transfer process. According to experimental data, it was found that carbonation has obvious influence on chloride diffusion [3, 4]. Hence, the study on this combined durability is of great significance.

After the depassivation of steel reinforcement, a macrocell corrosion with a larger cathode area and smaller anode area is formed [5, 6]. The corrosion product of steel reinforcement will expand 3 to 6 times in volume [7, 8], which generates tensile stress on the inner surface of concrete. As a brittle material, the compressive stress of concrete is greater than that of tensile strength [9]. If the tensile stress of concrete is greater than the tensile strength, cracks are propagated and developed. When the cracks reach the concrete cover, more aggressive agents including oxygen, carbon dioxide, and moisture will penetrate into the RC structure, which accelerates the corrosion process [9–11].

Spalling and deterioration caused by the expansive cracks have significant damage on the mechanical performance of the RC structure. Because cracks can reduce the confinement between concrete and rebars the bond behavior of the RC structure declines drastically [12]. The carrying capacity of the RC structure is also impaired by the corrosion-induced reduction of cross-sectional area of the steel reinforcement [9, 12–15]. Therefore, the research studies on the corrosion rate, corrosion product distribution, and cracks pattern are attached to the utmost importance. An accurate model is needed to predict the service life and durability.

Many scholars studied the corrosion process and mechanical damage in the RC structure. For simplicity, these works all assume that the corrosion products are uniformly distributed [1, 16, 17]. However, that case is only suitable for the laboratory condition, in which the external current is attached to accelerate the corrosion process [9, 13, 18, 19]. According to actual observations, it was found that most of the corrosion distribution patterns are nonuniform [15, 20]. In terms of calculation results, recent studies have verified that errors of uniform distribution cannot be neglected [21]. The service life and bearing capacity are overestimated in evenly distributed models [14, 22]. Hence, those uniform distribution models are very limited.

Additionally, numerous scholars regarded the corrosion-induced expansive displacement as the swelling displacement of the concrete layer [1, 22–27], which is applied to the mechanical part directly. However, this method is incompatible with the actual cases. Note that Young’s modulus of concrete is approximately 30 GPa, while Young’s modulus of rust merely varies from 60 MPa to 100 MPa which is far smaller than that of concrete. Therefore, the deformation of rust layers increases dramatically with the rise of compression stress of the concrete cover. As a consequence, the expansive displacement and displacement of concrete should be considered independently [21]. Furthermore, there are few comprehensive models depicting the whole process from corrosion initiation to cracks reaching the concrete cover. Establishing a simplified full-scale model is attached to great importance.

In this paper, a comprehensive model for the entire process of corrosion-induced concrete deterioration is proposed. After this introduction, the transport of various harmful masses and the determination of depassivation time are described in Section 2. Then, Section 3 presents the process of the electrochemical reaction and mechanical damage. Experimental verification is presented in Section 4. Numerical implementation and an illustrative example are provided in Section 5. The conclusion is given in Section 6.

2. Transport of Various Harmful Masses

2. 1. Process of Carbon Dioxide Diffusion and Carbonation

Because the diffusion process of carbon dioxide in the air is four times faster than that in water diffusion in the porous water can be neglected. Therefore, the equation depicting carbon dioxide diffusion can be drawn by

(1)

where ϕ_a is the volume fraction in the pore of the concrete;

is the molar concentration of gaseous carbon dioxide in concrete;

is the flux of carbon dioxide; and Q_C is the depletion rate of carbon dioxide, and Q_C can be determined in literature [28].

Based on literature [29–31], parameters mentioned in (1) can be defined by the following equations:

(2)

(3)

(4)

where ϕ is the porosity of concrete,

is the diffusion coefficient of carbon dioxide (m²/sec), and ϕ_hc is the porosity of hardened concrete. More details to formulate ϕ_hc can be found in literature [32].

2.2. Chloride Penetration considering the Effect of Carbonation

In the combined case, we consider that there are three forms of existence of chloride in the concrete. The first form is chloride ions in the pore solution of concrete; the second is the bond chloride which is depicted by the isotherm; and the last form of existence is chlorine salt which can be turned into chloride ions through the reaction with carbon dioxide. Therefore, the total chloride content in the unit volume of concrete can be drawn by

(5)

where C_wc is the whole concentration of chloride per volume of the concrete, ϕ_we is the volume fraction of volatile water in pore volume, C_fc is the concentration of free chloride ions, C_bc is the bound chloride, and C_cs is the concentration of chloride salts. Note that chloride salts can be turned into chloride ions through reaction with carbon dioxide. Consequently, with the consideration of convective term, the governing equation can be depicted by

(6)

where

is the diffusion coefficient of free chloride ions and

is diffusion coefficient of moisture.

varies with the degree of carbonation.

Based on the employment of isotherm between bound chloride and chloride ions, (1) can be arranged according to chloride ions, which can be given by

(7)

which can be then expressed as

(8)

where J_fc is the flux of chloride ions; Q_rc is the source term which shows shifts from Friedel’s salts to free chloride ions because of carbonation. Additionally, variables used in (4) can be depicted more explicitly by the following equations:

(9)

(10)

(11)

where κ_r is the rate of the releasing from chloride salts to chloride ions, and we regard it as the same with the rate of concrete binding which is 1 × 10⁻⁵ sec⁻¹.

Due to the fact that carbonation has an obvious effect on porosity of concrete and pore structure, the chloride diffusion process is combined with the process of carbonation. Hence, the governing equation can be given by

(12)

where D_fc and D_h are the initial diffusion coefficients of chloride and moisture,

and

are the diffusion coefficients of chloride and moisture with the consideration of carbonation, and f_p(Ω, δ) is the function depicting the effect of change of pore structures due to carbonation. According to literature [33, 34], the most significant features that influence ions transfer process are Ω tortuosity and δ constrictivity, which can be determined in literature [33, 34]. Besides, function depicting the carbonation effect on chloride diffusion can be given by

(13)

where Ω₀ is the initial tortuosity and δ₀ is the initial constrictivity.

2.3. Transport of Moisture

Based on sections mentioned previously, moisture has a significant impact on the diffusion process of carbon dioxide and chloride, so the study about the transfer of moisture is of great importance. The governing equation can be given by

(14)

(15)

where J_h is the flux of moisture, I_we is the water production because of the carbonation process, and κ is the correction factor which is taken as 1 for the sake of simplicity.

2.4. Corrosion Initiation

When ignoring the impact of carbonation, the corrosion of steel reinforcement begins once chloride content reaches a certain threshold. However, the carbonation can reduce the threshold. According to literature [35, 36], the threshold varying with the carbonation degree can be given by

(16)

where

is the molar concentration of dissolved calcium hydroxide without considering carbonation, C_th is the chloride threshold without considering carbonation, and C_ch,d is the molar concentration of dissolved calcium hydroxide.

Once the pH value is lower than 11 [21], the depassivation process initiates. Hence, the pH value can be calculated based on the content of dissolved calcium hydroxide:

(17)

3. Mechanical Damage Process

3.1. Formula of Corrosion Rate on Steel Reinforcement

There are various models of the steel corrosion rate, most of which do not consider the change of the corrosion rate after the concrete cover is cracked. In this article, a comprehensive forecast model mentioned in literature [37] is employed. It proposes methods to determine the parameters and simplify equations. It also takes full account of the change of the corrosion rate before and after cracking of the concrete surface.

The model divides steel corrosion into two situations: high humidity (relative humidity greater than 90%) and general humidity (relative humidity less than 90%). Under high humidity conditions, the corrosion rate of reinforcement steel is controlled by the diffusion of cathode oxygen, which follows Fick’s first law. As for the RC structure in marine environments, their environment conditions match high humidity conditions. Before the longitudinal cracks penetrate the concrete cover, the corrosion current density of the steel reinforcement can be expressed by

(18)

(19)

where D_c0 is the initial O₂ diffusion coefficient in the concrete cover in high humidity environment; α is the O₂ solubility in water, and the value is generally 0.025–0.028; n_c=4 is the number of electrons for the cathodic reaction unit of oxygen; F = 96500C/mol is the Faraday constant, [O₂]⁰ is O₂ concentration in the external environment, and the value is 8.67 mol/m³ in normal atmospheric conditions; d is the diameter of the steel reinforcement; c is the thickness of the concrete cover; W/C is the concrete water-cement ratio; T_c is the ambient temperature; H_w is environmental relative humidity; t₁ is the time from the corrosion process initiating to concrete surface cracking; and L_c is the length of oxygen permeable range on steel reinforcement.

The length range of the central rebars where oxygen is permeable can be defined as

(20)

where r is the radius of steel reinforcement (m) and s is the spacing of longitudinal steel reinforcement.

The length range of the angle rebars where oxygen is permeable can be defined as

(21)

After the longitudinal cracks penetrate the concrete cover, the corrosion rate is mainly controlled by macrocell corrosion due to differences in oxygen concentration [32, 38]. Hence, the corrosion rate is related to the width of longitudinal cracks. According to the experimental data [39], the corrosion current density along the longitudinal cracks is given by

(22)

where w is the width of the corrosion crack.

Literature [40] shows that the corrosion rate of steel reinforcement first decreases. Then, the corrosion rate reaches a steady state before cracking of the concrete surface. After the cracking of the concrete cover, the corrosion rate first increases rapidly and then reaches a stationary state.

In order to simplify the formula, based on the experimental results, the corrosion rate when the crack width is 0.2 mm is adopted. It is regarded as the average corrosion rate after the cracking of the concrete surface. In the analysis of rust swelling and cracking, we assume that when the crack width reaches 0.2 mm, the crack will completely penetrate through the concrete cover. When the crack width reaches 0.8 mm, the concrete cover will be completely destroyed [40].

In the general humidity environment, the corrosion rate of steel reinforcement is controlled by factors such as the O₂ diffusion rate and the concrete resistivity. For the inland RC structures, most of them are in the general humidity environment. Before the longitudinal cracks penetrate the concrete cover, the corrosion current density of the steel reinforcement is given by

(23)

where ΔE is the voltage of steel reinforcement; I_a is the standard current density; D_cl is the initial value of O₂ diffusion coefficient of the concrete cover before corrosion, in general humidity environment; ρ_con is the resistivity of concrete; k is a coefficient associated with the water-cement ratio W/C, when W/C = 0.3∼0.4, k = −11.1, and W/C = 0.5∼0.6.

When longitudinal cracks penetrate the concrete cover, the corrosion current density of the steel reinforcement can be calculated by (5). According to Faraday’s law, from the initiation of corrosion to t time, the loss of corrosion of steel reinforcement can be defined as

(24)

where S_a is the corrosion area of the anode zone, S_c is the corrosion area of the cathode zone, and A_s is the total corrosion area. The ratio of anodic and cathodic corrosion areas can be determined as follows [41, 42]:

(25)

where PS is the concrete pore moisture content.

In real cases, the temperature T_c and humidity H_w vary with time, so the current density I₀ is related to the time t. In order to simplify the calculation, the mean value of temperature and humidity is taken in this paper, and the change of time is not considered. So the current density is independent of time.

3.2. Formula of Corrosion Expanding Displacement

Currently, there are mainly three models depicting corrosion distribution on the cross-sectional area, namely, the linearly decreased model [43], ellipse model [44, 45], and Gaussian model [22, 46], respectively. According to experimental data, the ellipse model and Gaussian model have relatively higher correspondence with the corrosion distribution pattern in real cases.

Exponential formula and elliptical formula depicting the corrosion distribution pattern are given in literature [47, 48]. By comparison, there are no distinct differences between experimental results and these two models. Here, given difficulties in determining variables and integral calculation of the exponential formula, the ellipse model is employed in this article.

According to the displacement distribution theory of the elliptical model, distribution of the corrosion product on cross section is shown in Figure 1. Hence, the thickness of the corrosion layer at any polar angle can be calculated by the following equations: before cracks penetrating concrete cover,

(26)

where d_a is the maximum thickness of the corrosion layer. After cracks penetrating concrete cover,

(27)

where d_b is the thickness of the corrosion layer at the side far away from the cover, and it can be defined as d_b = m · d_a and m is a fitting parameter. Through comparison between experimental results of [42] and [49], we regard m as 0.25.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Oval rust expansion displacement theoretical model.

Because the diffusion rate of Fe²⁺ and Fe³⁺ is far less than that of OH⁻ we assume that the corrosion product all occurred at the anode area of rebars. Therefore, the thickness of the corrosion product on the original reinforcement surface can be calculated by the following equations: before cracks penetrating concrete cover,

(28)

after cracks penetrating concrete cover,

(29)

where β is the volume expansion ratio of the corrosion product, which varies with different corrosion products. Here, due to corrosion products being regarded as Fe(OH)₃, we adopt 4.20 as the volume expansion ratio_.

Because the only unknown parameter is d_a, the relationship between d_a and m_s can be drawn by following formulae: before cracks penetrating concrete cover,

(30)

after cracks penetrating concrete cover,

(31)

where ρ_s is the density of steel reinforcement. Substituting d_s into (13)–(16), we can get the formula depicting relationship between ΔL_s(θ), ΔL_r(θ), and time t.

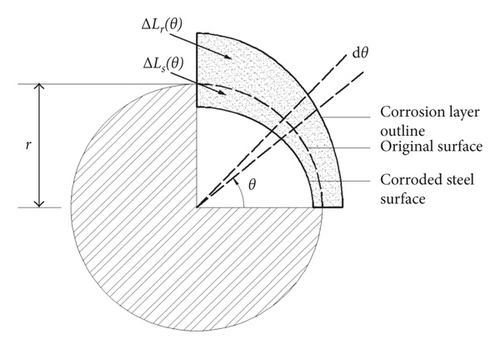
As for the corner rebars, Zhao et al. presumed that it can be derived by deflecting the corrosion displacement model of central rebars. By experimental results comparison, when there is little difference between concrete cover thicknesses of the two directions, this model can simulate the corrosion distribution pattern of corner rebars with little errors. When the cover of the side direction is far thicker than that of the forward direction, this model tends to be irrational with lots of errors, which cannot be applied. Therefore, when corrosion occurs on the side near the concrete cover, the corrosion expansive displacement can be calculated by superimposing displacements at different angles. Then, the corrosion expansive displacement is obtained.

Compared with the radius of steel reinforcement, the corrosion layer is thinner. The elastic modulus of the corrosion layer is about 100 MPa. It is far less than that of concrete. Consequently, we simply regard corrosion displacement expansion thickness ΔL_r(θ) as the displacement of the concrete in the radial direction. In this paper, we adopt an elliptical model to depict the corrosion distribution pattern. We discretize expansion thickness of corrosion ΔL_r(θ) and corrosion thickness ΔL_s(θ) along the polar angle. For each microelement dθ, we can assume that it complies the formulae of the ring structure, as shown in Figure 2. In Figure 2, u_c(θ) is the radial direction displacement of concrete; u_r(θ) is the displacement of corrosion products due to pressure of concrete; and

is the expansive thickness of the equivalent corrosion products on the original surface of reinforcement, which can be drawn as

(32)

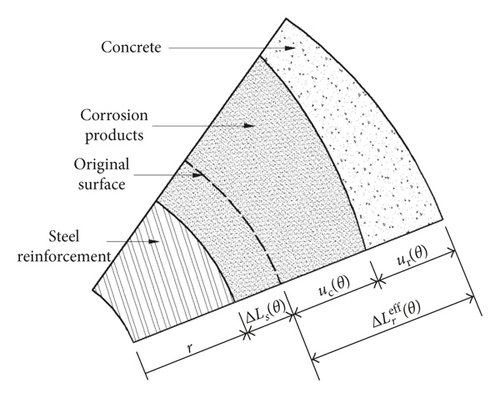
According to previous studies, corrosion products can diffuse in concrete internal void and the interface between reinforcement and concrete. Hence, when corrosion thickness is less than a certain constant δ₀, there is no expansive pressure on the concrete cover. In the calculation, we adopt δ₀ as 20 μm [50], and equals 0 when ΔL_r(θ) is less than δ₀.

As shown in Figure 2, we can draw the relational expression between u_r(θ) and u_c(θ) as follows:

(33)

Formula depicting the radial direction displacement of concrete is

(34)

where C_d is the thickness of the concrete cover, E_c is the elastic modulus of concrete, v_c is the Poisson ratio of concrete, and q(θ) is the radial pressure on contact interface between concrete and corrosion.

Formula depicting radial direction displacement of corrosion can be given by

(35)

where E_r is the elastic modulus of the corrosion product and v_r is the Poisson ratio of corrosion.

Substituting (20) and (19) into (18), we can get a comprehensive formula about u_c(θ):

(36)

3.3. Definition of Concrete Cracking and Initial Cracks Setting

After obtaining the radial displacement of the concrete layer, the development of cracks in concrete can be predicted by the fictitious crack model in expanding finite element method (XFEM). Here, the material is supposed to be linear elastic. Once the maximum tensile stress reaches the tensile strength of concrete, f_t, cracks initiate and develop. The crack expansion is always perpendicular to the maximum tensile stress direction.

Note that there is a virtual fracture area behind the tip of the crack. In this area, the stress of the surface area is not 0, whereas the stress is a function monotonically decreasing with the crack opening displacement. This is called material softening. The softening curve of the concrete material is controlled by its fracture energy G_f. When the crack opening displacement reaches a threshold, the stress of the surface area decreases to 0. Therefore, this point is the tip of the crack in real cases, so the crack surface behind this point is called free surface.

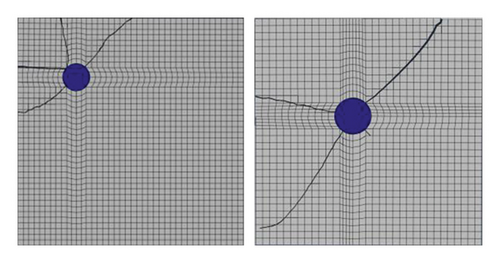
In the XFEM model, initial cracks need to be set in advance. Then, the development of cracks can be simulated more accurately. In our model, 8 initial cracks are set uniformly along the interaction surface between the steel reinforcement and the concrete. After the beginning of calculation, 2 or 3 fastest-developed main cracks are selected, and they can develop freely. Then, under the element birth and death control, the initial cracks are closed when the changes are not obvious, for the sake of simplicity.

4. Experimental Verification

4.1. Verification of the Influence of Carbonation on the Chloride Penetration

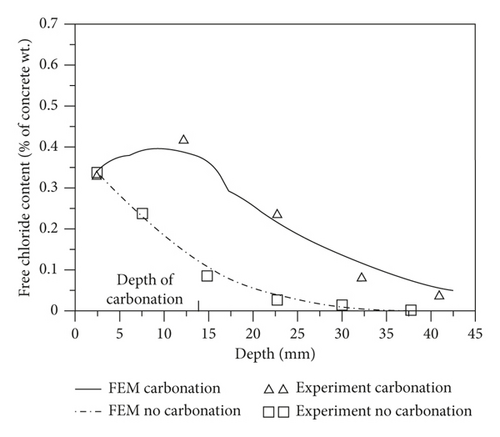
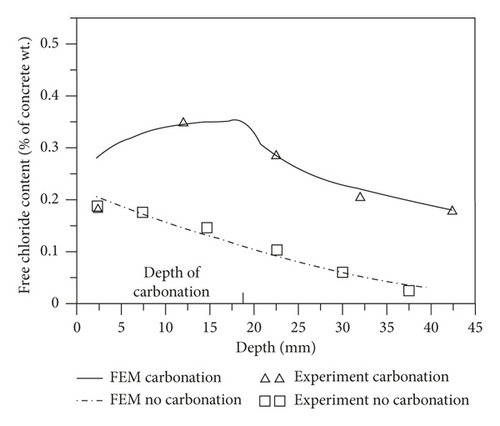
Based on the numerical model established by the theoretical model mentioned above, the transfer process of chloride in fully carbonized concrete can be stimulated. In most cases, the chloride transfer process and carbonation alternate. This more complicated situation can also be stimulated precisely. In the alternate experiment of carbonation and chloride penetration, concrete specimens are placed in an accelerated carbonation tank and the chloride tank alternately. Hence, the transfer process of chloride ions with carbonation can be determined. Because the alternate experiment is very close to the actual use of the RC structure, we employ alternate experiment testing data for the verification.

In literature [28], the influence of carbonation on the chloride transport properties in ordinary Portland concrete and fly ash concrete was tested, respectively. Concrete specimens were immersed in 5% NaCl solution for one week at the temperature of 25°C. In the next week, they are placed in an accelerated carbonation tank. In the carbonation tank, the temperature is 25°C, and humidity is 60%, and carbon dioxide content is 10%. A 56-week circulation is adopted.

As for the coupled effect of carbonation and chloride ions, the comparison of results obtained by the experiment and numerical model is shown in Figure 3. It is obvious that carbonation accelerates the chloride ions transfer rate significantly, and the chloride ions content is increased. Besides, the reaction between carbon dioxide and Friedel salt can cause the free chloride ions release effect. It can lead to an obvious jump of free chloride ions content at the edge of carbonation front (the interface between carbonized area and noncarbonized area). Because there is no enough time for the released free chloride ions to spread to two sides increasingly more free chloride ions accumulate at the reaction area. This phenomenon was precisely depicted by our numerical model. The numerical results agree well with the test results. Consequently, it shows good accuracy of the coupled mathematical model of carbonation and chloride ion penetration possesses.

4.2. Verification of the Mechanical Damage Model

Here, to determine the accuracy of the mechanical damage model, we compare the results of the numerical model and the experiment conducted in literature [51]. In the experiment, the cross section of specimens is 200 × 200 mm². In the first case, there is a steel reinforcement of 12 mm diameter with a 20 mm concrete cover; in the second case, there is a steel reinforcement of 16 mm with a 35 mm concrete cover. The embedment length of rebars is 180 mm, while the rest part is protected by a plastic sleeve. In two cases, each longitudinal side is saturated by 1% chloride solution for 1 minute and 3 minutes, respectively. Additionally, there is a potential of +500 mV NHE to accelerate the corrosion process. As shown in Figure 4, it can be found that results derived from our proposed model agree extremely well with the experiment results.

5. Illustrative Example

5.1. Problem Description and Procedure of Numerical Implementation

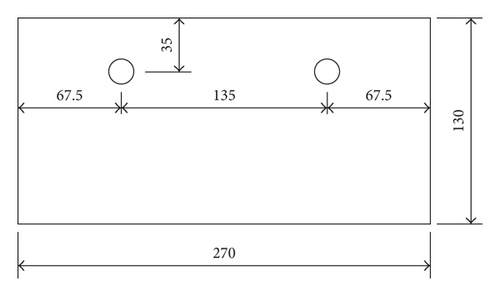
Here, a steel-reinforced concrete beam is used for the parametric study. The thickness of the concrete cover is 27 mm, the diameter of rebars is 16 mm, and the space between each steel reinforcement is 135 mm. Its cross section is shown in Figure 5. There is confinement on the Y direction on the lower boundary of the beam. The left and right sides are confined on the X direction. Parameters used in the numerical example are listed in Table 1.

Table 1. Material parameters summary.

Parameter	Value
Elastic modulus of concrete, E_c (Pa)	3.25 × 10¹⁰
Poisson’s ratio of concrete, v_c	0.20
Elastic modulus of corrosion products, E_r (Pa)	100 × 10⁶
Poisson’s ratio of corrosion products, v_r	0.49
Density of steel, ρ_s (kg·m⁻³)	7800
Water-cement ratio, W/C	0.35
Environment temperature, T_c (°C)	5
Environment humidity, H_w	0.9 (0.75)
Water content of concrete, PS (%)	35
Chloride content, C_fc (%)	0.2
Fracture energy, (G/J·m⁻²)	140
Concrete tensile strength, f_t (N·m⁻²)	1.71 × 10⁶

To determine the radial displacement variation of concrete along time order, we have to first determine the time when reaching the threshold of corrosion amount. In this paper, t₁ is regarded as the time when the cracks width reaches 0.2 mm. t₂ is regarded as the time when cracks reache 0.8 mm. From (11), it is notable that the corrosion product is in direct proportion to time, so the process to calculate t₁ (t₂) can be divided in to 5 steps:

(1)
If we assume a time period t, based on the MATLAB and theoretical formulae, we can calculate the corrosion expansive displacement distribution at t moment. Then, the rust expansion displacement is discretized into 24 points along the circumferential direction of the steel bar. Each point is applied on the surface of rebars.
(2)
With the application of XFEM of ABAQUS, we simulate the crack development under corrosion expansive displacement. In addition, the calculation of the crack width can be achieved. Therefore, we can determine time steps when the crack width reaches 0.2 mm and 0.8 mm, respectively.
(3)
According to the linear relationship between corrosion amount and time, we can determine the corrosion expansive displacement at each time step.
(4)
Based on MATLAB, the corresponding time of rust expansion displacement distribution can be deduced by the theoretical formula, which is the approximant value of t₁ (t₂).
(5)
Repeating step (1)–step (4), we can get the more accurate value of t₁ and t_2.

5.2. Radial Displacement Curve of Concrete under Corrosion Expansion Pressure

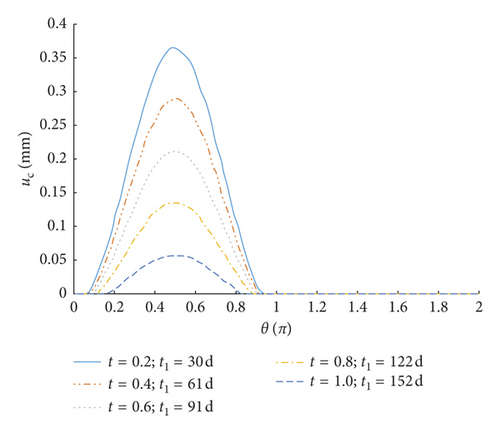
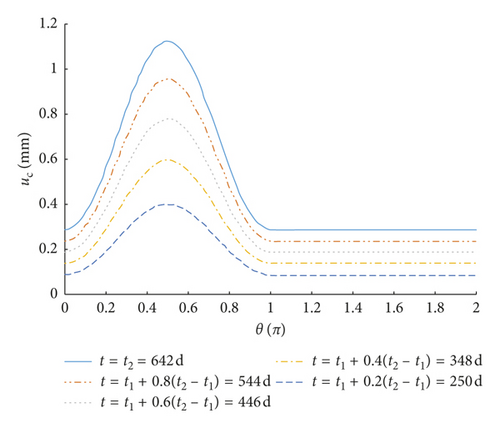
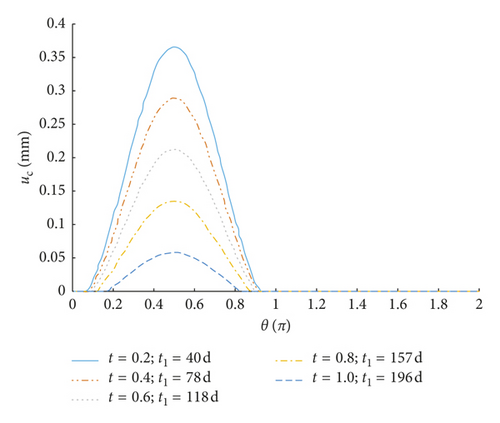
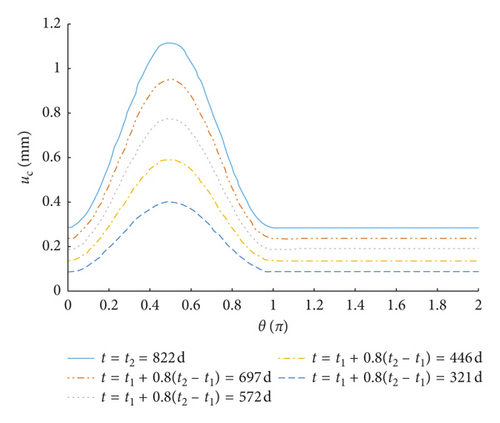
Figures 6 and 7 show the radial displacement of concrete u_c(θ) under corrosion expansive pressure at different time periods, when the environmental relative humidity is 90% and 75%, respectively. According to Figures 6(a) and 6(b), the corrosion before the cracking of the concrete surface mainly distributes on the half surface facing the side of the protective layer. The thickness of the corrosion layer turns smaller when it is farther from the concrete surface. Note that there is no corrosion on the half cross section which is far away from the protective layer. On the contrary, situation after cracks penetrating the concrete cover is completely different. Although less than the corrosion product on the surface close to the protective layer, corrosion appears on the surface far away from the protective layer. Additionally, under the same corrosion expansive pressure, when the structure is in high humidity, it takes less time to reach the same radial displacement of concrete. It suggests that high humidity environment contributes a lot to the corrosion process.

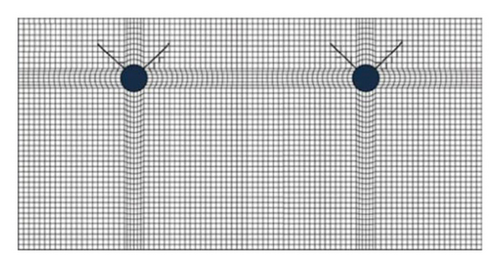
5.3. Crack Development under Nonuniform Corrosion Expanding Pressure

Having determined the distribution curve of radial displacement of concrete u_c(θ) along the circumferential direction of steel reinforcement, we input them as displacement load into the XFEM model of ABAQUS. Then, crack development of the concrete cover is obtained. It is more explicit and intuitional for researchers to study and analyze crack development.

Under the assumption that the environmental relative humidity is 90%, we analyze the crack development changing with time, as shown in Figure 5. Through calculation, when the corrosion expansive displacement of rebars u_c(θ) reaches what is shown in Figure 6(a) (the maximum of displacement is 0.365 mm), the surface of concrete is cracked (the crack width reaches 0.2 mm), and t₁ is 152 d. When the corrosion expansive displacement of rebars reaches Figure 6(b) (the maximum of displacement is 1.130 mm), the concrete cover is completely deteriorated (the crack width reaches 0.8 mm), and t₂ is 642 d. Development of corrosion-induced cracks is shown in Figure 8. It demonstrates that the concrete cover is cracked by corrosion-induced cracks after 5 months since the depassivation process. With the development of cracks, the concrete cover will be completely destroyed 16 months later. Consequently, as for the structure mentioned in this paper, anticorrosion methods and strengthening measures are required within 16 months when the cracks are discovered on the concrete cover.

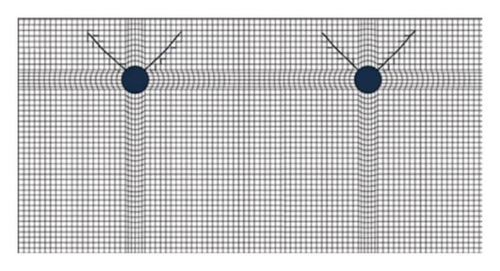
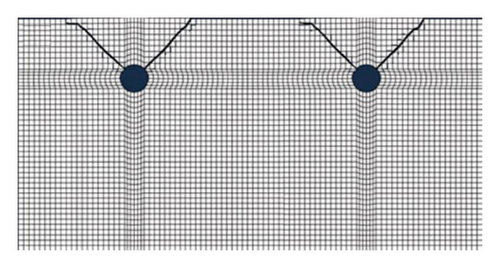
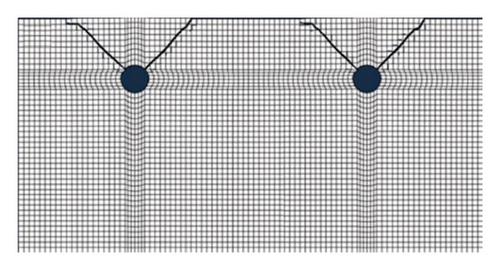
5.4. Comparison of Crack Development under Uniform and Nonuniform Corrosion Process

Numerous studies have verified that the corrosion product distribution is nonuniform in actual cases. As mentioned previously, most researches focusing on crack development of concrete are based on the uniform pattern. Therefore, it has been attached to the utmost significance to compare differences in crack pattern, initiation process, and cracking time. We analyze the structure shown in Figure 5 on the basis of the uniform distribution model, and the crack expanding process is shown in Figure 9.

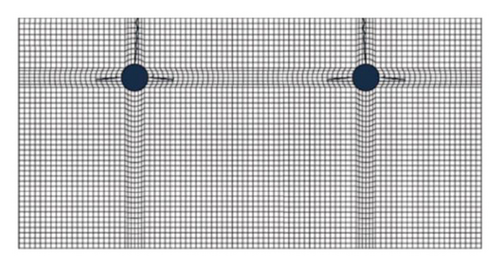
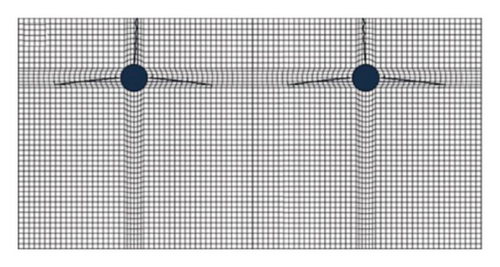
Comparing the crack development figures of uniform corrosion distribution and nonuniform corrosion distribution, respectively, we can find distinct differences in terms of the crack pattern. The cracking process of the uniform corrosion pattern is obviously slower than that of nonuniform corrosion pattern. Under uniform distribution, it takes 19 months for cracks to penetrate the concrete cover under the uniform corrosion pattern. Then, it takes 46 months to entirely destroy the concrete layer. Therefore, if employing uniform distribution pattern in the actual cases, the load capacity and service-life of structures will be severely overestimated, which can lead to undesirable consequences.

6. Conclusion

(1)
The transport of various harmful masses is described by a series of mathematical formulae, including chloride ions, carbon dioxide, and moisture. The combined effect of carbonation and chloride ingress is also studied.
(2)
The expansive displacement of concrete at different time periods of corrosion can be obtained directly by our proposed mathematical model.
(3)
By linking ABAQUS with MATLAB, the prediction for the evolution of corrosion-induced cracking damage for the concrete cover can be numerically implemented.
(4)
Various experimental data were compared with the results obtained by our model and verified its accuracy.
(5)
The numerical results of an illustrative example show that there are significant differences in the crack pattern and crack development between the uniform and nonuniform corrosion. If the uniform distribution theory is used to guide actual projects, the carrying capacity of the structure will be seriously overestimated.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was financially supported by the Natural Science Foundation of Shandong Province (no. ZR2018BEE044) and the National Natural Science Foundation of China (nos. 51678208 and 51678199). The authors also appreciate the support of the Major Training Program of Natural Science Research Innovation Foundation of Harbin Institute of Technology (HIT.NSRIF.201709) and the Major Program of Mutual Foundation of Weihai City with Harbin Institute of Technology (Weihai).

Open Research

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

1 Guzmán S., Gálvez J. C., and Sancho J. M., Modelling of corrosion-induced cover cracking in reinforced concrete by an embedded cohesive crack finite element, Engineering Fracture Mechanics. (2012) 93, 92–107, https://doi.org/10.1016/j.engfracmech.2012.06.010, 2-s2.0-84865415692.
10.1016/j.engfracmech.2012.06.010
Web of Science® Google Scholar
2 Muthulingam S. and Rao B. N., Non-uniform corrosion states of rebar in concrete under chloride environment, Corrosion Science. (2015) 93, 267–282, https://doi.org/10.1016/j.corsci.2015.01.031, 2-s2.0-84925362649.
10.1016/j.corsci.2015.01.031
CAS Web of Science® Google Scholar
3 Zhu X. J. and Zi G., Probabilistic analysis of reinforcement corrosion due to the combined action of carbonation and chloride ingress in concrete, Construction and Building Materials. (2016) 124, 667–680, https://doi.org/10.1016/j.conbuildmat.2016.07.120, 2-s2.0-84982740644.
10.1016/j.conbuildmat.2016.07.120
CAS Web of Science® Google Scholar
4 Zhu X. J., Zi G., Cao Z. F. et al., Combined effect of carbonation and chloride ingress in concrete, Construction and Building Materials. (2016) 110, 369–380, https://doi.org/10.1016/j.conbuildmat.2016.02.034, 2-s2.0-84958985459.
10.1016/j.conbuildmat.2016.02.034
CAS Web of Science® Google Scholar
5 Zhang R. J., Castel A., and François R., The corrosion pattern of reinforcement and its influence on serviceability of reinforced concrete members in chloride environment,, Cement and Concrete Research. (2009) 39, no. 11, 1077–1086, https://doi.org/10.1016/j.cemconres.2009.07.025, 2-s2.0-70349626276.
10.1016/j.cemconres.2009.07.025
CAS Web of Science® Google Scholar
6 Ožbolt J., Oršanić F., Balabanić G. et al., Modeling damage in concrete caused by corrosion of reinforcement: coupled 3D FE model, International Journal of Fracture. (2012) 178, no. 1-2, 233–244, https://doi.org/10.1007/s10704-012-9774-3, 2-s2.0-84870688831.
10.1007/s10704-012-9774-3
CAS Web of Science® Google Scholar
7 Ye H. L., Jin N. G., Fu C. Q. et al., Rust distribution and corrosion-induced cracking patterns of corner-located rebar in concrete cover, Construction and Building Materials. (2017) 156, 684–691, https://doi.org/10.1016/j.conbuildmat.2017.09.033, 2-s2.0-85029496530.
10.1016/j.conbuildmat.2017.09.033
Web of Science® Google Scholar
8 Bažant Z. P., Physical model for steel corrosion in concrete sea structures theory, Journal of the Structural Division. (1979) 105, 1137–1153.
10.1061/JSDEAG.0005168
Web of Science® Google Scholar
9 Zhao Y. X., Yu J., Wu Y. Y. et al., Critical thickness of rust layer at inner and out surface cracking of concrete cover in reinforced concrete structures, Corrosion Science. (2012) 59, 316–323, https://doi.org/10.1016/j.corsci.2012.03.018, 2-s2.0-84860230442.
10.1016/j.corsci.2012.03.018
CAS Web of Science® Google Scholar
10 Alonso C., Andrade C., Rodriguez J. et al., Factors controlling cracking of concrete affected by reinforcement corrosion, Materials & Structures. (1998) 31, no. 211, 435–441, https://doi.org/10.1007/bf02480466.
10.1007/BF02480466
CAS Web of Science® Google Scholar
11 Cao C., Cheung M. M. S., and Chan B. Y. B., Modelling of interaction between corrosion-induced concrete cover crack and steel corrosion rate, Corrosion Science. (2013) 69, 97–109, https://doi.org/10.1016/j.corsci.2012.11.028, 2-s2.0-84873750310.
10.1016/j.corsci.2012.11.028
CAS Web of Science® Google Scholar
12 Chernin L. and Val D. V., Prediction of corrosion-induced cover cracking in reinforced concrete structures, Construction and Building Materials. (2011) 25, no. 4, 1854–1869, https://doi.org/10.1016/j.conbuildmat.2010.11.074, 2-s2.0-78650913449.
10.1016/j.conbuildmat.2010.11.074
Web of Science® Google Scholar
13 Ma Y. F., Guo Z. Z., Wang L. et al., Experimental investigation of corrosion effect on bond behavior between reinforcing bar and concrete, Construction and Building Materials. (2017) 152, 240–249, https://doi.org/10.1016/j.conbuildmat.2017.06.169, 2-s2.0-85021697419.
10.1016/j.conbuildmat.2017.06.169
Web of Science® Google Scholar
14 Dasar A., Hamada H., Sagawa Y. et al., Deterioration progress and performance reduction of 40-year-old reinforced concrete beams in natural corrosion environments, Construction and Building Materials. (2017) 149, 690–704, https://doi.org/10.1016/j.conbuildmat.2017.05.162, 2-s2.0-85019971808.
10.1016/j.conbuildmat.2017.05.162
Web of Science® Google Scholar
15 Zhu W. J., François R., and Liu Y., Propagation of corrosion and corrosion patterns of bars embedded in RC beams stored in chloride environment for various periods, Construction and Building Materials. (2017) 145, 147–156, https://doi.org/10.1016/j.conbuildmat.2017.03.210, 2-s2.0-85017147631.
10.1016/j.conbuildmat.2017.03.210
CAS Web of Science® Google Scholar
16 Zhao Y. X., Dong J. F., Wu Y. Y. et al., Corrosion-induced concrete cracking model considering corrosion product-filled paste at the concrete/steel interface, Construction and Building Materials. (2016) 116, 273–280, https://doi.org/10.1016/j.conbuildmat.2016.04.097, 2-s2.0-84967334666.
10.1016/j.conbuildmat.2016.04.097
CAS Web of Science® Google Scholar
17 Isgor O. B. and Razaqpur A. G., Advanced modelling of concrete deterioration due to reinforcement corrosion, Canadian Journal of Civil Engineering. (2006) 33, no. 6, 707–718, https://doi.org/10.1139/l06-007, 2-s2.0-33751211191.
10.1139/l06-007
CAS Web of Science® Google Scholar
18 Zhao Y. X., Dong J. F., Ding H. J. et al., Shape of corrosion-induced cracks in recycled aggregate concrete, Corrosion Science. (2015) 98, 310–317, https://doi.org/10.1016/j.corsci.2015.05.028, 2-s2.0-84937970437.
10.1016/j.corsci.2015.05.028
CAS Web of Science® Google Scholar
19 Zhang R. J., Arnaud C., and François R., Concrete cover cracking with reinforcement corrosion of RC beam during chloride-induced corrosion process, Cement and Concrete Research. (2009) 40, no. 3, 415–425.
10.1016/j.cemconres.2009.09.026
CAS Web of Science® Google Scholar
20 Du X. L., Jin L., and Zhang R. B., Modeling the cracking of cover concrete due to non-uniform corrosion of reinforcement, Corrosion Science. (2014) 89, 189–202, https://doi.org/10.1016/j.corsci.2014.08.025, 2-s2.0-85027918410.
10.1016/j.corsci.2014.08.025
CAS Web of Science® Google Scholar
21 Zhu X. J. and Zi G., A 2D mechano-chemical model for the simulation of reinforcement corrosion and concrete damage, Construction and Building Materials. (2017) 137, 330–334, https://doi.org/10.1016/j.conbuildmat.2017.01.103, 2-s2.0-85011844349.
10.1016/j.conbuildmat.2017.01.103
CAS Web of Science® Google Scholar
22 Zhao Y. X., Karimi A. R., Wong H. S. et al., Comparison of uniform and non-uniform corrosion induced damage in reinforced concrete based on a Gaussian description of the corrosion layer, Corrosion Science. (2011) 53, no. 9, 2803–2814, https://doi.org/10.1016/j.corsci.2011.05.017, 2-s2.0-80053438646.
10.1016/j.corsci.2011.05.017
CAS Web of Science® Google Scholar
23 Chen E. and Leung C. K. Y., A coupled diffusion-mechanical model with boundary element method to predict concrete cover cracking due to steel corrosion, Corrosion Science. (2017) 126, 180–196, https://doi.org/10.1016/j.corsci.2017.07.001, 2-s2.0-85026531328.
10.1016/j.corsci.2017.07.001
CAS Web of Science® Google Scholar
24 Zhao Y. X., Yu J., and Jin W. L., Damage analysis and cracking model of reinforced concrete structures with rebar corrosion, Corrosion Science. (2011) 53, no. 10, 3388–3397, https://doi.org/10.1016/j.corsci.2011.06.018, 2-s2.0-79960706210.
10.1016/j.corsci.2011.06.018
CAS Web of Science® Google Scholar
25 Zhao Y. X., Yu J., Hu B. Y., and Jin W. L., Crack shape and rust distribution in corrosion-induced cracking concrete, Corrosion Science. (2012) 55, 385–393, https://doi.org/10.1016/j.corsci.2011.11.002, 2-s2.0-83555172262.
10.1016/j.corsci.2011.11.002
CAS Web of Science® Google Scholar
26 Tran K. K., Nakamura H., Kawamura K. et al., Analysis of crack propagation due to rebar corrosion using RBSM, Cement and Concrete Composites. (2011) 33, no. 9, 906–917, https://doi.org/10.1016/j.cemconcomp.2011.06.001, 2-s2.0-80052965030.
10.1016/j.cemconcomp.2011.06.001
CAS Web of Science® Google Scholar
27 Šavija B., Luković M., Pacheco J. et al., Cracking of the concrete cover due to reinforcement corrosion: A two-dimensional lattice model study, Construction and Building Materials. (2013) 44, 626–638, https://doi.org/10.1016/j.conbuildmat.2013.03.063, 2-s2.0-84876575753.
10.1016/j.conbuildmat.2013.03.063
Web of Science® Google Scholar
28 Cheng X. D., Sun L. F., Cao Z. F. et al., Cracking process analysis of concrete cover caused by non-uniform corrosion, Journal of Chinese Society for Corrosion and Protection. (2015) 35, no. 3, 257–264.
Google Scholar
29 Papadakis V., Vayenas C., and Fardis M., Physical and chemical characteristics affecting the durability of concrete, ACI Materials Journal. (1991) 88, no. 2, 186–196.
CAS Web of Science® Google Scholar
30 Saetta A. and Vitaliani R., Experimental investigation and numerical modeling of carbonation process in reinforced concrete structures part I: theoretical formulation, Cement and Concrete Research. (2004) 34, no. 4, 571–579, https://doi.org/10.1016/j.cemconres.2003.09.009, 2-s2.0-1542303583.
10.1016/j.cemconres.2003.09.009
CAS Web of Science® Google Scholar
31 Saetta A., Scotta R., and Vitaliani R., Mechanical behavior of concrete under physical-chemical attacks, Journal of Engineering Mechanics ASCE. (1998) 124, no. 10, 1100–1109, https://doi.org/10.1061/(asce)0733-9399(1998)124:10(1100).
10.1061/(ASCE)0733-9399(1998)124:10(1100)
Web of Science® Google Scholar
32 Liang C. H., The Introduction of Metal Corrosion, 1999, China Machine Press, Beijing, China.
Google Scholar
33 Ishida T., Iqbal P., and Anh H., Modeling of chloride diffusivity coupled with non-linear binding capacity in sound and cracked concrete, Cement and Concrete Research. (2009) 39, no. 10, 913–923, https://doi.org/10.1016/j.cemconres.2009.07.014, 2-s2.0-69249205455.
10.1016/j.cemconres.2009.07.014
CAS Web of Science® Google Scholar
34 Nakarai K., Ishida T., and Maekawa K., Multi-scale physicochemical modeling of soil-cementitious material interaction, Soils and Foundations. (2006) 46, no. 5, 635–664, https://doi.org/10.3208/sandf.46.653, 2-s2.0-62349083356.
10.3208/sandf.46.653
Web of Science® Google Scholar
35 Böhni H., Corrosion in Reinforced Concrete Structures, 2005, Woodhead Publishing, Oxford, UK.
10.1533/9781845690434
Google Scholar
36 Bertolini L., Elsener B., Pedeferri P. et al., Corrosion of Steel in Concrete–Prevention, Diagnosis, Repair, 2013, Wiley-VCH Verlag GmbH and Co. KGaA, Weinheim, Germany.
10.1002/9783527651696
Google Scholar
37 Geng O., Prediction models of steel bar corrosion rate in concrete member, 2008, China University of Mining and Technology, Xuzhou, China, Ph.D. thesis.
Google Scholar
38 Wei B. M., Metallic Corrosion Theories and Applications, 1984, Chemical Industry Press, Beijing, China.
Google Scholar
39 Mu Y. J., Reinforcement Corrosion Dilation Effect and Forecasting Model in Concrete, 2006, China University of Mining and Technology, Xuzhou, China.
Google Scholar
40 Zhao Y. X. and Jin W. L., Analysis on the cracking of concrete cover due to rebar corrosion, Journal of Hydraulic Engineering. (2005) 36, no. 8, 939–945.
Google Scholar
41 Song X. B. and Liu X. L., Experiment research on corrosion of reinforcement in concrete through cathode-to-anode area ratio, ACI Structural Journal. (2000) 97, no. 2, 148–155.
CAS Google Scholar
42 Song X. B., Corrosion of steel in concrete, 1999, Tsinghua University, Beijing, China, Ph.D. thesis.
Google Scholar
43 Jang B. S. and Oh B. H., Effects of non-uniform corrosion on the cracking and service life of reinforced concrete structures, Cement and Concrete Research. (2010) 40, no. 9, 1441–1450, https://doi.org/10.1016/j.cemconres.2010.03.018, 2-s2.0-77955327302.
10.1016/j.cemconres.2010.03.018
CAS Web of Science® Google Scholar
44 Du X. L., Jin L., and Zhang R. B., Modeling the cracking of cover concrete due to non-uniform corrosion of reinforcement, Corrosion Science. (2014) 89, 189–202, https://doi.org/10.1016/j.corsci.2014.08.025, 2-s2.0-85027918410.
10.1016/j.corsci.2014.08.025
CAS Web of Science® Google Scholar
45 Yuan Y. S., Ji Y. S., and Mou Y. J., Propagation and model of distribution for corrosion of steel bars in concrete, China Civil Engineering Journal. (2007) 40, no. 7, 5–10.
Google Scholar
46 Zhao Y. X., Hu B. Y., Yu J., and Jin W. L., Non-uniform distribution of rust layer around steel bar in concrete, Corrosion Science. (2011) 53, no. 12, 4300–4308, https://doi.org/10.1016/j.corsci.2011.08.045, 2-s2.0-80053453251.
10.1016/j.corsci.2011.08.045
CAS Web of Science® Google Scholar
47 Zhao Y. X., Hu B. Y., Yu J. et al., Non-uniform distribution of rust layer around steel bar in concrete, Corrosion Science. (2011) 53, no. 12, 4300–4308, https://doi.org/10.1016/j.corsci.2011.08.045, 2-s2.0-80053453251.
10.1016/j.corsci.2011.08.045
CAS Web of Science® Google Scholar
48 Yuan Y. S., Ji Y. S., and Mu Y. J., Propagation and model of distribution for corrosion of steel bars in concrete, China Civil Engineering Journal. (2007) 40, no. 7, 5–10.
Google Scholar
49 Ji Y. S., Correlation of reinforced concrete degradation processes in natural and artificial climate environment, 2007, China University of Mining and Technology, Xuzhou, China, Ph.D. thesis.
Google Scholar
50 Leon C. and Dimitri V. V., Prediction of corrosion-induced cover cracking in reinforced concrete structures, Construction and Building Materials. (2011) 25, no. 4, 1854–1869.
10.1016/j.conbuildmat.2010.11.074
Web of Science® Google Scholar
51 Ožbolt J., Oršanić F., and Balabanić G., Modeling pull-out resistance of corroded reinforcement in concrete: coupled three-dimensional finite element model, Cement and Concrete Composites. (2014) 46, no. 2, 41–45, https://doi.org/10.1016/j.cemconcomp.2013.10.014, 2-s2.0-84890071341.
10.1016/j.cemconcomp.2013.10.014
CAS Web of Science® Google Scholar

Citing Literature

All articles

Entire Process Simulation of Corrosion due to the Ingress of Chloride Ions and CO₂ in Concrete

Abstract

1. Introduction

2. Transport of Various Harmful Masses

2. 1. Process of Carbon Dioxide Diffusion and Carbonation

2.2. Chloride Penetration considering the Effect of Carbonation

2.3. Transport of Moisture

2.4. Corrosion Initiation

3. Mechanical Damage Process

3.1. Formula of Corrosion Rate on Steel Reinforcement

3.2. Formula of Corrosion Expanding Displacement

3.3. Definition of Concrete Cracking and Initial Cracks Setting

4. Experimental Verification

4.1. Verification of the Influence of Carbonation on the Chloride Penetration

4.2. Verification of the Mechanical Damage Model

5. Illustrative Example

5.1. Problem Description and Procedure of Numerical Implementation

5.2. Radial Displacement Curve of Concrete under Corrosion Expansion Pressure

5.3. Crack Development under Nonuniform Corrosion Expanding Pressure

5.4. Comparison of Crack Development under Uniform and Nonuniform Corrosion Process

6. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Entire Process Simulation of Corrosion due to the Ingress of Chloride Ions and CO2 in Concrete

Abstract

1. Introduction

2. Transport of Various Harmful Masses

2. 1. Process of Carbon Dioxide Diffusion and Carbonation

2.2. Chloride Penetration considering the Effect of Carbonation

2.3. Transport of Moisture

2.4. Corrosion Initiation

3. Mechanical Damage Process

3.1. Formula of Corrosion Rate on Steel Reinforcement

3.2. Formula of Corrosion Expanding Displacement

3.3. Definition of Concrete Cracking and Initial Cracks Setting

4. Experimental Verification

4.1. Verification of the Influence of Carbonation on the Chloride Penetration

4.2. Verification of the Mechanical Damage Model

5. Illustrative Example

5.1. Problem Description and Procedure of Numerical Implementation

5.2. Radial Displacement Curve of Concrete under Corrosion Expansion Pressure

5.3. Crack Development under Nonuniform Corrosion Expanding Pressure

5.4. Comparison of Crack Development under Uniform and Nonuniform Corrosion Process

6. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information

Entire Process Simulation of Corrosion due to the Ingress of Chloride Ions and CO₂ in Concrete