Advances in Materials Science and Engineering
Volume 2018, Issue 1 8707929
Research Article
Open Access

An Integral Formulation of Two-Parameter Fatigue Crack Growth Model

Jianguo Wu, 

Jianguo Wu

Science and Technology on Reliability and Environmental Engineering Laboratory, Beijing Institute of Structure and Environment Engineering, Beijing, China

Search for more papers by this author
Shan Jiang, 

Corresponding Author

Shan Jiang

Science and Technology on Reliability and Environmental Engineering Laboratory, School of Reliability and Systems Engineering, Beihang University, Beijing, China buaa.edu.cn

Search for more papers by this author
Wei Zhang, 

Wei Zhang

Science and Technology on Reliability and Environmental Engineering Laboratory, School of Reliability and Systems Engineering, Beihang University, Beijing, China buaa.edu.cn

Search for more papers by this author
Zili Wang, 

Zili Wang

Science and Technology on Reliability and Environmental Engineering Laboratory, School of Reliability and Systems Engineering, Beihang University, Beijing, China buaa.edu.cn

Search for more papers by this author
First published: 13 March 2018
https://doi.org/10.1155/2018/8707929
Citations: 1
Academic Editor: Dariusz Rozumek

Abstract

A two-parameter fatigue crack growth algorithm in integral form is proposed, which can describe the continuous crack growth process over the time period. In this model, the fatigue crack propagation behavior is governed by the temporal crack-tip state including the current applied load and the physical condition due to the previous load sequence. The plasticity-induced crack closure, left by the historical loading sequence, controls the following fatigue crack growth behavior and typically leads to the interaction effects. In the proposed method, a modified crack closure model deriving from the local plastic deformation is employed to account for this load memory effect. In general, this model can simulate the fatigue crack growth under variable amplitude loading. Additionally, this model is established on the physical state of crack tip in the small spatial and temporal scale, and it is used to evaluate the macroscopic crack propagation and fatigue life under irregular tension-tension loading. A special superimposed loading case is discussed to demonstrate the advantage of the proposed model, while the traditional two-parameter approach is not proper functional. Moreover, the typical various load spectra are also employed to validate the method. Good agreements are observed.

1. Introduction

Since the damage tolerance concept is of great significance to the engineering design, the prediction of fatigue crack growth life under the service environment becomes a prerequisite. Many fatigue-critical structures are usually subjected to variable amplitude (VA) loading condition. The fatigue analysis in this case has to encounter high nonlinear mechanisms of damage accumulation. An appropriate solution to the interaction effects in crack propagation process under VA loading is necessary and valuable.

Many references have focused to evaluate the interaction effects and further predict the fatigue crack growth under complex loading condition [1–4]. Wheeler and Willenborg et al. state that the yield zone size correlates with the fatigue crack growth rate [5, 6]. Afterwards, the forward and reverse plastic zone interaction is considered to be an essential characteristic of load sequence effects [7, 8]. Based on this hypothesis, Zhang et al. introduced a novel parameter, da/dS, to define the fatigue crack propagation rate with the stress variation at any moment of a cycle [7]. Furthermore, Zhang derived the relationship between da/dS and the traditional da/dN parameter that represented the fatigue crack growth rate per cycle. Lu and Liu proposed a small time scale fatigue crack growth model, in which the incremental crack growth kinetics was calculated [8]. Zhang and Liu stated that the crack-tip opening displacement (CTOD) is the driving parameter of fatigue crack growth and developed a time-based formulation [9]. Nevertheless, the computation results in the internal of a cycle are discontinuous by using these aforementioned methods. The requirement of cycle counting before predicting the fatigue crack growth is inevitable, which leads to the fundamental incapacity to utilize the load sequence information. Sadananda and Vasudevan suggested that the fatigue crack propagation rate is determined by two parameters, the maximum stress intensity factor, Kmax, and the stress intensity factor range, ΔK [10]. Therefore, this paper presents a novel integral formulation of two-parameter model to calculate the continuous fatigue crack propagation process without cycle counting. An equivalent physical state is proposed. It is assumed that the various physical states can be quantized by the several mechanism parameters. This hypothesis is beneficial to characterize the previous loading effects through the measurable physical function. Hence, the fatigue crack growth behavior is simultaneously determined by the current applied loads and the physical state ahead of the crack tip. In this investigation, the driving parameters are designated to be the current loading and the CTOD variation which is under the influence of the plastic-induced crack closure. Based on that, an integral two-parameter fatigue crack growth model is derived in the small spatial and temporal scale. The macroscopic crack propagation behavior under irregular tension-tension loading condition at arbitrary time can be estimated.

The paper is organized in four sections. Firstly, the model in integral form is proposed to calculate the fatigue crack growth rate. Next, the modified crack closure model is reviewed. Especially, the superimposed loading condition is discussed. In addition, Section 3 validates this model by comparison with the experimental data of aluminum alloy under VA loading. Finally, Section 4 summarizes and concludes this investigation.

2. Methodology

2.1. The Integral Fatigue Crack Growth Model

As it is shown in Figure 1, the fatigue crack growth model is derived in the small spatial and temporal scale, which can describe the continuous fatigue propagation process over the time period. For the tension-tension loading condition, it is proven that the crack growth only occurs during the loading process [11]. In the loading path, the crack remains closed initially until the applied stress increases beyond the crack closure level. “Δa” is the crack increment in one cycle. “ΔKeff” represents the effective stress intensity range. “dt” is the arbitrary small-scale time within one cycle; “dK” is the corresponding stress intensity factor range. “da” is the crack increment in “dt,” which represents the transient crack growth. Therefore, the basic fatigue crack growth formulation can be written as an integrated formulation:
(1)
where δa is the crack increment in arbitrary time period, Ki is the initial stress intensity factor, Kf is the final stress intensity factor, Kop is the stress intensity factor of crack closure level, and H is the Heaviside step function.
Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
Schematic illustration of the state-based fatigue crack model.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
Schematic illustration of the state-based fatigue crack model.
From the recent in situ SEM fatigue experiment observations [12, 13], it is revealed that the fatigue crack growth kinetics is highly correlated with CTOD variation under cyclic loadings. The CTOD variation is the fundamental for the fatigue crack growth prediction at any arbitrary time, which is the consequence of the elastic and plastic deformation around the crack tip. The CTOD variation, a function of the effective stress intensity factor range, is a quantity that has a definitude physical significance. Additionally, at present many investigations show that the crack growth is not only determined by the stress intensity factor range ΔK, but also by the maximum stress Kmax [14, 15]. Therefore, the crack increment can be expressed as follows:
(2)
where K is the current stress intensity factor, f(K, CTOD) is a function of the current stress intensity factor and the CTOD variation, and dCTOD is the derivative of CTOD variation. The CTOD variation can be expressed as follows [9]:
(3)
where E is Young’s modulus and σy is the yield strength. The function f(K, ΔCTOD) is the differential form of the two-parameter model, which can be written as follows:
(4)
where C is the material parameter and α and β are the fitting parameters. From (2–4), the fatigue crack increment can be obtained as follows:
(5)
where CI is equal to C/(Eσy), which depends on the material only. The crack increment “da” is substituted into (1), and the fatigue crack growth formulation can be rewritten as follows:
(6)
The general expression of fatigue crack growth can be expressed as follows:
(7)
where “t” is the given time, a0 is the initial crack length, and at is the fatigue crack length at “t”. The power of effective stress intensity factor range (β in the integral model) is the fitting parameters. Many researches show that β = 2 is a reasonable fitting result for aluminum alloy [16, 17].
The proposed model can calculate the continuous crack propagation within one cycle, whereas the cycle-based model is nonfunctional in the internal of the cycle. The general cycle-based two-parameter method can be written as follows [15]:
(8)
where da/dN is the crack increment per cycle and CT, αT, and βT are the material parameters. Similarly, the power of stress intensity factor range (βT in the two-parameter model) is 2.

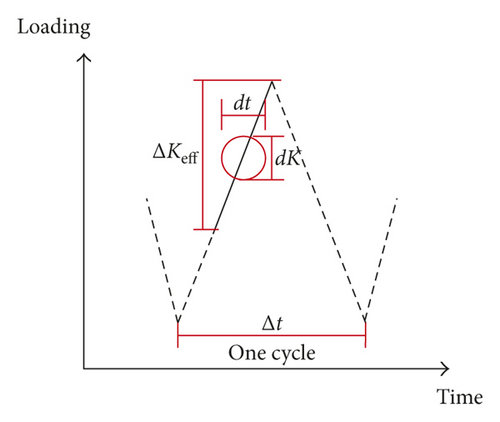
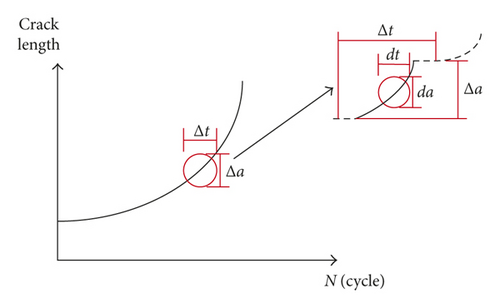
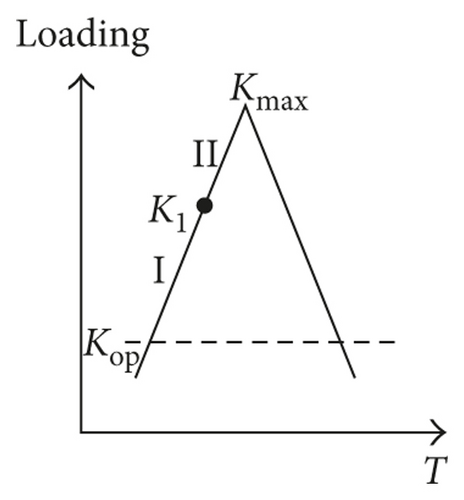
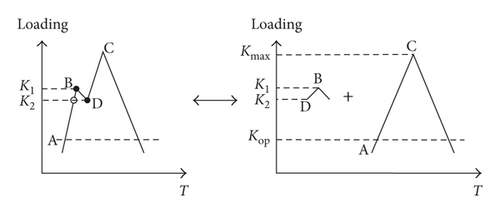
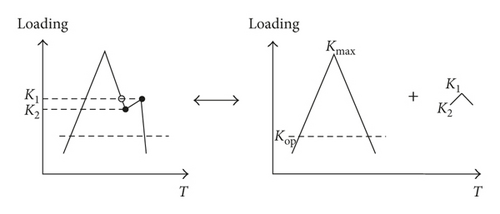
The simplified loading cases are shown in Figure 2. Firstly, the constant amplitude (CA) loading condition is discussed. K1 is the intermediate stage in the loading process. The comparison between the integral model and the traditional two-parameter method is carried out. The crack increments in these two stages can be calculated, as shown in Table 1.

Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
The simplified loading cases. (a) Constant amplitude loading. (b) Superimposed loading condition. (c) Superimposed loading condition.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
The simplified loading cases. (a) Constant amplitude loading. (b) Superimposed loading condition. (c) Superimposed loading condition.
Details are in the caption following the image
Figure 2 (c)
Open in figure viewerPowerPoint
The simplified loading cases. (a) Constant amplitude loading. (b) Superimposed loading condition. (c) Superimposed loading condition.
Table 1. The crack increments in the two stages of loading path.
The integral model The traditional two-parameter model

For both of these two models, if the load level directly increases from Kop to Kmax, the crack growth rates during this cycle can be calculated as shown in Table 2.

Table 2. The crack increments in the whole loading path [15].
The integral model The traditional two-parameter model
Obviously, the equation δaI + δaII = δaCA is satisfied by using the integral model, whereas that is untenable for the cycle-based method. It indicates that the crack increment during continuous loading process only depends on the initial and ultimate state, instead of the calculation path. Moreover, this can be extended to the superimposed loading conditions, as shown in Figures 2(b) and 2(c). For these two cases, the crack growth during these “complex cycles” should be equivalent to that under the small and large cycle. Taking the case (b) for example, δaAB represents the crack increment when the applied stress level increases from A to B, and so on. For the integral model, the following equation can be established:
(9)

Especially, when K2 is infinitely approaching to K1, the crack increment will approximate to that in the CA load cycle. It is manifested that the proposed model can handle the continuous crack growth prediction under the complex loads without cycle counting.

2.2. The Analytical Crack Closure Model

With the purpose of calculating the crack closure level, the analytical model is modified. Since the crack closure is caused by residual plastic deformation, the plastic state due to the preceding large cycles is traced to depict the interaction effect. The equivalent plastic zone concept is introduced, which can be expressed as follows:
(10)
where Deq·i is the equivalent plastic zone size in the ith cycle, di is the current plastic zone size in the ith cycle, and i is the current cycle number. Figure 3 shows the plastic state variation under arbitrary loading sequence case. In the upper plot, the crack length is “a” and high-amplitude load is applied at “t1,” which gives rise to the large plastic zones. When the current load is applied at “t2,” the crack grows to “a” in distance. In the lower plot, the dashed ellipse is the current plastic zone that does not exceed the previous one. Hence, the remaining plastic state will persist to affect the fatigue crack growth at that moment.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Schematic illustration of equivalent plastic zone.

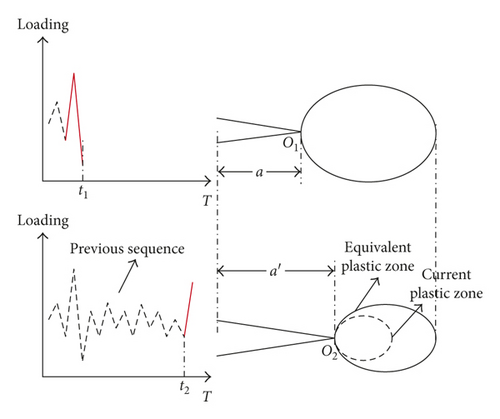
In [12], an analytical crack closure model is developed and verified under CA loading. This model is modified in this paper, and the schematic illustration is shown in Figure 4. The plastic state after the unloading process is shown in the upper plot of Figure 4. There is a reverse plastic zone with dr in diameter ahead of the crack tip “O.” The crack equably closes with length “b.” It is assumed that the crack “annealing” happens once it is fully closed. Therefore, the crack length can be perceived as a − b, and the reverse plastic zone diameter is Dr. The equation Dr = b + dr can be established. In the next loading process, the closed part of crack gradually opens until completes. Eventually, the forward plastic zone is df in diameter. The aforementioned equation can be written as df = Dr − dr.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Schematic illustration of crack closure.
The equivalent plastic zone is substituted, and the hardening is taken into account. Thus, the above equation can be rewritten as follows:
(11)
where γ is the hardening factor that is related to material only and can be obtained by calibration, dm·eq is the equivalent monotonic zone size, σy is the tensile yield strength, and σmin·eq is the equivalent minimum stress level that is calculated based on the reverse plastic state. Solving this equation, the theoretical expression of σop can be achieved:
(12)
where σop is the crack closure level.

3. Model Validation

3.1. Model Validation under Superimposed Loading Condition

The superimposed of high-frequency and low-frequency load cycle condition is one of the most common service environments in many engineering projects. For example, the wing of an aircraft is always subjected to the slow cycle superimposed with faster loads which occurs in turbulent air prominently during the climb and descent period at low altitudes [18]. In order to verify the superiority of the proposed model, the fatigue testing data of Al 7075-T6 under this condition is employed [9]. The yield strength of operational Al 7075-T6 is σy = 520 MPa. The specimens used in this experiment are made of 40 mm wide and 4.7 mm thick, as shown in Figure 5. The initial crack length is 11.3 mm. Zhang and Liu provide the geometric factor algorithm of the stress intensity factor [9]:
(13)
where η = a/w in which w is the width of specimen. Figure 6 shows the applicable loading conditions in detail. The low-frequency baseline loading is CA load with the maximum tensile force Pmax = 2000 N, R = 0.1. Five different specimens were used as the control group. The two high-frequency loads are 20% and 10% of the maximum load level, respectively. Three different specimens were used for each of these two superimposed loads.
Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
Geometry of CT specimen and precracked specimen.
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
Geometry of CT specimen and precracked specimen.
Details are in the caption following the image
Figure 6 (a)
Open in figure viewerPowerPoint
Applicable loading conditions: (a) baseline; (b) 10% low ratio; (c) 20% high ratio; (d) superimposed loading with 10% low ratio; (e) superimposed loading with 20% high ratio.
Details are in the caption following the image
Figure 6 (b)
Open in figure viewerPowerPoint
Applicable loading conditions: (a) baseline; (b) 10% low ratio; (c) 20% high ratio; (d) superimposed loading with 10% low ratio; (e) superimposed loading with 20% high ratio.
Details are in the caption following the image
Figure 6 (c)
Open in figure viewerPowerPoint
Applicable loading conditions: (a) baseline; (b) 10% low ratio; (c) 20% high ratio; (d) superimposed loading with 10% low ratio; (e) superimposed loading with 20% high ratio.
Details are in the caption following the image
Figure 6 (d)
Open in figure viewerPowerPoint
Applicable loading conditions: (a) baseline; (b) 10% low ratio; (c) 20% high ratio; (d) superimposed loading with 10% low ratio; (e) superimposed loading with 20% high ratio.
Details are in the caption following the image
Figure 6 (e)
Open in figure viewerPowerPoint
Applicable loading conditions: (a) baseline; (b) 10% low ratio; (c) 20% high ratio; (d) superimposed loading with 10% low ratio; (e) superimposed loading with 20% high ratio.

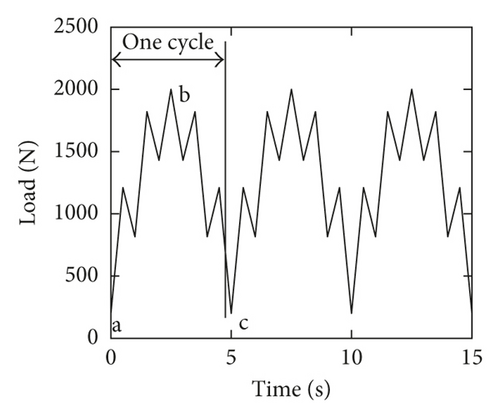
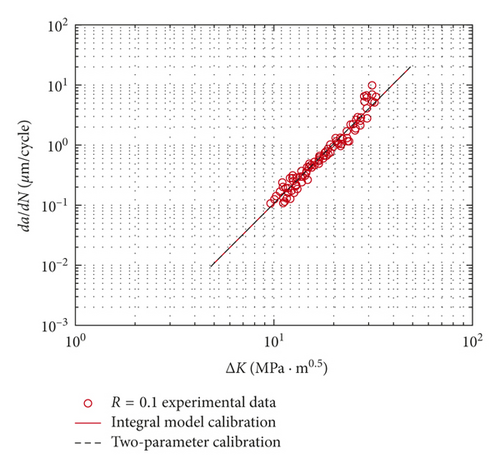
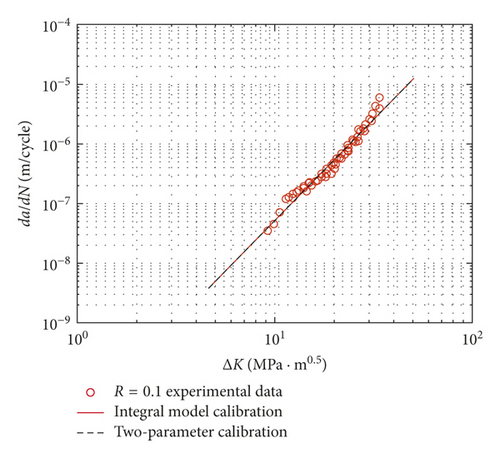
There are several unknown parameters in the fatigue crack growth formulation (6) and (8). The da/dN-ΔK testing data under baseline loading are employed to identify these calibration parameters [9], as shown in Figure 7. The calibration curves of these two models are coincident. The results are CI = 1.3469e − 10, α = 1.3268, and γ = 0.95 for the integral model, and CT = 4.5832e − 11 and mT = 3.3268 for the two-parameter method.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
da/dN-ΔK calibration of Al 7075-T6.

Taking the high ratio loading condition (Figure 6(e)) as an example, the comparison between the integral model and the two-parameter method is shown in Table 3.

Table 3. The crack increments in the whole loading path.
The loading path The integral model The traditional two-parameter model
image

The comparison between the proposed model and the traditional method is also shown in Figure 8. Under the baseline condition, the predicted a-N curves of these two models coincide with each other. The reason is that the integral model is equivalent to the two-parameter method under constant amplitude loading. Nevertheless, in the superimposed loading cases, the predictions of the traditional approach are slower than the baseline results, which is inconsistent with the experiment observation. It is noted that the integral approach can give the better predictions. The proposed model is verified to be appropriate under the superimposed loading condition. It is clear that the interaction effects can be evaluated well.

Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
a-N curves for superimposed loading condition.

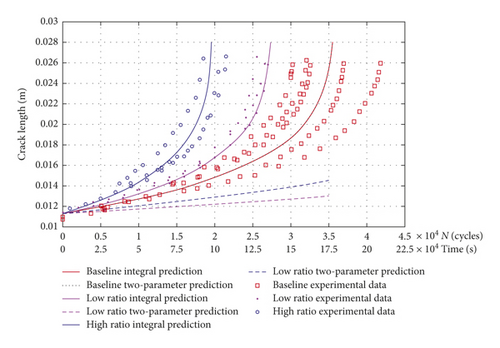
It is natural that the crack-tip damage occurs because of the current loading and the loading history and does not depend upon future loading, in the cycle-counting algorithm [19]. In these cases, as shown in Figure 6(e), when the applied load reaches to the point b, the large cycle cannot be identified without the future loading (point c). Hence, the traditional two-parameter approach is unable to calculate the fatigue crack growth under superimposed loading conditions, whereas the integral model is functional.

3.2. Model Validation under Variable Amplitude Loading

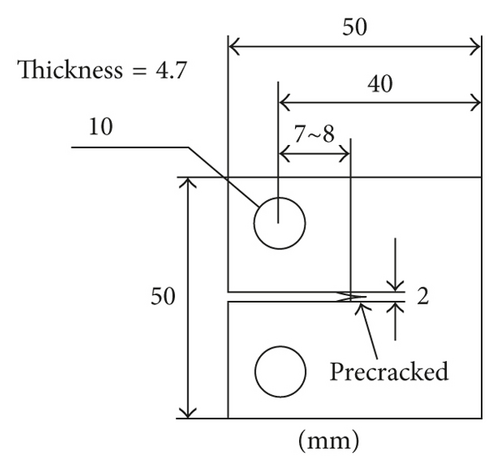
McMillan and Pelloux collected the fatigue testing data on the Al 2024-T3 specimen with center through crack under complex VA loading [20]. The specimens geometry parameters are as follows: width = 229 mm, length = 610 mm, and thickness = 4.1 mm. Two types of spectrum are discussed in this section. Two kinds of the Al 2024-T3 composition are used, and the materials mechanism properties are ultimate strength σult = 473.3 MPa and yield strength σy = 327.9 MPa.

One set of da/dN-ΔK testing data under CA loading (R = 0.1) are employed to calibrate the fitting parameters, as shown in Figure 9 [21]. The calibration results are CI = 6.6619e − 11, α = 1.3874, and γ = 0.9 for the integral model, and CT = 2.1283e − 11 and mT = 3.3874 for the two-parameter model. Good agreements are observed, which proved that the calibration results are available.

Details are in the caption following the image
Figure 9
Open in figure viewerPowerPoint
da/dN-ΔK calibration of Al2024-T6.

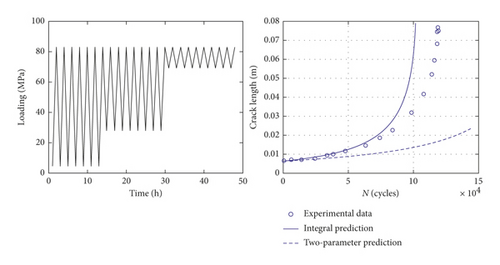
For the constant loading condition, the integral model is equivalent to the two-parameter method, so the predictions of these two approaches are the same. In this section, six types of VA loading condition are used to further validate the proposed model. These spectra and the corresponding prediction results are shown in Figure 10. Taking spectrum 1 as an example, the comparison between the integral model and the two-parameter method is shown in Table 4. For the variable loading case, the calculation results between these two models are obviously different. As it is shown in Figure 10, there is little difference between the first two spectra (spectrum 1 and 2). The reason might be that the crack closure level is stable and almost the same. Thus, the interaction effects under these two cases have no obvious difference, and the predicted a-N curves approximately coincide with each other. It is indicated that the proposed model is able to depict the interaction effects well and give the better predictions than the two-parameter method. In general, the results of the proposed model can match the testing data better.

Details are in the caption following the image
Figure 10 (a)
Open in figure viewerPowerPoint
a-N curves under VA loading. (a) Spectrum 1, (b) spectrum 2, (c) spectrum 3, (d) spectrum 4, (e) spectrum 5, and (f) spectrum 6.
Details are in the caption following the image
Figure 10 (b)
Open in figure viewerPowerPoint
a-N curves under VA loading. (a) Spectrum 1, (b) spectrum 2, (c) spectrum 3, (d) spectrum 4, (e) spectrum 5, and (f) spectrum 6.
Details are in the caption following the image
Figure 10 (c)
Open in figure viewerPowerPoint
a-N curves under VA loading. (a) Spectrum 1, (b) spectrum 2, (c) spectrum 3, (d) spectrum 4, (e) spectrum 5, and (f) spectrum 6.
Details are in the caption following the image
Figure 10 (d)
Open in figure viewerPowerPoint
a-N curves under VA loading. (a) Spectrum 1, (b) spectrum 2, (c) spectrum 3, (d) spectrum 4, (e) spectrum 5, and (f) spectrum 6.
Details are in the caption following the image
Figure 10 (e)
Open in figure viewerPowerPoint
a-N curves under VA loading. (a) Spectrum 1, (b) spectrum 2, (c) spectrum 3, (d) spectrum 4, (e) spectrum 5, and (f) spectrum 6.
Details are in the caption following the image
Figure 10 (f)
Open in figure viewerPowerPoint
a-N curves under VA loading. (a) Spectrum 1, (b) spectrum 2, (c) spectrum 3, (d) spectrum 4, (e) spectrum 5, and (f) spectrum 6.
Table 4. The crack length in the loading path.
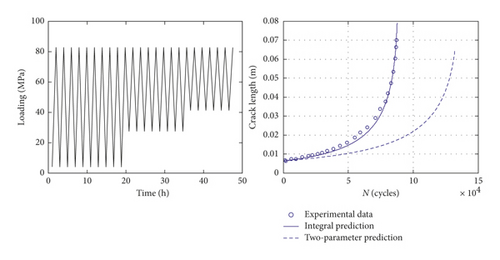
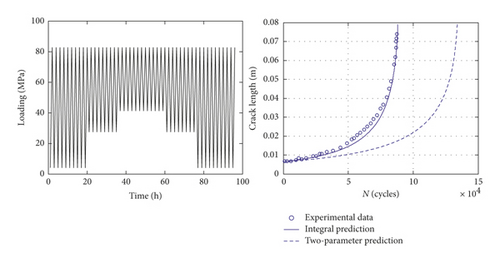
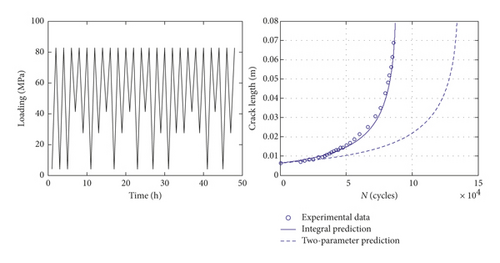
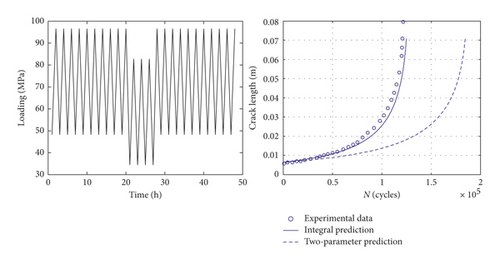
The loading path The integral model The traditional two-parameter model
image

4. Conclusions

In this paper, an integral fatigue crack growth model is proposed. Based on the current investigation, several conclusions can be drawn.

This approach is a general form of the traditional model. One advantage of the proposed model is that it can calculate the fatigue crack propagation under VA loading without cycle counting. Another advantage is that it can be used for fatigue analysis at arbitrary time periods and scales. In general, the model validation shows overall good agreements between the predictions and testing data under CA/VA loading cases. The interaction effects can be described well by considering the plasticity-induced crack closure. Furthermore, a typical loading condition is used to validate this model, which is the superimposed of the high-frequency small load cycles and low-frequency baseline. In this case, the proposed model can calculate the continuous crack propagation, while the traditional two-parameter approach is not proper functional.

Nomenclature

  • δa:
  • Crack increment in arbitrary time period
  • Δt:
  • Time of one cycle
  • Δa:
  • Crack increment in one cycle
  • a:
  • Crack length
  • da:
  • Infinitesimal crack increment
  • σmin, σmax:
  • Minimum and maximum stress in one loading cycle
  • σop:
  • Stress level at which the crack begins to grow
  • Kmax, Kmin:
  • Maximum/minimum stress intensity factor
  • ΔK:
  • Stress intensity factor range
  • Kop:
  • Stress intensity factor at which the crack begins to grow
  • CI, ress:
  • Material parameters in the integral model
  • CT, αT, βT:
  • Material parameters in the two-parameter model
  • Deq:
  • Equivalent plastic zone size
  • Dm:
  • Monotonic plastic zone size
  • df:
  • Forward plastic zone size
  • dr, Dr:
  • Reverse plastic zone size
  • σy:
  • Material yield strength
  • Y:
  • Geometry factor of the stress intensity factor.

    • Conflicts of Interest

    The authors declare no conflicts of interest.

    Acknowledgments

    This work was supported by the National Natural Science Foundation of China (grant no. 51405009) and the Academic Excellence Foundation of BUAA for PhD Students.

        The full text of this article hosted at iucr.org is unavailable due to technical difficulties.