The Riemann solutions of a deposition model are shown. A singular flux-function limit of the obtained Riemann solutions is considered. As a result, it is shown that the Riemann solutions of the deposition model just converge to the Riemann solutions of the limit system, the scalar conservation law with a linear flux function involving discontinuous coefficient. Especially, for some initial data, the two-shock Riemann solution of the deposition model tends to the delta-shock Riemann solution of the limit system; by contrast, for some initial data, the two-rarefaction-wave Riemann solution of the deposition model tends to the vacuum Riemann solution of the limit system. Some numerical results exhibiting the formation processes of delta-shocks and vacuum states are presented.

1. Introduction

Consider the following deposition model of conservation laws:

(1)

where v⩾0 denotes the density of the population performing the deposition, u = −∂_xh(x, t) with h(x, t) being the deposition height, and ϵ is a positive parameter. The first equation describes the conservation of total population. The second one is derived from the rules governing the time evolution of the deposition system: the deposition rate is proportional to the density of the population, and the population is driven by a velocity field proportional to the negative gradient of height. It was also derived as a decent hydrodynamic limit of some systems of interacting particles with two conserved quantities [1, 2]. This system can also describe the macroscopic behaviors of some (so-called chemotactic) bacterial populations, which are attracted by a chemical substrate [3–5].

The first task of this paper is to solve the Riemann problem, one of the fundamental problems associated with nonlinear hyperbolic conservation laws, for (1) with initial data

(2)

where v_± > 0. System (1) is nonstrictly hyperbolic, and both characteristic fields are genuinely nonlinear. The elementary waves include shocks and rarefaction waves. By the analysis method in phase plane, the unique global Riemann solution is constructed with five different kinds of structures containing shock(s) and/or rarefaction wave(s).

As ϵ → 0⁺, system (1) formally becomes

(3)

which can be rewritten in the form of scalar conservation law with a linear flux function involving discontinuous coefficient

(4)

The scalar hyperbolic conservation laws with the discontinuous flux functions arise in many areas, such as the continuous sedimentation of solid particles in a liquid, the two-phase flow in porous media, and the traffic flow theory. System (3) has been studied very extensively; for example, see [6–8] and the references cited therein. It has been shown that delta-shocks and vacuum states do occur in the Riemann solutions of (3).

Let us recall some knowledge with respect to delta-shocks and vacuum states. Delta-shocks are an important kind of nonclassical wave for systems of conservation laws. Mathematically, they are characterized by the delta functions appearing in the state variables. Physically, they can describe the concentration phenomenon. As for delta-shocks, see [9–18]. The other extreme situation is the vacuum state. It describes the cavitation phenomenon. Recently, the phenomena of concentration and cavitation and the formation of delta-shock and vacuum state have attracted wide attention from researchers. For example, Li [19] and Chen and Liu [20, 21] discussed this topic by considering the vanishing pressure limits of solutions of the isentropic and nonisentropic Euler equations. With respect to this topic, also see [22–24].

The second task of this paper is to study the behaviors of solutions of system (1) as the flux ϵv vanishes (i.e., ϵ → 0⁺) by the Riemann problem. We are especially concerned with the phenomena of concentration and cavitation and the formation of delta-shocks and vacuum states in the limit. As a result, we rigorously show that as ϵ → 0⁺, the Riemann solutions of (1) just converge to the Riemann solutions of (3) with the same initial data. Especially, when u₊ ⩽ 0 ⩽ u₋, the two-shock solution of (1) and (2) tends to the delta-shock solution of (3) and (2), where the intermediate density between the two shocks tends to a weighted δ-measure which forms the delta-shock; by contrast, when u₊⩾0⩾u₋, the two-rarefaction-wave solution of (1) and (2) tends to the two-contact-discontinuity solution of (3) and (2), in which the nonvacuum intermediate state between the two rarefaction waves tends to a vacuum state. It can also be seen that such a flux-function limit may be very singular: the limit functions of solutions are no longer in the spaces of functions BV or L^∞, and the space of Radon measures is a natural space in order to deal with such a limit.

The rest of the paper is organized as follows. In Section 2, we recall the Riemann problem for system (3). In Section 3, we solve the Riemann problem for (1) by the analysis method in phase plane. Sections 4 and 5 are devoted to the studies of the limits of solutions of the Riemann problem for (1) as ϵ → 0⁺. In Section 6, we present some numerical results to examine the formation processes of delta-shocks and vacuum states as ϵ decreases. Finally, we give the conclusions in Section 7.

2. Solutions of the Riemann Problem for (3)

In this section, we briefly recall the Riemann problem for (3) with initial data (2), for which we also refer the readers to the papers [6, 7]. The characteristic roots of (3) are λ₁(u, v) = 0 and λ₂(u, v) = u, and the corresponding right characteristic vectors are and , respectively. They satisfy , where, in what follows, ∇ = (∂/∂u, ∂/∂v) is the gradient operator. Therefore, (3) is nonstrictly hyperbolic because of λ₁ = λ₂ at u = 0, and λ_i (i = 1,2) is linearly degenerate.

Since the equations and the Riemann initial data are invariant under uniform stretching of coordinates (x, t)→(βx, βt) (β > 0), we consider the self-similar solutions (u, v)(x, t) = (u, v)(ξ), where ξ = x/t. Then this Riemann problem turns into

(5)

This is a two-point boundary value problem of first-order ordinary differential equations with the boundary values in the infinity.

Besides the constant states and the vacuum states (v ≡ 0), the self-similar wave (u, v)(ξ) (ξ = x/t) of the first family is a standing wave discontinuity

(6)

and that of the second family is a contact discontinuity

(7)

where the indices l and r denote the left and right states, respectively.

Using the above waves, by the analysis in phase plane, one can construct the solutions of Riemann problem (3) and (2) in the following cases.

(1)
When u₋ > 0, u₊ > 0, the solution is SW + J:
(8)
(2)
When u₋ < 0, u₊ < 0, the solution is J + SW:
(9)
(3)
When u₋ ⩽ 0 ⩽ u₊, the solution is J + Vac + J:
(10)

However, for the case u₊ ⩽ 0 ⩽ u₋, the singularity cannot be a jump with finite amplitude; that is, there is no solution which is piecewise smooth and bounded. Hence a solution containing a weighted δ-measure (i.e., delta-shock) supported on a line should be introduced in order to establish the existence in a space of measures from the mathematical point of view.

Denote by the space of bounded Borel measures on , then the definition of a measure solution of (3) in can be given as follows.

Definition 1. A pair (u, v)(x, t) is called a measure solution of (3) if it satisfies that

And (3) is satisfied in the measure and distributional senses; that is,

(11)

for all

Remark 2. The continuity conditions in may be used to give an interpretation for (u, v)(x, t) to take on initial values [25].

Definition 3. A two-dimensional weighted delta function w(s)δ_L supported on a smooth curve L parameterized as x = x(s), t = t(s) (c ≤ s ≤ d) is defined by

(12)

for all

We propose to find a solution of (3) of the form

(13)

where u_δ(t), w(t), x(t) ∈ C¹[0, ∞), and (u₁, v₁)(x, t) and (u₂, v₂)(x, t) are respective bounded smooth solutions of (3).

We assert that (13) is a measure solution of (3) if the relation

(14)

is satisfied, where

is the jump of g across the discontinuity with

being the limit value of g on the discontinuity. The proof is similar to that in [11, 17], and we omit it. System (14) is called the generalized Rankine-Hugoniot relation.

In addition, to guarantee uniqueness of solution, we propose the following admissible condition:

(15)

which means that all characteristics on both sides of discontinuity line are not outgoing.

A discontinuity in the form (13) satisfying (14) and (15) will be called a delta-shock, symbolized by δ.

Remark 4. Here the delta-shock is defined as a measure solution just as in [10, 17, 18, 25]. In fact, like [14, 15], it can also be defined as a solution in the sense of distributions, which gives a natural generalization of the classical definition of the weak L^∞-solution and specifies the definition of measure solution.

Remark 5. Here in a delta-shock, we assign u to be u_δ(t) on the discontinuity line. Physically, for instance, in adhesion particle dynamics, the formation of delta-shock can describe the process of the concentration of particles, and such an assignment can be interpreted as the velocity of colliding particles [17].

Now we consider the Riemann problem (3) and (2) for the case u₊ ⩽ 0 ⩽ u₋. At this time, the solution is a delta-shock in the form

(16)

Solving the generalized Rankine-Hugoniot relation (14) under the admissible condition (15) gives

(17)

3. Solutions of the Riemann Problem for (1)

In this section, we solve the Riemann problem for system (1) with initial data (2) and examine the dependence of the Riemann solutions on the parameter ϵ > 0. For (1), the characteristic roots and corresponding right characteristic vectors are

(18)

It is easy to calculate that

(19)

So (1) is nonstrictly hyperbolic because of

as u = v = 0, and both characteristic fields are genuinely nonlinear in virtue of (19).

As usual, we seek the self-similar solutions (u, v)(x, t) = (u, v)(ξ), where ξ = x/t. Then the Riemann problem turns into the two-point boundary value problem

(20)

(21)

For any smooth solution, (20) becomes

(22)

Besides the constant states, the smooth solutions are composed of the backward rarefaction waves

(23)

and the forward rarefaction waves

(24)

For them, we have

(25)

Let (u_l, v_l) and (u_r, v_r) denote the states connected by a rarefaction wave on the left and right sides, respectively. Then the conditions

and

are required for the forward and backward rarefaction waves, respectively. From (25), we have that both forward and backward rarefaction wave should satisfy

(26)

By solving the differential equations in (23) and (24), we further have the backward and forward rarefaction waves as follows:

(27)

For a given state (u_l, v_l), all possible states which can connect to (u_l, v_l) on the right by a backward rarefaction wave must be located on the curve

(28)

For a given state (u_r, v_r), all possible states which can connect to (u_r, v_r) on the left by a forward rarefaction wave must be located on the curve

(29)

It is easy to check that the backward shock curve

is monotonously decreasing and convex, and the forward shock curve

is monotonously increasing and convex. Furthermore,

has the u-axis as the asymptote as K_l > 0 and interacts with the u-axis at

as K_l ⩽ 0, where

(30)

has the u-axis as the asymptote as M_r > 0 and interacts with the u-axis at

as M_r ⩽ 0, where

(31)

Let us turn to the discontinuous solutions. For a bounded discontinuity at x = x(t), the Rankine-Hugoniot relation reads

(32)

where σ = dx/dt, [u] = u_l − u_r with u_l = u(x(t) − 0, t) and u_r = u(x(t) + 0, t), and so forth.

From (32), one easily obtains

(33)

By noticing

(34)

we solve (33) to obtain

(35)

Then we obtain two kinds of discontinuities

(36)

(37)

Notice that the second equations in (36) and (37) are equivalent to

(38)

(39)

respectively.

In order to identity the admissible solutions, the discontinuity (36) associating with λ₁ should satisfy

(40)

while the discontinuity (37) associating with λ₂ should satisfy

(41)

Then one can check that both inequalities (40) and (41) are equivalent to

(42)

The discontinuity (36) with (42) is called a backward shock and symbolized by , and (37) with (42) is called a forward shock and symbolized by .

For a given state (u_l, v_l), all possible states which can connect to (u_l, v_l) on the right by a backward shock must be located on the curve

(43)

For a given state (u_r, v_r), all possible states which can connect to (u_r, v_r) on the left by a forward shock must be located on the curve

(44)

One can check that the backward shock curve

is monotonously decreasing, convex, and lim_u→−∞v = +∞, and the forward shock curve

is monotonously increasing, convex, and lim_u→+∞v = +∞.

Denote and . Then the curve is monotonously decreasing, convex, and lim_u→−∞v = +∞; besides, it has the u-axis as the asymptote as K_l > 0 and interacts with the u-axis at as K_l ⩽ 0. The curve is monotonously increasing, convex, and lim_u→+∞v = +∞; besides, it has the u-axis as the asymptote as M_r > 0 and interacts with the u-axis at as M_r ⩽ 0.

We can construct the solutions of the Riemann problem by using the standard analysis method in the phase plane [26, 27]. Draw the backward wave curve passing the left state (u₋, v₋) and the forward wave curve passing the right state (u₊, v₊). According to the different locations of the intersection point of and , one can construct the unique global Riemann solution with five different structures as follows:

(i) a backward rarefaction wave + nonvacuum intermediate state + a forward rarefaction wave,

(ii) a backward rarefaction wave + nonvacuum intermediate state + a forward shock,

(iii) a backward shock + nonvacuum intermediate state + a forward rarefaction wave,

(iv) a backward shock + nonvacuum intermediate state + a forward shock,

(v) a backward rarefaction wave + vacuum intermediate state (v ≡ 0) + a forward rarefaction wave.

The conclusion can be stated in the following theorem.

Theorem 6. The Riemann problem for (1) with initial data (2) has a unique piecewise smooth solution consisting of waves of constant states, vacuums, shocks, and rarefaction waves.

4. Limits of Solution of (1) and (2) for u₋ > u₊, u₋v₋ > u₊v₊

In this section, we study the limits of solution of (1) and (2) as ϵ → 0⁺ for the case u₋ > u₊, u₋v₋ > u₊v₊. We especially pay more attention on the phenomenon of concentration and the formation of delta-shocks in the limit.

Lemma 7. If u₋ > u₊, u₋v₋ > u₊v₊, then there exists ϵ₀ > 0 such that for any ϵ < ϵ₀.

Proof. All states (u, v) connected with (u₋, v₋) by S₁ or S₂ satisfy

(45)

(46)

If v₊ = v₋, ϵ₀ may be taken as any real positive number. If v₊ ≠ v₋, we have the conclusion by taking

(47)

The proof is finished.

For fixed ϵ < ϵ₀, let U^ϵ(ξ) denote the two-shock Riemann solution for (1) and (2):

(48)

where (u₋, v₋) and

are connected by a shock

with speed

, and

and (u₊, v₊) are connected by a shock

with speed

(49)

(50)

The following lemmas describe the limit behaviors of the intermediate state and the speeds of two shocks as ϵ → 0⁺.

Lemma 8. is monotonously decreasing with respect to ϵ.

Proof. From (49) and (50), we have the equation with respect to

(51)

For ϵ₁ > ϵ₂, assume

; then we have

, which contradicts with

. Therefore, for ϵ₁ > ϵ₂, we must have

, which gives the conclusion. The proof is complete.

Lemma 9. is monotonously increasing with respect to ϵ.

Proof. For ϵ₁ > ϵ₂, assume ; then we have , which contradicts with . Therefore, for ϵ₁ > ϵ₂, we must have .

Lemma 10. One has

(52)

Proof. When u₋ > u₊ > 0, u₋v₋ > u₊v₊ or 0 > u₋ > u₊, u₋v₋ > u₊v₊, assume ; then from (51), we have

(53)

which is impossible. So when u₋ > u₊ > 0, u₋v₋ > u₊v₊ or 0 > u₋ > u₊, u₋v₋ > u₊v₊, we have

. Then from (51), we can deduce

(54)

which gives the desired conclusions. When u₋⩾0⩾u₊, similarly, there must be

Lemma 11. One has

(55)

Proof. Let . When u₋ > u₊ > 0, u₋v₋ > u₊v₊ or 0 > u₋ > u₊, u₋v₋ > u₊v₊, in virtue of Lemma 10, M = 0 is obvious. When u₋⩾0⩾u₊, from (51), one has

(56)

when M = 0.

Lemma 12. One has

(57)

Proof. From the second equation in (50), we have

(58)

Then the conclusions can be easily obtained by virtue of Lemmas 10 and 11.

Lemma 13. One has

(59)

Proof. Taking

(60)

and the Lemma 11 into account, one can easily get the conclusions.

Let

. Then when u₋ > u₊ > 0, u₋v₋ > u₊v₊,

(61)

where σ₁ = 0, σ₂ = u₊ and v_∗ = u₋v₋/u₊. When 0 > u₋ > u₊, u₋v₋ > u₊v₊,

(62)

σ₁ = u₋, σ₂ = 0, and v_∗ = u₊v₊/u₋. It can be seen that U⁰(ξ) coincides with the Riemann solution for (3) with the same initial data.

For the case u₋⩾0⩾u₊, it has been shown that two shocks will coincide at ξ = 0 as ϵ → 0⁺. Furthermore, for the component u^ϵ(ξ), it has been proven that

(63)

For the component v^ϵ(ξ), we have proven that the intermediate state

becomes infinity as ϵ → 0⁺. Next let us study in more detail the limit behaviors of v^ϵ(ξ).

Lemma 14. One has

(64)

Proof. With (49)–(51), it follows that

(65)

The proof is finished.

Take

such that ϕ(ξ) ≡ ϕ(0) for ξ in a neighborhood Ω of ξ = 0 (ϕ is called a sloping test function). Assume when ϵ < M₀ it holds that

and

. It is well known that solution (48) satisfies the weak formula

(66)

Since

(67)

we have

(68)

where

(69)

Returning to (66), we get

(70)

for all sloping test functions

For an arbitrary

, we take a sloping function ϕ(ξ) such that ϕ(0) = φ(0) and

(71)

We have

(72)

For the first limit on the right side, it follows that

(73)

For the second limit on the right side, it follows that

(74)

which converges to 0 by sending μ → 0 and recalling Lemma 14. Thus we have that

(75)

for all test functions

Let

be a smooth test function, and let

. Then it follows that

(76)

and from (75)

(77)

Combining the two relations above yields

(78)

The last term, by the definition,

(79)

with

(80)

Thus we have the following result.

Theorem 15. Let u₋⩾0⩾u₊, and (u^ϵ(x, t), v^ϵ(x, t)) is the two-shock solution of (1) and (2). Then (u^ϵ(x, t), v^ϵ(x, t)) converges in the sense of distributions. Denote the limit function by U⁰(x, t); then

(81)

where w(t) = (u₋v₋ − u₊v₊)t, which is just the delta-shock Riemann solution of (3).

5. Limits of Solutions of (1) and (2) for u₊⩾0⩾u₋

In this section, we study the limits of solutions of (1) and (2) as ϵ → 0⁺ for the case u₊⩾0⩾u₋ and show the phenomenon of cavitation and the formation of vacuum states in the limit.

Lemma 16. If u₊⩾0⩾u₋, then there exists ϵ₁ > 0 such that for any ϵ < ϵ₁.

Proof. If v₊ = v₋, ϵ₁ may be taken as any real positive number. If v₊ > v₋, ϵ₁ may be taken as the value of ϵ satisfying

(82)

If v₊ < v₋, ϵ₁ may be taken as the value of ϵ satisfying

(83)

The proof is complete.

Let and , which mean and . Denote ϵ₂ = min{ϵ₋, ϵ₊}.

When ϵ₁ > ϵ > ϵ₂, the Riemann solution for (1) and (2) contains two rarefaction waves with a nonvacuum intermediate state. This implies that, for a larger ϵ, no vacuum occurs in the solution.

However, when ϵ decreases so that ϵ ⩽ ϵ₁, the Riemann solution becomes two rarefaction waves with a vacuum intermediate state as follows:

(84)

where

(85)

with

and

(86)

with

. The intermediate states

and

satisfy

(87)

When ϵ → 0⁺, from (87), we have

(88)

then it follows that

(89)

In summary, as ϵ → 0⁺, the limit function U⁰(ξ) = (u, v)(ξ) of U^ϵ(ξ) is

(90)

which is just a solution of (3) and (2) containing a vacuum state that fills up the region formed by the two contact discontinuities ξ = u_±.

In Sections 4 and 5, we have proven that when u₋ > u₊, u₋v₋ > u₊v₊ or u₊⩾0⩾u₋, the limits of solutions of the Riemann problem for (1) just are the solutions of the Riemann problem for (3) with the same initial data. The same conclusions are true for the rest of the cases, and we omit the discussions.

6. Numerical Simulations

To understand the formation processes of delta-shocks and vacuum states in the Riemann solutions of (1) and (2) as the flux ϵv vanishes, we present some representative numerical results. To discretize the system, we employ the Nessyahu-Tadmor scheme [28] with 500 cells and CFL = 0.475.

To simulate the formation process of delta-shocks, we take the initial data as follows:

(91)

The numerical simulations for different choices of ϵ are presented in Figures 1–4.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Velocity and density for ϵ = 0.2 at t = 0.4.

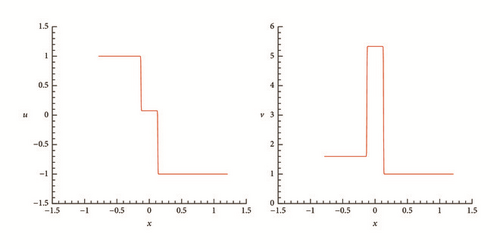
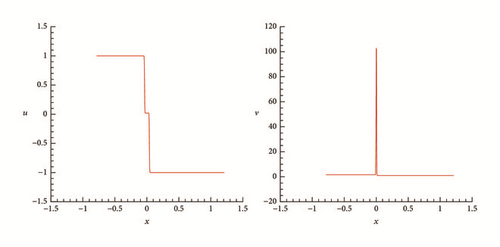
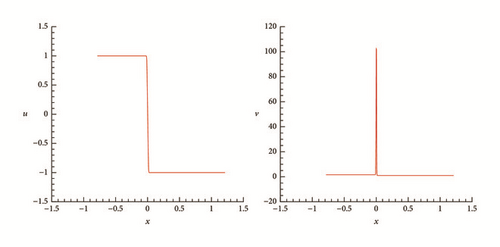
One can observe clearly from these numerical results that, when ϵ decreases, the location of the two shocks becomes closer and closer, and the density of the intermediate state increases dramatically, while the velocity is closer to a step function. The numerical simulations are in complete agreement with the theoretical analysis in Section 4.

To simulate the formation process of vacuum states, we take the initial data as follows:

(92)

The numerical simulations for different choices of ϵ are presented in Figures 5–8.

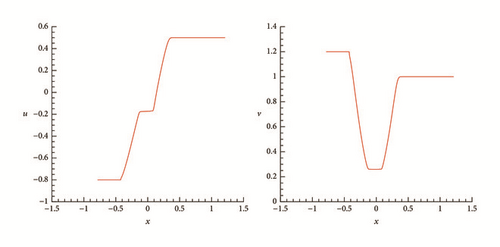
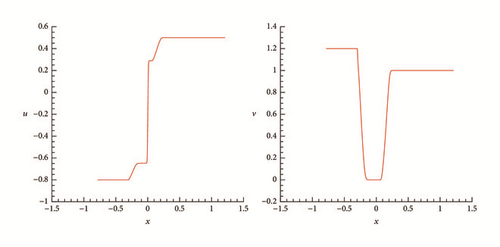
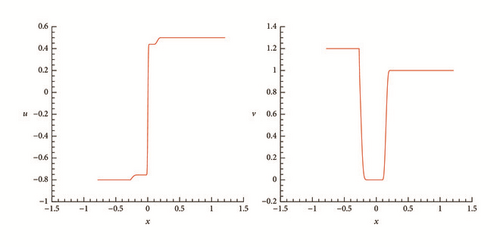
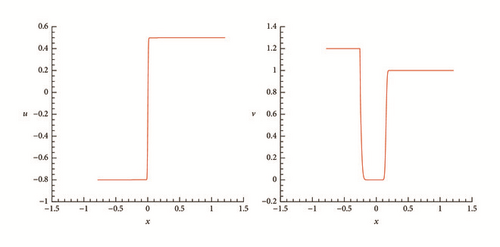
One can see that when ϵ = 0.6, the vacuum does not appear; when ϵ = 0.1, the vacuum appears; when ϵ decreases to zero, the two rarefaction waves become two contact discontinuities. The numerical simulations are also in complete agreement with the theoretical analysis in Section 5.

7. Conclusions and Discussions

In the paper [2], Toth and Valko proposed the model of conservation laws

(93)

where γ and ϵ > 0 are constants. It can describe a deposition/domain growth mechanism. When the term ϵv vanishes, system (93) becomes

(94)

This is a typical model admitting delta-shocks.

In this paper, we consider (93) for the case γ = 0, that is, model (1), which arose in the context of the true self-repelling motion constructed by Toth and Werner [1]. Firstly, we solve the Riemann problem, which is very useful for the understanding of equations because all properties, such as shocks and rarefaction waves, appear as characteristics in the solution. By the analysis method in phase plane, we obtain five kinds of structures of solutions containing shock(s) and/or rarefaction wave(s). Secondly, we consider the flux-function limits of solutions of system (1). We prove that the Riemann solutions of system (1) just converge to the Riemann solutions of the limit system (3). We especially identify and analyze the formation of delta-shocks and vacuum states in the limit.

For (93), the parameter γ is of crucial importance: different values of γ lead to completely different behaviors. One can carry out the investigation similar to that in this paper for some other cases, such as γ = 1 (Leroux equation) and γ = 1/2 (shallow water equation).

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

This work is supported by Applied Basic Research Projects of Yunnan Province (2015FB104).

References

1 Toth B. and Werner W., Hydrodynamic Equation for a Deposition Model, Progress in Probability. (2002) 51, 227–248.
Google Scholar
2 Toth B. and Valko B., Perturbation of singular equilibria of hyperbolic two-component systems: a universal hydrodynamic limit, Communications in Mathematical Physics. (2005) 256, no. 1, 111–157, https://doi.org/10.1007/s00220-005-1314-9, MR2134338.
10.1007/s00220-005-1314-9
Web of Science® Google Scholar
3 Nossal R., Boundary movement of chemotactic bacterial populations, Mathematical Biosciences. (1972) 13, no. 3-4, 397–406, 2-s2.0-0343125630, https://doi.org/10.1016/0025-5564(72)90058-2, Zbl0337.92017.
10.1016/0025-5564(72)90058-2
Google Scholar
4 Rascle M., The riemann problem fora nonlinear non-strictly hyperbolic system arising in biology, Computers & Mathematics with Applications. (1985) 11, no. 1-3, 223–238, 2-s2.0-0346248056, https://doi.org/10.1016/0898-1221(85)90148-8.
10.1016/0898-1221(85)90148-8
Web of Science® Google Scholar
5 Rascle M., On some viscous perturbations of quasi-linear first order hyperbolic systems arising in biology, Nonlinear Partial Differential Equations. (1983) 17, 133–142.
10.1090/conm/017/706094
Google Scholar
6 Hu J., The Riemann problem for a resonant nonlinear system of conservation laws with Dirac-measure solutions, Proceedings of the Royal Society of Edinburgh, Section: A Mathematics. (1998) 128, no. 1, 81–94, https://doi.org/10.1017/S0308210500027165, MR1606345, Zbl0893.35071, 2-s2.0-21944446807.
10.1017/S0308210500027165
Web of Science® Google Scholar
7 Gosse L. and James F., Numerical approximations of one-dimensional linear conservation equations with discontinuous coefficients, Mathematics of Computation. (2000) 69, no. 231, 987–1015, https://doi.org/10.1090/S0025-5718-00-01185-6, MR1670896, Zbl0949.65094, 2-s2.0-0034401759.
10.1090/S0025-5718-00-01185-6
Web of Science® Google Scholar
8 Gallouet T., Hyperbolic equations and systems with discontinunous coefficients of source terms, Proceedings of Equadiff-11, 2005, 105–114.
Google Scholar
9 Tan D. C., Zhang T., and Zheng Y. X., Delta-shock waves as limits of vanishing viscosity for hyperbolic systems of conservation laws, Journal of Differential Equations. (1994) 112, no. 1, 1–32, https://doi.org/10.1006/jdeq.1994.1093, MR1287550, 2-s2.0-0002178812.
10.1006/jdeq.1994.1093
Web of Science® Google Scholar
10 Bouchut F., On zero pressure gas dynamics, Advances in Kinetic Theory and Computing, Series on Advances in Mathematics for Applied Sciences, 1994, 22, World Scientific, River Edge, NJ, USA, 171–190, MR1323183.
10.1142/9789814354165_0006
Google Scholar
11 Sheng W. and Zhang T., The Riemann problem for the transportation equations in gas dynamics, Memoirs of the American Mathematical Society. (1999) 137, no. 654, https://doi.org/10.1090/memo/0654, MR1466909.
10.1090/memo/0654
Web of Science® Google Scholar
12 Le Floch P., An existence and uniqueness result for two nonstrictly hyperbolic systems, Nonlinear Evolution Equations that Change Type, 1990, 27, Springer, New York, NY, USA, 126–138, https://doi.org/10.1007/978-1-4613-9049-7_10, MR1074190, Zbl0727.35083.
10.1007/978-1-4613-9049-7_10
Google Scholar
13 Keyfitz B. L. and Kranzer H. C., A viscosity approximation to a system of conservation laws with no classical Riemann solution, Nonlinear Hyperbolic Problems, 1990, 1402, Springer, Berlin, Germany, 185–197, https://doi.org/10.1007/bfb0083875, MR1033283, Zbl0704.35094.
Google Scholar
14 Danilov V. G. and Shelkovich V. M., Dynamics of propagation and interaction of δ-shock waves in conservation laws systems, Journal of Differential Equations. (2005) 211, no. 2, 333–381, https://doi.org/10.1016/j.jde.2004.12.011, MR2125546.
10.1016/j.jde.2004.12.011
Web of Science® Google Scholar
15 Danilov V. G. and Shelkovich V. M., Delta-shock wave type solution of hyperbolic systems of conservation laws, Quarterly of Applied Mathematics. (2005) 63, no. 3, 401–427, https://doi.org/10.1090/S0033-569X-05-00961-8, MR2169026, 2-s2.0-14844358903.
10.1090/S0033-569X-05-00961-8
Web of Science® Google Scholar
16 Cheng H. and Yang H., Delta shock waves in chromatography equations, Journal of Mathematical Analysis and Applications. (2011) 380, no. 2, 475–485, https://doi.org/10.1016/j.jmaa.2011.04.002, MR2794406, Zbl1217.35120, 2-s2.0-79955048909.
10.1016/j.jmaa.2011.04.002
Web of Science® Google Scholar
17 Li J., Zhang T., and Yang S., The Two-Dimensional Riemann Problem in Gas Dynamics, 1998, 98, Longman, Harlow, England, Pitman Monographs and Surveys in Pure and Applied Mathematics, MR1697999.
Google Scholar
18 Yang H., Riemann problems for a class of coupled hyperbolic systems of conservation laws, Journal of Differential Equations. (1999) 159, no. 2, 447–484, https://doi.org/10.1006/jdeq.1999.3629, MR1730728, Zbl0948.35079, 2-s2.0-0033544732.
10.1006/jdeq.1999.3629
Web of Science® Google Scholar
19 Li J., Note on the compressible Euler equations with zero temperature, Applied Mathematics Letters. (2001) 14, no. 4, 519–523, https://doi.org/10.1016/S0893-9659(00)00187-7, MR1824197, Zbl0986.76079, 2-s2.0-0035340876.
10.1016/S0893-9659(00)00187-7
Web of Science® Google Scholar
20 Chen G.-Q. and Liu H., Formation of delta-shocks and vacuum states in the vanishing pressure limit of solutions to the isentropic Euler equations, SIAM Journal on Mathematical Analysis. (2003) 34, no. 4, 925–938, https://doi.org/10.1137/S0036141001399350, MR1969608.
10.1137/S0036141001399350
Web of Science® Google Scholar
21 Chen G.-Q. and Liu H., Concentration and cavitation in the vanishing pressure limit of solutions to the Euler equations for nonisentropic fluids, Physica D: Nonlinear Phenomena. (2004) 189, no. 1-2, 141–165, https://doi.org/10.1016/j.physd.2003.09.039, MR2044721, Zbl1098.76603, 2-s2.0-0842278905.
10.1016/j.physd.2003.09.039
Web of Science® Google Scholar
22 Yin G. and Sheng W., Delta shocks and vacuum states in vanishing pressure limits of solutions to the relativistic Euler equations for polytropic gases, Journal of Mathematical Analysis and Applications. (2009) 355, no. 2, 594–605, https://doi.org/10.1016/j.jmaa.2009.01.075, MR2521736, 2-s2.0-62549142645.
10.1016/j.jmaa.2009.01.075
Web of Science® Google Scholar
23 Yin G. and Sheng W., Delta wave formation and vacuum state in vanishing pressure limit for system of conservation laws to relativistic fluid dynamics, Zamm Journal of Applied Mathematics & Mechanics. (2013) 95, 49–65.
10.1002/zamm.201200148
Web of Science® Google Scholar
24 Mitrovic D. and Nedeljkov M., Delta shock waves as a limit of shock waves, Journal of Hyperbolic Differential Equations. (2007) 4, no. 4, 1–25, https://doi.org/10.1142/S021989160700129X, MR2374219.
10.1142/S021989160700129X
Web of Science® Google Scholar
25 Zheng Y., Systems of conservation laws with incomplete sets of eigenvectors everywhere, Advances in Nonlinear Partial Differential Equations & Related Areas. (1998) Zbl0929.35089.
10.1142/9789812815811_0023
Google Scholar
26 Chang T. and Hsiao L., The Riemann Problem and Interaction of Waves in Gas Dynamics, 1989, Longman Scientific & Technical.
Google Scholar
27 Zheng Y., Systems of Conservation Laws: Two-Dimensional Riemann Problems, 2001, Birkhauser.
10.1007/978-1-4612-0141-0
Google Scholar
28 Nessyahu H. and Tadmor E., Nonoscillatory central differencing for hyperbolic conservation laws, Journal of Computational Physics. (1990) 87, no. 2, 408–463, https://doi.org/10.1016/0021-9991(90)90260-8, MR1047564, 2-s2.0-28144455569.
10.1016/0021-9991(90)90260-8
Web of Science® Google Scholar

All articles

A Deposition Model: Riemann Problem and Flux-Function Limits of Solutions

Abstract

1. Introduction

2. Solutions of the Riemann Problem for (3)

3. Solutions of the Riemann Problem for (1)

4. Limits of Solution of (1) and (2) for u₋ > u₊, u₋v₋ > u₊v₊

5. Limits of Solutions of (1) and (2) for u₊⩾0⩾u₋

6. Numerical Simulations

7. Conclusions and Discussions

Conflicts of Interest

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Deposition Model: Riemann Problem and Flux-Function Limits of Solutions

Abstract

1. Introduction

2. Solutions of the Riemann Problem for (3)

3. Solutions of the Riemann Problem for (1)

4. Limits of Solution of (1) and (2) for u− > u+, u−v− > u+v+

5. Limits of Solutions of (1) and (2) for u+⩾0⩾u−

6. Numerical Simulations

7. Conclusions and Discussions

Conflicts of Interest

Acknowledgments

References

Figures

References

Related

Information

4. Limits of Solution of (1) and (2) for u₋ > u₊, u₋v₋ > u₊v₊

5. Limits of Solutions of (1) and (2) for u₊⩾0⩾u₋