This paper is devoted to introduce a novel method of the operational matrix of integration for Legendre wavelets in order to predict the thermal behavior of stratospheric balloons on float at high altitude in the stratosphere. Radiative and convective heat transfer models are also developed to calculate absorption and emission heat of the balloon film and lifting gas within the balloon. Thermal equilibrium equations (TEE) for the balloon system at daytime and nighttime are shown to predict the thermal behavior of stratospheric balloons. The properties of Legendre wavelets are used to reduce the TEE to a nonlinear system of algebraic equations which is solved by using a suitable numerical method. The approximations of the thermal behavior of the balloon film and lifting gas within the balloon are derived. The diurnal variations of the film and lifting gas temperature at float conditions are investigated, and the efficiency of the proposed method is also confirmed.

1. Introduction

Stratospheric balloons or airships have been paid attention since they can provide persistent observation platforms by keeping on station at an altitude about 20~30 km for a long time. They have some potential advantages, such as station keeping, long endurance, low cost, broadcasting, and telecommunication relay [1–3]. When the balloons stay at an altitude about 20~30 km, they should be filled with a huge gas volume of several hundred thousand cubic meters. Even a small temperature variation between the inner gas and the outer environment can lead to a huge buoyancy difference. So the thermal behavior of the stratospheric balloon should have attracted some interest from all over the world [4, 5].

It is important to predict the thermal behavior of the stratospheric balloon before it launches. Understanding the temperature variation of the stratospheric balloon will be helpful for balloon design and flight prediction. During the research of the thermal behavior of the stratospheric balloon, the average film and lifting gas temperature are the main focus. Carlson et al. [6] studied the trajectory and thermal behavior of the high-altitude balloons. Stefan [5] used a two-node model to solve the day-night airship temperature numerically. Farley [7] established a code to calculate the ascent and float thermal behavior of the stratospheric balloon. Dai et al. [8] developed a simulation program to investigate the thermal performance of a super pressure balloon by using the thermal models and dynamic models. Yao et al. [9] proposed a multinode heat transient model for stratospheric airships to predict the thermal behaviors of the ascent and descent processes. In these articles, the thermal models are established for different conditions. The thermal performance of the film and lifting gas can be obtained by solving TEE. The main method to solve these equations is discrete collocation method. The computation efficiency is low when the number of surface elements of film are very large.

In this paper, we adopt the thermal models given by Xia et al. [10] and present a novel technique to solve the TEE. The thermal performance of the film and lifting gas will be got by applying the method to solve the TEE. The method is based on Legendre wavelet integration operational matrix method. In the proposed method, the TEE is reduced to a system of nonlinear algebraic equations, which can be solved easily. The proposed method is of high computing efficiency and simple operation.

2. Thermal Model

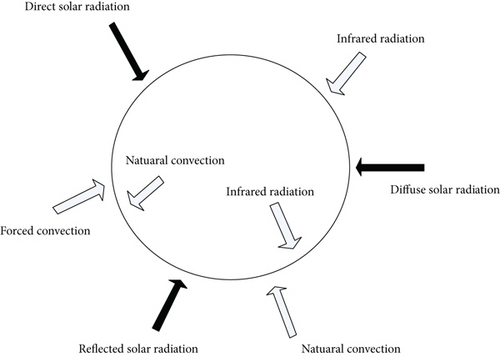
In this section, the same thermal environment and assumptions of the stratospheric balloon shown in [11, 12] will be considered. The thermal environment (shown in Figure 1) of the high-altitude stratospheric balloon includes infrared radiation, solar radiation, and convection. The balloon film is so thin that the conductive resistance can be neglected.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Thermal environment of a stratosphere balloon.

The transient temperature distribution of the film is expressed by the following [10]:

(1)

where δ_t, ρ, and c are the film thickness, density, and specific heat, respectively. h_ex and h_in are the convective heat transfer coefficients for the external and internal surfaces of the film. T, T_a, and T_g are the film temperature, atmosphere temperature, and lifting gas temperature, respectively. q_i(i = 1, 2, and 3) are the absorbed direct solar radiation, the absorbed diffuse solar radiation, and the absorbed reflected solar radiation. ε_ex and ε_in are the external and internal emissivities of the film. α_in denotes the internal absorptivity. G is the total irradiation falling on the film. σ is the Stefan Boltzmann constant.

The total irradiation G at the internal film segment

can be obtained by the following:

(2)

where F_i,k is the angle factor from element i to element k. M_s is the total number of surface elements of the balloon. J_k is the infrared radiation away from the internal surface, and it can be calculated as follows:

(3)

Then the average temperature of the lifting gas is written in the following equation [8]:

(4)

where c_g is the specific heat. m_g is mass of the lifting gas.

2.1. Atmosphere Model

The relation between the atmosphere temperature, pressure, and the altitude are given by the following [13]:

(5)

where H is the altitude of the balloon.

2.2. Solar Position and Solar Radiation Models

Before we introduce the solar radiation models, the computational method of solar position should be given as follows.

Suppose that η denotes the solar altitude angle and ψ denotes the solar azimuth angle, then we have the solar direction vector

(6)

The solar altitude angle η and the solar azimuth angle ψ can be expressed by the following [14]:

(7)

where ϕ is the local latitude, δ is the declination of the sun, and ω is the hour angle of the sun. They are defined as

(8)

where Γ is solar day angle and E_t is the value of time correction. The calculate method will be

(9)

where d_n is the day of the year.

The absorbed direct solar radiation heat flux is shown as [15]

(10)

where δ_s is the index which considers the self-shadowing and δ_s = 1 is the direct solar radiation; otherwise, δ_s = 0. α_s is the solar absorptivity of the external surface. τ_s is the atmosphere transmissivity. E_s = 1353 W/m² is the solar constant. β is the included angle between the solar radiation and surface external normal.

The absorbed diffuse and reflected solar radiation heat flux is written as [16]

(11)

where γ is the empirical diffuse coefficient. ρ_e is the Earth’s reflectivity. F_e is the angle factor between the film and the Earth.

The infrared radiation heat flux from the Earth and atmosphere can be given by [16]

(12)

where α_ex is the absorptivity of the external surface in the infrared spectrum. τ_atm is the transmissivity of the atmosphere in the infrared spectrum. q_e is the Earth’s atmosphere infrared flux.

2.3. Convective Heat Transfer Coefficient Models

Convective heat transfer happens to both inner and external surfaces of the balloon hull. For the inner surface, the heat convection is usually considered as a natural convection. For the external surface, the heat convection is either a forced one or natural one. It depends on the relative speed of the balloon and the atmosphere characteristic. According to the theory of Leland and Walter [17], the convective heat transfer coefficients for both inner and external surfaces are calculated by

(13)

where Nu is the Nusselt number, λ is the thermal conductivity of the gas, and L is the length of the balloon.

For the inner surface, the Nusselt number Nu is

(14)

For the external surface, natural convection case, Nusselt number Nu is

(15)

For the external surface, forced one, Nusselt number Nu is

(16)

where Ra is Rayleigh number and Re is Reynolds number. They can be obtained by

(17)

where Gr is the Grashof number, Pr is Prandtl number, g_n is the gravitational acceleration, ξ and υ are the coefficient of thermal expansion and the kinematic viscosity, respectively, ΔT is the temperature difference between the surface and the gas, and V is the airspeed of the balloon. The kinematic viscosity υ can be got as follows:

(18)

where μ is the dynamic viscosity. The computational method of these parameters (λ, μ, and Pr) for helium and air will be found in [18].

3. Legendre Wavelets and Their Properties

The Legendre wavelet polynomials are defined on the interval [0, 1) as [19]

(19)

where k = 1, 2, …,

, n = 1, 2, …, 2^k−1, m = 0, 1, …, M − 1 is the degree of the Legendre polynomials and M is a fixed positive integer, and P_m(t) are the Legendre polynomials of degree m.

For any function T(t) ∈ L²[0, 1) may be expressed by the Legendre wavelets as follows:

(20)

where c_nm = 〈T(t), ψ_nm(t)〉 are the Legendre wavelet coefficients and 〈, 〉 is the inner product of T(t) and ψ_nm(t).

If (20) is truncated, then it can be rewritten as

(21)

where C and Ψ(x) are

column vectors, given by

(22)

We can also rewrite (21) as

(23)

where c_i = c_nm and ψ_i = ψ_nm. The index i is determined by the relation i = M(n − 1) + m + 1. Then, we have

(24)

(25)

To illustrate the effectiveness of (23), we have shown the theorem as follows.

Theorem 1. Suppose that the function obtained by using Legendre wavelets is the approximation of T(t) and T(t) is with bounded second derivative, say ; then the series converges uniformly to the function T(t); that is,

(26)

Proof. See [20].

Next, we will derive the operational matrix of integration of Legendre wavelets. In order to do this, another basis set of Block pulse functions should be considered as follows [21]:

(27)

with a positive integer value for

and

Let

. Suppose that

(28)

where J is called the Block pulse operational matrix of integration [21] and

(29)

The Legendre wavelets may be expanded into an m term Block pulse function as

(30)

where

, and

The integration of the vector function Ψ(t) can be expressed as

(31)

where P is the operational matrix of integration. It is known (see [22]) that the matrix P can be approximated by

(32)

Then we have

(33)

The integrations of the function e^t and sint are selected to verify the effectiveness of matrix P. The integrations of e^t and sint are obtained as follows and . Take , the results are shown in Figure 2 and Figure 3, respectively.

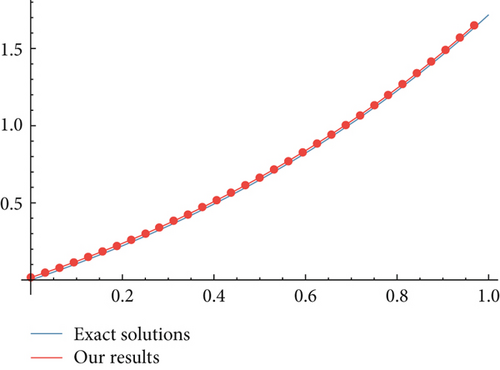
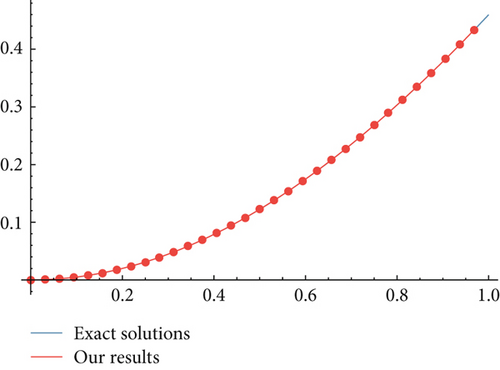
From Figure 2 and Figure 3, we can find that the matrix P is very credible to calculate the integration of any functions.

4. Solution Procedure for TEE (1) and (4)

In this section, the proposed method based on the Legendre wavelet expansion together with their operational matrices of integration to obtain numerical solutions of the TEE (1) and (4) is described. To obtain such numerical approximate solution, we apply the following steps:

(1)
Let , then , .
(2)
Express on and in the following form:
(34)

(35)
where and are unknown vector and is the vector which is defined in (25). By using initial conditions and integrating (34) and (35), we have
(36)
(3)
Expand the initial T(0) and T_g(0) by wavelets as follows:
(37)
Since , from (36) to (37) we have
(38)

(39)
which can be written as
(40)

(41)
(4)
Let and ; then we have
(42)

(43)
By using the disjointness of Block pulse functions, we get [21]
(44)
(5)
Substituting (34), (38), (40), and (44) into (1), we obtain
(45)
where .
Using and (42), we have
(46)

Discreting (46) by collocation points, we can get a nonlinear system of algebraic equations for the unknown vector

as follows:

(47)

where

(48)

The nonlinear system (47) can be solved by applying the Newton iteration method. Therefore, T(t) as the solution of (1) is given by .

Substituting (35), (40), and (41) into (4), we get

(49)

Applying

and (43), we have

(50)

Discreting (50) by the same collocation points, we can acquire a linear system of algebraic equations for the unknown vector

as follows:

(51)

where

(52)

S is the area of the balloon.

Solving this system, we can obtain the approximation of (4).

5. Error Analysis

To show the effectiveness of ∂T/∂t ≈ C^TΨ(t), we discuss error analysis of Legendre wavelets. Let ∂T_k,M(t)/∂t be the approximation of ∂T(t)/∂t, . Then, .

Theorem 2. Suppose that the function ∂T_k,M(t)/∂t obtained by using Legendre wavelets are the approximation of ∂T(t)/∂t, and ∂T(t)/∂t is with bounded second derivative; then one has the following estimation.

(53)

where

, c_nm = 〈∂T(t)/∂t, ψ_nm(t)〉, and Γ^′(t)/Γ(t) is double gamma function.

Proof. Let ∂T(t)/∂t be a function in the interval [0, 1] such that

(54)

where K is a positive constant.

Using the property

(I is the identity matrix), we have

(55)

where

; then we can obtain

(56)

Let

; then

(57)

Suppose

(58)

Therefore,

(59)

where

. Using Cauchy-Schwarz inequality

(60)

Then

(61)

Thus,

(62)

where

Since

(63)

then

(64)

Therefore, we have

(65)

Then we get

(66)

namely,

(67)

From Theorem 2, we can find that when M is fixed and k → +∞.

6. Numerical Implementation of Legendre Wavelet Method for Solving TEE

In order to show the validation of the proposed method, the same stratospheric balloon model [10] at float condition is selected. A spherical balloon with radius R = 20 m is shown in Figure 4. The film of the balloon is divided into 3018 elements by the software ANSYS 14.0. Other parameters in this part are for ε_ex = ε_in = α_ex = α_in = 0.53, α_s = 0.12, and ρ_e = 0.35. The surface density is 150 g/m², and the specific heat is 1500 J/(kg·K). The lifting gas is helium and the wind speed is 10 m/s. The floating altitude is 20 km. The floating latitude and longitude are 40 degrees and 120 degrees, respectively. The balloon was launched during daytime on Spring Equinox 2010.

Figure 5 shows the day-night variation of the film element temperature for and compares it with the measured data. The degree of the Legendre polynomials is 3. From Figure 5, we can see that the predicted data obtained by our method are in good agreement with measured data [23], which indicates the validation to simulate thermal behavior of the balloon. Due to the solar irradiation, the actual balloon temperature begins to increase before sunrise and after sunset it continues to decrease. The maximum and minimum temperatures are 274 K and 229 K. The variation of the actual balloon temperature is as high as 45 K.

The predicted data of the temperature day-night variation for are shown in Figure 6. From Figure 6, we can conclude that the temperature of the film varies nonlinearly with time. The reason for this variation is that the solar irradiation appeared at 6 o’clock and vanished at 18 o’clock.

The comparison between the predicted data for and the measured data is displayed in Figure 7. Table 1 reveals the CPU time on examples 1–4 for different . From Table 1, it is seen that the CPU time on examples 1–4 are less than 1 minute, which implies high efficiency for the method. It can be seen from Figure 7 that the proposed method can predict the thermal behavior of stratospheric balloon effectively, and the simulated results are more credible with increasing. Table 1 reveals the CPU time on simulation for different . From Table 1, it is seen that the CPU time are less than 20 seconds, which implies high efficiency for the method.

Table 1. CPU time (in seconds) for different

	CPU time
	15.881
	18.254

Figure 8 shows the comparison of day-night variation of helium temperature obtained by our proposed method and Xia et al.’s [10] method, respectively. From Figure 8, we may find that the maximum and minimum helium temperatures are 262.2 K and 229.1 K, respectively. We can also see that the calculated results are close to Xia et al.’s results by taking a closer look at Figure 8. The effectiveness of the proposed method is demonstrated by the coincidence.

Comparing Xia et al.’s results with ours, there exist some divergences in Figure 8. These are mainly due to the influence of computational errors by using (51). The errors consist of two parts: one is the approximation of the film’s area and the other is the inverse of matrices product. The difference, on the other hand, comes from the number of comparisons.

In summary, the main characteristics of the wavelet-based approach which leads to a sparse matrix are (1) the vanishing moments property and (2) having a small interval of support. In fact, the sparseness of the system coefficient and good adaptation in dealing with continuous functions are good advantages of using Legendre wavelets, as shown by numerical example. What is more, the approximate explicit expressions of the temperatures of lifting gas and balloon film are obtained generally, which can calculate the temperatures at any time.

7. Conclusion

In the proposed method, we used the properties of the Legendre wavelets to reduce TEE to solve a system of algebraic equations. The temperatures of lifting gas and balloon film will be got by solving the linear and nonlinear system of algebraic equations. The solution is expressed as a truncated Legendre wavelet series and so it can be easily evaluated for arbitrary values of time using any computer program. From the illustrative example, we can conclude that using this approach obtains very satisfactory results. To illustrate the validity and the great potential of the technique, comparisons are made between the predictions obtained by ours and results obtained in previous literature. The proposed method is not only simple but also practical.

Conflicts of Interest

The authors declare that they have no conflict of interest.

References

1 Colozza A. and Dolce J. L., High-altitude, long-endurance airships for coastal surveillance, 2005, NASA/TM-2005 e213427.
Google Scholar
2 Zheng Z. and Wu Z., Global path following control for underactuated stratospheric airship, Advances in Space Research. (2013) 52, no. 7, 1384–1395, https://doi.org/10.1016/j.asr.2013.07.011, 2-s2.0-84883802417.
10.1016/j.asr.2013.07.011
Web of Science® Google Scholar
3 Jamison L., Sommer G. S., and Porche I. R., High-altitude airships for the future force army, 2005, RAND Corporation Technical Report, Santa Monica, CA, USA.
Google Scholar
4 Cathey H. M., Advances in the thermal analysis of scientific balloons, 34th Aerospace Science Meeting and Exhibit, January 1996, Reno, NV, USA, https://doi.org/10.2514/6.1996-695.
10.2514/6.1996-695
Google Scholar
5 Stefan K., Thermal effects on a high altitude airship, 5th Lighter-Than Air Conference, July 1983, Anaheim, CA, USA, https://doi.org/10.2514/6.1983-1984.
10.2514/6.1983-1984
Google Scholar
6 Carlson L. A. and Horn W. J., New thermal and trajectory model for high-altitude balloons, Journal of Aircraft. (1983) 20, no. 6, 500–507, https://doi.org/10.2514/3.44900, 2-s2.0-0020765608.
10.2514/3.44900
Web of Science® Google Scholar
7 Farley R. E., BalloonAscent: 3-D simulation tool for the ascent and float of high-altitude balloons, AIAA 5th ATIO and 16th Lighter-Than-Air Sys Tech. and Balloon Systems Conferences, September 2005, Arlington, Virginia, https://doi.org/10.2514/6.2005-7412.
10.2514/6.2005-7412
Google Scholar
8 Dai Q., Fang X., Li X., and Tian L., Performance simulation of high altitude scientific balloons, Advances in Space Research. (2012) 49, no. 6, 1045–1052, https://doi.org/10.1016/j.asr.2011.12.026, 2-s2.0-84862806425.
10.1016/j.asr.2011.12.026
Web of Science® Google Scholar
9 Yao W., Lu X. C., Wang C., and Ma R., A heat transient model for the thermal behavior prediction of stratospheric airships, Applied Thermal Engineering. (2014) 70, no. 1, 380–387, https://doi.org/10.1016/j.applthermaleng.2014.05.050, 2-s2.0-84902265888.
10.1016/j.applthermaleng.2014.05.050
Web of Science® Google Scholar
10 Xia X. L., Li D. F., Sun C., and Ruan L. M., Transient thermal behavior of stratospheric balloons at float conditions, Advances in Space Research. (2010) 46, no. 9, 1184–1190, https://doi.org/10.1016/j.asr.2010.06.016, 2-s2.0-80052565521.
10.1016/j.asr.2010.06.016
CAS Web of Science® Google Scholar
11 Louchev O. A., Steady state model for the thermal regimes of shells of airships and hot air balloons, International Journal of Heat and Mass Transfer. (1992) 35, no. 10, 2683–2693, https://doi.org/10.1016/0017-9310(92)90109-6, 2-s2.0-0026938606.
10.1016/0017-9310(92)90109-6
Web of Science® Google Scholar
12 Modest M. F., Radiative Heat Transfer, 1993, McGraw-Hill, New York, NY, USA.
Google Scholar
13 Colozza A., Initial feasibility assessment of a high altitude long endurance airship, 2003, NASA/CR-2003-212724.
Google Scholar
14 Jui S. H., Solar Energy Engineering, 1986, Prentice-Hall Inc., Upper Saddle River, NJ, USA.
Google Scholar
15 Ran H., Thomas R., and Mavtis D., A comprehensive global model of broadband direct solar radiation for solar cell simulation, 45th AIAA Aerospace Sciences Meeting and Exhibit, January 2007, Reno, NV, USA, https://doi.org/10.2514/6.2007-33.
10.2514/6.2007-33
Google Scholar
16 Li X. J., Fang X. D., and Dai Q. M., Research on thermal characteristics of photovoltaic array of stratospheric airship, Journal of Aircraft. (2011) 48, no. 4, 1380–1386, https://doi.org/10.2514/1.C031295, 2-s2.0-79961061752.
10.2514/1.C031295
Web of Science® Google Scholar
17 Leland A. C. and Walter J. H., A unified thermal and vertical trajectory model for the prediction of high altitude balloon performance, 1981, NASA-CR-156884.
Google Scholar
18 Kreith F. and Kreider J., Principles of Solar Engineering, 1978, Hemisphere Publishing Corp, New York, NY, USA.
Google Scholar
19 Jafari H. and Yousefi S. A., Application of Legendre wavelets for solving fractional differential equations, Computers & Mathematics with Applications. (2011) 62, no. 3, 1038–1045, https://doi.org/10.1016/j.camwa.2011.04.024, 2-s2.0-79960994078.
10.1016/j.camwa.2011.04.024
Web of Science® Google Scholar
20 Liu N. and Lin E. B., Legendre wavelet method for numerical solutions of partial differential equations, Numerical Methods for Partial Differential Equations. (2010) 26, no. 1, 81–94, https://doi.org/10.1002/num.20417, 2-s2.0-73449118638.
10.1002/num.20417
Web of Science® Google Scholar
21 Li Y. L. and Sun N., Numerical solution of fractional differential equations using the generalized block pulse operational matrix, Computers & Mathematics with Applications. (2011) 62, no. 3, 1046–1054, https://doi.org/10.1016/j.camwa.2011.03.032, 2-s2.0-79961013964.
10.1016/j.camwa.2011.03.032
Web of Science® Google Scholar
22 Ur Rehman M. and Ali Khan R., The Legendre wavelet method for solving fractional differential equations, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, 4163–4173, https://doi.org/10.1016/j.cnsns.2011.01.014, 2-s2.0-79957889333.
10.1016/j.cnsns.2011.01.014
Web of Science® Google Scholar
23 Yang Y. Q., Research on the Pressure Resistance Ability of Stratospheric Aerostats Based on Multi-Field Coupling Method, 2014, Beihang Univeristy, Beijing, China.
Google Scholar

Citing Literature

All articles

A Novel Technique for Predicting the Thermal Behavior of Stratospheric Balloon

Abstract

1. Introduction

2. Thermal Model

2.1. Atmosphere Model

2.2. Solar Position and Solar Radiation Models

2.3. Convective Heat Transfer Coefficient Models

3. Legendre Wavelets and Their Properties

4. Solution Procedure for TEE (1) and (4)

5. Error Analysis

6. Numerical Implementation of Legendre Wavelet Method for Solving TEE

7. Conclusion

Conflicts of Interest

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Novel Technique for Predicting the Thermal Behavior of Stratospheric Balloon

Abstract

1. Introduction

2. Thermal Model

2.1. Atmosphere Model

2.2. Solar Position and Solar Radiation Models

2.3. Convective Heat Transfer Coefficient Models

3. Legendre Wavelets and Their Properties

4. Solution Procedure for TEE (1) and (4)

5. Error Analysis

6. Numerical Implementation of Legendre Wavelet Method for Solving TEE

7. Conclusion

Conflicts of Interest

References

Citing Literature

Figures

References

Related

Information