A comprehensive linear model for an elastic solid reinforced with fibers resistant to extension and flexure is presented. This includes the analysis of both unidirectional and bidirectional fiber-reinforced composites subjected to in-plane deformations. Within the prescription of the superposed incremental deformations, the fiber kinematics are approximated and used to determine the Euler equilibrium equations. The constraints of bulk incompressibility and admissible boundary conditions are also discussed for completeness. In particular, the complete systems of differential equations are obtained for the cases of Neo-Hookean and Mooney–Rivlin types of materials from which analytical solutions can be obtained.

1. Introduction

The mechanics of microstructured solids have consistently been the subject of intense research [1–5] for their practical importance in materials science and engineering. In particular, a considerable amount of attention is committed to the development of continuum models and analyses in an effort to predict the mechanical responses of fiber-matrix systems subjected to external forces and/or induced deformations (see, for example, [6, 7] and references therein). Continuum-based approaches postulate continuous distribution of fibers within the matrix materials so as to establish the idealized description of homogenized fiber-matrix composites. This is framed in the setting of anisotropic elasticity where the response function depends on the first gradient of deformations, typically augmented by the constraints of bulk incompressibility and/or fiber inextensibility. The latter condition often results highly constrained prediction models so that the corresponding deformation fields are essentially kinematically determinate, especially that arises in fibers [6, 7]. The approach has clear advantages in the prediction of deformation profiles of the system via the deformation mapping of an individual fiber, yet rather insufficient in the estimation of overall material properties of the fiber-matrix system. Nonetheless, the aforementioned models have been widely adopted in the analysis of composite materials for their merit in the continuum description and the associated mathematical framework [5–7]. For the estimation of resultant properties, one may also consider multiscale modeling method which integrates the material properties of continua assigned in different length scales by means of the Cauchy–Born rule. Examples of such practice can be found in the works of Shahabodini et al. [8, 9].

A considerable advance in the continuum theory of fiber-reinforced solids was made in recent years. This includes the incorporation of the bending resistance of fibers into the models of deformations where elastic resistance is assigned to changes in curvature of the fibers [10–12]. More precisely, the fibers are regarded as convected curves so that the bending deformation of fibers can be formulated via the second gradient of deformations explicitly [13]. The concept has been successfully adopted in a wide range of problems arising in materials science [14–17], and the mathematical perspective of the subject is discussed in [18–20]. The authors in [21] proposed a general theory for the mechanics of an elastic solids with fibers resistant to flexure, stretch, and twist within the simplified setting of the Cosserat theory of nonlinear elasticity [10, 22]. Further, the second gradient theory of elasticity for the mechanics of meshed structures is presented in [23–25]. To this end, the authors in [26–29] developed continuum-based models in the analysis of fiber-reinforced composites, where the extension and bending resistance of fibers are incorporated via the computations of the first and second gradient of deformations. The majority of the aforementioned studies address nonlinear continuum theory of fiber composites so that little has been devoted to the development of compatible linear models describing the mechanics of an elastic medium reinforced with fibers.

In the present work, we present comprehensive linear theory of the strain gradient elasticity for the mechanics of fiber-reinforced composites with fibers resistant to bending and extension. The kinematics of fibers is approximated with the prescription of the superposed incremental deformations. We formulate, in cases of Neo-Hookean types of materials, complete expressions of the linearized Piola stresses from which the Euler equilibrium equations and the admissible boundary conditions are obtained. Bidirectional fiber composites are accommodated via the decomposition of the deformation gradient tensor along the directions of fibers. In addition, the reduction of simultaneous differential equations into a single differential equation is demonstrated by utilizing the compatibility conditions of the response function. More importantly, we show that, even with the introduction of the second gradient of deformations, two different bases (referential and current coordinate) do indeed merge for “small” deformations superposed in large. Lastly, Mooney–Rivlin types of materials are elaborated where we show that the resulting Euler equilibrium equations are of the same form as those obtained from the Neo-Hookean model. The corresponding Piola stresses, on the other hand, are distinguished in that they demonstrate clear dependency on both the first and second invariant of the deformations gradient tensor. The obtained model can be easily adopted in the study of composite structures subjected to small in-plane deformations. For example, in the design stage of crystalline nanocelluloses (CNCs) composite, the overall responses and deformation profiles can be predetermined by utilizing the proposed model. In addition, the underlined theory can also be extended to the deformation analysis of lipid membranes (e.g., budding and thickness distension) [30–32], where phospholipids (microstructure) are aligned to the normal direction of the membrane, and therefore, their deformations can be mapped and computed using the proposed model.

Throughout the paper, we make use of a number of well-established symbols and conventions such as A^T, A⁻¹, A^∗, and tr(A). These are the transpose, the inverse, the cofactor, and the trance of a tensor A, respectively. The tensor product of vectors is indicated by interposing the symbol ⊗ , and the Euclidian inner product of tensors A and B is defined by A · B = tr(AB^T); the associated norm is . The symbol |∗| is also used to denote the usual Euclidian norm of three vectors. Latin and Greek indices take values in {1, 2} and, when repeated, are summed over their ranges. Lastly, the notation F_A stands for the tensor-valued derivatives of a scalar-valued function F(A).

2. Incremental Elastic Deformations and Equilibrium Equations

The incremental deformation is defined by (see, for example, [33] and the references therein) the following equation:

(1)

where (∗)_o denotes configurations of ∗ evaluated at ε = 0 and

. In the forthcoming derivations, we define

for the sake of convenience and clarity. From equation (1), the gradient of the deformation function χ(X) can be approximated up to the leading order as shown in the following equation:

(2)

where

In the above equation, we assume that the body is initially undeformed and stress free at ε = 0, that is, F_o = I and P_o = 0, where P is the Piola stress. Thus, equation (2) becomes the following equation:

(3)

and successively yields

(4)

which can be found by using the identity FF⁻¹ = I. The determinant of F can be approximated similarly as

(5)

where we evaluate

and

. Since

, we obtain from equation (5) that

(6)

In addition, the Euler equilibrium equation can be expanded as the following equation:

(7)

Dividing the above equation by ε and letting ε⟶0, we obtain

(8)

which serves as the linearized Euler equilibrium equation. The expression of Piola stresses in the case of fiber composites reinforced with fibers resistant to flexure is given by [27]:

(9)

where W, p, and C are the energy density function, Lagrange multiplier, and material constant of fibers (C = constant), respectively. Also, g is the geodesic curvature of fibers’ trajectory (i.e., g = G(D ⊗ D)) and D is the initial director filed of fibers’ where D = (∂X(S))/∂S. Here, S is the arc length parameter on the reference configuration. In general, most of fibers are straight prior to deformations. Even slightly curved fibers can be regarded as “fairly straight” fibers, considering their length scales with respect to that of matrix materials. Thus, from here and forthcoming derivations, it is assumed that

(10)

Accordingly, we find Div(D) = 0 and thereby reduce equation (10) to the following equation:

(11)

where the last term of the above equation is obtained by using the identity g_i,BD_AD_B(e_i ⊗ E_A) = ∇g(D ⊗ D). Thus, from equation (11),

can be evaluated as the following equation:

(12)

In the case of an incompressible Neo-Hookean material, the energy density function is given by the following equation:

(13)

and we find

(14)

In view of equations (8) and (14), the linearized Euler equilibrium equation then satisfies

(15)

The evaluation of equation (15) is essential to extract boundary value problems (BVPs); nonetheless, the details are often heavily omitted in the literature (see, for example, [26–29]). To see this, we first compute the following equation:

(16)

In the above equation, caution needs to be taken, in which ∇(∗) and div(∗) are the operators in the reference frame. Although, there are no clear distinction between the reference and current configurations for “small” incremental deformations, the mathematical procedure should reasonably address their connections especially when dealing with tensors with mixed bases (e.g., ∇u, F). The collapse of bases for the present problem will be discussed in the later sections. The second term in equation (15) becomes

(17)

where we use the Piola identity (i.e.,

) and

. Similarly, it can be easily shown that

(18)

However, in order to recover the initial stress free state at ε = 0, we require from equations (11) and (13) that

(19)

and thus find p_o = μ = constant. Therefore, equation (18) becomes

(20)

and Div(F^∗) = 0 (Piola’s identity). Also,

can be evaluated as

(21)

where g_i = G_iABD_AD_B (see [27]) and G = G_iAB(e_i ⊗ E_A ⊗ E_B) is the second gradient of deformations (i.e., ∇F = G). Consequently, by substituting equations (16), (17), (20), and (21) into equation (15), the linearized Euler equation can be obtained as follows:

(22)

For a single family of fibers (i.e., D = E₁, D₁ = 1, D₂ = 0), equation (22) reduces to

(23)

3. Boundary Conditions and Solution to the Linearized System

The corresponding boundary conditions are given by [27]

(24)

where t, m, and f are, respectively, the expressions of edge tractions, edge moments, and the corner forces. Further, N and T are unit normal and tangent to the boundary. The “small” increment of boundary forces are then computed as follows:

(25)

The expression of

can be obtained from equation (14) that

(26)

(27)

In order to apply boundary tractions (e.g.,

), it is necessary to compute equation (26) as a function of u = u(X₁, X₂). For the purpose, we first find the following equation:

(28)

where

at ε = 0. Also, to compute

, we use the chain rule in the form of the following equation:

(29)

Here, the expression of

can be found via the connection [34]:

(30)

Thus, at ε = 0, we have from the above equation that

(31)

and thereby obtain

(32)

Consequently, substituting equations (27), (28), and (32) into equation (26) furnishes

(33)

from which the expression of boundary tractions is completely determined in terms of u.

Remark 1. In the above equation, δ_iAδ_jBu_j,B is interpreted as δ_iAu_B,B resulting δ_iAδ_jBu_j,B = δ_iADivu in the reference configuration (Eulerian). However, one may also find δ_iAδ_jBu_j,B = u_j,j and thus obtain δ_iAδ_jBu_j,B = δ_iAdivu in the current configuration (Lagrangian). This confirms the well-known result from the linear elasticity theory that the bases collapse in the event of small deformations superposed on large (i.e., Divu = divu and E_A = e_i). In the present problem, the result allows one to formulate linearized Euler equations without conflicting bases mismatch especially when operating linear transform of mixed basis tensors. Although there are no clear distinctions between the current and deformed configurations, caution needs to be taken that the Euler equation () is, in principal, defined in the reference frame together with the boundary conditions.

Now, in view of equations (5) and (6), the constraints of bulk incompressibility reduce to the following equation:

(34)

Equation (34) serves as the linearized bulk incompressibility condition (i.e., u_i,i = 0), which needs to be solved together with equation (23). In addition, since Divu = Divu for small deformations (see Remark 1), we find Divu = Divu = 0 and thereby reduce equation (33) to the following equation:

(35)

which serves as an explicit form of the linearized Piola stress for elastic solids reinforced with single family of fibers. In particular, if the fibers’ directions are either normal or tangential to the boundary (i.e., (D · T)(D · N) = 0), equation (25) becomes

(36)

and therefore, we compute, for example,

(37)

where N is assumed to be parallel to the fiber’s director field (i.e., N = D = E₁). Lastly, from equations (27) and (36), the expression of boundary moments are obtained by

(38)

3.1. Solutions to the Linearized System

In the case of single family of fibers (i.e., D = E₁), the linearized system of partial differential equations (PDEs) is given by

(39)

The second one in the above equation can be automatically satisfied by introducing the following scalar field φ:

(40)

so that u_1,1 + u_2,2 = φ₁₂ − φ₂₁ = 0. Now, we recast the first one of equation (39) and thereby find the following equation:

(41)

In addition, using the compatibility conditions of p_i (i.e.,

), the first one of equation (41) becomes

(42)

Consequently, equation (42) further reduces to

(43)

An analytical solution of the above exists (see [27]) and is completely determined by imposing admissible boundary conditions as discussed in equation (25). For example, the symmetric bending can be imposed as

(44)

which serves as the boundary conditions for the equation (42).

4. Extensible Fibers

The Piola stress in the case of initially straight and extensible fibers is given by Zeidi and Kim [28]:

(45)

where E is the elastic modulus of fibers (extension). Further, the fibers’ stretch λ can be computed as

(46)

In the case of Neo-Hookean type materials (see equation (13)), equation (45) becomes

(47)

Thus, equations (1) and (47) can be approximated as

(48)

Since

, the above equation further reduces to the following equation:

(49)

where F_oD · F_oD = D · D = 1. To obtain the desired expression, it is required to compute the following equation:

(50)

In the above equation, the initial director field (D) is represented by the current frame (i.e., e_i). However, D is, in principal, a vector in the reference coordinate (i.e., D = D_AE_A). This is due to the collapse of bases as discussed in Remark 1. Caution needs to be taken when applying the Einstein summation. Thus, we obtain from equations (32), (34), (49), and (50) that

(51)

where

. Equation (51) can be used as the expression of boundary tractions in the case of extensible fibers. For example, if D = E₁ (single family of fibers), the above equation yields the following equation:

(52)

Further, from equations (8) and (49), the corresponding equilibrium equation then satisfies the following equation:

(53)

The evaluation of the above equation is well discussed through equations (16)–(21) except the stretch term which is now equated as

(54)

Therefore, we obtain the following equation:

(55)

The linearized boundary conditions in the case of extensible fibers remain intact (see [28]), except the expression of

where the explicit expression is obtained in equation (52). Thus, for example, in the case of unidirectional fiber composited where a boundary vector N is parallel to the fiber’s director field (i.e., N = D = E₁), the complete set of equations can be found as

(56)

Also, the corresponding boundary conditions are given by

(57)

where from equation (52),

. Lastly, we note here that the value of p_o, in the case of extensible fibers, can be obtained by evaluating the corresponding stresses (see equation (47)) at ε = 0 which is again found to be p_o = μ. By applying the similar scheme as applied in Section 3.1, we rearrange equation (56) and thereby obtain

(58)

The solution of equation (58) is not accommodated by conventional methods such as the separation of variables method, Fourier transform, and polynomial solutions. Instead, a particular form of solution (φ = X(x)sin(my)) can be proposed, inspired by the modified Helmholtz equation.

5. Extensible Bidirectional Fibers

In the forthcoming derivations, we confine our attention to the case of initially orthogonal fiber families. The bidirectional fibers can be accommodated by using the following decompositions of the deformation gradient:

(59)

where L and M are the director fields of each fiber family in the reference configuration and l and m are their counterparts in the current configuration. The fibers’ stretches are computed similarly as in equation (46) that

(60)

Equations (59) and (60) complete the deformation mapping, for example, L = L_AE_A and l = l_ie_i to yield

(61)

Further, by employing the variational principles, the Piola stress for the bidirectional and extensible fiber composites can be found as

(62)

where E_i and C_i are the material constants of fiber families, respectively, to extension and flexure. Applying the similar scheme as in Section 4, we approximate equation (62) and successively obtain

(63)

Therefore, equations (8) and (63) furnish

(64)

where we evaluate

(65)

Compatible results can be also found directly from equations (17) and (20) (i.e.,

and

). In the case of bidirectional and extensible fibers, the corresponding boundary conditions are given by (see [26]) the following equation:

(66)

Now, we approximate the above boundary conditions and thus obtain

(67)

If the fibers’ directions are aligned with the axes of Cartesian coordinates (i.e., L = E₁ and M = E₂) and are either normal or tangential to the boundary (i.e., (L · T)(L · N) = (M · T)(M · N) = 0), equations (64) and (67) further reduces to the following equation:

(68)

which together with the incompressibility condition (u_i,i = 0) constitutes the complete set of the PDEs system to solve the final deformation profiles. Similarly, equation (63) now becomes

(69)

For example, if the unit normal of a boundary is N = E₁, the boundary traction can be computed as follows:

(70)

Again, by introducing the scalar field φ (see equation (40)) and employing the compatibility conditions (i.e.,

), we reduce the above equation to the following equation:

(71)

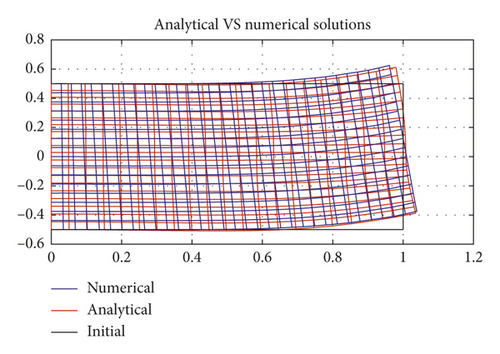
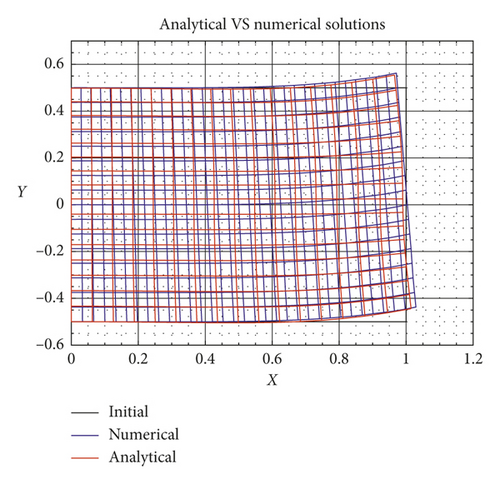
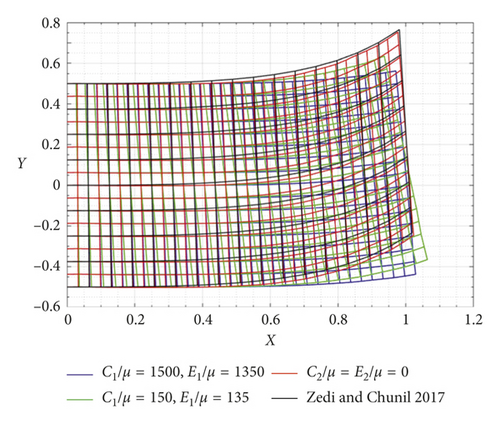
A complete analytical solution for equation (71) is available via the methods of iterative reduction and the principle of eigenfunction expansion (see, more details, [35–37]). Figures 1–4 illustrate the deformation profiles for the cases discussed through Sections 3–5. As the equations become mathematically compact, the corresponding deformation fields experience less oscillatory behaviors. This is clearly demonstrated by the results in Figures 3-4, bidirectional cases, which show a close agreement with the predictions from nonlinear models. We also mention here that equation (71) reduces to equations (42) and (58) in the limit of vanishing C₂ and E₂, respectively. This, in turn, suggests that unidirectional cases can be assimilated within the systems of equation (71) by setting C₂ = E₂ = 0 (see Figure 5). In fact, the latter model is recommended to use, since the bidirectional and extension fibers case is the most general and compact form (with minimal singular behaviors) and therefore produces more accurate prediction results.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Unidirectional fibers.

To elaborate the proposed model, we present comparisons with the experimental data obtained from the 3-point bending test of CNC fiber composite (C = 150 GPa, μ = 1 GPa). This is a particular case of the proposed model, when C/μ = 150 and vanishing E (i.e., equation (20)). Using the method presented in Section 3.1, we find the solution of equation (20) as

(72)

where

(73)

and the unknowns C_m and D_m can be determined via the applied moment in the form of Fourier expansion; i.e.,

(74)

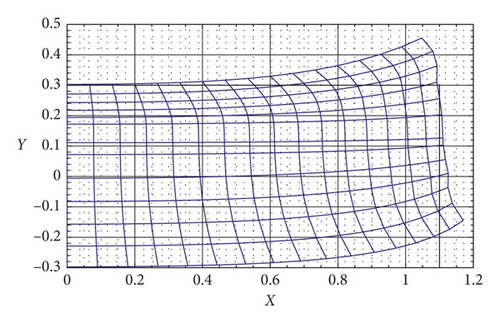
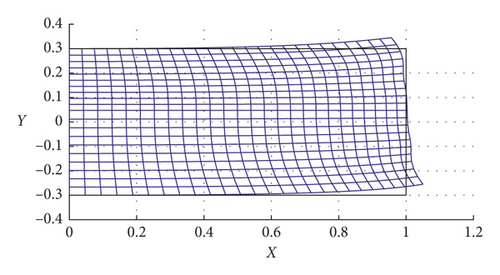
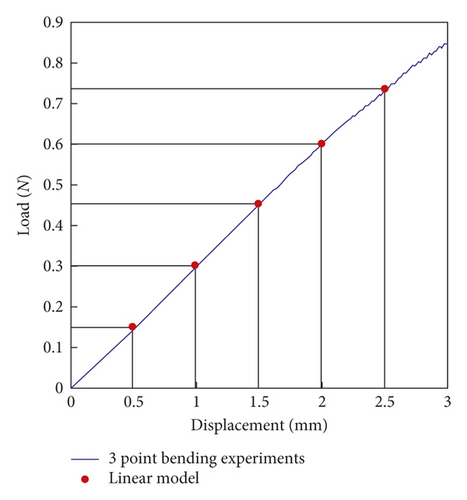
Using equation (74), we compute the maximum deflections of the CNC composite and illustrate the results in Figure 6. It is shown in Figure 6 that the proposed model successfully predicts the normal deflections of the CNC composite strip. Since the slope of the graph in Figure 6 indicates the moduli of the composite (when divided by the corresponding length scale), it can also be used in the estimation of the overall material properties of the composite. However, due to the paucity of available data, we are not able to provide the quantitative analysis other than those presented in Figure 6 at this time. The study is currently underway, and our intention is to present elsewhere when ready. We also mention here that the overall responses of composite materials can also be estimated using multiscale modeling methods (see, for example, Shahabodini et al. [8, 9]).

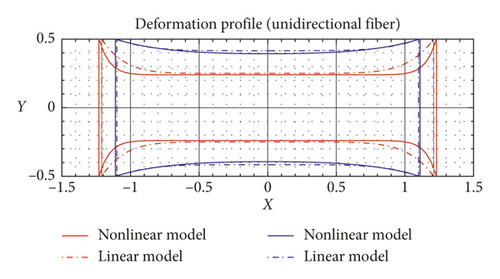
Lastly, we assimilate the case of single family of fiber composites subjected to the axial tension. The linear solution obtained from equation (56) demonstrates good agreement with the compatible nonlinear model [28] for small deformations superposed on large, while it shows discrepancies in the prediction of large deformations (See Figure 7). It is also noted here that we reserve the details in solving the corresponding differential equations (equation (56)) for the sake of conciseness. However, the procedures for the particular case of the present example can be found in [28].

6. Further Considerations

For the analysis of soft materials-based composites, such as carbon rubber-fiber composites and polymer composites, a different type of energy potential may be suggested instead of the Neo-Hookean model discussed in the previous sections. The Mooney–Rivlin model is one of the most commonly used energy potentials for the aforementioned cases (see, for example, [33]). In the forgoing development, we present a compatible linear model for the Mooney–Rivlin types of materials for the desired applications. The expression of the Mooney–Rivlin potential is given by the following equation:

(75)

The derivative of equation (75) with respect to the deformation gradient tensor then yields the following equation:

(76)

Substituting equation (76) into equation (9) furnishes the following expression of the Piola stresses:

(77)

Now, by applying the same schemes as adopted in the previous sections, we find the following equation:

(78)

where the second term of the right side of equation (78) can be evaluated at ε = 0 as

(79)

Since

, the above equation becomes the following equation:

(80)

Thus, from the results in equations (2), (27), (28), (33), (78), and (80), we find the following stress expression for the cases of unidirectional fiber composites as

(81)

where

from the conditions of bulk incompressibility (see equation (34)). Consequently, the corresponding Euler equilibrium equation satisfies the following equation:

(82)

Using the compatibility condition of u_A,iA (i.e. u_A,iA = u_A,Ai) and the constraints of bulk incompressibility, we find that

and thereby reduce equation (83) to the following equation:

(83)

The resulting equilibrium equation (equation (83)) implies that there is no clear distinction between the Neo-Hookean model and Mooney–Rivlin model as far as the superposed incremental deformations with the augmented bulk incompressibility conditions are considered. This is due to the fact that the divergence of high-strain terms identically vanishes upon the imposition of linearized bulk incompressibility conditions (i.e., Divu = divu = 0). However, the expressions of Piola stresses are affected by the introduction of Mooney–Rivlin type materials (see equations (33) and (81)). Thus, for example, if N = D = E₁, we compute from equation (25) that

(84)

which is the boundary tractions for the case of the Mooney–Rivlin energy potential. Lastly, from equation (77), we find at ε = 0 that

(85)

and thereby obtain μ = p_o. Equation (83) together with the imposed boundary conditions (i.e., equations (25) and (84)) constitutes a complete set of PDEs system which can be solved using the similar schemes as presented in Section 3.1. Further, because the resulting equilibrium equations are of the same form (see equations (22) and (84)), equations (81) and (84) may be used in the determination of the parameters associated with high-strain terms (λ) by comparing stresses in equations (33) and (81). Investigations in this respect (including the implementations of the developed linear theory) are currently underway. Our intention is to report elsewhere.

7. Conclusions

We present complete linear models for the mechanics of an elastic solid reinforced with fibers resistant to flexure and extension. Within the prescription of the superposed incremental deformations, the first and second gradient of deformations is approximated through which the kinematics of fibers is explicitly determined. The linearized Euler equilibrium equations and the Piola stress are then formulated for the Neo-Hookean types of materials. We also derive the corresponding boundary conditions and the conditions of bulk incompressibility for the sake of completeness. In addition, the cases of the bidirectional fiber composites are considered via the fiber decomposition of the deformation gradient tensor. It is found that the systems of PDEs for the bidirectional and extensible fibers reduce to those from single family of fibers in the limit of vanishing material parameters of fibers.

In particular, we demonstrate the well-known result from the linear theory of elasticity that the merging of the bases remains valid even with the incorporation of fibers’ bending and extension into the models of deformations. A Mooney–Rivlin material is also elaborated, where we show that there is no clear distinctions in the resulting Euler equations obtained from the two different strain energy models (i.e., Neo-Hookean and Mooney–Rivlin) as long as the small deformations are concerned. However, the resulting Piola stresses are of different forms in that the one from the Mooney–Rivlin model demonstrates clear dependency on both the first and second invariant of deformation gradient tensors, whereas the Piola stress, in the case of the Neo-Hookean model, depends only on the first invariant. Lastly, we mention here that the present model can be used in the approximation of the nonlinear theory of strain gradient elasticity arising in finite plane elastostatics.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by the Natural Sciences and Engineering Research Council of Canada via Grant #RGPIN 04742 and the University of Alberta through a start-up grant. The author would like to thank Dr. David Steigmann for many useful discussions.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Adkins J. E., Finite plane deformation of thin elastic sheets reinforced with inextensible cords, Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. (1956) 249, no. 961, 125–150, https://doi.org/10.1098/rsta.1956.0017.
10.1098/rsta.1956.0017
Google Scholar
2 Ericksen J. L. and Rivlin R. S., Large elastic deformations of homogeneous anisotropic materials, Indiana University Mathematics Journal. (1954) 3, no. 3, 281–301, https://doi.org/10.1512/iumj.1954.3.53014.
10.1512/iumj.1954.3.53014
Google Scholar
3 Spencer A. J. M., Deformations of Fibre-Reinforced Materials, 1972, Oxford University Press, Oxford, UK.
Google Scholar
4 Pipkin A. C., Stress analysis for fiber-reinforced materials, Advances in Applied Mechanics. (1979) 19, 1–51, https://doi.org/10.1016/s0065-2156(08)70308-9, 2-s2.0-0018752694.
10.1016/S0065-2156(08)70308-9
Google Scholar
5 Mulhern J. F., Rogers T. G., and Spencer A. J. M., A continuum model for fibre-reinforced plastic materials, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. (1967) 301, no. 1467, 473–492, https://doi.org/10.1098/rspa.1967.0220.
10.1098/rspa.1967.0220
CAS Google Scholar
6 Mulhern J. F., Rogers T. G., and Spencer A. J. M., A continuum theory of a plastic-elastic fibre-reinforced material, International Journal of Engineering Science. (1969) 7, no. 2, 129–152, https://doi.org/10.1016/0020-7225(69)90053-6.
10.1016/0020-7225(69)90053-6
Web of Science® Google Scholar
7 Pipkin A. C. and Rogers T. G., Plane deformations of incompressible fiber-reinforced materials, Journal of Applied Mechanics. (1971) 38, no. 3, https://doi.org/10.1115/1.3408866, 2-s2.0-0015128605.
10.1115/1.3408866
Google Scholar
8 Shahabodini A., Ansari R., and Darvizeh M., Atomistic-continuum modeling of vibrational behavior of carbon nanotubes using the variational differential quadrature method, Composite Structures. (2018) 185, 728–747, https://doi.org/10.1016/j.compstruct.2017.11.028, 2-s2.0-85036461325.
10.1016/j.compstruct.2017.11.028
Web of Science® Google Scholar
9 Shahabodini A., Ansari R., and Darvizeh M., Multiscale modeling of embedded graphene sheets based on the higher-order Cauchy-Born rule: nonlinear static analysis, Composite Structures. (2017) 165, 25–43, https://doi.org/10.1016/j.compstruct.2016.12.067, 2-s2.0-85009174897.
10.1016/j.compstruct.2016.12.067
Web of Science® Google Scholar
10 Toupin R. A., Theories of elasticity with couple-stress, Archive for Rational Mechanics and Analysis. (1964) 17, no. 2, 85–112, https://doi.org/10.1007/bf00253050, 2-s2.0-34250940617.
10.1007/BF00253050
Web of Science® Google Scholar
11 Mindlin R. D. and Tiersten H. F., Effects of couple-stresses in linear elasticity, Archive for Rational Mechanics and Analysis. (1962) 11, no. 1, 415–448, https://doi.org/10.1007/bf00253946, 2-s2.0-33947128429.
10.1007/BF00253946
Web of Science® Google Scholar
12 Koiter W. T., Couple-stresses in the theory of elasticity, Proceedings of the Knononklijke Nederlandse Akademie van Wetenschappen B. (1964) 67, 17–44.
Google Scholar
13 Spencer A. J. M. and Soldatos K. P., Finite deformations of fibre-reinforced elastic solids with fibre bending stiffness, International Journal of Non-Linear Mechanics. (2007) 42, no. 2, 355–368, https://doi.org/10.1016/j.ijnonlinmec.2007.02.015, 2-s2.0-34247515144.
10.1016/j.ijnonlinmec.2007.02.015
Web of Science® Google Scholar
14 Park H. C. and Lakes R. S., Torsion of a micropolar elastic prism of square cross-section, International Journal of Solids and Structures. (1987) 23, no. 4, 485–503, https://doi.org/10.1016/0020-7683(87)90013-8, 2-s2.0-0023215153.
10.1016/0020-7683(87)90013-8
Web of Science® Google Scholar
15 Maugin G. A. and Metrikine A. V., Mechanics of Generalized Continua: One Hundred Years after the Cosserats, 2010, Springer, New York, NY, USA.
10.1007/978-1-4419-5695-8
Google Scholar
16 Neff P., A finite-strain elastic.plastic Cosserat theory for polycrystals with grain rotations, International Journal of Engineering Science. (2006) 44, no. 8-9, 574–594, https://doi.org/10.1016/j.ijengsci.2006.04.002, 2-s2.0-33746562367.
10.1016/j.ijengsci.2006.04.002
Web of Science® Google Scholar
17 Munch I., Neff P., and Wagner W., Transversely isotropic material: nonlinear Cosserat vs. classical approach, Continuum Mechanics and Thermodynamics. (2011) 23, no. 1, 27–34, https://doi.org/10.1007/s00161-010-0150-0, 2-s2.0-79551528357.
10.1007/s00161-010-0150-0
Web of Science® Google Scholar
18 Neff P., Existence of minimizers for a finite-strain micro-morphic elastic solid, Proceedings of the Royal Society of Edinburgh: Section A Mathematics. (2006) 136, no. 5, 997–1012, https://doi.org/10.1017/s0308210500004844, 2-s2.0-33751038039.
10.1017/S0308210500004844
Web of Science® Google Scholar
19 Park S. K. and Gao X. L., Variational formulation of a modified couple-stress theory and its application to a simple shear problem, Zeitschrift für angewandte Mathematik und Physik. (2008) 59, no. 5, 904–917, https://doi.org/10.1007/s00033-006-6073-8, 2-s2.0-51349157575.
10.1007/s00033-006-6073-8
Web of Science® Google Scholar
20 Fried E. and Gurtin M. E., Gradient nanoscale polycrystalline elasticity: intergrain interactions and triple-junction conditions, Journal of the Mechanics and Physics of Solids. (2009) 57, no. 10, 1749–1779, https://doi.org/10.1016/j.jmps.2009.06.004, 2-s2.0-68949194439.
10.1016/j.jmps.2009.06.004
Web of Science® Google Scholar
21 Steigmann D. J., Theory of elastic solids reinforced with fibers resistant to extension, flexure and twist, International Journal of Non-Linear Mechanics. (2012) 47, no. 7, 734–742, https://doi.org/10.1016/j.ijnonlinmec.2012.04.007, 2-s2.0-84861329973.
10.1016/j.ijnonlinmec.2012.04.007
Web of Science® Google Scholar
22 Truesdell C. and Noll W., S. Flugge, The non-linear field theories of mechanics, Handbuch der Physik, III/3, 1965, Springer, Berlin, Germany.
10.1007/978-3-642-46015-9_1
Google Scholar
23 Isola F. D., Cuomo M., Greco L., and Della Corte A., Bias extension test for pantographic sheets: numerical simulations based on second gradient shear energies, Journal of Engineering Mathematics. (2017) 103, no. 1, 127–157.
10.1007/s10665-016-9865-7
Web of Science® Google Scholar
24 Isola F. D., Della Corte A., Greco L., and Luongo A., Plane bias extension test for a continuum with two inextensible families of fibers: a variational treatment with Lagrange multipliers and a perturbation solution, International Journal of Solids and Structures. (2016) 81, 1–12, https://doi.org/10.1016/j.ijsolstr.2015.08.029, 2-s2.0-84956614739.
10.1016/j.ijsolstr.2015.08.029
Web of Science® Google Scholar
25 Turco E., Non-standard coupled extensional and bending bias tests for planar pantographic lattices. Part I: numerical simulations, Zeitschrift für angewandte Mathematik und Physik. (2016) 67, no. 5, https://doi.org/10.1007/s00033-016-0713-4, 2-s2.0-84988493691.
10.1007/s00033-016-0713-4
PubMed Web of Science® Google Scholar
26 Kim C. and Zeidi M., Gradient elasticity theory for fiber composites with fibers resistant to extension and flexure, International Journal of Engineering Science. (2018) 131, 80–99, https://doi.org/10.1016/j.ijengsci.2018.06.002.
10.1016/j.ijengsci.2018.06.002
Web of Science® Google Scholar
27 Zeidi M. and Kim C., Finite plane deformations of elastic solids reinforced with fibers resistant to flexure: complete solution, Archive of Applied Mechanics. (2017) 88, no. 5, 819–835, https://doi.org/10.1007/s00419-018-1344-3, 2-s2.0-85040539877.
10.1007/s00419-018-1344-3
Web of Science® Google Scholar
28 Zeidi M. and Kim C., Mechanics of fiber composites with fibers resistant to extension and flexure, Mathematics and Mechanics of Solids. (2017) 108128651772854, https://doi.org/10.1177/1081286517728543, 2-s2.0-85045048020.
10.1177/1081286517728543
Web of Science® Google Scholar
29 Zeidi M. and Kim C., Mechanics of an elastic solid reinforced with bidirectional fiber in finite plane elastostatics: complete analysis, Continuum Mechanics and Thermodynamics. (2018) 30, no. 3, 573–592, https://doi.org/10.1007/s00161-018-0623-0, 2-s2.0-85041099676.
10.1007/s00161-018-0623-0
Web of Science® Google Scholar
30 Zeidi M. and Kim C., The effects of intra-membrane viscosity on lipid membrane morphology: complete analytical solution, Scientific Reprots. Nature. (2018) 8, no. 1, https://doi.org/10.1038/s41598-018-31251-6.
10.1038/s41598-018-31251-6
Google Scholar
31 Belay T., Kim C. I., and Schiavone P., Analytical solution of lipid membrane morphology subjected to boundary forces on the edges of rectangular membrane, Continuum Mechanics and Thermodynamics. (2015) 28, no. 1-2, 305–315, https://doi.org/10.1007/s00161-015-0426-5, 2-s2.0-84953639189.
10.1007/s00161-015-0426-5
Web of Science® Google Scholar
32 Kim C. and Steigmann D. J., Distension-induced gradient capillarity in lipid membranes, Continuum Mechanics and Thermodynamics. (2015) 27, no. 4-5, 609–315, https://doi.org/10.1007/s00161-014-0333-1, 2-s2.0-84932197815.
10.1007/s00161-014-0333-1
CAS Web of Science® Google Scholar
33 Ogden R. W., Non-Linear Elastic Deformations, 1984, Ellis Horwood Ltd., Chichester, England.
10.1016/0955-7997(84)90049-3
Google Scholar
34 Steigmann D. J., Invariants of the stretch tensors and their application to finite elasticity theory, Mathematics and Mechanics of Solids. (2002) 7, no. 4, 393–404, https://doi.org/10.1177/108128028481, 2-s2.0-0036695284.
10.1177/108128028481
Web of Science® Google Scholar
35 Read W. W., Analytical solutions for a Helmholtz equation with dirichlet boundary conditions and arbitrary boundaries, Mathematical and Computer Modelling. (1996) 24, no. 2, 23–34, https://doi.org/10.1016/0895-7177(96)00087-8, 2-s2.0-0030186108.
10.1016/0895-7177(96)00087-8
Google Scholar
36 Read W. W., Series solutions for Laplace’s equation with nonhomogeneous mixed boundary conditions and irregular boundaries, Mathematical and Computer Modelling. (1993) 17, no. 12, 9–19, https://doi.org/10.1016/0895-7177(93)90023-r, 2-s2.0-38249002868.
10.1016/0895-7177(93)90023-R
Web of Science® Google Scholar
37 Huang Y. and Zhang X., General analytical solution of transverse vibration for orthotropic rectangular thin plates, Journal of Marine Science and Application. (2002) 1, no. 2, 78–82, https://doi.org/10.1007/bf02935845.
10.1007/BF02935845
Google Scholar

Citing Literature

All articles

Superposed Incremental Deformations of an Elastic Solid Reinforced with Fibers Resistant to Extension and Flexure

Abstract

1. Introduction

2. Incremental Elastic Deformations and Equilibrium Equations

3. Boundary Conditions and Solution to the Linearized System

3.1. Solutions to the Linearized System

4. Extensible Fibers

5. Extensible Bidirectional Fibers

6. Further Considerations

7. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Superposed Incremental Deformations of an Elastic Solid Reinforced with Fibers Resistant to Extension and Flexure

Abstract

1. Introduction

2. Incremental Elastic Deformations and Equilibrium Equations

3. Boundary Conditions and Solution to the Linearized System

3.1. Solutions to the Linearized System

4. Extensible Fibers

5. Extensible Bidirectional Fibers

6. Further Considerations

7. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information