International Journal of Aerospace Engineering

Volume 2018, Issue 1 5213249

Research Article

Open Access

Reliability Analysis of the Reconfigurable Integrated Modular Avionics Using the Continuous-Time Markov Chains

Changxiao Zhao,

Changxiao Zhao

orcid.org/0000-0002-4065-8718

College of Airworthiness, Civil Aviation University of China, Tianjin 300300, China cauc.edu.cn

Key Laboratory of Civil Aircraft Airworthiness Technology, CAAC, Tianjin 300300, China caac.gov.cn

Search for more papers by this author

Peng Wang,

Corresponding Author

Peng Wang

[email protected]

orcid.org/0000-0002-8738-0602

College of Airworthiness, Civil Aviation University of China, Tianjin 300300, China cauc.edu.cn

Key Laboratory of Civil Aircraft Airworthiness Technology, CAAC, Tianjin 300300, China caac.gov.cn

Search for more papers by this author

Fang Yan,

Fang Yan

orcid.org/0000-0001-7994-5389

College of Airworthiness, Civil Aviation University of China, Tianjin 300300, China cauc.edu.cn

Key Laboratory of Civil Aircraft Airworthiness Technology, CAAC, Tianjin 300300, China caac.gov.cn

Search for more papers by this author

Changxiao Zhao,

Changxiao Zhao

orcid.org/0000-0002-4065-8718

College of Airworthiness, Civil Aviation University of China, Tianjin 300300, China cauc.edu.cn

Key Laboratory of Civil Aircraft Airworthiness Technology, CAAC, Tianjin 300300, China caac.gov.cn

Search for more papers by this author

Peng Wang,

Corresponding Author

Peng Wang

[email protected]

orcid.org/0000-0002-8738-0602

College of Airworthiness, Civil Aviation University of China, Tianjin 300300, China cauc.edu.cn

Key Laboratory of Civil Aircraft Airworthiness Technology, CAAC, Tianjin 300300, China caac.gov.cn

Search for more papers by this author

Fang Yan,

Fang Yan

orcid.org/0000-0001-7994-5389

College of Airworthiness, Civil Aviation University of China, Tianjin 300300, China cauc.edu.cn

Key Laboratory of Civil Aircraft Airworthiness Technology, CAAC, Tianjin 300300, China caac.gov.cn

Search for more papers by this author

First published: 18 September 2018

https://doi.org/10.1155/2018/5213249

Citations: 4

Academic Editor: Seid H. Pourtakdoust

Share a link

Email
Wechat
Bluesky

Abstract

The integrated modular avionics (IMA) has been widely deployed on the new designed aircraft to replace the traditional federated avionics. Hosted in different partitions which are isolated by the virtual boundaries, different functions are able to share the common resources in the IMA system. The IMA system can dynamically reconfigure the common resources to perform the hosted functions when some modules fail, which makes the system more robust. Meanwhile, the reliability of the reconfigurable integrated modular avionics becomes more complicated. In this paper, we firstly model the IMA as a joint (m, k)-failure tolerant system with the consideration of its reconfigurable capability. Secondly, the continuous-time Markov chains are introduced to analyze the reliability of the IMA system. Thirdly, we take the comprehensive display function hosted in the IMA system as an example to show the practical use of the proposed reliability analysis model. Through the parameter sensitivity analysis, different failure rate λ and priority order of different modules are chosen to analyze their impact on system reliability, which can provide guidance to improve the reliability of the IMA system during a dynamic reconstruction process and optimize resource allocation.

1. Introduction

In recent years, the integrated modular avionics (IMA) concept has been introduced to replace the traditional federated avionics [1]. In the federated avionics system, each function (e.g., autopilot, yaw damping, and displays) which uses dedicated communication, I/O, and computing resources is only loosely coupled to other functions [2]. Because the demand for more powerful and cost-effective avionic systems emerges, the federated avionics becomes not suitable for large-scale avionics. The IMA provides a common shared resource for several functions, which reduces the space, weight, and power requirements of the aircraft; therefore, both maintenance and operating costs are reduced [3]. Many newly designed civil and military aircrafts, such as COMAC C919, Boeing 787, and US Air force F-22, have chosen the IMA architecture.

Using shared resource, IMA has the potential to proliferate faults among functions, for example, a faulty function might monopolize the computer and deny service to all the other functions sharing the processor. It is almost impossible for individual functions to protect themselves against this kind of faults since their functions depended on the shared resources [4]. Furthermore, IMA implementations would allow applications with different safety-criticality levels to reside on the same platform. So, various partitioning technologies are introduced to the IMA to guarantee that each function will not be affected by other corrupt functions. In [5], spatial partitioning and temporal partitioning were proposed to isolate the memory and time resources for each function. The industry standard ARINC 653 [6] standardized a partitioned software architecture for IMA; it defined the application executive (APEX) interface which ensures the spatial and temporal partitioning of the avionics functions. Taking the communication needs of each function into account, Tu et al. [7] and He and Li [8] proposed the concept of network partition to allocate specified network bandwidth for each function. Zhou et al. [9] and Zhou and Xiong [10] proposed a resource allocation method for different functions to meet their various needs.

All the mentioned works tried to achieve the goal of robust partitioning [11] that offers the same level of isolation equivalent to the federated avionics. In fact, the partitioning mechanisms are provided either by hardware (such as memory management unit [12]) or software (such as intended segment analysis [13]). The failure or defect of the hardware and software can affect the robustness of the partitioning mechanism. In addition to the effectiveness analysis of the partitioning mechanism, the reliability of the partitioning mechanism themselves should also be considered. Chen et al. [14] analyzed the reliability of the avionics networks. Conmy and McDemid [15] illustrated the failure models of IMA. Suo et al. [16] analyzed the safety of the IMA from the airworthiness aspect. Wan et al. [17] used the stochastic Petri net (SPN) method to analyze the performability of the HM/FM strategies. The papers that focused on the reliability analysis of the IMA system reconfiguration are rare.

In this paper, the (m, k)-failure tolerant model is proposed to model the reconfigurable features of the IMA system and the continuous-time Markov chains are introduced to describe the state of the IMA reconfiguration. Then, a numerical example is given to show the practical use of the proposed reliability analysis model by listing reliability expressions. Finally, the sensitivity of the parameters λ and P_ij that affect the reliability of the comprehensive display system is analyzed. The influence rules of parameters λ and P_ij on system reliability are obtained, which can provide guidance for the resource allocation optimization of IMA.

2. The Reconfigurable Integrated Modular Avionics

2.1. Integrated Modular Avionics

The IMA is comprised as a set of shared hardware and software resources. The IMA platform is partitioned into several partitions which can host one or more functions. Different partitions are isolated by the virtual system boundaries in both spatial and temporal dimensions. The platform manages all the resources to provide communications, computing capabilities, and interfaces to different functions. This architecture qualifies IMA with highly configurable capability of resources, which means that it is convenient to allocate resources to meet different needs of different functions and reallocate resources if any functions fail. So, the reliability analysis of the IMA partitioning mechanisms should take the failure tolerance of the IMA architecture into consideration. The system model is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Model of the IMA system.

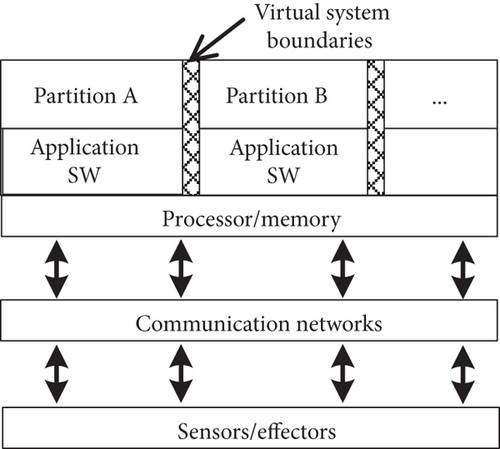
In the actual IMA system, different IMA system functions are configured by different types of core processing modules. As shown in Table 1, the A380 aircraft configures most of the aircraft functions to 7 types of 22 CPIOMs to support the system’s requirements of residing functions [18].

Table 1. CPIOMs in the A380.

Module type	Number
CPIOM-A	4
CPIOM-B	4
CPIOM-C	2
CPIOM-D	2 + 1 (optional)
CPIOM-E	2
CPIOM-F	4
CPIOM-G	4
IOM	8

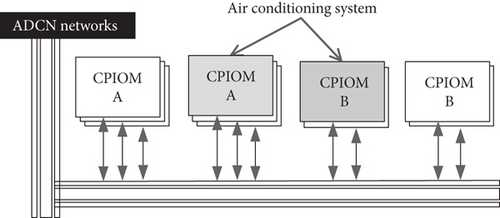
The same function can host in different CPIOMs to implement multiple backup systems, such as the ATA 21 air conditioning system in the A380 residing on two different types of hardware modules, CPIOM-A and CPIOM-B as shown in Figure 2.

2.2. Reconfiguration Process

Dynamic reconfiguration capability is the core technology of the IMA system, which not only reduces hardware redundancy and unexpected maintenance costs but also improves resource utilization, increases system flexibility, and enhances the ability of avionics systems to response to different missions and resource failures. Moreover, it can improve aircraft operational reliability while maintaining the current safety levels.

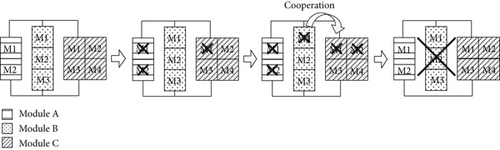
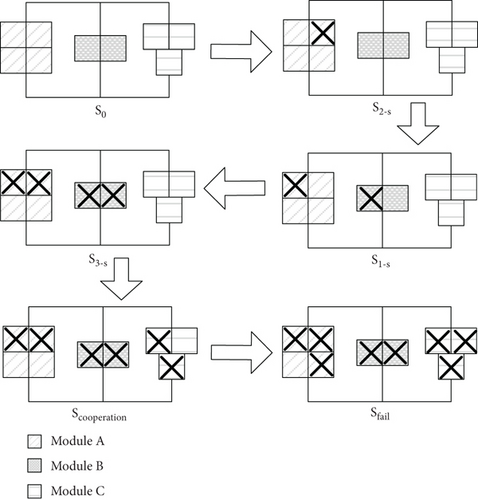
The reconfiguration behavior of the IMA system is controlled by the generic system management. When the reconfiguration is triggered due to the module failure, the generic system management obtains the configuration information from the blueprint system to realize the system reconfiguration. The following example illustrates the reconfiguration process of the IMA system. Assuming that an IMA system has 3 different types of modules, module A, module B, and module C. And function X can be implemented by any types of modules independently, while the amount of different types of modules required by function X varies due to the capability of each type of modules which is different. As shown in Figure 3, the system function is firstly implemented by the module A. When the number of type A modules is insufficient, it is implemented by the module B. When the module fails and the single -type module is not enough to implement the system function, the cooperative working mode is adopted. Function X will be implemented by a combination of module B and module C.

3. System Reliability Model

3.1. Assumptions

The assumptions made by this paper are shown below:

(1)
Each module in the IMA system works in a binary state model that it is either functional or failed. Our work also can be extended to a multistate system which will take the performance degradation into account
(2)
Module failures are independent and are not repairable
(3)
The reconfiguration mechanism is reliable and will not fail
(4)
All standby modules are in a hot backup state

3.2. Model of the Integrated Modular Avionics System

We assume that the IMA platform is consisted by N types of modules, P_IMA = {M₁, M₂, …, M_N}. And there are K functions hosted in the IMA platform, F = {f₁, f₂, …, f_K}. We use an array to describe each kind of the module, M_i(Com_i, Mem_i, Cal_i, P_i, Num_i), where Com_i is the communication capacity in which each module M_i can provide, Mem_i is the storage capacity in which each module M_i can provide, Cal_i is the calculation capacity in which each module M_i can provide, and Num_i is the number of module M_i configured in the IMA platform. P_i = {p_i1, p_i2, …, p_ij}, where p_ij denotes the priority of module M_i for host function f_j, which means the priority of module M_i is different for different host function f_j. Because the requirement of different functions is varied and the capability of each type of module is different, functions can be implemented by different types of modules. denotes the number of module M_i required to perform function f_j.

3.3. Reliability Model of the Reconfigurable Integrated Modular Avionics System

We use the continuous-time Markov model to describe the reconfigurable IMA system; the state of the IMA can be cataloged into four types.

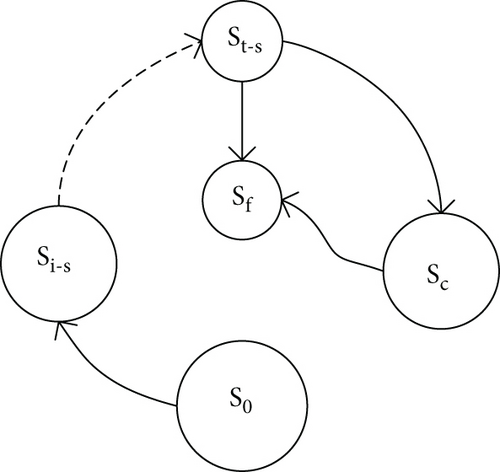
S₀: all the m modules are functioning correctly
S_i−s: the system works in a single-type module manner, which means that some modules fail, but the number of certain modules is sufficient to perform the function
S_c: the system works in a cooperative manner, which means that no single-type module can perform the function independently, but several types of modules can cooperatively work to perform the function
S_f: this state represents that the IMA system fails

The reconfiguration of the IMA system for certain functions is implemented according to the priority of the module for certain host function. In this paper, the reconfiguration mechanism for function f_j is shown in the following steps.

Step 1. All the modules are functional, and the function f_j is performed by module M_i. The system is in the state S₀.

Step 2. When some module M_i fail and if the number of functional module M_i is more than , the function f_j is still performed by module M_i. The system is in the state S_i−s.

Step 3. When more module M_i fail and the number of functional module M_i is less than , the IMA platform reconfigures according to the priority of the module for host function f_j. The function f_j is performed by module M_t with p_tj < p_ij. The system is in the state S_t−s.

Step 4. When more modules fail and no single-type module can perform the function independently, the IMA platform reconfigures in a cooperative manner. The system is in the state S_c.

Step 5. When the IMA platform cannot perform the function f_j either in a single-type module manner or in a cooperative manner, the system is in the state S_f.

To simplify the model, the cooperative working mode among different modules is unidirectional, which means that the lower priority module for function f_j can be replaced by a higher priority module but not vice versa.

The state transition diagram is shown in Figure 4.

Let R(t) denotes the system’s reliability, that is, the probability that the IMA system is functional in [0, t]. Then, the reliability of the reconfigurable IMA system can be expressed as the system in the S₀, S_i−s, and S_c states. We derive the reliability of the IMA system as follows:

(1)

For each S_i−s state, it is a (m, k)-failure tolerant model, and the reliability model of the system is as follows:

(2)

There is at least one type of the module that satisfies , i = 1, 2, …, N, and l_u = 0, 1, 2, …, m_u, u ≠ i. It is specified that the same type of the module has the same failure rate, and its reliability is expressed as r_i(t). The definitions l_i and l_u, respectively, represent the number of working modules M_i and M_u in the system. The vector m represents the number of modules configured, m = (m₁, m₂, …, m_N). Other parameters are consistent with the previous definition. In the formula, the reliability of any module M_i that satisfies the condition is calculated and then, the reliability of the remaining N − 1 types of module M_u(u ≠ i) is calculated, as shown in the multiplication operation, by multiplying the two and finally adding all the conditions that satisfy , that is, the reliability of the system in the S_i−s state.

For state S_c, it is a dynamic (m, k)-failure tolerant model. Different types of modules enter the cooperation mode according to the priority. The corresponding k and available m values also show dynamic changes. At this time, the reliability model of the system is as follows:

(3)

All types of modules satisfy , and the equation is established. y_c is defined as the state vector of the system, indicating the working state of various modules in the S_c state, y_c = (l₁, l₂, …, l_N). Define ψ_c(m) as the state vector set of the system. Other parameters are consistent with the previous definition. The reliability of each state vector y_c is calculated, as shown in the multiplication operation, then calculated the reliability of each type of the module and multiplied it, and finally added all the conditions in the state vector set ψ_c(m), that is, the reliability of the system in the S_c state.

The entire system is a joint (m, k)-failure tolerant model, so the reliability model of the reconfigurable IMA system is established as follows:

(4)

4. Model Example

4.1. Numerical Model

This section will give a numerical example to illustrate the feasibility of the proposed reliability analysis model. Suppose an IMA system has three types of modules: A, B, and C, that is, N = 3. The number of configuration for each type of the module is m = (4, 2, 3). For a function f_j, the number of requirements for each type of the module is . The priority of each type of the module for function f_j is p_ij = (1, 0, 2).

As shown in Figure 5, the reconfiguration process of IMA system function f_j includes a total of six states. At the beginning, the system has no module failure and the system prefers the second-type module with the highest priority to execute the function f_j. As the system runs, some modules fail. At this time, if , the system still prefers the type B module to execute function f_j (S_2−s), if , then the system will automatically perform the reconfiguration; it will reconfigure the function fj residing on the type B module to the higher priority type A module, and the system state is S_1−s. Until the three types of modules satisfy , the system will not be able to implement f_j through a single type of module and the system enters the joint working mode, that is, the high priority modules work in place of the low priority modules; this optimizes the performance of the system under limited resource conditions and enhances the system’s ability to cope with different missions. When the number of working modules of the system cannot meet the functional requirements, the system fails (S_fail).

The failure rates of the three types of modules are set to λ₁, λ₂, and λ₃. The probability that the system is in five working states is as follows:

(5)

Finally, we get the system reliability model of function f_j reconfiguration process as follows:

(6)

4.2. Reliability Model of Display Function

In order to further study the impact of module configuration on the reliability of the reconfigurable IMA system, this section takes parameter sensitivity analysis by taking the comprehensive display function residing on the IMA platform as an example; by changing the failure rate and priority of each module, the reliability of the system is compared and analyzed.

4.2.1. Reliability Modeling

Based on the core processing module of IMA, the comprehensive display system cross-links with multiple systems such as aircraft communication, navigation, identification, and air data and attitude heading reference to realize the display of parameter information such as flight attitude, airspeed, and air pressure altitude [19]. The FAA Advisory Circular AC 25-11B provides clear guidelines for criticality of the display information [20], as shown in Table 2.

Table 2. Critical requirements for display information.

Number	Display information	Criticality
1	Attitude	Critical
2	Airspeed	Critical
3	Barometric altitude	Critical
4	Vertical speed	Necessary
5	Corner velocity	Unnecessary
6	Sideslip/taxi, navigation, crew alerting	Necessary
7	Heading	Necessary
8	Power plant	Critical
9	Weather radar	Unnecessary

The IMA system encapsulates these display information in different types of processing modules in the form of functional applications. According to the safety related section of part 6 of STANAG 4626 [21], functional applications of the same critical level are packaged in the same module. Therefore, the resource configuration of the IMA display function is shown in Table 3.

Table 3. Resource configuration of display function of IMA.

Display information	1, 8	2, 3	4, 6, 7	5	9
Number of module A	1	1	1	1	1

Display information	1, 8	2	4, 6, 7	3	5	9
Number of module B	1	1	1	1	1	1

So far, the establishment of the joint reliability model of the display function of the IMA system is completed, as shown in Figure 6.

The IMA system performs display functions by configuring two types of modules, module A and module B, N = 2, m = (5, 6), , and P_iDis. = (0, 1). Three type A modules reside for all critical, necessary display information functions, and two reside with unnecessary display information functions. Four type B modules reside for all critical, necessary display information functions, and two reside with unnecessary display information functions. When the module fails and the reconfiguration is triggered, the system can only turn off the unnecessary display information function, the key and necessary display information functions cannot be discarded. Therefore, the module that resides the unnecessary display information function will turn off its resident function according to the system requirements and reconfigure the critical and necessary display information functions. In addition, the system prefers the type A module to perform the display function.

4.2.2. Sensitivity Analysis of Parameter λ

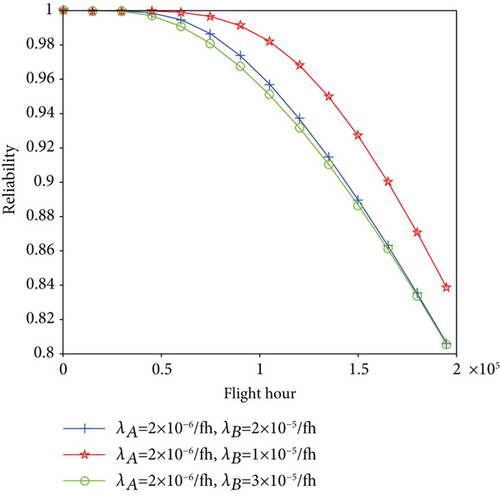
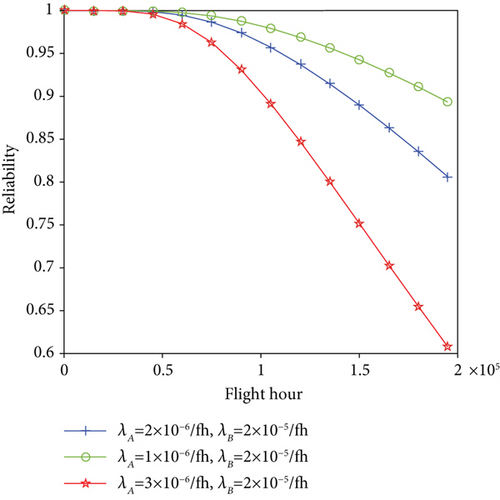
The parameter λ indicates the failure rate of the module, set the initial λ value of the type A module to λ_A = 2 × 10⁻⁶/fh and the type B module to λ_B = 2 × 10⁻⁵/fh. Then, keep the λ value of type A module unchanged and take the λ value of type B module as λ_B = 1 × 10⁻⁵/fh and λ_B = 3 × 10⁻⁵/fh, respectively; then, we obtain the relationship between system reliability and time as shown in Figure 7. Similarly, keep the λ value of type B module unchanged and take the λ value of type A module as λ_A = 1 × 10⁻⁶/fh and λ_A = 3 × 10⁻⁶/fh, respectively, as shown in Figure 8. Through observation, we found that for both types A and B of modules, when the value of λ is increased, the system reliability is reduced and when the λ value is reduced, the system reliability is improved. Meanwhile, we also found that the priority of the type A module is higher for the display function, so the system is more sensitive to the change of the λ value of the type A module. So, we can effectively improve the system reliability by configuring high priority modules with lower λ values.

4.2.3. Sensitivity Analysis of Parameter P_ij

Since the different system function requirements for modules are different, we set the P_ij value to characterize the priority of the module for function f_j to better implement the reconfigurable configuration of the IMA system. For the display function, we change the priority of module A and module B, that is, P_iDis. = (1, 0), the changes of the system reliability as shown in Figure 9. It can be seen from Figure 8 that the system reliability is significantly reduced. This is because after adjusting the priority of the type A module and the type B module, the system preferentially selects the type B module to perform the display function, but since the type B module has a larger λ value, the system reliability is degraded.

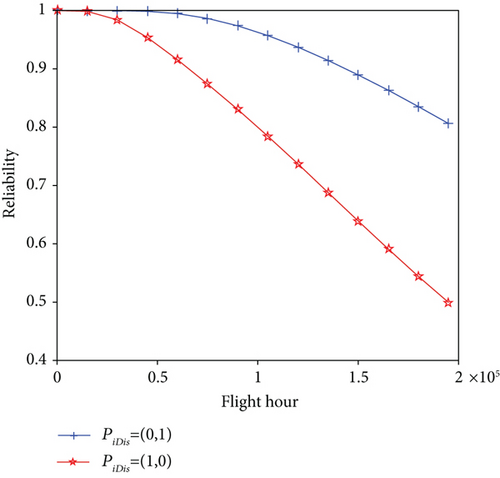
In summary, with the increase of the system module configuration, the economic cost of the system will be correspondingly improved and the correct and proper balance of the relationship between system reliability and economic benefits can provide effective guidance for system design.

5. Conclusion

This paper proposes a reliability methodology for the integrated modular avionics. Firstly, the reconfigurable ability of the IMA system is illustrated. Secondly, the joint (m, k)-failure tolerant model is introduced to analyze the reliability of the IMA system with the reconfigurable features. And a numerical example is given to show the practical use of the proposed reliability analysis model. The sensitivity of the parameters λ and P_ij that affect the reliability of the comprehensive display system is analyzed. The influence rules of parameters λ and P_ij on system reliability are obtained, which can provide guidance for the system design.

The Markov model can effectively describe the state transition of the system, while finding analytic solutions for Markov chain of complex systems is a big problem to overcome. We may pay great effort to find approximate solutions for the proposed Markov model of the reconfigurable IMA system.

Conflicts of Interest

The authors declare that they have no competing interests.

Acknowledgments

This paper was funded by Joint Funds of the National Natural Science Foundation of China and the Civil Aviation Administration of China (no. U1533105).

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Xiong H. G. and Wang Z. H., Advanced Avionics Integration Techniques, 2009, National Defense Industry Press, Beijing, China.
Google Scholar
2 Wang G. and Gu Q., Research on distributed integrated modular avionics system architecture design and implementation, 2013 IEEE/AIAA 32nd Digital Avionics Systems Conference (DASC), 2013, East Syracuse, NY, USA, 7D6-1–7D6-10, IEEEhttps://doi.org/10.1109/DASC.2013.6712647, 2-s2.0-84894426398.
10.1109/DASC.2013.6712647
Google Scholar
3 Wilson A. and Preyssler T., Incremental certification and integrated modular avionics, IEEE Aerospace and Electronic Systems Magazine. (2009) 24, no. 11, 10–15, https://doi.org/10.1109/MAES.2009.5344176, 2-s2.0-72449156070.
10.1109/MAES.2009.5344176
Web of Science® Google Scholar
4 Rushby J., Partitioning in avionics architectures: requirements, mechanisms, and assurance, 1999, NASA Langley Technical Report Server.
Google Scholar
5 RTCA Special Committee 200, Integrated Modular Avionics (IMA) development guidance and certification considerations, Rtca/Do-297, 2005, 1–18.
Google Scholar
6 Aeronautical Radio Inc, ARINC 653, Avionics Application Software Standard Interface, 1997, Aeronautical Radio Inc.
Google Scholar
7 Tu X., He F., Xiong H., and Liu C., Network partition method of distributed IMA and its real-time performance evaluation, Acta Aeronautica et Astronautica Sinica. (2013) 34, no. 1, 112–120.
Google Scholar
8 He F. and Li E., Deterministic bound for avionics switched networks according to networking features using network calculus, Chinese Journal of Aeronautics. (2017) 30, no. 6, 1941–1957, https://doi.org/10.1016/j.cja.2017.08.010, 2-s2.0-85034051577.
10.1016/j.cja.2017.08.010
Web of Science® Google Scholar
9 Zhou T., Xionq H., and Zhang Z., Hierarchical resource allocation for integrated modular avionics systems, Journal of Systems Engineering and Electronics. (2011) 22, no. 5, 780–787, https://doi.org/10.3969/j.issn.1004-4132.2011.05.009, 2-s2.0-84555178767.
10.3969/j.issn.1004-4132.2011.05.009
Web of Science® Google Scholar
10 Zhou T. and Xiong H., Design of energy-efficient hierarchical scheduling for integrated modular avionics systems, Chinese Journal of Aeronautics. (2012) 25, no. 1, 109–114, https://doi.org/10.1016/S1000-9361(11)60368-3, 2-s2.0-84858758097.
10.1016/S1000-9361(11)60368-3
Web of Science® Google Scholar
11 Rufino J. and Craveiro J., Robust partitioning and composability in ARINC 653 conformant real-time operating systems, 1st INTERAC Research Network Plenary Workshop, 2008, Braga, Portugal, 1–3.
Google Scholar
12 Jensen D. W. and Koenck S. E., Partition processing system and method for reducing computing problems, US Patent 8,489,846, 2013.
Google Scholar
13 Simpson M., Middha B., and Barua R., Segment protection for embedded systems using run-time checks, Proceedings of the 2005 International Conference on Compilers, Architectures and Synthesis for Embedded Systems - CASES ′05, 2005, San Francisco, CA, USA, 66–77, https://doi.org/10.1145/1086297.1086307.
10.1145/1086297.1086307
Google Scholar
14 Chen Y., Li Q., Zhao C. X., and Xiong Y., OBDD-based reliability analysis for avionics networks, Systems Engineering and Electronics. (2013) 35, no. 1, 230–236.
Google Scholar
15 Conmy P. and McDermid J., High level failure analysis for Integrated Modular Avionics, 3, Proceedings of the Sixth Australian Workshop on Safety Critical Systems and Software - SCS ‘01, 2001, Brisbane, Australia, 13–21, Australian Computer Society, Inc.
Google Scholar
16 Suo D., An J., Wu J., and Zhu J., Filling the gap between IMA development and safety assessment through safety-driven model-based system engineering, 2012 IEEE/AIAA 31st Digital Avionics Systems Conference (DASC), 2012, Williamsburg, VA, USA, 6C6-1–6C6-9, IEEEhttps://doi.org/10.1109/DASC.2012.6382394, 2-s2.0-84872441327.
10.1109/DASC.2012.6382394
Google Scholar
17 Wan J., Xiang X., Bai X., Lin C., Kong X., and Li J., Performability analysis of avionics system with multilayer HM/FM using stochastic Petri nets, Chinese Journal of Aeronautics. (2013) 26, no. 2, 363–377, https://doi.org/10.1016/j.cja.2013.02.014, 2-s2.0-84876798929.
10.1016/j.cja.2013.02.014
Web of Science® Google Scholar
18 Wang G. Q., Gu Q. F., Wang M., and Zhang L. H., Research on the architecture technology for new generation integrated avionics system, Acta Aeronautica et Astronautica Sinica. (2014) 35, no. 6, 1473–1486.
Google Scholar
19 Song C. Y., Yang Y. H., and Yang M., The integrated information display system of aircraft based on APEX, First China Aviation Science and Technology Conference, 2013, Beijing, China, 171–175.
Google Scholar
20 FAA, AC 25-11B, Advisory Circular: Transport Category, Airplane Electronic Display System, 2014, Federal Aviation Authority, Washington, DC, USA.
Google Scholar
21 ASAAC, Final Draft of Proposed Guidelines for System Issues, Vol. 7: Safety: ASAAC-STANAG 4626 (Part VI), 2004, North Atlantic Treaty Organization, Brussels, Belgium.
Google Scholar

Citing Literature

All articles

Reliability Analysis of the Reconfigurable Integrated Modular Avionics Using the Continuous-Time Markov Chains

Abstract

1. Introduction