Abstract and Applied Analysis
Volume 2018, Issue 1 1705409
Research Article
Open Access

Optimal Rational Approximations by the Modified Fourier Basis

Arnak V. Poghosyan, 

Corresponding Author

Arnak V. Poghosyan

Institute of Mathematics, Armenian National Academy of Sciences, 24/5 Marshal Baghramyan Ave., 0019 Yerevan, Armenia nas.gov.ua

Search for more papers by this author
Tigran K. Bakaryan, 

Tigran K. Bakaryan

Institute of Mathematics, Armenian National Academy of Sciences, 24/5 Marshal Baghramyan Ave., 0019 Yerevan, Armenia nas.gov.ua

Search for more papers by this author
First published: 01 April 2018
https://doi.org/10.1155/2018/1705409
Citations: 3
Academic Editor: Beong In Yun

Abstract

We consider convergence acceleration of the modified Fourier expansions by rational trigonometric corrections which lead to modified-trigonometric-rational approximations. The rational corrections contain some unknown parameters and determination of their optimal values for improved pointwise convergence is the main goal of this paper. The goal was accomplished by deriving the exact constants of the asymptotic errors of the approximations with further elimination of the corresponding main terms by appropriate selection of those parameters. Numerical experiments outline the convergence improvement of the optimal rational approximations compared to the expansions by the modified Fourier basis.

1. Introduction

The modified Fourier basis
(1)
was originally proposed by Krein [1] and thoroughly investigated in a series of papers [2–10].
Let MN(f, x) be the truncated modified Fourier series
(2)
where
(3)
Obviously, for even functions on [−1,1], expansions by the modified Fourier basis coincide with the expansions by the classical Fourier basis
(4)
Moreover, the modified Fourier basis can be derived from the other classical basis on [0,1]
(5)
by means of a change of variable.

The first results concerning the convergence of the expansions by the modified Fourier basis appeared in the works [2, 8–10]. We present two theorems for further comparisons.

Theorem 1 (see [10].)Assume f ∈ C2[−1,1] and f′′ ∈ BV[−1,1]. If |x| < 1, then

(6)
Otherwise,
(7)

Under some additional requirements, the convergence rate is faster.

Theorem 2 (see [2], [10].)Assume f ∈ C2q+2(−1,1), f(2q+2) ∈ BV[−1,1], q ≥ 1, and f obeys the first q derivative conditions:

(8)
If |x | < 1, then
(9)
Otherwise,
(10)

Overall, we see better convergence rates compared to the classical Fourier expansions [11]. This can be explained by faster decay of coefficients :
(11)
compared to the classical ones when f is smooth enough but nonperiodic on [−1,1]. Estimate (11) can be explained by a nonperiodicity of the basis functions sin⁡π(n − 1/2)x on [−1,1].
Convergence acceleration of the modified Fourier expansions by means of rational corrections was considered in [6]. Here, we continue those investigations. More specifically, consider a finite sequence of real numbers , p ≥ 1 and, by , denote the following generalized finite differences:
(12)
By , we denote the classical finite differences which correspond to generalized differences with θ ≡ 1. It is easy to verify that
(13)
Let
(14)
where
(15)
Consider two sequences of real numbers and . Let and . Let μj(k, θ) be defined by the following identities:
(16)
By means of sequential Abel transformations (see details in [6]), we derive the following expansions of errors (15):
(17)
where
(18)
(19)
These expansions lead to the following modified-trigonometric-rational (MTR-) approximations:
(20)
with the error
(21)
A crucial step for realization of the rational approximations is determination of parameters θc and θs. Different approaches are known for solution of this problem (see [12–19]). In general, appropriate determination of these parameters leads to rational approximations with improved accuracy compared to the classical ones in case of smooth f. However, the rational approximations are essentially nonlinear in the sense that
(22)
as for each approximation we need to determine its own θc and θs vectors.
In [6], those parameters were determined from the following systems of equations:
(23)
which led to the Fourier-Pade type approximations [12] with better convergence for smooth functions (see [6]) compared to the expansions by the modified Fourier basis. It is rather complex approach as parameters θc and θs depend on N and systems (23) must be solved for each N.
In this paper, assuming that f is smooth on [−1,1], we consider simpler alternative approach, where θs and θc are determined as follows [14, 16, 19]:
(24)
with and independent of N. Actually, in this approach, we take into consideration only the first two terms of the asymptotic expansions of θk = θk(N) in terms of 1/N. Although parameters θc and θs in (24) depend on N, we need only to determine τc and τs which are independent of N. Hence, this approach is less complex than the modified Fourier-Pade approximations.

The main results of this paper are exact constants of the main terms of asymptotic errors and optimal parameters for improved pointwise convergence of rational approximations. First, we derive the exact estimates for the main terms of asymptotic errors without specifying parameters τc and τs. Second, we determine the optimal values of parameters τc and τs which vanish the main terms and lead to approximations with substantially better pointwise convergence rates. We found that optimal values of parameters and , k = 1, …, p, are the roots of some polynomials depending on p and q, where q indicates the number of zero derivatives in (8). Moreover, the choice of optimal parameters depends on the parity of p and also on the location of x, whether |x| < 1 or x = ±1.

For example, when p is odd and |x| < 1, the roots of the generalized Laguerre polynomial (see Appendix A) could be used for τc and τs. In this case, the convergence rate of the MTR-approximations is O(N−2q−p−[(p + 1)/2]−2) as N → ∞. It means better convergence compared to the expansions by the modified Fourier basis with improvement by factor O(Np+[(p + 1)/2]). When p is odd and x = ±1, the roots of the generalized Laguerre polynomial could be used. In this case, the convergence rate is O(N−2q−[(p + 1)/2]−1) with the improvement by factor O(N[(p + 1)/2]). The problem that we encountered is impossibility to get simultaneous optimality on |x| < 1 and at x = ±1. One must decide whether to use parameters that provide the minimal error on [−1,1], but with worse accuracy on |x| < 1, or work with optimal parameters on |x| < 1 with worse accuracy at x = ±1. We expose similar observations for even values of p.

It is important that the values of parameters τc and τs depend only on p and q and are independent of f. It means that if functions f, g, and f + g have enough smoothness and obey the same derivative conditions, the optimal approach leads to linear rational approximations in the sense that
(25)
with the same parameters θc and θs for all included functions.

The paper is organized as follows. Section 2 presents some preliminary lemmas. Section 3 explores the pointwise convergence of the MTR-approximations away from the endpoints when |x| < 1. Section 4 considers the pointwise convergence of the MTR-approximations when x = ±1. In these sections, we show also the results of numerical experiments which confirm and explain the theoretical findings. Section 5 presents some concluding remarks. Appendix A recalls some results concerning the Laguerre polynomials and Appendix B proves some combinatorial identities that we used in the proofs of lemmas and theorems.

2. Preliminaries

Throughout the paper, we assume that parameters θk, k = 1, …, p are defined by (see (24))
(26)
Let τ = {τ1, …, τp} and let coefficients γk(τ) be defined by the following identity:
(27)
For f ∈ C2q+1[−1,1], q ≥ 0, we put
(28)

The following estimates can be simply obtained by means of integration by parts of the integrals in (3).

Lemma 3. Assume f ∈ C2m+1[−1,1], m ≥ 0, and f(2m+1) ∈ BV[−1,1]. Then, the following asymptotic expansions are valid:

(29)

Lemma 4. Assume f ∈ C2m+2[−1,1], m ≥ 0, and f(2m+2) ∈ BV[−1,1]. Then, the following asymptotic expansions are valid:

(30)

Next lemma unveils the asymptotic expansions of and , where
(31)

Lemma 5. Assume f ∈ C2q+p+r+1[−1,1], f(2q+p+r+1) ∈ BV[−1,1], q ≥ 0, r ≥ 0, p ≥ 1, and

(32)
Let θk, k = 1, …, p, be defined by (26). Then, the following estimates hold for n > N as N → ∞:
(33)
(34)
where
(35)
(36)
with
(37)

Proof. In view of (12) and (26), we have

(38)
Taking into account the fact that and using (13), we get
(39)
Application of Lemma 3, when p + r is even, and Lemma 4, when p + r is odd, leads to the following asymptotic expansion (h = p − k + r):
(40)
Then,
(41)
Finally,
(42)

It remains to notice that for (see [20]). Hence, t − 2s ≥ w + p − k, and s ≤ [(t − w)/2].

3. Pointwise Convergence Away from the Endpoints

In this section, we explore the pointwise convergence of the MTR-approximations away from the endpoints. Next theorem reveals the asymptotic behavior of the MTR-approximations for |x| < 1 without specifying the selection of parameters τc and τs.

Theorem 6. Assume f ∈ C2q+p+2[−1,1], f(2q+p+2) ∈ BV[−1,1], q ≥ 0, p ≥ 1, and

(43)
Let θk, k = 1, …, p, be defined by (26). Then, the following estimates hold for |x | < 1 as N → ∞:
(44)
(45)
where
(46)

Proof. We prove only estimate (44). Estimate (45) can be handled similarly.

Taking into account the fact that θk → 1 as N → ∞, we estimate only the sums on the right-hand side of (18). By the Abel transformation, we get

(47)
Lemma 5 estimates sequences , , and as N → ∞ and n ≥ N + 1. It shows that, for r = 1 and w = 2, we have
(48)
and the third term in the right-hand side of (47) is o(N−p−2q−2). Then, with r = 1 and w = 1, we have
(49)
and the second term is O(N−p−2q−3). Finally, using the exact estimate for , we derive
(50)
which completes the proof as
(51)

Note that Theorem 6 is valid also for p = 0 which corresponds to the modified Fourier expansions (compare with Theorems 1 and 2). In that case, the exact constants of the main terms in (44) and (45) coincide with similar estimate in [3] (Theorem 2.22, page 29).

Theorem 6 shows that
(52)
if parameters θc and θs are defined by (24). We see improvement in convergence rate by factor O(Np) and this result is obtained without specifying parameters τc and τs.
Let us compare the modified Fourier expansions and MTR-approximations for a specific smooth function. Consider the following one:
(53)
for which
(54)
Hence, this function obeys first q = 1 derivative conditions (8).

Figures 1 and 2 show the behaviors of |RN| (p = 0) and |RN,p| (p = 1, 2, 3, 4), respectively, on interval [−0.7,0.7] for N = 64 while approximating (53). We used , k = 1, …, p in the rational approximations.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The graph of |RN(f, x)| on [−0.7,0.7] for N = 64 while approximating (53) by the modified Fourier expansion (2).
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The graphs of |RN,p(f, θc, θs, x)| on [−0.7,0.7] for N = 64 and different p while approximating (53) by the MTR-approximations with , k = 1, …, p.

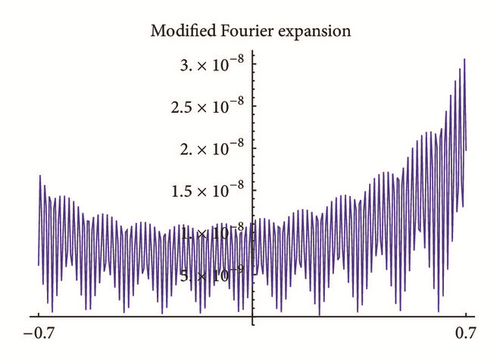
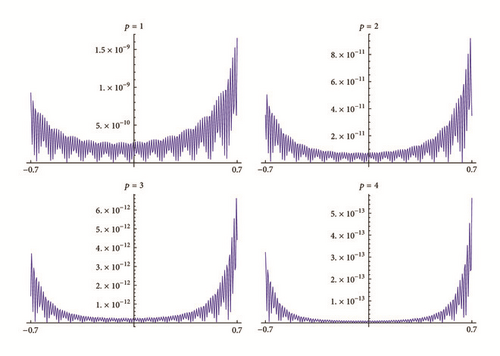
According to the results of Theorem 6, the bigger the value of p is, the higher the accuracy of the corresponding approximations is. We observe it empirically. We see that max[−0.7,0.7]⁡|RN,p| is 3 · 10−8 for p = 0, is 1.6 · 10−9 for p = 1, is 9 · 10−11 for p = 2, is 6.6 · 10−12 for p = 3, and is 5.7 · 10−13 for p = 4.

Can we improve the accuracy of the rational approximations by appropriate selection of parameters τs and τc? Further, in this section, we give positive answer to this question and show how the optimal values can be chosen.

Estimates of Theorem 6 show that improvement can be achieved if parameters are chosen such that τs = τc = τ and
(55)
By looking into the definition of hp,2q+1(τ), we observe that condition (55) can be achieved, for example, if
(56)
where Qr(k) is a polynomial of order r ≤ p − 1
(57)
with unknown coefficients cj, j = 1, …, r. Then, condition (55) follows from the well-known identity
(58)
Further, we determine the values of cj, j = 1, …, r, for improved convergence of the rational approximations.

Next result is an immediate consequence of those observations and estimates of Theorem 6.

Theorem 7. Let f ∈ C2q+p+2[−1,1], f(2q+p+2) ∈ BV[−1,1], q ≥ 0, p ≥ 1, and

(59)
Assume the polynomial
(60)
has only real-valued and nonzero roots x = zk, k = 1, …, p, and let
(61)
Then, the following estimate holds for |x| < 1:
(62)

Theorem 7 is valid only if, for given p and q, polynomial (60) has only real-valued and nonzero roots. Further, we clarify this statement by showing those cases when it is true.

By imposing extra smoothness on the underlying functions, we derive more precise estimate of (62).

First, we need estimates for and .

Lemma 8. Assume f ∈ C2q+p+[(p + 1)/2]+2[−1,1], f(2q+p+[(p + 1)/2]+2) ∈ BV[−1,1], q ≥ 0, p ≥ 1, and

(63)
Assume polynomial (60) has only real-valued and nonzero roots x = zk, k = 1, …, p, and θk is defined by (26) with τk = zk. Let w ≤ p, when w and p have the same parity, and w ≤ p + 1, otherwise. Then, the following estimates hold as N → ∞:
(64)
(65)
where
(66)
with β and defined in Lemma 5.

Proof. We prove only (64). By taking n = N in (33) and using (56), we get

(67)
This completes the proof in view of (B.15) and (B.16).

Further, in Theorems 9 and 10, we show that the pointwise convergence rate of the rational approximations depends on the asymptotic and . From the other side, Lemma 8 reveals that the convergence rates of those sequences depend on the value of (as w = 0)
(68)
When p is odd, for the highest power of 1/N, parameter j can be only j = 0. It means that Qr(k) ≡ 1. When p is even, parameter j can be j ≤ 1 which means that Qr(k) = 1 + c1k. We determine parameter c1 later.

Next theorem unveils the convergence rate of the MTR-approximations for odd values of p, when Qr(k) = Q0(k) ≡ 1. Note that, in this case, the roots of polynomial (60) coincide with the roots of generalized Laguerre polynomial (see Appendix A).

Theorem 9. Let parameter p ≥ 1 be odd, f ∈ C2q+p+(p + 1)/2+2[−1,1], q ≥ 0, f(2q+p+(p + 1)/2+2) ∈ BV[−1,1], and

(69)
Let θk, k = 1, …, p, be defined by (26), where τk are the roots of the generalized Laguerre polynomial . Then, the following estimates hold for |x| < 1:
(70)
where σ and are defined in Lemma 8.

Proof. We use (18) to estimate . The error can be estimated similarly.

Taking into account the fact that θk → 1 as N → ∞, we estimate only the sums on the right-hand side of (18). An application of the Abel transformation to the sums of leads to the following expansion of the error:

(71)
According to Lemma 5, we have
(72)
and hence the last term on the right-hand side of (71) is o(N−2q−p−(p + 1)/2−2) as N → ∞. It follows from Lemma 8 that the third term in (71) is O(N−2q−p−(p + 1)/2−3) as N → ∞. Therefore,
(73)
By Lemma 8, we have
(74)

Taking into account the fact that (see (B.16))

(75)
we conclude that σs,2q+(p + 1)/2,0(0) and σs,2q+(p + 1)/2,0(1) are nonzero only for s = q which leads to the following estimates:
(76)
From here, we get
(77)
which completes the proof.

Figure 3 shows the result of approximation of (53) by the MTR-approximations with optimal parameters , k = 1, …, p as the roots of . We see better accuracy on [−0.7,0.7] compared to nonoptimal parameters as in Figure 2. For p = 1, the improvement is almost 25 times, and for p = 3, the improvement is almost 240 times.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The graphs of |RN,p(f, θc, θs, x)| on interval [−0.7,0.7] for N = 64 while approximating (53) by MTR-approximations. Parameters and , k = 1, …, p, are the roots of which are optimal for odd p on |x | < 1 (see Theorem 9).

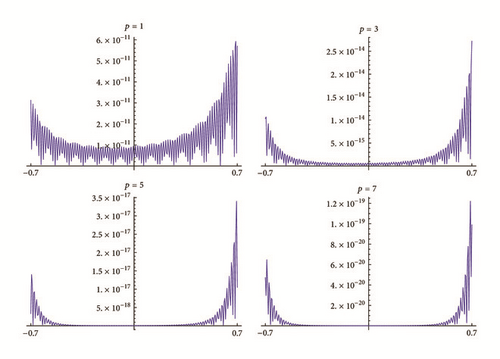
Next theorem deals with even values of p. As we mentioned above, the best convergence rate is possible if Qr(k) = Q1(k) = 1 + c1k and τk, k = 1, …, p, are the roots of (60). We need to assume that polynomial (60) has only real-valued and nonzero roots x = zk, k = 1, …, p, for fixed p and q. In two cases, we can prove that it is true. When c1 = 0, the roots of polynomial (60) coincide with the roots of the generalized Laguerre polynomial (see Appendix A). When c1 = −1/(2q + 1 + p), the roots coincide with the ones of .

We saw from our experiments (which we cannot prove theoretically) that polynomial (60) has only real-valued and nonzero roots also for other values of parameter c1. However, based on our experiments, we observed that the rational approximations have almost similar accuracy for different values of c1 while approximating smooth functions on |x| < 1.

Theorem 10. Let parameter p ≥ 2 be even, f ∈ C2q+p+p/2+2[−1,1], q ≥ 0, f(2q+p+p/2+2) ∈ BV[−1,1], and

(78)
Assume the polynomial
(79)
has only real-valued and nonzero roots x = zk, k = 1, …, p, and let θk be defined by (26) with τk = zk. Then, the following estimates hold for |x| < 1:
(80)
(81)
where σ and are defined in Lemma 8.

Proof. We prove only (80) and need only to estimate the sums on the right-hand side of (18). Similar to (71), we apply the Abel transformation and get the following expansion of the error:

(82)
Taking into account Lemma 5, we obtain
(83)
And the last term on the right-hand side of (82) is o(N−2q−p−p/2−2) as N → ∞. According to Lemma 8, the third term in the right-hand side of (82) is O(N−2q−p−p/2−3) as N → ∞. Therefore,
(84)
According to Lemma 8, we get
(85)

According to (B.16), we have

(86)
Hence, σs,2q+(p + 1)/2,j(0),   j = 0,1 and σs,2q+(p + 1)/2,1(1) are nonzero only for s = q, which leads to the following estimates:
(87)

Finally, from (84), we get

(88)
which completes the proof.

Theorems 9 and 10 conclude that by appropriate determination of parameters and , k = 1, …, p, we get extra improvement of the convergence rate of the MTR-approximations by factor O(N[(p + 1)/2]) compared to Theorem 6. Final improvement compared to the modified expansion is by factor O(Np+[(p + 1)/2]).

Let us return to MTR-approximations of (53). Figure 4 shows the results of approximation of (53) by the MTR-approximations with even p. Parameters , k = 1, …, p are selected as the roots of . Compared with Figure 2, we see better accuracy on |x| < 1. For p = 2, the improvement is almost 27 times, and for p = 4, the improvement is almost 200 times.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The graphs of |RN,p(f, θc, θs, x)| on interval [−0.7,0.7] for N = 64 while approximating (53). Parameters and , k = 1, …, p, are the roots of .

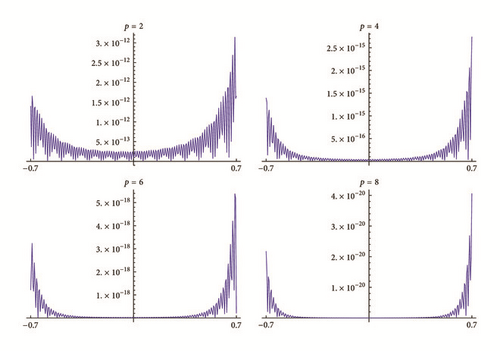
Figure 5 shows similar results with parameters , k = 1, …, p, as the roots of . In the next section, we will prove that those parameters provide improved accuracy also at x = ±1 for some p and q. We see that both choices of parameters provide similar results on |x| < 1.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
The graphs of |RN,p(f, θc, θs, x)| on interval [−0.7,0.7] for N = 64 while approximating (53). Parameters and , k = 1, …, p, are the roots of .

4. Pointwise Convergence at the Endpoints

In this section, we explore the pointwise convergence of the MTR-approximations at the endpoints x = ±1. Next theorem explores the convergence of the rational approximations without determining parameters τc and τs.

Theorem 11. Assume f ∈ C2q+p+1[−1,1], f(2q+p+1) ∈ BV[−1,1], q ≥ 0, p ≥ 1, and

(89)
Let θk, k = 1, …, p be defined by (26). Then, the following estimates hold:
(90)
where hp,m(τ) is defined by (46).

Proof. In view of (18) and (19), we write

(91)
(92)

Now, the proof immediately follows from the estimates of Lemma 5 by taking w = 0, r = 0 and by recalling that αp−k,p−k = (−1) p−k(p − k)!.

Note that this theorem is valid also for p = 0 which corresponds to the expansions by the modified Fourier basis (compare with Theorems 1 and 2).

Exact constants of the main terms in (90), for p = 0, can be found also in [10] (Theorem 3.2). We see that, in general, rational corrections do not increase the convergence rates of modified Fourier expansions at the endpoints x = ±1 without specifying appropriately parameters τc and τs. Both approaches have the same convergence rates O(N−2q−1).

Moreover, as Figure 6 shows, without reasonable selection of the parameters, modified Fourier expansions have better accuracy compared to “nonoptimal” rational approximations at x = ±1.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
The graphs of |RN,p(f, θc, θs, x)| for p = 0,1, 2,3 and N = 64 while approximating (53) at the points x = ±1. In rational approximations, we took , k = 1, …, p.
Is it possible to improve the accuracy by appropriate selection of parameters τc and τs? The answer is positive and the solution is in the estimates of Theorem 11. Like the previous section, we put
(93)
where
(94)
Now, the property hp,2q(τ) = 0 follows from the identity
(95)

Next theorem is the result of these observations and Theorem 11.

Theorem 12. Let f ∈ C2q+p+1[−1,1], q ≥ 0, p ≥ 1, f(2q+p+1) ∈ BV[−1,1], and

(96)
Assume the polynomial
(97)
has only real-valued and nonzero roots x = zk, k = 1, …, p, and let
(98)
Then,
(99)

Note that Theorem 12 is valid only for those parameters p and q when polynomial (97) has only real-valued and nonzero roots. Further, we clarify this property with more details.

Our next goal is derivation of the exact convergence rate of (99).

Lemma 13. Assume f ∈ C2q+p+[(p + 1)/2]+1[−1,1], q ≥ 0, p ≥ 1, f(2q+p+[(p + 1)/2]+1) ∈ BV[−1,1], and

(100)
Assume the polynomial
(101)
has only real-valued and nonzero roots x = zk, k = 1, …, p, and let θk be defined by (26) with τk = zk. Then, the following asymptotic expansions hold:
(102)
(103)
where is the th Bernoulli number and
(104)
(105)
with β and defined in Lemma 5.

Proof. We prove only (102). In view of Lemma 5 (with w = 0) and (91), we write

(106)
We estimate the infinite sum on the right-hand side of (106) by the Euler-Maclaurin formula (see [21]). We have
(107)
where bw is the wth Bernoulli number. Then,
(108)
which completes the proof in view of (B.2) and (B.3) (see Appendix B).

By repeating the observations of previous section, it is possible to deduce that, for getting the maximal convergence rate for odd values of p, the polynomial Qr(k) can be at most degree 0 polynomial, Qr(k) = Q0(k) ≡ 1. For even values of p, Qr(k) = Q1(k) = 1 + d1k. In the first case, parameters τk are the roots of . In the second case, if d1 = 0, we get the roots of and if d1 = −1/(2q + p), we get the roots of . The next two theorems immediately follow from Lemma 13 and identity (B.12) and, we omit the proofs.

Theorem 14. Let parameter p ≥ 1 be odd, f ∈ C2q+p+(p + 1)/2+2[−1,1], q ≥ 0, f(2q+p+(p + 1)/2+2) ∈ BV[−1,1], and

(109)
Let θk, k = 1, …, p, be defined by (26), where τk, k = 1, …, p, are the roots of the generalized Laguerre polynomial . Then, the following estimates hold as N → ∞:
(110)
where δ and are defined in Lemma 13.

Figure 7 shows the result of approximation of (53) by the rational approximations with optimal values of parameters τk, k = 1, …, p, as in Theorem 14. We see that, by increasing p (p is odd), we increase the accuracy of approximations at the points x = ±1. Note that p = 0 corresponds to the classical expansion by the modified basis and we see that, in contrary to Figure 6, the optimal choice of parameters do have big positive impact on the accuracy.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
The values of −log10⁡(max⁡|RN,p(f, θc, θs, ±1)|) while approximating (53) for different N and p. Parameters and , k = 1, …, p, are the roots of the generalized Laguerre polynomial .

Comparison of Theorems 9 and 14 reveals the problem of the optimal rational approximations which is in the difference of optimal values of parameters τk for |x| < 1 and x = ±1. On |x| < 1 and x = ±1, the optimal values are the roots of and , respectively. The choice of will result in better accuracy on overall [−1,1] by the uniform norm, but on |x| < 1 the rate of convergence will be worse by factor O(N).

Next theorem explores even values of p.

Theorem 15. Let parameter p ≥ 2 be even, f ∈ C2q+p+p/2+2[−1,1], q ≥ 0, f(2q+p+p/2+2) ∈ BV[−1,1], and

(111)
Assume the polynomial
(112)
has only real-valued and nonzero roots x = zk, k = 1, …, p, and let θk be defined by (26) with τk = zk. Then, the following asymptotic expansions hold:
(113)
(114)
where
(115)
with δ and defined in Lemma 13.

Estimates (113) and (114) are valid if polynomial (112) has only real-valued and nonzero roots. As we mentioned above, in two particular cases when d1 = 0 and d1 = −1/(2q + p), the roots of the polynomial coincide with the roots of and , respectively. Both Laguerre polynomials have only real-valued and positive roots and Theorem 15 is valid in both cases. The choice of polynomial is reasonable as it will provide optimal rational approximation both on |x| < 1 (see Theorem 10) and at x = ±1 for some p and q.

Figure 8 shows the result of application of the rational approximations to function (53) with optimal values of parameters τk, k = 1, …, p, as the roots of .

Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
The values of −log10⁡(max⁡|RN,p(f, θc, θs, ±1)|) while approximating (53) for different N and p. Parameters and , k = 1, …, p, are the roots of the generalized Laguerre polynomial .
Now, we show that, for some p and q, estimates (113) and (114) can be improved with appropriate selection of parameter d1. Assume that, for given p and q, it is possible to vanish Φq,p(d1) by appropriate selection of d1 in (113). Then, we derive
(116)
or
(117)
in case of smoother functions. Similarly, if by appropriate selection of parameter d1, then,
(118)
or
(119)
in case of smoother functions.
The problem is that we cannot vanish both Φq,p(d1) and simultaneously by the same d1. Hence, we decompose a function into even and odd parts and perform separate optimizations in terms of parameter d1. In order to choose parameter d1 appropriately, we need to have
(120)
(121)
for even and odd functions, respectively.
Then, we put
(122)
Finally, we put and into (112) and if that polynomials have only real-valued and nonzero roots, the optimization process will succeed. Tables 1 and 2 show that, except some special cases, we can optimize estimates of Theorem 15.
Table 1. The values of and the roots of (112) for p = 2,4, 6 and 0 ≤ q ≤ 6.
 q 0 1 2 3 4 5 6
  −1 1 1/3 1/5 1/7 1/9 1/11
 τ1 −1.41 2.71 4.26 5.89 7.57 9.28 11.01
 τ2 1.41 13.29 11.74 13.31 15.29 17.39 19.53
  
  −3/14 −3/2 3/10 3/22 3/34 3/46 3/58
 τ1 0.12 −27.44 2.61 3.81 5.10 6.45 7.85
 τ2 1.09 1.57 5.86 7.50 9.23 10.99 12.78
 τ3 3.46 4.44 10.85 12.72 14.76 16.86 18.98
 τ4 7.91 9.43 22.28 21.43 23.15 25.36 27.71
  
  −1/11 −1/5 1 1/7 1/13 1/19 1/25
 τ1 0.18 −0.74 1.96 2.90 3.95 5.07 6.25
 τ2 1.00 1.34 4.28 5.57 6.98 8.46 9.98
 τ3 2.60 3.41 7.51 9.04 10.76 12.54 14.35
 τ4 5.15 6.45 11.99 13.62 15.55 17.59 19.67
 τ5 8.96 10.74 18.54 19.91 21.87 24.08 26.38
 τ6 14.84 17.18 75.72 31.25 31.35 33.32 35.69
Table 2. The values of and the roots of (112) for p = 2,4, 6 and 0 ≤ q ≤ 4.
 q 0 1 2 3 4 5 6
  − − 1/2   1/4 1/6 1/8 1/10
 τ1 − − 4.417 6 7.653 9.347 11.07
 τ2 − − 13.58 14 15.68 17.65 19.73
  
  −3/20 −3/8 3/4 3/16 3/28 3/40 3/52
 τ1 0.23 −1.95 2.70 3.87 5.14 6.48 7.87
 τ2 1.35 1.83 6.09 7.63 9.31 11.05 12.83
 τ3 3.77 4.96 11.41 13.01 14.93 16.98 19.07
 τ4 8.249 10.16 35.80 22.99 23.76 25.69 27.92
  
  −1/14 −1/8 −1/2 1/4 1/10 1/16 1/22
 τ1 0.20 0.53 −16.59 2.94 3.98 5.09 6.27
 τ2 1.06 1.80 2.07 5.67 7.04 8.50 10.01
 τ3 2.71 3.88 4.52 9.23 10.86 12.60 14.40
 τ4 5.29 6.92 7.93 13.95 15.73 17.70 19.74
 τ5 9.14 11.23 12.62 20.58 22.21 24.28 26.52
 τ6 15.04 17.65 19.45 37.63 32.58 33.82 35.98

Figures 9 and 10 show the errors at x = ±1 while approximating (53) with rational approximations, where parameters and , k = 1, …, p, are selected according to Tables 1 and 2 for even and odd parts of the function, respectively. We called this approach “optimal” in the figures. For comparison, we showed also the result of approximations with parameters and , k = 1, …, p, as the roots of (see Figure 8 and Theorem 15). We called the latest “nonoptimal” in the figures. We see the impact of optimizations on the accuracy of the rational approximations at x = ±1.

Details are in the caption following the image
Figure 9
Open in figure viewerPowerPoint
The values of −log10⁡(max⁡|RN,p(f, θc, θs, ±1)|) for p = 4 and different N while approximating (53). In “nonoptimal” case, parameters and , k = 1, …, p, are the roots of . In “optimal” case, the parameters are chosen from Tables 1 and 2 for p = 4 and q = 1.
Details are in the caption following the image
Figure 10
Open in figure viewerPowerPoint
The values of −log10⁡(max⁡|RN,p(f, θc, θs, ±1)|) for p = 6 and different N while approximating (53). In “nonoptimal” case, parameters and , k = 1, …, p, are the roots of . In “optimal” case, the parameters are chosen from Tables 1 and 2 for p = 6 and q = 1.
Throughout the paper, we systematically required that approximated function f obeys first derivative conditions (8). Without those conditions, the convergence rate will remain slow. This is due to function jumps in certain derivatives at the endpoints x = ±1. If these jumps are known, the convergence acceleration can be achieved by well-known polynomial subtraction approach. For the classical Fourier series this approach has a very long history (see [3, 22–28]). For modified expansions this approach is explored in [3, 5, 7]. More specifically, we write f (see [3]) in the terms of its Lanczos representation:
(123)
where functions (polynomials) gk are chosen as such to satisfy the conditions:
(124)
Since f − gk obeys the first k derivative conditions, the new approximation
(125)
will converge with the same rate as if f obeyed those conditions. This is the polynomial subtraction technique known also as Krylov-Lanczos approach. If the jumps of f are unknown, their values can be approximated by solution of the corresponding system of linear equations (see [22]).

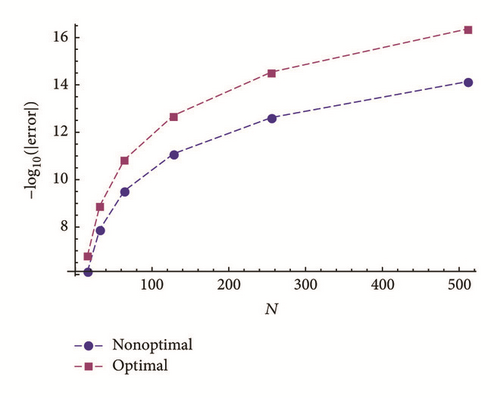
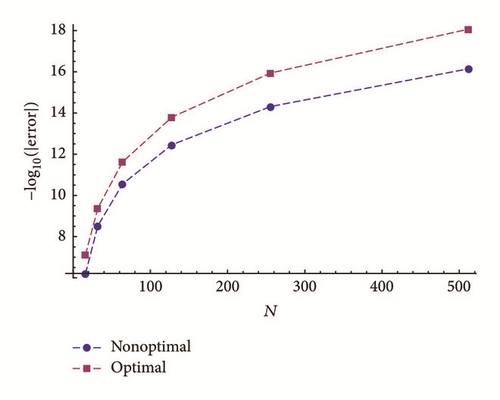
The same approach can be applied also for the MTR-approximations and in that case all theorems of this paper will remain valid without the requirements of the derivatives at the endpoints x = ±1.

5. Conclusion

In this paper, we investigated the convergence of the MTR-approximations MN,p with parameters θc and θs defined by (24). The main goal of the paper was to show that by appropriate selection of parameters τc and τs it was possible to improve substantially the pointwise convergence of the approximations. We accomplished the main goal by calculating the exact constants of the main terms of asymptotic errors and by eliminating those constants through appropriate selection of the approximation parameters. We showed that the optimization depends whether |x| < 1 or x = ±1 and also whether parameter p is odd or even.

Theorem 6 provides general estimate on |x| < 1 proving that, without optimal selection of parameters and , k = 1, …, p, the rational approximations have convergence rate O(N−2q−p−2) as N → ∞ if an approximated function has enough smoothness and obeys the first q derivative conditions (see (8)). Compared with the modified Fourier expansions (see Theorems 1 and 2 or the same theorem with p = 0), the improvement is by factor O(Np) as N → ∞.

Theorem 9 gave the optimal choice for parameters τk when |x| < 1 and p was odd. If , k = 1, …, p, were the roots of the generalized Laguerre polynomial then the rational approximations had convergence rate O(N−2q−p−[(p + 1)/2]−2) with improvement by factor O(N[(p + 1)/2]) compared to nonoptimal choice of parameters (Theorem 6). The improvement was by factor O(N[(p + 1)/2]+p) compared to the expansions by the modified Fourier basis.

In case of even values of p and |x| < 1 (Theorem 10), possible selection set of optimal parameters is wider. If for given p and q the polynomial
(126)
has only nonzero and real-valued roots x = zk, k = 1, …, p, then, selection provides better convergence rate O(N−2q−p−[p/2]−2) compared to the estimate of Theorem 6 and improvement is by factor O(N[p/2]). Improvement is by factor O(N[p/2]+p) compared to the expansions by the modified Fourier basis. The problem is to find the values of c1 in (126) for which it will have only real-valued and nonzero roots. In two cases it is obvious. When c1 = 0, the roots of (126) coincide with the roots of . When c1 = −1/(2q + p + 1), the roots coincide with the ones of . In both cases all roots are positive.

Theorem 11 imparts the convergence rate O(N−2q−1) of the rational approximations at x = ±1 without optimal selection of parameters. Comparison with Theorems 1 and 2 shows no improvement. Moreover, as our experiments show (see Figure 6) rational approximations without reasonable selection of parameters τk can perform worse at x = ±1 compared to the expansions by the modified Fourier basis.

Theorem 14 found the optimal values of parameters for odd p for better convergence rate at x = ±1. It proved that the best accuracy could be achieved when parameters were the roots of the generalized Laguerre polynomial . For that choice, the convergence rate was O(N−2q−[(p + 1)/2]−1) and improvement was by factor O(N[(p + 1)/2]) compared to the modified Fourier expansions.

We see that when p is odd, the optimal choices for |x| < 1 and x = ±1 are different. The choice of polynomial will provide the minimal uniform error on [−1,1], but, for |x| < 1, the convergence rate will be worse by factor O(N) compared to the optimal choice .

In case of even p, we obtained similar results. Theorem 15 outlines the set of optimal parameters. If for given p and q the polynomial
(127)
has only real-valued and nonzero roots x = zk for some d1, then, selection will provide convergence rate O(N−2q−[p/2]−1) with improvement by factor O(N[p/2]) compared to the modified Fourier expansions. The problem is the same as that for polynomial (126). Polynomial (127) must have only real-valued and nonzero roots for the selected d1. Fortunately, two such selections are known. When d1 = 0 or d1 = −1/(2q + p), the roots of (127) coincide with the ones of and , respectively. The choice of is better as it will provide optimal approximations for both |x| < 1 and x = ±1. However, estimates of Theorem 15 allow determining parameter d1 for even more better convergence rate. Tables 1 and 2 show some values of d1 and parameters τk that will provide convergence rate O(N−2q−[p/2]−2) with improvement by factor O(N). The problem is that the latest choice is not optimal for |x| < 1. It will give worse accuracy compared to the optimal selection for |x| < 1. Convergence rate will degrade by factor O(N). As in case of odd p, a user of the algorithms must decide which choice will be more appropriate to select, the best approximation on overall [−1,1] with worse accuracy on |x| < 1, or the best accuracy on the latest one.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

The research of the second author was supported by SCS Grant 16A-1a40.

    Appendix

    A. Laguerre Polynomials

    The differential equation [29]
    (A.1)
    is known as Laguerre differential equation. If p is a natural number, the solution of (A.1) reduces to a polynomial. When properly normalized, the polynomial is known as the Laguerre polynomial Lp(x). One of the normalizations is given by the Rodrigues formula:
    (A.2)
    This choice leads to the following closed form for the Laguerre polynomials:
    (A.3)
    Generalized Laguerre polynomials are defined by the following relation:
    (A.4)
    with the closed form
    (A.5)
    The generalized Laguerre polynomials are orthogonal over [0, ∞) with the weight function xαe−x
    (A.6)
    which leads to the property that has p real-valued and strictly positive simple roots.

    B. Some Combinatorial Identities

    In Section 2, we defined δs,t(w) by the following equation (see (104)):
    (B.1)
    where βk,s,t are defined by (35). We explore some properties of δs,t,j(w).
    First, we prove that
    (B.2)
    when
    (B.3)
    We have
    (B.4)
    Then,
    (B.5)
    where S(n, k) are the Stirling numbers of the second kind (see [30]). Applying the well-known property [30] of the Stirling numbers
    (B.6)
    where ct(m) are the associated Stirling numbers of the second kind, we can write
    (B.7)
    Thus, for δs,t,j(w), we obtain
    (B.8)
    It remains to notice that the expression
    (B.9)
    is a (2t − 2s − u + r − 2q + j + w)-degree polynomial of k, and hence we can write
    (B.10)
    with some coefficients dm. Therefore,
    (B.11)
    where αm,p are defined by (37). It is easy to verify that 2t + j + w − 2s − u + r − 2q < p, which completes the proof as αm,p = 0 for m < p.
    Second, in view of (B.11), we similarly prove that
    (B.12)
    In Section 3, we defined coefficients σs,t,j(w) as follows:
    (B.13)
    where βk,s,t are defined in Lemma 5. Similar to (B.11), we derive that
    (B.14)
    and, here, we observe that
    (B.15)
    (B.16)

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.