International Journal of Rotating Machinery
Volume 2017, Issue 1 8761375
Research Article
Open Access

Influence of Critical Flow Rates on Characteristics of Enforced and Shear Flows in Circular Convergent-Divergent Channels

Leonid A. Savin, 

Leonid A. Savin

Department of Mechatronics and International Engineering, Orel State University Named after I. S. Turgenev, Orel 302026, Russia oreluniver.ru

Search for more papers by this author
Alexey V. Kornaev, 

Alexey V. Kornaev

Mechatronics and International Engineering Research Center, Orel State University Named after I. S. Turgenev, Orel 302026, Russia oreluniver.ru

Search for more papers by this author
Elena P. Kornaeva, 

Corresponding Author

Elena P. Kornaeva

Modeling of Hydro and Mechanical Systems Research Laboratory, Orel State University Named after I. S. Turgenev, Orel 302026, Russia oreluniver.ru

Search for more papers by this author
First published: 12 June 2017
https://doi.org/10.1155/2017/8761375
Academic Editor: Steven Chatterton

Abstract

Analysis of the reasons of critical flow rate occurrence in hydraulic tracts of cryogenic machines has been carried out. Theoretical expressions have been derived to calculate critical velocities in a boiling multiphase medium. Applied to hybrid fluid-film bearings with throttles for lubricant supply, a mathematical model has been developed to calculate pressure distribution and hydrodynamic reaction forces of a lubricant considering the influence of steam content and critical flows in throttle devices. Numerical results of phase state and load capacity calculations of a hybrid fluid-film bearing under lubricant’s critical flow rates condition have been presented.

1. Introduction

One could note the tendency to widen the field of application of cryogenic and low-boiling liquids, for example, liquid O2, H2, methane, and noble gases, as fuel components and parts of technological machines and cooling systems. These materials have particular thermophysical properties, namely, low viscosity, compressibility in liquid state, and low boiling temperatures Tboil. For instance, under pressure of 1 atm Tboil of oxygen is around 90 K, hydrogen—around 20 K, methane—around 110 K, propane—around 230 K, and neon—around 28 K [1]. Phase state diagram presented in Figure 1 in P-T (pressure-temperature) coordinates shows the following zones of states of aggregation: gas, liquid, plasma, and solid. Under ultrahigh pressures (P > 10 MPa) even hydrogen can have liquid and solid metal state. Triple (critical) point K separates liquid and gas from some metastatic zones where no difference between phase properties can be observed [2].

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Phase state diagram of Н2.

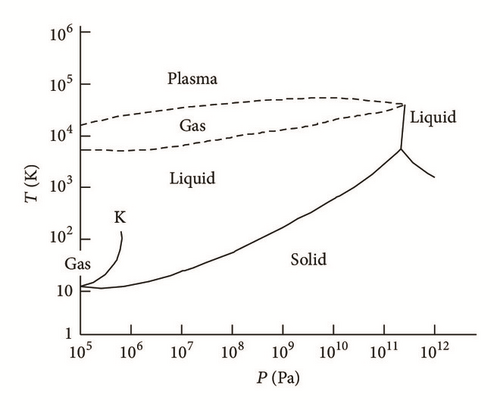
Under real conditions, these materials exist in liquid state under pressures of 1–50 MPa and are transported in special tanks. During throttling and dissipative and heat exchange processes in elements and hydraulic tracts, some phase transitions can occur as a result of boiling or vaporous cavitation resulting in multiphase flows.

Research of multiphase phenomena in hydraulic tracts of cryogenic machines has been covered in many papers. For instance, in [3] modeling of cavitation has been considered taking thermal effects into account. In [4] a joint problem of rotor’s axial and radial oscillations has been considered in case of presence of hydrodynamic forces in a multiphase flow. Cooling of impulse systems of high energy by means of using cryogenic fluids and implication of micro gas turbines in aircrafts in order to generate energy have been presented in [5]. Study of multiphase phenomena in case of fluid hammer in propulsion systems with liquid nitrogen is presented in [6]. Theoretical and experimental research of processes occurring in bearings of turbopumps of cryogenic rocket engines have been considered in [7–9]. Influence of boiling and steam-fluid content on characteristics of fluid-film bearings is considered in [10, 11]. Generally, the effect of steam phase occurrence is marked negative for the fluid film of bearings due to decrease of effective viscosity and rapid increase of compressibility which results in decrease of load capacity and damping properties and also in the increase of rotor’s oscillation amplitudes and occurrence of nonlinear biharmonic oscillations. As for positive effects, it could be noted that there are a slight decrease of power losses due to friction and some (~20%) increase of load capacity due to anticipatory boiling of lubricant in the unloaded area of a bearing which results in redistribution of pressure and change in the main reaction force vector’s direction of a fluid film. In [12–17], there is information on evaluation of operation of fluid-film bearings and hydrodynamic and gas dynamic seals under multiphase conditions of lubricants. In [14], the results of investigation of multiphase critical flows of liquid oxygen and liquid nitrogen through channels of fixed geometry are presented. The experimental results demonstrate the possibility of application of obtained results to the theory of two-phase flows. It has also been shown that the observed relations could be extrapolated and applied to other types of fluids. In [18], a hydrodynamic analysis is shown in a nonisothermal formulation for elliptic bearings based on the joint solution of the Navier-Stokes equation, continuity equation, and energy equation for multiphase flows. In order to provide the continuity condition for the area of cavitation the steam transfer equation has been introduced along with the Rayleigh–Plesset equation to take into account the growth and collapse of cavitation bubbles. This approach spares the need to impose artificial outlet boundary conditions in the form of various cavitation algorithms that are often employed to deal with lubricant film rupture and reformation. In [16], a quite critical review has been presented of the published studies, namely, of the 10 models of critical water flows, and the application limits have been set considering the industrial energy field. In [17], a homogenous model of a one-dimensional multiphase flow has been presented considering the boundary slip in the area of gas/fluid separation. It has been shown that the developed model matches experimental data better than the well-known Fauske model.

Fluid-film bearings occupy a particular niche as parts of rotor machines, and, in some cases, their application has practically no alternative. It is true, first of all, for the heavy energy machines, internal combustion engines, and high-speed machines with a turbine driver. During the hydrodynamic lubrication regime, when the surfaces are fully separated by the fluid film, their lifetime is almost unlimited and is defined by the endurance of the materials used. To provide such regime, a few requirements have to be met, namely, absence of misalignment, significant force and thermal deformations, sufficient load capacity of the fluid film, and also preservation of thermophysical and rheological properties of the film in a certain operational range. It is related largely to viscosity, on which pressure distribution is dependent, and hydrodynamic reaction forces, load capacity, and power losses due to friction, stiffness, and damping of hydrodynamic bearings. In a number of cases heat capacity, thermal conductivity, compressibility, and coefficient of expansion are also of great significance in formation of load bearing fluid film.

2. Mathematical Model

The present paper focuses on studying the influence of a physical effect of rapid decrease of the speed of sound in a liquid medium when steam phase occurs due to boiling. A good example of such effect’s occurrence is the fact that the speed of sound in water at T = 20°С and atmospheric pressure is 1450 m/s, and with steam content χ = 0.001–0.01 the same value decreases to 3–5 m/s [12]; that is, the value changes hundreds of times. Generally the dependence of the speed of sound on the steam content can be represented by a curve with an apparent peak at χ lower than 0.1%. In Figure 2 the same curve is shown for Freon-113 with various values of dryness rate.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Speed of sound-steam content relation.
Distribution of small disturbances in a multiphase medium is accompanied by a complex of specific physical processes which are subjects of thermodynamics, gas kinetics, acoustics, and gas dynamics [19, 20]. Presently there are a number of approaches: thermodynamic, based on the molecular-kinetic theory of gases, acoustic, and gas dynamics. For multiphase medium the thermodynamic theory is used more often and is based on single velocity continuum. The processes in the medium are assumed to be stationary, the influence of amplitude and frequency on the speed of sound is neglected, and nonadiabaticity is also neglected of the processes of compression and expansion due to the heat supply and energy dissipation. Generally, the Laplace equation is used in thermodynamic methods to determine the value of speed of sound:
(1)
where P is pressure, T is temperature, ρ is density, υ is specific volume, Cυ is isochoric heat capacity of liquid and steam phase along the saturation line, and χ is mass steam content.
The following expression can be obtained after a few transformations:
(2)
where ϕ is gas content, ρ′ is density of liquid phase, and ρ′′ is density of gas phase.
Considering the liquid phase incompressible (dρ′/dP = 0), one could obtain the expression to determine the speed of sound waves of low frequency distribution in some multiphase medium without considering the curvature of the surfaces of bubbles:
(3)
For a fine multiphase medium (dp < 10−5 m) when the surface tension σ and the bubble’s diameter db influence pressure in the gas phase, the expression takes the following form:
(4)
For gas lubrication there is also a possibility of occurrence of critical flows in throttle channels of a bearing. During supersonic drops, the flow rate of an ideal gas through a cylindrical channel is maximal and counterpressure does not affect it. If this process is considered isentropic and in equilibrium, then the critical velocity of a gas is determined as follows:
(5)
where indexes 1 and 2 correspond to the parameters of the flow before and after the drop of condensation, V1 is flow velocity, and αi = iρ/P is a function of enthalpy, density, and pressure, determined using the phase state diagram (or corresponding tables), where
(6)
where k is isentropic index.
For the ideal gas, the expression for critical velocity at the outlet of the channel takes the following form:
(7)
For a case of a multiphase boiling medium, expression (1) is transformed to the following form [11]:
(8)
where is isobaric heat capacity of liquid and is isobaric heat capacity of gas.

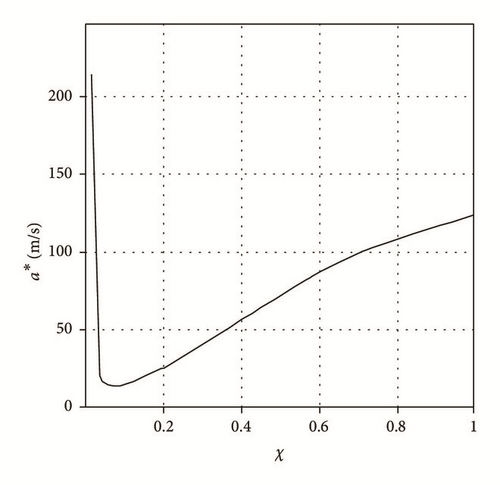
The derivatives in this expression are approximated as the ratio of finite increments Δυ′′ and Δυ′ and increments of pressure ΔP and temperature using the tables of saturated gas [1].

In hydraulic channels with fixed geometry, the chocked flow regime could occur at the outlet cross-sectional areas where local flow velocity is equal to the speed of sound. If the calculated value of the velocity V at the outlet of the throttle is higher than the critical a∗, which is principally impossible in the channels of the considered shape, then the critical flow rate through the cylindrical channel is as follows:
(9)
where ξ = 1.1–1.3 is an empirical coefficient of flow rate during the critical regime of a multiphase medium flow and dH is diameter of a throttle.
When the lubricant is supplied under pressure by means of a pump, in case of a hydrostatic bearing (see Figure 3), the presence of gas or steam medium (see Figure 4) can result in occurrence of critical flow rates when the velocity of the medium in the elements of the hydraulic tract reaches the value V = a∗, which can result in a radical change of the lubrication regime and all bearing’s characteristics. The values of the critical flow rate in throttle devices of hybrid bearings are most directly linked to the pressure in feeding chambers , MPa, that are determined based on the flow rate balance equation:
(10)
where is mass flow rate through the throttling devices in a bearing, n is number of throttle channels, Qx, Qz, Kg/s is flow rate from the chamber along the circumferential and axial coordinate, and ψ is loss coefficient at the inlet of the channel.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Calculation scheme of a hybrid bearing.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Phase diagram of a lubricant film.
When the flow velocity in the channels of a throttling device reaches the speed of sound, the chocking flow regime can be observed, that is, attainment of maximal possible flow rate of a lubricant with the given parameters
(11)
The values are internal boundary conditions when determining the pressure distribution P(x, y) in the lubricant film. The values and P(x, z) are obtained by means of joint solution of (10) and the modified Reynolds equation (12) using Seidel iteration method. For a steady-state flow, the characteristics of a fluid film are determined, given the fixed position of a rotor in the bearing (e = const, φ = 0), and the Reynolds equation is as follows:
(12)
where ρ is density, kg/m3, h = h(x) is a radial gap function, m, Ux and Uy are accordingly the tangential and normal components of the rotor’s surface velocity, m/s, μ is dynamic viscosity, Pa·s, kx, kz are turbulence coefficients, and P is pressure, Pa.
Calculation of pressure distribution in the fluid film P(x, y) under possible phase transition conditions unavoidably implies an isothermal formulation of the problem, assuming there is a change in temperature, in this case enthalpy, that depends on dissipative and heat exchange processes [10]. The energy equation for an adiabatic process taking thermal conductivity across the fluid film and dissipation into account is as follows:
(13)
where i is lubricant’s enthalpy, m2/s2, λ is heat conduction coefficient W/(m·K), Vx, Vz are velocities in circumferential and axial direction accordingly, m/s, and μ is dynamic viscosity, Pa·s.
In the set of (12) and (13), the following parameters are to be determined: pressure, temperature (enthalpy), density, viscosity, heat capacity, and turbulence coefficients. To close the system, a number of additional expressions are used: gap function h(x) = h0 − e · cos(α(x)), approximate relations between thermophysical parameters, and coefficients of turbulence kx and kz [21] as follows:
(14)
Total load capacity of a bearing can be determined as follows:
(15)
where Ri, Rj are reaction forces of a lubricant film in a corresponding direction, obtained by means of integrating the pressure distribution over the bearing’s area:
(16)
where D, L are diameter and length of the bearing accordingly and φ is position angle of the center line.

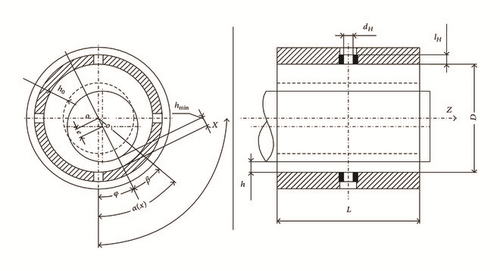
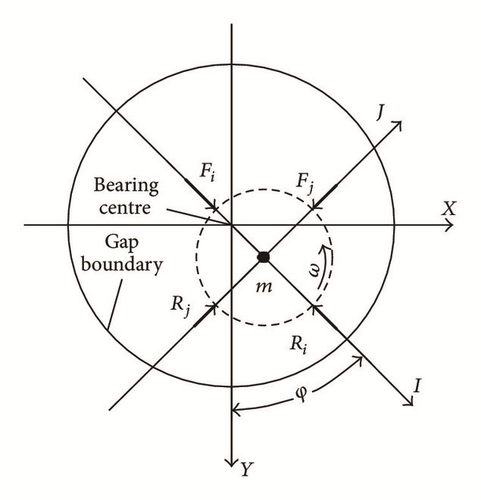
Scheme to calculation of rotor trajectories is presented in Figure 5.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Rotor trajectory calculation scheme.
Rotor is represented by a point mass on a bearing. Motion is studied in the perpendicular plane relative to the bearing’s axis. Rotor trajectories are sets of points that describe the location of a center of a shaft in the fluid film at some fixed points in time and are results of numerical integration of rotor motion equations, which in polar coordinates are as follows:
(17)
where m, q are rotor mass and imbalance accordingly, e and φ are eccentricity and rotation angle of the center lines, and Ri, Rj are reaction forces of the lubricant film:
(18)
where q is rotor’s imbalance and g is free fall acceleration.

3. Test Rig

In order to verify the obtained theoretical results and to check the working capacity of the bearing under the conditions of boiling and multiphase state of the lubricant, a series of experimental studies have been carried out using a specially designed test rig which includes a rotor machine (see Figure 6(a)), rotational driver, the data acquisition system, and the Freon contour (see Figure 6(b)). The test rig consists of two bearings (3 and 4), a shaft (16), a loading device (13), and a number of sensors.

Details are in the caption following the image
Figure 6 (a)
Open in figure viewerPowerPoint
Rotor machine test rig (a) with the scheme of the Freon contour (b).
Details are in the caption following the image
Figure 6 (b)
Open in figure viewerPowerPoint
Rotor machine test rig (a) with the scheme of the Freon contour (b).

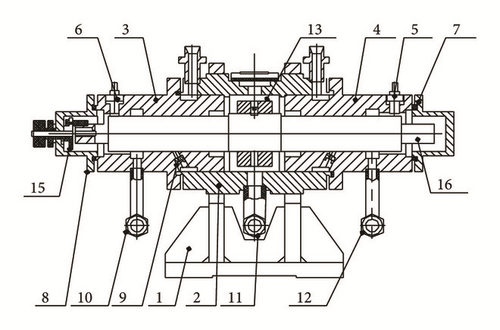
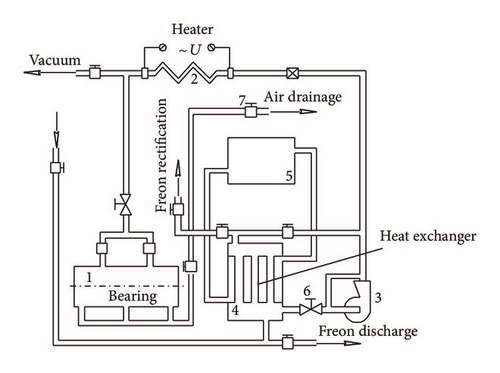
Freon-113 is used as a lubricant and allows provision of multiphase boiling in the elements of the hydraulic tract in an acceptable range of pressures. The supply system is used to store and refine Freon, to feed it to the tested bearings under certain pressure and temperature, to condensate the vapor, and to cool it down to the storage temperature. The system consists of filters, pumps, and so on.

4. Results and Discussion

In Figure 7, the numerical results are presented of the relative rotor position (similar to the load capacity in vertical direction) in a hybrid bearing with the following parameters: rotor’s mass mR = 12 Kg; imbalance q = 42 · 10−5 Kg·m; angular velocity ω = 0–2000 rad/s; diameter and length of the bearing D = 0.054 m, L = 0.07 m; diameter and length of a throttle dH = 8 · 10−4 m, lH = 3 · 10−3 m; number of throttles n = 8 (1 row); radial gap h0 = 7.5 · 10−5 m; pressure and temperature of supplied medium P0 = 0.5–0.6 MPa, T0 = 340–350 K; lubricant—Freon-113, thermodynamic properties of which under atmospheric pressure are ρ = 1540 Kg/m3, μ = 1.3 · 10−4 Pa·s/m2, and Tboil = 320 K.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Influence of steam phase concentration on the position of rotor in the bearing.

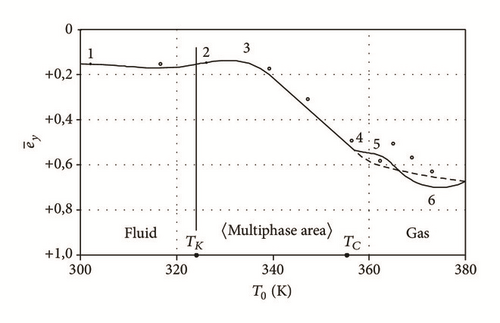
The presented temperature range along the horizontal axis which partially occupies the areas of liquid, gas, and multiphase flow is arbitrarily divided into a few character areas, the borders of which are marked with corresponding numbers. With the increase of temperature on the inlet of a hybrid bearing in the area of liquid flow (1-2), a slight decrease of bearing capacity is observed due to decrease of dynamic viscosity and density of the lubricant. Here, enthalpy of a single-phase flow is insignificantly increased due to energy dissipation as a result of friction, which also results in the decrease of load capacity W.

It shall be noted that it has been experimentally proven that load capacity of a hybrid bearing increased in the beginning of the multiphase area (2-3), which can be explained with boiling in the unloaded area of the film. The load capacity is increased due to redistribution of pressures in the lubricant’s film in the direction of pressures’ drop in the hemisphere with a big radial gap, which provides additional lifting force. The width of temperature interval of increasing load capacity is 8–12°С, and the increment of load capacity W, given certain supply pressure, eccentricity, and rotational speed, could be 5–20%. With the increase of temperature of the supplied lubricant (given that P0 = const) the boiling process spreads across the whole radial gap and results in rapid decrease of load capacity (3-4) due to a general decrease of pressure in the film. This phenomenon occurs due to decreasing density and viscosity of the steam-fluid medium with increasing steam content. Occurrence of gas phase in the feeding chambers of the unloaded part results in the flow rate limitation through them and violation of the flow rate balance equation, which results in decreasing hydrostatic pressure and provides the displacement of a rotor (4-5). The shift of the process of critical flows in pressure compensators towards the loaded part evens the pressure distribution in circumferential direction and decreases the combined reaction force (5-6). Here the critical velocity of the flow through the throttles begins to increase, which increases the volumetric flow rate through them and the hydrodynamic and gas dynamic pressure in this area of the lubricant’s film. In the surroundings of the point (6), load capacity is formed to a high extent only due to the gas dynamic effect.

It is assumed that operation in this regime is unwanted, since it is quite possible for a bearing to seize functioning due to low stiffness of the film. Increase of critical velocity with increasing steam content in the throttles provides increasing load capacity (6) and operation in a more stable gas dynamic and gas static regime, where with the increase of T0 some slight increase of W is observed due to increased viscosity of the gas. It should also be noted that critical flow can occur in the throttles at P0 > P∗ in case of a gas flow. The relative curvature in the areas (4, 5, 6, and 7) depends mainly on P0, e, G, q, and ω and is 5–15% in terms of load capacity W and 10–20 K in terms of temperature.

The numerical results (solid line) of flow rate relative to increasing temperature T0, eccentricity, and angular velocity match the experimental results (slash-dotted line) quite well (see Figure 8). There is some increase of volumetric flow rate to be observed with increasing temperature and decreasing of Q due to chocked flow through the throttle as a result of rapid decrease of the speed of sound in the multiphase medium.

Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Volumetric flow rate of the lubricant and the concentration of steam content relation.

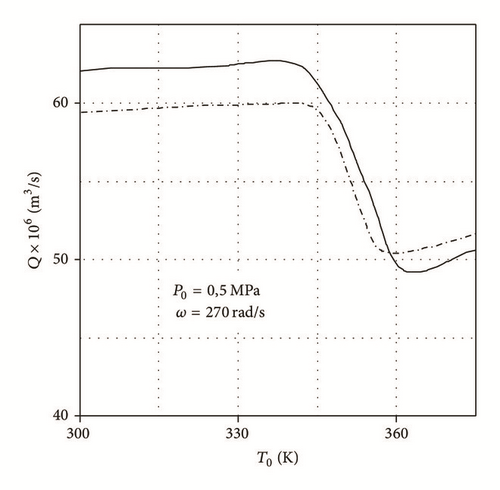
Mass flow with increasing temperature of the liquid insignificantly decreases due to a decrease in density. When the speed of sound is reached, a sharp decrease in the lubricant flow in the throttle devices in the unloaded area is observed. With an increase in temperature of the supplied lubricant process of critical flows proceeds to other throttles, which reduces the total flow rate through the bearing.

5. Conclusion

Based on the developed mathematical and simulation models, a complex of numerical experiments has been carried out in order to evaluate the influence of critical flows and flow rates of lubricants on the characteristics of pressure-shear flows. In particular, a hybrid bearing with throttles and point feeding chambers was considered. It has been identified that load capacity decreases and amplitudes of oscillations increase, once the critical flows occur in all throttling devices. This happens due to rapid pressure drop in the throttling devices and, consequently, in the fluid film. So, decrease of flow rate of the lubricant due to rapid drop in speed of sound in a multiphase medium shall not be considered positive. During critical regimes of flow almost all characteristics of a bearing change, and in case of a low value of critical flow rate a regime of “oil starvation” could occur. This could lead to the boundary friction regime and increased wear rate of surfaces of the journal and the sleeve. The obtained theoretical results have been substantiated using the developed test rig with a Freon contour.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

This work was supported by the Russian Science Foundation under Project no. 16-19-00186 and under Grant no. 14.Z56.17.1643-MK of the President of the Russian Federation. The authors gratefully acknowledge this support.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.