International Journal of Stochastic Analysis
Volume 2017, Issue 1 8019498
Research Article
Open Access

Option Price Decomposition in Spot-Dependent Volatility Models and Some Applications

Raúl Merino, 

Corresponding Author

Raúl Merino

Universitat de Barcelona, Departament de Matemàtiques i Informàtica, Gran Via 585, 08007 Barcelona, Spain ub.edu

VidaCaixa S.A., Investment Control Department, Juan Gris 2-8, 08014 Barcelona, Spain vidacaixa.es

Search for more papers by this author
Josep Vives, 

Josep Vives

Universitat de Barcelona, Departament de Matemàtiques i Informàtica, Gran Via 585, 08007 Barcelona, Spain ub.edu

Search for more papers by this author
First published: 31 July 2017
https://doi.org/10.1155/2017/8019498
Citations: 4
Academic Editor: Henri Schurz

Abstract

We obtain a Hull and White type option price decomposition for a general local volatility model. We apply the obtained formula to CEV model. As an application we give an approximated closed formula for the call option price under a CEV model and an approximated short term implied volatility surface. These approximated formulas are used to estimate model parameters. Numerical comparison is performed for our new method with exact and approximated formulas existing in the literature.

1. Introduction

In [1], a decomposition of the price of a plain vanilla call under the Heston model is obtained using Itô calculus. Recently, in [2], the decomposition obtained in [1] has been used to infer a closed form approximation formula for a plain vanilla call price in the Heston case, and on the basis of this approximated price, a method to calibrate model parameters has been developed and successfully applied. In this paper, we use the ideas presented in [1] to obtain a closed form approximation to plain vanilla call option price under a spot-dependent volatility model.

The model presented here assumes the volatility is a deterministic function of the underlying stock price, and therefore, there is only one source of randomness in the model. These models are sometimes called local volatility models in the industry and GARCH-type volatility models in financial econometrics. Recall that these models are different from the so-called stochastic volatility models, like Heston model, where the volatility process is driven by an additional source of randomness, not perfectly correlated with the stock price innovations.

As an application, for the particular case of CEV model, we obtain an approximation of the at-the-money (ATM) implied volatility curve as a function of time and an approximation of the implied volatility smile as a function of the log-moneyness, close to the expiry date. We use these approximations to calibrate the CEV model parameters.

2. Preliminaries and Notations

Let S = {St,   t ∈ [0, T]} be a positive price process under a market chosen risk neutral probability that follows the model
()
where W is a standard Brownian motion, r ≥ 0 is the constant interest rate, and θ : [0, ∞)→[0, ∞) is a function of C2([0, ∞)) such that θ(St) is a square integrable random variable that satisfies enough conditions to ensure the existence and uniqueness of a solution of (1).
The following notation will be used in all the paper:
  • (i)

    We define the Black-Scholes function as a function of t ∈ [0, T] and x, y ∈ [0, ∞) such that

    ()

  •  

    where Φ(·) denotes the cumulative probability function of the standard normal law, K and T are strictly positive constants, and

    ()

  •  

    Note that the price of a plain vanilla European call under the classical Black-Scholes theory is BS(t, St, σ) where St is the price of the underlying process at t, σ is the constant volatility, K is the strike price, and T is the expiry date.

  • (ii)

    We will denote frequently by τ≔T − t the time to maturity.

  • (iii)

    We use in all the paper the notation , where is the completed natural filtration of S.

  • (iv)

    In our setting, the call option price is given by

    ()

  • (v)

    Recall that from the Feynman-Kac formula, the operator

    ()

  •  

    satisfies .

  • (vi)

    We define the operators Λ≔x∂x, , and Γ2 = Γ∘Γ. In particular, we have that

    ()

Lemma 1. Then, for any n ≥ 2, and for any positive quantities x, y, p, and q, one has

()
where C is a constant that depends on p, q, and n.

Proof. For any n ≥ 2 we have

()
where Pn−2 is a polynomial of order n − 2 and the exponential decreasing on x of the Gaussian kernel compensates the possible increasing of x and ln⁡x.

3. A General Decomposition Formula

Here we obtain a general abstract decomposition formula for a certain family of functionals of S that will be the basis of all later computations.

Assume we have a functional of the form
()
where B is a function of C2([0, T]) and A(t, x, y) is a function of C1,2,2([0, T]×[0, ∞)×[0, ∞)).

Then we have the following lemma.

Lemma 2 (generic decomposition formula). For all t ∈ [0, T], one has

()

Proof. Applying the Itô formula to process e−rtA(t, St, θ2(St))B(t) we obtain

()

Now, applying Feynman-Kac formula for , multiplying by ert, and taking conditional expectations, we obtain

()

On the other hand, using Itô calculus rules, it is easy to see that

()

Finally, substituting this expression in (12) we finish the proof.

For the Black-Scholes function previous lemma reduces to the following corollary.

Corollary 3 (BS decomposition formula). For all t ∈ [0, T], one has

()

Proof. Applying Lemma 2 to A(t, St, θ2(St))≔BS(t, St, θ(St)) and B(t) ≡ 1, and using equalities

()
the corollary follows straightforward. Note that to apply Itô formula to Black-Scholes function, because the derivatives of this function are not bounded, we have to use an approximation to the identity and the dominated convergence theorem as it is done, for example, in [3]. For simplicity we skip this mollifying argument across the paper.

Remark 4. For clarity, in the following we will refer to terms of the previous decomposition as

()

Remark 5. In [4], an alternative formula that can be used for local volatility models is proved. The formula presented in [4] uses, as a base function, function BS(t, St, σ), but this formula is numerically worse than the new formula presented here that uses as a base function BS(t, St, θ(St)). This happens because in the formula presented in [4] the volatility is put into the approximated term, instead of keeping it on the Black-Scholes term as we do here. It is precisely because volatility is a deterministic function of the underlying asset price that we can do that.

4. Approximation Formula

In this section we obtain an approximation formula to plain vanilla call price by approximating terms (I)–(IV). The main idea is to use again Lemma 2 to estimate the errors.

Theorem 6 (BS decomposition formula with error term). For all t ∈ [0, T], one has

()
where Ω is an error. Terms of Ω are written in Appendix A.

Proof. We apply Lemma 2 to terms (I)–(IV). Concretely, functions A and B in every case are

(I)

()

(II)

()

(III)

()

(IV)

()

5. CEV Model

The constant elasticity of variance (CEV) model is a diffusion process that solves the stochastic differential equation
()
Note that, writing , CEV model can be seen as a local volatility model. This model, introduced in [5], is one of the first alternatives to Black-Scholes point of view that appeared in the literature. The parameter β ≥ 0 is called the elasticity of the volatility and σ ≥ 0 is a scale parameter. Note that for β = 1, the model reduces to Osborne-Samuelson model, for β = 0, the model reduces to Bachelier model, and for β = 1/2, the model reduces to Cox-Ingersoll-Ross model. Parameter β controls the steepness of the skew exhibited by the implied volatility.

There exists a closed form formula for call options; see [5, 6]. An approximated formula is given in [7].

5.1. Approximation of the CEV Model

Applying Corollary 3 to CEV model, we obtain the following.

Corollary 7 (CEV exact formula). For all t ∈ [0, T], one has

()

We will write
()

The exact formula can be difficult to use in practice, so we will use the following approximation.

Corollary 8 (CEV approximation formula). For all t ∈ [0, T], one has

()
where Ω is an error. Terms of Ω are written in Appendix B. We have that Ω ≤ (β − 1) 2Π(t, T, r, σ, β) and Π is an increasing function on every parameter.

Proof. The proof is a direct consequence of applying Lemma 1 to (ICEV)–(IVCEV). In Appendix C, the upper-bounds for every term are given.

5.2. Numerical Analysis of the Approximation for the CEV Case

In this section, we compare our numerically approximated price of a CEV call option with the following different pricing methods:
  • (i)

    The exact formula, see [5, 6, 8]. The Matlab code is available in [9].

  • (ii)

    The Singular Perturbation Technique, see [7].

The results for a call option with parameters β = 0.25, S0 = 100, K = 100, σ = 20%, and r = 1% are presented in Table 1.

Table 1. Call option β = 0.25, S0 = 100, K = 100, σ = 20%, and r = 1%.
Parameters Exact formula Approximation HW
 T − t Price Price Error Price Error
0.25 0.2882882 0.2882884 −1.92E − 07  0.2882019 8.64E − 05 
1 1.0103060 1.0103070 −9.78E − 07  1.0100377 2.68E − 04 
2.5 2.4709883 2.4709894 −1.04E − 06  2.4708310 1.57E − 04 
5 4.8771276 4.8771278 −2.22E − 07  4.8771099 1.77E − 05 

The results in the case that β = 0.50 are presented in Table 2.

Table 2. Call option β = 0.50, S0 = 100, K = 100, σ = 20%, and r = 1%.
Parameters Exact formula Approximation HW
 T − t Price Price Error Price Error
0.25 0.5356736 0.5356765   − 2.89E − 06  0.5354323  2.41E − 04 
1 1.3886303 1.3886529   − 2.26E − 05  1.3868801  1.75E − 03 
2.5 2.8506826 2.8507669   − 8.42E − 05  2.8450032  5.68E − 03 
5 5.1658348 5.1660433   − 2.09E − 04  5.1543092  1.15E − 02 

The results in the case that β = 0.75 are presented in Table 3.

Table 3. Call option β = 0.75, S0 = 100, K = 100, σ = 20%, and r = 1%.
Parameters Exact formula Approximation HW
 T − t Price Price Error Price Error
0.25 1.3887209 1.3887438   − 2.30E − 05  1.3883284  3.92E − 04 
1 3.0389972 3.0391797   − 1.83E − 04  3.0359001  3.10E − 03 
2.5 5.2954739 5.2961870   − 7.13E − 04  5.2835621  1.19E − 02 
5 8.2781049 8.2800813   − 1.98E − 03  8.2459195  3.22E − 02 

Finally, the results in the case that β = 0.90 are presented in Table 4.

Table 4. Call option β = 0.90, S0 = 100, K = 100, σ = 20%, and r = 1%.
Parameters Exact formula Approximation HW
 T − t Price Price Error Price Error
0.25 2.6404164 2.6404455   − 2.92E − 05  2.6401025  3.14E − 04 
1 5.5191736 5.5194053   − 2.32E − 04  5.5166821  2.49E − 03 
2.5 9.1446125 9.1455159   − 9.03E − 04  9.1349142  9.70E − 03 
5 13.5553379 13.5578351   − 2.50E − 03  13.5286009  2.67E − 02 

Note that the new approximation is more accurate than the approximation obtained in [7].

In Figure 1, we plot the surface of errors between the exact formula and our approximation.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Error surface between exact formula and our approximation for S0 = 100, σ = 20%, and r = 5%.

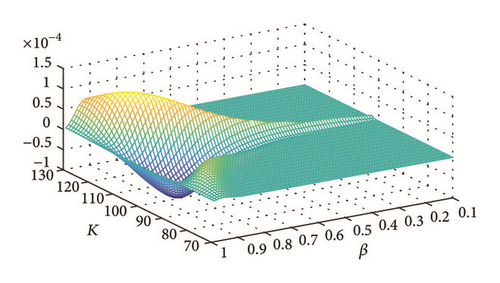
We calculate also the speed time of execution (in seconds) of every method running the function timeit of Matlab 1.000 times. The computer used is an Intel Core i7 CPU Q740 @1.73 GHz 1.73 GHz with 4 GB of RAM with a Windows 10 (×64). The results are presented in Table 5.

Table 5. Call option β = 0.9, S0 = 100, K = 100, σ = 20%, T − t = 5, and r = 1%.
Measure Exact formula Approximation HW
Average  2.56E − 02   1.73E − 04   1.67E − 04 
Standard deviation  3.03E − 03   2.86E − 05   2.52E − 05
Max  4.68E − 02   3.65E − 04   3.67E − 04
Min  2.42E − 02   1.64E − 04   1.59E − 04

We observe that singular perturbation method is the fastest method to calculate the price of CEV call option. The method developed in this work is a little more expensive in computation time. But to compute the exact price is much more expensive than any of the other two methods. Note that, in our method, we also are able to calculate at the same time the price and the Gamma of the log-normal price.

6. The Approximated Implied Volatility Surface under CEV Model

In the above section we have computed a bound for the error between the exact and the approximated pricing formulas for the CEV model. Now, we are going to derive an approximated implied volatility surface of second order in the log-moneyness. This approximated implied volatility surface can help us to understand better the volatility dynamics. Moreover we obtain an approximation of the ATM implied volatility dynamics.

6.1. Deriving an Approximated Implied Volatility Surface for the CEV Model

In this section, for simplicity and without losing generality, we assume t = 0. So T = τ denotes time to maturity. The price of an European call option with strike K and maturity T is an observable quantity which will be referred to as . The implied volatility is defined as the value I(T, K) that makes
()
Using the results from the previous section, we are going to derive an approximation to the implied volatility as in [10]. We use the idea to expand the function with respect to an asymptotic sequence converging to 0. Thus, we can write
()
and assuming β ∈ (0,2) we can choose δ = β − 1. Then, we can expand I(T, K) with respect to this scale as
()
and write
()
Let Write BS(v0) as a shorthand for BS(0, S0, v0). We can rewrite Corollary 8 as
()
On the other hand we can consider the Taylor expansion of BS(0, S0, I(T, K)) around v0. We have that
()
and this expression can be rewritten as
()
Then, equating this expression to we have
()

Note that I1(T, K) is linear with respect to the log-moneyness, while I2(T, K) is quadratic.

Remark 9. Note that the pricing formula has an error of O((β − 1) 2) as we have proved in Corollary 8, and this is translated into an error of O((β − 1) 2) into our approximation of the implied volatility. The quadratic term of the volatility shape is not accurate.

We calculate now the short time behavior of the approximated implied volatility . We write the approximated equations in terms of 1 − β, because the case β < 1 is the most interesting, and in terms of the log-moneyness ln⁡K − ln⁡S0.

Lemma 10. For T close to 0 one has

()

Proof. Note that

()

Remark 11. Note that (34) is a parabolic equation in the log-moneyness. Also, from the above expression it is easy to see that the slope with respect to ln⁡K is negative when K < S0exp⁡(3/2(1 − β)) and positive when K > S0exp⁡(3/2(1 − β)), showing that the implied volatility for short times to maturity is smile-shaped. This is consistent with the result in [11]. Furthermore, there is a minimum of the implied volatility with respect to ln⁡K attained at K = S0exp⁡(3/2(1 − β)).

Remark 12. Note that, in stochastic volatility models, the implied volatility depends homogeneously on the pair (S, K), and in fact it is a function of the log-moneyness ln⁡(S0/K). As extensively discussed in [12] and exemplified for GARCH option pricing in [13], this homogeneity property is at odds with any type of GARCH option pricing. We found also this phenomenon in the quadratic expansion (34).

The behavior of the approximated implied volatility when the option is ATM is easy to obtain:
()

6.2. Numerical Analysis of the Approximation of the Implied Volatility for the CEV Case

In this section, we compare numerically our approximated implied volatilities with implied volatility computed from call option prices calculated with the exact formula and with the ones obtained using the following formula obtained in [7]:
()
where fav = (1/2)(F0 − K) and F0 is the forward price.

In Figure 2, we can see that the implied volatility dynamics behaves well for long dated maturities and short dated maturities when β is close to 1. When this is not the case, the formula behaves well at-the-money but the error increases far from the ATM value. This behavior is a consequence of the quadratic error of our approximation.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Comparative of implied volatility approximations for S0 = 100, σ = 20%, and r = 5%.

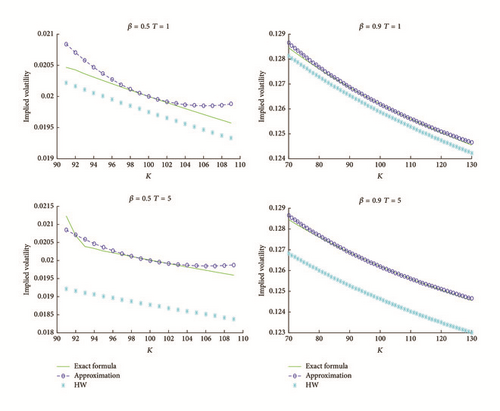
Comparing the ATM volatility structure, we have the following graphics.

In Figure 3, we observe that, for ATM options, the approximated implied volatility surface fits really well the real implied volatility structure.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Comparative of ATM implied volatility approximations for S0 = 100, σ = 20%, and r = 5%.

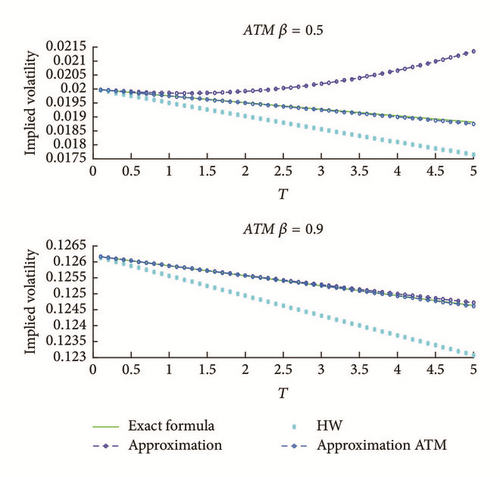
Now, we put the implied volatility approximation found in (34) into Black-Scholes formula and compare the obtained results with Hagan and Woodward results. The results for a call option with parameters β = 0.25, S0 = 100, K = 100, σ = 20%, and r = 1% are presented in Table 6.

Table 6. Call option β = 0.25, S0 = 100, K = 100, σ = 20%, and r = 1%.
Parameters Exact formula BS with implied volatility (34) HW
 T Price Price Error Price Error
0.25 0.2882882 0.2882882  3.51E − 08  0.28820185  8.64E − 05 
1 1.0103060 1.0103057  2.36E − 07  1.010037675  2.68E − 04 
2.5 2.4709883 2.4709880  2.94E − 07  2.470830954  1.57E − 04 
5 4.8771276 4.8771275  6.72E − 08  4.877109923  1.77E − 05 

The results in the case that β = 0.50 are presented in Table 7.

Table 7. Call option β = 0.50, S0 = 100, K = 100, σ = 20%, and r = 1%.
Parameters Exact formula BS with implied volatility (34) HW
 T Price Price Error Price Error
0.25 0.5356736 0.5356732  4.27E − 07   0.53543231   2.41E − 04 
1 1.3886303 1.3886267  3.65E − 06   1.386880117   1.75E − 03 
2.5 2.8506826 2.8506672  1.54E − 05   2.845003212   5.68E − 03 
5 5.1658348 5.1657911  4.36E − 05   5.154309238   1.15E − 02 

The results in the case that β = 0.75 are presented in Table 8.

Table 8. Call option β = 0.75, S0 = 100, K = 100, σ = 20%, and r = 1%.
Parameters Exact formula BS with implied volatility (34) HW
 T Price Price Error Price Error
0.25 1.3887209 1.3887176  3.29E − 06   1.388328423   3.92E − 04 
1 3.0389972 3.0389707  2.64E − 05   3.035900123   3.10E − 03 
2.5 5.2954739 5.2953686  1.05E − 04   5.283562121   1.19E − 02 
5 8.2781049 8.2778040  3.01E − 04   8.245919491   3.22E − 02 

And the results in the case that β = 0.90 are presented in Table 9.

Table 9. Call option β = 0.90, S0 = 100, K = 100, σ = 20%, and r = 1%.
Parameters Exact formula BS with implied volatility (34) HW
 T Price Price Error Price Error
0.25 2.6404164  2.6404122   4.17E − 06   2.640102524   3.14E − 04 
1 5.5191736  5.5191404   3.31E − 05   5.51668209   2.49E − 03 
2.5 9.1446125  9.1444830   1.29E − 04   9.134914233   9.70E − 03 
5 13.5553379  13.5549787   3.59E − 04   13.52860091   2.67E − 02 

Our approximation is better than Hagan and Woodward one.

We compare also execution times (see Table 10).

Table 10. Call option β = 0.9, S0 = 100, K = 100, σ = 20%, T = 5, and r = 1%.
Measure HW BS with implied volatility (34)
Average  1.67E − 04   1.66E − 04
Standard deviation  2.52E − 05   2.37E − 05
Max  3.67E − 04   3.48E − 04
Min  1.59E − 04   1.58E − 04

We can observe that both formulas are similar in computation time, with the new approximation formula being a bit faster.

6.3. Calibration of the Model

Following the ideas of [2], we propose a method to calibrate the model. This method will allow us to find σ and β using quadratic linear regression. We can recover the parameters with a set of options of the same maturity with (34) or with ATM options of different maturities (36).

6.3.1. Calibration Using the Smile of Volatility

Using a set of options with the same maturity and the parameters S0 = 100, σ = 20%, r = 5%, K = 98 ⋯ 102, T = 1, and β = 0.5. We calculate the price and their implied volatilities with the exact formula. We do a quadratic regression adjusting a parabola a + bc + cx2 with x = ln⁡K − ln⁡S0 to the implied volatilities. Using (34), it is easy to see that β = 2b/a + 1 and σ = a/Sβ−1. In this case, we have
()
from which we obtain β = 0.50233 and σ = 19.787%.
Using the same procedure, for T = 5 and β = 0.5, we find that
()
from which we obtain β = 0.51219 and σ = 18.921%.
Using the same procedure, for T = 1 and β = 0.9, we find that
()
from which we obtain β = 0.89997 and σ = 20.002%.
Using the same procedure, for T = 5 and β = 0.9, we find that
()
from which we obtain β = 0.90041 and σ = 19.963%.

6.3.2. Calibration Using ATM Implied Volatilities

Using a set of ATM options with the same maturity and parameters S0 = 100, σ = 20%, r = 5%, T = 0.3,0.5,0.8,0.9,1, and β = 0.5, we calculate the price and their implied volatilities with the exact formula. Then we do a quadratic regression adjusting a parabola a + bc + cx2 with x = T to the implied volatilities. Using (36), it is easy to see that and σ = a/Sβ−1. In this case, we have
()
from which we obtain β = 0.48324 (or β = −185.94 which we can discard) and σ = 21.607%.
Using the same procedure, for T = 1,2, 3,4, 5 and β = 0.5, we find that
()
from which we obtain β = 0.49970 (or β = −186.0055 which we can discard) and σ = 20.028%.
Using the same procedure, for T = 0.3,0.5,0.8,0.9,1 and β = 0.9, we find that
()
from which we obtain β = 0.90040 (or β = −3.6103 which we can discard) and σ = 19.963%.
Using the same procedure, for T = 1,2, 3,4, 5 and β = 0.9, we find that
()
from which we obtain β = 0.89822 (or β = −3.6081 which we can discard) and σ = 20.164%.

We have seen that to do a quadratic regression is enough to recover a good approximation of the parameters.

7. Conclusion

In this paper, we notice that ideas developed in [1] for Heston model can be used for spot-dependent volatility models. It is interesting to realize that the approximation found in this case has more terms than the one obtained for stochastic volatility models (see [4]). We have applied this technique to the CEV model, doing a comparison between exact prices, Black-Scholes using Hagan and Woodward implied volatility, and our price approximation. We have seen that our approximation is better than Hagan and Woodward approximation for pricing, but a bit more expensive in computation time. As well, we have calculated an approximation of the implied volatility as the limit of the implied volatility close to zero as a function of log-moneyness and an approximation of the ATM implied volatility as a function of time. We have compared our approximation with the exact implied volatility and Hagan and Woodward approximation. We note that if we put our implied volatility approximation into Black-Scholes function, we get a better approximation than Hagan and Woodward in the same computation time. So we have developed an easy way to calibrate CEV model that consists essentially in doing a quadratic regression.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this article.

Acknowledgments

Josep Vives was partially supported by Grant MEC MTM 2013 40782 P.

    Appendix

    In the following appendices we obtain the error terms of the decomposition in Theorem 6 (Appendix A), the same formulas in the particular case of CEV model (Appendix B), and upper-bounds for those terms using Lemma 1 (Appendix C). In all the section we write τu≔T − u.

    A. Decomposition Formulas in the General Model

    A.1. Decomposition of Term (I)

    The term (I) can be decomposed by
    ()

    A.2. Decomposition of Term (II)

    The term (II) can be decomposed by
    ()

    A.3. Decomposition of Term (III)

    The term (III) can be decomposed by
    ()

    A.4. Decomposition of Term (IV)

    The term (IV) can be decomposed by
    ()

    B. Decomposition Formulas for the CEV Model

    B.1. Decomposition of the Term (ICEV)

         
    ()

    B.2. Decomposition of the Term (IICEV)

         
    ()

    B.3. Decomposition of the Term (IIICEV)

         
    ()

      

    B.4. Decomposition of the Term (IVCEV)

         
    ()

    C. Upper-Bound First-Order Decomposition Formulas

    C.1. Upper-Bound of the Term (ICEV)

         
    ()
    where Π1(t, T, r, σ, β) is an increasing function for every parameter, Ci (i = 1, …, 5) are some constants, and C = max⁡(Ci).

    C.2. Upper-Bound of the Term (IICEV)

         
    ()
    where Π2(t, T, r, σ, β) is an increasing function for every parameter, Ci (i = 1, …, 10) are some constants, and C = max⁡(Ci).

    C.3. Upper-Bound of the Term (IIICEV)

         
    ()
    where Π3(t, T, r, σ, β) is an increasing function for every parameter, Ci (i = 1, …, 10) are some constants, and C = max⁡(Ci).

    C.4. Decomposition of the Term (IVCEV)

         
    ()
    where Π4(t, T, r, σ, β) is an increasing function for every parameter, Ci (i = 1, …, 10) are some constants, and C = max(Ci).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.