International Journal of Differential Equations

Volume 2017, Issue 1 1946304

Research Article

Open Access

Finite Time Synchronization of Extended Nonlinear Dynamical Systems Using Local Coupling

A. Acosta

School of Mathematical Sciences and Information Technology, Department of Mathematics, Yachay Tech, Urcuqui, Ecuador yachaytech.edu.ec

Search for more papers by this author

P. García,

Corresponding Author

P. García

[email protected]

orcid.org/0000-0001-8164-6759

Facultad de Ingeniería en Ciencias Aplicadas, Universidad Técnica del Norte, Ibarra, Ecuador utn.edu.ec

Search for more papers by this author

H. Leiva,

H. Leiva

School of Mathematical Sciences and Information Technology, Department of Mathematics, Yachay Tech, Urcuqui, Ecuador yachaytech.edu.ec

Search for more papers by this author

A. Merlitti,

A. Merlitti

Departamento de Estadística, Facultad de Ciencias Económicas y Sociales, Universidad Central de Venezuela, Caracas, Venezuela ucv.ve

Search for more papers by this author

A. Acosta,

A. Acosta

School of Mathematical Sciences and Information Technology, Department of Mathematics, Yachay Tech, Urcuqui, Ecuador yachaytech.edu.ec

Search for more papers by this author

P. García,

Corresponding Author

P. García

[email protected]

orcid.org/0000-0001-8164-6759

Facultad de Ingeniería en Ciencias Aplicadas, Universidad Técnica del Norte, Ibarra, Ecuador utn.edu.ec

Search for more papers by this author

H. Leiva,

H. Leiva

School of Mathematical Sciences and Information Technology, Department of Mathematics, Yachay Tech, Urcuqui, Ecuador yachaytech.edu.ec

Search for more papers by this author

A. Merlitti,

A. Merlitti

Departamento de Estadística, Facultad de Ciencias Económicas y Sociales, Universidad Central de Venezuela, Caracas, Venezuela ucv.ve

Search for more papers by this author

First published: 07 December 2017

https://doi.org/10.1155/2017/1946304

Citations: 1

Academic Editor: Peiguang Wang

Share a link

Email
Wechat
Bluesky

Abstract

We consider two reaction-diffusion equations connected by one-directional coupling function and study the synchronization problem in the case where the coupling function affects the driven system in some specific regions. We derive conditions that ensure that the evolution of the driven system closely tracks the evolution of the driver system at least for a finite time. The framework built to achieve our results is based on the study of an abstract ordinary differential equation in a suitable Hilbert space. As a specific application we consider the Gray-Scott equations and perform numerical simulations that are consistent with our main theoretical results.

1. Introduction

The synchronization of the evolution of systems that are sensitive to changes in the initial condition is a phenomenon that occurs spontaneously in systems ranging from biology to physics. As a matter of fact, starting from publications by Fujisaka and Yamada [1] and later by Pecora and Carroll [2], there have been many explanations about the occurrence of this phenomenon as well as new practical applications [3]; among these we highlight [4]. For localized systems (ODE) the problem is well understood; see, for example, [4, 5] and the references therein. On the other hand, a much smaller number of results are available for extended systems represented by partial differential equations (PDE). Among these in [6, 7], the authors have considered a pair of unidirectionally coupled systems with a linear term that penalizes the separation between the actual states of the systems. When the coupling function is linear, the synchronization problem has been addressed through different approaches like invariant manifold method via Galerkin’s approximations [8], via an abstract formulation using semigroup theory [7, 9], or numerically [6].

With the exception of works [6, 10], in the rest of the references [7–9, 11, 12] the coupling function disturbs the system in its entirety. In contrast, in [6, 10], the authors propose a synchronization scheme that does need to disturb the whole driven system. Moreover, the subset of sites in the driven system is chosen arbitrarily.

In this work we present a general procedure for two reaction-diffusion equations connected through a one-directional coupling function. We study the synchronization problem in the case where the coupling function affects the driven system in some specific regions and our approach, which is based in an abstract formulation coming from semigroup theory, allows establishing a relation between the conditions to obtain synchronization in finite time and the intensity of the coupling. To illustrate the theoretical results we consider a pair of equations of Gray-Scott [13].

The paper is organized as follows: in Section 2 we set the problem, in Section 3 we give an abstract representation of the problem in a suitable Hilbert space, in Section 4 we give the main theoretical results, as the existence of bounded solutions of the abstract equation, in Section 5 we give an example and numerical simulations of the performance of the strategy, and finally in Section 6 we give some final remarks.

2. Setting of the Problem

We consider the following system with boundary Dirichlet conditions:

()

where 0 < x < l, t > 0. D = diag(d₁, d₂, …, d_n) is a diagonal matrix with positive entries, the function

is a continuous locally Lipschitz function, and p(x) is defined as

()

where, for i ∈ {1,2, …, m}, each

and

is the characteristic function of the interval [a_i, b_i], with 0 < a₁ < b₁ < ⋯<a_m < b_m < l.

We show that the evolution of (2) closely tracks the evolution of (1) which means v behaves, in some sense, like u. To set precisely our problem and consider it in an abstract framework we start with a bounded solution

of (1). Thus, there exists N > 0 such that

()

where

are the components of the vector valued function

. Also, we assume that for any interval J = [a, b]⊂(0, +∞) there exists a constant K > 0, depending on J, such that

()

Let us define a function

()

and consider the transformation

()

If v is a solution of (2), with input

, then (6) and (7) lead us to the equation

()

Now, we consider (8) together with Dirichlet boundary conditions:

()

Our efforts will focus on problem (8)-(9). Concretely, we are interested in solutions such that the driven systems closely track the evolution of the driver systems at least for a finite time interval.

3. Preliminaries and Abstract Formulation of the Problem

In this section, by choosing an appropriate Hilbert space, we discuss some preliminaries and set our problem as an abstract ordinary differential equation. Let us start considering the Hilbert space

with the usual inner product; that is, if Φ = (Φ¹, …, Φⁿ) ^T, Ψ = (Ψ¹, …, Ψⁿ) ^T ∈ H, then

()

and the induced norm is given by

()

Next, we consider the linear unbounded operator A : D(A) ⊂ H → H defined by

()

where

()

We summarize some very well-known important properties related to the operator A:

(i)
A is a sectorial operator. As a consequence −A generates an analytic semigroup, e^−At, which is, for each t > 0, compact.
(ii)
The spectrum σ(A), of A, consists of just eigenvalues λ_i,j = d_j(iπ/l) ², with i = 1,2, … and j = 1,2, …, n. We order the set of eigenvalues {λ_i,j} according to the sequence 0 < λ₁ ≤ λ₂ ≤ ⋯→∞, where
()
(iii)
There exists a complete orthonormal set , of eigenvectors of A, such that
()
(iv)
e^−At is given by
()

In the remainder of this section we mainly follow [14, 15] and the notations used come from [15]. In order to study the nonlinear part of the abstract equation corresponding to (8)-(9), we consider the fractional power spaces and the interpolation spaces associated with the operator A. For any α ≥ 0, the domain D(A^α) of the fractional power operator A^α is defined by

()

and the operator A^α is given by

()

V^α itself becomes a Hilbert space with the V^α-inner product given by 〈Φ, Ψ〉_α

and the V^α-norm is the graph norm associated with A^α; that is, ‖Φ‖_α = ‖A^αΦ‖. Moreover, if α ≥ β, then V^α is a continuous embedding into V^β that verifies the estimate

, for all Φ ∈ V^α. In particular,

()

Also, according to Theorem 1.6.1 in [14] and the discussion given there, for 1/4 < α ≤ 1 we have that V^2α is a continuous embedding into

. Thus, there exists a positive constant C such that

()

The next proposition, whose proof is similar to the one given in [7], contains estimates relating the semigroup {e^−At} with norms ‖·‖_α and ‖·‖. Also, it will play an important role in the discussion of our main theoretical results.

Proposition 1. For each Φ ∈ V^α, α > 0, one has the following estimates:

()

Now, we associate with system (8)-(9) an abstract ordinary differential equation on H with an initial condition

()

where F, acting on [0, ∞) × V^2α, is defined by

()

For some r > 0 and 1/4 < α < 1, we assume F maps [0, ∞) × U_r into H, where U_r = {Φ ∈ V^2α : ‖Φ‖_2α ≤ r}.

The following lemma establishes that F is Lipschitz continuous in the second variable on U_r.

Lemma 2. There exists a constant L = L(U_r) such that for Φ₁, Φ₂ ∈ U_r, t > 0,

()

Proof. Given a ball of radius and center 0 in , there exists a positive constant such that for all .

For any Φ₁, Φ₂ ∈ U_r, we consider Δ≔|F(t, Φ₁)(x) − F(t, Φ₂)(x)|, 0 < x < l, and t > 0. Now, let us consider N and C as in (4) and (20), respectively. If we choose , then there exists such that

()

Therefore,

()

Thus,

()

with

()

We finish this section with a lemma that will be used to obtain our main theoretical results. It can be established as an application of Lemma 3.3.2 in [14].

Lemma 3. A continuous function Φ : (0, t₁) → V^2α is a solution of the integral equation

()

if and only if Φ is a solution of (22).

4. Main Theoretical Results

Theorem 4. For any Φ₀ ∈ int(U_r) there exists t₁ = t₁(Φ₀) > 0 such that (22) has a unique solution Φ on (0, t₁) with initial condition Φ(0) = Φ₀.

Proof. By Lemma 3, it suffices to prove the corresponding result for integral equation (29).

Choose ρ > 0, with , such that the set

()

is contained in U_r. We have, applying Lemma 2, that F is Lipschitz continuous, in the second variable, on V. Moreover, for the estimate

()

we choose

, with

. Next, we select t₁ > 0 such that

()

Let us define S as the set of continuous functions Ψ : [0, t₁] → V^2α such that on [0, t₁]. If S is endowed with the supreme norm , then it is a complete metric space.

Now, for Ψ ∈ S we define T(Ψ) acting on [0, t₁] as

()

First, we show that T maps S into itself. In fact,

()

The fact that T(Ψ) is continuous from [0, t₁] to V^2α is easily proved.

Next, we shall prove that T is a contraction. In fact, if Ψ₁, Ψ₂ ∈ S and 0 ≤ t ≤ t₁, then for we have that

()

Therefore,

for all Ψ₁, Ψ₂ ∈ S.

Finally, by the Banach fixed point theorem, T has a unique fixed point Φ in S, which is a continuous solution of integral equation (29). By Lemma 3, this is the unique solution of (22) on (0, t₁) with initial value Φ(0) = Φ₀.

The previous theorem does not tell anything about the maximal interval where Φ is defined. In this regard we have the following.

Theorem 5. Assume that for every closed set B ⊂ int(U_r), F([0, ∞) × B) is bounded in H. If Φ is a solution of (22) on (0, t₁) and t₁ is maximal, then either t₁ = +∞ or else there exists a sequence as n → ∞ such that Φ(t_n) → ∂U_r.

Proof. Suppose t₁ < ∞ and there is not neighborhood N of ∂U_r such that Φ(t) enters N for t in an interval [t₁ − ϵ, t₁), with ϵ small enough. We may take N of the form N = U_r − B where B is a closed subset of int(U_r), and Φ(t) ∈ B for t ∈ [t₁ − ϵ, t₁).

We are going to prove that there exists Φ₁ ∈ B such that Φ(t) → Φ₁ in V^2α as , and this implies that the solution may be extended beyond time t₁ (with Φ(t₁) = Φ₁), contradicting maximality of t₁.

Now let M≔sup{‖F(t, Φ)‖ : t ≥ 0, Φ ∈ B}. We first show that ‖Φ(t)‖_2α remains bounded on the interval (0, t₁); in fact

()

Now we consider the difference Φ(t) − Φ(τ) with t and τ such that t₁ − ϵ ≤ τ < t < t₁. It is obtained that

()

For each term in the right hand side we get an estimate. Let us call

, and

; now we have

()

Since e^−At is compact for t > 0, then {e^−At} is a uniformly continuous semigroup, which implies that ‖e^{−A(t−τ+ϵ)} − e^−Aϵ‖ → 0 as t → τ.

Finally from the estimates given for I₁, I₂, and I₃ we conclude that there exists Φ₁ ∈ B such that , and the proof is complete.

Corollary 6. There exists ϵ > 0 such that the solution Φ, of problem (22), satisfies the estimate

()

for all t belonging to the interval [0, ϵ).

Proof. Let B a closed subset of V^2α that contains the initial condition Φ₀ in its interior and M≔sup{‖F(t, Φ)‖ : t ≥ 0, Φ ∈ B}. There exists such that

()

Therefore

()

and the result follows due to the fact that

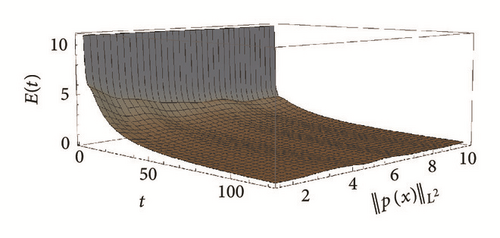
5. Example and Numerical Simulations

To illustrate our theoretical results we consider the particular case of system (1)-(2):

()

where 0 < x < l, t > 0. System (43) corresponds to the Gray-Scott cubic autocatalysis model [13] which is related to two irreversible chemical reactions and exhibits mixed mode spatiotemporal chaos. Here a, b, d₁, and d₂ are dimensionless constants, where b corresponds to the rate of conversion of a component into another, a is the rate of the process that feeds a component and drains another, and d_i, i = 1,2, are the diffusion rates. In the context of (1) the function f is defined as

and the (8), that is, e_t = De_xx + g(x, t, e), becomes in

()

Proposition 7. There exists a real value function h, continuous and increasing on the interval (0, ∞) such that |g(x, t, e)| ≤ h(|e|) for all (x, t, e) in .

Proof. The estimates

()

where

is a constant that depends on a, b, and the function p, imply that

. Thus, h could be defined by

To apply Theorem 4, we observe that for the abstract problem the extended function given in (23) becomes in

()

where

()

being Φ = (Φ₁, Φ₂) ^T,

Now, for Φ ∈ V^2α using (20) and Proposition 7 we obtain that

()

Hence F maps bounded sets in [0, ∞) × V^2α into bounded sets in H.

In order to realize a numerical implementation to illustrate the main result, the values for the constants d₁, d₂, a, and b appearing in system (43)-(44) are chosen as d₁ = 5 × 10⁻³, d₂ = 5 × 10⁻⁴, a = 0.028, and b = 0.053, and initial conditions are given by

()

In this case the Lipschitz constant L, appearing in (33), is given by

()

Figure 1 shows a qualitative result of the synchronization error as function of the time, defined as

()

and the intensity of the perturbation defined as

. There, for a fixed time, the error always is minor compared with the initial error, consistent with our main result.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Synchronization error as function of the time and the intensity of the perturbation defined as .

6. Concluding Remarks

We present a synchronization scheme of reaction-diffusion equations connected by a localized one-directional coupling function and give conditions that ensure the synchronization at least for a finite time. Conditions for synchronization depend on a sort of coupling intensity given by the L² norm of the coupling function. This norm is related to the intensity of local perturbation and its spatial extension, suggesting that this relation can be optimized in order to improve the synchronization or design of a control scheme.

Finally, although we have proven that the synchronization occurs in an interval of time, the numerical simulations suggest that this interval can be extended.

Disclosure

P. García’s permanent address is Laboratorio de Sistemas Complejos, Departamento de Física Aplicada, Facultad de Ingeniería, Universidad Central de Venezuela.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

References

1 Fujisaka H. and Yamada T., Stability theory of synchronized motion in coupled-oscillator systems, Progress of Theoretical and Experimental Physics. (1983) 69, no. 1, 32–47, https://doi.org/10.1143/PTP.69.32, MR699754.
10.1143/PTP.69.32
CAS Web of Science® Google Scholar
2 Pecora L. M. and Carroll T. L., Synchronization in chaotic systems, Physical Review Letters. (1990) 64, no. 8, 821–824, MR1038263, https://doi.org/10.1103/PhysRevLett.64.821, Zbl0938.37019, 2-s2.0-0343689904.
10.1103/PhysRevLett.64.821
CAS PubMed Web of Science® Google Scholar
3 Jovic B., Synchronization Techniques for Chaotic Communication Systems, 2001, Springer, Berlin, Germany.
Google Scholar
4 Boccaletti S., Kurths J., Osipov G., Valladares D. L., and Zhou C. S., The synchronization of chaotic systems, Physics Reports. (2002) 366, no. 1-2, 1–101, 2-s2.0-0036285235, https://doi.org/10.1016/S0370-1573(02)00137-0.
10.1016/S0370-1573(02)00137-0
CAS Web of Science® Google Scholar
5 Pecora L., Carroll T., Johnson G., Mar D., and Fink K. S., Synchronization stability in coupled oscillator arrays: solution for arbitrary configurations, International Journal of Bifurcation and Chaos. (2000) 10, no. 2, 273–290, MR1754078, https://doi.org/10.1142/S0218127400000189, 2-s2.0-0034134720.
10.1142/S0218127400000189
Web of Science® Google Scholar
6 Kocarev L., Tasev Z., and Parlitz U., Synchronizing spatiotemporal chaos of partial differential equations, Physical Review Letters. (1997) 79, no. 1, 51–54, 2-s2.0-0002636408, https://doi.org/10.1103/PhysRevLett.79.51.
10.1103/PhysRevLett.79.51
CAS Web of Science® Google Scholar
7 Acosta A., Garca P., and Leiva H., Synchronization of non-identical extended chaotic systems, Applicable Analysis: An International Journal. (2013) 92, no. 4, 740–751, https://doi.org/10.1080/00036811.2011.635654, MR3037138.
10.1080/00036811.2011.635654
Web of Science® Google Scholar
8 Xie L. and Zhao Y., Synchronization of some kind of PDE chaotic systems by invariant manifold method, International Journal of Bifurcation and Chaos. (2005) 5, no. 7, 2303–2309, https://doi.org/10.1142/S0218127405013174, MR2166348.
10.1142/S0218127405013174
Google Scholar
9 García P., Acosta A., and Leiva H., Synchronization conditions for master-slave reaction diffusion systems, Europhysics Letters. (2009) 88, no. 6, 60006-1–60006-6, https://doi.org/10.1209/0295-5075/88/60006.
10.1209/0295-5075/88/60006
Google Scholar
10 Xu Z. and Jiangsum W., Synchronization of two discrete Ginzburg-Landau equations using local coupling, International Journal of Nonlinear Science. (2006) 1, no. 1, 19–29.
Google Scholar
11 Grigoriev R. O. and Handel A., Non-normality and the localized control of extended systems, Physical Review E: Statistical, Nonlinear, and Soft Matter Physics. (2002) 66, no. 6, 067201/1–067201/4, 067201, https://doi.org/10.1103/PhysRevE.66.067201, 2-s2.0-84988745187.
10.1103/PhysRevE.66.067201
CAS Web of Science® Google Scholar
12 Wu K. and Chen B.-S., Synchronization of partial differential systems via diffusion coupling, IEEE Transactions on Circuits and Systems I: Regular Papers. (2012) 59, no. 11, 2655–2668, MR2996243, https://doi.org/10.1109/TCSI.2012.2190670, 2-s2.0-84869494789.
10.1109/TCSI.2012.2190670
Web of Science® Google Scholar
13 Gray P. and Scott S. K., Sustained oscillations and other exotic patterns of behavior in isothermal reactions, The Journal of Physical Chemistry. (1985) 89, no. 1, 22–32, https://doi.org/10.1021/j100247a009.
10.1021/j100247a009
CAS Web of Science® Google Scholar
14 Henry D., Geometric Theory of Semilinear Parabolic Equations, 1981, 840, Springer, New York, NY, USA, Lecture Notes in Mathematics.
10.1007/BFb0089647
Google Scholar
15 Sell G. R. and You Y., Dynamics of evolutionary equations, 2002, 143, Springer, Applied Mathematical Sciences, https://doi.org/10.1007/978-1-4757-5037-9, MR1873467.
10.1007/978-1-4757-5037-9
Google Scholar

Citing Literature

All articles

Finite Time Synchronization of Extended Nonlinear Dynamical Systems Using Local Coupling

Abstract

1. Introduction

2. Setting of the Problem

3. Preliminaries and Abstract Formulation of the Problem

4. Main Theoretical Results

5. Example and Numerical Simulations

6. Concluding Remarks

Disclosure

Conflicts of Interest

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Finite Time Synchronization of Extended Nonlinear Dynamical Systems Using Local Coupling

Abstract

1. Introduction

2. Setting of the Problem

3. Preliminaries and Abstract Formulation of the Problem

4. Main Theoretical Results

5. Example and Numerical Simulations

6. Concluding Remarks

Disclosure

Conflicts of Interest

References

Citing Literature

Figures

References

Related

Information