A second-order sliding mode control for chaotic synchronization with bounded disturbance is studied. A robust finite-time controller is designed based on super twisting algorithm which is a popular second-order sliding mode control technique. The proposed controller is designed by combining an adaptive law with super twisting algorithm. New results based on adaptive super twisting control for the synchronization of identical Qi three-dimensional four-wing chaotic system are presented. The finite-time convergence of synchronization is ensured by using Lyapunov stability theory. The simulations results show the usefulness of the developed control method.

1. Introduction

Synchronization of chaotic system has been of increasing interest in recent years owing to its effective applications in secure communication, power convertors, biological systems, information processing, and chemical reactions [1, 2]. A fundamental concept for chaos synchronization is to use the outputs of the master system to control the outputs of the slave system so that the states of the slave system track the states of master system. In practice, it is difficult to know the parameters of a chaotic system precisely and external disturbance always occurs in the system. Thus, synchronization of chaotic system in the presence of parameter uncertainties and external disturbances is effectively crucial in applications. Various nonlinear control methods have been proposed to deal with the problem of synchronization of uncertain chaotic systems such as adaptive control [3], passive control [4], sliding mode control [5, 6], backstepping control [7, 8], and fuzzy control [9].

Sliding mode control (SMC) [10, 11] is an effective nonlinear control method to deal with a system with uncertainties and external disturbance. However, there are two main drawbacks of sliding mode control. First, the convergence of system states to the equilibrium point is asymptotical, so the system states cannot converge to the equilibrium point within a finite time. The second drawback is the chattering phenomenon. Second-order sliding mode control (SOSMC) [12–14] is the enhanced SMC method which is developed to maintain good properties of SMC and reduce the chattering effect. Moreover, the recent SOSMC is designed based on the finite-time stability [15, 16]. This can improve the convergence speed of SMC and keep the desired properties of SMC.

The aim of this paper is to design a robust finite-time feedback control for chaotic synchronization. As is known, the super twisting algorithm is in a class of second-order SMC and is widely used in many practical applications [17–19]. Moreover, to deal with uncertainties and disturbance, the adaptive tuning law is combined with the super twisting algorithm. This adaptive law is used to update the controller gains and this relaxes the requirement of information of the bound of uncertainties and disturbances. The resulting controller is called adaptive-gain super twisting controller (AGSTC).

The rest of this paper is organized as follows. In Section 2.1, the synchronization problem is formulated and concepts and lemmas of finite-time stability are given. Section 2.2 presents the controller design for the synchronization problem via SMC. In Section 2.3, a robust finite-time controller design is proposed. The proposed adaptive super twisting controller is developed to achieve finite-time synchronization. Section 2.4 discusses the synchronization of identical Qi four-wing chaotic system. Section 3 presents the simulation results. Conclusions are provided in Section 4.

2. Materials and Methods

2.1. System Description and Problem Statement

Consider the chaotic system described by the following:

master system:
()
slave system:
()

where x ∈ Rⁿ and y ∈ Rⁿ are the states of the master and slave systems, A is the n × n matrix of the system parameters, f : Rⁿ → Rⁿ is the nonlinear part of the system, u ∈ R^m is the controller to be designed, and d_x, d_y ∈ R^m are external disturbances for master and slave systems, respectively. We define the synchronization error as

()

From master system (1) and slave system (2), we obtain the error dynamic as

()

where η(x, y) = f(y) − f(x) and

We consider the master and slave chaotic systems described by (1) and (2), respectively. The aim is to find a controller u so that the error state e converges to zero in a finite time represented by a constant T = T(e(0)) > 0. In other words, we need lim_t→T‖e(t)‖ = 0 and ‖e(t)‖ ≡ 0, when t ≥ T. This implies that the chaos synchronization between chaotic systems (1) and (2) is realized in the finite time T. We now restate the concepts related to finite-time stability presented by Bhat and Bernstein [15, 16].

Lemma 1 (Bhat and Bernstein [15]). Consider the system

()

where f : D → Rⁿ is continuous on an open neighborhood D ⊂ Rⁿ. Assume that there is a continuous differential positive definite function V(x) : D → R and real numbers p > 0 and 0 < η < 1, such that

()

Then, the origin of system (5) is a locally finite-time stable equilibrium, and the settling time, depending on the initial state x(0) = x₀, satisfies

()

In addition, if D = Rⁿ and V(x) is also radially unbounded, then the origin is a globally finite-time stable equilibrium of systems (5).

Lemma 2 (Yu et al. [20]). For any numbers λ₁ > 0, λ₂ > 0, and 0 < ϖ < 1, an extended Lyapunov condition of finite-time stability can be given in the form of fast terminal sliding mode as

()

where the settling time can be estimated by

()

2.2. Synchronization via Sliding Mode Controller

We define the sliding variable defined as

()

where

is a 1 × n constant matrix and

is the synchronization error. In the SMC, the motion of system (4) is driven to the sliding surface defined by

()

which is required to be invariant under the flow of the error dynamic (4). The necessary condition for state trajectory e(t) to stay on the sliding manifold s is

. We ignore the disturbance vector

and apply the constant plus proportional rate reaching law:

()

where sign⁡(s) is the sign function and the constant gains q > 0 and k > 0 are determined such that the sliding condition is satisfied. The proposed SMC is designed as

()

In the following theorem, under controller (13) we can ensure that the synchronization occurs asymptotically.

Theorem 3. Master system (1) and slave system (2) are globally and asymptotically synchronized for all initial conditions x(0), y(0) ∈ Rⁿ by the feedback control law (13).

Proof. Substituting (13) into (4), we obtain

()

We consider the Lyapunov function

()

which is positive definite function on R. Differentiating (15), we obtain

()

Substituting (12) into (16), we obtain

()

Using the fact that sign⁡(s) = |s|/s, one has

()

Obviously,

is negative definite. Thus, the error state e globally and asymptotically reaches the sliding surface s = 0.

2.3. Adaptive-Gain Super Twisting Controller

The super twisting control law is the most powerful second-order continuous sliding mode control algorithms. It generates the continuous control function that drives the sliding variable and its derivative to zero in finite time. Next, we add an adaptive law to the classical super twisting algorithm to tune the controller gains and avoid knowledge of upper bound of the vector .

We use the sliding variable e defined by (10) and introduce a new reaching law as

()

where k₁ and k₂ are positive gains defined as k₁ = λ₁μL(t) and k₂ = λ₂(μ²L²(t)/2), where λ₁ and λ₂ are positive constants and L(t) is updated by

()

with a continuous function l(t) > 0.

Considering the error dynamic (4), the adaptive super twisting controller is designed as

()

Substituting (21) into (4), one obtains

()

where

Let us define

()

Then, (22) can be written as

()

Next, for system (24) under the following assumption, the proof of finite-time convergence to the origin is given.

Assumption 4. The new disturbance ξ(t) and its first-time derivative δ(t) are bounded; that is, |ξ(t)| ≤ D₁ and |δ(t)| ≤ D₂, where D₁ and D₂ are positive constants.

Theorem 5. Let Assumption 4 hold. With μ > 0 and λ₁ > 0 and λ₂ > 0 and L(t) defined in (20), all states (z₁ and z₂) of system (24) converge to the origin in finite time.

Proof. We first introduce the new vector . Its time derivative is given by

()

Next, we change variable as ς = Γ⁻¹υ and obtain

()

where

. The derivative of ς is

()

where

()

We now construct the Lyapunov function by extending the ideas of Moreno and Osorio [21].

Let the Lyapunov function be chosen as

()

where P is the solution of the Lyapunov equation:

()

If the gains λ₁ and λ₂ are chosen such that the matrix A is Hurwitz and arbitrary symmetric positive definite matrix Q is selected, then the solution P is unique and symmetric positive definite. Finding the derivative of V₂, we obtain

()

We consider the term Γ⁻¹φ, and one obtains

()

Thus,

in (31) becomes

()

Using

, we obtain

()

where R = PN. It is observed that there exists a time t₀, where the gain L(t) is sufficiently large such that

is attained. Therefore, by Lemma 2, the states ς₁ and ς₂ converge to zero in finite time. This implies the finite-time convergence to zero in states z₁ and z₂. As a consequence the gain L(t) will stop growing in finite time and it will remain bounded.

2.4. Synchronization of Identical Qi Four-Wing Chaotic System

Qi four-wing chaotic systems are described as follows:

master system:
()
slave system:
()

where x_i and y_i (i = 1,2, 3) are state variables of the master and slave systems, respectively.

Note that systems (35) and (36) are obtained by considering (1) and (2), where A, x, y, f(x), f(y), d_x, and d_y are defined as follows:

()

In (36), the control laws u₁, u₂, u₃ can be designed together in the form of vector u which is more convenient for our proposed method. The parameters a, b, c, d, ε are positive constants. The synchronization error is defined by

()

We obtained the error dynamics as

()

We rewrite the error dynamics (39) as

()

where

()

with

()

3. Results and Discussion

In this section, numerical simulations are performed to compare the performances of sliding mode control (SMC) defined in (13) and adaptive-gain super twisting control (AGSTC) defined in (21).

The parameters for the chaotic systems (35) and (36) and the control laws (13) and (21) are set as a = 14, b = 43, c = −1, d = 16, ε = 4, k = 4, q = 0.2, k₁ = 2.5L(t), k₂ = 5(L²(t)/2), and

()

The initial values of the master system (1) are taken as x₁(0) = 5, x₂(0) = 12, and x₃(0) = 20 and initial values of the slave system (2) are taken as y₁(0) = 16, y₂(0) = 24, and y₃(0) = 7.

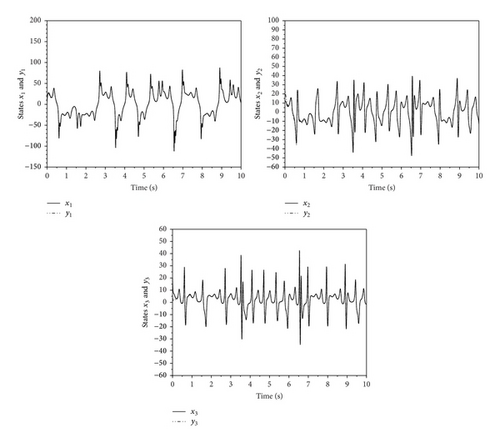
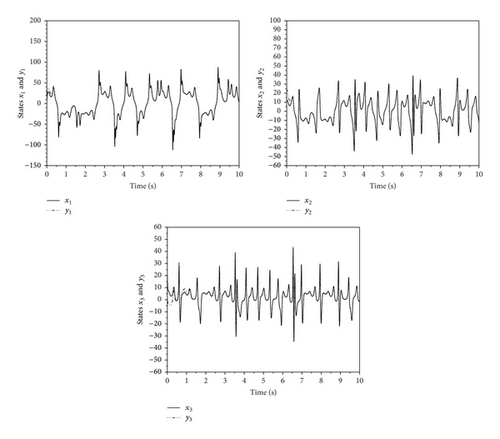
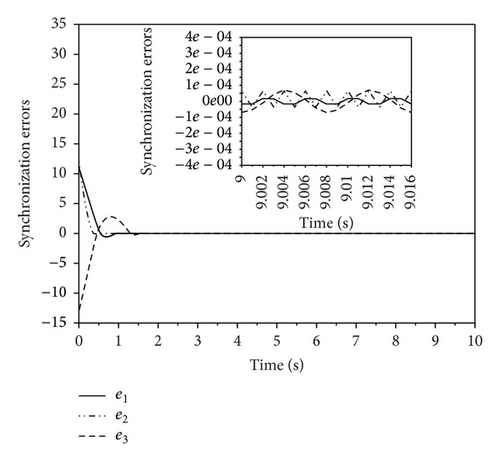
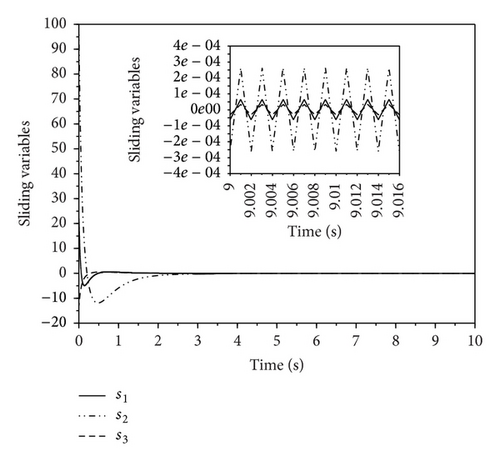
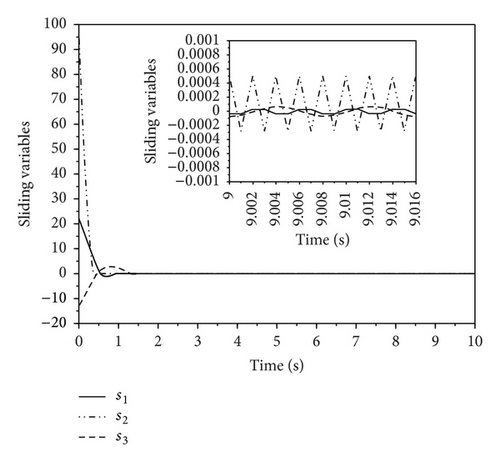
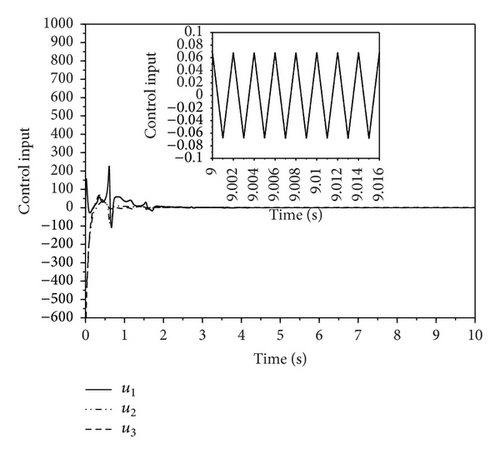
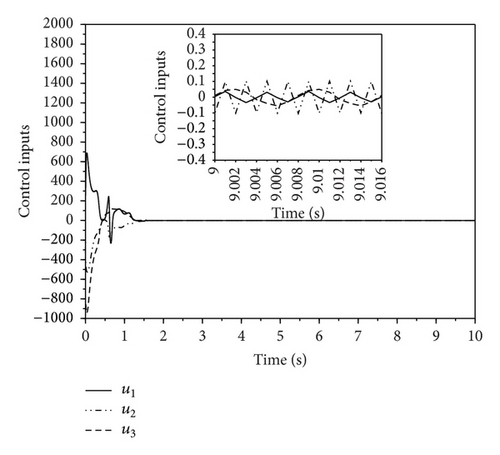
The simulation results of synchronization under SMC and AGSTC are shown in Figures 1–8. As shown in Figures 1 and 2, for AGSTC the states of slave system quickly track the states of master system when compared with SMC. Similarly, Figures 3 and 4 show the error of synchronization in which AGSTC provides faster rate of convergence. For AGSTC, the synchronization error is larger than the one obtained by SMC because the control parameters λ₁, μ, and L(t) updated by (43) are chosen large enough to ensure the disturbance rejection ability. This leads to larger synchronization errors obtained by AGSTC as shown in Figures 3 and 4. From Figures 5 and 6, we can see that, for AGSTC, the sliding variables reach zero quicker. In Figures 7 and 8, the control inputs obtained by AGSTC are smoother than SMC. From these simulation results, it is clearly shown that AGSTC gives better results of synchronization.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Synchronization of identical Qi four-wing system for SMC.

4. Conclusions

A robust finite-time controller has been successfully applied to synchronize identical Qi three-dimensional (3D) four-wing chaotic systems. The proposed control law is designed combining the super twisting algorithm with an adaptive tuning law. The finite-time convergence of synchronization error is proved using the Lyapunov stability theory. Numerical simulations are provided to validate synchronization results of the developed control method.

Competing Interests

The authors declare that they have no competing interests.

References

1 Kapitaniak T., Chaotic Oscillations in Mechanical Systems, 1991, Manchester University Press, New York, NY, USA, MR1116769.
Google Scholar
2 Lakshmanan M. and Murali K., Chaos in Nonlinear Oscillators: Controlling and Synchronization, 1996, World Scientific, Singapore.
10.1142/2637
Google Scholar
3 Bowong S., Adaptive synchronization between two different chaotic dynamical systems, Communications in Nonlinear Science and Numerical Simulation. (2007) 12, no. 6, 976–985, https://doi.org/10.1016/j.cnsns.2005.10.003, MR2309769, 2-s2.0-33846878521.
10.1016/j.cnsns.2005.10.003
Web of Science® Google Scholar
4 Wang F. and Liu C., Synchronization of unified chaotic system based on passive control, Physica D. (2007) 225, no. 1, 55–60, https://doi.org/10.1016/j.physd.2006.09.038, MR2304914, 2-s2.0-33845198445.
10.1016/j.physd.2006.09.038
Web of Science® Google Scholar
5 Wang H., Han Z., Xie Q., and Zhang W., Finite-time chaos synchronization of unified chaotic system with uncertain parameters, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 5, 2239–2247, https://doi.org/10.1016/j.cnsns.2008.04.015.
10.1016/j.cnsns.2008.04.015
Web of Science® Google Scholar
6 Wang H., Han Z.-Z., Xie Q.-Y., and Zhang W., Sliding mode control for chaotic systems based on LMI, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 4, 1410–1417, https://doi.org/10.1016/j.cnsns.2007.12.006, MR2468965, 2-s2.0-55549132257.
10.1016/j.cnsns.2007.12.006
Web of Science® Google Scholar
7 Yassen M. T., Controlling, synchronization and tracking chaotic Liu system using active backstepping design, Physics Letters, Section A: General, Atomic and Solid State Physics. (2007) 360, no. 4-5, 582–587, https://doi.org/10.1016/j.physleta.2006.08.067, 2-s2.0-33751216742.
10.1016/j.physleta.2006.08.067
CAS Google Scholar
8 Chen H.-H., Sheu G.-J., Lin Y.-L., and Chen C.-S., Chaos synchronization between two different chaotic systems via nonlinear feedback control, Nonlinear Analysis: Theory, Methods & Applications. (2009) 70, no. 12, 4393–4401, https://doi.org/10.1016/j.na.2008.10.069, MR2514770, 2-s2.0-63449125876.
10.1016/j.na.2008.10.069
Web of Science® Google Scholar
9 Yau H.-T. and Shieh C.-S., Chaos synchronization using fuzzy logic controller, Nonlinear Analysis: Real World Applications. (2008) 9, no. 4, 1800–1810, https://doi.org/10.1016/j.nonrwa.2007.05.009, MR2422581, 2-s2.0-43649107820.
10.1016/j.nonrwa.2007.05.009
Web of Science® Google Scholar
10 Utkin V. I., Sliding Modes in Control and Optimization, 1992, Springer, Berlin, Germany, Communications and Control Engineering Series, https://doi.org/10.1007/978-3-642-84379-2, MR1295845.
10.1007/978-3-642-84379-2
Google Scholar
11 C. Edwards, E. Fossas Colet, and L. Fridman, Advances in Variable Structure and Sliding Mode Control, 2006, Springer, Berlin, Germany, https://doi.org/10.1007/11612735, MR2229169.
10.1007/11612735
Google Scholar
12 Levant A., Higher-order sliding modes, differentiation and output-feedback control, International Journal of Control. (2003) 76, no. 9-10, 924–941, https://doi.org/10.1080/0020717031000099029, MR1999375, 2-s2.0-0142137682.
10.1080/0020717031000099029
Web of Science® Google Scholar
13 Perruquetti W. and Barbot J. P., Sliding Mode Control in Engineering, 2002, Marcel Dekker, New York, NY, USA.
10.1201/9780203910856
Web of Science® Google Scholar
14 Damiano A., Gatto G. L., Marongiu I., and Pisano A., Second-order sliding-mode control of dc drives, IEEE Transactions on Industrial Electronics. (2004) 51, no. 2, 364–373, https://doi.org/10.1109/TIE.2004.825268, 2-s2.0-1942423634.
10.1109/TIE.2004.825268
Web of Science® Google Scholar
15 Bhat S. P. and Bernstein D. S., Finite-time stability of continuous autonomous systems, SIAM Journal on Control and Optimization. (2000) 38, no. 3, 751–766, https://doi.org/10.1137/s0363012997321358, MR1756893, 2-s2.0-0000761428.
10.1137/S0363012997321358
Web of Science® Google Scholar
16 Bhat S. P. and Bernstein D. S., Geometric homogeneity with applications to finite-time stability, Mathematics of Control, Signals, and Systems. (2005) 17, no. 2, 101–127, https://doi.org/10.1007/s00498-005-0151-x, MR2150956, ZBL1110.34033, 2-s2.0-21344471250.
10.1007/s00498-005-0151-x
Web of Science® Google Scholar
17 Levant A., Pridor A., Gitizadeh R., Yaesh I., and Ben-Asher J. Z., Aircraft pitch control via second-order sliding technique, Journal of Guidance, Control, and Dynamics. (2000) 23, no. 4, 586–594, https://doi.org/10.2514/2.4591, 2-s2.0-0034226653.
10.2514/2.4591
Web of Science® Google Scholar
18 Shtessel Y. B., Shkolnikov I. A., and Levant A., Smooth second-order sliding modes: missile guidance application, Automatica. (2007) 43, no. 8, 1470–1476, https://doi.org/10.1016/j.automatica.2007.01.008, MR2320533, 2-s2.0-34347364560.
10.1016/j.automatica.2007.01.008
Web of Science® Google Scholar
19 Pukdeboon C., Finite-time second-order sliding mode controllers for spacecraft attitude tracking, Mathematical Problems in Engineering. (2013) 2013, 12, 930269, https://doi.org/10.1155/2013/930269, MR3080136.
10.1155/2013/930269
Web of Science® Google Scholar
20 Yu S., Yu X., Shirinzadeh B., and Man Z., Continuous finite-time control for robotic manipulators with terminal sliding mode, Automatica. (2005) 41, no. 11, 1957–1964, https://doi.org/10.1016/j.automatica.2005.07.001, MR2168660, 2-s2.0-24944498043.
10.1016/j.automatica.2005.07.001
Web of Science® Google Scholar
21 Moreno J. A. and Osorio M., Strict Lyapunov functions for the super-twisting algorithm, IEEE Transactions on Automatic Control. (2012) 57, no. 4, 1035–1040, https://doi.org/10.1109/tac.2012.2186179, MR2952337, 2-s2.0-84859727230.
10.1109/TAC.2012.2186179
Web of Science® Google Scholar

Citing Literature

All articles

Finite-Time Synchronization for Uncertain Master-Slave Chaotic System via Adaptive Super Twisting Algorithm

Abstract

1. Introduction

2. Materials and Methods

2.1. System Description and Problem Statement

2.2. Synchronization via Sliding Mode Controller

2.3. Adaptive-Gain Super Twisting Controller

2.4. Synchronization of Identical Qi Four-Wing Chaotic System

3. Results and Discussion

4. Conclusions

Competing Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Finite-Time Synchronization for Uncertain Master-Slave Chaotic System via Adaptive Super Twisting Algorithm

Abstract

1. Introduction

2. Materials and Methods

2.1. System Description and Problem Statement

2.2. Synchronization via Sliding Mode Controller

2.3. Adaptive-Gain Super Twisting Controller

2.4. Synchronization of Identical Qi Four-Wing Chaotic System

3. Results and Discussion

4. Conclusions

Competing Interests

References

Citing Literature

Figures

References

Related

Information