Periodicity, Stability, and Boundedness of Solutions to Certain Second Order Delay Differential Equations

Definition 1 (see [3].)A continuous function $$ with W(0) = 0, W(s) > 0 if s ≠ 0, and W strictly increasing is a wedge. (We denote wedges by W or W_i, where i is an integer.)

Definition 2 (see [3].)The zero solution of (8) is asymptotically stable if it is stable and if for each t₀ ≥ 0 there is an η > 0 such that ‖ϕ‖ ≤ η implies that

Definition 3 (see [2].)An element ψ ∈ C_H is in the ω-limit set of ϕ, say Ω(ϕ), if X(t, 0, ϕ) is defined on $$ and there is a sequence {t_n}, t_n → ∞ as n → +∞, with $$ as n → ∞, where $$ for −r ≤ θ < 0.

Definition 4 (see [26].)A set Q ⊂ C_H is an invariant set if for any ϕ ∈ Q, the solution X(t, 0, ϕ) of the system (8) is defined on $$, and X_t(ϕ) ∈ Q for $$.

Lemma 5 (see [7].)Suppose that $$ and F(t, ϕ) is periodic in t of period ω, ω ≥ r, and consequently for any α > 0 there exists an L(α) > 0 such that ϕ ∈ C_α implies |F(t, ϕ)| ≤ L(α). Suppose that a continuous Lyapunov functional V(t, ϕ) exists, defined on $$, ϕ ∈ S^∗, S^∗ is the set of ϕ ∈ C such that |ϕ(0)| ≥ H (H may be large), and V(t, ϕ) satisfies the following conditions:

• (i)

  a(|ϕ(0)|) ≤ V(t, ϕ) ≤ b(‖ϕ‖), where a(r) and b(r) are continuous, increasing, and positive for r ≥ H and a(r) → ∞ as r → ∞;

• (ii)

  $$, where c(r) is continuous and positive for r ≥ H.

Lemma 6 (see [7].)Suppose that F(t, ϕ) is defined and continuous on 0 ≤ t ≤ c, ϕ ∈ C_H and that there exists a continuous Lyapunov functional V(t, ϕ, φ) defined on 0 ≤ t ≤ c, ϕ, φ ∈ C_H which satisfy the following conditions:

• (i)

  V(t, ϕ, φ) = 0 if ϕ = φ;

• (ii)

  V(t, ϕ, φ) > 0 if ϕ ≠ φ;

• (iii)

  for the associated system

  $$ (11)

•  

  one has $$, where for ‖ϕ‖ = H or ‖φ‖ = H, one understands that the condition $$ is satisfied in the case V^′ can be defined.

Lemma 7 (see [7].)Suppose that a continuous Lyapunov functional V(t, ϕ) exists, defined on $$, ‖ϕ‖ < H, 0 < H₁ < H which satisfies the following conditions:

• (i)

  a(‖ϕ‖) ≤ V(t, ϕ) ≤ b(‖ϕ‖), where a(r) and b(r) are continuous, increasing, and positive;

• (ii)

  $$, where c(r) is continuous and positive for r ≥ 0.

Lemma 8 (see [2].)Let $$ be continuous and locally Lipschitz in ϕ. If

• (i)

  $$,

• (ii)

  $$, for some N > 0 where W_i  (i = 0,1, 2,3, 4) are wedges,

Theorem 9. In addition to the assumptions on the functions f, g, p, and ϕ, suppose that a, b, ϕ₀, B, α, β, L, M are positive constants and that for all t ≥ 0

• (i)

  a ≤ f(·)/y for all x and y ≠ 0;

• (ii)

  b ≤ g(x)/x ≤ B for all x ≠ 0;

• (iii)

  |g^′(x)| ≤ L for all x;

• (iv)

  1 < ϕ₀ ≤ ϕ(t) for all t ≥ 0;

• (v)

  0 ≤ τ(t) ≤ α, τ^′(t) ≤ β, 0 < β < 1, where

  $$ (14)

• (vi)

  |p(t, x, y)| ≤ M, 0 < M < ∞.

Remark 10. Below are some observations from previous results which the current results are addressing:

• (i)

  When $$, g(x(t − τ(t))) = bx and p(t, x, y) = 0, then system (7) reduces to linear constant coefficients differential equation $$, and conditions (i) to (vi) of Theorem 9 specialize to the corresponding Routh Hurwitz criteria a > 0 and b > 0.

• (ii)

  When ϕ(t)f(·) = cx^′, g(x(t − τ(t))) = g(t, x), and p(t, x, y) = h(t), system (7) specializes to ordinary differential equation discussed in [22]. Our result includes and extends the results in [22].

• (iii)

  If τ(t) = τ (a constant), ϕ(t)f(·) = p₁y^′(t) + p₂y^′(t − τ), and g(x(t − τ(t))) = q₁y(t) + q₂y(t − τ), system (7) is trimmed down to that discussed in [10, 24]. Thus our results improve the results in [10, 24].

• (iv)

  If τ(t) = 0, ϕ(t)f(·) = c(t, x, x^′), g(x(t − τ(t))) = q(t)b(x), and p(t, x, y) = f(t) then system (7) reduces to that considered in [17]. Thus the result in [17] is a special case of Theorem 9.

• (v)

  Whenever τ(t) = 0, (6) reduces to the cases discussed in [8, 9].

Lemma 11. Under the hypotheses of Theorem 9, there exist positive constants D₀ = D₀(b, 1), D₁ = D₁(a, b, B), and D₂ = D₂(λ₁, λ₂) such that

Furthermore, there exist positive constants D₃ = D₃(a, b, ϕ₀, α, β, L, 1) and D₄ = D₄(a, b, 1) such that

Proof. Let (x_t, y_t) be any solution of system (7). It is clear from (13) that V(0,0) = 0. Since the double integrals terms are nonnegative, g(x) ≥ bx for all x ≠ 0, and (ax + y) ² ≥ 0 for all x and y, then there exists a positive constant δ₀ such that

t ≥ 0, x and y, where

Next, let (x_t, y_t) be any solution of the system (7). The time derivative of the function V, defined in (13), along a solution path of the system (7) is

Proof of Theorem 9. Let (x_t, y_t) be any solution of system (7), hypothesis (vi) of Theorem 9, and the fact that |x | < 1 + x², and then there exist positive constants δ₅ and δ₆ such that inequality (31) yields

Theorem 12. Suppose that hypotheses (i) to (v) of Theorem 9 hold; then the zero solution of system (35) is uniformly asymptotically stable.

Remark 13. (i) The stability results in [2, 8–10] are special cases of Theorem 12.

(ii) When ϕ(t)f(·) = p(t)ϕ^′(t) and g(x(t − τ(t))) = q(t)ϕ(t) (34) reduces to the one discussed in [12].

(iii) Whenever ϕ(t)f(·) = cx^′ and g(x(t − τ(t))) = g(t, x) then (34) is a case studied in [22].

(iv) If ϕ(t)f(·) = 0 and g(x(t − τ(t))) = ax(t) then (34) reduces to the one discussed in [25].

Proof of Theorem 12. Let (x_t, y_t) be any solution of system (35), with hypotheses of Theorem 12; estimates (17), (21), and (22) hold. Furthermore, the derivative of the functional V defined in (13) with respect to the independent variable t along the solution path of the system (35) is

Theorem 14. If hypotheses (i) to (vi) of Theorem 9 hold, then there exists a unique periodic solution of period ω for the system (7).

Proof. Let (x_t, y_t) be any solution of system (7). In view of the hypotheses of Theorem 14 (19) and inequality (20) hold. Moreover, from hypothesis (vi) and the fact that

Example 1. Consider a second order delay differential equation

•  

  (i) The function

  $$ (43)

•  

  Since

  $$ (44)

•  

  for all t ≥ 0, it follows that

  $$ (45)

•  

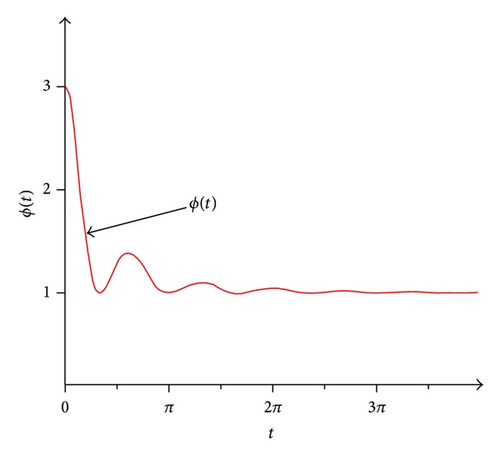
  for all t ≥ 0. The behaviour of ϕ(t) is shown in Figure 1.

•  

  (ii) The function

  $$ (46)

•  

  It is not difficult to show that

  $$ (47)

•  

  for all t ≥ 0, x and y ≠ 0. See the behaviour of f(·) in Figure 2.

•  

  (iii) The function

  $$ (48)

•  

  Since

  $$ (49)

•  

  for all x, then we assert that

  $$ (50)

•  

  (iv) The function

  $$ (51)

•  

  Clearly, g^′(x) is a bounded function; thus it is not difficult to show that

  $$ (52)

•  

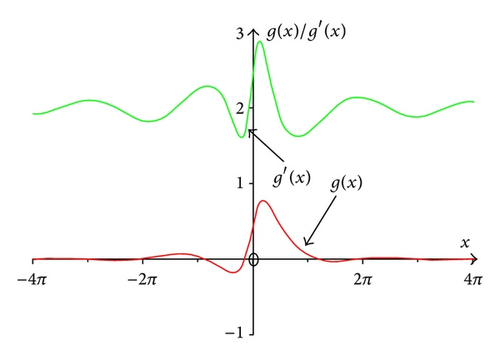
  The boundedness of g and g^′ is shown in Figure 3.

•  

  (v) The function

  $$ (53)

•  

  Since

  $$ (54)

•  

  for all t ≥ 0, x and y, it follows that

  $$ (55)

•  

  for all t ≥ 0, x and y; and if

•  

  (vi) β = 1/2, and with the values of a, b, B, L, M as above, then inequality (14) becomes

  $$ (56)

Example 2. Consider the second order delay differential equation

Equation (57) is equivalent to system of first order differential equation

•  (i)

  The function

  $$ (61)

•  

  Noting that

  $$ (62)

•  

  for all t ≥ 0, x and y, we assert that

  $$ (63)

•  

  for all t ≥ 0, x and y ≠ 0. The function f(·) is shown in Figure 4.

•  (ii)

  The function

  $$ (64)

•  

  Let

  $$ (65)

•  

  Since

  $$ (66)

•  

  for all x, it follows that

  $$ (67)

•  

  for all x ≠ 0.

•  (iii)

  Furthermore, from (ii) above we have

  $$ (68)

•  

  It is not difficult to show that

  $$ (69)

•  

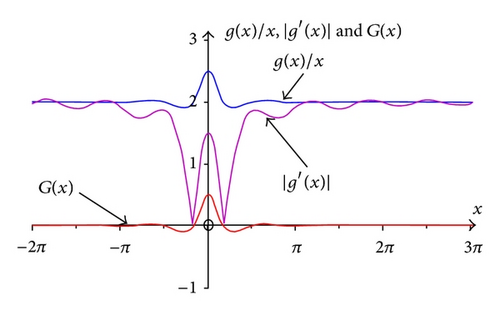
  for all x. The functions g(x)/x, G(x), and |g^′(x)| are shown in Figure 5.

•  (iv)

  The function

  $$ (70)

•  

  Since

  $$ (71)

•  

  for t ∈ [0,2π], it follows that

  $$ (72)

•  

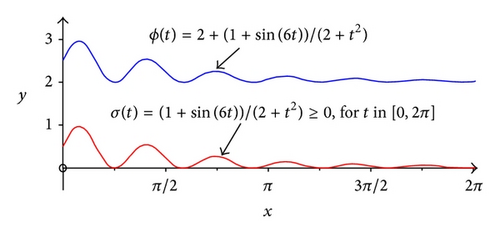
  for all t ≥ 0. The graph of function ϕ(t) is shown in Figure 6.

•  (v)

  Moreover, choose β₀ = 1/2 and from (i) to (iv) of Example 2 we have

  $$ (73)

•  

  so that

  $$ (74)

•  (vi)

  The function

  $$ (75)

•  

  Since

  $$ (76)

•  

  for all x and y, it follows that

  $$ (77)

•  

  for all t ≥ 0, x and y.

•  (i)

  solutions of system (59) are uniformly bounded and uniformly ultimately bounded;

•  (ii)

  there exists a unique periodic solution of period ω,

•  (iii)

  the trivial solution of the system (59) (when p(t, x, y) = 0) is uniformly asymptotically stable.